
Переосмысливаем классические стратегии (Часть VI): Анализ нескольких таймфреймов
Введение
Существует потенциально бесконечное множество способов, с помощью которых современный инвестор может интегрировать искусственный интеллект (ИИ) для улучшения своих трейдинговых решений. К сожалению, маловероятно, что вы сможете оценить все эти стратегии, прежде чем решите, какой стратегии доверить свой кровно заработанный капитал. В данной серии статей мы рассмотрим торговые стратегии, чтобы оценить, можем ли мы улучшить их с помощью ИИ. Мы стремимся предоставить вам информацию, необходимую для принятия обоснованного решения о том, подходит ли данная стратегия для вашего индивидуального инвестиционного профиля.
Обзор торговой стратегии
В данной статье мы вновь рассмотрим хорошо известную стратегию анализа нескольких таймфреймов. Большая группа успешных трейдеров по всему миру придерживается мнения, что прежде чем принимать инвестиционные решения, имеет смысл проводить анализ более одного таймфрейма. Существует множество различных вариантов данной стратегии. Однако все они, как правило, придерживаются общего мнения, что какой бы тренд ни был выявлен на более высоком таймфрейме, он сохранится и на всех более низких таймфремах.
Так, например, если мы наблюдаем бычье поведение цены на ежедневном графике, то вполне разумно ожидать появления бычьих ценовых паттернов на часовом графике. Данная стратегия также расширяет идею еще больше: согласно стратегии, нам следует придать больший вес колебаниям цен, которые соответствуют тренду, наблюдаемому на более высоком таймфрейме.
Другими словами, возвращаясь к нашему простому примеру, если бы мы наблюдали восходящий тренд на дневном графике, то были бы более склонны к возможностям совершения покупки на часовом графике и неохотно занимали бы позиции, противоположные тренду, наблюдаемому на дневном графике.
Вообще говоря, стратегия разваливается, когда тренд, наблюдаемый на более высоком таймфрейме, меняется на противоположный. Обычно это происходит потому, что разворот начинается только на более низком таймфрейме. Напомним, что при использовании данной стратегии лишь незначительный вес придается колебаниям, наблюдаемым на более низких таймфреймах, которые противоречат более высоким таймфреймам. Поэтому трейдеры, придерживающиеся данной стратегии, обычно ожидают, пока разворот не станет заметен на более высоком таймфрейме. Таким образом, они могут испытывать сильную волатильность в цене, ожидая подтверждения от более высоких таймфреймов.
Обзор методологии
Чтобы эмпирически оценить преимущества этой стратегии, нам пришлось тщательно извлечь значимые данные из нашего терминала MetaTrader 5. Нашей целью в данной статье было предсказать будущую цену закрытия пары EURUSD на 20 минут вперед. Для достижения этой цели мы создали 3 группы предикторов:
- Обычно это информация о цене открытия, максимума, минимума и закрытия.
- Изменения уровней цен на более высоких таймфреймах
- Надмножество из двух вышеперечисленных наборов.
Мы наблюдали относительно слабые уровни корреляции между обычными ценовыми данными и изменениями цен на более высоких таймфреймах. Самые сильные уровни корреляции, которые мы наблюдали, были между изменениями цен на M15 и уровнями цен на M1, приблизительно -0,1.
Нами создан большой набор различных моделей и испытан на всех трех наборах предикторов с целью наблюдения за изменениями в точности. Наши наилучшие уровни ошибок наблюдались при использовании первого набора предикторов - обычных рыночных данных. Из наших наблюдений следует, что наиболее эффективной является модель линейной регрессии, за которой следует модель Регрессора градиентного бустинга (РГБ).
Поскольку линейная модель не имеет каких-либо параметров настройки, представляющих для нас большой интерес, мы выбрали модель РГБ в качестве возможного решения, а уровни ошибок линейной модели стали нашим эталоном эффективности. Теперь нашей целью стало оптимизировать модель РГБ, чтобы превзойти эталон эффективности, установленный линейной моделью.
Прежде чем приступить к процессу оптимизации, мы выполнили отбор признаков с использованием алгоритма обратного отбора. Все признаки, связанные с изменениями цен на более высоких таймфреймах, были отброшены алгоритмом, что может указывать на то, что связь может быть ненадежной, либо мы также можем интерпретировать это как то, что мы не представили ассоциацию нашей модели в значимой форме.
Мы использовали алгоритм рандомизированного поиска с 1000 итерациями для поиска оптимальных настроек для нашей модели РГБ. После этого мы использовали результаты нашего рандомизированного поиска в качестве отправной точки для локальной оптимизации параметров непрерывного РГБ с использованием Алгоритма ограниченной памяти Бройдена-Флетчера-Гольдфарба-Шанно (L-BFGS-B)
Нам не удалось превзойти стандартную модель РГБ по проверке данных, что, возможно, указывает на то, что мы избыточно подстраивались под обучающие данные. Кроме того, нам также не удалось превзойти эталонные показатели линейной модели при валидации.
Извлечение данных
Мной созданы полезные MQL5-скрипты для извлечения данных из нашего терминала MetaTrader 5. Скрипт также извлекает изменения цены из выборки более высоких таймфреймов и создает путь файла: “MetaTrader 5\MQL5\Files\...”
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 5; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + " multiple timeframe 20 step look ahead .csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= -1;i<=size;i++) { if(i == -1) { FileWrite(file_handle,"Time","Open","High","Low","Close","M5","M15","M30","H1","D1"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i), (iClose(Symbol(),PERIOD_M5,i) - iClose(Symbol(),PERIOD_M5,i+20)), (iClose(Symbol(),PERIOD_M15,i) - iClose(Symbol(),PERIOD_M15,i+20)), (iClose(Symbol(),PERIOD_M30,i) - iClose(Symbol(),PERIOD_M30,i+20)), (iClose(Symbol(),PERIOD_H1,i) - iClose(Symbol(),PERIOD_H1,i+20)), (iClose(Symbol(),PERIOD_D1,i) - iClose(Symbol(),PERIOD_D1,i+20)) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Считывание данных
Начнем с загрузки нужных нам библиотек.
import pandas as pd imort numpy as np
Обратите внимание, что данные передаются из ближайшего настоящего в далекое прошлое. Нам нужно перевернуть данные таким образом, чтобы они передавались из прошлого в ближайшее настоящее.
#Let's format the data so it starts with the oldest date market_data = market_data[::-1] market_data.reset_index(inplace=True)
Теперь определим наш горизонт прогноза.
look_ahead = 20 Маркировка данных. Нашей целью будет будущая цена закрытия пары EURUSD.
#Let's label the data market_data["Target"] = market_data["Close"].shift(-look_ahead)
Теперь отбросим все строки с пропущенными значениями.
#Drop rows with missing values
market_data.dropna(inplace=True)
Разведочный анализ данных
Анализ уровней корреляции.
#Let's see if there is any correlation market_data.iloc[:,2:-1].corr()
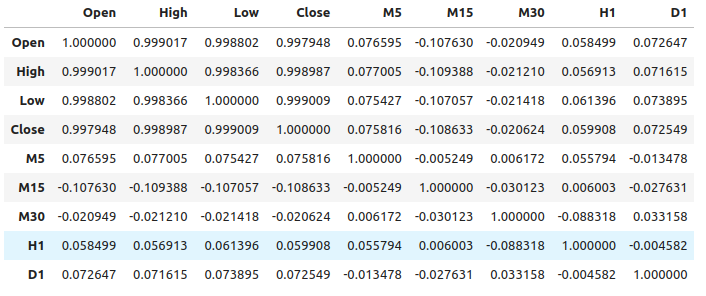
Рис 1: Уровни корреляции по разным таймфреймам
Как видно, в нашем наборе данных наблюдаются умеренно слабые уровни корреляции. Обратите внимание, что корреляция не обязательно доказывает наличие взаимосвязи между наблюдаемыми переменными.
Взаимная информация - это показатель потенциала, которым обладает предиктор для объяснения нашей цели. Начнем с рассмотрения переменной, которая, как мы знаем, определенно обладает большим потенциалом для прогнозирования цели - цены открытия.
from sklearn.feature_selection import mutual_info_regression
Теперь, в качестве точки отсчета, это хороший показатель взаимной информации (ВИ, MI).
#MI Score for the Open price
print(f'Open price has MI score: {mutual_info_regression(market_data.loc[:,["Open"]],market_data.loc[:,"Target"])[0]}') Теперь посмотрим на показатель MI на предмет изменения цены на таймфрейме M5 относительно будущей цены на таймфрейме M1.
#MI Score for the M5 change in price
print(f'M5 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M5"]],market_data.loc[:,"Target"])[0]}') Наш показатель MI значительно меньше, это означает, что мы, возможно, не раскрыли взаимосвязь значимым образом, или, возможно, нет зависимости между уровнями цен на разных таймфреймах!
#MI Score for the M15 change in price
print(f'M15 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M15"]],market_data.loc[:,"Target"])[0]}') Это верно и в отношении выбранных нами оставшихся таймфреймов.
Моделирование взаимосвязи
Определим наши предикторы и цель.
#Let's define our predictors and our target ohlc_predictors = [ "Open", "High", "Low", "Close" ] time_frame_predictors = [ "M5", "M15", "M30", "H1", "D1" ] all_predictors = ohlc_predictors + time_frame_predictors target = "Target"
Теперь импортируем необходимые нам библиотеки.
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import SGDRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit,RandomizedSearchCV from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
Define the parameters for our time-series split object.
#Define the time series split object gap = look_ahead splits = 10
Теперь подготовим наши модели, а также создадим фреймы данных для хранения наших уровней точности. Таким образом, мы можем наблюдать изменение точности по мере изменения вводных данных нашей модели.
#Store our models in a list models = [ LinearRegression(), SGDRegressor(), RandomForestRegressor(), BaggingRegressor(), GradientBoostingRegressor(), AdaBoostRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), MLPRegressor(hidden_layer_sizes=(100,20),early_stopping=True) ] #Create a list of column titles for each model columns = [ "Linear Regression", "SGD Regressor", "Random Forest Regressor", "Bagging Regressor", "Gradient Boosting Regressor", "AdaBoost Regressor", "K Neighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neurla Network" ] #Create data frames to store our accuracy ohlc_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) multiple_time_frame_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) all_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns)
Now let us prepare the predictors and scale our data.
#Preparing to perform cross validation
current_predictors = all_predictors
scaled_data = pd.DataFrame(RobustScaler().fit_transform(market_data.loc[:,all_predictors]),columns=all_predictors)
Создаём объект разделения временного ряда.
#Create the time series split object
tscv = TimeSeriesSplit(gap=gap,n_splits=splits)
Теперь проведем перекрестную проверку. Первый цикл выполняет перебор списка моделей, которые мы создали ранее, второй цикл выполняет перекрестную проверку каждой модели по очереди.
#First we will iterate over all the available models for i in np.arange(0,len(models)): #First select the model model = models[i] #Now we will cross validate this current model for j , (train,test) in enumerate(tscv.split(scaled_data)): #First define the train and test data train_X = scaled_data.loc[train[0]:train[-1],current_predictors] train_y = market_data.loc[train[0]:train[-1],target] test_X = scaled_data.loc[test[0]:test[-1],current_predictors] test_y = market_data.loc[test[0]:test[-1],target] #Now we will fit the model model.fit(train_X,train_y) #And finally record the accuracy all_accuracy.iloc[j,i] = root_mean_squared_error(test_y,model.predict(test_X))
Наши уровни точности при использовании обычных вводных данных для нашей модели.
ohlc_accuracy
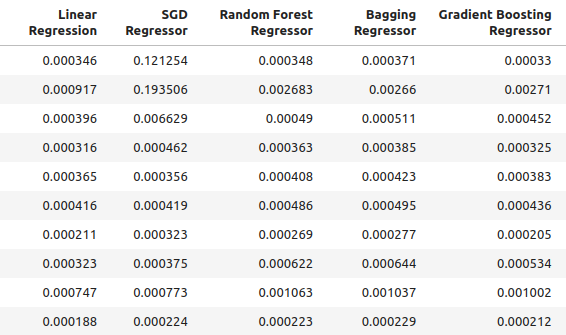
Рис 2: Наши обычные уровни точности.
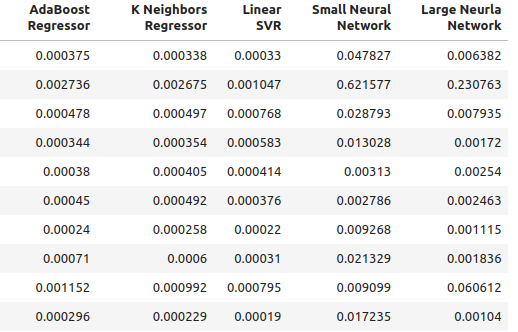
Рис 3: Наши обычные уровни точности II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {ohlc_accuracy.iloc[:,i].mean()}")
Linear Regression имел уровни ошибок 0.00042256332959154886
SGD Regressor имел уровни ошибок 0.0324320107406244
Random Forest Regressor имел уровни ошибок 0.0006954883552094012
Bagging Regressor имел уровни ошибок 0.0007030697054783931
Gradient Boosting Regressor имел уровни ошибок 0.0006588749449742309
AdaBoost Regressor имел уровни ошибок 0.0007159624774453208
K Neighbors Regressor имел уровни ошибок 0.0006839218661791973
Linear SVR имел уровни ошибок 0.000503277800807813
Small Neural Network имел уровни ошибок 0.07740701832606754
Large Neural Network имел уровни ошибок 0.03164056895135391
Наша точность при использовании новых исходных данных, которые мы создали.
multiple_time_frame_accuracy
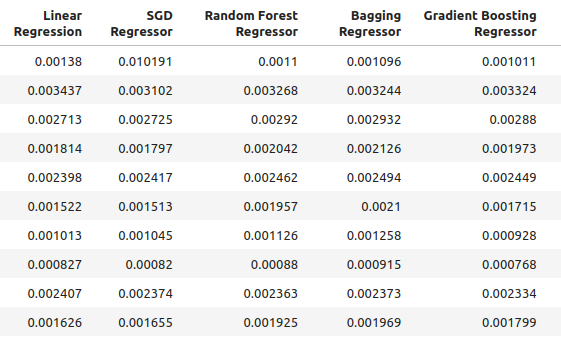
Рис 4: Наши новые уровни точности
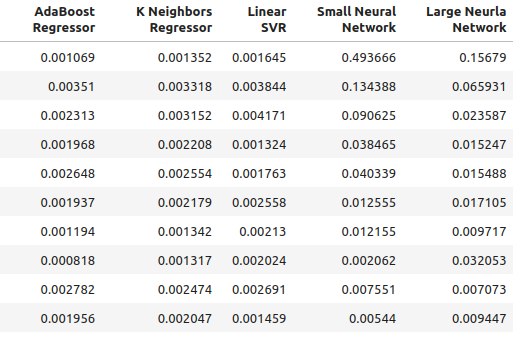
Рис 5: Наши новые уровни точности II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {multiple_time_frame_accuracy.iloc[:,i].mean()}")
Linear Regression имел уровни ошибок 0.001913639795583766
SGD Regressor имел уровни ошибок 0.0027638553835377206
Random Forest Regressor имел уровни ошибок 0.0020041047670504254
Bagging Regressor имел уровни ошибок 0.0020506512726394415
Gradient Boosting Regressor имел уровни ошибок 0.0019180687958290775
AdaBoost Regressor имел уровни ошибок 0.0020194136735787625
K Neighbors Regressor имел уровни ошибок 0.0021943350208868213
Linear SVR имел уровни ошибок 0.0023609474919917338
Small Neural Network имел уровни ошибок 0.08372469596701271
Large Neural Network имел уровни ошибок 0.035243897461061074
Наконец, давайте рассмотрим нашу точность при использовании всех доступных предикторов.
all_accuracy
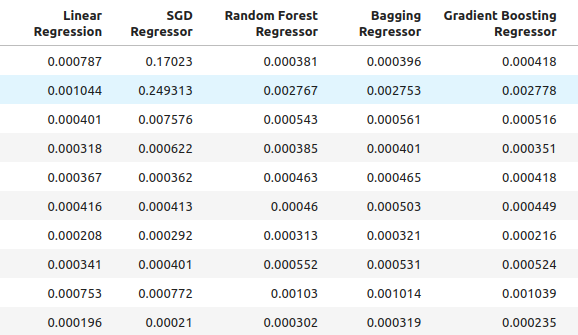
Рис 6: Наши уровни точности при использовании всех имеющихся предикторов.
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {all_accuracy.iloc[:,i].mean()}")
Linear Regression имел уровни ошибок 0.00048307488099524497
SGD Regressor имел уровни ошибок 0.043019079499194125
Random Forest Regressor имел уровни ошибок 0.0007196920919204373
Bagging Regressor имел уровни ошибок 0.0007263444909545053
Gradient Boosting Regressor имел уровни ошибок 0.0006943964783049555
AdaBoost Regressor имел уровни ошибок 0.0007217149661087063
K Neighbors Regressor имел уровни ошибок 0.000872811528292862
Linear SVR имел уровни ошибок 0.0006457525216512596
Small Neural Network имел уровни ошибок 0.14002618062102
Large Neural Network имел уровни ошибок 0.06774795252887988
Как видно, линейная модель оказалась наиболее эффективной во всех тестах. Кроме того, он лучше всего работал при использовании обычных данных OHLC. Однако у модели нет интересующих нас параметров настройки. Поэтому выберем вторую по эффективности модель, Регрессор градиентного бустинга (РГБ, GBR), и попытаемся превзойти линейную модель.
Выбор признаков
Теперь посмотрим, какие признаки были наиболее важны для нашей модели РГБ.
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS
Выбираем модель.
#We'll select the Gradient Boosting Regressor as our chosen model model = GradientBoostingRegressor()
Используем алгоритм обратного выбора. Начнем с модели, содержащей все предикторы и будем непрерывно удалять признаки друг за другом. Признак будет удален только в том случае, если это приведет к повышению производительности модели.
#Let us prepare the Feature Selector Object sfs = SFS(model, k_features=(1,len(all_predictors)), forward=False, n_jobs=-1, scoring="neg_root_mean_squared_error", cv=10 )
Выполняем выбор признаков.
#Select the best feature sfs_results = sfs.fit(scaled_data.loc[:,all_predictors],market_data.loc[:,"Target"])
The algorithm only retained the high price and discarded all other features.
#The best feature we found
sfs_results.k_feature_names_
Визуализируем наши результаты.
#Prepare the plot fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev") plt.title("Backward Selection on Gradient Boosting Regressor") plt.grid()
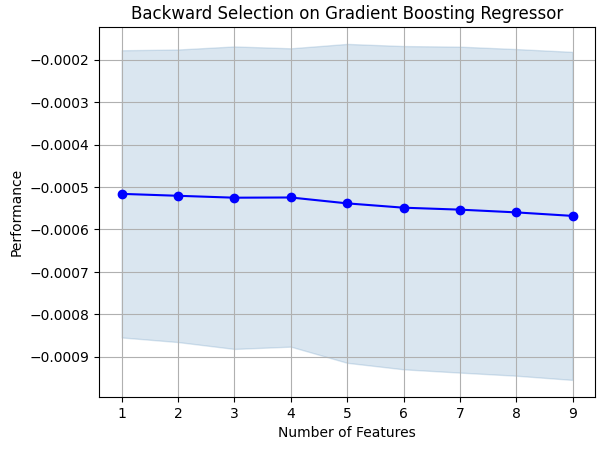
Рис 7: Визуализация процесса выбора признака
Как видно, размер нашей модели и уровни ошибок были прямо пропорциональны. Или, другими словами, по мере того, как наша модель становилась больше, увеличивался и уровень ошибок.
Настройка параметров
Теперь выполним настройку параметров нашей модели РГБ. Мы определили 11 параметров модели, которые стоит настроить, и мы выполним 1000 циклов объекта настройки, прежде чем завершим процесс оптимизации.
#Let us try to tune our model
from sklearn.model_selection import RandomizedSearchCV
Прежде чем начать настраивать нашу модель, разделим наши данные на две части. Одна половина будет направлена на обучение и оптимизацию нашей модели, вторая будет использоваться для валидации и тестирования на предмет переобучения.
#Before we try to tune our model, let's first create a train and test set train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = market_data.loc[:(market_data.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = market_data.loc[(market_data.shape[0]//2):,"Target"]
Определяем объект настройки.
#Time the process import time start_time = time.time() #Prepare the tuning object tuner = RandomizedSearchCV(GradientBoostingRegressor(), { "loss": ["squared_error","absolute_error","huber"], "learning_rate": [0,(10.0 ** -1),(10.0 ** -2),(10.0 ** -3),(10.0 ** -4),(10.0 ** -5),(10.0 ** -6),(10.0 ** -7)], "n_estimators": [5,10,25,50,100,200,500,1000], "max_depth": [1,2,3,5,9,10], "min_samples_split":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0], "criterion":["friedman_mse","squared_error"], "min_samples_leaf":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9], "min_weight_fraction_leaf":[0.0,0.1,0.2,0.3,0.4,0.5], "max_features":[1,2,3,4,5,20], "max_leaf_nodes": [2,3,4,5,10,20,50,90,None], "min_impurity_decrease": [0,1,10,(10.0 ** 2),(10.0 ** 3),(10.0 ** 4)] }, cv=5, n_iter=1000, return_train_score=False, scoring="neg_mean_squared_error" )
Настройка РГБ модели.
#Tune the GradientBoostingRegressor tuner.fit(train_X,train_y) end_time = time.time() print(f"Process completed in {end_time - start_time} seconds.")
Посмотрим на результаты в порядке от лучших к худшим.
#Let's observe the results tuner_results = pd.DataFrame(tuner.cv_results_) params = ["param_loss", "param_learning_rate", "param_n_estimators", "param_max_depth", "param_min_samples_split", "param_criterion", "param_min_samples_leaf", "param_max_features", "param_max_leaf_nodes", "param_min_impurity_decrease", "param_min_weight_fraction_leaf", "mean_test_score"] tuner_results.loc[:,params].sort_values(by="mean_test_score",ascending=False)
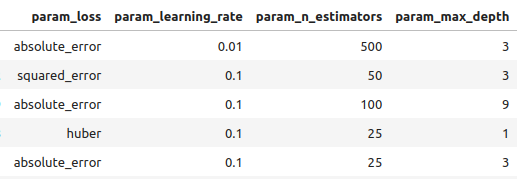
Рис 8: Некоторые из наших лучших результатов.
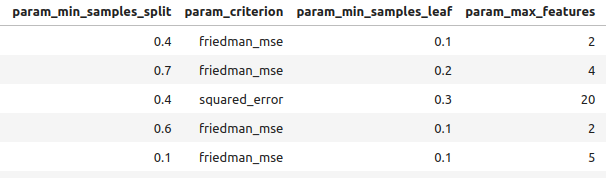
Рис 9: Некоторые из наших лучших результатов II
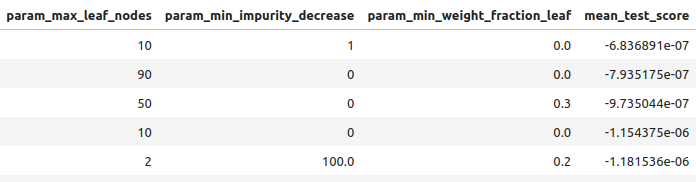
Рис 10: Некоторые из наших лучших результатов III
Лучшие параметры, обнаруженные нами.
#Best parameters we found
tuner.best_params {'n_estimators': 500,
'min_weight_fraction_leaf': 0.0,
'min_samples_split': 0.4,
'min_samples_leaf': 0.1,
'min_impurity_decrease': 1,
'max_leaf_nodes': 10,
'max_features': 2,
'max_depth': 3,
'loss': 'absolute_error',
'learning_rate': 0.01,
'criterion': 'friedman_mse'}
Более глубокая настройка параметров

Рис 11: Логотип SciPy
SciPy — это библиотека Python, используемая для научных вычислений. SciPy означает «scientific python (научный python)». Посмотрим, получится ли найти еще лучшие параметры. Чтобы попытаться найти параметры, которые улучшат производительность нашей модели, нами будет использоваться библиотека SciPy optimize.
#Let's see if we can't find better parameters #We may be overfitting the training data! from scipy.optimize import minimize
Для использования библиотеки SciPy optimize, нам нужно определить целевую функцию. Нашей целевой функцией будет среднее значение перекрестно проверенных уровней ошибок, которые достигает наша модель на обучающем наборе. Наш оптимизатор SciPy выполнит поиск коэффициентов, которые уменьшат нашу ошибку обучения.
#Define the objective function def objective(x): #Create a dataframe to store our new accuracy current_error = pd.DataFrame(index=[0],columns=["error"]) #x is an array of possible values to use for our Gradient Boosting Regressor model = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=x[0], min_samples_split=x[1], min_samples_leaf=x[2], learning_rate=x[3]) model.fit(train_X.loc[:,:],train_y.loc[:]) current_error.iloc[0,0] = root_mean_squared_error(train_y.loc[:],model.predict(train_X.loc[:,:])) #Record our progress mean_error = current_error.loc[:].mean() #Return the average error return mean_error
Теперь приступим к процессу оптимизации. Обратите внимание, что некоторые параметры в модели РГБ не допускают отрицательных значений, а наш оптимизатор SciPy будет передавать отрицательные значения, если мы не укажем границы для оптимизатора. Более того, оптимизатор ожидает, что мы предоставим начальную точку. Мы будем использовать конечную точку предыдущего алгоритма оптимизации в качестве начальной точки для данного алгоритма.
#Let's optimize these parameters again #Fist define the bounds bounds = ((0.0,0.5),(0.3,0.5),(0.001,0.2),(0.001,0.1)) #Then define the starting points for the L-BFGS-B algorithm pt = np.array([tuner.best_params_["min_weight_fraction_leaf"], tuner.best_params_["min_samples_split"], tuner.best_params_["min_samples_leaf"], tuner.best_params_["learning_rate"] ])
Сведение к минимуму ошибки обучения.
lbfgs = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
Посмотрим на результаты.
lbfgs
success: True
status: 0
fun: 0.0005766670348377334
x: [ 5.586e-06 4.000e-01 1.000e-01 1.000e-02]
nit: 3
jac: [-6.216e+00 -4.871e+02 -2.479e+02 8.882e+01]
nfev: 180
njev: 36
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
Тестирование на переобучение
Теперь сравним точность наших двух оптимизированных моделей по сравнению с моделью РГБ по умолчанию. Кроме того, мы также обратим внимание на то, превзошли ли мы в смысле эффективности линейную модель.
#Let us now see how well we're performing on the validation set linear_regression = LinearRegression() default_gbr = GradientBoostingRegressor() grid_search_gbr = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=0, min_samples_split=0.4, min_samples_leaf=0.1, learning_rate=0.01 ) lbfgs_grid_search_gbr = GradientBoostingRegressor( n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=lbfgs.x[0], min_samples_split=lbfgs.x[1], min_samples_leaf=lbfgs.x[2], learning_rate=lbfgs.x[3] )Наша точность при использовании линейной модели.
#Linear Regression
linear_regression.fit(train_X,train_y)
root_mean_squared_error(test_y,linear_regression.predict(test_X)) Наша точность при использовании модели РГБ.
#Default Gradient Boosting Regressor
default_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,default_gbr.predict(test_X)) Наша точность с использованием модели РГБ, оптимизированной методом случайного поиска.
#Random Search Gradient Boosting Regressor
grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,grid_search_gbr.predict(test_X)) Наша точность при использовании модели РГБ, оптимизированной методом случайного поиска и L-BFGS-B.
#L-BFGS-B Random Search Gradient Boosting Regressor
lbfgs_grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,lbfgs_grid_search_gbr.predict(test_X))
Как видно, нам не удалось превзойти линейную модель. Также, нам не удалось превзойти стандартную модель РГБ. Соответственно, в целях демонстрации мы продолжим работу со стандартной моделью РГБ. Однако обратите внимание, что выбор линейной модели обеспечил бы нам больше точности.
Экспортирование в ONNX
Open Neural Network Exchange (ONNX) — это протокол, позволяющий представлять модели машинного обучения в виде вычислительного графа, состоящего из узлов и рёбер. Где узлы представляют собой математические операции, а ребра - поток данных. Экспортировав нашу модель машинного обучения в формат ONNX, мы сможем с легкостью использовать наши модели искусственного интеллекта в нашем Expert Advisor.
Подготовимся к экспорту нашей модели ONNX.
#We failed to beat the linear regression model, in such cases we should pick the linear model! #However for demonstrational purposes we'll pick the gradient boosting regressor #Let's export the default GBR to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnx
Теперь нам нужно масштабировать наши данные таким образом, чтобы можно было воспроизвести их в MetaTrader 5. Самое простое преобразование - это простое вычитание среднего значения и деление на стандартное отклонение.
#We need to save the scale factors for our inputs scale_factors = pd.DataFrame(index=["mean","standard deviation"],columns=all_predictors) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = market_data.iloc[:,i+2].mean() scale_factors.iloc[1,i] = market_data.iloc[:,i+2].std() market_data.iloc[:,i+2] = ((market_data.iloc[:,i+2] - market_data.iloc[:,i+2].mean()) / market_data.iloc[:,i+2].std()) scale_factors

Рис 12: Наши коэффициенты масштабирования
Определим типы вводных данных для нашей модели ONNX.
#Define our initial types initial_types = [("float_input",FloatTensorType([1,test_X.shape[1]]))]
Подгонка модели по всем имеющимся у нас данным.
#Fit the model on all the data we have model = GradientBoostingRegressor().fit(market_data.loc[:,all_predictors],market_data.loc[:,"Target"])
Создадим представление ONNX.
#Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
Сохраним модель ONNX.
#Now save the ONNX model onnx_model_name = "GBR_M1_MultipleTF_Float.onnx" onnx.save(onnx_model,onnx_model_name)
Визуализация модели
Netron — это инструмент с открытым исходным кодом для визуализации и анализа моделей машинного обучения. В настоящее время netron предлагает поддержку ограниченного числа платформ. Однако со временем и по мере развития библиотеки, поддержка будет распространяться на различные платформы машинного обучения.
Импортируем необходимые нам библиотеки.
#Import netron so we can visualize the model
import netron
Запускаем netron.
netron.start(onnx_model_name)
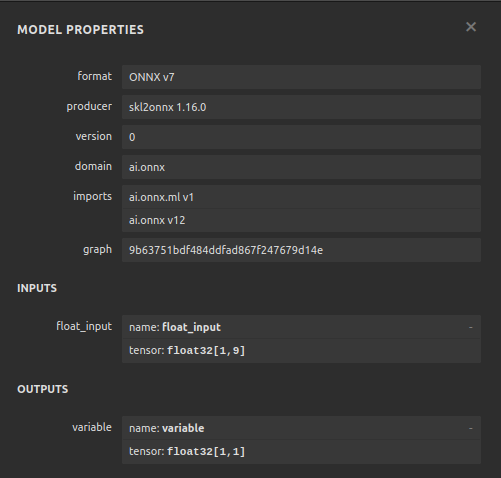
Рис. 13: Свойства нашей ONNX модели Регрессора градиентного бустинга
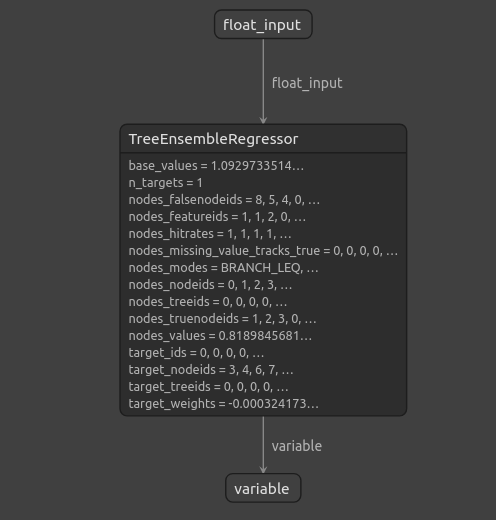 \
\
Рис 14: Структура нашего Регрессора градиентного бустинга
Поскольку мы видим, что входные и выходные данные нашей модели ONNX соответствуют нашим ожиданиям, это дает нам уверенность в том, что можно продолжить развитие советника на основе нашей модели ONNX.
Реализация средствами MQL5
Чтобы приступить к созданию нашего советника с интегрированным модулем искусственного интеллекта, нам сначала нужна модель ONNX.//+------------------------------------------------------------------+ //| Multiple Time Frame.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the onnx file | //+------------------------------------------------------------------+ #resource "\\Files\\GBR_M1_MultipleTF_Float.onnx" as const uchar onnx_model_buffer[];
Теперь загрузим торговую библиотеку.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Определим входные данные, которые может изменить наш конечный пользователь.
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input double max_risk = 20; //How much profit/loss should we allow before closing input double sl_width = 1; //How wide should out sl be?
Теперь определим глобальные переменные, которые будут использоваться во всей нашей программе.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_variance[9],std_variance[9]; //Our scaling factors vector model_forecast = vector::Zeros(1); //Model forecast vector model_inputs = vector::Zeros(9); //Model inputs double ask,bid; //Market prices double trading_volume; //Our trading volume int lot_multiple = 20; //Our lot size int state = 0; //System state
Определим вспомогательные функции, которые мы будем использовать во всей нашей программе. Во-первых, нам нужна функция для обнаружения разворотов и оповещения конечного пользователя о предстоящей опасности, которую предсказала наша система искусственного интеллекта. Если наша система искусственного интеллекта обнаружит разворот, мы закроем открытые позиции, которые у нас есть на этом рынке.
//+------------------------------------------------------------------+ //| Check reversal | //+------------------------------------------------------------------+ void check_reversal(void) { //--- Check for reversal if(((state == 1) && (model_forecast[0] < iClose(Symbol(),PERIOD_M1,0))) || ((state == 2) && (model_forecast[0] > iClose(Symbol(),PERIOD_M1,0)))) { Alert("Reversal predicted."); Trade.PositionClose(Symbol()); } //--- Check if we have breached our maximum risk levels if(MathAbs(PositionGetDouble(POSITION_PROFIT) > max_risk)) { Alert("We've breached our maximum risk level."); Trade.PositionClose(Symbol()); } }
Теперь определим функцию для поиска возможностей выхода на рынок. Мы будем считать выход действительным только в случае наличия подтверждения от более высоких таймфреймов относительно движения. В данном советнике мы хотим, чтобы наши сделки соответствовали движению цены на недельном графике.
//+------------------------------------------------------------------+ //| Find an entry | //+------------------------------------------------------------------+ void find_entry(void) { //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bullish momentum if(model_forecast[0] > iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a buy Trade.Buy(trading_volume,Symbol(),ask,(ask - sl_width),(ask + sl_width),"Multiple Time Frames AI"); state = 1; } } //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bearish momentum if(model_forecast[0] < iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a sell Trade.Sell(trading_volume,Symbol(),bid,(bid + sl_width),(bid - sl_width),"Multiple Time Frames AI"); state = 2; } } }
Нам также нужна функция для получения текущих рыночных цен.
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); }
Наша модель ONNX не может быть использована до тех пор, пока мы не стандартизируем и не нормализуем входные данные. Данная функция будет извлекать коэффициенты масштабирования, которые мы использовали при обучении нашей модели ONNX.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ void load_scaling_factors(void) { //--- EURUSD OHLC mean_variance[0] = 1.0930010861272836; std_variance[0] = 0.0017987600829890852; mean_variance[1] = 1.0930721822927123; std_variance[1] = 0.001810556238082839; mean_variance[2] = 1.092928371812889; std_variance[2] = 0.001785041172362313; mean_variance[3] = 1.093000590242923; std_variance[3] = 0.0017979420556511476; //--- M5 Change mean_variance[4] = (MathPow(10.0,-5) * 1.4886568962056413); std_variance[4] = 0.000994902152654042; //--- M15 Change mean_variance[5] = (MathPow(10.0,-5) * 1.972093957036524); std_variance[5] = 0.0017104874192072138; //--- M30 Change mean_variance[6] = (MathPow(10.0,-5) * 1.5089339490060967); std_variance[6] = 0.002436078407827825; //--- H1 Change mean_variance[7] = 0.0001529512146155358; std_variance[7] = 0.0037675774501395387; //--- D1 Change mean_variance[8] = -0.0008775667536639223; std_variance[8] = 0.03172437243836734; }
Определяя функцию, ответственную за получение прогнозов из нашей модели, обратите внимание, что мы масштабируем входные данные перед передачей их в нашу модель ONNX. Прогнозы получаются из модели с помощью команды OnnxRun.
//+------------------------------------------------------------------+ //| Model predict | //+------------------------------------------------------------------+ void model_predict(void) { //--- EURD OHLC model_inputs[0] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[0]) / std_variance[0]); model_inputs[1] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[1]) / std_variance[1]); model_inputs[2] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[2]) / std_variance[2]); model_inputs[3] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[3]) / std_variance[3]); //--- M5 CAHNGE model_inputs[4] = (((iClose(Symbol(),PERIOD_M5,0) - iClose(Symbol(),PERIOD_M5,20)) - mean_variance[4]) / std_variance[4]); //--- M15 CHANGE model_inputs[5] = (((iClose(Symbol(),PERIOD_M15,0) - iClose(Symbol(),PERIOD_M15,20)) - mean_variance[5]) / std_variance[5]); //--- M30 CHANGE model_inputs[6] = (((iClose(Symbol(),PERIOD_M30,0) - iClose(Symbol(),PERIOD_M30,20)) - mean_variance[6]) / std_variance[6]); //--- H1 CHANGE model_inputs[7] = (((iClose(Symbol(),PERIOD_H1,0) - iClose(Symbol(),PERIOD_H1,20)) - mean_variance[7]) / std_variance[7]); //--- D1 CHANGE model_inputs[8] = (((iClose(Symbol(),PERIOD_D1,0) - iClose(Symbol(),PERIOD_D1,20)) - mean_variance[8]) / std_variance[8]); //--- Fetch forecast OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
Теперь определим функцию для загрузки нашей модели Onnx, а также определим форму ввода и вывода.
//+------------------------------------------------------------------+ //| Load our onnx file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- Set the input shape ulong input_shape [] = {1,9}; //--- Check if the input shape is valid if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model)); return(false); } //--- Set the output shape ulong output_shape [] = {1,1}; //--- Check if the output shape is valid if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
Теперь можем определить процедуру инициализации программы. Наш советник загрузит файл Onnx, загрузит коэффициенты масштабирования и извлечет рыночные данные.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX file if(!load_onnx_file()) { //--- We failed to load our onnx model return(INIT_FAILED); } //--- Load scaling factors load_scaling_factors(); //--- Get trading volume trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
Всякий раз, когда наша программа не используется, мы освобождаем ресурсы, которые нам больше не нужны. Мы отключим модель Onnx и удалим советника из графика.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Release the expert advisor ExpertRemove(); }
Всякий раз, когда нам предлагают новые цены, мы сначала получаем прогноз из нашей модели, а затем обновляем наши рыночные цены. Если у нас нет открытой позиции, мы попытаемся найти вход. В противном случае, если у нас есть позиция, которой необходимо управлять, мы будем внимательно следить за возможным разворотом.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a prediction from our model model_predict(); //--- Show the model forecast Comment("Model forecast ",model_forecast); //--- Fetch market prices update_market_prices(); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find entry find_entry(); //--- Update state state = 0; } //--- If we have an open position, manage it else { //--- Check if our AI is predicting a reversal check_reversal(); } }
Теперь мы можем увидеть наше приложение в действии.
Рис 15: Интерфейс нашего советника
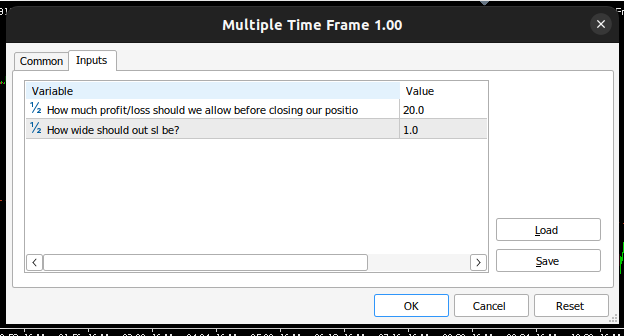
Рис 16: Входные данные нашего советника
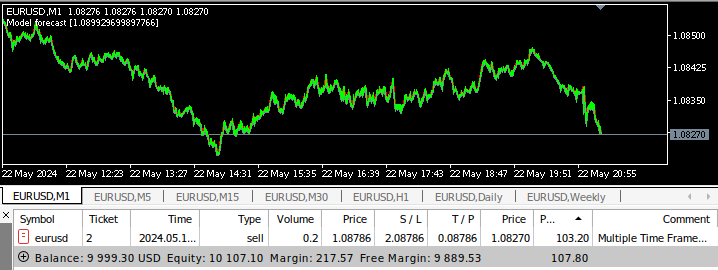
Рис 17: Советник на нескольких таймфреймах проходит бэк-тестирование
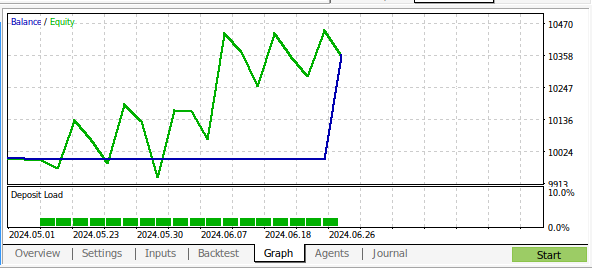
Рис 18: Результаты бэк-тестирования нашей программы на основе данных M1 за 1 месяц
Заключение
В данной статье мы продемонстрировали, что можно создать советника на базе искусственного интеллекта, который анализирует несколько таймфреймов. Несмотря на то, что нами получены более высокие уровни точности при использовании обычных данных OHLC, существует много различных вариантов, которые мы не рассматривали, например, мы не добавляли какие-либо индикаторы в отношении более высоких таймфреймов. Существует множество способов применения искусственного интеллекта в нашей торговой стратегии. Надеемся, что теперь у вас появились новые идеи о возможностях, которые вы можете использовать при установке MetaTrader 5.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15610
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Интеграция теории хаоса в прогнозирование временных рядов (Attraos)
Нейросети в трейдинге: Интеграция теории хаоса в прогнозирование временных рядов (Attraos)
 Разрабатываем мультивалютный советник (Часть 24): Подключаем новую стратегию (I)
Разрабатываем мультивалютный советник (Часть 24): Подключаем новую стратегию (I)
 Как опередить любой рынок (Часть III): Индекс расходов Visa
Как опередить любой рынок (Часть III): Индекс расходов Visa
 Анализ всех вариантов движения цены на квантовом компьютере IBM
Анализ всех вариантов движения цены на квантовом компьютере IBM
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Спасибо за пошаговый и подробный анализ. Это действительно полезно в качестве шаблона для тех, кто не знаком с анализом данных, чтобы работать через . Результат захватывает (и неожиданный), Означает ли это, что мы должны тестировать другие параметры, а также, например, объем, спред Предыдущий день действия или это больше перебор. Спасибо за шаблон, теперь у меня есть инструменты, чтобы проверить это самостоятельно :)