
古典的な戦略を再構築する(第6回):多時間枠分析
はじめに
現代の投資家が人工知能(AI)を統合して取引判断を強化する方法は無限にある可能性があります。残念ながら、苦労して稼いだ資金をどの戦略に託すかを決める前に、これらの戦略をすべて評価できる可能性は低いです。この連載では、AIを使って戦略を改善できるかどうかを評価するために、取引戦略を探っていきます。この戦略が個々の投資家のプロファイルに適しているかどうかを、十分な情報に基づき判断していただくために必要な情報を提供することを目的としています。
取引戦略の概要
この記事では、よく知られた多時間枠分析の戦略を再検討します。世界中の成功したトレーダーの多くは、投資判断を下す前に多時間枠を分析することに美徳があるという信念を持っています。この戦略には多くの異なるバリエーションがありますが、すべてのバリエーションは、上位時間枠で特定されたトレンドが、それよりも下位の時間枠のすべてでも持続するという一般的な考え方を持っています。
例えば、日足チャートで強気な値動きが観察されれば、時間足チャートでも強気な値動きが観察されると予想されます。この戦略はさらにその考えを拡張しており、戦略によれば、上位時間枠で観察されたトレンドに沿った価格変動により重みを加えるべきです。
言い換えれば、単純な例に戻ると、もし日足チャートで上昇トレンドを観察した場合、1時間足チャートでの買いの機会に対してより偏りを持ち、日足チャートで観察されたトレンドに反するポジションを取ることに消極的になるでしょう。
一般的に言えば、上位時間枠で観察されたトレンドが逆転すると、この戦略はうまく機能しなくなります。これは通常、逆転は下位時間枠でのみ始まるからです。この戦略を使用する場合、上位時間枠に反して下位時間枠で観測される変動はほとんど重視されないことを思い出してください。したがって、この戦略に従うトレーダーは、通常、上位時間枠で反転が観察できるようになるのを待つことになります。上位時間枠からの確認を待つ間、価格の変動が大きくなる可能性があります。
方法論の概要
この戦略のメリットを実証的に評価するには、MetaTrader 5端末から意味のあるデータを慎重に抽出する必要がありました。この記事の目標は、20分先のEURUSDの終値を予測することでした。この目標を達成するために、予測因子を3つのグループに分けました。
- 通常の始値、高値、安値、終値の情報
- 上位時間枠での価格水準の変化
- 1.と2.の上位集合
通常の価格データと上位時間枠の価格変動との間には比較的弱い相関が観察されました。最も強い相関が見られたのは、M15の価格変動とM1の価格水準の間で、約-0.1でした。
精度の変化を観察するために、様々なモデルの大規模なセットを作成し、予測因子の3つのセットすべてでそれらを訓練しました。最良の誤差レベルは、最初の予測因子のセットである通常の市場データを使用したときに観察されました。観察から、線形回帰モデルが最も良いパフォーマンスを示すモデルであり、次いで勾配ブースティング回帰(GBR)モデルであるようです。
線形モデルには、私たちにとってあまり興味のあるチューニングパラメータがないため、GBRモデルを候補解として選択し、線形モデルの誤差レベルが性能ベンチマークとなりました。私たちの目標は、線形モデルが設定したベンチマークの性能を上回るようにGBRモデルを最適化することになりました。
最適化プロセスを開始する前に、後方選択アルゴリズムを用いて特徴量を選択しました。上位時間枠における価格の変動に関連するすべての特徴量はアルゴリズムによって除外されました。これは、おそらくその関係が信頼できないことを示唆しているか、あるいは私たちがこの関連性をモデルに対して意味のある形で提示していないことを示唆していると解釈することもできます。
GBRモデルの最適設定を見つけるために、1000回の反復による無作為化探索アルゴリズムを使用しました。その後、Limited Memory Broyden Fletcher Goldfarb And Shanno(L-BFGS-B)アルゴリズムを用いた連続GBRパラメータの局所最適化の出発点として、ランダムサーチの結果を採用しました。
検証データではデフォルトのGBRモデルを上回りませんでしたが、これはおそらく訓練データに過剰適合していたことを示しています。さらに、検証においても線形モデルのベンチマーク性能を上回ることはできませんでした。
データ抽出
MetaTrader 5端末からデータを抽出するための便利なMQL5スクリプトを作成しました。スクリプトはまた、上位時間枠の選択から価格の変化を取得し、パス「MetaTrader 5\MQL5\Files\...」にファイルを出力します。
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/ja/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 5; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + " multiple timeframe 20 step look ahead .csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= -1;i<=size;i++) { if(i == -1) { FileWrite(file_handle,"Time","Open","High","Low","Close","M5","M15","M30","H1","D1"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i), (iClose(Symbol(),PERIOD_M5,i) - iClose(Symbol(),PERIOD_M5,i+20)), (iClose(Symbol(),PERIOD_M15,i) - iClose(Symbol(),PERIOD_M15,i+20)), (iClose(Symbol(),PERIOD_M30,i) - iClose(Symbol(),PERIOD_M30,i+20)), (iClose(Symbol(),PERIOD_H1,i) - iClose(Symbol(),PERIOD_H1,i+20)), (iClose(Symbol(),PERIOD_D1,i) - iClose(Symbol(),PERIOD_D1,i+20)) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
データを読み解く
必要なライブラリをロードすることから始めましょう。
import pandas as pd imort numpy as np
データが現在から過去へと遡っているので、逆転させ、過去から現在に近づける必要があります。
#Let's format the data so it starts with the oldest date market_data = market_data[::-1] market_data.reset_index(inplace=True)
次に、予測期間を定義します。
look_ahead = 20 データにラベルを付けます。ターゲットはEURUSDの将来の終値とします。
#Let's label the data market_data["Target"] = market_data["Close"].shift(-look_ahead)
欠損値のある行を削除します。
#Drop rows with missing values
market_data.dropna(inplace=True)
探索的データ分析
相関レベルの分析
#Let's see if there is any correlation market_data.iloc[:,2:-1].corr()
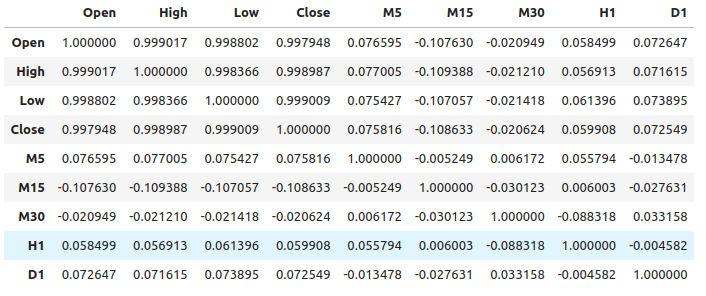
図1:異なる時間枠における相関レベル
見てわかるように、データセットには中程度に弱いレベルの相関があります。なお、相関関係は必ずしも観測される変数間に関係があることを証明するものではありません。
相互情報とは、予測因子がターゲットを説明できる可能性を示す尺度です。まず、ターゲットを予測する可能性が高いことがわかっている変数、すなわち始値について考えてみましょう。
from sklearn.feature_selection import mutual_info_regression
ベンチマークとして、これは良い相互情報(MI)スコアです。
#MI Score for the Open price
print(f'Open price has MI score: {mutual_info_regression(market_data.loc[:,["Open"]],market_data.loc[:,"Target"])[0]}') 次に、M1時間枠の将来価格に関するM5時間枠の価格変動のMIスコアを見てみましょう。
#MI Score for the M5 change in price
print(f'M5 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M5"]],market_data.loc[:,"Target"])[0]}') このMIスコアはかなり小さくなっています。これは、私たちがその関係を意味のある形で示していないか、あるいは異なる時間枠における価格レベルの間に依存関係がない可能性があることを意味します。
#MI Score for the M15 change in price
print(f'M15 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M15"]],market_data.loc[:,"Target"])[0]}') 私たちが選んだ残りの時間枠についても同様です。
関係のモデル化
予測因子とターゲットを定義しましょう。
#Let's define our predictors and our target ohlc_predictors = [ "Open", "High", "Low", "Close" ] time_frame_predictors = [ "M5", "M15", "M30", "H1", "D1" ] all_predictors = ohlc_predictors + time_frame_predictors target = "Target"
必要なライブラリをインポートします。
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import SGDRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit,RandomizedSearchCV from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
時系列分割オブジェクトのパラメータを定義します。
#Define the time series split object gap = look_ahead splits = 10
モデルを準備し、精度レベルを保存するデータフレームを作成します。こうすることで、モデルの入力を変えたときの精度の変化を観察することができます。
#Store our models in a list models = [ LinearRegression(), SGDRegressor(), RandomForestRegressor(), BaggingRegressor(), GradientBoostingRegressor(), AdaBoostRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), MLPRegressor(hidden_layer_sizes=(100,20),early_stopping=True) ] #Create a list of column titles for each model columns = [ "Linear Regression", "SGD Regressor", "Random Forest Regressor", "Bagging Regressor", "Gradient Boosting Regressor", "AdaBoost Regressor", "K Neighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neurla Network" ] #Create data frames to store our accuracy ohlc_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) multiple_time_frame_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) all_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns)
予測因子を準備し、データをスケーリングします。
#Preparing to perform cross validation
current_predictors = all_predictors
scaled_data = pd.DataFrame(RobustScaler().fit_transform(market_data.loc[:,all_predictors]),columns=all_predictors)
時系列分割オブジェクトを作成します。
#Create the time series split object
tscv = TimeSeriesSplit(gap=gap,n_splits=splits)
交差検証をおこないます。最初のループは先ほど作成したモデルのリストを反復処理し、2番目のループは各モデルを順番に交差検証します。
#First we will iterate over all the available models for i in np.arange(0,len(models)): #First select the model model = models[i] #Now we will cross validate this current model for j , (train,test) in enumerate(tscv.split(scaled_data)): #First define the train and test data train_X = scaled_data.loc[train[0]:train[-1],current_predictors] train_y = market_data.loc[train[0]:train[-1],target] test_X = scaled_data.loc[test[0]:test[-1],current_predictors] test_y = market_data.loc[test[0]:test[-1],target] #Now we will fit the model model.fit(train_X,train_y) #And finally record the accuracy all_accuracy.iloc[j,i] = root_mean_squared_error(test_y,model.predict(test_X))
以下は、モデルに通常の入力を使用した場合の精度レベルです。
ohlc_accuracy
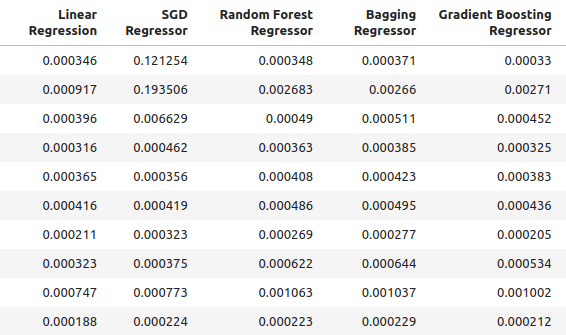
図2:通常の精度レベル
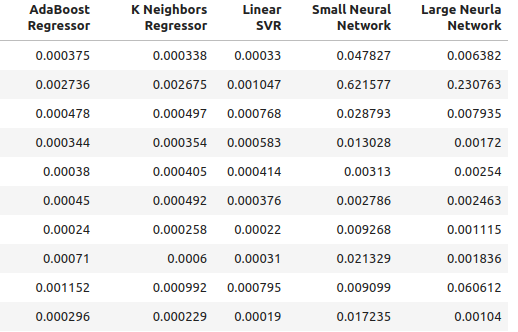
図3:通常の精度レベル II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {ohlc_accuracy.iloc[:,i].mean()}")
Linear Regression had error levels 0.00042256332959154886
SGD Regressor had error levels 0.0324320107406244
Random Forest Regressor had error levels 0.0006954883552094012
Bagging Regressor had error levels 0.0007030697054783931
Gradient Boosting Regressor had error levels 0.0006588749449742309
AdaBoost Regressor had error levels 0.0007159624774453208
K Neighbors Regressor had error levels 0.0006839218661791973
Linear SVR had error levels 0.000503277800807813
Small Neural Network had error levels 0.07740701832606754
Large Neural Network had error levels 0.03164056895135391
以下は、私たちが作成した新しい入力を使用した場合の精度です。
multiple_time_frame_accuracy
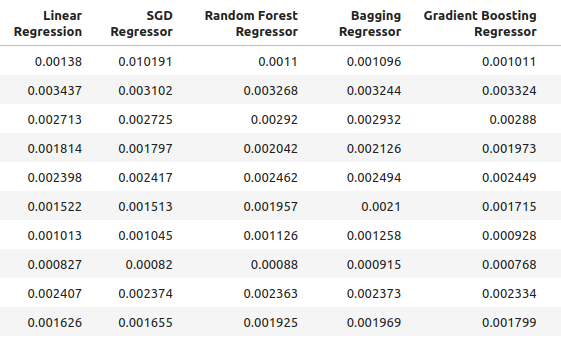
図4:新しい精度レベル
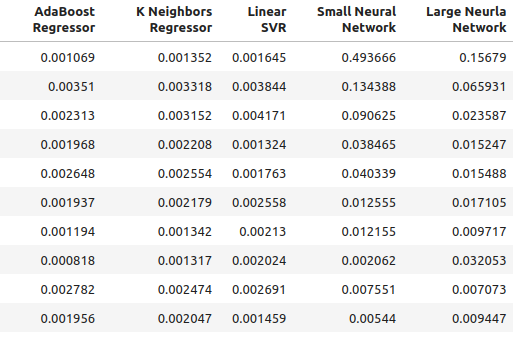
図5:新しい精度レベル II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {multiple_time_frame_accuracy.iloc[:,i].mean()}")
Linear Regression had error levels 0.001913639795583766
SGD Regressor had error levels 0.0027638553835377206
Random Forest Regressor had error levels 0.0020041047670504254
Bagging Regressor had error levels 0.0020506512726394415
Gradient Boosting Regressor had error levels 0.0019180687958290775
AdaBoost Regressor had error levels 0.0020194136735787625
K Neighbors Regressor had error levels 0.0021943350208868213
Linear SVR had error levels 0.0023609474919917338
Small Neural Network had error levels 0.08372469596701271
Large Neural Network had error levels 0.035243897461061074
最後に、利用可能なすべての予測因子を使用した場合の精度を観察してみましょう。
all_accuracy
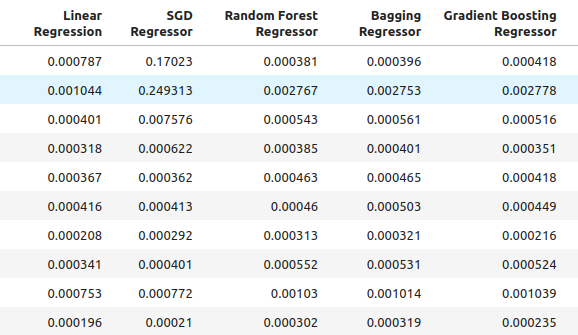
図6:私たちが持っているすべての予測因子を使用した場合の精度レベル
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {all_accuracy.iloc[:,i].mean()}")
Linear Regression had error levels 0.00048307488099524497
SGD Regressor had error levels 0.043019079499194125
Random Forest Regressor had error levels 0.0007196920919204373
Bagging Regressor had error levels 0.0007263444909545053
Gradient Boosting Regressor had error levels 0.0006943964783049555
AdaBoost Regressor had error levels 0.0007217149661087063
K Neighbors Regressor had error levels 0.000872811528292862
Linear SVR had error levels 0.0006457525216512596
Small Neural Network had error levels 0.14002618062102
Large Neural Network had error levels 0.06774795252887988
見てわかるように、線形モデルはすべてのテストにおいて最高のパフォーマンスを示しました。さらに、通常のOHLCデータを使用した場合に最高のパフォーマンスを発揮しました。しかし、このモデルには私たちが関心を持つチューニングパラメータがありません。そこで、2番目に優れたモデルである勾配ブースティング回帰(GBR)を選択し、線形モデルを上回ることを試みます。
特徴量の選択
それでは、GBRモデルにとってどの機能が最も重要だったかを見てみましょう。
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS
モデルを選択します。
#We'll select the Gradient Boosting Regressor as our chosen model model = GradientBoostingRegressor()
後方選択アルゴリズムを使用します。まず、すべての予測因子を含むモデルから始めて、連続的に特徴を1つずつ落としていきます。特徴量が削除されるのは、その機能によってモデルのパフォーマンスが向上する場合に限られます。
#Let us prepare the Feature Selector Object sfs = SFS(model, k_features=(1,len(all_predictors)), forward=False, n_jobs=-1, scoring="neg_root_mean_squared_error", cv=10 )
特徴量を選択します。
#Select the best feature sfs_results = sfs.fit(scaled_data.loc[:,all_predictors],market_data.loc[:,"Target"])
アルゴリズムは高値だけを残し、それ以外の特徴量はすべて除外しました。
#The best feature we found
sfs_results.k_feature_names_
結果を可視化してみましょう。
#Prepare the plot fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev") plt.title("Backward Selection on Gradient Boosting Regressor") plt.grid()
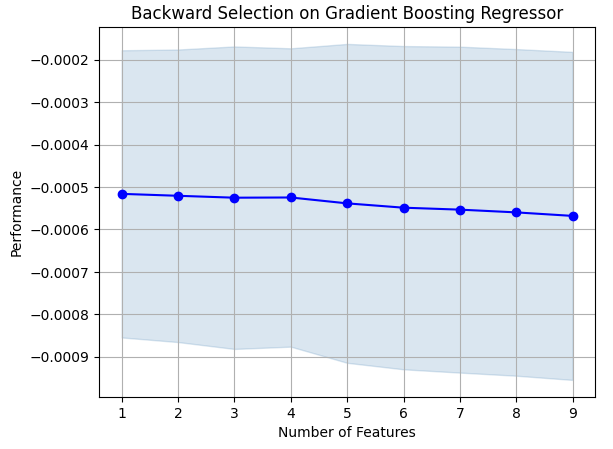
図7:特徴量選択プロセスの可視化
ご覧の通り、モデルサイズと誤差レベルは正比例しています。言い換えれば、モデルが大きくなればなるほど、誤差のレベルも大きくなったということです。
パラメータチューニング
それでは、GBRモデルのパラメータチューニングをおこなってみましょう。チューニングする価値のある11のパラメータをモデルから特定しました。最適化プロセスを終了する前に、チューニングオブジェクトを1000回反復させます。
#Let us try to tune our model
from sklearn.model_selection import RandomizedSearchCV
モデルのチューニングを始める前に、データを2つに分けてみましょう。一方はモデルの訓練と最適化に、もう一方は検証や過剰適合のテストに使われます。
#Before we try to tune our model, let's first create a train and test set train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = market_data.loc[:(market_data.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = market_data.loc[(market_data.shape[0]//2):,"Target"]
チューニングオブジェクトを定義します。
#Time the process import time start_time = time.time() #Prepare the tuning object tuner = RandomizedSearchCV(GradientBoostingRegressor(), { "loss": ["squared_error","absolute_error","huber"], "learning_rate": [0,(10.0 ** -1),(10.0 ** -2),(10.0 ** -3),(10.0 ** -4),(10.0 ** -5),(10.0 ** -6),(10.0 ** -7)], "n_estimators": [5,10,25,50,100,200,500,1000], "max_depth": [1,2,3,5,9,10], "min_samples_split":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0], "criterion":["friedman_mse","squared_error"], "min_samples_leaf":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9], "min_weight_fraction_leaf":[0.0,0.1,0.2,0.3,0.4,0.5], "max_features":[1,2,3,4,5,20], "max_leaf_nodes": [2,3,4,5,10,20,50,90,None], "min_impurity_decrease": [0,1,10,(10.0 ** 2),(10.0 ** 3),(10.0 ** 4)] }, cv=5, n_iter=1000, return_train_score=False, scoring="neg_mean_squared_error" )
GBRモデルを調整します。
#Tune the GradientBoostingRegressor tuner.fit(train_X,train_y) end_time = time.time() print(f"Process completed in {end_time - start_time} seconds.")
結果を良いものから悪いものまで見ていきます。
#Let's observe the results tuner_results = pd.DataFrame(tuner.cv_results_) params = ["param_loss", "param_learning_rate", "param_n_estimators", "param_max_depth", "param_min_samples_split", "param_criterion", "param_min_samples_leaf", "param_max_features", "param_max_leaf_nodes", "param_min_impurity_decrease", "param_min_weight_fraction_leaf", "mean_test_score"] tuner_results.loc[:,params].sort_values(by="mean_test_score",ascending=False)
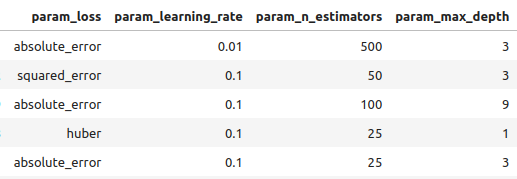
図8:最良結果の一部
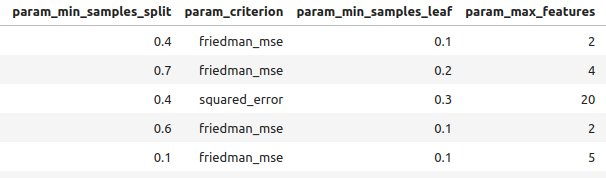
図9:最良結果の一部
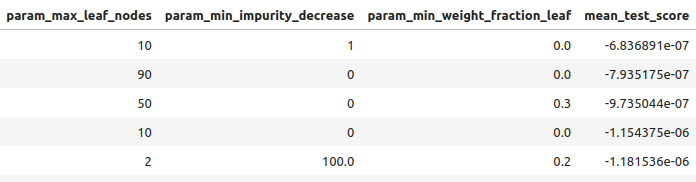
図10:最良結果の一部III
以下が、見つかった最高のパラメータです。
#Best parameters we found
tuner.best_params {'n_estimators':500,
'min_weight_fraction_leaf':0.0,
'min_samples_split':0.4,
'min_samples_leaf':0.1,
'min_impurity_decrease':1,
'max_leaf_nodes':10,
'max_features':2,
'max_depth':3,
'loss': 'absolute_error',
'learning_rate':0.01,
'criterion': 'friedman_mse'}
より詳細なパラメーターチューニング

図11:SciPyのロゴ
SciPyは科学計算に使用されるPythonライブラリです。SciPyはScientific PYthonの略です。もっといいパラメータがないか探してみましょう。SciPyのoptimizeライブラリを使って、モデルの性能を向上させるパラメータを見つけようとします。
#Let's see if we can't find better parameters #We may be overfitting the training data! from scipy.optimize import minimize
SciPyのoptimizeライブラリを使用するには、目的関数を定義する必要があります。目的関数は、モデルが訓練セットで達成した交差検証誤差レベルの平均となります。SciPyのオプティマイザは、学習誤差を減らす係数を探索します。
#Define the objective function def objective(x): #Create a dataframe to store our new accuracy current_error = pd.DataFrame(index=[0],columns=["error"]) #x is an array of possible values to use for our Gradient Boosting Regressor model = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=x[0], min_samples_split=x[1], min_samples_leaf=x[2], learning_rate=x[3]) model.fit(train_X.loc[:,:],train_y.loc[:]) current_error.iloc[0,0] = root_mean_squared_error(train_y.loc[:],model.predict(train_X.loc[:,:])) #Record our progress mean_error = current_error.loc[:].mean() #Return the average error return mean_error
では、最適化プロセスを始めましょう。GBRモデルのいくつかのパラメータは負の値を許さないので、オプティマイザに境界を指定しない限り、SciPyオプティマイザは負の値を渡します。さらに、オプティマイザは私たちが出発点を与えることを期待しています。前回の最適化アルゴリズムの終点を、今回の最適化アルゴリズムの出発点とします。
#Let's optimize these parameters again #Fist define the bounds bounds = ((0.0,0.5),(0.3,0.5),(0.001,0.2),(0.001,0.1)) #Then define the starting points for the L-BFGS-B algorithm pt = np.array([tuner.best_params_["min_weight_fraction_leaf"], tuner.best_params_["min_samples_split"], tuner.best_params_["min_samples_leaf"], tuner.best_params_["learning_rate"] ])
訓練エラーを最小限に抑えます。
lbfgs = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
結果を見てみましょう。
lbfgs
success:True
status:0
fun:0.0005766670348377334
x: [ 5.586e-06 4.000e-01 1.000e-01 1.000e-02]
nit:3
jac: [-6.216e+00 -4.871e+02 -2.479e+02 8.882e+01]
nfev:180
njev:36
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
過剰適合のテスト
それでは、2つのカスタマイズモデルの精度を、デフォルトのGBRモデルと比較してみましょう。さらに、線形モデルを上回ったかどうかにも注目します。
#Let us now see how well we're performing on the validation set linear_regression = LinearRegression() default_gbr = GradientBoostingRegressor() grid_search_gbr = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=0, min_samples_split=0.4, min_samples_leaf=0.1, learning_rate=0.01 ) lbfgs_grid_search_gbr = GradientBoostingRegressor( n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=lbfgs.x[0], min_samples_split=lbfgs.x[1], min_samples_leaf=lbfgs.x[2], learning_rate=lbfgs.x[3] )以下は、線形モデルでの精度です。
#Linear Regression
linear_regression.fit(train_X,train_y)
root_mean_squared_error(test_y,linear_regression.predict(test_X)) 以下は、デフォルトのGBRモデルでの精度です。
#Default Gradient Boosting Regressor
default_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,default_gbr.predict(test_X)) 以下は、ランダムサーチによってカスタマイズされたGBRモデルでの精度です。
#Random Search Gradient Boosting Regressor
grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,grid_search_gbr.predict(test_X)) 以下は、ランダムサーチとL-BFGS-BによってカスタマイズされたGBRモデルを使用した場合の精度です。
#L-BFGS-B Random Search Gradient Boosting Regressor
lbfgs_grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,lbfgs_grid_search_gbr.predict(test_X))
ご覧の通り、線形モデルを上回ることはできませんでした。また、デフォルトのGBRモデルを上回ることもできませんでした。したがって、デモンストレーションのために、デフォルトのGBRモデルで進めていきますが、線形モデルを選択した方がより精度が高くなることに注意してください。
ONNXへのエクスポート
Open Neural Network Exchange(ONNX)は、機械学習モデルをノードとエッジの計算グラフとして表現することを可能にするプロトコルです。ノードは数学的操作を、エッジはデータの流れを表します。機械学習モデルをONNX形式にエクスポートすることで、AIモデルをEA内で簡単に使用できるようになります。
ONNXモデルをエクスポートする準備をしましょう。
#We failed to beat the linear regression model, in such cases we should pick the linear model! #However for demonstrational purposes we'll pick the gradient boosting regressor #Let's export the default GBR to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnx
ここで、MetaTrader 5で再現できる方法でデータをスケールする必要があります。最も簡単な変換は、単純に平均を引き、標準偏差で割ることです。
#We need to save the scale factors for our inputs scale_factors = pd.DataFrame(index=["mean","standard deviation"],columns=all_predictors) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = market_data.iloc[:,i+2].mean() scale_factors.iloc[1,i] = market_data.iloc[:,i+2].std() market_data.iloc[:,i+2] = ((market_data.iloc[:,i+2] - market_data.iloc[:,i+2].mean()) / market_data.iloc[:,i+2].std()) scale_factors

図12:スケール係数
ONNXモデルの入力タイプを定義します。
#Define our initial types initial_types = [("float_input",FloatTensorType([1,test_X.shape[1]]))]
手持ちの全データにモデルを適合します。
#Fit the model on all the data we have model = GradientBoostingRegressor().fit(market_data.loc[:,all_predictors],market_data.loc[:,"Target"])
ONNX表現を作成します。
#Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
ONNXモデルを保存します。
#Now save the ONNX model onnx_model_name = "GBR_M1_MultipleTF_Float.onnx" onnx.save(onnx_model,onnx_model_name)
モデルの可視化
Netronは、機械学習モデルを検査するためのオープンソースのビジュアライザーです。現在、Netronは限られた数のフレームワークをサポートしていますが、時間が経過し、ライブラリが成熟するにつれて、さまざまな機械学習フレームワークへのサポートが拡張されていくでしょう。
必要なライブラリをインポートします。
#Import netron so we can visualize the model
import netron
Netronを立ち上げます。
netron.start(onnx_model_name)
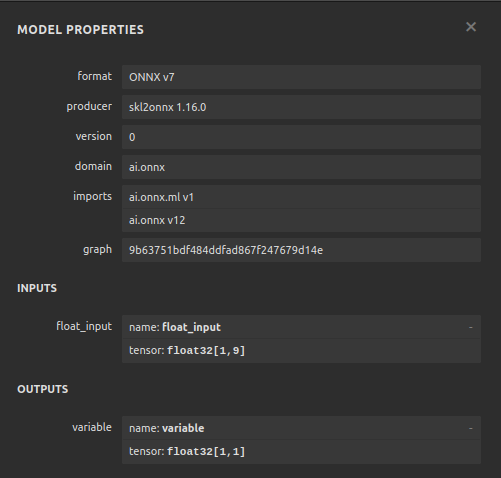
図13:勾配ブースティング回帰ONNXモデルの特性
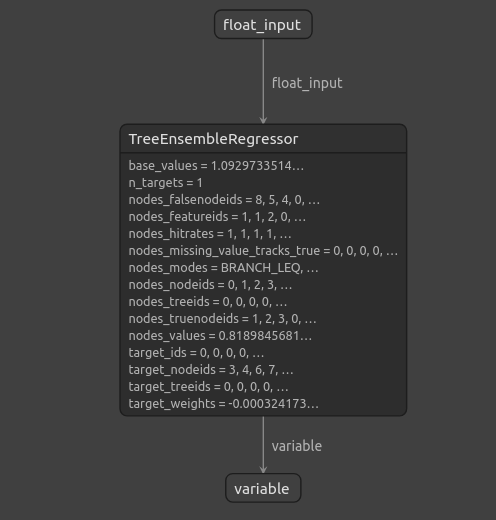
図14:勾配ブースティング回帰の構造
ご覧の通り、ONNXモデルの入力と出力の形状は期待通りの場所にあり、これにより自信を持って、ONNXモデルの上にEAを構築することができます。
MQL5での実装
AIモジュールを組み込んだEAを構築するには、まずONNXモデルが必要です。//+------------------------------------------------------------------+ //| Multiple Time Frame.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/ja/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/ja/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the onnx file | //+------------------------------------------------------------------+ #resource "\\Files\\GBR_M1_MultipleTF_Float.onnx" as const uchar onnx_model_buffer[];
次に、取引ライブラリをロードします。
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
エンドユーザーが変更できる入力を定義します。
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input double max_risk = 20; //How much profit/loss should we allow before closing input double sl_width = 1; //How wide should out sl be?
次に、プログラム全体で使用するグローバル変数を定義します。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_variance[9],std_variance[9]; //Our scaling factors vector model_forecast = vector::Zeros(1); //Model forecast vector model_inputs = vector::Zeros(9); //Model inputs double ask,bid; //Market prices double trading_volume; //Our trading volume int lot_multiple = 20; //Our lot size int state = 0; //System state
プログラム全体で使用するヘルパー関数を定義します。まず、逆転を検知し、AIシステムが予測した前方の危険をエンドユーザーに警告する関数が必要です。AIシステムが反転を検知したら、その市場で保有するポジションを決済します。
//+------------------------------------------------------------------+ //| Check reversal | //+------------------------------------------------------------------+ void check_reversal(void) { //--- Check for reversal if(((state == 1) && (model_forecast[0] < iClose(Symbol(),PERIOD_M1,0))) || ((state == 2) && (model_forecast[0] > iClose(Symbol(),PERIOD_M1,0)))) { Alert("Reversal predicted."); Trade.PositionClose(Symbol()); } //--- Check if we have breached our maximum risk levels if(MathAbs(PositionGetDouble(POSITION_PROFIT) > max_risk)) { Alert("We've breached our maximum risk level."); Trade.PositionClose(Symbol()); } }
次に、市場参入の機会を見つけるための関数を定義します。上位時間枠から、その動きに関する確認が取れた場合のみ、エントリが有効であると判断します。このEAでは、週足チャートのプライスアクションに合わせて取引をおこないます。
//+------------------------------------------------------------------+ //| Find an entry | //+------------------------------------------------------------------+ void find_entry(void) { //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bullish momentum if(model_forecast[0] > iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a buy Trade.Buy(trading_volume,Symbol(),ask,(ask - sl_width),(ask + sl_width),"Multiple Time Frames AI"); state = 1; } } //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bearish momentum if(model_forecast[0] < iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a sell Trade.Sell(trading_volume,Symbol(),bid,(bid + sl_width),(bid - sl_width),"Multiple Time Frames AI"); state = 2; } } }
また、現在の市場価格を取得する関数も必要です。
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); }
入力を標準化および正規化しない限り、ONNXモデルは使用できません。この関数は、ONNXモデルの訓練時に使用したスケーリング係数を取得します。
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ void load_scaling_factors(void) { //--- EURUSD OHLC mean_variance[0] = 1.0930010861272836; std_variance[0] = 0.0017987600829890852; mean_variance[1] = 1.0930721822927123; std_variance[1] = 0.001810556238082839; mean_variance[2] = 1.092928371812889; std_variance[2] = 0.001785041172362313; mean_variance[3] = 1.093000590242923; std_variance[3] = 0.0017979420556511476; //--- M5 Change mean_variance[4] = (MathPow(10.0,-5) * 1.4886568962056413); std_variance[4] = 0.000994902152654042; //--- M15 Change mean_variance[5] = (MathPow(10.0,-5) * 1.972093957036524); std_variance[5] = 0.0017104874192072138; //--- M30 Change mean_variance[6] = (MathPow(10.0,-5) * 1.5089339490060967); std_variance[6] = 0.002436078407827825; //--- H1 Change mean_variance[7] = 0.0001529512146155358; std_variance[7] = 0.0037675774501395387; //--- D1 Change mean_variance[8] = -0.0008775667536639223; std_variance[8] = 0.03172437243836734; }
モデルから予測を取得する関数を定義する際、入力をONNXモデルに渡す前にスケーリングしていることに注意してください。OnnxRunコマンドを使ってモデルから予測を得ます。
//+------------------------------------------------------------------+ //| Model predict | //+------------------------------------------------------------------+ void model_predict(void) { //--- EURD OHLC model_inputs[0] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[0]) / std_variance[0]); model_inputs[1] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[1]) / std_variance[1]); model_inputs[2] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[2]) / std_variance[2]); model_inputs[3] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[3]) / std_variance[3]); //--- M5 CAHNGE model_inputs[4] = (((iClose(Symbol(),PERIOD_M5,0) - iClose(Symbol(),PERIOD_M5,20)) - mean_variance[4]) / std_variance[4]); //--- M15 CHANGE model_inputs[5] = (((iClose(Symbol(),PERIOD_M15,0) - iClose(Symbol(),PERIOD_M15,20)) - mean_variance[5]) / std_variance[5]); //--- M30 CHANGE model_inputs[6] = (((iClose(Symbol(),PERIOD_M30,0) - iClose(Symbol(),PERIOD_M30,20)) - mean_variance[6]) / std_variance[6]); //--- H1 CHANGE model_inputs[7] = (((iClose(Symbol(),PERIOD_H1,0) - iClose(Symbol(),PERIOD_H1,20)) - mean_variance[7]) / std_variance[7]); //--- D1 CHANGE model_inputs[8] = (((iClose(Symbol(),PERIOD_D1,0) - iClose(Symbol(),PERIOD_D1,20)) - mean_variance[8]) / std_variance[8]); //--- Fetch forecast OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
次に、Onnxモデルをロードする関数を定義し、入力と出力のシェイプを定義します。
//+------------------------------------------------------------------+ //| Load our onnx file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- Set the input shape ulong input_shape [] = {1,9}; //--- Check if the input shape is valid if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model)); return(false); } //--- Set the output shape ulong output_shape [] = {1,1}; //--- Check if the output shape is valid if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
次にプログラムの初期化手順を定義します。EAはONNXファイルをロードし、スケーリング係数をロードし、市場データを取得します。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX file if(!load_onnx_file()) { //--- We failed to load our onnx model return(INIT_FAILED); } //--- Load scaling factors load_scaling_factors(); //--- Get trading volume trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
プログラムが使われなくなったときはいつでも、もう必要のないリソースを解放します。ONNXモデルをリリースし、チャートからEAを削除します。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Release the expert advisor ExpertRemove(); }
新しい価格が提示されるたびに、まずモデルから予測を取得し、それから市場価格を更新します。ポジションがない場合は、エントリを探します。それ以外の場合、管理すべきポジションがあれば、反転の可能性に注意深く目を光らせます。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a prediction from our model model_predict(); //--- Show the model forecast Comment("Model forecast ",model_forecast); //--- Fetch market prices update_market_prices(); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find entry find_entry(); //--- Update state state = 0; } //--- If we have an open position, manage it else { //--- Check if our AI is predicting a reversal check_reversal(); } }
これで、アプリケーションの動作を見ることができます。
図15:EAインターフェイス
図16:EAの入力
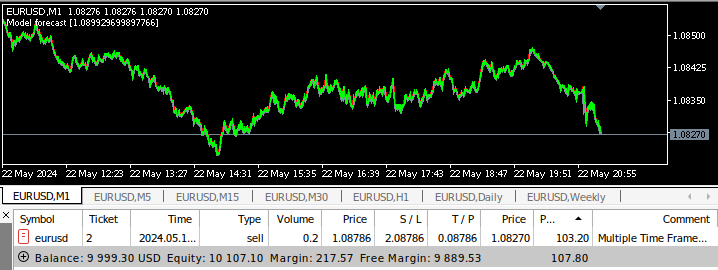
図17:多時間枠EAのバックテスト
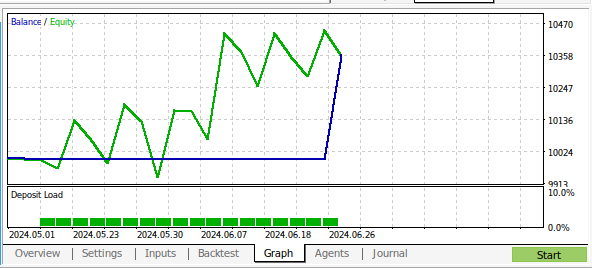
図18:1ヶ月のM1データに対するバックテストの結果
結論
この記事では、多時間枠を分析するAI搭載のEAを構築することが可能であることを実証しました。通常のOHLCデータを使用して高い精度レベルを達成しましたが、例えば上位時間枠の指標を追加するなど、検証しなかった選択肢もいくつかあります。AIを取引戦略に応用する方法は多岐にわたりますが、MetaTrader 5にインストールして活用できる機能に関して、新たなアイデアが浮かんだのではないでしょうか。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15610
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 どんな市場でも優位性を得る方法(第3回):VISA消費指数
どんな市場でも優位性を得る方法(第3回):VISA消費指数
 古典的な戦略を再構築する(第5回):USDZARの多銘柄分析
古典的な戦略を再構築する(第5回):USDZARの多銘柄分析
 知っておくべきMQL5ウィザードのテクニック(第32回):正則化
知っておくべきMQL5ウィザードのテクニック(第32回):正則化
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

ステップ・バイ・ステップで詳細な分析をありがとうございます。これは、データ分析に不慣れな人が作業するためのテンプレートとして本当に役に立ちます。結果は魅力的です(そして予想外でした)。テンプレートをありがとう、自分でチェックするツールができたよ。)