Reimaginando las estrategias clásicas (Parte VI): Análisis de múltiples marcos temporales
234
0
Introducción
Hay potencialmente infinitas formas en las que un inversor moderno puede integrar Inteligencia Artificial (IA) para mejorar sus decisiones comerciales. Lamentablemente, es poco probable que pueda evaluar todas estas estrategias antes de decidir en cuál estrategia confiar su capital ganado con tanto esfuerzo. En esta serie de artículos, exploraremos estrategias comerciales para evaluar si podemos mejorar la estrategia con IA. Nuestro objetivo es brindarle la información que necesita para tomar una decisión informada sobre si esta estrategia es adecuada para su perfil de inversor individual.
Descripción general de la estrategia comercial
En este artículo, revisamos una estrategia bien conocida de análisis de múltiples marcos temporales. Un gran grupo de traders exitosos de todo el mundo cree que es ventajoso analizar más de un período de tiempo antes de tomar decisiones de inversión. Hay muchas variantes diferentes de la estrategia. Sin embargo, todos tienden a mantener la creencia general de que cualquier tendencia identificada en un marco temporal superior persistirá en todos los marcos temporales inferiores.
Entonces, por ejemplo, si observamos un comportamiento de precios alcista en el gráfico diario, entonces esperaríamos razonablemente ver patrones de precios alcistas en el gráfico horario. Esta estrategia también extiende la idea más allá: según la estrategia, deberíamos agregar más peso a las fluctuaciones de precios que están alineadas con la tendencia observada en el marco temporal superior.
En otras palabras, volviendo a nuestro ejemplo simple, si observamos una tendencia alcista en el gráfico diario, entonces estaríamos más inclinados a comprar oportunidades en el gráfico horario y tomaríamos a regañadientes posiciones opuestas a la tendencia observada en el gráfico diario.
En términos generales, la estrategia se desmorona cuando se revierte la tendencia observada en el marco temporal superior. Generalmente, esto se debe a que la reversión comenzará solo en un marco temporal inferior. Recuerde que al utilizar esta estrategia, se atribuye poco peso a las fluctuaciones observadas en los marcos temporales inferiores que son contrarias al marco temporal superior. Por lo tanto, los traders que siguen esta estrategia normalmente esperarían a que la reversión sea observable en el marco temporal superior. Por lo tanto, pueden experimentar mucha volatilidad en el precio mientras esperan la confirmación del marco temporal superior.
Descripción general de la metodología
Para evaluar empíricamente los méritos de esta estrategia, tuvimos que extraer cuidadosamente datos significativos de nuestro terminal MetaTrader 5. Nuestro objetivo en este artículo sera predecir el precio de cierre futuro del EURUSD 20 minutos en el futuro. Para lograr este objetivo, creamos 3 grupos de predictores:
- Información de precios ordinarios de apertura, máximos, mínimos y cierre.
- Cambios en los niveles de precios en marcos temporales más largos.
- Un superconjunto de los dos conjuntos anteriores.
Observamos niveles relativamente débiles de correlación entre los datos de precios ordinarios y los cambios de precios en marcos temporales más altos. Los niveles de correlación más fuertes que observamos fueron entre los cambios en el precio del M15 y los niveles de precios del M1, aproximadamente -0,1.
Creamos un amplio conjunto de varios modelos y los entrenamos con los 3 conjuntos de predictores para observar los cambios en la precisión. Nuestros mejores niveles de error se observaron al utilizar el primer conjunto de predictores, datos de mercado ordinarios. De nuestras observaciones se desprende que el modelo de regresión lineal es el que ofrece mejores resultados, seguido del modelo Gradient Boosting Regressor (GBR).
Como el modelo lineal no tiene ningún parámetro de ajuste que nos interese mucho, seleccionamos el modelo GBR como solución candidata, y los niveles de error del modelo lineal se convirtieron en nuestra referencia de rendimiento. Nuestro objetivo ahora era optimizar el modelo GBR para superar el rendimiento de referencia establecido por el modelo lineal.
Antes de iniciar el proceso de optimización, realizamos la selección de características mediante el algoritmo de selección hacia atrás. El algoritmo descartó todas las características relacionadas con los cambios en el precio a lo largo de plazos más largos, lo que posiblemente sugiere que la relación puede no ser fiable o, alternativamente, también podemos interpretar que esto sugiere que no hemos expuesto la asociación a nuestro modelo de forma significativa.
Utilizamos un algoritmo de búsqueda aleatoria con 1000 iteraciones para encontrar los ajustes óptimos de nuestro modelo GBR. Después, empleamos los resultados de nuestra búsqueda aleatoria como punto de partida para una optimización local de los parámetros GBR continuos utilizando el algoritmo de memoria limitada Broyden Fletcher Goldfarb And Shanno (L-BFGS-B).
No superamos el modelo GBR por defecto en los datos de validación, lo que posiblemente indica que nos ajustamos en exceso a los datos de entrenamiento. Además, tampoco superamos el rendimiento de referencia del modelo lineal en la validación.
Extracción de datos
He creado unos scripts MQL5 muy útiles para extraer datos de nuestro terminal MetaTrader 5. El script también obtendrá los cambios en el precio de una selección de plazos más altos y la salida del archivo en la ruta: «MetaTrader 5\MQL5\Files\...»
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 5; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + " multiple timeframe 20 step look ahead .csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= -1;i<=size;i++) { if(i == -1) { FileWrite(file_handle,"Time","Open","High","Low","Close","M5","M15","M30","H1","D1"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i), (iClose(Symbol(),PERIOD_M5,i) - iClose(Symbol(),PERIOD_M5,i+20)), (iClose(Symbol(),PERIOD_M15,i) - iClose(Symbol(),PERIOD_M15,i+20)), (iClose(Symbol(),PERIOD_M30,i) - iClose(Symbol(),PERIOD_M30,i+20)), (iClose(Symbol(),PERIOD_H1,i) - iClose(Symbol(),PERIOD_H1,i+20)), (iClose(Symbol(),PERIOD_D1,i) - iClose(Symbol(),PERIOD_D1,i+20)) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Leyendo los datos
Comencemos cargando las bibliotecas que necesitamos.
import pandas as pd imort numpy as np
Observe que los datos van desde el presente cercano hasta el pasado distante. Necesitamos invertir los datos para que vayan desde el pasado hasta el presente cercano.
#Let's format the data so it starts with the oldest date market_data = market_data[::-1] market_data.reset_index(inplace=True)
Ahora definiremos nuestro horizonte de pronóstico.
look_ahead = 20 Etiquetado de los datos. Nuestro objetivo será el precio de cierre futuro del EURUSD.
#Let's label the data market_data["Target"] = market_data["Close"].shift(-look_ahead)
Ahora eliminemos todas las filas que tengan valores faltantes.
#Drop rows with missing values
market_data.dropna(inplace=True)
Análisis exploratorio de datos
Analizando los niveles de correlación.
#Let's see if there is any correlation market_data.iloc[:,2:-1].corr()
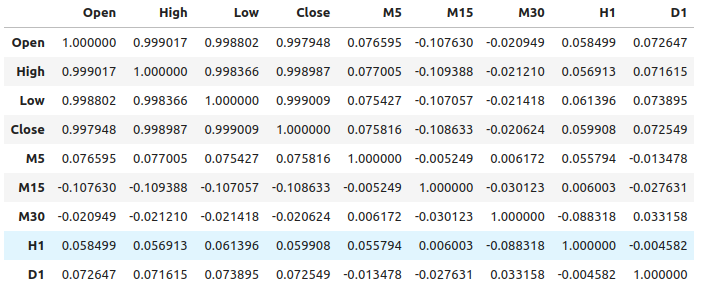
Figura 1: Niveles de correlación en diferentes períodos de tiempo.
Como podemos ver, hay niveles moderadamente débiles de correlación en nuestro conjunto de datos. Tenga en cuenta que la correlación no prueba necesariamente que exista una relación entre las variables observadas.
La información mutua es una medida del potencial que tiene un predictor para explicar nuestro objetivo. Comencemos considerando una variable que sabemos definitivamente que tiene un fuerte potencial para predecir el objetivo: el precio de apertura.
from sklearn.feature_selection import mutual_info_regression
Ahora bien, como punto de referencia, este es un buen puntaje de información mutua (Mutual Information, MI) .
#MI Score for the Open price
print(f'Open price has MI score: {mutual_info_regression(market_data.loc[:,["Open"]],market_data.loc[:,"Target"])[0]}') Veamos ahora la puntuación MI para los cambios en el precio en el marco temporal M5 con respecto al precio futuro en el marco temporal M1.
#MI Score for the M5 change in price
print(f'M5 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M5"]],market_data.loc[:,"Target"])[0]}') Nuestra puntuación MI es considerablemente menor, esto significa que es posible que no hayamos expuesto la relación de manera significativa, o tal vez no haya dependencia entre los niveles de precios en diferentes marcos temporales.
#MI Score for the M15 change in price
print(f'M15 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M15"]],market_data.loc[:,"Target"])[0]}') Lo mismo ocurre con el resto de los períodos de tiempo que hemos seleccionado.
Modelando la relación
Definamos nuestros predictores y objetivos.
#Let's define our predictors and our target ohlc_predictors = [ "Open", "High", "Low", "Close" ] time_frame_predictors = [ "M5", "M15", "M30", "H1", "D1" ] all_predictors = ohlc_predictors + time_frame_predictors target = "Target"
Now we import the libraries we need.
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import SGDRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit,RandomizedSearchCV from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
Defina los parámetros para nuestro objeto de división de series de tiempo.
#Define the time series split object gap = look_ahead splits = 10
Ahora preparemos nuestros modelos y también creemos marcos de datos para almacenar nuestros niveles de precisión. De esta manera, podemos observar el cambio en la precisión a medida que cambiamos las entradas de nuestro modelo.
#Store our models in a list models = [ LinearRegression(), SGDRegressor(), RandomForestRegressor(), BaggingRegressor(), GradientBoostingRegressor(), AdaBoostRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), MLPRegressor(hidden_layer_sizes=(100,20),early_stopping=True) ] #Create a list of column titles for each model columns = [ "Linear Regression", "SGD Regressor", "Random Forest Regressor", "Bagging Regressor", "Gradient Boosting Regressor", "AdaBoost Regressor", "K Neighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neurla Network" ] #Create data frames to store our accuracy ohlc_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) multiple_time_frame_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) all_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns)
Ahora preparemos los predictores y escalemos nuestros datos.
#Preparing to perform cross validation
current_predictors = all_predictors
scaled_data = pd.DataFrame(RobustScaler().fit_transform(market_data.loc[:,all_predictors]),columns=all_predictors)
Crear el objeto de división de series de tiempo.
#Create the time series split object
tscv = TimeSeriesSplit(gap=gap,n_splits=splits)
Ahora realizaremos la validación cruzada. El primer bucle itera sobre la lista de modelos que creamos anteriormente y el segundo bucle valida de forma cruzada cada modelo por turno.
#First we will iterate over all the available models for i in np.arange(0,len(models)): #First select the model model = models[i] #Now we will cross validate this current model for j , (train,test) in enumerate(tscv.split(scaled_data)): #First define the train and test data train_X = scaled_data.loc[train[0]:train[-1],current_predictors] train_y = market_data.loc[train[0]:train[-1],target] test_X = scaled_data.loc[test[0]:test[-1],current_predictors] test_y = market_data.loc[test[0]:test[-1],target] #Now we will fit the model model.fit(train_X,train_y) #And finally record the accuracy all_accuracy.iloc[j,i] = root_mean_squared_error(test_y,model.predict(test_X))
Nuestros niveles de precisión al utilizar entradas ordinarias para nuestro modelo.
ohlc_accuracy
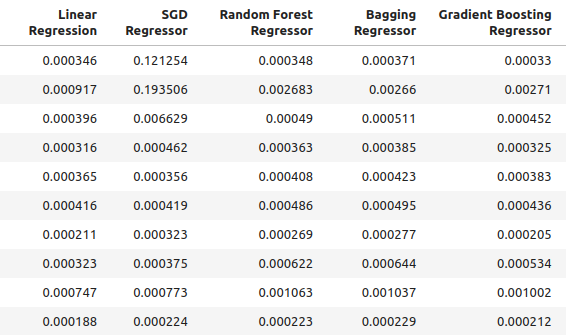
Figura 2: Nuestros niveles normales de precisión.
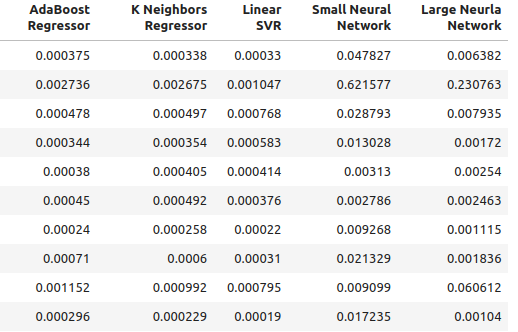
Figura 3: Nuestros niveles normales de precisión II.
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {ohlc_accuracy.iloc[:,i].mean()}")
La regresión lineal tuvo niveles de error de 0,00042256332959154886
El regresor SGD tuvo niveles de error de 0,0324320107406244
El regresor Random Forest tuvo niveles de error de 0,0006954883552094012
El regresor Bagging tuvo niveles de error de 0,0007030697054783931
El regresor Gradient Boosting tuvo niveles de error de 0,0006588749449742309
El regresor AdaBoost tuvo niveles de error de 0,0007159624774453208
K Neighbors Regressor tuvo niveles de error de 0,0006839218661791973
El SVR lineal tuvo niveles de error de 0,000503277800807813
La red neuronal pequeña tuvo niveles de error de 0,07740701832606754
La red neuronal grande tuvo niveles de error de 0,03164056895135391
Nuestra precisión al utilizar las nuevas entradas que hemos creado.
multiple_time_frame_accuracy
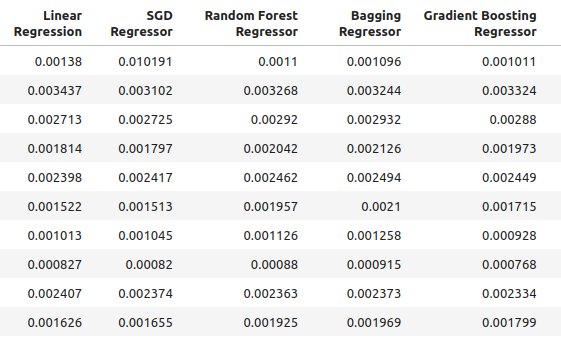
Figura 4: Nuestros nuevos niveles de precisión
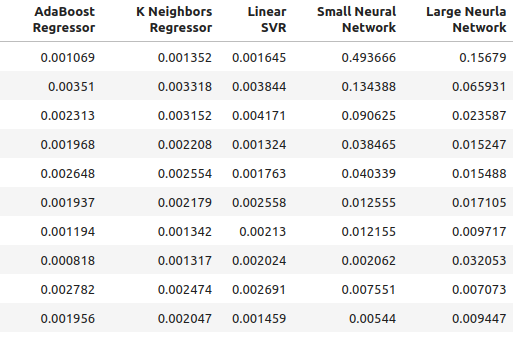
Figura 5: Nuestros nuevos niveles de precisión II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {multiple_time_frame_accuracy.iloc[:,i].mean()}")
La regresión lineal tuvo niveles de error de 0,001913639795583766
El regresor SGD tuvo niveles de error de 0,0027638553835377206
El regresor Random Forest tuvo niveles de error de 0,0020041047670504254
El regresor Bagging tuvo niveles de error de 0,0020506512726394415
El regresor Gradient Boosting tuvo niveles de error de 0,0019180687958290775
El regresor AdaBoost tuvo niveles de error de 0,0020194136735787625
K Neighbors Regressor tuvo niveles de error de 0,0021943350208868213
El SVR lineal tuvo niveles de error de 0,0023609474919917338
La red neuronal pequeña tuvo niveles de error de 0,08372469596701271
La red neuronal grande tuvo niveles de error de 0,035243897461061074
Por último, observemos nuestra precisión al utilizar todos los predictores disponibles.
all_accuracy
Figura 6: Nuestros niveles de precisión al utilizar todos los predictores de que disponemos.
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {all_accuracy.iloc[:,i].mean()}")
La regresión lineal tuvo niveles de error de 0,00048307488099524497
El regresor SGD tuvo niveles de error de 0,043019079499194125
El regresor de Random Forest tuvo niveles de error de 0,0007196920919204373
El regresor Bagging tuvo niveles de error de 0,0007263444909545053
El regresor Gradient Boosting tuvo niveles de error de 0,0006943964783049555
El regresor AdaBoost tuvo niveles de error de 0,0007217149661087063
K Neighbors Regressor tuvo niveles de error de 0,000872811528292862
El SVR lineal tuvo niveles de error de 0,0006457525216512596
La red neuronal pequeña tuvo niveles de error de 0,14002618062102
La red neuronal grande tuvo niveles de error de 0,06774795252887988
Como se puede ver, el modelo lineal fue el que obtuvo mejores resultados en todas las pruebas. Además, funcionó mejor cuando se utilizaron datos OHLC ordinarios. Sin embargo, el modelo no tiene parámetros de ajuste que sean de interés para nosotros. Por lo tanto, seleccionaremos el segundo mejor modelo, el Gradient Boosting Regressor (GBR), e intentaremos superar al modelo lineal.
Selección de funciones
Veamos ahora qué características fueron las más importantes para nuestro modelo GBR.
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS
Seleccione el modelo.
#We'll select the Gradient Boosting Regressor as our chosen model model = GradientBoostingRegressor()
Vamos a utilizar el algoritmo de selección hacia atrás. Comenzaremos con un modelo que contiene todos los predictores y eliminaremos características continuamente una por una. Solo se eliminará una característica si su resultado es un mejor rendimiento del modelo.
#Let us prepare the Feature Selector Object sfs = SFS(model, k_features=(1,len(all_predictors)), forward=False, n_jobs=-1, scoring="neg_root_mean_squared_error", cv=10 )
Realizar selección de características.
#Select the best feature sfs_results = sfs.fit(scaled_data.loc[:,all_predictors],market_data.loc[:,"Target"])
El algoritmo solo mantuvo el precio alto y descartó todas las demás características.
#The best feature we found
sfs_results.k_feature_names_
Visualicemos nuestros resultados.
#Prepare the plot fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev") plt.title("Backward Selection on Gradient Boosting Regressor") plt.grid()
Figura 7: Visualización del proceso de selección de características.
Como se puede ver, el tamaño de nuestro modelo y los niveles de error eran directamente proporcionales. O en otras palabras, a medida que nuestro modelo se hizo más grande, también lo hicieron nuestros niveles de error.
Ajuste de parámetros
Ahora realizaremos el ajuste de parámetros en nuestro modelo GBR. Hemos identificado 11 parámetros del modelo que vale la pena ajustar y permitiremos 1000 iteraciones del objeto de ajuste antes de finalizar el proceso de optimización.
#Let us try to tune our model
from sklearn.model_selection import RandomizedSearchCV
Antes de comenzar a ajustar nuestro modelo, dividamos nuestros datos en dos. La mitad se utilizará para entrenar y optimizar nuestro modelo, la otra mitad se utilizará para la validación y para probar si hay sobreajuste.
#Before we try to tune our model, let's first create a train and test set train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = market_data.loc[:(market_data.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = market_data.loc[(market_data.shape[0]//2):,"Target"]
Definir el objeto de ajuste.
#Time the process import time start_time = time.time() #Prepare the tuning object tuner = RandomizedSearchCV(GradientBoostingRegressor(), { "loss": ["squared_error","absolute_error","huber"], "learning_rate": [0,(10.0 ** -1),(10.0 ** -2),(10.0 ** -3),(10.0 ** -4),(10.0 ** -5),(10.0 ** -6),(10.0 ** -7)], "n_estimators": [5,10,25,50,100,200,500,1000], "max_depth": [1,2,3,5,9,10], "min_samples_split":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0], "criterion":["friedman_mse","squared_error"], "min_samples_leaf":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9], "min_weight_fraction_leaf":[0.0,0.1,0.2,0.3,0.4,0.5], "max_features":[1,2,3,4,5,20], "max_leaf_nodes": [2,3,4,5,10,20,50,90,None], "min_impurity_decrease": [0,1,10,(10.0 ** 2),(10.0 ** 3),(10.0 ** 4)] }, cv=5, n_iter=1000, return_train_score=False, scoring="neg_mean_squared_error" )
Ajuste del modelo GBR.
#Tune the GradientBoostingRegressor tuner.fit(train_X,train_y) end_time = time.time() print(f"Process completed in {end_time - start_time} seconds.")
Veamos los resultados en orden de mejor a peor.
#Let's observe the results tuner_results = pd.DataFrame(tuner.cv_results_) params = ["param_loss", "param_learning_rate", "param_n_estimators", "param_max_depth", "param_min_samples_split", "param_criterion", "param_min_samples_leaf", "param_max_features", "param_max_leaf_nodes", "param_min_impurity_decrease", "param_min_weight_fraction_leaf", "mean_test_score"] tuner_results.loc[:,params].sort_values(by="mean_test_score",ascending=False)
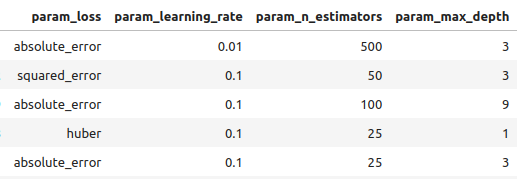
Figura 8: Algunos de nuestros mejores resultados.
Figura 9: Algunos de nuestros mejores resultados II.
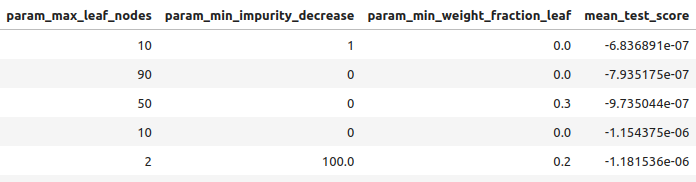
Figura 10: Algunos de nuestros mejores resultados III.
Los mejores parámetros que encontramos.
#Best parameters we found
tuner.best_params {'n_estimators': 500,
'min_weight_fraction_leaf': 0.0,
'min_samples_split': 0.4,
'min_samples_leaf': 0.1,
'min_impurity_decrease': 1,
'max_leaf_nodes': 10,
'max_features': 2,
'max_depth': 3,
'loss': 'absolute_error',
'learning_rate': 0.01,
'criterion': 'friedman_mse'}
Ajuste más profundo de parámetros
Figura 11: Logotipo de SciPy.
SciPy es una biblioteca de Python utilizada para cálculos científicos. SciPy significa Python científico. Veamos si podemos encontrar parámetros aún mejores. Utilizaremos la biblioteca de optimización SciPy para intentar encontrar parámetros que mejoren el rendimiento de nuestro modelo.
#Let's see if we can't find better parameters #We may be overfitting the training data! from scipy.optimize import minimize
Para utilizar la biblioteca de optimización SciPy, necesitamos definir una función objetivo. Nuestra función objetivo será el promedio de los niveles de error validados de forma cruzada que nuestro modelo alcanza en el conjunto de entrenamiento. Nuestro optimizador SciPy buscará coeficientes que reduzcan nuestro error de entrenamiento.
#Define the objective function def objective(x): #Create a dataframe to store our new accuracy current_error = pd.DataFrame(index=[0],columns=["error"]) #x is an array of possible values to use for our Gradient Boosting Regressor model = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=x[0], min_samples_split=x[1], min_samples_leaf=x[2], learning_rate=x[3]) model.fit(train_X.loc[:,:],train_y.loc[:]) current_error.iloc[0,0] = root_mean_squared_error(train_y.loc[:],model.predict(train_X.loc[:,:])) #Record our progress mean_error = current_error.loc[:].mean() #Return the average error return mean_error
Ahora comencemos el proceso de optimización. Tenga en cuenta que algunos parámetros en el modelo GBR no permiten valores negativos y nuestro optimizador SciPy pasará valores negativos a menos que especifiquemos límites para el optimizador. Además, el optimizador espera que le demos un punto de partida. Utilizaremos el punto final del algoritmo de optimización anterior como punto de partida para este.
#Let's optimize these parameters again #Fist define the bounds bounds = ((0.0,0.5),(0.3,0.5),(0.001,0.2),(0.001,0.1)) #Then define the starting points for the L-BFGS-B algorithm pt = np.array([tuner.best_params_["min_weight_fraction_leaf"], tuner.best_params_["min_samples_split"], tuner.best_params_["min_samples_leaf"], tuner.best_params_["learning_rate"] ])
Minimizar el error de entrenamiento.
lbfgs = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
Veamos los resultados.
lbfgs
success: True
status: 0
fun: 0.0005766670348377334
x: [ 5.586e-06 4.000e-01 1.000e-01 1.000e-02]
nit: 3
jac: [-6.216e+00 -4.871e+02 -2.479e+02 8.882e+01]
nfev: 180
njev: 36
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
Prueba de sobreajuste
Comparemos ahora la precisión de nuestros dos modelos personalizados con el modelo GBR predeterminado. Además, también prestaremos atención para ver si superamos el modelo lineal.
#Let us now see how well we're performing on the validation set linear_regression = LinearRegression() default_gbr = GradientBoostingRegressor() grid_search_gbr = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=0, min_samples_split=0.4, min_samples_leaf=0.1, learning_rate=0.01 ) lbfgs_grid_search_gbr = GradientBoostingRegressor( n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=lbfgs.x[0], min_samples_split=lbfgs.x[1], min_samples_leaf=lbfgs.x[2], learning_rate=lbfgs.x[3] )Nuestra precisión con el modelo lineal.
#Linear Regression
linear_regression.fit(train_X,train_y)
root_mean_squared_error(test_y,linear_regression.predict(test_X)) Nuestra precisión con el modelo GBR predeterminado.
#Default Gradient Boosting Regressor
default_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,default_gbr.predict(test_X)) Nuestra precisión con el modelo GBR personalizado mediante búsqueda aleatoria.
#Random Search Gradient Boosting Regressor
grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,grid_search_gbr.predict(test_X)) Nuestra precisión al utilizar el modelo GBR personalizado por búsqueda aleatoria y L-BFGS-B.
#L-BFGS-B Random Search Gradient Boosting Regressor
lbfgs_grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,lbfgs_grid_search_gbr.predict(test_X))
Como podemos ver, no logramos superar el modelo lineal. Además, no logramos superar el modelo GBR predeterminado. Por lo tanto, continuaremos con el modelo GBR predeterminado a modo de demostración. Sin embargo, tenga en cuenta que seleccionar el modelo lineal nos habría dado más precisión.
Exportar a ONNX
Open Neural Network Exchange (ONNX) es un protocolo que nos permite representar modelos de aprendizaje automático como un gráfico computacional de nodos y aristas. Donde los nodos representan operaciones matemáticas y las aristas representan el flujo de datos. Al exportar nuestro modelo de aprendizaje automático al formato ONNX, podremos utilizar nuestros modelos de IA dentro de nuestro Asesor Experto con facilidad.
Preparémonos para exportar nuestro modelo ONNX.
#We failed to beat the linear regression model, in such cases we should pick the linear model! #However for demonstrational purposes we'll pick the gradient boosting regressor #Let's export the default GBR to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnx
Ahora necesitamos escalar nuestros datos de manera que podamos reproducirlos en MetaTrader 5. La transformación más fácil es simplemente restar la media y dividir por la desviación estándar.
#We need to save the scale factors for our inputs scale_factors = pd.DataFrame(index=["mean","standard deviation"],columns=all_predictors) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = market_data.iloc[:,i+2].mean() scale_factors.iloc[1,i] = market_data.iloc[:,i+2].std() market_data.iloc[:,i+2] = ((market_data.iloc[:,i+2] - market_data.iloc[:,i+2].mean()) / market_data.iloc[:,i+2].std()) scale_factors
Figura 12: Nuestros factores de escala.
Definir los tipos de entrada para nuestro modelo ONNX.
#Define our initial types initial_types = [("float_input",FloatTensorType([1,test_X.shape[1]]))]
Ajustando el modelo a todos los datos que tenemos.
#Fit the model on all the data we have model = GradientBoostingRegressor().fit(market_data.loc[:,all_predictors],market_data.loc[:,"Target"])
Crear la representación ONNX.
#Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
Guarde el modelo ONNX.
#Now save the ONNX model onnx_model_name = "GBR_M1_MultipleTF_Float.onnx" onnx.save(onnx_model,onnx_model_name)
Visualizando el modelo
Netron es un visualizador de código abierto para inspeccionar modelos de aprendizaje automático. Actualmente, Netron ofrece soporte para un número limitado de frameworks. Sin embargo, a medida que pase el tiempo y la biblioteca madure, el soporte se ampliará a diferentes marcos de aprendizaje automático.
Importamos las librerías que necesitamos.
#Import netron so we can visualize the model
import netron
Lanzar Netron.
netron.start(onnx_model_name)
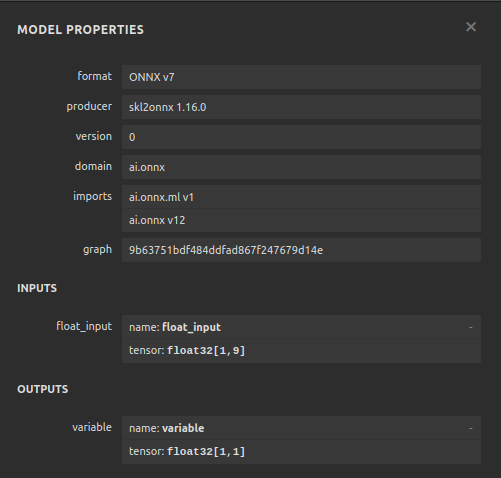
Figura 13: Propiedades de nuestro modelo Gradient Boosting Regressor (GBR) en ONNX.
\
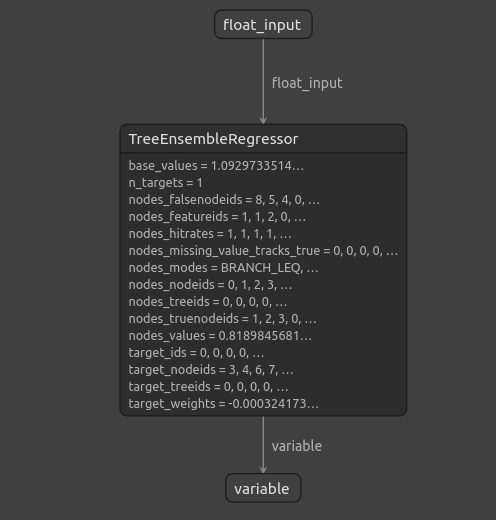
Figura 14: La estructura de nuestro Gradient Boosting Regressor (GBR).
Como podemos ver, la forma de entrada y salida de nuestro modelo ONNX está donde esperamos que esté, esto nos da confianza para continuar y construir un Asesor Experto sobre nuestro modelo ONNX.
Implementación en MQL5
Para comenzar a construir nuestro Asesor Experto con un módulo de IA integrado, primero debemos requerir el modelo ONNX.//+------------------------------------------------------------------+ //| Multiple Time Frame.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the onnx file | //+------------------------------------------------------------------+ #resource "\\Files\\GBR_M1_MultipleTF_Float.onnx" as const uchar onnx_model_buffer[];
Ahora cargaremos la biblioteca comercial.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Definamos las entradas que nuestro usuario final puede cambiar.
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input double max_risk = 20; //How much profit/loss should we allow before closing input double sl_width = 1; //How wide should out sl be?
Ahora definiremos las variables globales que se utilizarán en todo nuestro programa.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_variance[9],std_variance[9]; //Our scaling factors vector model_forecast = vector::Zeros(1); //Model forecast vector model_inputs = vector::Zeros(9); //Model inputs double ask,bid; //Market prices double trading_volume; //Our trading volume int lot_multiple = 20; //Our lot size int state = 0; //System state
Definamos funciones de ayuda que utilizaremos a lo largo de nuestro programa. En primer lugar, necesitamos una función para detectar retrocesos y alertar al usuario final sobre el peligro que se avecina y que nuestro sistema de IA ha predicho. Si nuestro sistema de IA detecta una reversión, cerraremos las posiciones abiertas que tengamos en ese mercado.
//+------------------------------------------------------------------+ //| Check reversal | //+------------------------------------------------------------------+ void check_reversal(void) { //--- Check for reversal if(((state == 1) && (model_forecast[0] < iClose(Symbol(),PERIOD_M1,0))) || ((state == 2) && (model_forecast[0] > iClose(Symbol(),PERIOD_M1,0)))) { Alert("Reversal predicted."); Trade.PositionClose(Symbol()); } //--- Check if we have breached our maximum risk levels if(MathAbs(PositionGetDouble(POSITION_PROFIT) > max_risk)) { Alert("We've breached our maximum risk level."); Trade.PositionClose(Symbol()); } }
Ahora definiremos una función para encontrar oportunidades de entrada al mercado. Solo consideraremos que una entrada es válida si tenemos confirmación de plazos superiores con respecto al traslado. En este Asesor Experto, queremos que nuestras operaciones se alineen con la acción del precio en el gráfico semanal.
//+------------------------------------------------------------------+ //| Find an entry | //+------------------------------------------------------------------+ void find_entry(void) { //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bullish momentum if(model_forecast[0] > iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a buy Trade.Buy(trading_volume,Symbol(),ask,(ask - sl_width),(ask + sl_width),"Multiple Time Frames AI"); state = 1; } } //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bearish momentum if(model_forecast[0] < iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a sell Trade.Sell(trading_volume,Symbol(),bid,(bid + sl_width),(bid - sl_width),"Multiple Time Frames AI"); state = 2; } } }
También necesitamos una función para obtener los precios actuales del mercado.
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); }
Nuestro modelo ONNX no se puede utilizar a menos que estandaricemos y normalicemos las entradas, esta función obtendrá los factores de escala que usamos al entrenar nuestro modelo ONNX.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ void load_scaling_factors(void) { //--- EURUSD OHLC mean_variance[0] = 1.0930010861272836; std_variance[0] = 0.0017987600829890852; mean_variance[1] = 1.0930721822927123; std_variance[1] = 0.001810556238082839; mean_variance[2] = 1.092928371812889; std_variance[2] = 0.001785041172362313; mean_variance[3] = 1.093000590242923; std_variance[3] = 0.0017979420556511476; //--- M5 Change mean_variance[4] = (MathPow(10.0,-5) * 1.4886568962056413); std_variance[4] = 0.000994902152654042; //--- M15 Change mean_variance[5] = (MathPow(10.0,-5) * 1.972093957036524); std_variance[5] = 0.0017104874192072138; //--- M30 Change mean_variance[6] = (MathPow(10.0,-5) * 1.5089339490060967); std_variance[6] = 0.002436078407827825; //--- H1 Change mean_variance[7] = 0.0001529512146155358; std_variance[7] = 0.0037675774501395387; //--- D1 Change mean_variance[8] = -0.0008775667536639223; std_variance[8] = 0.03172437243836734; }
Al definir la función responsable de obtener predicciones de nuestro modelo, tenga en cuenta que estamos escalando las entradas antes de pasarlas a nuestro modelo ONNX. Las predicciones se obtienen del modelo utilizando el comando OnnxRun.
//+------------------------------------------------------------------+ //| Model predict | //+------------------------------------------------------------------+ void model_predict(void) { //--- EURD OHLC model_inputs[0] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[0]) / std_variance[0]); model_inputs[1] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[1]) / std_variance[1]); model_inputs[2] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[2]) / std_variance[2]); model_inputs[3] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[3]) / std_variance[3]); //--- M5 CAHNGE model_inputs[4] = (((iClose(Symbol(),PERIOD_M5,0) - iClose(Symbol(),PERIOD_M5,20)) - mean_variance[4]) / std_variance[4]); //--- M15 CHANGE model_inputs[5] = (((iClose(Symbol(),PERIOD_M15,0) - iClose(Symbol(),PERIOD_M15,20)) - mean_variance[5]) / std_variance[5]); //--- M30 CHANGE model_inputs[6] = (((iClose(Symbol(),PERIOD_M30,0) - iClose(Symbol(),PERIOD_M30,20)) - mean_variance[6]) / std_variance[6]); //--- H1 CHANGE model_inputs[7] = (((iClose(Symbol(),PERIOD_H1,0) - iClose(Symbol(),PERIOD_H1,20)) - mean_variance[7]) / std_variance[7]); //--- D1 CHANGE model_inputs[8] = (((iClose(Symbol(),PERIOD_D1,0) - iClose(Symbol(),PERIOD_D1,20)) - mean_variance[8]) / std_variance[8]); //--- Fetch forecast OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
Ahora definiremos una función para cargar nuestro modelo ONNX y definir la forma de entrada y salida.
//+------------------------------------------------------------------+ //| Load our onnx file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- Set the input shape ulong input_shape [] = {1,9}; //--- Check if the input shape is valid if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model)); return(false); } //--- Set the output shape ulong output_shape [] = {1,1}; //--- Check if the output shape is valid if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
Ahora podemos definir el procedimiento de inicialización del programa. Nuestro experto cargará el archivo ONNX, cargará los factores de escala y obtendrá los datos del mercado.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX file if(!load_onnx_file()) { //--- We failed to load our onnx model return(INIT_FAILED); } //--- Load scaling factors load_scaling_factors(); //--- Get trading volume trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
Cada vez que nuestro programa no esté en uso, liberaremos los recursos que ya no necesitemos. Lanzaremos el modelo ONNX y eliminaremos el asesor experto del gráfico.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Release the expert advisor ExpertRemove(); }
Siempre que se ofrezcan nuevos precios, primero obtendremos una predicción de nuestro modelo y luego actualizaremos nuestros precios de mercado. Si no tenemos ninguna posición abierta, intentaremos encontrar una entrada. De lo contrario, si tenemos una posición que necesita ser gestionada, estaremos atentos a una posible reversión.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a prediction from our model model_predict(); //--- Show the model forecast Comment("Model forecast ",model_forecast); //--- Fetch market prices update_market_prices(); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find entry find_entry(); //--- Update state state = 0; } //--- If we have an open position, manage it else { //--- Check if our AI is predicting a reversal check_reversal(); } }
Ahora podemos ver nuestra aplicación en acción.
Figura 15: Nuestra interfaz de asesor experto.
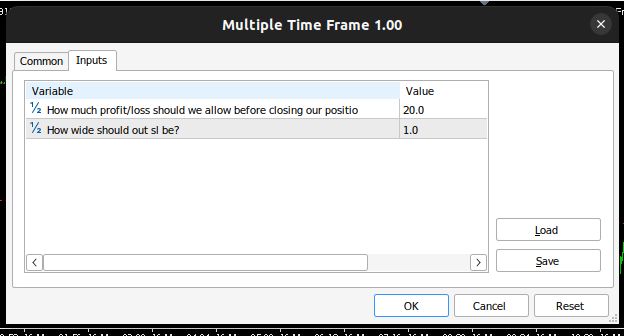
Figura 16: Nuestras entradas en el asesor experto.
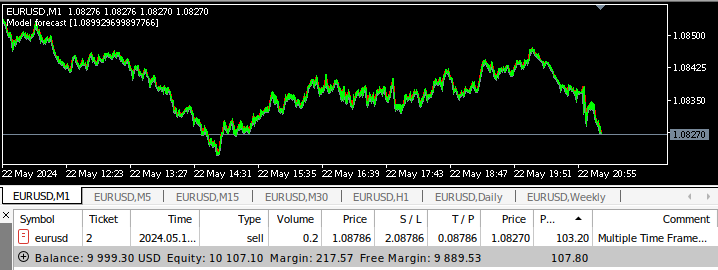
Figura 17: Asesor experto de múltiples marcos temporales en retrospectiva.
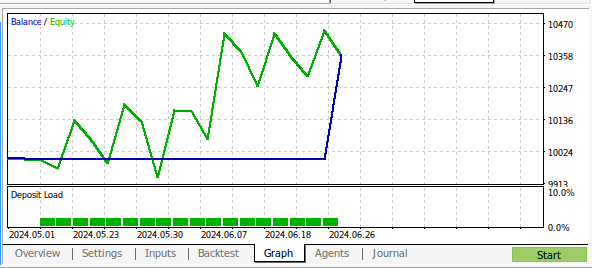
Figura 18: Resultados de las pruebas retrospectivas de nuestro programa con un mes de datos en M1.
Conclusión
En este artículo, hemos demostrado que es posible construir un Asesor Experto potenciado por IA que analiza múltiples marcos temporales. Aunque obtuvimos niveles de precisión más altos utilizando datos OHLC ordinarios, hay muchas opciones diferentes que no examinamos, por ejemplo, no añadimos ningún indicador en marcos temporales más altos. Hay muchas maneras en que podemos aplicar la IA en nuestra estrategia de negociación, esperemos que ahora tenga nuevas ideas de las capacidades que esperan ser aprovechadas en su instalación de MetaTrader 5.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15610
Gestión de Riesgo (parte 3): Construyendo la Clase Principal para la Gestión de Riesgo
Redes neuronales en el trading: Resultados prácticos del método TEMPO
Algoritmo de colmena artificial — Artificial Bee Hive Algorithm (ABHA): Teoría y métodos
Reimaginando las estrategias clásicas (Parte V): Análisis de múltiples símbolos en USDZAR
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso