Redes neuronales en el trading: Modelos "ligeros" de pronóstico de series temporales
343
0
Introducción
La predicción de los próximos movimientos de precios resulta fundamental para desarrollar una estrategia comercial. Para conseguir predicciones precisas generalmente se requiere el uso de modelos de aprendizaje profundo potentes y complejos.
La base para una previsión precisa de series temporales a largo plazo reside en la periodicidad y la tendencia inherentes de los datos. Además, desde hace tiempo se viene observando que el movimiento de precios de los pares de divisas está estrechamente relacionado con las sesiones comerciales individuales. Por ejemplo, si discretizamos una serie temporal de secuencias diarias en un momento particular del día, cada subsecuencia exhibirá tendencias similares o consistentes. En este caso, la periodicidad y la tendencia de la secuencia original se descompone y transforma. Es decir, los patrones periódicos se transforman en dinámicas de inter-subsecuencias, mientras que los patrones de tendencia se reinterpretan como características de intra-subsecuencias. Esta descomposición abre nuevas perspectivas en el desarrollo de modelos ligeros para la previsión de series temporales a largo plazo, a las que prestaron atención los autores del artículo "SparseTSF: Modeling Long-term Time Series Forecasting with 1k Parameters".
En su artículo, son quizás los primeros en explorar cómo explotar esta periodicidad y descomposición en los datos para construir modelos especializados y ligeros de pronóstico de series temporales. Esto les permite proponer el algoritmo SparseTSF, un modelo extremadamente ligero para la previsión de series temporales a largo plazo.
Técnicamente, proponen un método de pronóstico disperso entre periodos. En primer lugar, los datos de origen se dividen en secuencias con periodicidad constante. Luego se realiza una predicción para cada subsecuencia con discretización reducida. De esta forma, el problema original de pronóstico de series temporales se reduce al problema de pronosticar la tendencia interperiodo.
Este enfoque posee dos ventajas:
- La separación eficiente de la periodicidad y la tendencia de los datos, que permite que el modelo identifique y extraiga de manera estable características periódicas mientras se centra en predecir cambios de tendencia;
- La compresión extrema del tamaño de los parámetros del modelo, que reduce significativamente la necesidad de recursos computacionales.
1. Algoritmo SparseSTF
El problema del pronóstico de series temporales a largo plazo (Long-term Time Series Forecasting — LTSF) consiste en pronosticar valores futuros durante un horizonte extendido utilizando datos de series temporales multidimensionales observados previamente. El objetivo principal del LTSF es ampliar el horizonte de planificación H, ya que ofrece recomendaciones más ricas y avanzadas para la aplicación práctica. Sin embargo, ampliar el horizonte de planificación a menudo produce un aumento de la complejidad del modelo entrenado. Para abordar este problema, los autores del método SparseTSF se han centrado en desarrollar modelos que no solo sean extremadamente ligeros, sino también robustos y eficientes.
Los avances recientes en LTSF han llevado a un cambio hacia enfoques de pronóstico de canal independiente al trabajar con datos de series temporales multidimensionales. Esta estrategia simplifica el proceso de pronóstico al centrarse en series temporales unidimensionales individuales en el conjunto de datos, lo cual reduce la complejidad de considerar las relaciones entre canales. Como resultado, el objetivo principal de los modelos modernos dominantes ha cambiado en los últimos años hacia la previsión efectiva usando el modelado de dependencias de largo plazo, incluidas periodicidades y tendencias, en secuencias unidimensionales.
Como los datos pronosticados a menudo exhiben una periodicidad persistente a priori, los autores del método SparseTSF proponen utilizar pronósticos dispersos entre periodos para mejorar la extracción de dependencias seriales de largo plazo y, al mismo tiempo, reducir la escala de los parámetros del modelo. La solución propuesta usa una capa lineal para modelar la tarea de LTSF.
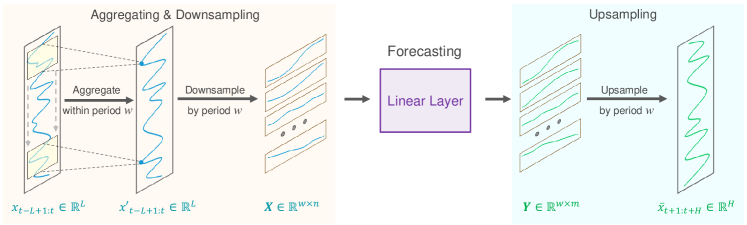
Se supone que la serie temporal X t de longitud L tiene una periodicidad conocida w. El primer paso del algoritmo propuesto será reducir la resolución de la secuencia original en w subsecuencias de longitud n (n = L/w). Luego se aplicará un modelo de predicción con parámetros comunes a estas subsecuencias. Como resultado de esta operación, obtendremos w subsecuencias predichas, cada una de las cuales tiene una longitud m (m=H/w), que forman la secuencia predicha completa de longitud H.
Intuitivamente, este proceso de pronóstico parece un pronóstico continuo con un intervalo disperso w, realizado por una capa completamente conectada de intercambio de parámetros durante un periodo de tiempo constante w. Esto puede verse como un modelo que realiza pronósticos móviles dispersos a lo largo de los periodos.
Técnicamente, el proceso de reducción de discretización es equivalente a cambiar la forma del tensor de datos original X t a una matriz n*w, seguida de su transposición a w*n. Predecir la trayectoria subsiguiente con deslizamiento disperso es equivalente a aplicar una capa lineal de tamaño n*m a la última dimensionalidad de la matriz. El resultado de esta operación será una matriz w*m.
Durante la discretización ascendente, realizamos las operaciones inversas: transponemos la matriz w*m y luego la reformateamos en una secuencia predicha completa de longitud H.
No obstante, el enfoque propuesto enfrenta dos problemas:
- La pérdida de información, porque solo se utiliza un punto de datos por periodo para pronosticar y el resto se ignoran;
- La mejora de la influencia de los valores atípicos, ya que la presencia de valores extremos en las subsecuencias con discretización reducida puede influir directamente en la predicción.
Para abordar estos problemas, los autores del método SparseTSF introducen la agregación deslizante de la secuencia original antes de realizar una predicción dispersa. Cada punto de datos agregado incorpora información de otros puntos durante el periodo circundante, resolviendo así el primer problema. Además, como el valor agregado es esencialmente un promedio ponderado de los puntos circundantes, este mitiga el impacto de los valores atípicos, resolviendo así el segundo problema.
Técnicamente, esta agregación continua de datos se puede implementar usando una capa convolucional de rellenado con ceros.
Con frecuencia, los datos de series temporales muestran cambios en la distribución entre los conjuntos de datos de entrenamiento y de prueba. El uso de estrategias simples de normalización de muestras entre los datos de origen y la secuencia prevista puede ayudar a mitigar este problema. El algoritmo SparseTSF usa una estrategia de normalización sencilla. En particular, el valor medio de una secuencia se resta de los datos de origen antes de introducirlos en el modelo. Y luego se vuelve a sumar a los resultados obtenidos.
A continuación le presentamos la visualización del autor del método SparseTSF.
2. Implementación con MQL5
Tras revisar los aspectos teóricos del método SparseTSF, podemos proceder a implementar los enfoques propuestos utilizando MQL5. Para ello, crearemos una nueva clase CNeuronSparseTSF dentro de nuestra biblioteca.
2.1 Creando la clase SparseTSF
Nuestra nueva clase heredará la funcionalidad principal de la clase básica de la capa completamente conectada CNeuronBaseOCL. A continuación mostramos la estructura de la clase CNeuronSparseTSF.
class CNeuronSparseTSF : public CNeuronBaseOCL { protected: CNeuronConvOCL cConvolution; CNeuronTransposeOCL acTranspose[4]; CNeuronConvOCL cForecast; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSparseTSF(void) {}; ~CNeuronSparseTSF(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSparseTSF; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
En la estructura de la nueva clase añadiremos 2 capas convolucionales. Una de ellas realiza la función de agregación de datos, mientras que la segunda predice las secuencias posteriores. Además, usaremos toda una serie de transposiciones para reformatear los datos. Todos los objetos internos agregados se declararán estáticamente, lo cual permitirá dejar el constructor y el destructor de la clase "vacíos", mientras que la inicialización directa del objeto de clase se realizará en el método Init.
En los parámetros del método de inicialización, transmitiremos los parámetros principales del objeto creado:
- sequence — longitud de la secuencia de los datos de origen;
- variables — número de parámetros analizados (secuencias unitarias en datos fuente multimodales);
- period — periodicidad de los datos iniciales;
- forecast — profundidad del pronóstico.
bool CNeuronSparseTSF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch ) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch)) return false;
En el cuerpo del método, como es habitual, llamaremos al método homónimo de la clase padre, en el que ya está construido el proceso de inicialización de objetos y variables heredados.
Tenga en cuenta que al llamar al método de inicialización de la clase principal, especificaremos un tamaño de capa igual al producto de la profundidad de predicción y el número de secuencias unitarias en los datos multimodales.
Tras inicializar con éxito los objetos y variables heredados, pasaremos a la etapa de inicialización de los objetos internos agregados. Los inicializaremos en la secuencia de realización de la pasada directa. Y aquí, como dicen, "tenga cuidado con lo que hace", en nuestro caso, con la dimensionalidad del tensor de datos procesados.
En la entrada de la capa, esperamos recibir un tensor de datos de origen de dimensionalidad L*v, donde L será la longitud de la secuencia de datos de origen, mientras que v será el número de series unitarias en los datos de origen multimodales. Como hemos mencionado en la primera parte de este artículo, el método SparseTSF funciona en el paradigma de predicción de secuencias unitarias independientes. Y para organizar dicho proceso, transpondremos la matriz de los datos de origen a v*L.
if(!acTranspose[0].Init(0, 0, OpenCL, sequence, variables, optimization, iBatch)) return false;
A continuación, planeamos agregar los datos de origen usando una capa convolucional. En esta operación realizaremos una convolución dentro de 2 periodos de los datos de origen con un paso de 1 periodo. Para preservar la dimensionalidad, el número de filtros de convolución será igual al tamaño del periodo.
if(!cConvolution.Init(0, 1, OpenCL, 2 * period, period, period, sequence / period, variables, optimization, iBatch)) return false; cConvolution.SetActivationFunction(None);
Tenga en cuenta que realizaremos la agregación de datos dentro de secuencias unitarias independientes.
El siguiente paso del algoritmo SparseTSF consistirá en discretizar los datos de origen. En esta etapa, los autores del método proponen cambiar la dimensionalidad y transponer el tensor de los datos de origen. En nuestro caso trabajaremos con búferes de datos unidimensionales. Y el cambio en la dimensionalidad de los datos de origen será de naturaleza declarativa: no provocará una reorganización de los datos en la memoria, lo cual no puede decirse de la transposición. A continuación, inicializaremos la siguiente capa de transposición de datos.
if(!acTranspose[1].Init(0, 2, OpenCL, variables * sequence / period, period, optimization, iBatch)) return false;
Usar una segunda capa de transposición de datos puede parecer un poco extraño, después de todo, a primera vista, realiza una operación que es la inversa de la transposición anterior de los datos de origen. Pero esto no es cierto en absoluto. No en vano nos hemos centrado en las dimensionalidades de los datos anteriores. El tamaño total de nuestro búfer de datos permanecerá sin cambios: L*v. Solo después de cambiar declarativamente la dimensionalidad de la matriz de datos podremos decir que su tamaño es igual a (v * L/w) * w, donde w será la periodicidad de los datos de origen. Y lo transpondremos a w * (L/w * v). Después de realizar dicha operación, nuestro búfer de datos mostrará una secuencia de etapas individuales de periodicidad de los datos de origen, considerando la independencia de la serie unitaria de los datos de origen.
Gráficamente, podemos representar el resultado de las 2 etapas de transposición de datos de la siguiente manera:
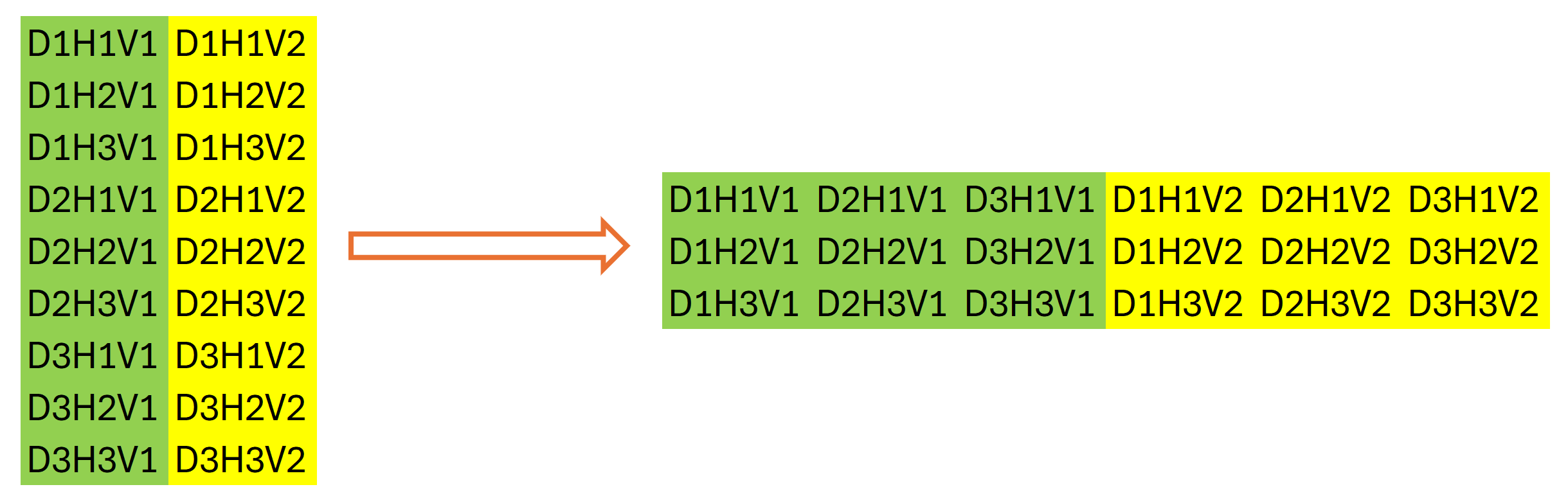
Luego usaremos una capa convolucional para predecir de forma independiente los pasos individuales dentro de la periodicidad de los datos de entrada para secuencias unitarias durante un horizonte de planificación determinado.
if(!cForecast.Init(0, 3, OpenCL, sequence / period, sequence / period, forecast / period, variables, period, optimization, iBatch)) return false; cForecast.SetActivationFunction(TANH);
Tenga en cuenta que el tamaño de la ventana de datos de origen analizados y su paso es igual a "sequence / period", mientras que el número de filtros de convolución es igual a "forecast / period". Esto nos permite obtener valores de pronóstico para todo el horizonte de planificación en una sola pasada. En este caso, usaremos filtros separados para cada paso del periodo de los datos analizados.
Como pretendemos trabajar con datos normalizados, usaremos la tangente hiperbólica como función de activación para los valores predichos. Esto nos permitirá limitar los resultados del pronóstico al rango [-1, 1].
A continuación, deberemos llevar los valores predichos a la secuencia requerida. Realizaremos esta operación usando 2 capas sucesivas de transposición de datos, que realizarán las operaciones de permutación inversa de los valores.
if(!acTranspose[2].Init(0, 4, OpenCL, period, variables * forecast / period, optimization, iBatch)) return false; if(!acTranspose[3].Init(0, 5, OpenCL, variables, forecast, optimization, iBatch)) return false;
Y para evitar el copiado innecesario de datos, organizaremos la sustitución de los búferes de resultados y los gradientes de error de la capa actual.
if(!SetOutput(acTranspose[3].getOutput()) || !SetGradient(acTranspose[3].getGradient()) ) return false; //--- return true; }
En cada iteración, comprobaremos los resultados de las operaciones. Y retornaremos el resultado lógico final de la operación del método al programa que ha realizado la llamada.
Tenga en cuenta que durante el proceso de inicialización del objeto no guardaremos los parámetros de arquitectura de la capa que se está creando. En este caso, solo necesitaremos transmitir los parámetros correspondientes a los objetos anidados. Su arquitectura definirá de forma única el funcionamiento de la clase, lo que hará innecesario el almacenamiento adicional de los parámetros obtenidos.
Tras inicializar el objeto de clase, procederemos a crear el método de pasada directa CNeuronSparseTSF::feedForward, en el cual construiremos el algoritmo del método SparseTSF con transferencia de datos entre objetos internos.
En los parámetros del método de pasada directa, recibiremos el puntero al objeto de la capa anterior, que contendrá los datos de origen.
bool CNeuronSparseTSF::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[0].FeedForward(NeuronOCL)) return false;
Y como recrearemos el algoritmo usando métodos previamente creados de objetos anidados, no organizaremos la verificación de la relevancia del puntero recibido. Simplemente lo transmitiremos al método de pasada directa de la primera capa de transposición de datos, en el que ya está organizada una comprobación similar junto con las operaciones de la funcionalidad principal de permutación de datos en el búfer de datos. Solo verificaremos el resultado lógico de la ejecución de las operaciones del método llamado.
A continuación, se realizará la agregación de datos llamando al método de pasada directa de la capa convolucional.
if(!cConvolution.FeedForward(acTranspose[0].AsObject())) return false;
Según el algoritmo del método SparseTSF, los datos agregados se sumarán con los datos de origen. No obstante, para mantener la consistencia de los datos, sumaremos la versión transpuesta de los datos de origen con los resultados de la agregación.
if(!SumAndNormilize(cConvolution.getOutput(), acTranspose[0].getOutput(), cConvolution.getOutput(), 1, false)) return false;
El siguiente paso consistirá en llamar al método de pasada directa de la siguiente capa de transposición de datos, que completará el proceso de discretización de la secuencia original.
if(!acTranspose[1].FeedForward(cConvolution.AsObject())) return false;
Después de ello, pronosticaremos la continuación más probable de la serie temporal analizada utilizando la segunda capa convolucional anidada.
if(!cForecast.FeedForward(acTranspose[1].AsObject())) return false;
Permítanme recordarles que la previsión de subsecuencias se realizará sobre la base del análisis de pasos individuales dentro de la periodicidad dada de los datos de origen. En este caso, realizaremos pronósticos independientes para cada secuencia unitaria de la serie temporal multimodal de los datos de origen. Y para cada paso del ciclo cerrado de periodicidad de datos de origen, se utilizarán sus propios parámetros de entrenamiento.
La reordenación de los valores previstos en el orden requerido de la secuencia de salida esperada se realizará utilizando dos capas posteriores de transposición de datos.
if(!acTranspose[2].FeedForward(cForecast.AsObject())) return false; if(!acTranspose[3].FeedForward(acTranspose[2].AsObject())) return false; //--- return true; }
Obviamente, para el paso del cambio de orden de los valores predichos en el búfer de datos, podríamos crear un nuevo kernel y reemplazarlo con una sola llamada a 2 capas de transposición de datos. Esto nos ofrecería cierta ganancia de rendimiento al eliminar la operación de transferencia de datos innecesaria. Pero dado el tamaño del modelo, se espera que la ganancia de rendimiento sea insignificante, por lo que en este experimento hemos decidido reducir el código del programa y el trabajo del programador.
Tenga en cuenta que las operaciones del método de pasada directa se completan ejecutando los métodos de pasada directa de los objetos anidados. En este caso, no transferiremos valores al búfer de resultados de la capa actual heredado de la clase principal. No obstante, las capas posteriores de nuestro modelo no tienen acceso a los objetos anidados y trabajan con los datos en el búfer de resultados de nuestra capa. Así que hemos compensado la interrupción visible en el flujo de datos reemplazando los búferes de resultados y los gradientes de error en la etapa de inicialización de nuestra clase. De esta forma, el búfer de resultados de nuestra capa ha obtenido un puntero al búfer de resultados de la última capa de transposición de datos. Y al realizar la última operación de transposición, en realidad estamos escribiendo los datos en el búfer de resultados de nuestra capa. Esto elimina operaciones innecesarias de transferencia de datos entre objetos.
Como siempre, en cada etapa comprobaremos el resultado de las operaciones y retornaremos el valor lógico final al programa que realiza la llamada.
Con esto damos por completada la implementación de la pasada directa del método SparseTSF y podemos pasar a la construcción de los algoritmos de pasada inversa. Aquí tendremos que distribuir el gradiente de error entre todos los participantes del proceso según su influencia en el resultado y ajustar los parámetros del modelo en la dirección de la minimización del error en la predicción de la continuación de la serie temporal multimodal analizada.
Primero construiremos el método de distribución del gradiente de error CNeuronSparseTSF::calcInputGradients. Al igual que en el caso de la pasada directa, en los parámetros del método recibiremos el puntero al objeto de la capa anterior, en el que, en esta etapa, deberemos escribir el gradiente de error según la influencia de los datos de origen en el resultado del modelo.
bool CNeuronSparseTSF::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[2].calcHiddenGradients(acTranspose[3].AsObject())) return false;
Luego distribuiremos el gradiente de error de acuerdo con las operaciones de pasada directa, pero en orden inverso. Como ya sabrá, al sustituir los punteros a los búferes de datos, el gradiente de error obtenido de la siguiente capa del modelo termina en el búfer de la última capa de transposición de datos internos. Y nosotros, sin realizar operaciones de transferencia de datos adicionales, pasamos inmediatamente a trabajar con objetos internos.
Primero pasaremos el gradiente de error a través de 2 capas de transposición de datos para lograr la discretización de gradiente requerida.
if(!cForecast.calcHiddenGradients(acTranspose[2].AsObject())) return false;
Si es necesario, ajustaremos el gradiente obtenido por la derivada de la función de activación de la capa de predicción de datos.
if(cForecast.Activation() != None && !DeActivation(cForecast.getOutput(), cForecast.getGradient(), cForecast.getGradient(), cForecast.Activation())) return false;
Después de lo cual bajaremos el gradiente de error al nivel de los datos agregados.
if(!acTranspose[1].calcHiddenGradients(cForecast.AsObject())) return false; if(!cConvolution.calcHiddenGradients(acTranspose[1].AsObject())) return false;
Y pasaremos el gradiente de error a través de la capa de agregación.
if(!acTranspose[0].calcHiddenGradients(cConvolution.AsObject())) return false;
Permítanme recordarles que al agregar datos, usaremos relaciones residuales sumando los datos agregados y la secuencia original. Por consiguiente, el gradiente de error también pasará a través de 2 flujos de datos y sumaremos los valores de los 2 búferes de gradiente de error.
if(!SumAndNormilize(cConvolution.getGradient(), acTranspose[0].getGradient(), acTranspose[0].getGradient(), 1, false)) return false;
Después de lo cual transferimos el gradiente de error obtenido al nivel de la capa anterior y, de ser necesario, los corregiremos por la derivada de la función de activación.
if(!NeuronOCL || !NeuronOCL.calcHiddenGradients(acTranspose[0].AsObject())) return false; if(NeuronOCL.Activation() != None && !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), NeuronOCL.Activation())) //--- return true; }
Al final del método, retornaremos el resultado lógico de las operaciones realizadas al programa que ha realizado la llamada.
Después de distribuir el gradiente de error a todos los objetos de nuestro modelo según su influencia en el resultado final, necesitaremos ajustar los parámetros del modelo en la dirección de la minimización del error de pronóstico de datos. Esta funcionalidad se realizará en el método CNeuronSparseTSF::updateInputWeights. Aquí todo es también bastante prosaico y simple. Nuestra nueva clase contendrá solo 2 capas convolucionales internas con los parámetros entrenables. Como ya sabe, la transposición de datos no usa parámetros entrenables. Por ello, como parte del proceso de ajuste de los parámetros del modelo, solo necesitaremos llamar a los métodos homónimos de las capas convolucionales anidadas y verificar el valor lógico de la ejecución de las operaciones de los métodos llamados. El proceso completo de ajuste de parámetros ya está integrado en los objetos internos.
bool CNeuronSparseTSF::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cConvolution.UpdateInputWeights(acTranspose[0].AsObject())) return false; if(!cForecast.UpdateInputWeights(acTranspose[1].AsObject())) return false; //--- return true; }
Con esto concluye nuestro análisis del algoritmo para construir los métodos de la funcionalidad principal de nuestra nueva clase CNeuronSparseTSF. Todos los métodos auxiliares de esta clase se construyen según los esquemas ya conocidos por los artículos anteriores de esta serie. Por consiguiente, no nos detendremos en ellos en el marco de este artículo y los dejaremos para un estudio independiente. Encontrará el código completo de todos los métodos de la nueva clase en el archivo adjunto.
2.2 Arquitectura de los modelos entrenados
Más arriba, hemos implementado los principales enfoques del método SparseTSF usando MQL5 dentro de la nueva clase CNeuronSparseTSF. Ahora tendremos que implementar un objeto de la nueva clase en nuestro modelo. Creo que resulta obvio que, al igual que antes, utilizaremos el algoritmo de pronóstico de series temporales en el modelo del Codificador del estado del entorno. La arquitectura de este modelo se presenta en el método CreateEncoderDescriptions, en cuyos parámetros transmitiremos el puntero a un objeto de array dinámico para registrar la arquitectura del modelo estamos creando.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
En el cuerpo del método, verificaremos la relevancia del puntero recibido y, de ser necesario, crearemos un nuevo objeto de array dinámico.
A continuación, como de costumbre, utilizaremos una capa básica totalmente conectada para escribir los datos iniciales.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
Luego transferiremos los datos iniciales "brutos" (sin procesar) al modelo, lo cual nos permitirá minimizar el trabajo de preparación de los datos iniciales en el lado del programa principal, mientras que los datos obtenidos se someterán a un procesamiento preliminar en la capa de normalización por lotes,
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
tras la cual colocaremos nuestra nueva capa del método SparseTSF.
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSparseTSF; descr.count = HistoryBars; descr.window = BarDescr;
Permítanme recordarles que para entrenar y probar los modelos en esta serie de artículos usamos los datos históricos del periodo H1, y en estas condiciones, estableceremos un tamaño del periodo de datos inicial igual a 24, lo que se corresponderá con 1 día del calendario.
descr.step = 24; descr.window_out = NForecast; descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
Vale la pena señalar aquí que el uso de los modelos analizados no se limita al periodo H1. No obstante, la prueba y el entrenamiento de diferentes modelos en las mismas condiciones nos permitirá evaluar el rendimiento de los modelos minimizando la influencia de factores externos en su efectividad.
A pesar de su aparente simplicidad, el método SparseTSF es bastante complejo y autosuficiente. Y para obtener la previsión deseada del próximo movimiento de precios, solo necesitaremos añadir los indicadores de distribución de los datos de origen, extraídos en la capa de normalización por lotes.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Para coordinar las características de frecuencia de los valores predichos, utilizaremos los enfoques del método FreDF.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Como podemos ver, la arquitectura del modelo del Codificador del estado del entorno es bastante corta. lo cual resulta bastante coherente con la naturaleza ligera del método SparseTSF declarado por los autores.
Los modelos del Actor y el Crítico del artículo anterior los hemos trasladado sin cambios. Lo mismo se aplicará a los programas de entrenamiento de modelos y de interacción con el entorno. Por ello, en el marco de este artículo no nos detendremos en su consideración. En el archivo adjunto encontrará el código completo de todos los programas y clases utilizados en la preparación de este artículo.
3. Simulación
En los anteriores apartados del presente artículo, nos hemos familiarizado con los aspectos teóricos del método SparseTSF y hemos implementado los enfoques propuestos por los autores del método utilizando las herramientas de MQL5. Ahora es el momento de evaluar la eficacia de los enfoques propuestos en el campo de la previsión de los próximos movimientos de precios utilizando datos históricos reales. Asimismo, comprobaremos la posibilidad de utilizar las previsiones obtenidas para construir una política eficaz de acciones de nuestro Actor.
Durante la construcción del nuevo modelo, no hemos realizado ningún cambio en la estructura de los datos de origen ni en los resultados previstos esperados, lo cual nos ha permitido utilizar la interacción con el entorno y los programas de entrenamiento de modelos de trabajos anteriores sin ninguna modificación. Esto también nos permite usar las muestras de entrenamiento recopiladas previamente para el entrenamiento inicial de los modelos. De esta manera, entrenaremos el Codificador del estado del entorno utilizando el búfer de reproducción de modelos entrenados previamente.
Como recordará, el Codificador de Estado del Entorno trabaja únicamente con el movimiento de precios y los valores de los indicadores analizados que no dependen de las acciones del Actor. En consecuencia, según la comprensión del Codificador, todas las pasadas en la muestra de entrenamiento en un intervalo histórico serán idénticas. Esto nos permite entrenar el modelo del Codificador sin tener que actualizar el conjunto de entrenamiento, mientras que la ligereza del modelo propuesto permitirá reducir significativamente el coste de los recursos y el tiempo de entrenamiento del Codificador.
No podemos decir que el proceso de entrenamiento del modelo haya producido predicciones altamente precisas de estados posteriores pero, en general, la calidad de las previsiones resulta comparable a la de modelos más complejos cuyo entrenamiento requiere más recursos y tiempo. Por eso, en este sentido, podemos decir que en parte hemos conseguido el resultado deseado.
La segunda etapa consistirá en entrenar la política del Actor usando como base los valores predichos obtenidos. En esta etapa, realizaremos un entrenamiento iterativo de los modelos con la actualización periódica del conjunto de entrenamiento, lo cual nos permitirá tener un conjunto de entrenamiento actualizado con una recompensa real por la distribución de acciones cercanas a la política actual del Actor. Y debo admitir que en esta etapa nos hemos llevado una grata sorpresa: a primera vista, los pronósticos inexpresivos del próximo movimiento de precios han resultado ser lo suficientemente informativos para construir una política del Actor capaz de generar ganancias tanto en las muestras de entrenamiento como en las de prueba.
Permítanme recordarles que para entrenar los modelos usamos los datos históricos del instrumento EURUSD y el marco temporal H1 para todo el año 2023. Para todos los indicadores analizados se han usado los parámetros por defecto. Las pruebas de los modelos entrenados se han realizado con los datos históricos de enero de 2024, manteniendo todos los demás parámetros. De esta forma hemos acercado lo más posible las pruebas del modelo a sus condiciones reales de funcionamiento.
A continuación le presentamos los resultados de la prueba del modelo entrenado.
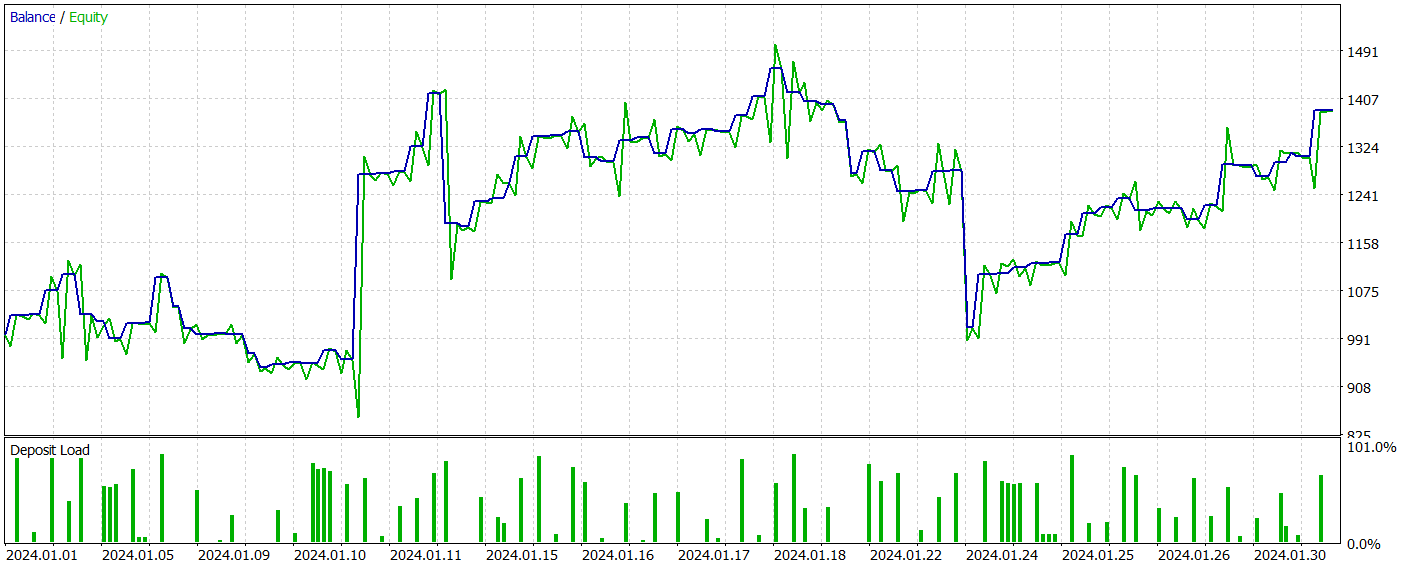
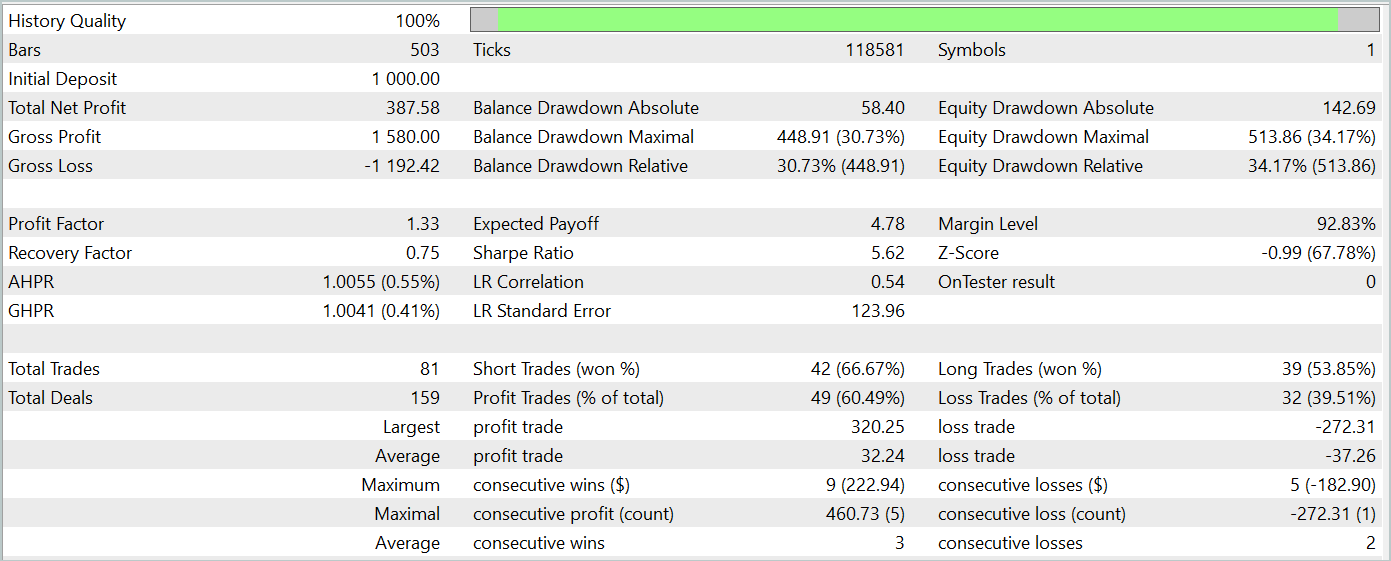
Durante el periodo de prueba, el modelo ha realizado 81 transacciones. Al mismo tiempo, tenemos una distribución casi igual entre posiciones cortas y largas: 42 frente a 39, respectivamente. Más del 60% de las transacciones se han cerrado con beneficios, lo cual nos ha permitido obtener un factor de beneficio de 1,33.
Una de las características del método SparseTSF es la previsión de datos como pasos individuales del periodo cíclico de los datos de origen. Permítanme recordarles que en el modelo entrenado del Codificador del estado del entorno, analizamos los datos horarios con un periodo cíclico de 24 horas, y en este aspecto, la rentabilidad horaria del modelo resulta de especial interés.
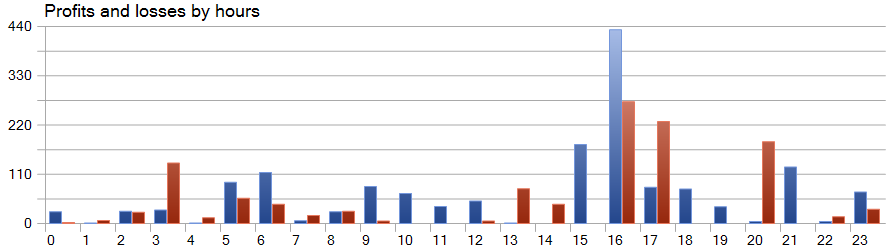
En el gráfico presentado vemos una ausencia virtual de pérdidas en la primera mitad de la sesión europea de 9 a 12 horas. La duración media de apertura de una transacción de 1 hora y 6 minutos nos permite hablar de un cambio mínimo entre la apertura de una transacción y la fijación de las ganancias/pérdidas. La máxima rentabilidad se observa al inicio de la sesión americana (15-16 horas).
Conclusión
En este artículo, presentamos el método SparseTSF, que muestra ventajas en el campo del pronóstico de series temporales debido a su arquitectura ligera y al uso eficiente de recursos. El uso de un número mínimo de parámetros hace que el modelo propuesto resulte particularmente útil para aplicaciones con recursos computacionales limitados y tiempos cortos de toma de decisiones.
SparseTSF permite analizar pasos individuales de series temporales con una periodicidad dada y realizar pronósticos independientes para cada secuencia unitaria, lo cual garantiza una alta flexibilidad y adaptabilidad del modelo.
En la parte práctica del artículo, hemos implementado los enfoques propuestos utilizando MQL5, y también hemos entrenado y probado el modelo entrenado con datos históricos reales. Como resultado, hemos obtenido un modelo capaz de generar ganancias tanto en muestras de entrenamiento como de prueba, lo que demuestra la eficacia de los enfoques propuestos.
Sin embargo, me gustaría recordarle una vez más que en este artículo presentamos programas destinados únicamente a demostrar una de las opciones a la hora de implementar los enfoques propuestos y su uso. No obstante, los programas presentados no están listos para su uso en los mercados financieros reales.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15392
Reconocimiento de patrones mediante deformación dinámica del tiempo (Dynamic Time Warping, DTW) en MQL5
Integración en MQL5: Python
Redes neuronales en el trading: Uso de modelos de lenguaje para la predicción de series temporales
Monitoreo de transacciones usando notificaciones push: ejemplo de un servicio en MetaTrader 5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso