取引におけるニューラルネットワーク:時系列予測のための軽量モデル
はじめに
将来の価格変動を予測することは、効果的な取引戦略を構築する上で不可欠です。正確な予測をおこなうには、一般的に高度で複雑なディープラーニングモデルが必要とされます。
長期時系列予測の精度を左右する要素は、データ内に潜む固有の周期性と傾向です。加えて、通貨ペアの価格変動は特定の取引セッションと密接に関連していることが長年の観察で明らかになっています。たとえば、日次の時系列データを特定の時間で区切ると、各サブシーケンスが類似した傾向や連続したパターンを示すことがわかります。この場合、元のシーケンスの周期性と傾向は、それぞれ分解・変換されます。周期的なパターンはサブシーケンス間のダイナミクスへ、トレンドパターンはサブシーケンス内部の特性へと再解釈されるのです。この分解手法は、長期時系列予測向けの軽量モデル開発に新たな道を開きます。そのアプローチは、論文「SparseTSF:Modeling Long-term Time Series Forecasting with 1k Parameters」で詳しく論じられています。
本論文の著者は、おそらく初めて、周期性とデータ分解を活用し、特殊な軽量時系列予測モデルを構築する手法を研究しました。このアプローチにより、長期時系列予測向けの**超軽量モデル「SparseTSF」が提案されました。
著者は、期間間のスパース予測を実現する技術的アプローチを提示しています。まず、入力データを一定周期のシーケンスに分割し、それぞれをダウンサンプリングします。次に、得られたサブシーケンスごとに予測を実行することで、元の「時系列予測」という問題を「期間間の傾向予測」へと簡略化します。
このアプローチには2つの利点があります。
- データの周期性と傾向を効率的に分離し、傾向変化の予測に焦点を当てながら、モデルが周期的な特徴を安定して識別・捉えられるようにする。
- モデルパラメータのサイズを大幅に圧縮し、コンピューティングリソースの要件を大幅に削減する。
1. SparseSTFアルゴリズム
長期時系列予測(LTSF)の目的は、過去に観測された多変量時系列データをもとに、長期間にわたる将来の値を予測することです。LTSFの主な目標は、予測期間Hの延長であり、これにより、実際の用途においてより包括的かつ高度な洞察を提供できます。しかし、予測期間を延ばすほどモデルの複雑性が増すという問題がありました。これに対処するため、SparseTSFの著者は、軽量かつ堅牢で効率的なモデルの開発に重点を置きました。
近年のLTSFの進歩により、多変量時系列データを扱う際のアプローチが独立したチャネル予測へと移行しつつあります。この戦略では、データセット内の個々の単変量時系列に焦点を当てることで、予測プロセスを簡素化し、チャネル間の依存関係の複雑性を軽減します。その結果、近年のモデル開発の主要な方向性は、単変量シーケンス内の周期性や傾向といった長期的な依存関係をモデル化し、より効率的な予測を行うことへとシフトしています。
多くの場合、予測データは一貫した事前周期性を示すため、SparseTSFの著者は、モデルパラメータの複雑性を抑えつつ、長期的な連続依存関係を抽出するための「期間間スパース予測」を提案しました。この手法では、LTSFタスクを単一の線形層でモデル化します。
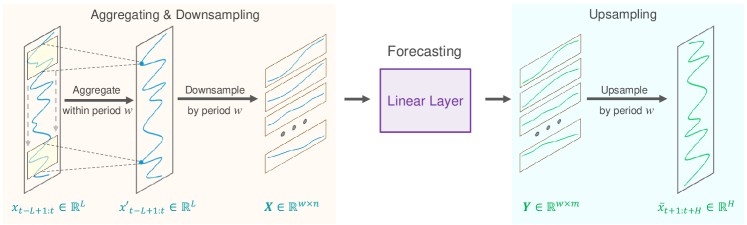
長さLの時系列Xtは、既知の周期性wを持つと仮定します。提案されたアルゴリズムの最初のステップでは、元のシーケンスを長さn(n=L/w)のw個のサブシーケンスにダウンサンプリングします。次に、共有パラメータを持つ予測モデルをこれらのサブシーケンスに適用します。この結果、長さm(m=H/w)のw個の予測サブシーケンスが生成され、それらが結合して長さHの完全な予測シーケンスを形成します。
直感的に、この予測プロセスは、固定周期wにわたりパラメータを共有する全結合層によって実行される「スパース間隔wのスライディング予測」と類似しています。これは、期間全体にわたるスパーススライディング予測をおこなうモデルとして解釈できます。
技術的な観点では、ダウンサンプリング処理は、元のデータ Xtのテンソルをn*w行列に変換し、その後w*n行列に転置する処理と同等です。また、スパーススライディング予測は、サイズn*mの線形層をマトリクスの最終次元に適用する処理と同じになります。この演算の結果、w*mの行列が得られます。
アップサンプリングの際には、この操作を逆にし、w*mの行列を転置して、長さHの完全な予測シーケンスに再フォーマットします。
しかし、このアプローチには2つの問題点が存在します。
- 各期間の予測には1つのデータポイントしか使用されず、その他のデータが無視されるため、情報が失われる。
- ダウンサンプリングされたサブシーケンス内の極端な値が予測に直接影響を与えるため、外れ値に対する感度が高くなる。
これらの問題を軽減するため、SparseTSFの著者らは、スパース予測をおこなう前に「スライディング集約ステップ」を導入しました。この手法では、各データポイントに対し、同じ期間内の周囲のデータポイントの情報を統合することで、最初の問題を軽減します。さらに、集約値は周囲のデータポイントの加重平均として計算されるため、外れ値の影響が抑えられ、2番目の問題も解決されます。
技術的には、このスライディングデータ集約は、ゼロパディングを施した畳み込み層を用いて実装できます。
時系列データでは、訓練データセットとテストデータセット間で分布のシフトが生じることがよくあります。この問題を軽減するために、元のデータと予測されたシーケンスの間でシンプルな正規化戦略を適用することが有効です。SparseTSFアルゴリズムでは、シンプルな正規化手法が採用されています。具体的には、シーケンスの平均値を、モデルに入力する前に入力データから減算し、予測結果に加算するというアプローチを取っています。
以下に、著者によるSparseTSF法の視覚化を示します。
2.MQL5での実装
SparseTSF法の理論的側面を考慮した後、 MQL5を使用して提案されたアプローチの実装に移りましょう。ライブラリの一部として、新しいクラスCNeuronSparseTSFを作成します。
2.1SparseTSFクラスの作成
新しいクラスは、基底クラスCNeuronBaseOCLからコア機能を継承します。CNeuronSparseTSFクラスの構造を以下に示します。
class CNeuronSparseTSF : public CNeuronBaseOCL { protected: CNeuronConvOCL cConvolution; CNeuronTransposeOCL acTranspose[4]; CNeuronConvOCL cForecast; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSparseTSF(void) {}; ~CNeuronSparseTSF(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSparseTSF; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
新しいクラスの構造に、2つの畳み込み層を追加します。1つはデータ集約の役割を果たし、もう1つは後続のシーケンスを予測します。さらに、転置の配列全体を使用してデータを再フォーマットします。追加されたすべての内部オブジェクトは静的に宣言されるため、クラスのコンストラクタとデストラクタは「空」のままになります。クラスオブジェクトの初期化はInitメソッドで実行されます。
初期化メソッドのパラメータでは、作成されたオブジェクトの主なパラメータを渡します。
- シーケンス—初期データのシーケンスの長さ
- 変数—分析された多峰性時系列内の単変量シーケンスの数
- 周期—入力データの周期性
- 予測—予測の深さ。
bool CNeuronSparseTSF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch ) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch)) return false;
メソッドの本体では、通常どおり、同じ名前を持つ親クラスのメソッドを呼び出します。このメソッドは、継承されたオブジェクトと変数を初期化するプロセスをすでに実装しています。
親クラスの初期化メソッドを呼び出すときに、予測深度とマルチモーダルデータ内のユニタリ シーケンスの数の積に等しい層 サイズを指定することに注意してください。
継承されたオブジェクトと変数の初期化が正常に完了したら、追加された内部オブジェクトの初期化の段階に進みます。フィードフォワードパスの順序で初期化します。ここで、処理しているデータテンソルの次元に特に注意してください。
層の入力では、次元L*vの入力データテンソルを受け取ることが想定されます。ここで、Lは入力シーケンスの長さ、vはマルチモーダルソースデータ内のユニタリシリーズの数です。この記事の最初の部分で述べたように、SparseTSFメソッドは独立したユニタリシーケンスを予測するパラダイムで機能します。このようなプロセスを実装するには、入力データ行列をv*L行列に転置します。
if(!acTranspose[0].Init(0, 0, OpenCL, sequence, variables, optimization, iBatch)) return false;
次に、畳み込み層を使用して入力データを集約する予定です。この操作では、元のデータの2周期内で1周期ずつ畳み込みを実行します。次元を保持するために、畳み込みフィルタの数は周期サイズと等しくなります。
if(!cConvolution.Init(0, 1, OpenCL, 2 * period, period, period, sequence / period, variables, optimization, iBatch)) return false; cConvolution.SetActivationFunction(None);
データの集約は独立した単一シーケンス内で実行されることに注意してください。
SparseTSFアルゴリズムの次のステップは、元のデータの離散化です。この段階で、この方法の著者は次元を変更し、元のデータのテンソルを転置することを提案しています。私たちの場合、1次元のデータバッファを操作しています。元のデータの次元の変更は、純粋に宣言的なものであり、メモリ内のデータの再配置は伴いません。しかし、転置については同じことが言えません。したがって、データ転置のために次の層を初期化して進めます。
if(!acTranspose[1].Init(0, 2, OpenCL, variables * sequence / period, period, optimization, iBatch)) return false;
2番目のデータ転置層を使用するのは少し奇妙に思えるかもしれません。一見すると、元のデータの以前の転置の逆の操作を実行します。しかし、それは必ずしも真実ではありません。上記のデータの次元を強調しました。データバッファの合計サイズは変更されません。L*v。データ行列の次元を宣言的に変更した後にのみ、そのサイズは(v*L/w)*wに等しいと言えます。ここで、wは初期データの周期性です。これをw*(L/w*v)に転置します。この操作の後、データバッファには、元のデータのユニタリシリーズの独立性を考慮して、元のデータの周期的な各段階のシーケンスが得られます。
2段階のデータ転置の結果は、グラフィカルに次のように表すことができます。
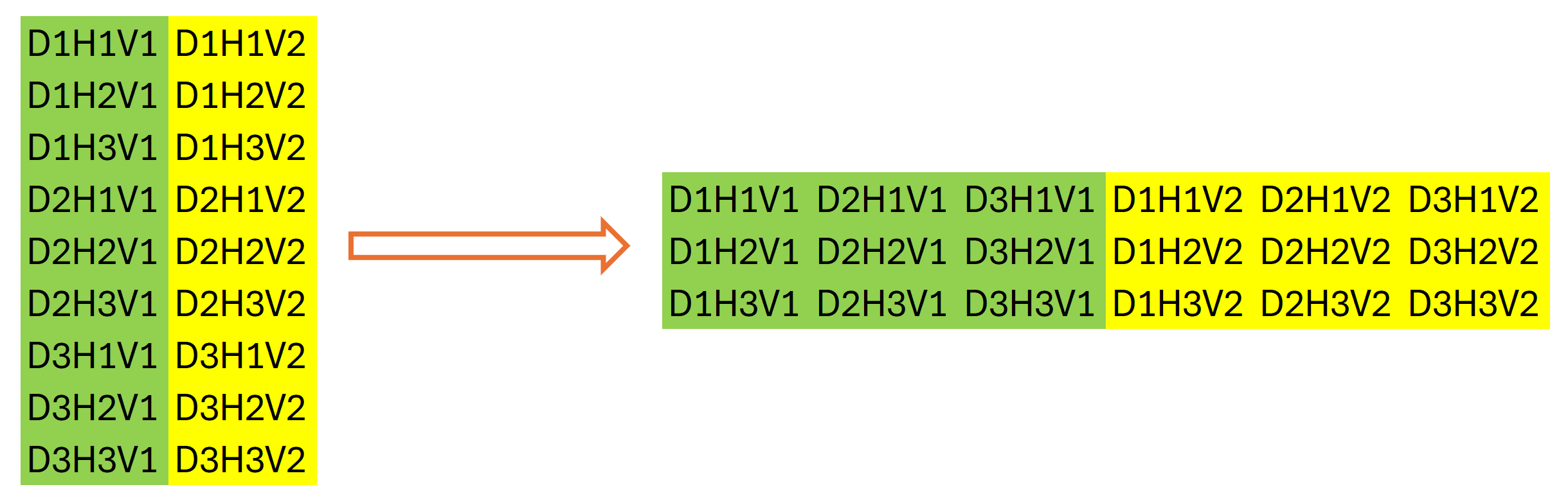
次に、畳み込み層を使用して、特定の計画期間内のユニタリシーケンスの入力データの周期性内で個々のステップを独立して予測します。
if(!cForecast.Init(0, 3, OpenCL, sequence / period, sequence / period, forecast / period, variables, period, optimization, iBatch)) return false; cForecast.SetActivationFunction(TANH);
分析されるソースデータウィンドウのサイズとそのステップは「シーケンス/期間」であり、畳み込みフィルタの数は「予測/期間」であることに注意してください。これにより、計画期間全体の予測値を1回のパスで取得できます。この場合、分析対象データの期間の各ステップに個別のフィルタを使用します。
正規化されたデータを使用する予定なので、予測値の活性化関数として双曲正接を使用します。これにより、予測結果を[-1,1]の範囲に制限できます。
次に、予測された値を必要なシーケンスに変換する必要があります。この操作は、値の逆順列操作を実行する2つの連続するデータ転置層を使用して実行します。
if(!acTranspose[2].Init(0, 4, OpenCL, period, variables * forecast / period, optimization, iBatch)) return false; if(!acTranspose[3].Init(0, 5, OpenCL, variables, forecast, optimization, iBatch)) return false;
不要なデータのコピーを避けるために、現在の層の結果バッファと誤差勾配の置換を整理します。
if(!SetOutput(acTranspose[3].getOutput()) || !SetGradient(acTranspose[3].getGradient()) ) return false; //--- return true; }
各反復で、操作の結果を確認します。メソッドの操作の最終的な論理結果が呼び出し元に返されます。
オブジェクトの初期化プロセス中に、作成している層のアーキテクチャパラメータを保存しなかったことに注意してください。この場合、ネストされたオブジェクトに適切なパラメータを渡すだけです。アーキテクチャによってクラスの操作が独自に定義されるため、受信したパラメータを追加で保存する必要はありません。
クラスオブジェクトを初期化した後、フィードフォワードメソッドCNeuronSparseTSF::feedForwardの作成に進みます。このメソッドでは、内部オブジェクト間のデータ転送を使用してSparseTSFメソッドのアルゴリズムを構築します。
フィードフォワードメソッドのパラメータでは、元のデータが含まれる前の層のオブジェクトへのポインタを受け取ります。
bool CNeuronSparseTSF::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[0].FeedForward(NeuronOCL)) return false;
ネストされたオブジェクトの以前に作成されたメソッドを使用してアルゴリズムを再作成するため、受信したポインタの検証は追加しません。これを最初のデータ転置層のフィードフォワードメソッドに渡すだけです。このメソッドでは、データバッファ内のデータ順列に関連する主要な機能の操作とともに、同様のチェックがすでに実装されています。呼び出されたメソッドの操作を実行した論理的な結果のみをチェックします。
次に、畳み込み層のフィードフォワード方メソッドを呼び出してデータの集約を行います。
if(!cConvolution.FeedForward(acTranspose[0].AsObject())) return false;
SparseTSFアルゴリズムに従って、集約されたデータは元のデータと合計されます。ただし、データの一貫性を維持するために、元のデータの転置バージョンと集約結果を合計します。
if(!SumAndNormilize(cConvolution.getOutput(), acTranspose[0].getOutput(), cConvolution.getOutput(), 1, false)) return false;
次のステップでは、次のデータ転置層のフィードフォワードメソッドを呼び出し、元のシーケンスの離散化プロセスを完了します。
if(!acTranspose[1].FeedForward(cConvolution.AsObject())) return false;
その後、2番目のネストされた畳み込み層を使用して、分析された時系列の最も可能性の高い継続を予測します。
if(!cForecast.FeedForward(acTranspose[1].AsObject())) return false;
サブシーケンスの予測は、初期データの所定の周期内での個々のステップの分析に基づいて実行されることに注意してください。この場合、マルチモーダル入力時系列の各単位シーケンスに対して独立した予測を行います。入力データの周期性のクローズドサイクルの各ステップでは、個別の訓練パラメータを使用します。
予測値を期待される出力シーケンスの必要な順序に並べ替えることは、連続する2つのデータ転置層を使用して実行されます。
if(!acTranspose[2].FeedForward(cForecast.AsObject())) return false; if(!acTranspose[3].FeedForward(acTranspose[2].AsObject())) return false; //--- return true; }
もちろん、データバッファ内の予測値を並べ替える手順では、新しいカーネルを作成し、2つの転置層を1回のカーネル呼び出しで置き換えることができます。これにより、不要なデータ転送操作が排除され、パフォーマンスが向上します。ただし、モデルのサイズを考えると、期待されるパフォーマンスの向上はごくわずかです。この実験では、プログラムコードを簡素化し、プログラマーの作業負荷を軽減することを選択しました。
フォワードパスメソッドの操作は、ネストされたオブジェクトのフィードフォワードパスメソッドの実行で終了することに注意することが重要です。同時に、親クラスから継承された現在の層の結果バッファに値を転送しません。ただし、モデルの後続の層はネストされたオブジェクトにアクセスできず、層の結果バッファに対して操作をおこないます。この明らかなデータフローのギャップを補うために、クラスの初期化中に結果とエラーの勾配バッファを置き換えました。その結果、層の結果バッファは、最後の転置層の結果バッファへのポインタを受け取りました。したがって、最終的な転置操作を実行することで、層の結果バッファにデータを効果的に書き込み、オブジェクト間の不要なデータ転送操作を排除します。
いつものように、各段階で操作の結果を確認し、最終的な論理結果を呼び出し元プログラムに返します。
これで、SparseTSF法のフィードフォワードパスの実装が完了し、バックプロパゲーションアルゴリズムの構築に進みます。ここでは、結果への影響に応じてプロセスのすべての参加者間で誤差勾配を分散し、分析されたマルチモーダル時系列の予測誤差を最小限に抑えるようにモデルパラメータを調整する必要があります。
最初のステップは、誤差勾配を分配するメソッドCNeuronSparseTSF::calcInputGradientsを開発することです。フィードフォワードパスと同様に、メソッドパラメータには前の層のオブジェクトへのポインタが含まれており、ここで元のデータがモデル出力に与える影響に基づいて誤差勾配を記録します。
bool CNeuronSparseTSF::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[2].calcHiddenGradients(acTranspose[3].AsObject())) return false;
フィードフォワード操作に従って、逆の順序で誤差勾配を分散します。ご存知のように、データバッファのポインタ置換により、次のモデル層から受信した誤差勾配は、最後の内部転置層のバッファに格納されます。これにより、追加のデータ転送操作なしで内部オブジェクトを直接処理できるようになります。
まず、誤差勾配を2つの転置層に渡して、必要な勾配の離散化を実現します。
if(!cForecast.calcHiddenGradients(acTranspose[2].AsObject())) return false;
必要に応じて、データ予測層の活性化関数の微分によって得られた勾配を調整します。
if(cForecast.Activation() != None && !DeActivation(cForecast.getOutput(), cForecast.getGradient(), cForecast.getGradient(), cForecast.Activation())) return false;
その後、誤差勾配を集約データのレベルに伝播します。
if(!acTranspose[1].calcHiddenGradients(cForecast.AsObject())) return false; if(!cConvolution.calcHiddenGradients(acTranspose[1].AsObject())) return false;
次に、集約層を通じて誤差勾配を伝播します。
if(!acTranspose[0].calcHiddenGradients(cConvolution.AsObject())) return false;
データを集約する際には、集約データと元のシーケンスを合計して残差関係を使用しました。したがって、誤差勾配も2つのデータストリームを通過し、2つの誤差勾配バッファの値を合計します。
if(!SumAndNormilize(cConvolution.getGradient(), acTranspose[0].getGradient(), acTranspose[0].getGradient(), 1, false)) return false;
その後、得られた誤差勾配を前の層に伝播し、必要に応じて活性化関数の導関数に合わせて調整します。
if(!NeuronOCL || !NeuronOCL.calcHiddenGradients(acTranspose[0].AsObject())) return false; if(NeuronOCL.Activation() != None && !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), NeuronOCL.Activation())) //--- return true; }
メソッドの最後に、実行された操作の論理結果を呼び出し元プログラムに返します。
最終結果への影響に応じてモデルのすべてのオブジェクトに誤差勾配を分配した後、データ予測誤差を最小限に抑えるためにモデルパラメータを調整する必要があります。この機能は、CNeuronSparseTSF::updateInputWeightsメソッドで実行されます。ここではすべてが非常に簡単です。新しいクラスには、訓練可能なパラメータを含む2つの内部畳み込み層のみが含まれています。ご存知のとおり、データ転置では訓練可能なパラメータは使用されません。したがって、モデルパラメータを調整するプロセスの一環として、同じ名前のネストされた畳み込み層のメソッドを呼び出し、呼び出されたメソッドの操作の実行の論理値を確認するだけで済みます。パラメータを調整するプロセス全体は、すでに内部オブジェクトに組み込まれています。
bool CNeuronSparseTSF::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cConvolution.UpdateInputWeights(acTranspose[0].AsObject())) return false; if(!cForecast.UpdateInputWeights(acTranspose[1].AsObject())) return false; //--- return true; }
これで、新しいCNeuronSparseTSFクラスの主な機能のメソッドの説明は終了です。このクラスのすべての補助メソッドは、本連載の以前の記事で説明したロジックに従います。従って、この記事ではそれについては触れないことにします。新しいクラスのすべてのメソッドの完全なコードは添付ファイルにあります。
2.2 学習可能なモデルのアーキテクチャ
SparseTSFアルゴリズムの主なアプローチをMQL5の新しいクラスCNeuronSparseTSF内に実装しました。ここで、新しいクラスのオブジェクトをモデルに実装する必要があります。環境状態がわかれば、エンコーダーモデルで時系列予測アルゴリズムを使用することは明らかだと思います。このモデルのアーキテクチャは、CreateEncoderDescriptionsメソッドで説明されています。そのパラメータでは、モデルのアーキテクチャを書き込むための動的配列オブジェクトへのポインタを渡します。
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
メソッド本体では、受信したポインタの関連性を検証し、必要に応じて新しい動的配列オブジェクトを作成します。
次に、いつものように、基本的な完全接続層を使用して初期データを書き込みます。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
未処理の「生の」入力データをモデルに入力します。これにより、メインプログラム側で初期データを大規模に準備する必要がなくなります。受信したデータはバッチ正規化層で前処理されます。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
この層の後に、新しいSparseTSFメソッド層が続きます。
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSparseTSF; descr.count = HistoryBars; descr.window = BarDescr;
本連載では、H1期間の履歴データを使用してモデルを訓練およびテストしていることを思い出してください。これらの条件では、初期データ期間のサイズを24に設定します。これは1暦日に対応します。
descr.step = 24; descr.window_out = NForecast; descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
ここで注目すべきは、検討中のモデルの使用はH1時間枠に限定されないということです。ただし、同じ条件下でさまざまなモデルをテストおよび訓練することで、外部要因の影響を最小限に抑えながらモデルのパフォーマンスを評価することができます。
一見単純そうに見えますが、SparseTSFメソッドは非常に複雑で自己完結的です。今後の価格変動の望ましい予測を得るには、バッチ正規化層で抽出された元のデータの分布指標を追加するだけです。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
予測値の周波数特性を揃えるために、FreDF法のアプローチを使用します。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
ご覧のとおり、環境状態エンコーダーモデルのアーキテクチャは非常に簡潔です。これは、SparseTSFメソッドの作成者が述べた軽量性と一致しています。
前回の記事のActorとCriticを変更せずにコピーします。同じことが、モデルの訓練や環境との相互作用のためのプログラムにも当てはまります。したがって、この記事ではそれらについて詳細には説明しません。この記事で使用されているすべてのプログラムの完全なコードは添付ファイルに含まれています。
3.テスト
この記事の前のセクションでは、SparseTSF法の理論的側面を検討し、この手法の著者が提案したアプローチをMQL5を使用して実装しました。ここで、実際の履歴データを使用して今後の価格変動を予測する能力の観点から、提案されたアプローチの有効性を評価します。また、得られた予測を使用して、Actorの行動方策を構築する上での有効性も検証する必要があります。
新しいモデルを構築する過程で、入力データの構造や予想される予測結果に変更は加えませんでした。そのため、以前の研究で使用された環境インタラクションやモデル訓練プログラムを、そのまま適用できます。また、モデルの初期訓練には、以前に収集した訓練データセットを使用することもできます。そこで、以前に訓練したモデルの経験再生バッファを使用して、環境状態エンコーダーを訓練します。
ご存知のとおり、環境状態エンコーダーは、Actorの行動に依存しない価格変動と分析されたインジケーターの値のみで動作します。したがって、エンコーダーは、1つの履歴間隔における訓練データセット内のすべてのパスを同一のものとして認識します。つまり、訓練データセットを更新しなくても、Encoderモデルを訓練できるということです。また、提案されたモデルの軽量性により、エンコーダーの訓練に必要なリソースと時間を大幅に削減することが可能になります。
モデルの訓練によって、完全に正確な状態予測が得られたわけではありません。しかし、全体的には、予測の品質は、訓練により多くのリソースと時間を必要とするより複雑なモデルに匹敵します。したがって、私たちは望んでいた結果を部分的に達成したと言えます。
2番目の段階では、取得した予測値に基づいてActor方策を訓練します。この段階では、訓練データセットを定期的に更新しながらモデルの反復訓練を実行します。これにより、Actorの現在の方策に近い行動の分布に対する実際の報酬を含む最新の訓練データセットを取得できます。正直に言うと、この段階では意外な発見がありました。一見、精度が低いように見える価格変動予測が、訓練データセットとテストデータセットの両方で利益を生み出すことができるActorの方策を構築する上で非常に有益であることが判明したのです。
モデルの訓練には、2023年全体のH1時間枠におけるEURUSD商品の履歴データを使用しました。分析されたすべての指標のパラメータはデフォルト値に設定されます。その後、他のすべてのパラメータを同じに保ちながら、訓練されたモデルを2024年1月の履歴データでテストしました。したがって、モデルのテストは実際の状況に厳密に適合するようになりました。
訓練されたモデルのテストの結果を以下に示します。
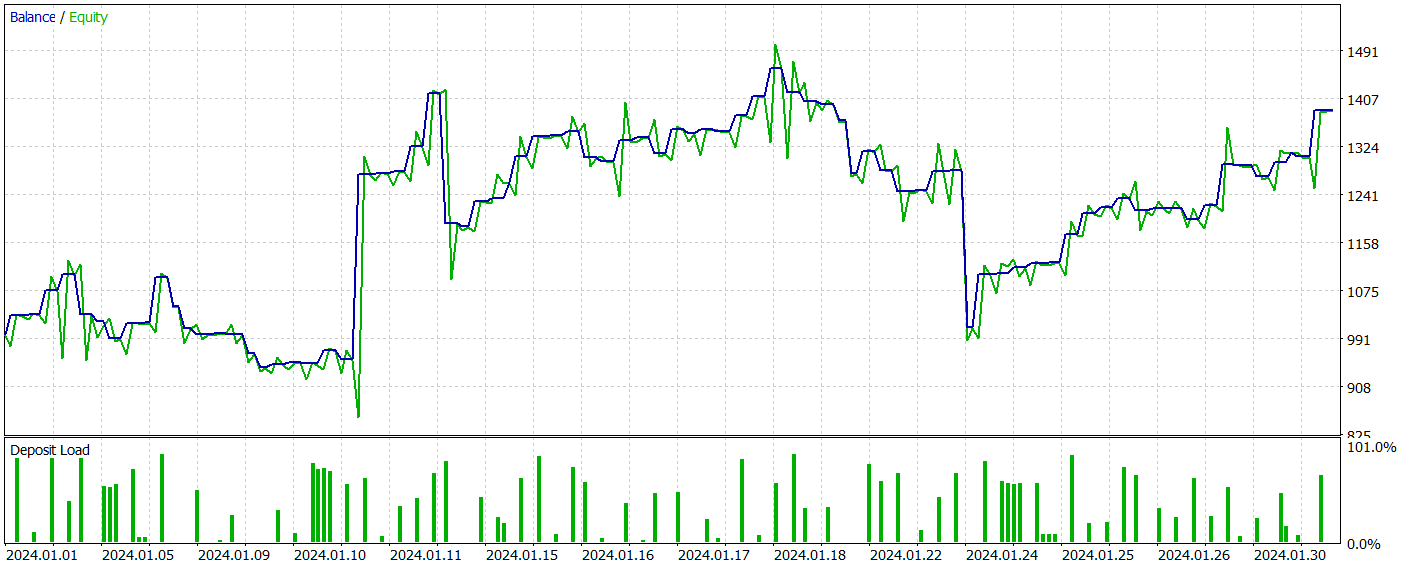
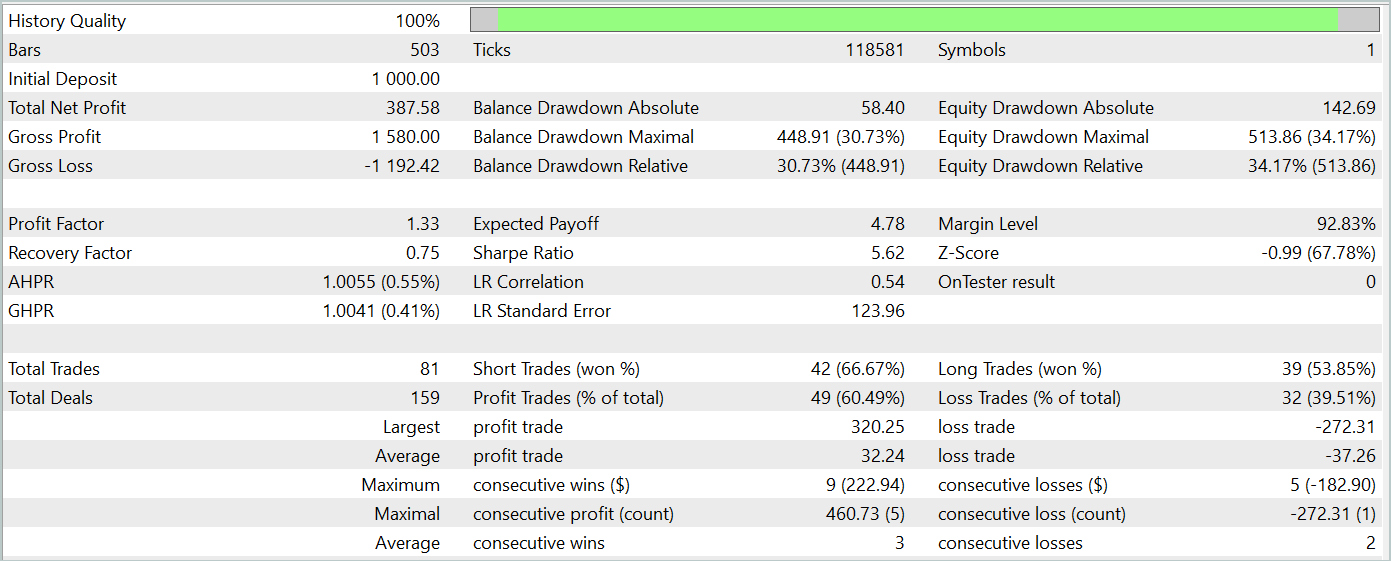
テスト期間中、モデルは81件の取引を実行しました。ショートポジションとロングポジションの分布はほぼ均等で、42対39でした。取引の60%以上が利益で終了し、利益率は1.33になりました。
SparseTSF法の特徴的な機能の1つは、元のデータの周期内の各ステップを基にデータを予測することです。念のため、訓練済みの環境状態エンコーダーモデルでは、24時間の周期で1時間ごとのデータを分析しました。この側面により、モデルの収益性は時間単位で見ると特に興味深いものになります。
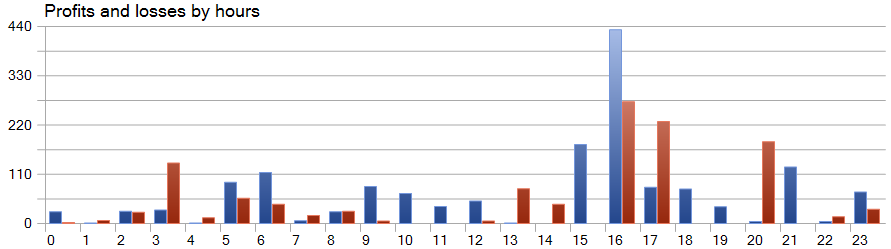
提示されたグラフでは、欧州セッションの前半、9:00から12:00の間に損失がほとんどないことがわかります。取引の平均所要時間は1時間6分であり、取引の開始から利益/損失の実現までの遅延が最小限であることを示しています。収益は、アメリカセッションの開始時(15:00~16:00)に最も高くなります。
結論
本記事では、軽量なアーキテクチャと効率的なリソース使用により、時系列予測に優れた利点をもたらすSparseTSF法を紹介しました。パラメータ数を最小限に抑えることで、計算リソースが限られた環境や、迅速な意思決定が求められる用途に特に有効なモデルとなっています。
SparseTSFを活用することで、特定の周期に基づいて時系列データの各ステップを分析し、各単位シーケンスに対して独立した予測をおこなうことが可能になります。これにより、モデルの柔軟性と適応性が向上します。
記事の実践部分では、MQL5を使用して提案手法を実装し、モデルの訓練と実際の履歴データによるテストをおこないました。その結果、訓練データセットとテストデータセットの両方で利益を生み出すモデルが得られ、提案手法の有効性が確認されました。
ただし、本記事で紹介したプログラムは、提案手法の実装例および使用方法の一例を示すことを目的としており、実際の金融市場での運用を想定したものではありません。
参照文献
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | StudyEncoder.mq5 | EA | エンコーダー訓練EA |
| 5 | Test.mq5 | EA | モデルをテストするEA |
| 6 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 7 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 8 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15392
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 初級から中級へ:変数(III)
初級から中級へ:変数(III)
 初心者からプロまでMQL5をマスターする(第4回):配列、関数、グローバルターミナル変数について
初心者からプロまでMQL5をマスターする(第4回):配列、関数、グローバルターミナル変数について
 多通貨エキスパートアドバイザーの開発(第16回):異なるクォート履歴がテスト結果に与える影響
多通貨エキスパートアドバイザーの開発(第16回):異なるクォート履歴がテスト結果に与える影響
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
