カオス理論アプローチによる買われ過ぎと売られ過ぎのトレンド分析

カオスがパターンになるとき

雪嵐の中で森を歩いている状況を想像してください。雪の結晶は一見すると無秩序で予測不可能に見えます。しかし、よく観察すると、雪の結晶は見えない空気の流れに沿って動き、一定のパターンを描いていることがわかります。金融市場の価格も、この雪の結晶のように独自の「踊り」をしており、一見ランダムにランダムに見えているにすぎません。

カオス理論は、驚くべき事実を示しています。それは、完全に予測不可能に見えるシステムの中にも、深いパターンや構造が隠されているということです。気象学者のエドワード・ローレンツは、天気モデルの研究中、初期値を丸めて入力したところ、予測結果が大きく変化することを発見しました。この現象は後に「バタフライ効果」と呼ばれ、初期条件のわずかな違いがシステム全体に大きな影響を与える可能性を示しています。

「ストレンジアトラクターを持つシステムは、一見完全にランダムに見えるが、そこには隠れた秩序が存在する」と、ローレンツは述べています。気象システムに目に見えないパターンが存在するように、金融市場にも一見予測困難でありながら、一定の規則性が存在します。

アトラクター：市場の目に見えない磁石

部屋でボールを投げることを想像してください。どれだけ強く投げても、どの方向に投げても、最終的にボールは床に落ちます。この場合、床がアトラクターとして機能しています。

金融市場におけるアトラクターも同様です。ただし物理的な引力ではなく、経済的な力が価格を特定の水準に戻そうとします。株価が過大評価されると売り圧力が、過小評価されると買い圧力が働き、市場はまるで「ゴムバンド」のように均衡点へ引き戻されます。

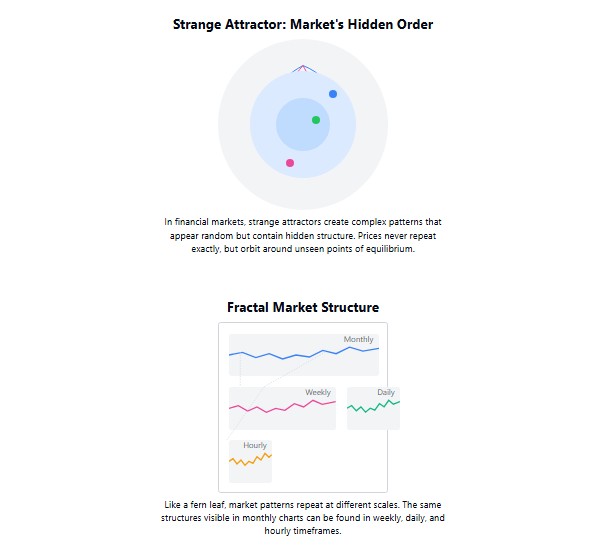
しかし、単純なボールとは異なり、市場にはストレンジアトラクターがあります。これは単なる一点ではなく、システムが目指す複雑な構造であり、同じ経路を繰り返すことはありません。まるで川が湖に流れ込むように、水は常に湖へ向かって流れますが、その経路は決して同じにはならないのです。

市場のフラクタルパターンを理解する方法

1960年代、ブノワ・マンデルブロはIBMでの研究中、綿花価格の長期的変動を分析しました。その結果、驚くべきことに気づきました。日次、月次、年次のデータを見ても、価格チャートの形はほとんど同じに見えたのです。この発見は、異なるスケールで自己相似する形状を研究するフラクタル幾何学の発展につながりました。

シダの葉を思い浮かべてください。葉全体の形は、小さな小葉にも繰り返され、さらに小さな部分にも同様のパターンが現れます。市場も同様に機能します。分足チャートで観察されるパターンは、時間足、日足、さらには月足でも繰り返されることが多いのです。

この自己相似性は偶然ではありません。市場は単なるランダムノイズではなく、内部構造を持つ複雑なシステムであることを示しています。この構造を理解することが、将来の価格変動を予測するための鍵となります。

平均への回帰：自然界の普遍的リズム

金融の世界には「木は天まで伸びない」という格言がありますば、歴史は、急激な成長や下落の後、市場は長期的な平均値に戻る傾向があることを示しています。

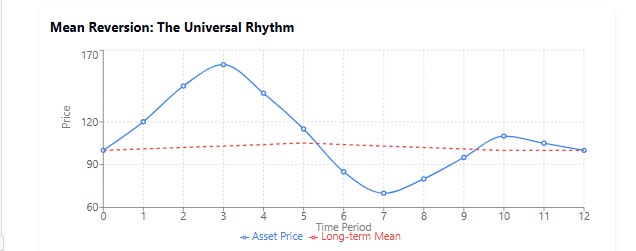
この現象は自然界のあらゆる場面で観察できます。振り子を思い浮かべてください。振り子を遠くに振るほど、中心の位置に戻ろうとする力が強く働きます。また、体温を考えてみてください。熱があるとき、体は36.6℃の正常値に戻そうと働きます。

この効果は市場にも常に見られます。一時的に突出したリターンを示す株は、次の期間に平凡な結果となることが多いです。長期間にわたって市場平均以上に成長した企業も、ほぼ例外なく成長のペースが鈍化します。伝説的投資家のピーター・リンチも次のように述べています。「平均への回帰は、偉大な企業であっても逃れられない重力の力である」。

しかし、Sensory Neural Attractorが革新的である点は、単なる静的な平均ではなく、市場が現在向かっている動的なレベルを特定できることです。これは、たとえ重力が突然変化したとしても、振り子がどこで止まるかを正確に予測できるようなものです。

初期条件への感度：ウォール街におけるバタフライ効果

「ブラジルで蝶が羽ばたくことで、テキサスに竜巻が発生することがあるか？」というローレンツの有名な問いは、カオス理論の重要な原理である初期条件への感度を示しています。

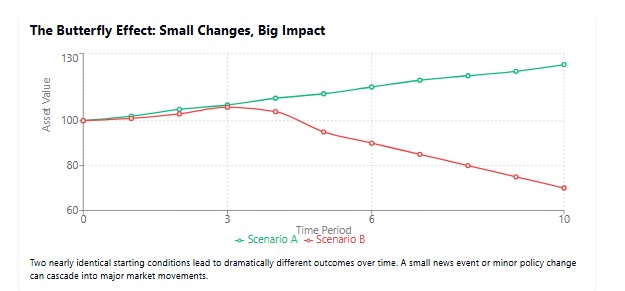
金融市場でも、このような「バタフライ効果」は日常的に観察されます。CEOのツイートによって企業の株価が急落することもありますし、連邦準備制度(FRB)の予想外の決定が世界的な調整を引き起こすこともあります。小規模銀行に関する問題の噂だけで、銀行セクター全体にパニックが広がることもありました。これは、2008年の金融危機で実際に見られた現象です。

このような感度の高さにより、長期的な正確な予測は原理的に困難です。ニールス・ボーアも冗談めかして「予測は非常に難しい、特に未来については」と述べています。しかし、システムの構造を理解し、アトラクターを特定することで、確率的な予測が可能となり、投資判断に優位性をもたらすことができます。

ニューラルアトラクターオシレーター：市場カオスの制御

理論から実践へ：インジケーターの作成

資産の価格が、まるで見えない力に引かれるかのように一定水準に戻ることに気づいたことはありませんか。荒々しい上昇の後に急激な調整が起きたり、長期下落の後に突然の回復が始まったりするのはなぜでしょうか。これは、価格を一方向に動かし続けさせない見えない力が働いているからです。この研究では、この「見えない力」をデジタルネットワークで捉えることを目指します。

従来のトレーダーが従来型のインジケーターを使い続ける一方で、本手法では、市場の隠れたリズムを認識できるインジケーターを作ることを目指します。この旅のコンパスはニューラルネットワークであり、地図はアトラクター理論です。

ニューラルネットワークの構造：インジケーターの頭脳

映画のハッカーものを思い浮かべると、主人公が数分の画面時間で超知能を作り出す場面がありますが、実際には少し複雑です。しかし、一般的なトレーダー兼プログラマでも十分に実装可能です。

本ネットワークは、雪上の足跡を分析する熟練の追跡者のように、過去価格を解析し、市場（動物）がどこに向かうかを予測します。その構造は比較的シンプルです。入力層でデータを収集し、隠れ層でパターン認識の「魔法」がおこなわれ、出力層で予測がおこなわれます。

これは、私たちの「脳」の初期化がどのように見えるかを示したものです。

void InitializeNetwork() {
   // Initializing hidden layer
   ArrayResize(Network.hidden, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      ArrayResize(Network.hidden[i].weights, InputNeurons);
      // Initializing weights with random values in the range [-0.5, 0.5]
      for(int j = 0; j < InputNeurons; j++) {
         Network.hidden[i].weights[j] = (MathRand() / 32767.0) - 0.5;
      }
      Network.hidden[i].bias = (MathRand() / 32767.0) - 0.5;
   }
   
   // Initializing output neuron
   ArrayResize(Network.output.weights, HiddenNeurons);
   for(int i = 0; i < HiddenNeurons; i++) {
      Network.output.weights[i] = (MathRand() / 32767.0) - 0.5;
   }
   Network.output.bias = (MathRand() / 32767.0) - 0.5;
}

重みが初期化されている行に注目してください。これは、研究を始める前に顕微鏡の感度を調整するようなものです。最初はランダムな値から開始し、その後、学習プロセスによってこれらの「調整ノブ」が徐々に最適化され、より正確な像を生み出すようになります。

ネットワークの学習：初心者から達人へ

子どもが歩くことを学ぶ様子を想像してください。最初は転び、数歩進み、また転びます。しかし、徐々に能力を向上させていきます。同様に、私たちのネットワークも過去データを用いて「歩く」ことを学び、常にステップを調整していきます。

このプロセスの重要な部分は、順方向パスと逆方向パスです。順方向パスではネットワークが予測をおこない、逆方向パスでは誤差に応じて重みを調整します。

double ForwardPass(double &inputs[]) {
   // Calculating outputs of the hidden layer
   for(int i = 0; i < HiddenNeurons; i++) {
      double sum = Network.hidden[i].bias;
      for(int j = 0; j < InputNeurons; j++) {
         sum += inputs[j] * Network.hidden[i].weights[j];
      }
      Network.hidden[i].output = Sigmoid(sum);
   }
   
   // Calculating neural network output
   double sum = Network.output.bias;
   for(int i = 0; i < HiddenNeurons; i++) {
      sum += Network.hidden[i].output * Network.output.weights[i];
   }
   Network.output.output = Sigmoid(sum);
   
   return Network.output.output;
}

この関数の内部を実行中に観察できたとしたら、脳のニューロンを通過する電気インパルスのようなものを見ることになるでしょう。情報が接続のネットワークを通じて伝達され、変換され、増幅されていく様子です。

活性化関数：ニューロンの発火

インジケーターの更新版では、従来のシグモイド関数を双曲線正接関数(tanh)に置き換えました。この関数は範囲が[-1, 1]であり、正負の値がともに重要となるカオス的システムのモデリングに特に適しています。

double Tanh(double x) {
   return (MathExp(x) - MathExp(-x)) / (MathExp(x) + MathExp(-x));
}

双曲線正接関数は中央付近の傾きがより急であるため、ネットワークはより速く学習し、データの急激な変化をより正確に捉えることができます。これは、状態間の遷移が急速に起こり得るカオス的市場において極めて重要です。

データの正規化：共通言語で話す

ニューラルネットワークにデータを入力する前に、正規化をおこなう必要があります。これは、対話相手に理解可能な言語へ翻訳することに似ています。もし自分がロシア語を話し、相手が英語しか理解できなければ、意思疎通は成立しません。

double NormalizePrice(double price) {
   double min = ArrayMin(PriceHistory);
   double max = ArrayMax(PriceHistory);
   return (price - min) / (max - min);
}

この関数は、すべての価格を0から1の範囲にスケーリングします。これは、シグモイド活性化関数への入力として最適な形式です。

オシレーターの計算：真実の瞬間

最後に、最も興味深い部分であるオシレーター値の計算に到達しました。どのように計算するのでしょうか。本質的には、現在価格と予測されたアトラクターを比較し、その乖離をパーセンテージとして表現します。

// Calculate oscillator value as ratio of current price to attractor
if(AttractorBuffer[i] > 0) {
   OscillatorBuffer[i] = (CurrentPriceBuffer[i] / AttractorBuffer[i] - 1.0) * 100.0;
} else {
   OscillatorBuffer[i] = 0; // Division-by-zero protection
}

このシンプルな式は、現在価格がその「自然な水準」からどれだけ乖離しているかを示します。オシレーターが+30%を示す場合、価格は「過熱」しており、近いうちにアトラクターへ回帰する可能性があります。-30%の場合、価格は「過冷却」状態にあり、上方への反発が起こる可能性があります。

インジケーターをニーズに合わせてカスタマイズする

「フリーサイズ」という言葉をご存じでしょうか。しかし、取引の世界ではそれが通用することはほとんどありません。市場ごとにも時間足ごとにも、それぞれ固有の特性や「気質」があります。そして、私たちのインジケーターもそれらの特性に適応しなければなりません。

input int    InputNeurons = 10;     // Number of input neurons (historical periods)
input int    HiddenNeurons = 20;    // Number of neurons in the hidden layer
input double LearningRate = 0.01;   // Learning rate
input int    TrainBars = 1000;      // Number of bars for training
input int    PredictionPeriod = 5;  // Prediction period (in bars)
input bool   Smoothing = false;     // Apply smoothing to the oscillator
input int    SmoothingPeriod = 3;   // Smoothing period

これらのパラメータは、高級オーディオアンプのコントロールのようなものです。より感度の高いインジケーターが必要であれば、ニューロン数を増やすか、予測期間を短くします。ノイズが多すぎる場合は、平滑化を有効にします。

予測期間：未来を見通す

PredictionPeriodパラメータは特に重要です。これは、どれだけ先の未来を予測しようとするかを決定します。分足チャートで取引をおこなうスキャルパーにとって、値が5であれば、5分先の予測を意味します。日足チャートで取引するポジショントレーダーにとっては、5日先の予測になります。

この設定については、ぜひ実験することを推奨します。まずは小さな値から始め、徐々に増やしながらインジケーターの挙動がどのように変化するかを観察してください。実際の科学と同様に、ここに決まった公式はありません。あるのは経験と実験のみです。

リアプノフ指数：市場ランダム性の測定

更新版インジケーターの中核を成す要素は、リアプノフ指数です。これは、システムの初期条件に対する感度を測定する指標です。この指数は、有名な「バタフライ効果」を数学的に記述します。すなわち、初期条件のわずかな違いが、長期的には大きな乖離を生み出す現象です。

double CalculateLyapunovExponent(const double &close[], int bars) {
   double epsilon = 0.0001; // Small perturbation
   double lyapunov = 0.0;
   int samples = MathMin(LyapunovPeriod, TrainBars/2);
   
   for(int i = 0; i < samples; i++) {
      int startIdx = MathRand() % (TrainBars - InputNeurons - PredictionPeriod);
      
      // Initial input data
      double inputs1[];
      ArrayResize(inputs1, InputNeurons);
      for(int j = 0; j < InputNeurons; j++) {
         inputs1[j] = NormalizePrice(close[bars - TrainBars + startIdx + j]);
      }
      
      // Slightly perturbed input data
      double inputs2[];
      ArrayResize(inputs2, InputNeurons);
      ArrayCopy(inputs2, inputs1);
      inputs2[MathRand() % InputNeurons] += epsilon;
      
      // Predictions for both data sets
      double pred1 = ForwardPass(inputs1);
      double pred2 = ForwardPass(inputs2);
      
      // Distance between predictions
      double distance = MathAbs(pred2 - pred1);
      
      // Lyapunov exponent
      if(distance > 0) {
         lyapunov += MathLog(distance / epsilon);
      }
   }
   
   // Average and normalize
   lyapunov = lyapunov / samples;
   
   // Limit the value for stability
   lyapunov = MathMax(-1.0, MathMin(1.0, lyapunov));
   
   return lyapunov;
}

フラクタルノイズ：自然な構造の付加

このインジケーターの最も革新的な要素のひとつは、Midpoint Displacementアルゴリズムによって生成されるフラクタルノイズを組み込んでいる点にあります。ブノワ・マンデルブロが金融市場に初めて応用したフラクタル幾何学は、市場の持つ自然な自己相似構造をモデル化することを可能にします。

void GenerateFractalNoise(int size) {
   ArrayResize(FractalNoiseBuffer, size);
   
   // Starting points
   FractalNoiseBuffer[0] = 0;
   FractalNoiseBuffer[size-1] = 0;
   
   // Recursive calculation of midpoints
   MidpointDisplacement(FractalNoiseBuffer, 0, size-1, 1.0, FractalDimension);
   
   // Normalization
   double min = ArrayMin(FractalNoiseBuffer, 0, size);
   double max = ArrayMax(FractalNoiseBuffer, 0, size);
   
   for(int i = 0; i < size; i++) {
      FractalNoiseBuffer[i] = 2.0 * (FractalNoiseBuffer[i] - min) / (max - min) - 1.0;
   }
}

フラクタル次元(FractalDimension)パラメータの値が高いほど、ノイズはよりギザギザでカオス的になります。これにより、ボラティリティの高い市場をより正確にモデル化することが可能になります。

インジケーターの実践的応用

ここまででインジケーターの仕組みを理解したので、次に実践的な応用について考察します。一般的なオシレーターと同様に、Neural Attractor Oscillatorは市場の買われすぎ・売られすぎを判断するために使用できます。

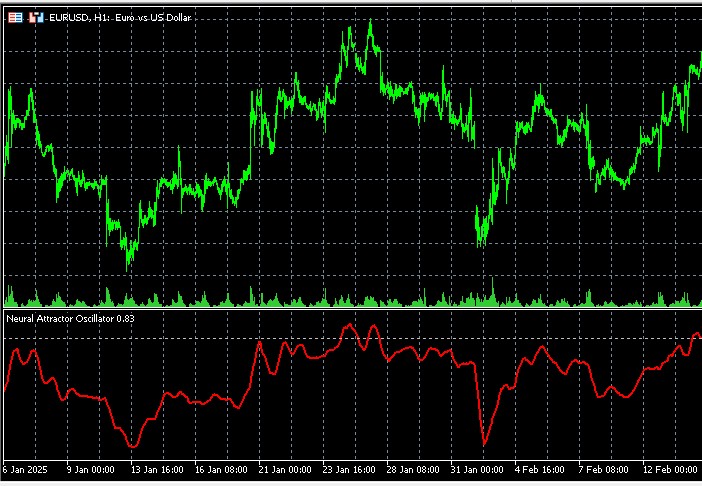
振り子を観察している場面を想像してください。右に大きく振れすぎた場合、まもなく左へ戻ることが分かります。左に大きく振れすぎた場合も同様に、やがて右へ戻ります。私たちのインジケーターも同様に機能します。ただし、振り子を中心へ戻すのが機械的な力であるのに対し、市場では均衡へ戻そうとする経済的な力が働きます。

カオスを考慮したエントリーシグナル

1. 買いシグナル：オシレーターがアトラクターの下限（リアプノフ指数に応じて動的に調整されます）を下回り、その後上昇に転じた場合、ロングポジションのエントリーポイントとなる可能性があります。この際、現在のリアプノフ指数の値を考慮することが重要です。値が低いほど、シグナルの信頼性は高くなります。
2. 売りシグナル：オシレーターがアトラクターの上限を上回り、その後下落に転じた場合、ショートポジションのエントリーポイントとなる可能性があります。ここでも、リアプノフ指数が低いほどシグナルの信頼性は高まります。
3. ダイバージェンス：インジケーターのピークと価格との間に生じるダイバージェンスは、特に価値が高く、精度の高いシグナルとなります。

なお、カオスが強い局面（リアプノフ指数が高い局面）では、強いシグナルであっても信頼性は低下します。そのため、ポジションサイズを縮小するか、市場へのエントリーを控えるべきです。

カオス理論の文脈におけるダイバージェンス

Chaos Attractorオシレーターは、従来のダイバージェンスに対して新たな視点を提供します。価格が新たな極値を形成しているにもかかわらず、オシレーターがそれに追随しない場合、それは単なるトレンドの弱まりではなく、アトラクター構造の変化、すなわち市場が向かおうとしている均衡点の変化を示唆している可能性があります。

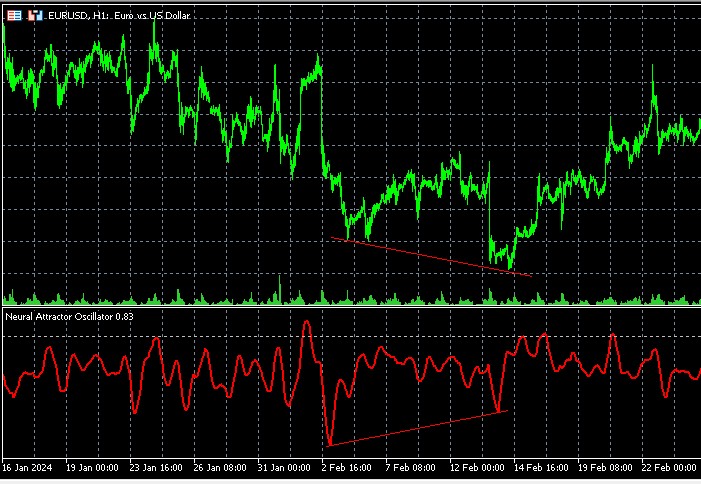
特に強力なシグナルは、ダイバージェンスがリアプノフ指数の変化と同時に発生する場合です。たとえば、指数が正から負へ転じる場合、それはカオス的局面の後に新たな安定トレンドが形成されることを示唆する可能性があります。

ネットワークのモメンタム最適化

更新版インジケーターでは、学習プロセスを大幅に向上させ、局所最小値に陥る可能性を低減するために、モメンタム法を適用しました。

// Updating the output layer weights with momentum
for(int j = 0; j < HiddenNeurons; j++) {
    double delta = LearningRate * Network.output.error * Network.hidden[j].output;
    Network.output.momentum[j] = momentum * Network.output.momentum[j] + (1.0 - momentum) * delta;
    Network.output.weights[j] += Network.output.momentum[j];
}

モメンタム手法は、物理世界における「慣性」のように機能します。最適化の過程でネットワークがある方向へ長時間移動している場合、小さな障害（局所最小値）に遭遇しても、その方向への移動を継続しようとします。これは、誤差関数の地形が非常に複雑になり得るカオス的システムにおいて特に有効です。

今後の改善点

私たちのインジケーターはすでに強力なツールですが、カオスアトラクター概念のさらなる発展に向けて、いくつかの方向性が考えられます。

1. リカレントニューラルネットワーク：現在のフィードフォワード型ニューラルネットワークをリカレントニューラルネットワーク（LSTMやGRU）に置き換えることで、カオス的システムにおける長期依存関係の捉え方を向上させることが可能です。
2. マルチフラクタル解析：異なる時間スケールにおけるボラティリティ構造を特定するために、マルチフラクタル解析手法を実装することが考えられます。
3. アトラクターのトポロジー解析：動的トポロジー手法を適用し、価格ダイナミクスにおけるストレンジアトラクターの識別および分類をおこなうことが可能です。
4. 量子アルゴリズム：将来的には、量子コンピューティングを用いて複雑なカオスシステムをモデル化することにより、市場予測において革新的なブレークスルーがもたらされる可能性があります。

そしてもちろん、このシステムに基づくエキスパートアドバイザー（EA）の作成についても、今後検討していく予定です。以下は、そのラフドラフト、いわば EA のスケッチです。

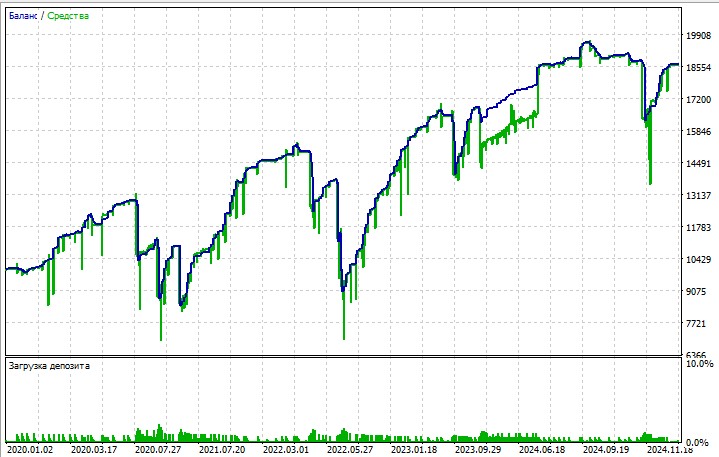
全体として、本システムは概ね良好に機能しています。飛び抜けて優れているわけではありませんが、決して悪いものでもありません。

柔軟な平滑化手法

更新版インジケーターでは、複数の平滑化手法を選択可能とし、市場環境に応じてインジケーターの反応特性をトレーダーが調整できるようにしました。

void ApplySmoothing(int rates_total, int prev_calculated, int period, ENUM_MA_METHOD method) {
   int start = prev_calculated == 0 ? InputNeurons + period : prev_calculated - 1;
   
   double temp[];
   ArrayResize(temp, rates_total);
   ArrayCopy(temp, OscillatorBuffer);
   
   for(int i = start; i < rates_total; i++) {
      switch(method) {
         case MODE_SMA: // Simple moving average
            {
               double sum = 0;
               for(int j = 0; j < period; j++) {
                  sum += temp[i - j];
               }
               OscillatorBuffer[i] = sum / period;
            }
            break;
            
         case MODE_EMA: // Exponential moving average
            {
               double alpha = 2.0 / (period + 1.0);
               OscillatorBuffer[i] = temp[i] * alpha + OscillatorBuffer[i-1] * (1.0 - alpha);
            }
            break;
            
         // ... other methods ...
      }
   }
}

リアプノフ指数が高いカオス的市場では、変化への反応が速いEMAを使用する方が適しています。一方、リアプノフ指数が低いより予測可能な市場では、SMA を用いることで、誤ったシグナルの発生を抑えつつ、より信頼性の高いシグナルを得ることができます。

結論

本研究では、単なるテクニカルインジケーターではなく、市場のカオスを分析するための完全なシステムを構築しました。Chaos Attractorオシレーターは、カオス理論、フラクタル幾何学、ニューラルネットワークにおける最新の成果を統合し、複雑かつ予測困難な市場環境をナビゲートするためのツールをトレーダーに提供します。

このインジケーターの特筆すべき価値は、売買シグナルを生成するだけでなく、リアプノフ指数を通じてその信頼性を評価できる点にあります。これにより、市場が予測可能なときには積極的に、カオス的なときには慎重にといった形で、戦略を現在の市場状況に適応させることが可能になります。

アルゴリズム取引と人工知能の時代において、市場の複雑な本質を最も的確にモデル化できる者が優位性を獲得します。Chaos Attractorオシレーターは、その方向への一歩であり、他者が単なるランダム性しか見いだせないところに秩序を見出すことを可能にします。

もっとも、どれほど高度なインジケーターであっても、成功を保証する魔法の公式ではありません。取引には常に、規律、リスク管理、市場環境への理解が求められます。しかし、市場カオスの本質を覗き込むことができるツールを手にすることで、一貫した利益への道において大きな優位性を得ることができます。

取引での成功を祈ります。そして、Chaos Attractorがあなたと共にありますように。