レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング

MetaTrader 5 — トレーディング | YYYY年08月DD日, 08:15

はじめに

この記事の目的は、トレーダーの方々に非常に効果的なニューラルネットワークの学習アルゴリズム、すなわちニュートン法の一種であるレーベンバーグ・マルカート法を提供することです。このアルゴリズムは順伝播型ニューラルネットワークの学習において最速の部類に入り、L-BFGS(Broyden-Fletcher-Goldfarb-Shanno)アルゴリズムと肩を並べる性能を持ちます。

確率的最適化法である確率的勾配降下法(SGD: Stochastic Gradient Descent)やAdam法は、長期間の学習によりニューラルネットワークが過学習するオフライン学習に適しています。しかし、トレーダーがニューラルネットワークを用いて、常に変化する市場状況に迅速に適応させたい場合には、各新しいバーの到来ごと、あるいは短期間ごとにオンラインで再学習させる必要があります。この場合、損失関数の勾配情報だけでなく、二階導函数に関する追加情報も用いて、わずか数エポックで損失関数の局所最小値を見つけられるアルゴリズムが最適です。

現時点で、私の知る限りMQL5でのレーベンバーグ・マルカート法の公開実装はありません。このギャップを埋めるとともに、記事の後半では勾配降下法、モーメンタム付き勾配降下法、確率的勾配降下法といった代表的でシンプルな最適化アルゴリズムについても簡単に解説します。最後に、レーベンバーグ・マルカート法とscikit-learn機械学習ライブラリのアルゴリズムの効率を比較する小さなテストをおこないます。

データセット

以降のすべての例では、説明を簡単にするために人工データを使用します。時間(time)が唯一の予測変数として使われ、ニューラルネットワークを用いて予測したい目的変数は次の関数です。

1 + sin(pi/4*time) + NormDistr(0,sigma)

この関数は、周期成分を持つ正弦波のような決定論的部分と、正規分布に従うホワイトノイズ（ランダム成分）から構成されています。データポイントは全部で81個あります。以下に、この関数と、それを三層パーセプトロンで近似したグラフを示します。

合成データ

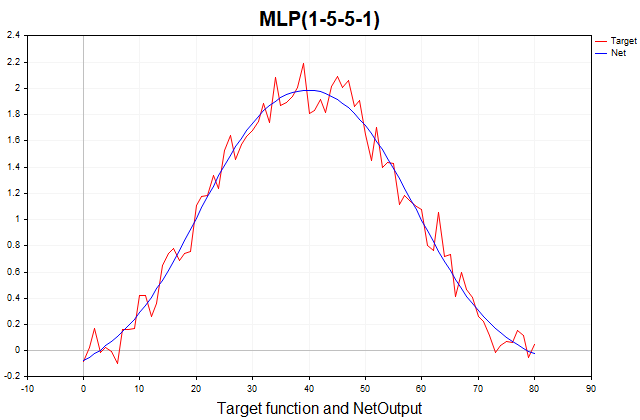
図1：目的関数と三層パーセプトロンによる近似

勾配降下法

まずは、ニューラルネットワークの学習における最も基本的な手法である通常の勾配降下法の実装から始めましょう。ここでは、MQL5リファレンス（行列とベクトルのメソッド/機械学習）にある非常に良い例をテンプレートとして使用します。私はこの例をいくつか修正し、ネットワークの最終層の活性化関数を選択可能にし、勾配降下法の実装を汎用的に変更し、リファレンスの例で暗黙的に想定されている二次損失関数だけでなく、MQL5で利用可能なすべての損失関数で学習できるようにしました。ニューラルネットワークの学習において、損失関数は非常に重要な役割を担っており、二次損失だけにこだわらず、さまざまな損失関数を試してみる価値があります。以下に、出力層の誤差（デルタ）を計算する一般的な式を示します。

デルタ最終層

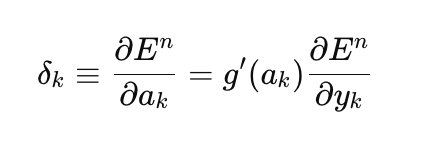
ここで

δₖ：出力層の誤差
E：損失関数
g′(aₖ)：活性化関数の導関数
aₖ：最終層の事前活性化値
yₖ：ネットワークの予測値

//--- Derivative of the loss function with respect to the predicted value       
matrix DerivLoss_wrt_y = result_.LossGradient(target,loss_func);  
matrix deriv_act;
  if(!result_.Derivative(deriv_act, ac_func_last)) 
     return false;      
 matrix  loss = deriv_act*DerivLoss_wrt_y;  // loss = delta_k

損失関数をネットワークの予測値に関して偏微分した結果は、LossGradient関数によって計算されます。一方、活性化関数の導関数はDerivative関数によって計算されます。リファレンスにある例では、出力層の誤差として、目標値とネットワークの予測値との差に2を掛けたものが使用されています。

matrix loss = (target - result_)*2;

機械学習の文献では、通常ネットワークの各層の誤差は「loss」ではなくdelta（たとえばD2、D1など）と呼ばれます（参考文献：Bishop (1995)）。これに従い、今後はコード中でもこのdeltaという表記を用います。

では、なぜこのような結果になるのでしょうか。ここでは暗黙的に、損失関数が目標値と予測値の残差平方和(SSE: Sum of Squared Errors)であると仮定されています。これは平均二乗誤差(MSE: Mean Squared Error)ではなく、学習サンプル数による正規化がされていないバージョンです。この損失関数を微分すると、導関数はちょうど「(target - result)*2」になります。そして、ネットワークの最後の層には恒等関数が活性化関数として使われており、その導関数は常に1です。したがって、上記の結果に自然とたどり着くわけです。そのため、任意の損失関数や出力層の活性化関数を用いてネットワークを学習させたい場合は、前述した一般的な出力層の誤差式を使用する必要があります。

それでは、実際に平均二乗誤差を使ってネットワークを学習させてみましょう。以下に、損失推移のグラフを対数スケールで表示しました。視認性を高めるためです。

損失SD

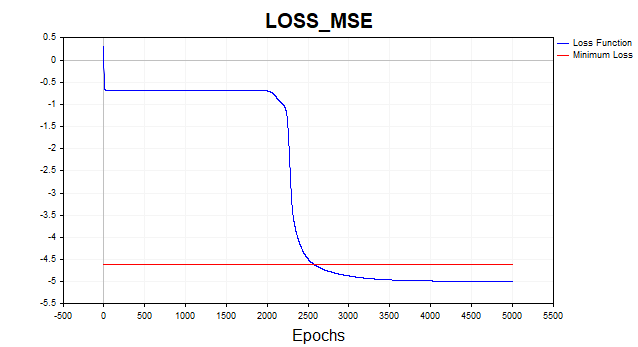
図2：MSE損失関数、勾配降下法

通常、勾配降下法アルゴリズムが損失関数の最小閾値に到達するまでには、平均して1500〜2000エポック（つまり、訓練データ全体に対する繰り返し回数）が必要です。今回の例では、各5ニューロンの隠れ層を2層使用しています。

グラフ上の赤い線は、損失関数の最小閾値を示しています。これは、ホワイトガウスノイズの分散によって定義されます。ここでは、分散0.01（つまり0.1σ * 0.1σ）のノイズを用いています。

では、この最小閾値以下までニューラルネットワークを学習させてしまうとどうなるでしょうか。その場合、過学習という望ましくない現象が発生します。訓練データに対する損失関数の誤差をこの最小閾値より下げようとするのは無意味であり、それをおこなうとテストデータに対する予測性能が低下してしまいます。ここで重要なポイントは、予測対象の系列の統計的なばらつきを超えて正確に予測することは不可能だということです。一方、最小閾値よりも高いところで学習を途中で止めてしまうと、今度は過小学習という問題が生じます。これは、ネットワークが系列の予測可能な成分を十分に捉えられていない状態を意味します。

ご覧の通り、勾配降下法は最適なパラメータを得るまでに非常に多くの反復を必要とします。ここで使っているデータセットは非常に単純なものですが、実際の実務的な問題では、この方法の学習時間は非現実的です。勾配降下法の収束性と速度を改善する最も単純な方法の一つが、次に紹介するモーメンタム法です。

モーメンタム付き勾配降下法

モーメンタム法の基本的な考え方は、ネットワークの学習中におけるパラメータの変化の軌跡を平滑化することです。これは、単純指数移動平均のようにパラメータを平均化することで実現されます。ちょうど、金融商品の価格の時系列データを移動平均で滑らかにして主要なトレンドを抽出するのと同じように、ここでは損失関数の局所最小点に向かって進むパラメータベクトルの軌跡を平滑化するのです。これをより直感的に理解するために、2つのパラメータの値が、学習の初期から損失関数の最小点に到達するまでにどのように変化したかを示したグラフを見てみましょう。図3は、モーメンタムを使用しなかった場合のパラメータの軌跡を示しています。

モーメンタムなしSD

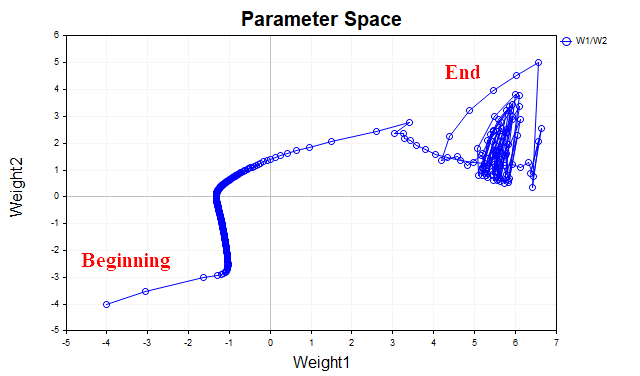
図3：勾配降下法（モーメンタムなし）

最小値に近づくにつれて、パラメータベクトルがカオス的に振動を始めることがわかります。このような現象が起きると、最適点にうまく到達できなくなります。この問題を解消するためには、学習率を下げる必要があります。もちろん、学習率を下げればアルゴリズムは収束に向かいますが、探索にかかる時間が大幅に増加する可能性があります。

図4は、モーメンタム（ここでは値を0.9）を使用した場合のパラメータベクトルの軌跡を示しています。今回は軌跡が明らかに滑らかになっており、最適点にもスムーズに到達できています。さらに、学習率を上げても問題なく学習が進むようになります。これこそが、モーメンタム付き勾配降下法の主な狙いです。つまり、収束速度を速めることです。

モーメンタム付きSD

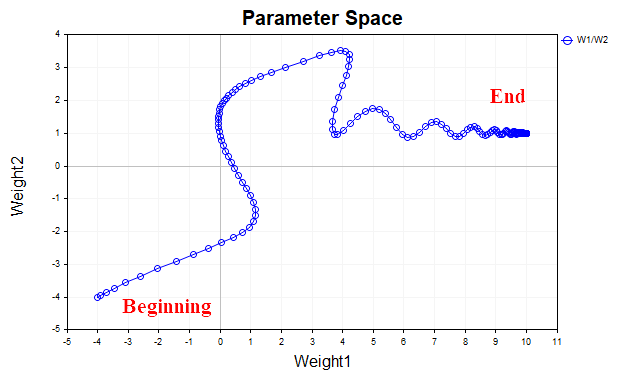
図4：勾配降下法、モーメンタム法(0.9)

Momentum_SDスクリプトでは、モーメンタム付き勾配降下法を実装しています。このアルゴリズムでは、ネットワークの重みとバイアスを分離し、構造をより明確に理解できるようにしました。また、隠れ層を1つに簡略化しています。具体的には、前の例では隠れ層が2つあり、それぞれに5個のニューロンがありましたが、今回は隠れ層を1つにして、20個のニューロンを持たせています。

//+------------------------------------------------------------------+
//|                                                  Momentum_SD.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,  
   target_netpredict_plot
  };
  
matrix weights1, weights2,bias1,bias2;                      // network parameter matrices
matrix dW1,db1,dW2,db2;                                     // weight increment matrices
matrix n1,n2,act1,act2;                                     // neural layer output matrices
input int    layer1                  = 20;                  // neurons Layer 1
input int    Epochs                  = 1000;                // Epochs
input double lr                      = 0.1;                 // learning rate coefficient
input double sigma_                  = 0.1;                 // standard deviation synthetic data
input double gamma_                  = 0.9;                 // momentum 
input Plots  plot_                   = LossFunction_plot;   // display graph
input bool   plot_log                = false;               // Plot Log graph
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;      // Activation Layer1
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR;    // Activation Layer2
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;     // Loss function

double LossPlot[],target_Plot[],NetOutput[];
matrix ones_;
int Sample_,Features; 

//+------------------------------------------------------------------+
//| Script start function                                            |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- generate a training sample
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }
   ones_ = matrix::Ones(1,Sample_);  
      
   ulong start=GetMicrosecondCount(); 
//--- train the model
   if(!Train(data, target, Epochs))
      return;
   ulong end = (GetMicrosecondCount()-start)/1000;  
   Print("Learning time = " + (string)end + " msc");
//--- generate a test sample
    Func(data,target);
    StandartScaler(data);
//--- test the model
   Test(data, target);
//--- display graphs  
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Model training method                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- create the model
   if(!CreateNet())
      return false;
   ArrayResize(LossPlot,Epochs);
//--- train the model
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- feed forward
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      LossPlot[ep] = act2.Loss(target, loss_func);
      //--- backpropagation and update of weight matrix
      if(!Backprop(data, target))
         return false;
     }
//---
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Cols(); i++)
     {
      NetOutput[i]  =act2.Transpose()[i,0];
     }
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Model creation method                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- initialize weight matrices
   if(!weights1.Init(layer1,Features)  || !weights2.Init(1,layer1)) 
      return false;
//--- initialize offset matrices
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))  
      return false;
//--- initialize the matrix of parameter increments
   dW1.Init(layer1,Features);
   dW2.Init(1, layer1);
   db1.Init(layer1,1);
   db2.Init(1,1);
   dW1.Fill(0);
   dW2.Fill(0);
   db1.Fill(0);
   db2.Fill(0);
//--- fill the parameter matrices with random values
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1,0.1);
   bias2.Random(-0.1,0.1);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Feed-forward method                                              |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  { 
//--- calculate the first neural layer
//--- n1 pre-activation of the first layer
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- calculate the activation function of the act1 first layer
   n1.Activation(act1, ac_func);
//--- calculate the second neural layer
//--- n2 pre-activation of the second layer
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- calculate the activation function of the act2 second layer
   n2.Activation(act2, ac_func_last);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Backpropagation method                                           |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- Derivative of the loss function with respect to the predicted value
   matrix DerivLoss_wrt_y = act2.LossGradient(target.Transpose(),loss_func);
   matrix deriv_act2;
   n2.Derivative(deriv_act2, ac_func_last);
//--- D2   
   matrix  D2 = deriv_act2*DerivLoss_wrt_y; // error(delta) of the network output layer
//--- D1
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = D1*deriv_act1; // error (delta) of the first layer of the network
//--- update network parameters
   matrix  ones = matrix::Ones(data.Rows(),1);
   dW1 = gamma_*dW1 + (1-gamma_)*(D1.MatMul(data)) * lr;
   db1 = gamma_*db1 + (1-gamma_)*(D1.MatMul(ones)) * lr;
   dW2 = gamma_*dW2 + (1-gamma_)*(D2.MatMul(act1.Transpose())) * lr;
   db2 = gamma_*db2 + (1-gamma_)*(D2.MatMul(ones)) * lr;
   weights1 =  weights1 - dW1;
   weights2 =  weights2 - dW2;
   bias1    =  bias1    - db1;
   bias2    =  bias2    - db2;
//--- return result
   return true;
  }

モーメンタムのおかげで、学習率を0.1から0.5に引き上げることができました。その結果、通常の勾配降下法では約500回の反復が必要だったところを、わずか150～200回の反復で収束するようになりました。

損失SDモーメンタム付き

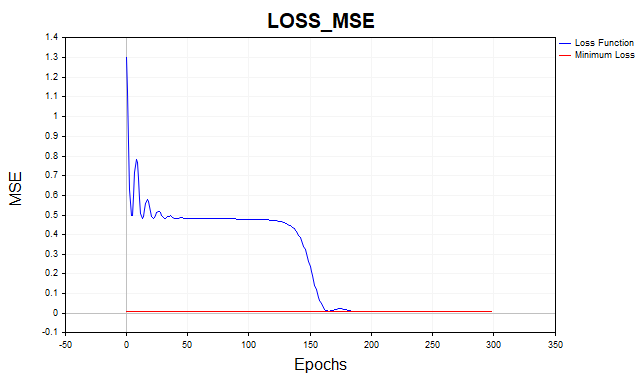
図5：MSE損失関数、MLP(1-20-1) SD_Momentum

確率的勾配降下法

モーメンタム法は有効ですが、データセットが私たちの例のように81個のデータポイントではなく、何万件ものデータインスタンスがある場合には、実績がありシンプルなアルゴリズムであるSGD（確率的勾配降下法）を使うのが理にかなっています。SGDは通常の勾配降下法と同様ですが、勾配を計算する際に訓練データ全体ではなく、そのごく一部（ミニバッチ）あるいは、場合によっては1つのデータポイントだけを用いる点が異なります。その後、ネットワークの重みを更新し、新たなデータポイントがランダムに選ばれ、プロセスが繰り返されます。このランダム性があるために「確率的」と呼ばれるのです。一方、通常の勾配降下法では、データセット全体で勾配を計算してから重みを一度だけ更新していました。これがいわゆるバッチ法です。

ここでは、1つのデータポイントのみを使ってミニバッチとするSGDのバリエーションを実装します。

損失SGD

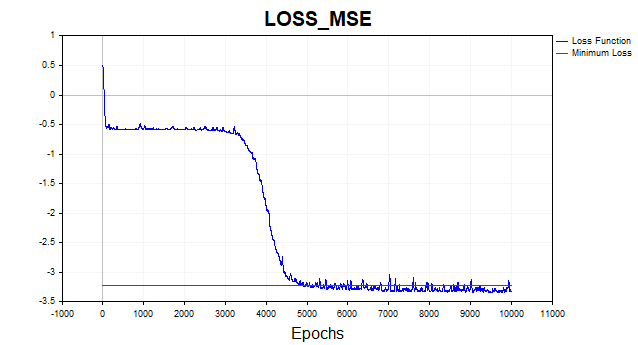
図6：対数スケールの損失関数、SGD

SGDアルゴリズム（バッチサイズ = 1）は、4,000〜6,000回の反復で最小値の境界に収束します。ただし、ここで忘れてはならないのは、81個ある訓練データのうちたった1つしか使ってパラメータベクトルを更新していないという点です。したがって、このアルゴリズムはおおよそ50〜75エポックで収束していることになります。前回のアルゴリズムと比べて、なかなかの改善だと思いませんか。ここでもモーメンタムを使用していますが、1つのデータポイントしか使わないため、収束速度への影響はあまり大きくありません。

レーベンバーグ・マルカートアルゴリズム

この古き良きアルゴリズムは、なぜか現在ではほとんど忘れ去られています。しかし、もしネットワークのパラメータ数が数百個程度であるならば、L-BFGSと並んでこれに勝るものはありません。

ただし、重要なポイントが1つあります。LMアルゴリズムは、他の非線形関数の二乗和の形をした関数を最小化するように設計されています。したがって、この手法では損失関数として二次損失またはRMSE(Root Mean Square Loss)のみに限定されます。条件が同じであれば、この損失関数は非常にうまく機能するため、大きな問題はありませんが、他の損失関数を使ってネットワークを学習させることはできないという制限があります。

それでは、このアルゴリズムがどのように登場したのか、詳しく見ていきましょう。まずはニュートン法から始めます。

ニュートン法

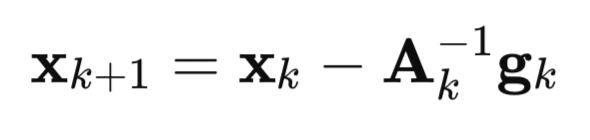
ここで

A：F(x)損失関数のヘッセ行列の逆行列

g：F(x)損失関数の勾配

x：パラメータベクトル

次に、二次損失関数を見てみましょう。

SSE

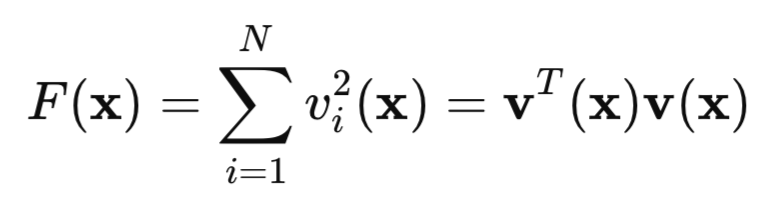
ここで、vはネットワークの誤差（予測値 − 目標値）、xはネットワークのすべての重みやバイアスを含むパラメータベクトルです。

この損失関数の勾配を見つけてみましょう。

勾配SSE損失関数

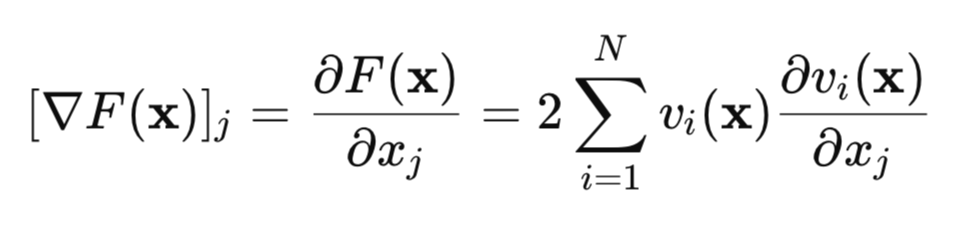
行列形式では、次のように記述できます。

行列表記の勾配

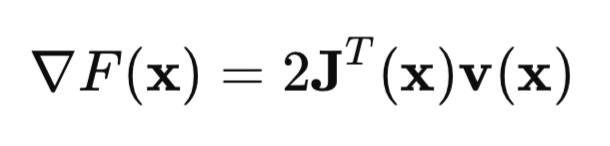
重要な点はヤコビ行列です。

ヤコビ行列

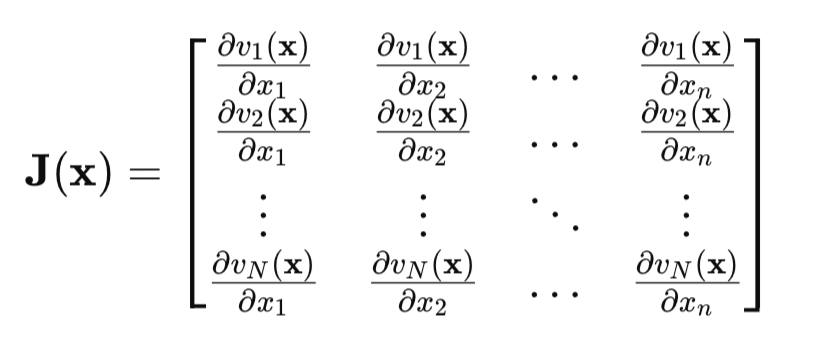
ヤコビ行列では、各行が「ネットワーク誤差をすべてのパラメータで偏微分したもの」を含んでいます。つまり、各行は訓練データの1つのサンプルに対応します。

それではヘッセ行列を見てみましょう。これは損失関数の二階導函数をすべて含む行列です。しかし、このヘッセ行列を正確に計算するのは非常に複雑かつ計算コストが高いため、代わりにヤコビ行列を使って近似します。

ヘッセ行列

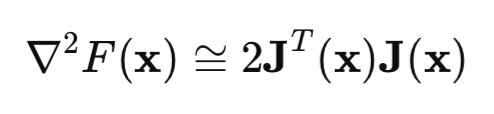
ヘッセ行列と勾配方程式をニュートン法の方程式に代入すると、ガウス・ニュートン法が得られます。

しかし、ガウス・ニュートン法には1つ大きな問題があります。それは、行列[J'J]が可逆でない可能性があるという点です。この問題を解決するために、単位行列に正のスカラー𝜇*Iを掛けたものを行列に加えます。この場合、レーベンバーグ・マルカートアルゴリズムが得られます。

レーベンバーグ・マルカート法

このアルゴリズムの特徴は、パラメータ𝜇が大きな正の値を取ると、記事の最初で述べた通常の勾配降下法に帰着する点です。逆に𝜇がゼロに近づくと、ガウス・ニュートン法に戻ります。

通常、学習は小さな𝜇の値から始まります。損失関数の値が減少しない場合、𝜇の値を増やします（たとえば10倍にする）。これは勾配降下法に近づくことを意味し、遅かれ早かれ損失関数の減少が得られます。損失関数が減少した場合、𝜇の値を小さくして、より高速に最小点へ収束するためにガウス・ニュートン法を適用します。これがレーベンバーグ・マルカート法の主なアイデアです。つまり、勾配降下法とガウス・ニュートン法の間を常に切り替えるというものです。

レーベンバーグ・マルカートアルゴリズムにおける誤差逆伝播法の実装には独自の特徴があります。ヤコビ行列の要素はネットワーク誤差の偏導関数であり、誤差の二乗ではないため、記事の最初で示したネットワークの最後の層のデルタを求める式が簡略化されます。今やデルタは単に最後の層の活性化関数の導関数に等しくなります。この結果は、ネットワーク誤差(y – target)をyで微分したときに得られ、その値は明らかに1だからです。

以下が詳しいコメント付きのニューラルネットワークのコードです。

//+------------------------------------------------------------------+
//|                                                           LM.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,
   mu_plot,
   gradient_plot,
   target_netpredict_plot
  };

matrix weights1,weights2,bias1,bias2;                    // network parameter matrices
matrix n1,n2,act1,act2,new_n1,new_n2,new_act1,new_act2;  // neural layer output matrices
input int    layer1     = 20;                            // neurons Layer 1
input int    Epochs     = 10;                            // Epochs
input double Initial_mu = 0.001;                         // mu
input double Incr_Rate  = 10;                            // increase mu
input double Decr_Rate  = 0.1;                           // decrease mu
input double Min_grad   = 0.000001;                      // min gradient norm
input double Loss_goal  = 0.001;                         // Loss goal
input double sigma_     = 0.1;                           // standard deviation synthetic data
input Plots  plot_      = LossFunction_plot;             // display graph
input bool   plot_log   = false;                         // logarithmic function graph 
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;   // first layer activation function
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR; // last layer activation function
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;  // Loss function

double LossPlot[],NetOutput[],mu_Plot[],gradient_Plot[],target_Plot[];
matrix ones_;
double old_error,gradient_NormP2;
double mu_ = Initial_mu;
bool break_forloop = false;
int Sample_,Features;

//+------------------------------------------------------------------+
//| Script start function                                            |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- generate a training sample
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }

   ones_ = matrix::Ones(1,Sample_);
//--- train the model
   ulong start=GetMicrosecondCount();
   Train(data, target, Epochs);
   ulong end = (GetMicrosecondCount()-start)/1000 ;
   Print("Learning time = " + (string)end + " msc");
   int NumberParameters = layer1*(Features+1) + 1*(layer1+1);
   Print("Number Parameters of NN = ",NumberParameters);

//--- generate a test sample
   Func(data,target);
   StandartScaler(data);
//--- test the model
   Test(data,target);
   
//--- display graphs
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Model training method                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- create the model
   if(!CreateNet())
      return false;
//--- train the model
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- feed forward
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      //--- arrays for graphs
      ArrayResize(LossPlot,ep+1,10000);
      ArrayResize(mu_Plot,ep+1,10000);
      ArrayResize(gradient_Plot,ep+1,10000);
      LossPlot[ep]       = act2.Loss(target, loss_func);
      mu_Plot [ep]       = mu_;
      gradient_Plot[ep]  = gradient_NormP2;
      //--- Stop training if the target value of the loss function is reached
      if(break_forloop == true){break;}
      //--- backpropagation and update of weight matrix
      if(!Backprop(data, target))
         return false;
     }
//--- Euclidean norm of gradient, mu parameter, RMSE metric
   Print("gradient_normP2 =  ", gradient_NormP2);
   Print(" mu_ = ", mu_);
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
//--- array of network output for graph
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Transpose().Rows(); i++)
     {
      NetOutput[i]  = act2.Transpose()[i,0];
     }
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Model creation method                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- initialize weight matrices
   if(!weights1.Init(layer1,Features) || !weights2.Init(1,layer1))
      return false;
//--- initialize offset matrices
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))
      return false;
//--- fill the weight matrices with random values
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1, 0.1);
   bias2.Random(-0.1, 0.1);   
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Feed-forward method                                              |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- calculate the first neural layer
//--- n1 pre-activation of the first layer
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- calculate the activation function of the act1 first layer
   n1.Activation(act1, ac_func);
//--- calculate the second neural layer
//--- n2 pre-activation of the second layer
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- calculate the activation function of the act2 second layer
   n2.Activation(act2, ac_func_last);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Backpropagation method                                           |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- current value of the loss function
   old_error = act2.Loss(target, loss_func);
//--- network error (quadratic loss function)
   matrix loss = act2.Transpose() - target ;
//--- derivative of the activation function of the last layer
   matrix D2;
   n2.Derivative(D2, ac_func_last);
//--- derivative of the first layer activation function
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
//--- first layer network error
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = deriv_act1 * D1;
//--- first partial derivatives of network errors with respect to the first layer weights
   matrix jac1;
   partjacobian(data.Transpose(),D1,jac1);
//--- first partial derivatives of network errors with respect to the second layer weights
   matrix jac2;
   partjacobian(act1,D2,jac2);
//--- Jacobian
   matrix j1_D1 = Matrixconcatenate(jac1,D1.Transpose(),1);
   matrix j2_D2 = Matrixconcatenate(jac2,D2.Transpose(),1);
   matrix jac   = Matrixconcatenate(j1_D1,j2_D2,1);
// --- Loss function gradient
   matrix je = (jac.Transpose().MatMul(loss));
//--- Euclidean norm of gradient normalized to sample size
   gradient_NormP2 = je.Norm(MATRIX_NORM_FROBENIUS)/Sample_;
   if(gradient_NormP2 < Min_grad)
     {
      Print("Local minimum. The gradient is less than the specified value.");
      break_forloop = true; // stop training
      return true;
     }
//--- Hessian
   matrix Hessian = (jac.Transpose().MatMul(jac));
   matrix I=matrix::Eye(Hessian.Rows(), Hessian.Rows());
//---
   break_forloop = true;
   while(mu_ <= 1e10 && mu_ > 1e-20)
     {
      matrix H_I = (Hessian + mu_*I);
      //--- solution via Solve
      vector v_je = je.Col(0);
      vector Updatelinsolve = -1* H_I.Solve(v_je);
      matrix Update = matrix::Zeros(Hessian.Rows(),1);
      Update.Col(Updatelinsolve,0); // increment of the parameter vector
      
      //--- inefficient calculation of inverse matrix
      //   matrix Update = H_I.Inv();
      //   Update = -1*Update.MatMul(je);
      //---

      //--- save the current parameters
      matrix  Prev_weights1 = weights1;
      matrix  Prev_bias1    = bias1;
      matrix  Prev_weights2 = weights2;
      matrix  Prev_bias2    = bias2;
      //---

      //--- update the parameters
      //--- first layer
      matrix updWeight1 = matrix::Zeros(layer1,Features);
      int count =0;
      for(int j=0; j <Features; j++)
        {
         for(int i=0 ; i <layer1; i++)
           {
            updWeight1[i,j] = Update[count,0];
            count = count+1;
           }
        }

      matrix updbias1 = matrix::Zeros(layer1,1);
      for(int i =0 ; i <layer1; i++)
        {
         updbias1[i,0] = Update[count,0];
         count = count +1;
        }
        
      weights1 = weights1 + updWeight1;
      bias1 = bias1 + updbias1;

      //--- second layer
      matrix updWeight2 = matrix::Zeros(1,layer1);
      for(int i =0 ; i <layer1; i++)
        {
         updWeight2[0,i] = Update[count,0];
         count = count +1;
        }
      matrix updbias2 = matrix::Zeros(1,1);
      updbias2[0,0] = Update[count,0];

      weights2 = weights2 + updWeight2;
      bias2 = bias2 + updbias2;

      //--- calculate the loss function for the new parameters
      new_n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
      new_n1.Activation(new_act1, ac_func);
      new_n2 = weights2.MatMul(new_act1) + bias2.MatMul(ones_);
      new_n2.Activation(new_act2, ac_func_last);
      //--- loss function taking into account new parameters
      double new_error = new_act2.Loss(target, loss_func);
      //--- if the loss function is less than the specified threshold, terminate training
      if(new_error < Loss_goal)
        {
         break_forloop = true;
         Print("Training complete. The desired loss function value achieved");
         return true;
        }
      break_forloop = false;
      //--- correct the mu parameter
      if(new_error >= old_error)
        {
         weights1 = Prev_weights1;
         bias1    = Prev_bias1;
         weights2 = Prev_weights2;
         bias2    =  Prev_bias2;
         mu_ = mu_*Incr_Rate;
        }
      else
        {
         mu_ = mu_*Decr_Rate;
         break; 
        }

     }
//--- return result
   return true;
  }

アルゴリズムは、勾配ノルムがあらかじめ定められた値より小さい場合、または損失関数が所定のレベルに達した場合に収束します。アルゴリズムは、𝜇パラメータがあらかじめ定められた値より小さくなるか大きくなるか、あるいは所定のエポック数に達した場合に停止します。

LMパラメータ

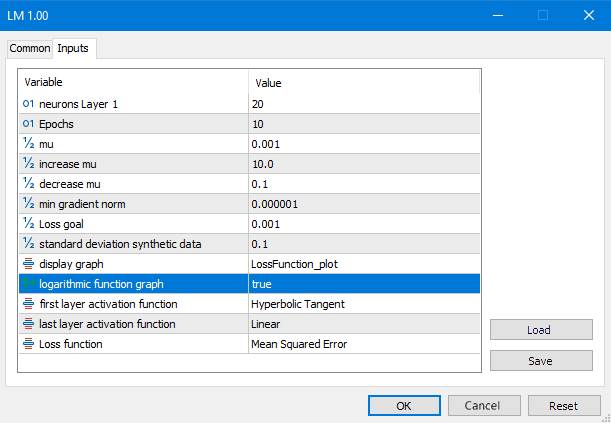
図7：LMスクリプトパラメータ

この計算の結果を見てみましょう。

損失LM

図8：対数スケールの損失関数、LM

今ではまったく異なる様相を呈しています。アルゴリズムはわずか6回の反復で最小値の境界に到達しました。では、もしこのネットワークを1000エポック学習させたらどうなるでしょうか。典型的な過学習が発生することになります。下の図がそれをよく示しています。ネットワークは単にガウスノイズを記憶し始めているのです。

過学習LM

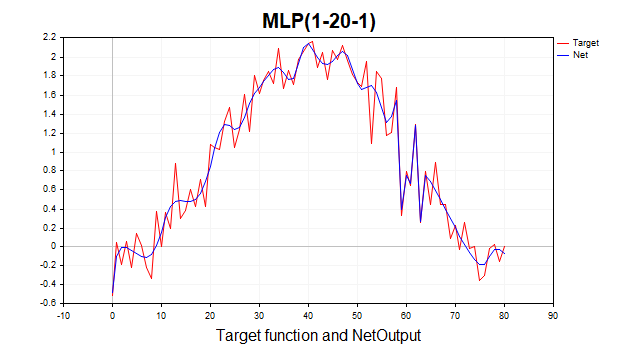
図9：典型的な過学習、LM、1000エポック

それでは、訓練データセットとテストデータセットにおける評価指標を見てみましょう。

パフォーマンスLM

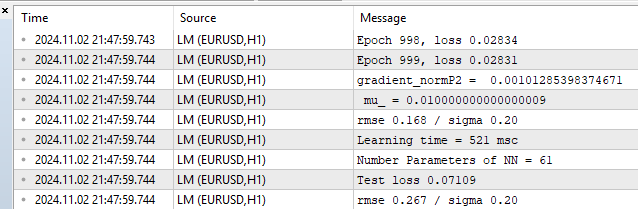
図10：パフォーマンス統計、LM、1000エポック

RMSEが0.168となっており、これは下限の0.20を下回っています。そしてその直後、テストセットでは過学習の代償としてRMSEが0.267に跳ね上がっています。

ビッグデータでのテストとPythonのsklearnライブラリとの比較

そろそろ、より現実的な例で我々のアルゴリズムをテストする時です。今回は、2つの特徴量を持つ1000個のデータポイントを使用しました。このデータとともに、記事の最後にあるLM_BigDataスクリプトをダウンロードすることができます。 LM（レーベンバーグ・マーカート法）は、Pythonライブラリのアルゴリズム、SGD、Adam、そしてL-BFGSと競います。

Pythonのテストスクリプトはこちらです。

# Eugene
# https://www.mql5.com

import numpy as np
import time 
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neural_network import MLPRegressor

# here is your path to the data
df = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Data.csv',delimiter=';')
X = df.to_numpy()
df1 = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Target.csv')
y = df1.to_numpy()
y = y.reshape(-1)

start = time.time() 

'''
clf = MLPRegressor(solver='sgd', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=700,batch_size=10,
                    learning_rate_init=0.01,momentum=0.9,
                    shuffle = False,n_iter_no_change = 2000, tol = 0.000001)
'''

'''
clf = MLPRegressor(solver='adam', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=3000,batch_size=100,                                    
                    learning_rate_init=0.01,
                    n_iter_no_change = 2000, tol = 0.000001)
'''

#'''
clf = MLPRegressor(solver='lbfgs', alpha=0.0, 
                    hidden_layer_sizes=(100),
                    activation='tanh',max_iter=300,
                    tol = 0.000001)
#'''                    
                       
clf.fit(X, y)
end = time.time() - start          # training time

print("learning time  =",end*1000) 
print("solver = ",clf.solver);      
print("loss = ",clf.loss_*2)
print("iter = ",clf.n_iter_)
#print("n_layers_ = ",clf.n_layers_)
#print("n_outputs_ = ",clf.n_outputs_)
#print("out_activation_ = ",clf.out_activation_)

coef = clf.coefs_
#print("coefs_ = ",coef)
inter = clf.intercepts_  
#print("intercepts_ = ",inter) 
plt.plot(np.log(pd.DataFrame(clf.loss_curve_)))
plt.title(clf.solver)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

アルゴリズムを正しく比較するために、Python側の損失関数に2を掛けました。というのも、このライブラリでは損失関数が以下のように計算されているためです。

return ((y_true - y_pred) ** 2).mean() / 2

つまり、開発者がMSEをさらに2で割っているのです。以下に、各最適化アルゴリズムによる典型的な結果を示します。これらのアルゴリズムに対しては、最適なハイパーパラメータ設定を見つけようと努めました。ただし、残念ながらこのライブラリではすべてのアルゴリズムがパラメトリック空間の同じ初期点から開始するように初期パラメータ値を設定する機能がありません。また、損失関数の目標閾値を設定する機能もありません。LMでは損失関数の目標値は0.01に設定されており、Pythonのアルゴリズムに対しては、おおよそ同じレベルに達するような反復回数を設定して比較しました。

1つの隠れ層（20ニューロン）を持つMLPのテスト結果：

1) 確率的勾配降下法

損失関数MSE：0.00278
学習時間：11459ミリ秒

SGD損失Python

図11：SGD、20ニューロン、損失 = 0.00278

2) Adam

損失関数MSE：0.03363
学習時間：8581ミリ秒

Adam損失

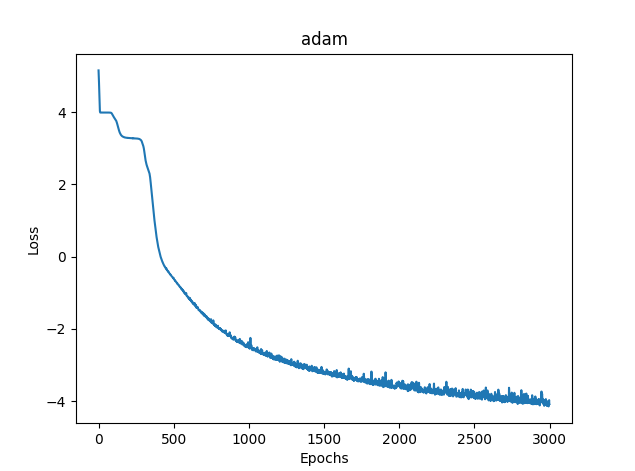
図12：Adam、20ニューロン、損失 = 0.03363

3) L-BFGS

損失関数MSE：0.02770
学習時間：277ミリ秒

残念ながら、L-BFGSの損失関数グラフを表示することはできません。

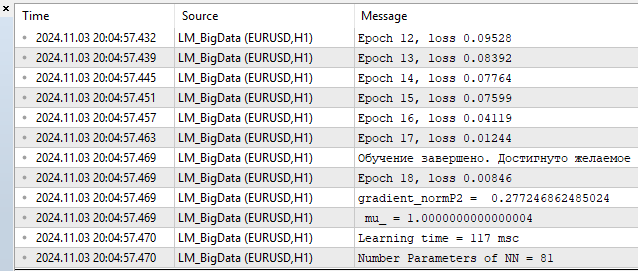
4) LM MQL5

損失関数MSE：0.00846
学習時間：117ミリ秒

LM損失

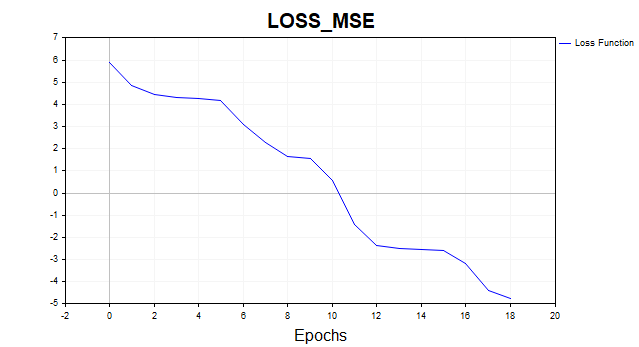
図13：LM、20ニューロン、損失 = 0.00846

パフォーマンスLM

私の感想としては、このアルゴリズムはL-BFGSと十分に競合でき、場合によってはそれに先行することすら可能です。しかし、完璧なものは存在しません。パラメータ数が増えるにつれて、レーベンバーグ・マルカート法はL-BFGSに劣り始めます。

100ニューロンL-BFGS：

損失関数MSE：0.00847
学習時間：671ミリ秒

100ニューロンLM：

損失関数MSE：0.00206
学習時間：1253ミリ秒

100ニューロンはネットワークパラメータ401個に相当します。これが「多い」と感じるか「少ない」と感じるかは読者次第ですが、個人的には明らかに過剰なパワーだと思います。ニューロン数が100未満のケースでは、LMは明確な優位性を示しています。

結論

本記事では、基本的かつ最もシンプルなニューラルネットワークの学習アルゴリズムについて解説・実装しました。

勾配降下法
モーメンタム付き勾配降下法
確率的勾配降下法

あわせて、ニューラルネットワークの収束と過学習の問題にも簡単に触れました。

そして何より、小規模なネットワークのオンライン学習に理想的な、非常に高速なレーベンバーグ・マルカートアルゴリズムを構築しました。

また、scikit-learnライブラリで使用されているニューラルネットワーク学習アルゴリズムとの性能比較もおこない、パラメータ数が400個（隠れ層で100ニューロン）以下のとき、本アルゴリズムが最速であることが示されました。それ以上の規模になると、L-BFGSが優位になります。

すべてのアルゴリズムについて、詳しいコメント付きの個別スクリプトを用意しています。

#	名前	種類	詳細
1	SD.mq5	スクリプト	勾配降下法
2	Momentum_SD.mq5	スクリプト	モーメンタム付き勾配降下法
3	SGD.mq5	スクリプト	確率的勾配降下法
4	LM.mq5	スクリプト	レーベンバーグ・マルカートアルゴリズム
5	LM_BigData.mq5	スクリプト	LMアルゴリズム、2次元特徴量のテスト
6	SklearnMLP.py	スクリプト	Pythonアルゴリズムのテスト
7	FileCSV.mqh	インクルード	データを含むテキストファイルの読み取り
8	Data.csv、Target.csv	CSVファイル	Pythonスクリプトの特徴量と目標変数
9	X1.txt、X2.txt、Target.txt	TXT	LM_BigData.mq5スクリプトの特徴と目的

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16296

添付されたファイル |

ZIPをダウンロード

SD.mq5 (26.15 KB)

SGD.mq5 (26.16 KB)

Momentum_SD.mq5 (22.59 KB)

LM.mq5 (36.21 KB)

LM_BigData.mq5 (36.15 KB)

FileCSV.mqh (10.45 KB)

X1.txt (19.26 KB)

X2.txt (19.26 KB)

Target.txt (17.62 KB)

Data.csv (37.56 KB)

Target.csv (17.62 KB)

SklearnMLP.py (1.83 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (6)

Evgeniy Chernish | 8 11月 2024 において 08:52

フィードバックありがとう。

パイソンではこれはエラーではなく、アルゴリズムが反復限界に達したため停止したことを警告しています。つまり、値tol = 0.000001に達する前にアルゴリズムが停止しました。そして、lbfgsオプティマイザが "loss_curve "属性、つまり損失関数のデータを持っていないことを警告します。adamとsgdにはあるのだが、lbfgsにはなぜかない。おそらく、lbfgsが起動したときにこのプロパティを要求しないようにスクリプトを作るべきだったのだろう。

SDについて。パラメータ空間の異なる点から毎回スタートするので、解への道筋も違ってきます。私は多くのテストを行いましたが、収束するまでに本当に多くの反復回数がかかることがあります。平均的な反復回数を示してみました。反復回数を増やせば、最終的にアルゴリズムが収束するのがわかるでしょう。

Andrey Dik | 8 11月 2024 において 09:32

Evgeniy Chernish #:

SDについて。パラメータ空間の異なる点から毎回スタートするので、解に収束するまでの経路も異なります。私は多くのテストを行いましたが、収束するまでに本当に多くの反復を要することもありました。平均的な反復回数を示してみました。反復回数を増やせば、アルゴリズムが最終的に収束するのがわかるでしょう。

それが私の言っていることです。ロバスト性、つまり結果の再現性です。結果のばらつきが大きいほど、そのアルゴリズムは与えられた問題に対してRNDに近いということです。

ここに3つの異なるアルゴリズムがどのように機能するかの例を示します。どれがベストでしょうか？一連の独立したテストを実行し、平均結果を計算しない限り（理想的には、最終結果の分散を計算して比較する）、比較することは不可能です。

Evgeniy Chernish | 8 11月 2024 において 09:52

Andrey Dik #:

私が言っているのはそのことだ。安定性、つまり結果の再現性です。結果のばらつきが大きいほど、そのアルゴリズムは与えられた問題に対してRNDに近いということです。

そこで、評価基準を定義する必要があります。

時間や最大結果（関数の最小値を求める場合は最小値）を基準にすることができます。

再スタートの回数を設定する。

この再試行回数で達成された最大値とそれにかかった時間を記録する。

このようなテストを1000回とする。

そしてこの一連の平均と分散、つまり最大値の平均と分散を計算する。

結果の分布密度の構築まで、ほとんど徹底的にやったわけではないので、1つの記事ですべてをカバーすることは不可能である。

Maxim Dmitrievsky | 8 11月 2024 において 11:43

この記事は追加テストなしで素晴らしく、アルゴリズムに関する一般的な結論と一致している :)これによって、すぐに何かに合意し、次のトピックに移ることができる。

Andrey Dik | 8 11月 2024 において 11:44

Evgeniy Chernish #:
次に評価基準を定義する必要がある。

評価基準としては、時間と最大結果を取ることができる（関数の最小値を求める必要がある場合は最小値を取ることもできる）。

再スタートの回数を設定する。

この再スタート回数で達成された最大値と、それにかかった時間を記録する。

このようなテストを1000回とする。

そしてこの一連の平均と分散、すなわち最大値の平均と分散を計算する。

結果の分布密度の構築まで，ほとんど徹底的にやったわけではないので，1つの記事ですべてをカバーすることは不可能である。

いや、この場合はそんな面倒なことをする必要はないが、もし異なる方法を比較するのであれば、もう1サイクル（独立試験）を追加して、個々の試験のグラフをプロットすることができる。そうすれば、誰が収束したのか、どの程度安定しているのか、何回繰り返せば収束するのか、すべてが明確になる。それで、結果は素晴らしいが、100万回に1回しかない「前回のような」結果になった。

とにかく、ありがとう。この記事は私に興味深い考えを与えてくれた。

取引におけるニューラルネットワーク：双曲潜在拡散モデル(HypDiff)

この記事では、異方性拡散プロセスを用いた双曲潜在空間における初期データのエンコーディング手法について検討します。これにより、現在の市場状況におけるトポロジー的特徴をより正確に保持でき、分析の質が向上します。

Pythonによる農業国通貨への天候影響分析

天候と外国為替にはどのような関係があるのでしょうか。古典的な経済理論は、天候のような要因が市場の動きに与える影響を長い間無視してきました。しかし、すべてが変わりました。天候条件と農業通貨の市場でのポジションとの間に、どのようなつながりがあるのかを探ってみましょう。

取引におけるニューラルネットワーク：双曲潜在拡散モデル（最終回）

HypDiffフレームワークで提案されているように、双曲潜在空間における初期データのエンコーディングに異方性拡散プロセスを用いることで、現在の市場状況におけるトポロジー的特徴を保持しやすくなり、分析の質を向上させることができます。前回の記事では、提案されたアプローチの実装をMQL5を用いて開始しました。今回はその作業を継続し、論理的な完結に向けて進めていきます。

リプレイシステムの開発（第73回）：異例のコミュニケーション(II)

この記事では、インジケーターとサービス間でリアルタイムに情報を伝達する方法について解説し、また時間軸を変更した際に発生しうる問題の原因とその解決方法について理解を深めます。おまけとして、最新バージョンのリプレイ/シミュレーションアプリへのアクセスも提供します。