Entrenamos un perceptrón multicapa usando el algoritmo de Levenberg-Marquardt

MetaTrader 5 — Trading | 27 mayo 2025, 07:41

149

Evgeniy Chernish

Introducción

El objetivo de este artículo será ofrecer a los tráders en activo un algoritmo eficaz para entrenar redes neuronales, una variante del método de optimización newtoniano conocido como algoritmo de Levenberg-Marquardt. Se trata de uno de los algoritmos más rápidos para entrenar redes neuronales de propagación directa, al que solo puede plantar cara el algoritmo Broyden-Fletcher-Goldfarb-Shanno (L-BFGS).

Los métodos de optimización estocástica, como el descenso de gradiente estocástico (SGD) y Adam, resultan muy adecuados para el entrenamiento offline cuando la red neuronal se reentrena durante largos periodos de tiempo. Si un tráder que utiliza redes neuronales quiere que el modelo se adapte rápidamente a unas condiciones comerciales en cambio constante, necesitará reentrenar la red online en cada nueva barra, o tras un breve periodo de tiempo. En tal caso, los algoritmos que, además de información sobre el gradiente de la función de pérdida, también usan información adicional sobre las segundas derivadas parciales, lo cual permitirá encontrar el mínimo local de la función de pérdida en unas pocas épocas de entrenamiento.

De momento, que yo sepa, no existe ninguna implementación de acceso abierto del algoritmo Levenberg-Marquardt en MQL5. Así que ha llegado la hora de llenar este vacío, y también de repasar brevemente los algoritmos de optimización más conocidos y sencillos, como el descenso de gradiente, el descenso de gradiente con impulso y el descenso de gradiente estocástico. Al final del artículo, realizaremos algunas pruebas de rendimiento del algoritmo Levenberg-Marquardt y de algoritmos de la biblioteca de aprendizaje automático scikit-learn.

El conjunto de datos

En todos los ejemplos siguientes se usarán datos sintéticos para simplificar la presentación. Como única variable predictiva se utilizará el tiempo, mientras que, en calidad de variable objetivo que queremos predecir utilizando la red neuronal, se usará la función:

1 + sin(pi/4*time) + NormDistr(0,sigma)

Esta función constará de una parte determinista, representada por un componente periódico en forma de seno, y una parte estocástica, representada por ruido blanco gaussiano. En total, tendremos 81 puntos de datos. A continuación le mostramos un gráfico de esta función y su aproximación mediante un perceptrón de tres capas.

SyntheticData

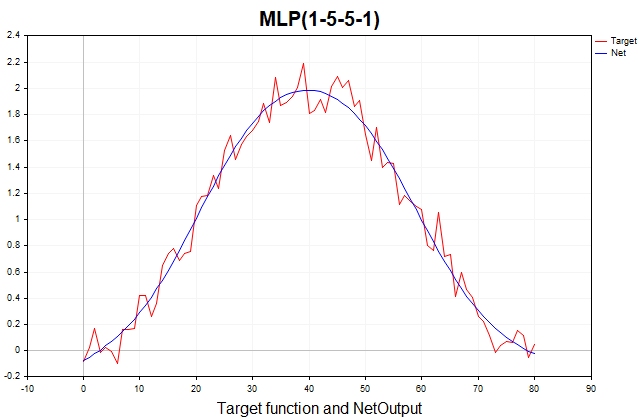
Fig.(1) La función objetivo y su aproximación usando un perceptrón de tres capas

Descenso de gradiente

Comenzaremos aplicando el descenso de gradiente ordinario como método más sencillo para entrenar redes neuronales. Para ello, utilizaremos como plantilla un ejemplo muy bueno del libro de referencia MQL5 (Métodos de matrices y vectores/Aprendizaje automático). Lo hemos modificado ligeramente añadiendo la posibilidad de seleccionar la función de activación para la última capa de la red y haciendo universal la implementación del descenso de gradiente, capaz de aprender no solo con la función de pérdida cuadrática, como se supone implícitamente en el ejemplo del libro de referencia, sino con todas las funciones de pérdida disponibles en MQL5. La función de pérdida resulta fundamental para el entrenamiento de redes neuronales, y a veces merecerá la pena experimentar con distintas funciones más allá de la pérdida cuadrática. Aquí tenemos la fórmula general para calcular el error de la capa de salida (delta):

delta last layer

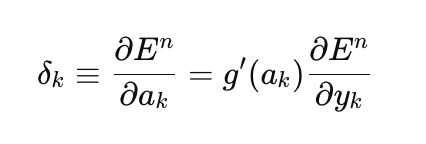
aquí,

delta_k — error de la capa de salida,
E — función de pérdida,
g'(a_k) — derivada de la función de activación,
a_k — preactivación de la última capa,
y_k — valor predicho de la red.

//--- Производная функции потерь по предсказанному значению       
matrix DerivLoss_wrt_y = result_.LossGradient(target,loss_func);  
matrix deriv_act;
  if(!result_.Derivative(deriv_act, ac_func_last)) 
     return false;      
 matrix  loss = deriv_act*DerivLoss_wrt_y;  // loss = delta_k

Las derivadas parciales de la función de pérdida sobre el valor predicho de la red se calcularán mediante la función LossGradient, mientras que la derivada de la función de activación se calculará mediante la función Derivative. En el ejemplo de la referencia, la diferencia entre el valor objetivo y el valor predicho de la red multiplicado por 2 se utilizará como error de la capa de salida.

matrix loss = (target - result_)*2;

En la literatura sobre aprendizaje automático, el error de cada capa de la red suele denominarse delta(D2,D1, etc.) en lugar de pérdida (véase, por ejemplo, Bishop(1995)). En el futuro, utilizaremos esta denominación concreta en el código.

Bien, ¿cómo hemos llegado a este resultado? Aquí asumiremos implícitamente que la función de pérdida es la suma de cuadrados de las diferencias entre el valor objetivo y el predicho, en lugar del error cuadrático medio (ECM), que además se normalizará por el tamaño de la muestra de entrenamiento. La derivada de esta función de pérdida será exactamente igual a (target - result)*2. Y como la última capa de la red utiliza una función de activación idéntica cuya derivada es igual a uno, llegaremos a este resultado. Por lo tanto, aquellos que deseen usar funciones de pérdida arbitrarias y funciones de activación de la capa de salida para entrenar la red deberán utilizar la fórmula general anterior.

Vamos a entrenar ahora nuestra red con la función de pérdida RMS. Aquí, para mayor claridad, hemos representado el gráfico en escala logarítmica.

Loss SD

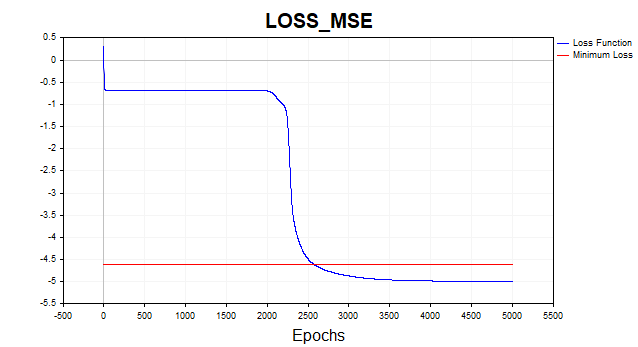
Fig.2 Función de pérdida MSE, descenso de gradiente

Por término medio, el algoritmo de descenso de gradiente necesita 1.500-2.000 épocas (es decir, pasadas por todo el conjunto de datos de entrenamiento) para alcanzar el umbral mínimo de la función de pérdida. Para ello, hemos utilizado dos capas ocultas de 5 neuronas cada una.

La línea roja del gráfico indica el umbral mínimo de la función de pérdida. Se define como la varianza del ruido blanco gaussiano. Aquí hemos utilizado ruido con una varianza igual a 0,01 (0,1 sigma* 0,1 sigma).

¿Qué ocurrirá si dejamos que el modelo de red neuronal se entrene por debajo de este umbral mínimo? Entonces nos encontraremos con un fenómeno indeseable como el sobreentrenamiento de la red. No tiene sentido intentar que el error de la función de pérdida con el conjunto de datos de entrenamiento sea inferior a un umbral mínimo, ya que esto afectará al poder predictivo del modelo con el conjunto de datos de prueba. Y aquí nos enfrentaremos al hecho de que es imposible predecir una serie con más exactitud de la que permite la dispersión estadística de dicha serie. Si dejamos de aprender por encima del umbral mínimo, nos enfrentaremos a otro problema: la red estará poco entrenada. Es decir, tendremos una red que no habrá comprendido plenamente el componente predictivo de la serie.

Como podemos ver, el descenso de gradiente necesita pasar por bastantes iteraciones para alcanzar el conjunto óptimo de parámetros. Y eso en el caso de un conjunto de datos sencillo como el nuestro. Para los problemas prácticos reales, el tiempo de entrenamiento del descenso de gradiente resulta inaceptable. Una de las formas más sencillas de mejorar la convergencia y la velocidad del descenso de gradiente es el método de impulso.

Descenso de gradiente con impulso

La idea que subyace al descenso de gradiente con impulso consiste en suavizar la trayectoria de los parámetros de la red durante el entrenamiento, promediando los parámetros mediante un tipo de media exponencial ordinaria. Del mismo modo que suavizamos la serie temporal de los precios de los instrumentos financieros con el promedio para resaltar la dirección principal, del mismo modo tendremos derecho a suavizar la trayectoria del vector paramétrico que se desplaza hacia el punto de mínimo local de nuestra función de pérdida. Para visualizarlo mejor, echemos un vistazo a este gráfico, que muestra cómo han cambiado los valores de los dos parámetros, desde el inicio del entrenamiento hasta el punto de mínimo de la función de pérdida. La figura 3 muestra la trayectoria sin utilizar el impulso.

SD without Momentum

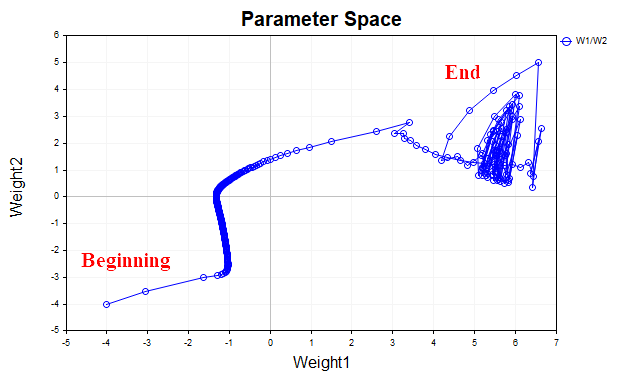
Fig.3 Descenso de gradiente sin impulso

Podemos ver que, a medida que nos acercamos al mínimo, el vector de parámetros empieza a oscilar caóticamente, lo cual nos impedirá alcanzar el punto óptimo. Para eliminar este fenómeno, deberemos reducir el coeficiente de aprendizaje. Entonces, obviamente, el algoritmo empezará a converger, pero el tiempo empleado en la búsqueda podría aumentar considerablemente.

La Fig. 4 muestra la trayectoria del vector de parámetros usando el impulso (con valor=0,9). Esta vez la trayectoria resulta más suave y llegaremos tranquilamente al punto óptimo. Y ahora podremos incluso aumentar el factor de velocidad de aprendizaje. En realidad, esta es la idea principal del descenso de gradiente con impulso: acelerar el proceso de convergencia.

SD with Momentum

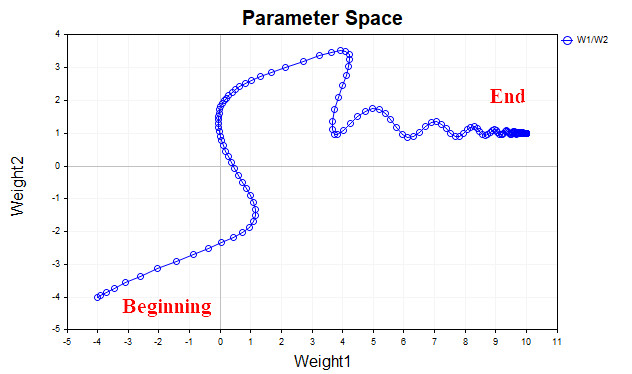
Fig.(4) Descenso de gradiente, momentum (0,9)

El script Momentum_SD implementa el algoritmo de descenso de gradiente con impulso. En él, hemos decidido deshacernos de una capa oculta y separar los pesos y los desplazamientos de la red, para mayor claridad de percepción. Ahora solo tendremos una capa oculta con 20 neuronas en lugar de dos capas ocultas de 5 neuronas cada una como en el ejemplo anterior.

//+------------------------------------------------------------------+
//|                                                  Momentum_SD.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,  
   target_netpredict_plot
  };
  
matrix weights1, weights2,bias1,bias2;                      // network parameter matrices
matrix dW1,db1,dW2,db2;                                     // weight increment matrices
matrix n1,n2,act1,act2;                                     // neural layer output matrices
input int    layer1                  = 20;                  // neurons Layer 1
input int    Epochs                  = 1000;                // Epochs
input double lr                      = 0.1;                 // learning rate coefficient
input double sigma_                  = 0.1;                 // standard deviation synthetic data
input double gamma_                  = 0.9;                 // momentum 
input Plots  plot_                   = LossFunction_plot;   // display graph
input bool   plot_log                = false;               // Plot Log graph
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;      // Activation Layer1
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR;    // Activation Layer2
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;     // Loss function

double LossPlot[],target_Plot[],NetOutput[];
matrix ones_;
int Sample_,Features; 

//+------------------------------------------------------------------+
//| Функция запуска скрипта                                          |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- генерируем обучающую выборку
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }
   ones_ = matrix::Ones(1,Sample_);  
      
   ulong start=GetMicrosecondCount(); 
//--- обучаем модель
   if(!Train(data, target, Epochs))
      return;
   ulong end = (GetMicrosecondCount()-start)/1000;  
   Print("Learning time = " + (string)end + " msc");
//--- генерируем тестовую выборку
    Func(data,target);
    StandartScaler(data);
//--- тестирование модели
   Test(data, target);
//--- отображаем графики  
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Метод обучения модели                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- создаем модель
   if(!CreateNet())
      return false;
   ArrayResize(LossPlot,Epochs);
//--- обучаем модель
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- прямой проход
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      LossPlot[ep] = act2.Loss(target, loss_func);
      //--- обратный проход и обновление матриц весов
      if(!Backprop(data, target))
         return false;
     }
//---
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Cols(); i++)
     {
      NetOutput[i]  =act2.Transpose()[i,0];
     }
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод создания модели                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- инициализируем матрицы весов
   if(!weights1.Init(layer1,Features)  || !weights2.Init(1,layer1)) 
      return false;
//--- инициализируем матрицы смещений
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))  
      return false;
//--- инициализируем матрицы приращений параметров
   dW1.Init(layer1,Features);
   dW2.Init(1, layer1);
   db1.Init(layer1,1);
   db2.Init(1,1);
   dW1.Fill(0);
   dW2.Fill(0);
   db1.Fill(0);
   db2.Fill(0);
//--- заполняем матрицы параметров случайными значениями
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1,0.1);
   bias2.Random(-0.1,0.1);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод прямого прохода                                            |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  { 
//--- вычисляем первый нейронный слой
//--- n1 предактивация первого слоя
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- вычисляем функцию активации первого слоя act1
   n1.Activation(act1, ac_func);
//--- вычисляем второй нейронный слой
//--- n2 предактивация второго слоя
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- вычисляем функцию активации второго слоя act2
   n2.Activation(act2, ac_func_last);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод обратного прохода                                          |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- Производная функции потерь по предсказанному значению
   matrix DerivLoss_wrt_y = act2.LossGradient(target.Transpose(),loss_func);
   matrix deriv_act2;
   n2.Derivative(deriv_act2, ac_func_last);
//--- D2   
   matrix  D2 = deriv_act2*DerivLoss_wrt_y; // ошибка(delta) выходного слоя сети
//--- D1
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = D1*deriv_act1; // ошибка (delta) первого слоя сети
//--- обновляем параметры  сети
   matrix  ones = matrix::Ones(data.Rows(),1);
   dW1 = gamma_*dW1 + (1-gamma_)*(D1.MatMul(data)) * lr;
   db1 = gamma_*db1 + (1-gamma_)*(D1.MatMul(ones)) * lr;
   dW2 = gamma_*dW2 + (1-gamma_)*(D2.MatMul(act1.Transpose())) * lr;
   db2 = gamma_*db2 + (1-gamma_)*(D2.MatMul(ones)) * lr;
   weights1 =  weights1 - dW1;
   weights2 =  weights2 - dW2;
   bias1    =  bias1    - db1;
   bias2    =  bias2    - db2;
//--- возвращаем результат
   return true;
  }

Gracias al impulso, hemos podido aumentar el ritmo de aprendizaje de 0,1 a 0,5. El algoritmo converge ahora en 150-200 iteraciones en lugar de las 500 del descenso de gradiente convencional.

Loss SD with Momentum

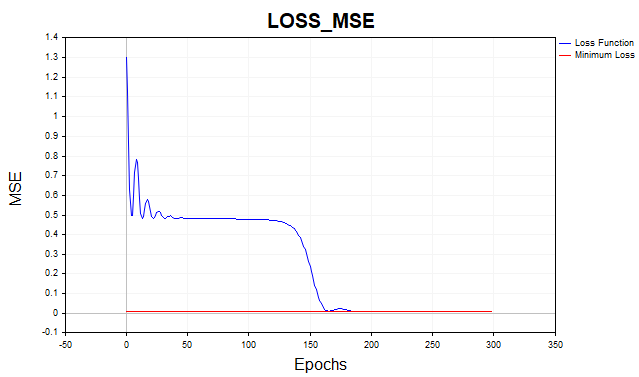
Fig.(5) Función de pérdida MSE, MLP(1-20-1) SD_Momentum

Descenso de gradiente estocástico

Momentum es bueno, pero cuando en el conjunto de datos no hay 81 puntos de datos, como en nuestro ejemplo, sino decenas de miles de instancias de datos, tiene sentido hablar de un algoritmo bien establecido (y sencillo) como el SGD. ¿Qué supone dicho algoritmo? Es lo mismo que el descenso de gradiente, pero el gradiente no se calcula sobre todo el conjunto de entrenamiento, sino solo sobre una parte muy pequeña de este conjunto (minilotes), o sobre un único punto de datos. A continuación, se actualizan los pesos de la red, se elige aleatoriamente un nuevo punto de datos y se repite el proceso hasta que el algoritmo converja. Por eso el algoritmo se llama estocástico, en el descenso de gradiente convencional actualizamos los pesos de la red solo después de haber calculado el gradiente en todo el conjunto de datos, es el llamado método por lotes.

Implementaremos una variante de SGD en la que solo se utilizará un punto de datos como minipaquete.

Loss SGD

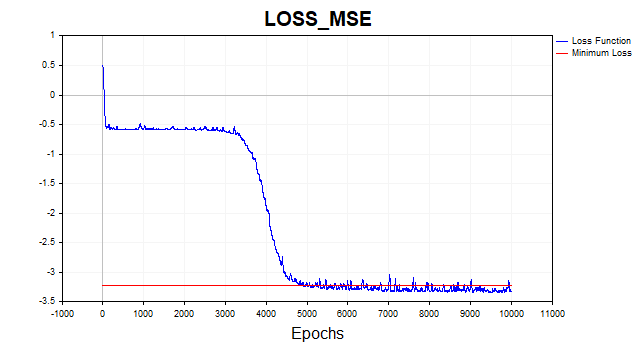
Fig.(6) Función de pérdida en escala logarítmica, SGD

El algoritmo SGD (batch_size = 1) converge al límite mínimo en 4-6 mil iteraciones, pero recordemos que solo usaremos un ejemplo de entrenamiento de 81 para actualizar el vector de parámetros. Por ello, el algoritmo convergirá en este conjunto de datos en aproximadamente 50-75 épocas. No es una mala mejora respecto al algoritmo anterior, ¿cierto? Aquí también hemos utilizado el impulso, pero como se usa un único punto de datos, no tendrá demasiado efecto en la velocidad de convergencia.

Algoritmo de Levenberg-Marquardt

Por alguna razón este viejo algoritmo está completamente olvidado hoy en día, aunque si nuestra red tiene hasta un par de cientos de parámetros, no encontrará nada igual a él junto con el L-BFGS.

Pero hay un punto importante a considerar. El algoritmo LM está diseñado para minimizar funciones que sean sumas de cuadrados de otras funciones no lineales. Por consiguiente, para este método, nos limitaremos únicamente a la función de pérdida cuadrática o RMS. En igualdad de condiciones, esta función de pérdida hace un gran trabajo y no existirá mayor problema, pero debemos saber que no podremos entrenar la red utilizando este algoritmo en otras funciones.

Vamos ahora a explicar cómo surgió este algoritmo. Empecemos por el método de Newton:

Newton’s method

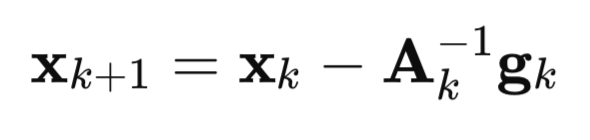
aquí,

A – matriz de Hesse inversa de la función de pérdida F(x),

g – gradiente de la función de pérdida F(x),

x – vector de parámetros

Ahora echaremos un vistazo a nuestra función de pérdida cuadrática:

SSE

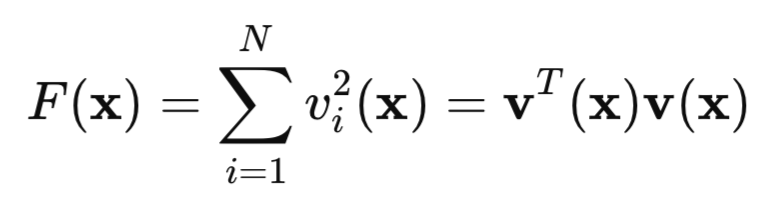
aquí, v será el error de la red (valor predicho menos objetivo), mientras que x será un vector de parámetros de red que incluirá todos los pesos y desplazamientos de cada capa.

Busquemos ahora el gradiente de esta función de pérdida:

gradient SSE Loss function

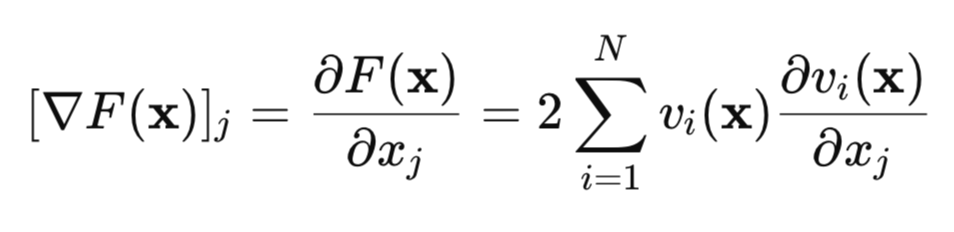
En forma de matriz, podemos escribirlo de la siguiente manera:

matrix notation gradient

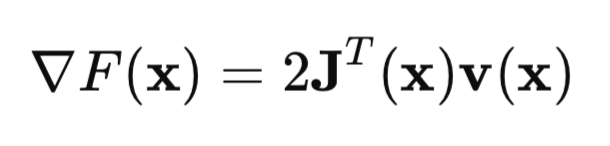
El punto clave será la matriz de Jacobi:

Jacobian

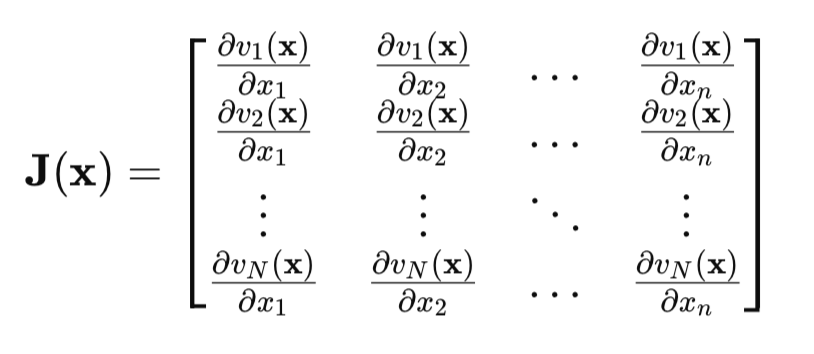
La matriz de Jacobi, en cada fila, contendrá todas las derivadas parciales del error de red sobre todos los parámetros. Cada fila se corresponderá con un ejemplo del conjunto de entrenamiento.

Veamos ahora la matriz de Hesse. Es la matriz de las segundas derivadas parciales de la función de pérdida. El cálculo del hessiano es una tarea difícil y costosa, por lo que utilizaremos la aproximación del hessiano usando la matriz de Jacobi:

Hessian

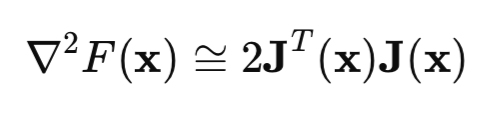
Si sustituimos las fórmulas del hessiano y del gradiente en la fórmula del método de Newton, obtendremos el método de Gauss-Newton:

Pero el problema del método Gauss-Newton es que la matriz [J'J] puede no ser reversible. Entonces, para resolver este problema, añadiremos a esta matriz una matriz unitaria multiplicada por un escalar positivo mu*I. En este caso, obtendremos exactamente el algoritmo de Levenberg-Marquardt:

Levenberg-Marquardt method

La peculiaridad de este algoritmo es que cuando el parámetro mu toma valores positivos grandes, el algoritmo se reducirá al descenso de gradiente habitual que hemos considerado al principio del artículo. Si el parámetro mu tiende a cero, volveremos al método de Gauss-Newton.

Normalmente, el entrenamiento comienza con un valor pequeño de mu; si el valor de la función de pérdida no se ha reducido, entonces se aumentará el parámetro mu (por ejemplo, se multiplicará por 10). Como esto nos acerca al método de descenso de gradiente, tarde o temprano lograremos una reducción de la función de pérdida. Si la función de pérdida ha disminuido, reduciremos el valor del parámetro mu usando el método Gauss-Newton para una convergencia más rápida al punto de mínimo. Esta es la idea básica del método Levenberg-Marquardt: alternar constantemente entre el método de descenso de gradiente y el método de Gauss-Newton.

La implementación del método de propagación inversa para el algoritmo de Levenberg-Marquardt tiene sus propias peculiaridades. Como los elementos de la matriz de Jacobi son derivadas parciales de los errores de la red, no los cuadrados de estos errores, la fórmula para calcular el delta de la última capa de la red que dimos al principio del artículo, se simplificará. Ahora delta será simplemente igual a la derivada de la función de activación de la última capa. Este resultado se obtendrá si hallamos la derivada del error de red (y - objetivo) en y, que obviamente será igual a uno.

De hecho, aquí tenemos el propio código de la red neuronal con comentarios detallados.

//+------------------------------------------------------------------+
//|                                                           LM.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,
   mu_plot,
   gradient_plot,
   target_netpredict_plot
  };

matrix weights1,weights2,bias1,bias2;                    // network parameter matrices
matrix n1,n2,act1,act2,new_n1,new_n2,new_act1,new_act2;  // neural layer output matrices
input int    layer1     = 20;                            // neurons Layer 1
input int    Epochs     = 10;                            // Epochs
input double Initial_mu = 0.001;                         // mu
input double Incr_Rate  = 10;                            // increase mu
input double Decr_Rate  = 0.1;                           // decrease mu
input double Min_grad   = 0.000001;                      // min gradient norm
input double Loss_goal  = 0.001;                         // Loss goal
input double sigma_     = 0.1;                           // standard deviation synthetic data
input Plots  plot_      = LossFunction_plot;             // display graph
input bool   plot_log   = false;                         // logarithmic function graph 
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;   // first layer activation function
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR; // last layer activation function
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;  // Loss function

double LossPlot[],NetOutput[],mu_Plot[],gradient_Plot[],target_Plot[];
matrix ones_;
double old_error,gradient_NormP2;
double mu_ = Initial_mu;
bool break_forloop = false;
int Sample_,Features;

//+------------------------------------------------------------------+
//| Функция запуска скрипта                                          |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- генерируем обучающую выборку
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }

   ones_ = matrix::Ones(1,Sample_);
//--- обучаем модель
   ulong start=GetMicrosecondCount();
   Train(data, target, Epochs);
   ulong end = (GetMicrosecondCount()-start)/1000 ;
   Print("Learning time = " + (string)end + " msc");
   int NumberParameters = layer1*(Features+1) + 1*(layer1+1);
   Print("Number Parameters of NN = ",NumberParameters);

//--- генерируем тестовую выборку
   Func(data,target);
   StandartScaler(data);
//--- тестирование модели
   Test(data,target);
   
//--- отображаем графики
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Метод обучения модели                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- создаем модель
   if(!CreateNet())
      return false;
//--- обучаем модель
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- прямой проход
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      //--- массивы для графиков
      ArrayResize(LossPlot,ep+1,10000);
      ArrayResize(mu_Plot,ep+1,10000);
      ArrayResize(gradient_Plot,ep+1,10000);
      LossPlot[ep]       = act2.Loss(target, loss_func);
      mu_Plot [ep]       = mu_;
      gradient_Plot[ep]  = gradient_NormP2;
      //--- Прекращаем обучение если достигнуто целевое значение функции потерь
      if(break_forloop == true){break;}
      //--- обратный проход и обновление матриц весов
      if(!Backprop(data, target))
         return false;
     }
//--- Евклидова норма градиента, параметр mu, метрика RMSE
   Print("gradient_normP2 =  ", gradient_NormP2);
   Print(" mu_ = ", mu_);
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
//--- массив выхода сети для графика
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Transpose().Rows(); i++)
     {
      NetOutput[i]  = act2.Transpose()[i,0];
     }
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод создания модели                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- инициализируем матрицы весов
   if(!weights1.Init(layer1,Features) || !weights2.Init(1,layer1))
      return false;
//--- инициализируем матрицы смещений
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))
      return false;
//--- заполняем матрицы весов случайными значениями
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1, 0.1);
   bias2.Random(-0.1, 0.1);   
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод прямого прохода                                            |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- вычисляем первый нейронный слой
//--- n1 предактивация первого слоя
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- вычисляем функцию активации первого слоя act1
   n1.Activation(act1, ac_func);
//--- вычисляем второй нейронный слой
//--- n2 предактивация второго слоя
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- вычисляем функцию активации второго слоя act2
   n2.Activation(act2, ac_func_last);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод обратного прохода                                          |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- текущее значение функции потерь
   old_error = act2.Loss(target, loss_func);
//--- ошибка сети (квадратичная функция потерь)
   matrix loss = act2.Transpose() - target ;
//--- производная функции активации последнего слоя
   matrix D2;
   n2.Derivative(D2, ac_func_last);
//--- производная функции активации первого слоя
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
//--- ошибка первого слоя сети
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = deriv_act1 * D1;
//--- первые частные производные ошибок сети по весам первого слоя
   matrix jac1;
   partjacobian(data.Transpose(),D1,jac1);
//--- первые частные производные ошибок сети по весам второго слоя
   matrix jac2;
   partjacobian(act1,D2,jac2);
//--- Якобиан
   matrix j1_D1 = Matrixconcatenate(jac1,D1.Transpose(),1);
   matrix j2_D2 = Matrixconcatenate(jac2,D2.Transpose(),1);
   matrix jac   = Matrixconcatenate(j1_D1,j2_D2,1);
// --- Градиент функции потерь
   matrix je = (jac.Transpose().MatMul(loss));
//--- Евклидова норма градиента нормируемая на обьем выборки
   gradient_NormP2 = je.Norm(MATRIX_NORM_FROBENIUS)/Sample_;
   if(gradient_NormP2 < Min_grad)
     {
      Print("Локальный минимум.Градиент меньше заданного значения.");
      break_forloop = true; // прекращаем обучение
      return true;
     }
//--- Гессиан
   matrix Hessian = (jac.Transpose().MatMul(jac));
   matrix I=matrix::Eye(Hessian.Rows(), Hessian.Rows());
//---
   break_forloop = true;
   while(mu_ <= 1e10 && mu_ > 1e-20)
     {
      matrix H_I = (Hessian + mu_*I);
      //--- решение через Solve
      vector v_je = je.Col(0);
      vector Updatelinsolve = -1* H_I.Solve(v_je);
      matrix Update = matrix::Zeros(Hessian.Rows(),1);
      Update.Col(Updatelinsolve,0); // приращение вектора параметров
      
      //--- неэффективное вычисление обратной матрицы
      //   matrix Update = H_I.Inv();
      //   Update = -1*Update.MatMul(je);
      //---

      //--- cохраняем текущие параметры 
      matrix  Prev_weights1 = weights1;
      matrix  Prev_bias1    = bias1;
      matrix  Prev_weights2 = weights2;
      matrix  Prev_bias2    = bias2;
      //---

      //--- обновляем параметры 
      //--- первый слой
      matrix updWeight1 = matrix::Zeros(layer1,Features);
      int count =0;
      for(int j=0; j <Features; j++)
        {
         for(int i=0 ; i <layer1; i++)
           {
            updWeight1[i,j] = Update[count,0];
            count = count+1;
           }
        }

      matrix updbias1 = matrix::Zeros(layer1,1);
      for(int i =0 ; i <layer1; i++)
        {
         updbias1[i,0] = Update[count,0];
         count = count +1;
        }
        
      weights1 = weights1 + updWeight1;
      bias1 = bias1 + updbias1;

      //--- второй слой
      matrix updWeight2 = matrix::Zeros(1,layer1);
      for(int i =0 ; i <layer1; i++)
        {
         updWeight2[0,i] = Update[count,0];
         count = count +1;
        }
      matrix updbias2 = matrix::Zeros(1,1);
      updbias2[0,0] = Update[count,0];

      weights2 = weights2 + updWeight2;
      bias2 = bias2 + updbias2;

      //--- вычисляем функцию потерь для новых параметров
      new_n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
      new_n1.Activation(new_act1, ac_func);
      new_n2 = weights2.MatMul(new_act1) + bias2.MatMul(ones_);
      new_n2.Activation(new_act2, ac_func_last);
      //--- функция потерь с учетом новых параметров
      double new_error = new_act2.Loss(target, loss_func);
      //--- если функция потерь меньше заданного порога завершаем обучение
      if(new_error < Loss_goal)
        {
         break_forloop = true;
         Print("Обучение завершено. Достигнуто желаемое значение функции потерь");
         return true;
        }
      break_forloop = false;
      //---корректируем параметр mu
      if(new_error >= old_error)
        {
         weights1 = Prev_weights1;
         bias1    = Prev_bias1;
         weights2 = Prev_weights2;
         bias2    =  Prev_bias2;
         mu_ = mu_*Incr_Rate;
        }
      else
        {
         mu_ = mu_*Decr_Rate;
         break; 
        }

     }
//--- возвращаем результат
   return true;
  }

El algoritmo convergirá si la norma de gradiente es inferior a un número predeterminado, o si se alcanza el nivel deseado de la función de pérdida. El algoritmo se detendrá si el parámetro mu es superior o inferior a un número predeterminado, o después de completar un número predeterminado de épocas.

LM parameters

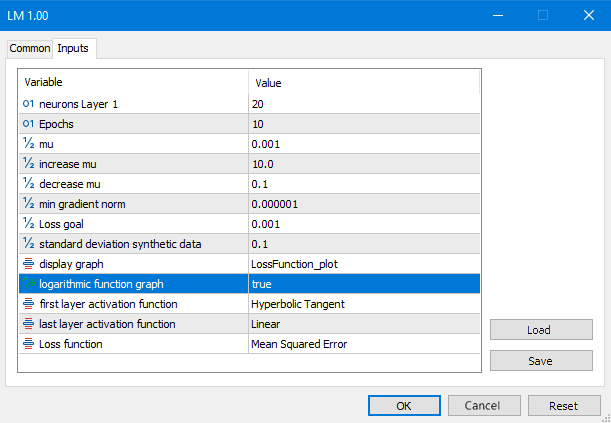
Fig.(7) Parámetros del script LM

Veamos el resultado de todos estos malabarismos matemáticos:

Loss LM

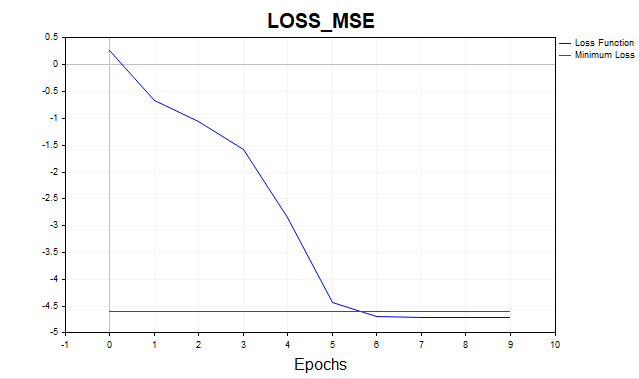
Fig.(8) Función de pérdida en escala logarítmica, LM

Ahora resulta bastante distinto, el algoritmo ha alcanzado el límite mínimo en 6 iteraciones. ¿Y si entrenamos la red con mil épocas? Obtendríamos el típico sobreajuste, la imagen de abajo lo demuestra bien. La red empieza a memorizar el ruido gaussiano.

Overfitting LM

Fig.(9) Sobreajuste típico, LM, 1000 épocas

Veamos las métricas del conjunto de entrenamiento y del conjunto de pruebas.

performance LM

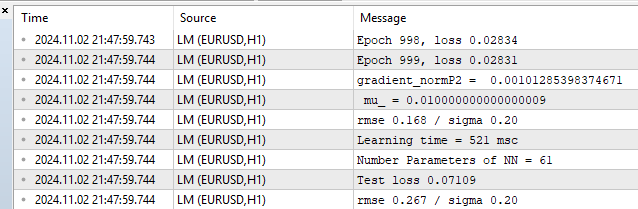
Fig.(10) estadísticas de rendimiento, LM, 1000 épocas

Podemos ver un RMSE de 0,168 con un límite inferior de 0,20 y, a continuación, una recuperación inmediata por sobreajuste en una prueba de 0,267.

Pruebas con big data y comparación con la biblioteca Python sklearn

Es hora de probar nuestro algoritmo con un ejemplo más realista. Ahora hemos tomado dos características de 1000 puntos de datos cada una. Podrá descargar estos datos junto con el script LM_BigData al final del artículo. Con LM competirán los algoritmos de la biblioteca Python: SGD, Adam y L-BFGS.

Aquí tenemos un script de prueba en Python

# Eugene
# https://www.mql5.com

import numpy as np
import time 
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neural_network import MLPRegressor

# здесь ваш путь к данным
df = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Data.csv',delimiter=';')
X = df.to_numpy()
df1 = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Target.csv')
y = df1.to_numpy()
y = y.reshape(-1)

start = time.time() 

'''
clf = MLPRegressor(solver='sgd', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=700,batch_size=10,
                    learning_rate_init=0.01,momentum=0.9,
                    shuffle = False,n_iter_no_change = 2000, tol = 0.000001)
'''

'''
clf = MLPRegressor(solver='adam', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=3000,batch_size=100,                                    
                    learning_rate_init=0.01,
                    n_iter_no_change = 2000, tol = 0.000001)
'''

#'''
clf = MLPRegressor(solver='lbfgs', alpha=0.0, 
                    hidden_layer_sizes=(100),
                    activation='tanh',max_iter=300,
                    tol = 0.000001)
#'''                    
                       
clf.fit(X, y)
end = time.time() - start          # время обучения

print("learning time  =",end*1000) 
print("solver = ",clf.solver);      
print("loss = ",clf.loss_*2)
print("iter = ",clf.n_iter_)
#print("n_layers_ = ",clf.n_layers_)
#print("n_outputs_ = ",clf.n_outputs_)
#print("out_activation_ = ",clf.out_activation_)

coef = clf.coefs_
#print("coefs_ = ",coef)
inter = clf.intercepts_  
#print("intercepts_ = ",inter) 
plt.plot(np.log(pd.DataFrame(clf.loss_curve_)))
plt.title(clf.solver)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

Para comparar correctamente los algoritmos, hemos multiplicado la función de pérdida en Python por 2, ya que en esta biblioteca se calcula así:

return ((y_true - y_pred) ** 2).mean() / 2

Es decir, los desarrolladores han dividido adicionalmente el MSE por 2. A continuación le mostramos algunos resultados típicos del optimizador. Hemos intentado elegir los mejores ajustes de hiperprámetros para estos algoritmos. Desafortunadamente, esta biblioteca carece de la capacidad de inicializar los valores de los parámetros de inicio para garantizar que todos los algoritmos partan del mismo punto en el espacio de parámetros. Tampoco hay forma de establecer un umbral objetivo para la función de pérdida. Para el LM el objetivo de la función de pérdida se ha fijado en 0,01, para los algoritmos Python he intentado fijar el número de iteraciones en las que se alcanza aproximadamente el mismo nivel.

Resultados de la prueba MLP con una capa oculta , 20 neuronas:

1) Descenso de gradiente estocástico

loss mse – 0,00278
tiempo de entrenamiento - 11459 msc

SGD Loss Python

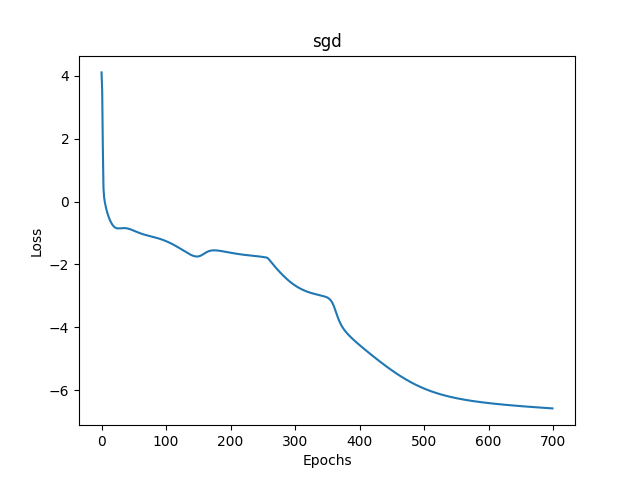
Fig.(11) SGD, 20 neuronas, pérdida = 0,00278

2) Adam

loss mse – 0,03363
tiempo de entrenamiento - 8581 msc

Adam loss

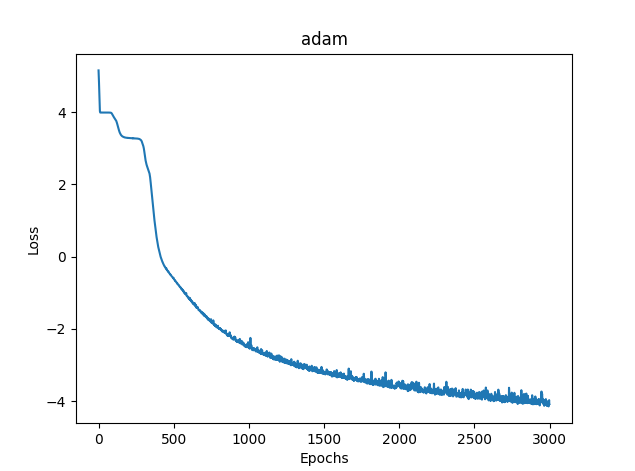
Fig.(12) Adam, 20 neuronas, pérdida = 0,03363

3)L-BFGS

loss mse – 0,02770
tiempo de entrenamiento - 277 msc

Desgraciadamente, para el L-BFGS no resulta posible mostrar el gráfico de la función de pérdida.

4) LM MQL5

loss – 0,00846
tiempo de entrenamiento - 117 msc

LM Loss

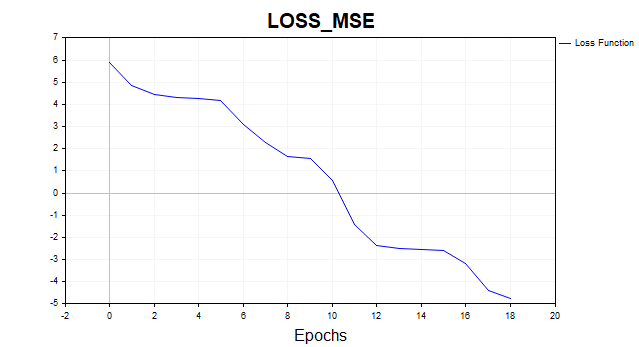
Fig.(13) LM, 20 neuronas, pérdida = 0,00846

performance LM

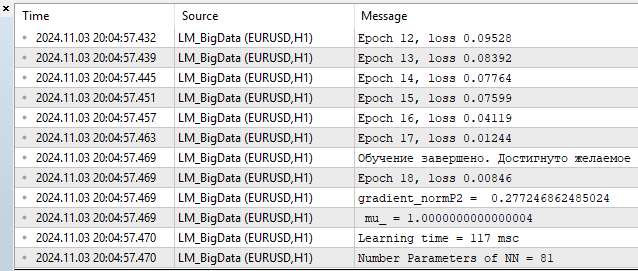
Bueno, en cuanto a nuestro caso, ha resultado bastante positivo, el algoritmo puede competir fácilmente con el L-BFGS y, como podemos ver, también puede ofrecer una cierta ventaja. Pero nada es perfecto, a medida que aumenta el número de parámetros, el método Levenberg-Marquardt empieza a perder frente al L-BFGS.

100 neuronas L-BFGS:

loss mse – 0,00847
tiempo de entrenamiento - 671 msc

100 neuronas LM:

loss mse – 0,00206
tiempo de entrenamiento - 1253 msc

100 neuronas corresponden a 401 parámetros de red. A usted, querido lector, le corresponde decidir si es mucho o poco, en mi humilde opinión hablamos de potencia sobrante. Y hasta 100 neuronas supone una ventaja para el LM.

Conclusión

En este artículo hemos analizado y aplicado algunos de los algoritmos más básicos y sencillos para entrenar redes neuronales:

descenso gradiente
descenso de gradiente con impulso
descenso de gradiente estocástico

Junto a esto, hemos abordado brevemente la convergencia y el reentrenamiento de las redes neuronales.

Pero lo más importante es que hemos creado un algoritmo de Levenberg-Marquardt muy rápido, ideal para el entrenamiento online de redes pequeñas.

Asimismo, hemos comparado el rendimiento de los algoritmos de entrenamiento de redes neuronales utilizados en la biblioteca de aprendizaje automático scikit-learn, y nuestro algoritmo ha sido el más rápido cuando el número de parámetros de la red neuronal no supera los 400 o 100 neuronas de la capa oculta. Además, a medida que aumenta el número de neuronas, el L-BFGS empieza a dominar.

Además hemos creado scripts independientes para cada algoritmo, con comentarios detallados:

#	Nombre	Tipo	Descripción
1	SD.mq5	Script	Descenso de gradiente
2	Momentum_SD.mq5	Script	Descenso de gradiente con impulso
3	SGD.mq5	Script	Descenso de gradiente estocástico
4	LM.mq5	Script	Algoritmo de Levenberg-Marquardt
5	LM_BigData.mq5	Script	Algoritmo LM, prueba de características bidimensionales
6	SklearnMLP.py	Script	Script de prueba de algoritmos Python
7	ArchivoCSV.mqh	Include	Lectura de archivos de texto con datos
8	Data.csv, Target.csv	Csv	Características y objetivo para el script de Python
9	X1.txt, X2.txt, Target.txt	Txt	Características y objetivo para el script de LM_BigData.mq5

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16296

Archivos adjuntos |

Descargar ZIP

SD.mq5 (26.11 KB)

SGD.mq5 (26.08 KB)

Momentum_SD.mq5 (22.58 KB)

LM.mq5 (36.08 KB)

LM_BigData.mq5 (36 KB)

FileCSV.mqh (10.46 KB)

X1.txt (19.26 KB)

X2.txt (19.26 KB)

Target.txt (17.62 KB)

Data.csv (37.56 KB)

Target.csv (17.62 KB)

SklearnMLP.py (1.94 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

De novato a experto: depuración colaborativa en MQL5

La resolución de problemas puede establecer una rutina concisa para dominar habilidades complejas, como la programación en MQL5. Este enfoque le permite concentrarse en la resolución de problemas al tiempo que desarrolla sus capacidades. Cuantos más problemas abordes, más conocimientos avanzados se transferirán a tu cerebro. Personalmente, creo que la depuración es la forma más efectiva de dominar la programación. Hoy repasaremos el proceso de limpieza de código y analizaremos las mejores técnicas para transformar un programa desordenado en uno limpio y funcional. Lea este artículo y descubra información valiosa.

Análisis del impacto del clima en las divisas de los países agrícolas usando Python

¿Cómo se relacionan el clima y el mercado de divisas? La teoría económica clásica no ha reconocido durante mucho tiempo la influencia de estos factores en el comportamiento del mercado. Pero ahora las cosas han cambiado. Hoy intentaremos encontrar conexiones entre el estado del tiempo y la posición de las divisas agrarias en el mercado.

Redes neuronales en el trading: Modelo hiperbólico de difusión latente (HypDiff)

El artículo estudiará formas de codificar los datos de origen en un espacio latente hiperbólico mediante procesos de difusión anisotrópica. Esto ayudará a preservar con mayor precisión las características topológicas de la situación actual del mercado y mejorará la calidad de su análisis.

Cómo crear un diario de operaciones con MetaTrader y Google Sheets

Crear un diario de operaciones con MetaTrader y Google Sheets! Aprenderá cómo sincronizar sus datos comerciales a través de HTTP POST y recuperarlos mediante solicitudes HTTP. Al final, tendrás un diario de operaciones que te ayudará a realizar un seguimiento de tus operaciones de manera eficaz y eficiente.