Обучение многослойного персептрона с помощью алгоритма Левенберга-Марквардта

Введение

Цель данной статьи дать практикующим трейдерам очень эффективный алгоритм обучения нейронных сетей — вариант ньютоновского метода оптимизации, известный как алгоритм Левенберга-Марквардта. Это один из самых быстрых алгоритмов обучения нейронных сетей прямого распространения, конкуренцию которому может составить разве что алгоритм Бройдена-Флетчера-Гольдфарба-Шанно(L-BFGS).

Стохастические методы оптимизации, такие как стохастический градиентный спуск(SGD) и Adam, хорошо подходят для оффлайн обучения, когда переобучение нейросети происходит через длительные отрезки времени. Если трейдер, применяющий нейронные сети, желает, чтобы модель быстро адаптировалась к постоянно меняющимся торговым условиям, ему нужно производить переобучение сети онлайн на каждом новом баре, или через небольшой отрезок времени. В таком случае, как нельзя лучше подойдут алгоритмы, которые кроме информации о градиенте функции потерь, используют также дополнительную информацию о вторых частных производных, что позволяет буквально за несколько эпох обучения найти локальный минимум функции потерь.

На данный момент насколько мне известно, реализации алгоритма Левенберга-Марквардта на языке MQL5 в открытом доступе нет. Пора этот пробел заполнить, а также, заодно, вкратце пройтись по хорошо известным и самым простым алгоритмам оптимизации, таким как градиентный спуск, градиентный спуск с импульсом (momentum) и стохастический градиентный спуск. В конце статьи проведем небольшое тестирование эффективности алгоритма Левенберга-Марквардта и алгоритмов из библиотеки машинного обучения scikit-learn.

Набор данных

Во всех последующих примерах для простоты изложения используются синтетические данные. В качестве единственной предсказывающей переменной используется время, а в качестве целевой переменной, которую мы хотим предсказать с помощью нейросети, используется функция:

1 + sin(pi/4*time) + NormDistr(0,sigma)

Эта функция состоит из детерминированной части, представленной периодической компонентой в виде синуса, и стохастической части — гауссовского белого шума. Всего 81 точка данных. Ниже представлен график этой функции и ее аппроксимация трехслойным персептроном.

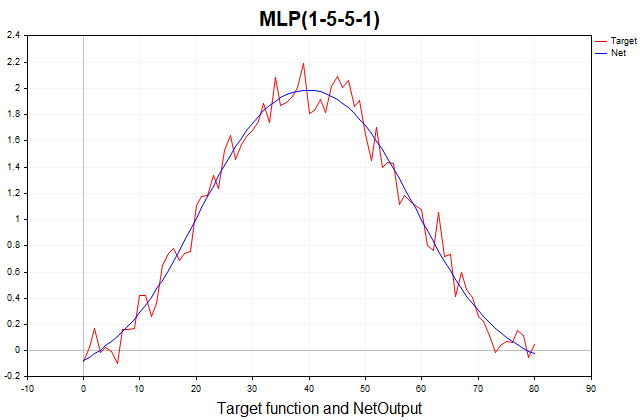
Рис.(1) Целевая функция и ее аппроксимация трехслойным персептроном

Градиентный спуск

Начнем с реализации обычного градиентного спуска, как самого простого метода обучения нейронных сетей. Для этого, в качестве шаблона я буду использовать очень хороший пример из справочника MQL5 (Методы матриц и векторов/Машинное обучение). Я немного изменил его, добавив возможность выбора функции активации для последнего слоя сети и сделав реализацию градиентного спуска универсальным, способным обучаться не только на квадратичной функции потерь, как это неявно предполагается в примере из справочника, а на всех доступных функциях потерь в MQL5. Функция потерь занимает центральное место в обучении нейронных сетей, и иногда стоит поэкспериментировать с разными функциями, не ограничиваясь только квадратичной потерей. Вот общая формула для вычисления ошибки выходного слоя(delta):

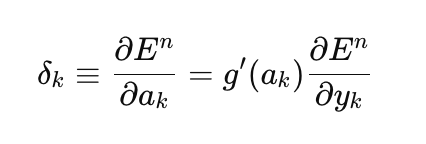
здесь,

• delta_k — ошибка выходного слоя,
• E — функция потерь,
• g'(a_k) — производная функции активации,
• а_k — предактивация последнего слоя,
• y_k — предсказанное значение сети.

//--- Производная функции потерь по предсказанному значению       
matrix DerivLoss_wrt_y = result_.LossGradient(target,loss_func);  
matrix deriv_act;
  if(!result_.Derivative(deriv_act, ac_func_last)) 
     return false;      
 matrix  loss = deriv_act*DerivLoss_wrt_y;  // loss = delta_k

Частные производные функции потерь по предсказанному значению сети вычисляет функция LossGradient, а производную функции активации — функция Derivative. В примере из справки, в качестве ошибки выходного слоя, используется разность между целевым и предсказанным значением сети умноженным на 2.

matrix loss = (target - result_)*2; 

В литературе по машинному обучению ошибку каждого слоя сети обычно называют delta(D2,D1 и т.д.), а не loss (смотрите, например, Bishop(1995)). В дальнейшем я буду использовать именно это обозначение в коде.         

Хорошо, как получился данный результат? Здесь неявно предполагается, что в качестве функции потерь выступает сумма квадратов разностей между целевым и предсказанным значением, а не среднеквадратичная ошибка (MSE), которая дополнительно нормируется на размер обучающей выборки. Производная данной функции потерь как раз и равна (target - result)*2. И так как в последнем слое сети используется тождественная функция активации, чья производная равна единице, то мы и приходим к данному результату. Поэтому тем, кто хочет использовать произвольные функции потерь и функции активации выходного слоя для обучения сети, нужно использовать вышеуказанную общую формулу.

Обучим теперь нашу сеть на среднеквадратичной функции потерь. Здесь, для наглядности, я отобразил график в логарифмическом масштабе.

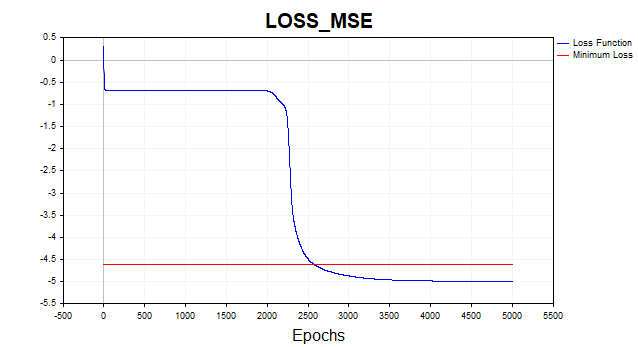
Рис.2 Функция потерь MSE, градиентный спуск

В среднем, алгоритму градиентного спуска требуется 1500-2000 эпох (то есть проходов по всему обучающему множеству данных), чтобы достичь минимального порога функции потерь. При этом я использовал два скрытых слоя по 5 нейронов в каждом.

Красной линией на графике обозначен минимальный порог функции потерь. Он определяется как дисперсия белого гауссовского шума. Здесь я использовал шум с дисперсией равной 0,01 (0,1 сигма* 0,1 сигма).

Что произойдет если мы позволим модели нейронной сети обучится ниже этого минимального порога? Тогда мы столкнемся с таким нежелательным явлением, как переобучение сети. Бессмысленно пытаться получить ошибку функции потерь на обучающем наборе данных ниже минимального порога, так как это скажется на предсказательной силе модели на тестовом наборе данных. Здесь мы сталкиваемся с тем фактом, что невозможно предсказать ряд точнее, чем позволяет статистический разброс этого ряда. Если мы остановим обучение выше уровня минимального порога, то столкнемся с другой проблемой — сеть окажется недообученной. То есть такой, которая не смогла до конца уловить предсказуемую компоненту ряда.

Как видите, градиентному спуску требуется пройти довольно много итераций, чтобы достичь оптимального набора параметров. И это в случае такого простого набора данных, как наш. Для реальных практических задач время обучения по градиентному спуску оказывается неприемлемым. Одним из самых простых способов улучшить сходимость и скорость градиентного спуска является метод импульса (momentum).

Градиентный спуск с импульсом

Идея градиентного спуска  с импульсом заключается в сглаживании  траектории параметров сети в ходе обучения, с помощью усреднения параметров по типу обыкновенной экспоненциальной средней. Так же как средней мы сглаживаем временной ряд цен финансовых инструментов, чтобы выделить главное направление, точно так же мы вправе сгладить траекторию параметрического вектора, который движется к точке локального минимума нашей функции потерь. Чтобы лучше себе это представить, давайте посмотрим на график, который демонстрирует, как менялись значения двух параметров — с начала обучения до точки минимума функции потерь.  Рис.3 демонстрирует траекторию без использования момента. 

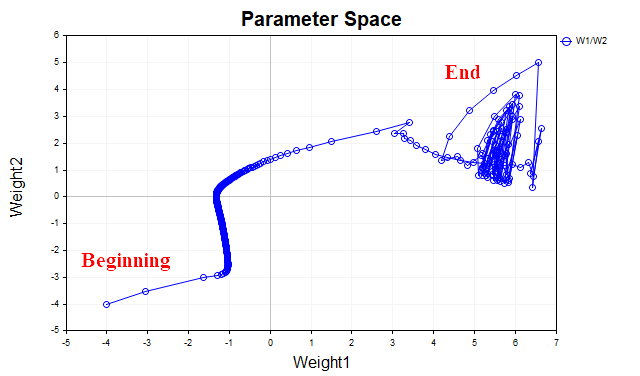
Рис.3 Градиентный спуск без момента

Мы видим, что с приближением минимума, вектор параметров начинает хаотически осциллировать, что не позволяет добраться до точки оптимума. Чтобы избавится от этого явления,  нам придется снижать коэффициент скорости обучения. Тогда алгоритм, конечно, начнет сходиться, но время, затраченное на поиск, может значительно увеличиться.

Рис. 4 демонстрирует траекторию вектора параметров с использованием момента (со значением=0,9). На этот раз траектория более сглажена, и мы спокойно добираемся к точке оптимума. И теперь даже можем увеличить коэффициент скорости обучения. В этом, собственно, основная идея градиентного спуска с импульсом и заключается — ускорить процесс сходимости.

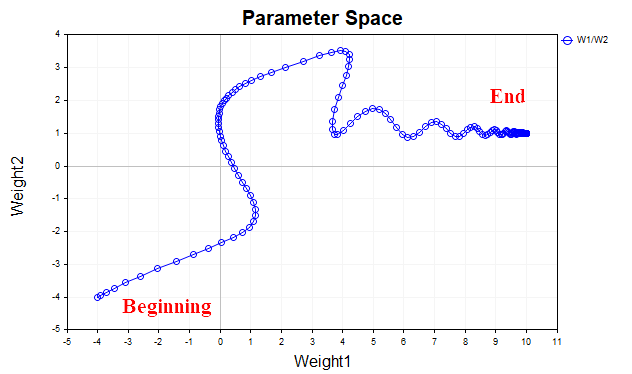
Рис.(4) Градиент спуск, momentum (0.9)

Скрипт Momentum_SD реализует алгоритм градиентного спуска с моментом. В нем я решил избавиться от одного скрытого слоя и разделить веса и смещения сети, для наглядности восприятия. Теперь у нас только один скрытый слой, в котором 20 нейронов вместо двух скрытых слоев по 5 нейронов в каждом, как в предыдущем примере.

//+------------------------------------------------------------------+
//|                                                  Momentum_SD.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,  
   target_netpredict_plot
  };
  
matrix weights1, weights2,bias1,bias2;                      // network parameter matrices
matrix dW1,db1,dW2,db2;                                     // weight increment matrices
matrix n1,n2,act1,act2;                                     // neural layer output matrices
input int    layer1                  = 20;                  // neurons Layer 1
input int    Epochs                  = 1000;                // Epochs
input double lr                      = 0.1;                 // learning rate coefficient
input double sigma_                  = 0.1;                 // standard deviation synthetic data
input double gamma_                  = 0.9;                 // momentum 
input Plots  plot_                   = LossFunction_plot;   // display graph
input bool   plot_log                = false;               // Plot Log graph
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;      // Activation Layer1
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR;    // Activation Layer2
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;     // Loss function

double LossPlot[],target_Plot[],NetOutput[];
matrix ones_;
int Sample_,Features; 

//+------------------------------------------------------------------+
//| Функция запуска скрипта                                          |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- генерируем обучающую выборку
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }
   ones_ = matrix::Ones(1,Sample_);  
      
   ulong start=GetMicrosecondCount(); 
//--- обучаем модель
   if(!Train(data, target, Epochs))
      return;
   ulong end = (GetMicrosecondCount()-start)/1000;  
   Print("Learning time = " + (string)end + " msc");
//--- генерируем тестовую выборку
    Func(data,target);
    StandartScaler(data);
//--- тестирование модели
   Test(data, target);
//--- отображаем графики  
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Метод обучения модели                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- создаем модель
   if(!CreateNet())
      return false;
   ArrayResize(LossPlot,Epochs);
//--- обучаем модель
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- прямой проход
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      LossPlot[ep] = act2.Loss(target, loss_func);
      //--- обратный проход и обновление матриц весов
      if(!Backprop(data, target))
         return false;
     }
//---
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Cols(); i++)
     {
      NetOutput[i]  =act2.Transpose()[i,0];
     }
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод создания модели                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- инициализируем матрицы весов
   if(!weights1.Init(layer1,Features)  || !weights2.Init(1,layer1)) 
      return false;
//--- инициализируем матрицы смещений
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))  
      return false;
//--- инициализируем матрицы приращений параметров
   dW1.Init(layer1,Features);
   dW2.Init(1, layer1);
   db1.Init(layer1,1);
   db2.Init(1,1);
   dW1.Fill(0);
   dW2.Fill(0);
   db1.Fill(0);
   db2.Fill(0);
//--- заполняем матрицы параметров случайными значениями
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1,0.1);
   bias2.Random(-0.1,0.1);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод прямого прохода                                            |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  { 
//--- вычисляем первый нейронный слой
//--- n1 предактивация первого слоя
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- вычисляем функцию активации первого слоя act1
   n1.Activation(act1, ac_func);
//--- вычисляем второй нейронный слой
//--- n2 предактивация второго слоя
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- вычисляем функцию активации второго слоя act2
   n2.Activation(act2, ac_func_last);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод обратного прохода                                          |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- Производная функции потерь по предсказанному значению
   matrix DerivLoss_wrt_y = act2.LossGradient(target.Transpose(),loss_func);
   matrix deriv_act2;
   n2.Derivative(deriv_act2, ac_func_last);
//--- D2   
   matrix  D2 = deriv_act2*DerivLoss_wrt_y; // ошибка(delta) выходного слоя сети
//--- D1
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = D1*deriv_act1; // ошибка (delta) первого слоя сети
//--- обновляем параметры  сети
   matrix  ones = matrix::Ones(data.Rows(),1);
   dW1 = gamma_*dW1 + (1-gamma_)*(D1.MatMul(data)) * lr;
   db1 = gamma_*db1 + (1-gamma_)*(D1.MatMul(ones)) * lr;
   dW2 = gamma_*dW2 + (1-gamma_)*(D2.MatMul(act1.Transpose())) * lr;
   db2 = gamma_*db2 + (1-gamma_)*(D2.MatMul(ones)) * lr;
   weights1 =  weights1 - dW1;
   weights2 =  weights2 - dW2;
   bias1    =  bias1    - db1;
   bias2    =  bias2    - db2;
//--- возвращаем результат
   return true;
  }

Благодаря моменту, я смог увеличить скорость обучения с 0.1 до 0.5. Теперь алгоритм сходится за 150-200 итераций вместо 500 для обычного градиентного спуска.

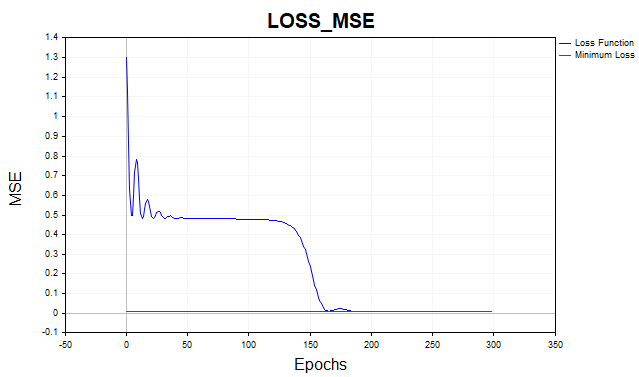
Рис.(5) Функция потерь MSE, MLP(1-20-1) SD_Momentum

Стохастический градиентный спуск

Моментум — это хорошо, но когда набор данных не 81 точка данных, как в нашем примере, а десятки тысяч экземпляров данных, то тут уже есть смысл поговорить о таком хорошо зарекомендовавшем себя (и простом) алгоритме, как SGD. Что он из себя представляет? Это тот же градиентный спуск, но градиент вычисляется не по всему обучающему множеству, а только на какой-то очень небольшой части этого множества (mini-batch), или вообще на одной точке данных. После чего, веса сети обновляются, далее случайно выбирается новая точка данных, и процесс повторяется, пока алгоритм не сойдется. Поэтому алгоритм и называется стохастическимм, в обычном градиентном спуске мы обновляли веса сети только после того, как вычислили градиент на всем множестве данных, это так называемый пакетный метод (batch метод).

Мы реализуем вариант SGD, когда в качестве мини пакета используется только одна точка данных.

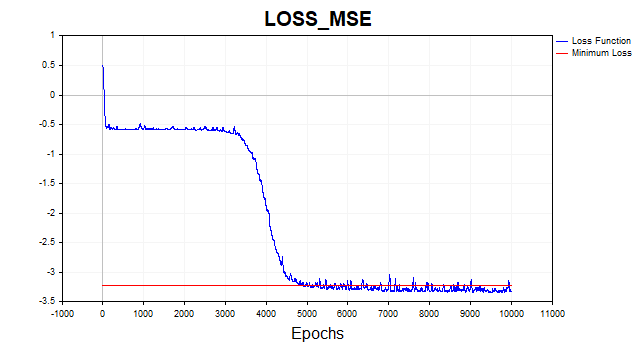
Рис.(6) Функция потерь в логарифмическом масштабе, SGD

Алгоритм SGD (batch_size = 1) сходится к минимальной границе за 4-6 тыс. итераций, но давайте вспомним, что мы ведь используем всего один обучающий пример из 81, чтобы обновить вектор параметров. Следовательно, алгоритм на данном датасете сходится приблизительно за 50-75 эпох. Неплохое улучшение по сравнению с предыдущим алгоритмом, не так ли? Я здесь также использовал момент, но из-за того, что используется одна точка данных, он оказывает не слишком большое влияние на скорость сходимости.

Алгоритм Левенберга-Марквардта

Этот старый добрый алгоритм почему-то совершенно забыт в наше время, хотя если ваша сеть насчитывает до пары сотни параметров, равных ему вместе с L-BFGS просто нет.

Но есть один важный момент. Алгоритм LM предназначен для минимизации функций, которые являются суммами квадратов других нелинейных функций. Поэтому для этого метода мы будем ограничены только квадратичной или среднеквадратичной функцией потерь. При прочих равных, данная функция потерь прекрасно справляется со своей задачей, и большой проблемы здесь нет, но нужно знать, что мы не сможем обучать сеть по этому алгоритму на других функциях.

Давайте теперь подробно разберем как возник этот алгоритм. Начнем с метода Ньютона:

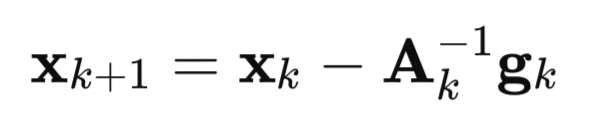
здесь,

A – это обратная матрица Гессе функции потерь F(x),

g – градиент функции потерь F(x),

x – вектор параметров

Теперь давайте взглянем на нашу квадратичную функцию потерь:

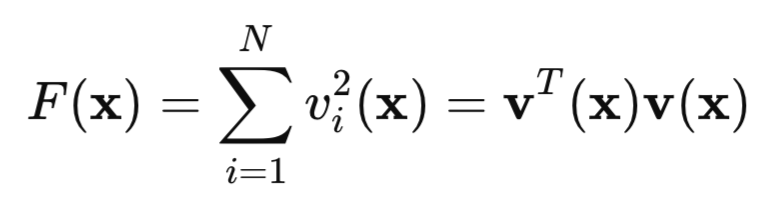
здесь, v это ошибка сети (предсказанное значение минус цель), а x это вектор параметров сети, который включает в себя все веса и смещения для каждого слоя.

Найдем градиент этой функции потерь:

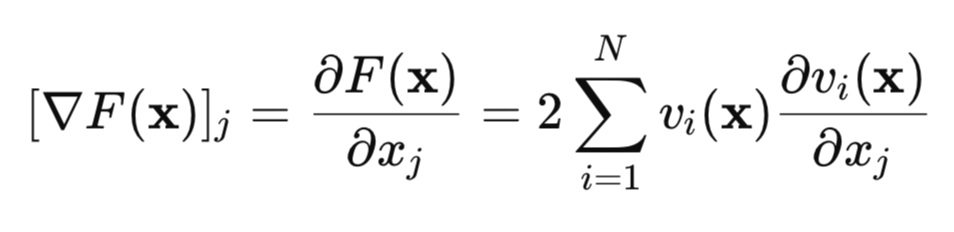
В матричной форме это можно записать так:

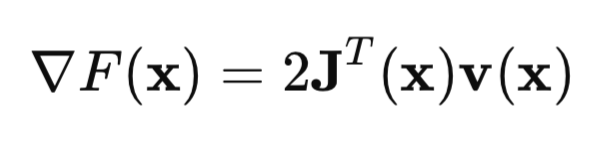
Ключевой момент — это матрица Якоби:

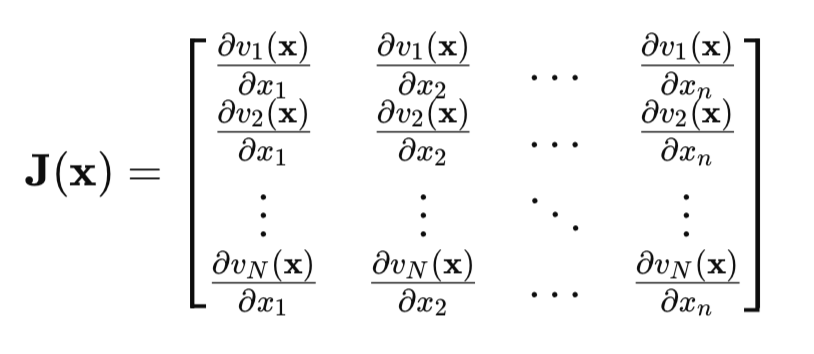
В матрице Якоби, в каждой строке, содержаться все частные производные ошибки сети по всем параметрам. Каждая строка соответствует одному примеру обучающего множества.

Теперь посмотрим на матрицу Гессе. Это матрица вторых частных производных функции потерь. Вычисление гессиана это непростая и затратная задача, поэтому используют аппроксимацию гессиана матрицей Якоби:

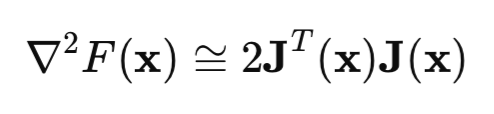
Если мы подставим формулы гессиана и градиента в формулу метода Ньютона, то получим метод Гаусса-Ньютона:

Но проблема с методом Гаусса-Ньютона заключается в том, что матрица [J'J] может не быть обратимой. Тогда, для решения этой проблемы, к этой матрице прибавляют единичную матрицу, умноженную на положительный скаляр mu*I. В этом случае мы как раз и получаем алгоритм Левенберга-Марквардта:

Особенность данного алгоритма заключается в том, что когда параметр mu принимает большие положительные значения, алгоритм сводится к обычному градиентному спуску, который мы с вами рассматривали в начале статьи. Если параметр mu стремится к нулю, мы возвращаемся к методу Гаусса-Ньютона.

Обычно обучение начинают с малого значения mu, если значение функции потерь при этом не стало меньше, тогда параметр mu увеличивают (например, умножают на 10). Так как это приближает нас к методу градиентного спуска, то рано или поздно мы добьемся снижения функции потерь. Если функция потерь уменьшилась, мы уменьшаем значение параметра mu, подключая метод Гаусса-Ньютона, для более быстрой сходимости к точке минимума. В этом и заключается основная идея метода Левенберга-Марквардта — постоянно переключаться между методом градиентного спуска и методом Гаусса-Ньютона.

Реализация метода обратного распространения для алгоритма Левенберга-Марквардта имеет свои особенности. Так как элементы матрицы Якоби представляют собой частные производные ошибок сети, а не квадратов этих ошибок, то формула для вычисления delta последнего слоя сети, которую я приводил в начале статьи, упрощается. Теперь delta равна просто производной функции активации последнего слоя. Этот результат получается, если мы найдем производную ошибки сети (y – target) по y, которая очевидно равна единице.

Вот, собственно, сам код нейронной сети с подробными комментариями.

//+------------------------------------------------------------------+
//|                                                           LM.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,
   mu_plot,
   gradient_plot,
   target_netpredict_plot
  };

matrix weights1,weights2,bias1,bias2;                    // network parameter matrices
matrix n1,n2,act1,act2,new_n1,new_n2,new_act1,new_act2;  // neural layer output matrices
input int    layer1     = 20;                            // neurons Layer 1
input int    Epochs     = 10;                            // Epochs
input double Initial_mu = 0.001;                         // mu
input double Incr_Rate  = 10;                            // increase mu
input double Decr_Rate  = 0.1;                           // decrease mu
input double Min_grad   = 0.000001;                      // min gradient norm
input double Loss_goal  = 0.001;                         // Loss goal
input double sigma_     = 0.1;                           // standard deviation synthetic data
input Plots  plot_      = LossFunction_plot;             // display graph
input bool   plot_log   = false;                         // logarithmic function graph 
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;   // first layer activation function
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR; // last layer activation function
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;  // Loss function

double LossPlot[],NetOutput[],mu_Plot[],gradient_Plot[],target_Plot[];
matrix ones_;
double old_error,gradient_NormP2;
double mu_ = Initial_mu;
bool break_forloop = false;
int Sample_,Features;

//+------------------------------------------------------------------+
//| Функция запуска скрипта                                          |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- генерируем обучающую выборку
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }

   ones_ = matrix::Ones(1,Sample_);
//--- обучаем модель
   ulong start=GetMicrosecondCount();
   Train(data, target, Epochs);
   ulong end = (GetMicrosecondCount()-start)/1000 ;
   Print("Learning time = " + (string)end + " msc");
   int NumberParameters = layer1*(Features+1) + 1*(layer1+1);
   Print("Number Parameters of NN = ",NumberParameters);

//--- генерируем тестовую выборку
   Func(data,target);
   StandartScaler(data);
//--- тестирование модели
   Test(data,target);
   
//--- отображаем графики
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Метод обучения модели                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- создаем модель
   if(!CreateNet())
      return false;
//--- обучаем модель
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- прямой проход
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      //--- массивы для графиков
      ArrayResize(LossPlot,ep+1,10000);
      ArrayResize(mu_Plot,ep+1,10000);
      ArrayResize(gradient_Plot,ep+1,10000);
      LossPlot[ep]       = act2.Loss(target, loss_func);
      mu_Plot [ep]       = mu_;
      gradient_Plot[ep]  = gradient_NormP2;
      //--- Прекращаем обучение если достигнуто целевое значение функции потерь
      if(break_forloop == true){break;}
      //--- обратный проход и обновление матриц весов
      if(!Backprop(data, target))
         return false;
     }
//--- Евклидова норма градиента, параметр mu, метрика RMSE
   Print("gradient_normP2 =  ", gradient_NormP2);
   Print(" mu_ = ", mu_);
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
//--- массив выхода сети для графика
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Transpose().Rows(); i++)
     {
      NetOutput[i]  = act2.Transpose()[i,0];
     }
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод создания модели                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- инициализируем матрицы весов
   if(!weights1.Init(layer1,Features) || !weights2.Init(1,layer1))
      return false;
//--- инициализируем матрицы смещений
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))
      return false;
//--- заполняем матрицы весов случайными значениями
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1, 0.1);
   bias2.Random(-0.1, 0.1);   
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод прямого прохода                                            |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- вычисляем первый нейронный слой
//--- n1 предактивация первого слоя
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- вычисляем функцию активации первого слоя act1
   n1.Activation(act1, ac_func);
//--- вычисляем второй нейронный слой
//--- n2 предактивация второго слоя
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- вычисляем функцию активации второго слоя act2
   n2.Activation(act2, ac_func_last);
//--- возвращаем результат
   return true;
  }
//+------------------------------------------------------------------+
//| Метод обратного прохода                                          |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- текущее значение функции потерь
   old_error = act2.Loss(target, loss_func);
//--- ошибка сети (квадратичная функция потерь)
   matrix loss = act2.Transpose() - target ;
//--- производная функции активации последнего слоя
   matrix D2;
   n2.Derivative(D2, ac_func_last);
//--- производная функции активации первого слоя
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
//--- ошибка первого слоя сети
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = deriv_act1 * D1;
//--- первые частные производные ошибок сети по весам первого слоя
   matrix jac1;
   partjacobian(data.Transpose(),D1,jac1);
//--- первые частные производные ошибок сети по весам второго слоя
   matrix jac2;
   partjacobian(act1,D2,jac2);
//--- Якобиан
   matrix j1_D1 = Matrixconcatenate(jac1,D1.Transpose(),1);
   matrix j2_D2 = Matrixconcatenate(jac2,D2.Transpose(),1);
   matrix jac   = Matrixconcatenate(j1_D1,j2_D2,1);
// --- Градиент функции потерь
   matrix je = (jac.Transpose().MatMul(loss));
//--- Евклидова норма градиента нормируемая на обьем выборки
   gradient_NormP2 = je.Norm(MATRIX_NORM_FROBENIUS)/Sample_;
   if(gradient_NormP2 < Min_grad)
     {
      Print("Локальный минимум.Градиент меньше заданного значения.");
      break_forloop = true; // прекращаем обучение
      return true;
     }
//--- Гессиан
   matrix Hessian = (jac.Transpose().MatMul(jac));
   matrix I=matrix::Eye(Hessian.Rows(), Hessian.Rows());
//---
   break_forloop = true;
   while(mu_ <= 1e10 && mu_ > 1e-20)
     {
      matrix H_I = (Hessian + mu_*I);
      //--- решение через Solve
      vector v_je = je.Col(0);
      vector Updatelinsolve = -1* H_I.Solve(v_je);
      matrix Update = matrix::Zeros(Hessian.Rows(),1);
      Update.Col(Updatelinsolve,0); // приращение вектора параметров
      
      //--- неэффективное вычисление обратной матрицы
      //   matrix Update = H_I.Inv();
      //   Update = -1*Update.MatMul(je);
      //---

      //--- cохраняем текущие параметры 
      matrix  Prev_weights1 = weights1;
      matrix  Prev_bias1    = bias1;
      matrix  Prev_weights2 = weights2;
      matrix  Prev_bias2    = bias2;
      //---

      //--- обновляем параметры 
      //--- первый слой
      matrix updWeight1 = matrix::Zeros(layer1,Features);
      int count =0;
      for(int j=0; j <Features; j++)
        {
         for(int i=0 ; i <layer1; i++)
           {
            updWeight1[i,j] = Update[count,0];
            count = count+1;
           }
        }

      matrix updbias1 = matrix::Zeros(layer1,1);
      for(int i =0 ; i <layer1; i++)
        {
         updbias1[i,0] = Update[count,0];
         count = count +1;
        }
        
      weights1 = weights1 + updWeight1;
      bias1 = bias1 + updbias1;

      //--- второй слой
      matrix updWeight2 = matrix::Zeros(1,layer1);
      for(int i =0 ; i <layer1; i++)
        {
         updWeight2[0,i] = Update[count,0];
         count = count +1;
        }
      matrix updbias2 = matrix::Zeros(1,1);
      updbias2[0,0] = Update[count,0];

      weights2 = weights2 + updWeight2;
      bias2 = bias2 + updbias2;

      //--- вычисляем функцию потерь для новых параметров
      new_n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
      new_n1.Activation(new_act1, ac_func);
      new_n2 = weights2.MatMul(new_act1) + bias2.MatMul(ones_);
      new_n2.Activation(new_act2, ac_func_last);
      //--- функция потерь с учетом новых параметров
      double new_error = new_act2.Loss(target, loss_func);
      //--- если функция потерь меньше заданного порога завершаем обучение
      if(new_error < Loss_goal)
        {
         break_forloop = true;
         Print("Обучение завершено. Достигнуто желаемое значение функции потерь");
         return true;
        }
      break_forloop = false;
      //---корректируем параметр mu
      if(new_error >= old_error)
        {
         weights1 = Prev_weights1;
         bias1    = Prev_bias1;
         weights2 = Prev_weights2;
         bias2    =  Prev_bias2;
         mu_ = mu_*Incr_Rate;
        }
      else
        {
         mu_ = mu_*Decr_Rate;
         break; 
        }

     }
//--- возвращаем результат
   return true;
  }

Алгоритм сходится, если норма градиента оказывается меньше наперед заданного числа, или если достигнут желаемый уровень функции потерь. Алгоритм останавливается, если параметр mu оказался меньше или больше наперед заданного числа, или после завершения заданного числа эпох.

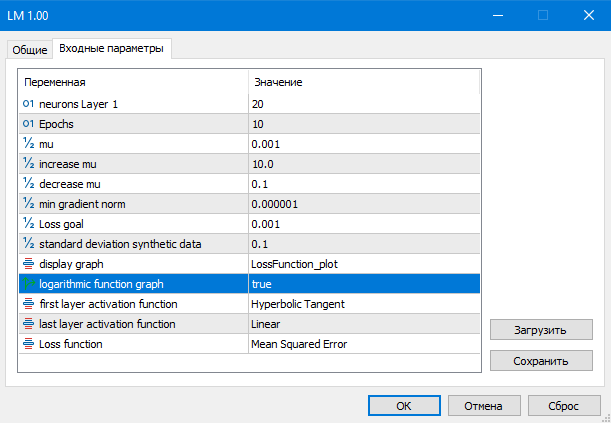
Рис.(7) параметры скрипта LM

Давайте посмотрим на результат всей этой математической эквилибристики:

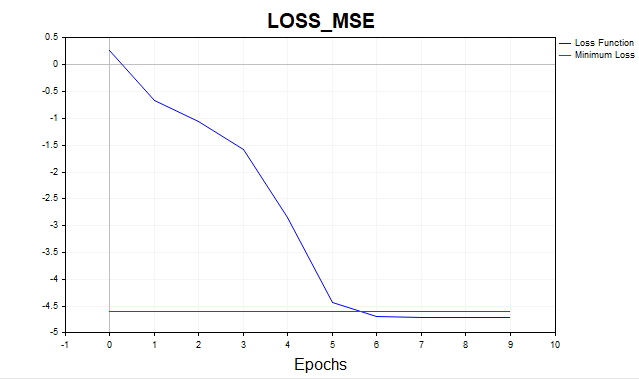
Рис.(8) Функция потерь в логарифмическом масштабе, LM

Теперь совсем другое дело, алгоритм достиг минимальной границы за 6 итераций.  А что, если бы мы обучили сеть на одной тысяче эпох? Получили бы типичный оверфиттинг, рисунок ниже это хорошо демонстрирует. Сеть просто начинает запоминать гауссовский шум.

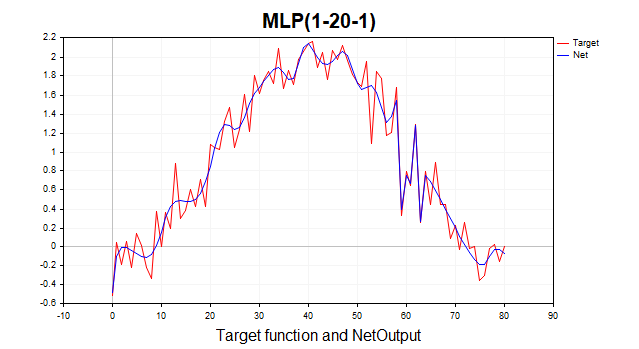
Рис.(9) Типичный оверфиттинг, LM, 1000 эпох

Посмотрим на метрики на обучающем и тестовом множестве.

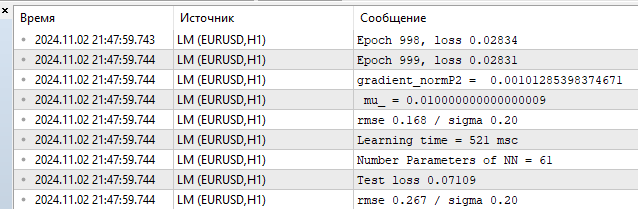
Рис.(10) статистика производительности, LM, 1000 эпох

Видим RMSE 0,168 при нижней границе в 0,20 и тут же — немедленная расплата за оверфиттинг на тесте 0,267.

Тестирование на больших данных и сравнение с библиотекой Python sklearn

Пришло время проверить наш алгоритм на более реалистичном примере. Теперь я взял два признака по 1000 точек данных. Эти данные вы сможете скачать вместе со скриптом LM_BigData в конце статьи.  Конкуренцию LM составят алгоритмы из библиотеки Python — SGD, Adam и L-BFGS.

Вот тестовый скрипт на Python

# Eugene
# https://www.mql5.com

import numpy as np
import time 
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neural_network import MLPRegressor

# здесь ваш путь к данным
df = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Data.csv',delimiter=';')
X = df.to_numpy()
df1 = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Target.csv')
y = df1.to_numpy()
y = y.reshape(-1)

start = time.time() 

'''
clf = MLPRegressor(solver='sgd', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=700,batch_size=10,
                    learning_rate_init=0.01,momentum=0.9,
                    shuffle = False,n_iter_no_change = 2000, tol = 0.000001)
'''

'''
clf = MLPRegressor(solver='adam', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=3000,batch_size=100,                                    
                    learning_rate_init=0.01,
                    n_iter_no_change = 2000, tol = 0.000001)
'''

#'''
clf = MLPRegressor(solver='lbfgs', alpha=0.0, 
                    hidden_layer_sizes=(100),
                    activation='tanh',max_iter=300,
                    tol = 0.000001)
#'''                    
                       
clf.fit(X, y)
end = time.time() - start          # время обучения

print("learning time  =",end*1000) 
print("solver = ",clf.solver);      
print("loss = ",clf.loss_*2)
print("iter = ",clf.n_iter_)
#print("n_layers_ = ",clf.n_layers_)
#print("n_outputs_ = ",clf.n_outputs_)
#print("out_activation_ = ",clf.out_activation_)

coef = clf.coefs_
#print("coefs_ = ",coef)
inter = clf.intercepts_  
#print("intercepts_ = ",inter) 
plt.plot(np.log(pd.DataFrame(clf.loss_curve_)))
plt.title(clf.solver)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()  

Для корректного сравнения алгоритмов, я умножил функцию потерь в Python на 2, так как в этой библиотеке она считается так:

return ((y_true - y_pred) ** 2).mean() / 2

То есть, разработчики дополнительно еще разделили MSE на 2. Ниже представлены типичные результаты оптимизаторов. Я старался подобрать самые лучшие настройки гиперпраметров для этих алгоритмов. К сожалению, в этой библиотеке отсутствует возможность инициализировать значения стартовых параметров для того, чтобы все алгоритмы стартовали с одной точки параметрического пространства. Также нет возможности установить целевой порог функции потерь. Для LM цель функции потерь установлена на уровне 0,01, для алгоритмов Python я старался задать то количество итераций, при котором приблизительно достигается тот же уровень.

Результаты тестирования MLP c одним скрытым слоем , 20 нейронов:

1) Стохастический градиентный спуск  

• loss mse – 0,00278
• время обучения  - 11459 msc

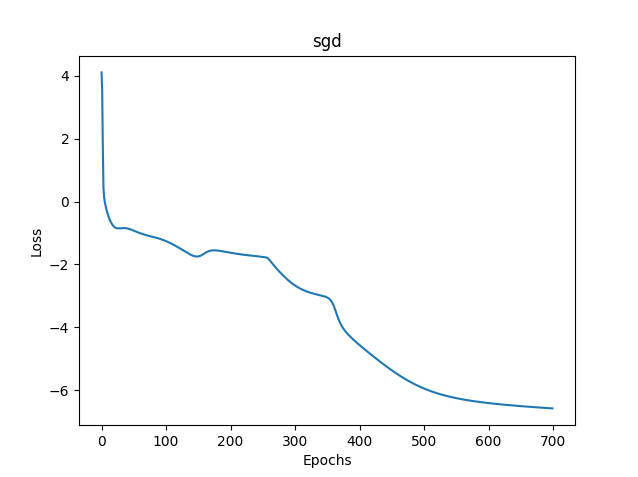
Рис.(11) SGD, 20 нейронов, loss = 0,00278

2) Adam          

•  loss mse – 0,03363
•  время обучения  - 8581 msc

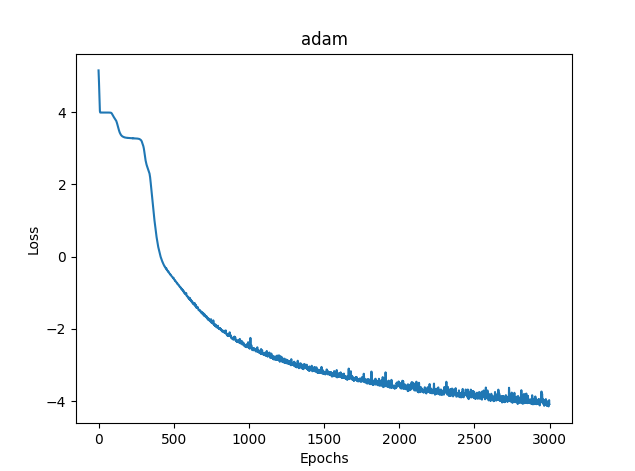
Рис.(12) Adam, 20 нейронов, loss = 0,03363

3)L-BFGS

• loss mse – 0,02770
• время обучения - 277 msc

К сожалению для L-BFGS нельзя отобразить график функции потерь.

4) LM MQL5

•  loss – 0,00846
•  время обучения — 117 msc

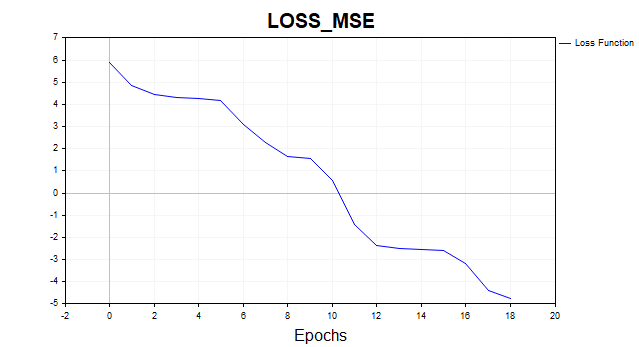
Рис.(13) LM, 20 нейронов, loss = 0,00846

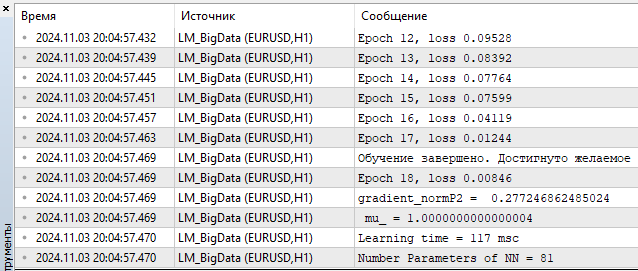
Ну что же, как по мне, так получилось неплохо, алгоритм спокойно конкурирует с L-BFGS и, как видите, еще и фору может дать. Но не бывает ничего идеального, с ростом количества параметров, метод Левенберга-Марквардта начинает проигрывать L-BFGS.

100 нейронов L-BFGS:

• loss mse – 0,00847
• время обучения - 671 msc

100 нейронов LM:

• loss mse – 0,00206
• время обучения  -  1253 msc

100 нейронов соответствуют 401 параметру сети. Решать вам, дорогой читатель, много это или мало, на мой скромный взгляд — это избыточная мощность. А до 100 нейронов — преимущество за LM.

Заключение

В данной статье мы обсудили и реализовали базовые, и самые простые, алгоритмы обучения нейронных сетей:

• градиентный спуск
• градиентный спуск с импульсом
• стохастический градиентный спуск

Вместе с этим, мы кратко затронули вопросы сходимости и переобучения нейронных сетей.

Но самое главное — мы построили очень быстрый алгоритм Левенберга-Марквардта, который идеально подходит для онлайн-обучения небольших сетей.

Мы провели сравнение результативности алгоритмов обучения нейронных сетей, используемых в библиотеке машинного обучения scikit-learn, и самым быстрым оказался именно наш алгоритм, когда количество параметров нейронной сети не превышает 400 или 100 нейронов скрытого слоя. Дальше, с ростом количества нейронов, уже начинает доминировать L-BFGS.

Для каждого алгоритма созданы отдельные скрипты, с подробными комментариями:

#	Имя	Тип	Описание
1	SD.mq5	Script	Градиентный спуск
2	Momentum_SD.mq5	Script	Градиентный спуск с моментом
3	SGD.mq5	Script	Стохастический градиентный спуск
4	LM.mq5	Script	Алгоритм Левенберга-Марквардта
5	LM_BigData.mq5	Script	Алгоритм LM, тест на двумерных признаках
6	SklearnMLP.py	Script	Тестовый скрипт алгоритмов Python
7	FileCSV.mqh	Include	Чтение текстовых файлов с данными
8	Data.csv, Target.csv	Csv	Признаки и цель для Python скрипта
9	X1.txt, X2.txt, Target.txt	Txt	Признаки и цель для скрипта LM_BigData.mq5