Спасибо за интересную статью.
Жаль по кодам мало объяснений.
И с питоновским кодом что-то не так, вроде все библиотеки установил, выдаёт в терминале следующее:
learning time = 1228.5106182098389
solver = lbfgs
loss = 0.0024399556870102
iter = 300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)
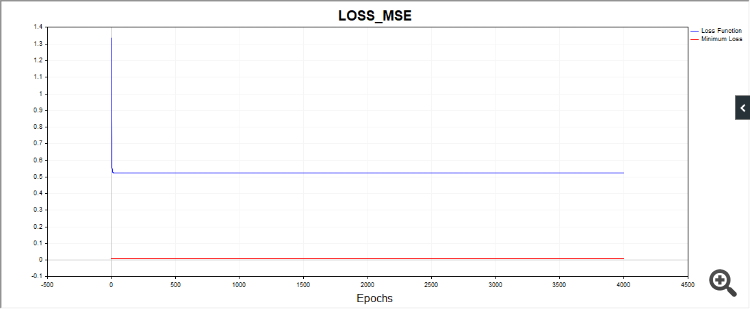
Ещё один момент, скрипт SD в некоторых случаях рисует такую картинку:
Т.е., алго застрял на, судя по всему, простой дате.
Остальные коды тоже выдают очень разные результаты по сходимости. Поэтому желательно приводить графики серии независимых испытаний, картинки единичных испытаний мало о чем говорят (практически ничего).
Спасибо за отзыв.
По пайтону. Это не ошибка, это он предупреждает, что алгоритм остановился из-за того, что мы достигли лимита итераций. То есть алгоритм остановился раньше чем достигнуто значение tol = 0.000001. А дальше он ругается, что оптимизатор lbfgs не имеет атрибута "loss_curve", то есть данных функции потерь. Для adam и sgd они сделали,а для lbfgs почему-то нет. Мне наверно нужно было сделать скрипт так, что бы когда запускается lbfgs то не запрашивать это свойство , что бы оно людей с толку не сбивало.
По SD. Так как мы стартуем каждый раз из различных точек пространства параметров, то и пути схождения к решению тоже будут разными. Я провел очень много проверок, иногда действительно требуется большее количество итераций что-бы сойтись. Я старался указывать среднее количество итераций. Вы можете увеличить количество эпох и увидите что в итоге алгоритм сходится.
По SD. Так как мы стартуем каждый раз из различных точек пространства параметров, то и пути схождения к решению тоже будут разными. Я провел очень много проверок, иногда действительно требуется большее количество итераций что-бы сойтись. Я старался указывать среднее количество итераций. Вы можете увеличить количество эпох и увидите что в итоге алгоритм сходится.
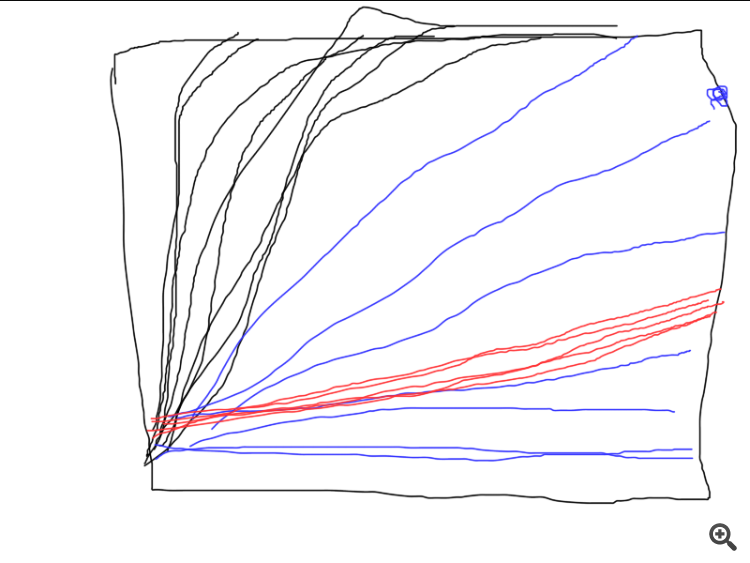
Об этом и веду речь. Это устойчивость, или, воспроизводимость результатов. Чем больше разброс результатов, тем ближе алгоритм по свойствам к RND для данной задачи.
Вот пример работы трёх разных алго. Какой из них лучше всего? Если не провести серию независимых испытаний и не посчитать средние результаты (в идеале посчитать и сравнить дисперсию итоговых результатов), то и сравнить невозможно.
Об этом и веду речь. Это устойчивость, или, воспроизводимость результатов. Чем больше разброс результатов, тем ближе алгоритм по свойствам к RND для данной задачи.
Вот пример работы трёх разных алго. Какой из них лучше всего? Если не провести серию независимых испытаний и не посчитать средние результаты (в идеале посчитать и сравнить дисперсию итоговых результатов), то и сравнить невозможно.
Нужно определится тогда с критерием оценки.
Не, в данном случае так заморачиваться не обязательно, просто если уж сравниваете разные методы, то можно было добавить ещё один цикл (независимые испытания) и вывести на картинку графики отдельных испытаний. Всё получилось бы очень наглядно, кто как сходится, насколько стабильно и сколько тратит на это итераций. А так получилось "как в прошлый раз", когда результат замечательный, но лишь один раз на миллион.
В любом случае спасибо, статья натолкнула на интересные мысли.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Обучение многослойного персептрона с помощью алгоритма Левенберга-Марквардта:
В статье представлена реализация алгоритма Левенберга-Марквардта для обучения нейронных сетей прямого распространения. Проведен сравнительный анализ результативности с алгоритмами из библиотеки scikit-learn Python. Предварительно обсуждаются более простые методы обучения такие как градиентный спуск, градиентный спуск с импульсом и стохастический градиентный спуск.
Цель данной статьи дать практикующим трейдерам очень эффективный алгоритм обучения нейронных сетей — вариант ньютоновского метода оптимизации, известный как алгоритм Левенберга-Марквардта. Это один из самых быстрых алгоритмов обучения нейронных сетей прямого распространения, конкуренцию которому может составить разве что алгоритм Бройдена-Флетчера-Гольдфарба-Шанно(L-BFGS).
Стохастические методы оптимизации, такие как стохастический градиентный спуск(SGD) и Adam, хорошо подходят для оффлайн обучения, когда переобучение нейросети происходит через длительные отрезки времени. Если трейдер, применяющий нейронные сети, желает, чтобы модель быстро адаптировалась к постоянно меняющимся торговым условиям, ему нужно производить переобучение сети онлайн на каждом новом баре, или через небольшой отрезок времени. В таком случае, как нельзя лучше подойдут алгоритмы, которые кроме информации о градиенте функции потерь, используют также дополнительную информацию о вторых частных производных, что позволяет буквально за несколько эпох обучения найти локальный минимум функции потерь.
На данный момент насколько мне известно, реализации алгоритма Левенберга-Марквардта на языке MQL5 в открытом доступе нет. Пора этот пробел заполнить, а также, заодно, вкратце пройтись по хорошо известным и самым простым алгоритмам оптимизации, таким как градиентный спуск, градиентный спуск с импульсом (momentum) и стохастический градиентный спуск. В конце статьи проведем небольшое тестирование эффективности алгоритма Левенберга-Марквардта и алгоритмов из библиотеки машинного обучения scikit-learn.
Автор: Evgeniy Chernish