使用莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法训练多层感知器

MetaTrader 5 — 交易 | 31 七月 2025, 14:50

706

Evgeniy Chernish

概述

本文的目的是为实践中的交易者提供一种非常有效的神经网络训练算法——一种被称为LM算法的牛顿优化方法的变体。它是训练前馈神经网络的最快算法之一，只有Broyden-Fletcher-Goldfarb-Shanno（L-BFGS）算法可以与之匹敌。

随机优化方法，如随机梯度下降（SGD）和Adam，非常适合于神经网络在长时间内过拟合时的离线训练。如果使用神经网络的交易者希望模型能够快速适应不断变化的交易条件，他需要在每根新K线或短时间内重新在线训练网络。在这种情况下，最好的算法是那些除了使用关于损失函数梯度的信息外，还使用关于二阶偏导数的额外信息的算法，这允许在仅仅几个训练周期内找到损失函数的局部最小值。

据我所知，目前还没有公开的MQL5中Levenberg-Marquardt算法的实现。是时候填补这一空白了，同时，也简要回顾一下众所周知的最简便的优化算法，如梯度下降、带动量的梯度下降和随机梯度下降。文章的最后，我们将对Levenberg-Marquardt算法和scikit-learn机器学习库中的算法进行一个小规模的效率测试。

数据集

为了便于展示，所有后续示例均使用合成数据。时间被用作唯一的预测变量，而我们希望通过神经网络预测的目标变量是以下函数：

1 + sin(pi/4*time) + NormDistr(0,sigma)

该函数由确定性部分（以正弦形式呈现的周期性分量）和随机部分（高斯白噪声）组成。总共有81个数据点。以下是该函数及其通过三层感知器近似的图表。

合成数据

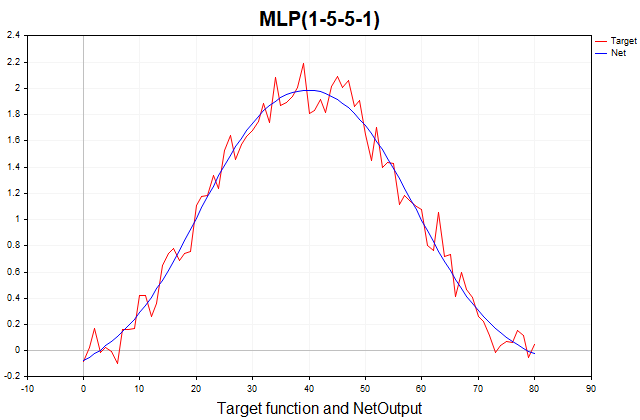
图例1. 目标函数及其通过三层感知器的近似

梯度下降

让我们从实现普通的梯度下降开始，这是训练神经网络的最简单方法。我将使用MQL5参考书中的一个非常好的例子作为模板（矩阵和向量方法/机器学习）。我对它进行了少量修改，增加了选择网络最后一层激活函数的能力，并使梯度下降的实现方式更加通用，不仅能够基于参考书中隐含假设的二次损失函数进行学习，还能基于MQL5中所有可用的损失函数进行学习。损失函数是训练神经网络的核心，有时值得尝试不同的损失函数，而不仅仅是二次损失函数。以下是计算输出层误差（δ）的通用方程：

最后一层的δ

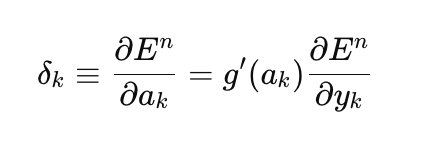
这里

δk — 输出层误差
E — 损失函数
g'(ak) — 激活函数的导数
ak — 最后一层预激活
yk — 网络的预测值

//--- Derivative of the loss function with respect to the predicted value       
matrix DerivLoss_wrt_y = result_.LossGradient(target,loss_func);  
matrix deriv_act;
  if(!result_.Derivative(deriv_act, ac_func_last)) 
     return false;      
 matrix  loss = deriv_act*DerivLoss_wrt_y;  // loss = delta_k

损失函数相对于网络预测值的偏导数由LossGradient函数计算，而激活函数的导数由Derivative函数计算。在参考示例中，将目标值与网络预测值之间的差乘以2作为输出层的误差。

matrix loss = (target - result_)*2;

在机器学习文献中，网络每一层的误差通常被称为δ（例如D2、D1等），而不是损失（例如，参见Bishop(1995)）。从现在开始，我将在代码中使用这种表示法。

我们是如何得到这个结果的？这里隐含地假设损失函数是目标值和预测值之间平方差的总和，而不是均方误差（MSE），后者还会根据训练样本的大小进行额外的标准化。这个损失函数的导数恰好等于(target - result)*2。由于网络的最后一层使用了恒等激活函数，其导数等于1，因此我们得到了这个结果。因此，对于那些希望使用任意损失函数和输出层激活函数来训练网络的人，需要使用上述通用方程。

现在让我们使用均方误差损失函数来训练网络。这里，我使用对数尺度显示图表，以便更清晰。

误差损失，梯度下降

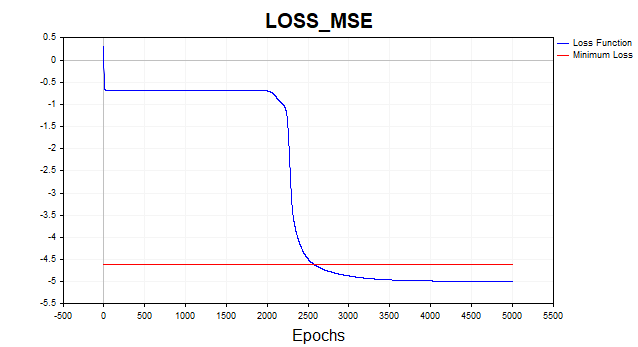
图例2. 图2展示了均方误差损失函数和梯度下降的结果

平均而言，梯度下降算法需要1500-2000个周期（即对整个训练数据集的遍历）才能达到最小损失函数阈值。在该情况下，我使用了两个隐藏层，每个隐藏层有5个神经元。

图上的红线表示损失函数的最小阈值。它被定义为白高斯噪声的方差。这里我使用了方差为0.01的噪声（0.1σ * 0.1σ）。

如果我们允许神经网络模型学习到低于这个最小阈值的水平，会发生什么？之后我们将遇到一个不希望出现的现象——网络过拟合。试图将训练数据集上的损失函数误差降低到最小阈值以下是没有意义的，因为这将影响模型在测试数据集上的预测能力。在此我们将面临这样一个事实：基于该序列的统计分布所允许的程度，无法更精准地预测一个序列。如果我们停止训练在最小阈值以上，将面临另一个问题——网络将训练不足。也就是说，它无法完全捕捉到序列的可预测成分。

正如所见，梯度下降需要经过相当多的迭代才能达到最优参数集。请注意，我们的数据集相当简单。对于实际问题，梯度下降的训练时间可能变得不可接受。改进梯度下降的收敛性和速度的最简单方法之一是动量方法。

带有动量的梯度下降

带有动量的梯度下降的思想是通过像简单指数平均一样平均参数，来平滑训练过程中网络参数的轨迹。正如我们利用求平均值的方法来平滑金融工具价格的时间序列，从而突显其主要走势一样，我们也会针对朝损失函数局部最小值点移动的参数向量的轨迹进行平滑处理。为了更好地可视化这一点，让我们看看一张图表，它显示了两个参数值的变化——从训练开始到损失函数的最小点。图3展示了不使用动量时的轨迹。

无动量的随机梯度下降（SD）

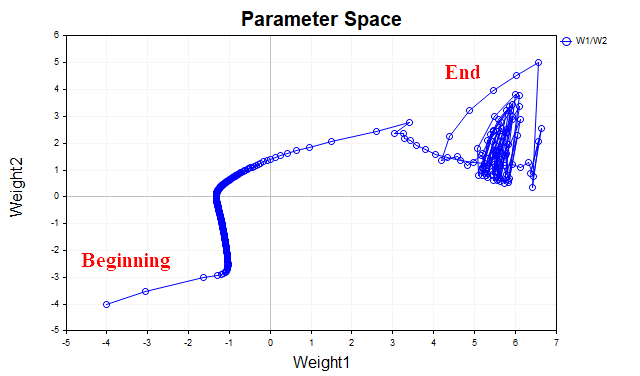
图例3. 无动量的梯度下降

我们可以看到，随着接近最小值点，参数向量开始无序振荡，这使得我们无法到达最优解。为了消除这一现象，我们不得不降低学习率。当然，这样一来算法会开始收敛，但搜索所需的时间可能会大幅增加。

图4展示了使用动量（动量值为0.9）时参数向量的轨迹。这一次，轨迹更加平滑，我们轻松地到达了最优解。现在，我们甚至可以增大学习率。这实际上就是带动量的梯度下降的主要理念——加速收敛过程。

带动量的随机梯度下降（SD）

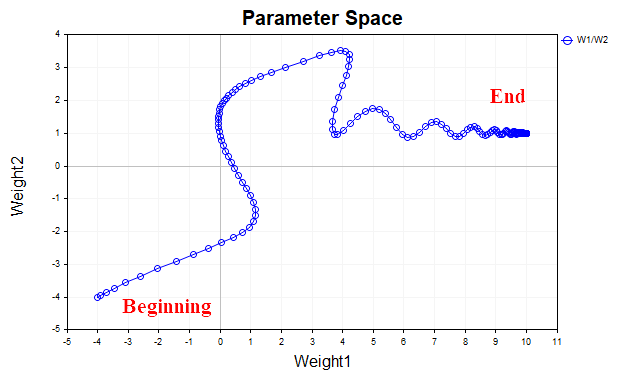
图例4. 带动量（0.9）的梯度下降

Momentum_SD脚本实现了带动量的梯度下降算法。在该算法中，为了提高可理解性，我决定去掉一个隐藏层，并将网络的权重和偏置分开。现在，我们只有一个包含20个神经元的隐藏层，而不是像前一个示例中有两个各包含5个神经元的隐藏层。

//+------------------------------------------------------------------+
//|                                                  Momentum_SD.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,  
   target_netpredict_plot
  };
  
matrix weights1, weights2,bias1,bias2;                      // network parameter matrices
matrix dW1,db1,dW2,db2;                                     // weight increment matrices
matrix n1,n2,act1,act2;                                     // neural layer output matrices
input int    layer1                  = 20;                  // neurons Layer 1
input int    Epochs                  = 1000;                // Epochs
input double lr                      = 0.1;                 // learning rate coefficient
input double sigma_                  = 0.1;                 // standard deviation synthetic data
input double gamma_                  = 0.9;                 // momentum 
input Plots  plot_                   = LossFunction_plot;   // display graph
input bool   plot_log                = false;               // Plot Log graph
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;      // Activation Layer1
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR;    // Activation Layer2
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;     // Loss function

double LossPlot[],target_Plot[],NetOutput[];
matrix ones_;
int Sample_,Features; 

//+------------------------------------------------------------------+
//| Script start function                                            |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- generate a training sample
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }
   ones_ = matrix::Ones(1,Sample_);  
      
   ulong start=GetMicrosecondCount(); 
//--- train the model
   if(!Train(data, target, Epochs))
      return;
   ulong end = (GetMicrosecondCount()-start)/1000;  
   Print("Learning time = " + (string)end + " msc");
//--- generate a test sample
    Func(data,target);
    StandartScaler(data);
//--- test the model
   Test(data, target);
//--- display graphs  
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Model training method                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- create the model
   if(!CreateNet())
      return false;
   ArrayResize(LossPlot,Epochs);
//--- train the model
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- feed forward
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      LossPlot[ep] = act2.Loss(target, loss_func);
      //--- backpropagation and update of weight matrix
      if(!Backprop(data, target))
         return false;
     }
//---
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Cols(); i++)
     {
      NetOutput[i]  =act2.Transpose()[i,0];
     }
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Model creation method                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- initialize weight matrices
   if(!weights1.Init(layer1,Features)  || !weights2.Init(1,layer1)) 
      return false;
//--- initialize offset matrices
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))  
      return false;
//--- initialize the matrix of parameter increments
   dW1.Init(layer1,Features);
   dW2.Init(1, layer1);
   db1.Init(layer1,1);
   db2.Init(1,1);
   dW1.Fill(0);
   dW2.Fill(0);
   db1.Fill(0);
   db2.Fill(0);
//--- fill the parameter matrices with random values
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1,0.1);
   bias2.Random(-0.1,0.1);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Feed-forward method                                              |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  { 
//--- calculate the first neural layer
//--- n1 pre-activation of the first layer
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- calculate the activation function of the act1 first layer
   n1.Activation(act1, ac_func);
//--- calculate the second neural layer
//--- n2 pre-activation of the second layer
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- calculate the activation function of the act2 second layer
   n2.Activation(act2, ac_func_last);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Backpropagation method                                           |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- Derivative of the loss function with respect to the predicted value
   matrix DerivLoss_wrt_y = act2.LossGradient(target.Transpose(),loss_func);
   matrix deriv_act2;
   n2.Derivative(deriv_act2, ac_func_last);
//--- D2   
   matrix  D2 = deriv_act2*DerivLoss_wrt_y; // error(delta) of the network output layer
//--- D1
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = D1*deriv_act1; // error (delta) of the first layer of the network
//--- update network parameters
   matrix  ones = matrix::Ones(data.Rows(),1);
   dW1 = gamma_*dW1 + (1-gamma_)*(D1.MatMul(data)) * lr;
   db1 = gamma_*db1 + (1-gamma_)*(D1.MatMul(ones)) * lr;
   dW2 = gamma_*dW2 + (1-gamma_)*(D2.MatMul(act1.Transpose())) * lr;
   db2 = gamma_*db2 + (1-gamma_)*(D2.MatMul(ones)) * lr;
   weights1 =  weights1 - dW1;
   weights2 =  weights2 - dW2;
   bias1    =  bias1    - db1;
   bias2    =  bias2    - db2;
//--- return result
   return true;
  }

归功于动量，我能够将学习速度从0.1提高到0.5。现在算法在150-200次迭代中收敛，而不是普通梯度下降的500次。

带动量的梯度下降（SD）损失

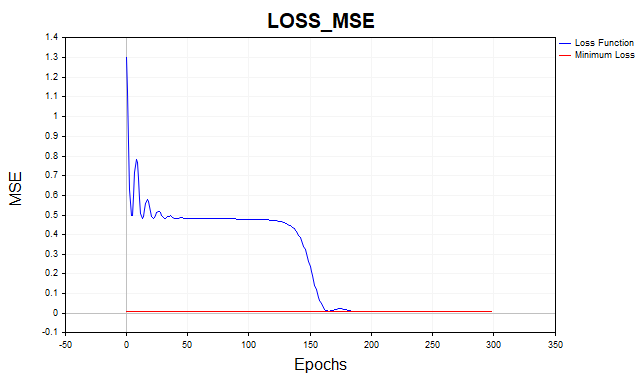
图例5. 均方误差损失函数，MLP(1-20-1) SD_Momentum

随机梯度下降

动量虽好，但如果数据集不是像我们例子中的81个数据点，而是成千上万个数据实例，那么就有理由讨论这样一个经过充分验证（且简便）的算法——SGD。SGD和梯度下降一样，但梯度不是在整个训练集上计算的，而是只在该集的某个非常小的部分（小批量）上，甚至只在一个数据点上计算。之后，网络权重会更新，随机选择一个新的数据点，然后重复这个过程，直到算法收敛。这就是为什么其被称为随机算法。在传统的梯度下降中，我们只有在整个数据集上计算梯度后才更新网络权重。这就是所谓的批量方法。

我们实现了一个SGD的变体，其中只使用一个数据点作为小的批量。

SGD损失

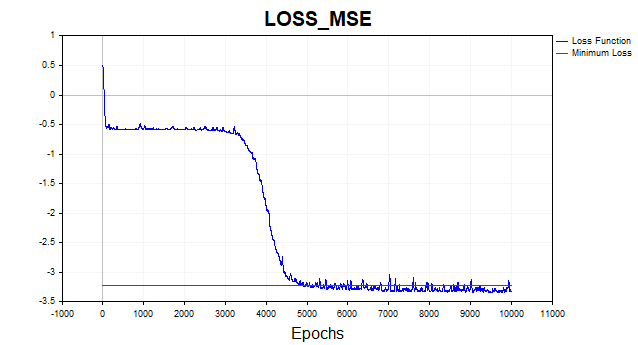
图例6. 对数尺度下的损失函数，SGD

SGD算法（batch_size = 1）在4-6千次迭代中收敛到最小边界，但请记住我们只使用81个中的一个训练样本来更新参数向量。因此，该算法在这个数据集上大约在50-75个周期内收敛。与前一个算法相比，改进效果还不算差，对吧？这里我也使用了动量，但由于只使用了一个数据点，它对收敛速度的影响不大。

莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法

这个古老的算法如今不知何故被完全遗忘了，尽管如果您的网络有几百个参数，与L-BFGS一起，简直无与伦比。

但是有一点很重要。LM算法旨在最小化其他非线性函数平方和形式的函数。因此，对于该方法，我们将仅限于使用二次或均方根损失函数。在其他条件相同的情况下，这种损失函数完全能够完成其工作，此处并没有什么大问题，但我们需要明白，无法使用该算法在其他函数上训练网络。

现在让我们详细看一下这个算法是如何起源的。从牛顿法开始：

牛顿法

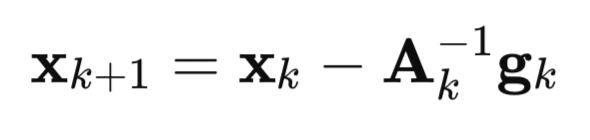
这里

A — 损失函数 F(x) 的逆海森矩阵（Hessian Matrix）

g — 损失函数 F(x) 的梯度（Gradient）

x — 参数向量（Parameter Vector）

现在让我们看看我们的二次损失函数：

SSE

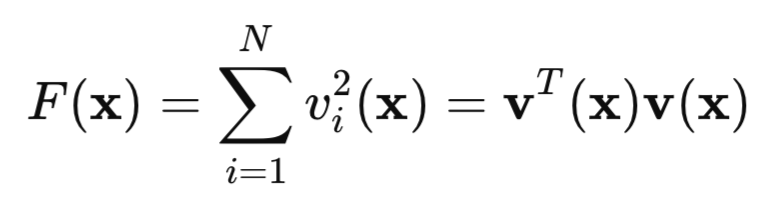
这里，v是网络误差（预测值减去目标值），而x是一个包含每层所有权重和偏置的网络参数向量。

让我们来求这个损失函数的梯度：

SSE损失函数的梯度

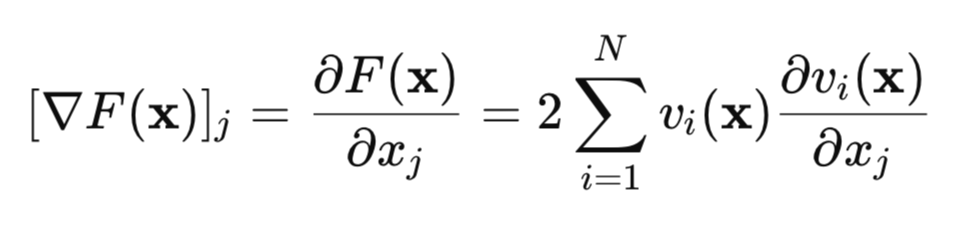
用矩阵形式表示，可以写成：

矩阵表示的梯度

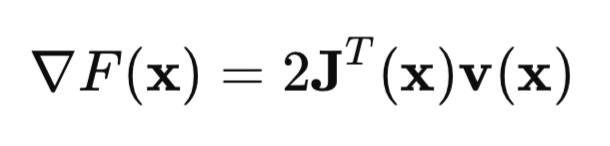
关键点是雅可比矩阵（Jacobian Matrix）：

雅可比矩阵

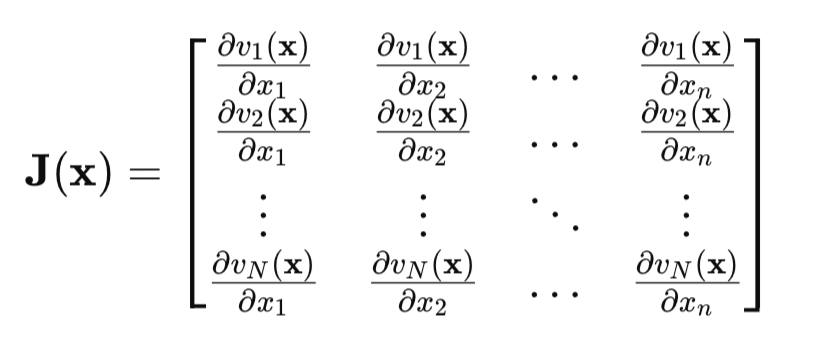
在雅可比矩阵中，每一行都包含网络误差相对于所有参数的偏导数。每一行对应训练集中的一个样本。

现在让我们看一下海森矩阵（Hessian Matrix）。这是损失函数的二阶偏导数矩阵。计算海森矩阵是一个困难且代价高昂的任务，因此通常使用雅可比矩阵来近似海森矩阵：

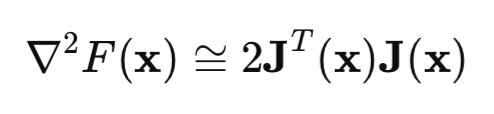
如果我们将海森矩阵和梯度方程代入牛顿法方程，我们得到高斯-牛顿方法（Gauss-Newton Method）：

但是高斯-牛顿方法的问题在于，[J'J] 矩阵可能不可逆。为了解决这个问题，我们将单位矩阵乘以正标量mu*I并加到该矩阵上。在此情况下，我们得出莱文贝格-马夸尔特（LM）算法：

莱文贝格-马夸尔特（LM）方法

该算法的特点是，当mu参数取较大正值时，算法简化为我们在文章开头讨论的普通梯度下降法。如果mu参数趋于0，我们则回归到高斯-牛顿方法。

通常训练从较小的mu值开始。如果损失函数值没有变小，那么mu参数就会增加（例如，乘以 10）。由于这使我们更接近梯度下降法，迟早会实现损失函数的减少。如果损失函数已经减小，我们通过连接高斯-牛顿方法来更快地收敛到最小点，从而减小mu参数的值。这就是LM方法的主要思想——在梯度下降法和高斯-牛顿方法之间不断地切换。

莱文贝格-马夸尔特算法的反向传播方法的实现有其自身的特点。由于雅可比矩阵的元素是网络误差的偏导数，而不是这些误差的平方，因此我在文章开头给出的计算网络最后一层的 delta 的方程被简化了。现在δ等于最后一层激活函数的导数。如果我们将网络误差（y – target）对y求导，显然结果为1，这就是我们得到的结果。

以下是附有详细注释的神经网络代码：

//+------------------------------------------------------------------+
//|                                                           LM.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,
   mu_plot,
   gradient_plot,
   target_netpredict_plot
  };

matrix weights1,weights2,bias1,bias2;                    // network parameter matrices
matrix n1,n2,act1,act2,new_n1,new_n2,new_act1,new_act2;  // neural layer output matrices
input int    layer1     = 20;                            // neurons Layer 1
input int    Epochs     = 10;                            // Epochs
input double Initial_mu = 0.001;                         // mu
input double Incr_Rate  = 10;                            // increase mu
input double Decr_Rate  = 0.1;                           // decrease mu
input double Min_grad   = 0.000001;                      // min gradient norm
input double Loss_goal  = 0.001;                         // Loss goal
input double sigma_     = 0.1;                           // standard deviation synthetic data
input Plots  plot_      = LossFunction_plot;             // display graph
input bool   plot_log   = false;                         // logarithmic function graph 
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;   // first layer activation function
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR; // last layer activation function
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;  // Loss function

double LossPlot[],NetOutput[],mu_Plot[],gradient_Plot[],target_Plot[];
matrix ones_;
double old_error,gradient_NormP2;
double mu_ = Initial_mu;
bool break_forloop = false;
int Sample_,Features;

//+------------------------------------------------------------------+
//| Script start function                                            |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- generate a training sample
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }

   ones_ = matrix::Ones(1,Sample_);
//--- train the model
   ulong start=GetMicrosecondCount();
   Train(data, target, Epochs);
   ulong end = (GetMicrosecondCount()-start)/1000 ;
   Print("Learning time = " + (string)end + " msc");
   int NumberParameters = layer1*(Features+1) + 1*(layer1+1);
   Print("Number Parameters of NN = ",NumberParameters);

//--- generate a test sample
   Func(data,target);
   StandartScaler(data);
//--- test the model
   Test(data,target);
   
//--- display graphs
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Model training method                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- create the model
   if(!CreateNet())
      return false;
//--- train the model
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- feed forward
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      //--- arrays for graphs
      ArrayResize(LossPlot,ep+1,10000);
      ArrayResize(mu_Plot,ep+1,10000);
      ArrayResize(gradient_Plot,ep+1,10000);
      LossPlot[ep]       = act2.Loss(target, loss_func);
      mu_Plot [ep]       = mu_;
      gradient_Plot[ep]  = gradient_NormP2;
      //--- Stop training if the target value of the loss function is reached
      if(break_forloop == true){break;}
      //--- backpropagation and update of weight matrix
      if(!Backprop(data, target))
         return false;
     }
//--- Euclidean norm of gradient, mu parameter, RMSE metric
   Print("gradient_normP2 =  ", gradient_NormP2);
   Print(" mu_ = ", mu_);
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
//--- array of network output for graph
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Transpose().Rows(); i++)
     {
      NetOutput[i]  = act2.Transpose()[i,0];
     }
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Model creation method                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- initialize weight matrices
   if(!weights1.Init(layer1,Features) || !weights2.Init(1,layer1))
      return false;
//--- initialize offset matrices
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))
      return false;
//--- fill the weight matrices with random values
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1, 0.1);
   bias2.Random(-0.1, 0.1);   
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Feed-forward method                                              |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- calculate the first neural layer
//--- n1 pre-activation of the first layer
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- calculate the activation function of the act1 first layer
   n1.Activation(act1, ac_func);
//--- calculate the second neural layer
//--- n2 pre-activation of the second layer
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- calculate the activation function of the act2 second layer
   n2.Activation(act2, ac_func_last);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Backpropagation method                                           |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- current value of the loss function
   old_error = act2.Loss(target, loss_func);
//--- network error (quadratic loss function)
   matrix loss = act2.Transpose() - target ;
//--- derivative of the activation function of the last layer
   matrix D2;
   n2.Derivative(D2, ac_func_last);
//--- derivative of the first layer activation function
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
//--- first layer network error
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = deriv_act1 * D1;
//--- first partial derivatives of network errors with respect to the first layer weights
   matrix jac1;
   partjacobian(data.Transpose(),D1,jac1);
//--- first partial derivatives of network errors with respect to the second layer weights
   matrix jac2;
   partjacobian(act1,D2,jac2);
//--- Jacobian
   matrix j1_D1 = Matrixconcatenate(jac1,D1.Transpose(),1);
   matrix j2_D2 = Matrixconcatenate(jac2,D2.Transpose(),1);
   matrix jac   = Matrixconcatenate(j1_D1,j2_D2,1);
// --- Loss function gradient
   matrix je = (jac.Transpose().MatMul(loss));
//--- Euclidean norm of gradient normalized to sample size
   gradient_NormP2 = je.Norm(MATRIX_NORM_FROBENIUS)/Sample_;
   if(gradient_NormP2 < Min_grad)
     {
      Print("Local minimum. The gradient is less than the specified value.");
      break_forloop = true; // stop training
      return true;
     }
//--- Hessian
   matrix Hessian = (jac.Transpose().MatMul(jac));
   matrix I=matrix::Eye(Hessian.Rows(), Hessian.Rows());
//---
   break_forloop = true;
   while(mu_ <= 1e10 && mu_ > 1e-20)
     {
      matrix H_I = (Hessian + mu_*I);
      //--- solution via Solve
      vector v_je = je.Col(0);
      vector Updatelinsolve = -1* H_I.Solve(v_je);
      matrix Update = matrix::Zeros(Hessian.Rows(),1);
      Update.Col(Updatelinsolve,0); // increment of the parameter vector
      
      //--- inefficient calculation of inverse matrix
      //   matrix Update = H_I.Inv();
      //   Update = -1*Update.MatMul(je);
      //---

      //--- save the current parameters
      matrix  Prev_weights1 = weights1;
      matrix  Prev_bias1    = bias1;
      matrix  Prev_weights2 = weights2;
      matrix  Prev_bias2    = bias2;
      //---

      //--- update the parameters
      //--- first layer
      matrix updWeight1 = matrix::Zeros(layer1,Features);
      int count =0;
      for(int j=0; j <Features; j++)
        {
         for(int i=0 ; i <layer1; i++)
           {
            updWeight1[i,j] = Update[count,0];
            count = count+1;
           }
        }

      matrix updbias1 = matrix::Zeros(layer1,1);
      for(int i =0 ; i <layer1; i++)
        {
         updbias1[i,0] = Update[count,0];
         count = count +1;
        }
        
      weights1 = weights1 + updWeight1;
      bias1 = bias1 + updbias1;

      //--- second layer
      matrix updWeight2 = matrix::Zeros(1,layer1);
      for(int i =0 ; i <layer1; i++)
        {
         updWeight2[0,i] = Update[count,0];
         count = count +1;
        }
      matrix updbias2 = matrix::Zeros(1,1);
      updbias2[0,0] = Update[count,0];

      weights2 = weights2 + updWeight2;
      bias2 = bias2 + updbias2;

      //--- calculate the loss function for the new parameters
      new_n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
      new_n1.Activation(new_act1, ac_func);
      new_n2 = weights2.MatMul(new_act1) + bias2.MatMul(ones_);
      new_n2.Activation(new_act2, ac_func_last);
      //--- loss function taking into account new parameters
      double new_error = new_act2.Loss(target, loss_func);
      //--- if the loss function is less than the specified threshold, terminate training
      if(new_error < Loss_goal)
        {
         break_forloop = true;
         Print("Training complete. The desired loss function value achieved");
         return true;
        }
      break_forloop = false;
      //--- correct the mu parameter
      if(new_error >= old_error)
        {
         weights1 = Prev_weights1;
         bias1    = Prev_bias1;
         weights2 = Prev_weights2;
         bias2    =  Prev_bias2;
         mu_ = mu_*Incr_Rate;
        }
      else
        {
         mu_ = mu_*Decr_Rate;
         break; 
        }

     }
//--- return result
   return true;
  }

算法会在梯度范数小于预设值，或者损失函数达到期望水平时收敛。如果mu参数小于或大于预设值，或者完成预设的训练周期数，算法就会停止。

LM参数

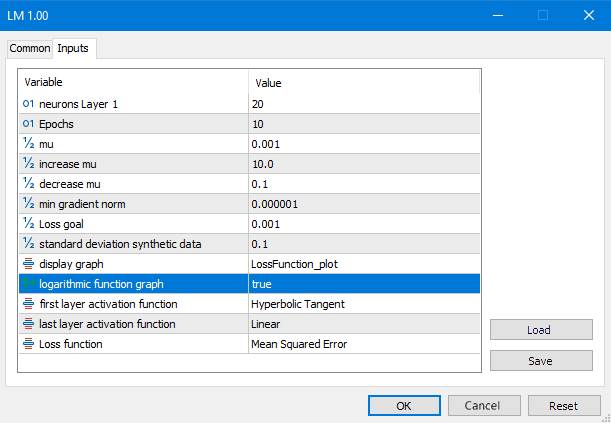
图例7. LM脚本参数

让我们看一下所有这些数学运算的结果：

LM损失

图例8. 以对数尺度表示的LM损失函数

现在情况完全不同了。算法在6次迭代中就达到了最小边界。如果我们在1000个周期内训练网络会怎样呢？我们会得到典型的过拟合现象。下图很好地展示了这一点。网络开始记住高斯白噪声。

LM过拟合

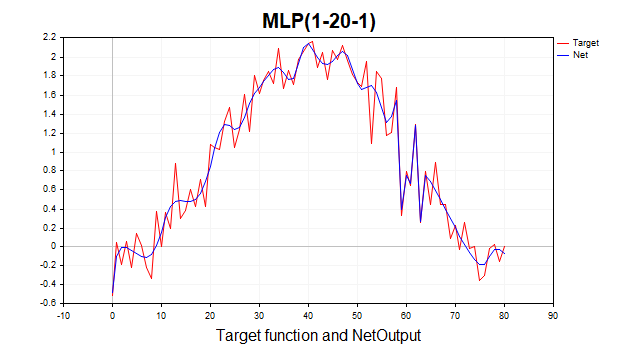
图例9. 典型的过拟合现象，LM，1000个周期

让我们看一下训练集和测试集上的性能指标。

LM性能

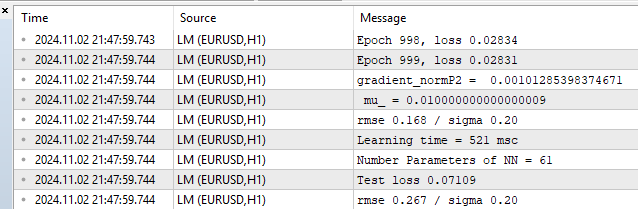
图例10. 性能统计，LM，1000个周期

我们看到训练集上的均方根误差（RMSE）为0.168，而测试集上的均方根误差为0.267，这就是过拟合的代价。

在大数据集上测试并与Python sklearn库进行比较

现在是时候在更真实的实例上测试我们的算法了。我选择了两个特征，包含1000个数据点。您可以在文章末尾下载这些数据以及LM_BigData 脚本。LM将与Python库中的SGD、Adam 和L-BFGS算法进行比较。

以下是Python测试脚本

# Eugene
# https://www.mql5.com

import numpy as np
import time 
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neural_network import MLPRegressor

# here is your path to the data
df = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Data.csv',delimiter=';')
X = df.to_numpy()
df1 = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Target.csv')
y = df1.to_numpy()
y = y.reshape(-1)

start = time.time() 

'''
clf = MLPRegressor(solver='sgd', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=700,batch_size=10,
                    learning_rate_init=0.01,momentum=0.9,
                    shuffle = False,n_iter_no_change = 2000, tol = 0.000001)
'''

'''
clf = MLPRegressor(solver='adam', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=3000,batch_size=100,                                    
                    learning_rate_init=0.01,
                    n_iter_no_change = 2000, tol = 0.000001)
'''

#'''
clf = MLPRegressor(solver='lbfgs', alpha=0.0, 
                    hidden_layer_sizes=(100),
                    activation='tanh',max_iter=300,
                    tol = 0.000001)
#'''                    
                       
clf.fit(X, y)
end = time.time() - start          # training time

print("learning time  =",end*1000) 
print("solver = ",clf.solver);      
print("loss = ",clf.loss_*2)
print("iter = ",clf.n_iter_)
#print("n_layers_ = ",clf.n_layers_)
#print("n_outputs_ = ",clf.n_outputs_)
#print("out_activation_ = ",clf.out_activation_)

coef = clf.coefs_
#print("coefs_ = ",coef)
inter = clf.intercepts_  
#print("intercepts_ = ",inter) 
plt.plot(np.log(pd.DataFrame(clf.loss_curve_)))
plt.title(clf.solver)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

为了正确比较这些算法，我在Python中将损失函数乘以2，因为在该库中它是这样计算的：

return ((y_true - y_pred) ** 2).mean() / 2

换句话说，开发者额外将均方误差（MSE）除以2。以下是这些优化器的典型结果。我尝试为这些算法找到最佳的超参数设置。不幸的是，这个库不提供初始化起始参数值的能力，以便所有算法都从参数空间的同一点开始。也没有办法设置损失函数的目标阈值。对于LM，损失函数的目标设置为0.01，对于 Python 算法，我尝试设置迭代次数，以大致达到相同的水平。

具有一个隐藏层（20个神经元）的MLP测试结果：

1) 随机梯度下降

损失（MSE）：0.00278
训练时间：11459毫秒

Python中的SGD损失

图例11. SGD，20个神经元，损失 = 0.00278

2) Adam

损失（MSE）：0.03363
训练时间：8581毫秒

Adam损失

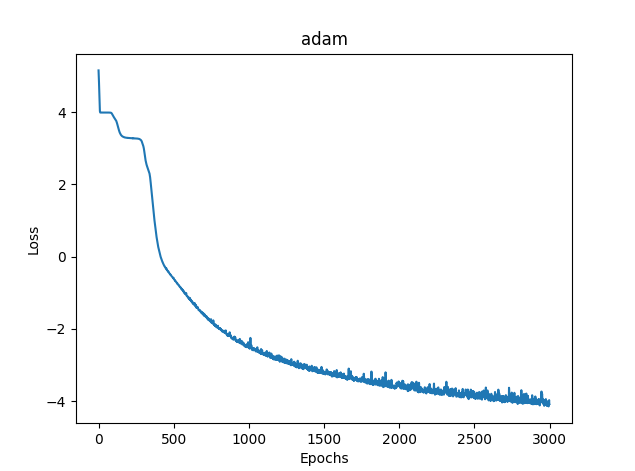
图例12. Adam，20个神经元，损失 = 0.03363

3)L-BFGS

损失（MSE）：0.02770
训练时间：277毫秒

遗憾的是，无法显示L-BFGS的损失函数图。

4) LM MQL5

损失： 0.00846
训练时间：117毫秒

LM损失

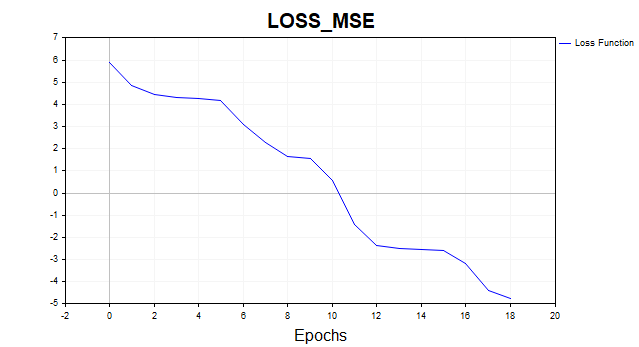
图例13. LM，20个神经元，损失 = 0.00846

LM性能

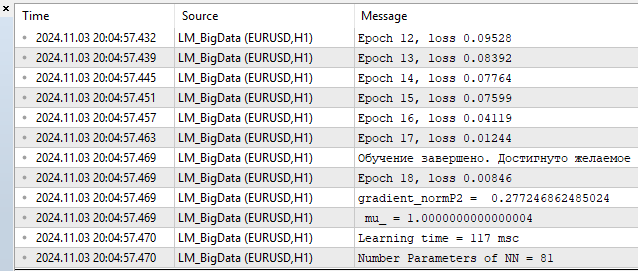
在我看来，该算法能够轻松地与L-BFGS竞争，甚至可以有领先的机会。但所有算法都不是完美的。随着参数数量的增加，Levenberg-Marquardt方法逐渐输给L-BFGS。

100个神经元的L-BFGS：

损失（MSE）：0.00847
训练时间：671毫秒

100个神经元的LM：

损失（MSE）：0.00206
训练时间：1253毫秒

100个神经元对应于401个网络参数。由您决定这样是否算多，但以我拙见，这算是多余的计算能力。在最多100个神经元的情况下，LM很明显具有优势。

结论

在本文中，我们讨论并实现了最基本的神经网络训练算法：

梯度下降
带有动量的梯度下降
随机梯度下降

同时，我们简要地探讨了神经网络的收敛和再训练问题。

但最重要的是，我们构建了一个非常快速的莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法，非常适合小网络的在线训练。

我们将scikit-learn机器学习库中使用的神经网络训练算法的性能进行了比较，结果表明，当神经网络参数数量不超过400或隐藏层中有100个神经元时，我们的算法是最快速的。之后，随着神经元数量的增加，L-BFGS开始占据主导地位。

我为每种算法都创建了单独的脚本，并附有详细的注释。

#	名称	类型	描述
1	SD.mq5	脚本	梯度下降
2	Momentum_SD.mq5	脚本	带有动量的梯度下降
3	SGD.mq5	脚本	随机梯度下降
4	LM.mq5	脚本	莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法
5	LM_BigData.mq5	脚本	LM算法，二维特征测试
6	SklearnMLP.py	脚本	Python算法测试脚本
7	FileCSV.mqh	库	读取包含数据的文本文件
8	Data.csv, Target.csv	Csv	Python脚本的特性和用途
9	X1.txt, X2.txt, Target.txt	Txt	LM_BigData.mq5脚本的功能和用途

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/16296

附加的文件 |

下载ZIP

SD.mq5 (26.15 KB)

SGD.mq5 (26.16 KB)

Momentum_SD.mq5 (22.59 KB)

LM.mq5 (36.21 KB)

LM_BigData.mq5 (36.15 KB)

FileCSV.mqh (10.45 KB)

X1.txt (19.26 KB)

X2.txt (19.26 KB)

Target.txt (17.62 KB)

Data.csv (37.56 KB)

Target.csv (17.62 KB)

SklearnMLP.py (1.83 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

最近评论 | 前往讨论 (6)

Evgeniy Chernish | 8 11月 2024 在 08:52

感谢您的反馈。

关于 python。这不是一个错误，它警告说算法已经停止，因为我们已经达到了迭代极限。也就是说，算法在达到 tol = 0.000001 值之前就停止了。然后警告说，lbfgs 优化器没有 "loss_curve "属性，即损失函数数据。adam 和 sgd 有，但 lbfgs 却没有。我也许应该编写一个脚本，这样当启动 lbfgs 时，它就不会询问这个属性，这样就不会让人感到困惑了。

关于 SD。由于我们每次都从参数空间的不同点出发，因此求解的路径也会不同。我做了很多测试，有时确实需要更多的迭代才能收敛。我尝试给出平均迭代次数。你可以增加迭代次数，你会发现算法最终会收敛。