記事「レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング」についてのディスカッション

新しいコメント
 

新しい記事「レーベンバーグ・マルカートアルゴリズムを用いた多層パーセプトロンのトレーニング」はパブリッシュされました:

この記事では、順伝播型（フィードフォワード）ニューラルネットワークの学習におけるレーベンバーグ・マルカートアルゴリズムの実装を紹介します。また、scikit-learn Pythonライブラリのアルゴリズムと性能比較もおこなっています。まずは、勾配降下法、モーメンタム付き勾配降下法、確率的勾配降下法などのより単純な学習法について簡単に触れます。

この記事の目的は、トレーダーの方々に非常に効果的なニューラルネットワークの学習アルゴリズム、すなわちニュートン法の一種であるレーベンバーグ・マルカート法を提供することです。このアルゴリズムは順伝播型ニューラルネットワークの学習において最速の部類に入り、L-BFGS(Broyden-Fletcher-Goldfarb-Shanno)アルゴリズムと肩を並べる性能を持ちます。

確率的最適化法である確率的勾配降下法(SGD: Stochastic Gradient Descent)やAdam法は、長期間の学習によりニューラルネットワークが過学習するオフライン学習に適しています。しかし、トレーダーがニューラルネットワークを用いて、常に変化する市場状況に迅速に適応させたい場合には、各新しいバーの到来ごと、あるいは短期間ごとにオンラインで再学習させる必要があります。この場合、損失関数の勾配情報だけでなく、二階導函数に関する追加情報も用いて、わずか数エポックで損失関数の局所最小値を見つけられるアルゴリズムが最適です。

現時点で、私の知る限りMQL5でのレーベンバーグ・マルカート法の公開実装はありません。このギャップを埋めるとともに、記事の後半では勾配降下法、モーメンタム付き勾配降下法、確率的勾配降下法といった代表的でシンプルな最適化アルゴリズムについても簡単に解説します。最後に、レーベンバーグ・マルカート法とscikit-learn機械学習ライブラリのアルゴリズムの効率を比較する小さなテストをおこないます。


作者: Evgeniy Chernish

 

興味深い記事をありがとう。

コードの説明が少ないのが残念です。

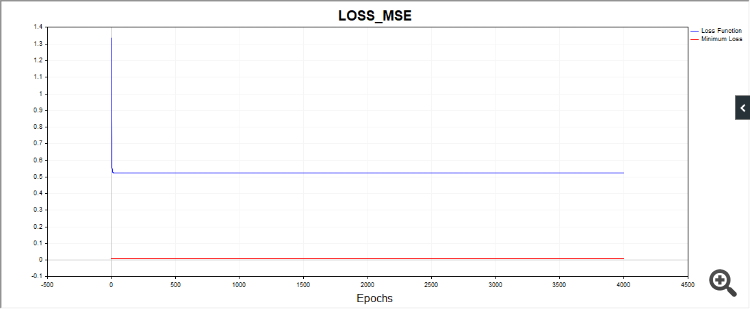
そして、pythonのコードがおかしいです。すべてのライブラリをインストールしたのですが、ターミナルでは次のようになります：

learning time  = 1228.5106182098389
solver =  lbfgs
loss =  0.0024399556870102
iter =  300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
    https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
  self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
    plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)

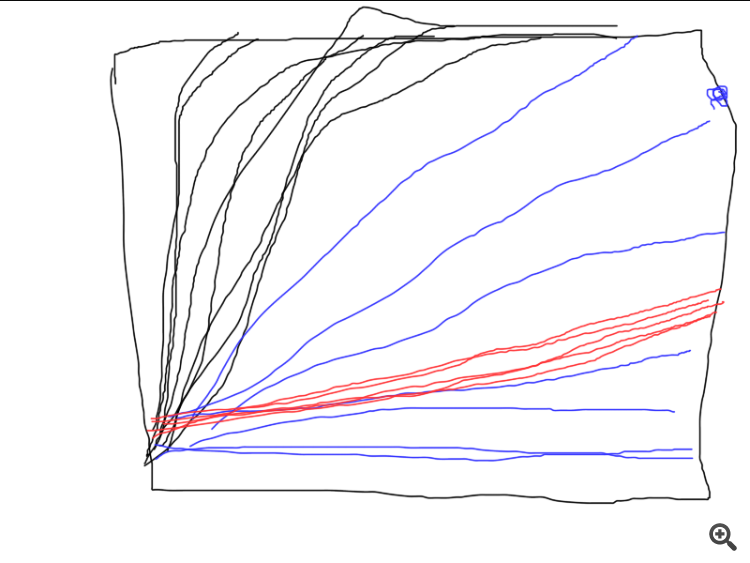
もうひとつ、SDスクリプトがこのような絵を描く場合があります：


つまり、アルゴはどうやら単純な日付に引っかかっている。

他のコードでも、非常に異なった収束結果が得られる。したがって、一連の独立したテストのグラフを与えることが望ましい。

 

フィードバックありがとう。

パイソンではこれはエラーではなく、アルゴリズムが反復限界に達したため停止したことを警告しています。つまり、値tol = 0.000001に達する前にアルゴリズムが停止しました。そして、lbfgsオプティマイザが "loss_curve "属性、つまり損失関数のデータを持っていないことを警告します。adamとsgdにはあるのだが、lbfgsにはなぜかない。おそらく、lbfgsが起動したときにこのプロパティを要求しないようにスクリプトを作るべきだったのだろう。

SDについて。パラメータ空間の異なる点から毎回スタートするので、解への道筋も違ってきます。私は多くのテストを行いましたが、収束するまでに本当に多くの反復回数がかかることがあります。平均的な反復回数を示してみました。反復回数を増やせば、最終的にアルゴリズムが収束するのがわかるでしょう。

 
Evgeniy Chernish #:

SDについて。パラメータ空間の異なる点から毎回スタートするので、解に収束するまでの経路も異なります。私は多くのテストを行いましたが、収束するまでに本当に多くの反復を要することもありました。平均的な反復回数を示してみました。反復回数を増やせば、アルゴリズムが最終的に収束するのがわかるでしょう。

それが私の言っていることです。ロバスト性、つまり結果の再現性です。結果のばらつきが大きいほど、そのアルゴリズムは与えられた問題に対してRNDに近いということです。

ここに3つの異なるアルゴリズムがどのように機能するかの例を示します。どれがベストでしょうか？一連の独立したテストを実行し、平均結果を計算しない限り（理想的には、最終結果の分散を計算して比較する）、比較することは不可能です。

 
Andrey Dik #:

私が言っているのはそのことだ。安定性、つまり結果の再現性です。結果のばらつきが大きいほど、そのアルゴリズムは与えられた問題に対してRNDに近いということです。

ここに3つの異なるアルゴリズムがどのように機能するかの例を示します。どれがベストでしょうか？一連の独立したテストを実行し、平均結果を計算しない限り（理想的には、最終結果の分散を計算して比較する）、比較することは不可能です。

そこで、評価基準を定義する必要があります。
時間や最大結果（関数の最小値を求める場合は最小値）を基準にすることができます。
再スタートの回数を設定する。
この再試行回数で達成された最大値とそれにかかった時間を記録する。
このようなテストを1000回とする。
そしてこの一連の平均と分散、つまり最大値の平均と分散を計算する。

結果の分布密度の構築まで、ほとんど徹底的にやったわけではないので、1つの記事ですべてをカバーすることは不可能である。
 
この記事は追加テストなしで素晴らしく、アルゴリズムに関する一般的な結論と一致している :)これによって、すぐに何かに合意し、次のトピックに移ることができる。
 
Evgeniy Chernish #:
次に評価基準を定義する必要がある。
評価基準としては、時間と最大結果を取ることができる（関数の最小値を求める必要がある場合は最小値を取ることもできる）。
再スタートの回数を設定する。
この再スタート回数で達成された最大値と、それにかかった時間を記録する。
このようなテストを1000回とする。
そしてこの一連の平均と分散、すなわち最大値の平均と分散を計算する。

結果の分布密度の構築まで，ほとんど徹底的にやったわけではないので，1つの記事ですべてをカバーすることは不可能である。

いや、この場合はそんな面倒なことをする必要はないが、もし異なる方法を比較するのであれば、もう1サイクル（独立試験）を追加して、個々の試験のグラフをプロットすることができる。そうすれば、誰が収束したのか、どの程度安定しているのか、何回繰り返せば収束するのか、すべてが明確になる。それで、結果は素晴らしいが、100万回に1回しかない「前回のような」結果になった。

とにかく、ありがとう。この記事は私に興味深い考えを与えてくれた。

新しいコメント