取引におけるカオス理論（第2回）：さらなる研究

前の記事の要約

最初の記事では、カオス理論の基本概念と、それが金融市場の分析にどのように応用されるかを検討しました。具体的には、アトラクター、フラクタル、バタフライ効果といった主要な概念を取り上げ、それらが市場の動向にどのように現れるのかを考察しました。特に、金融の文脈におけるカオスシステムの特性とボラティリティの関係に注目しました。

また、古典的なカオス理論とビル・ウィリアムズのアプローチを比較し、それぞれの科学的応用と実践的応用の違いを深く理解することを目指しました。さらに、金融時系列分析のツールとしてのリャプノフ指数を中心に据え、その理論的な意味とMQL5言語による実装の両面から考察しました。

記事の最後の部分では、リャプノフ指数を用いたトレンドの反転・継続に関する統計分析について説明しました。具体的な例として、EUR/USD のH1時間枠を用いた分析を紹介し、その適用方法と得られた結果の解釈について詳しく解説しました。

この記事では、金融市場におけるカオス理論の基礎を築くとともに、それを取引に応用するための実践的なツールを紹介しました。この2番目の記事では、より高度な概念と実践的な応用に焦点を当て、このトピックの理解をさらに深めていきます。

まず最初に、市場の混乱を測る尺度としてのフラクタル次元について説明します。

市場の混乱を測るフラクタル次元

フラクタル次元は、カオス理論や金融市場を含む複雑システムの分析において重要な役割を果たす概念です。これは、オブジェクトまたはプロセスの複雑さと自己相似性の定量的な尺度を提供するため、市場の動きのランダム性の程度を評価するのに特に役立ちます。

金融市場の文脈では、フラクタル次元は価格チャートの「ギザギザ感」を測定するために使用できます。フラクタル次元が高いほど、価格構造はより複雑で混沌としていることを示し、フラクタル次元が低いほど、動きはよりスムーズで予測可能であることを示します。

フラクタル次元を計算する方法はいくつかあります。最も人気のある方法の1つは、ボックスカウント法です。この方法では、さまざまなサイズのセルのグリッドでチャートを覆い、さまざまなスケールでチャートを覆うために必要なセルの数を数えます。

この方法を使用してフラクタル次元Dを計算する式は次のとおりです。

D = -lim(ε→0) [log N(ε) / log(ε)]

ここで、N(ε)はオブジェクトをカバーするために必要なサイズεのセルの数です。

フラクタル次元を金融市場分析に適用すると、トレーダーやアナリストは市場の動きの性質についてさらに深い洞察を得ることができます。以下が例です。

• 市場モードの特定：フラクタル次元の変化は、トレンド、横ばいの動き、混沌とした期間など、さまざまな市場状態間の遷移を示すことができる
• ボラティリティ評価：フラクタル次元が高い場合、多くの場合、ボラティリティが増加する期間に相当する
• 予測：時間の経過に伴うフラクタル次元の変化を分析すると、将来の市場の動きを予測するのに役立つ
• 取引戦略の最適化：市場のフラクタル構造を理解することは、取引アルゴリズムの開発と最適化に役立つ

それでは、MQL5言語でフラクタル次元を計算する実際の実装を見てみましょう。MQL5で価格チャートのフラクタル次元をリアルタイムで計算するインジケーターを開発します。

このインジケーターはボックスカウント法を使用してフラクタル次元を推定します。

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ja/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

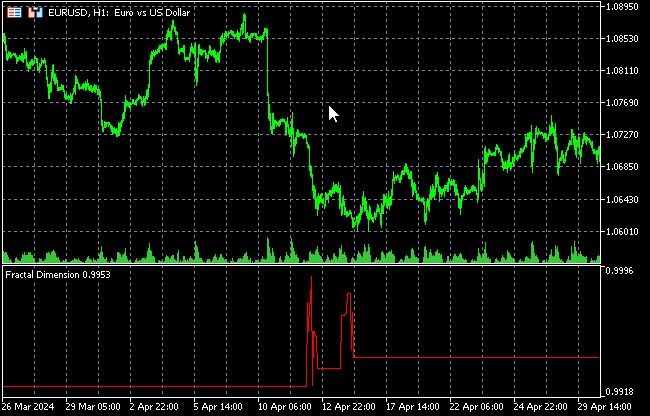
このインジケーターは、ボックスカウント法を使用して価格チャートのフラクタル次元を計算します。フラクタル次元は、チャートの「ギザギザ度」または複雑さを測る尺度であり、市場の混乱の度合いを評価するために使用できます。

入力

• InpBoxSizesCount：計算のための異なる「ボックス」サイズの数
• InpMinBoxSize：最小の「ボックス」サイズ
• InpMaxBoxSize：最大「ボックス」サイズ
• InpDataLength：計算に使用されるローソク足の数

インジケーター操作アルゴリズム

1. チャート上の各ポイントについて、インジケーターは最後のInpDataLengthローソク足のデータを使用してフラクタル次元を計算します。
2. ボックスカウントメソッドは、InpMinBoxSizeからInpMaxBoxSizeまでのさまざまな「ボックス」サイズに適用されます。
3. チャートをカバーするために必要な「ボックス」の数は、「ボックス」のサイズごとに計算されます。
4. 「ボックス」の数の対数と「ボックス」のサイズの対数の依存関係グラフが作成されます。
5. グラフの傾きは、フラクタル次元の推定値である線形回帰法を使用して計算されます。

フラクタル次元の変化は、市場モードの変化を示す可能性があります。

価格変動の隠れたパターンを発見するためのリカレンス分析

リカレンス分析は、金融市場の動向を研究するために効果的に適用できる強力な非線形時系列分析手法です。このアプローチにより、金融市場を含む複雑な動的システムにおける繰り返しパターンを視覚化し、定量化することができます。

リカレンス分析の中心的なツールはリカレンスプロットです。この図は、時間の経過に伴うシステムの繰り返される状態を視覚的に表現するものです。リカレンスプロットでは、時刻iと時刻jの状態が特定の意味で類似している場合、点(i, j)が着色されます。

金融時系列のリカレンスプロットを作成するには、次の手順に従います。

1. 位相空間の再構成：遅延法を使用して、1次元の価格時系列を多次元位相空間に変換します。
2. 類似性の閾値の設定：どの程度の差異を「類似」と見なすかの基準を決定します。
3. リカレンス行列の構築：各時点のペアについて、対応する状態が類似しているかどうかを判断します。
4. 可視化：リカレンス行列を2次元画像として表示し、類似した状態を点で示します。

リカレンスプロットを使用すると、システム内のさまざまな種類のダイナミクスを識別できます。

• 均質な領域は定常的な期間を示す
• 対角線は決定論的なダイナミクスを示す
• 垂直および水平構造は層流状態を示している可能性がある
• 構造がない領域はランダムプロセスの特徴である

リカレンスプロットの構造を定量化するために、リカレンス率、対角線のエントロピー、最長対角線長など、さまざまな繰返し尺度が使用されます。

金融時系列にリカレンス分析を適用すると、次のような効果が得られます。

1. さまざまな市場モード（トレンド、フラット、カオス状態）を識別する
2. モードの変更を検出する
3. さまざまな期間における市場の予測可能性を評価する
4. 隠された周期的なパターンを明らかにする

取引におけるリカレント分析の実際的な実装のために、リカレントプロットを構築し、繰返し尺度をリアルタイムで計算するインジケーターをMQL5言語で開発することができます。これにより、他のテクニカル分析手法と組み合わせることで、取引判断の補助ツールとして活用できます。

次のセクションでは、このインジケーターの具体的な実装方法を示し、その値を取引戦略の文脈でどのように解釈するかを解説します。

MQL5のリカレンス分析インジケーター

この指標は、金融市場の動向を研究するためのリカレンス分析法を実装します。リカレンスの3つの主要な尺度（繰返しレベル、決定性、層流性）を計算します。

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ja/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

インジケーターの主な特徴

インジケーターは価格チャートの下の別のウィンドウに表示され、3つのバッファを使用してデータを保存および表示します。このインジケーターは、全体的な繰返しのレベルを示す繰返し率（青線）、システムの予測可能性の尺度である決定性（赤線）、システムが特定の状態に留まる傾向を評価する層流性（緑線）の3つのメトリックを計算します。

インジケーターの入力には、位相空間再構成の埋め込み次元を定義するInpEmbeddingDimension（デフォルト：3）、再構成中の時間遅延を定義するInpTimeDelay（デフォルト：1）、ポイント単位の状態類似性閾値を定義するInpThreshold（デフォルト：10）、分析ウィンドウのサイズを設定するInpWindowSize（デフォルト：200）が含まれます。

インジケーターの動作アルゴリズムは、価格の1次元時系列から位相空間を再構築する遅延法に基づいています。分析ウィンドウ内の各ポイントについて、他のポイントに対する「繰返し」が計算されます。次に、得られた再帰構造に基づいて、すべての点における繰返し点の割合を決定する繰返し率、対角線を形成する繰返し点の割合を示す決定性、垂直線を形成する繰返し点の割合を推定する層流性の3つの尺度が計算されます。

ボラティリティ予測におけるターケンスの埋め込み定理の適用

ターケンスの埋め込み定理は、力学系の理論における基本定理であり、金融データを含む時系列解析において重要な応用を持ちます。この定理は、ある動的システムがタイムラグ法を用いることで、1つの観測変数から再構築可能であることを示しています。

金融市場の文脈では、ターケンスの定理により、価格または収益の1次元の時系列から多次元の位相空間を再構築することができます。これは、金融市場の重要な特性であるボラティリティを分析するときに特に役立ちます。

ターケンスの定理をボラティリティ予測に適用する基本的な手順は次のとおりです。

1. 位相空間の再構成：
   • 埋め込み次元(m)を選択する
   • 時間遅延(τ)を選択する
   • 元の時系列からm次元ベクトルを作成する
2. 再構築された空間の分析：
   • 各ポイントの最近傍点を見つける
   • 局所点密度を推定する
3. ボラティリティ予測：
   • 局所的密度情報を使用して将来のボラティリティを予測する

これらの手順を詳しく見てみましょう。

位相空間の再構成

終値の時系列{p(t)}を考えてみましょう。次のようにm次元ベクトルを作成します。

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

ここで、mは埋め込み次元であり、τは時間遅延です。

再構築を成功させるには、m とτの正しい値を選択することが重要です。通常、τは相互情報量法または自己相関関数法を使用して選択され、mは偽近傍(FNN: False Nearest Neighbor)法を使用して選択されます。

再構築された空間の分析

位相空間を再構築した後、システムアトラクターの構造を分析できます。ボラティリティ予測では、位相空間内の点の局所密度に関する情報が特に重要です。

各点x(t)について、そのk個の最も近い近傍点（通常、kは5から20の範囲で選択されます）を見つけ、これらの近傍点までの平均距離を計算します。この距離は、局所的な密度、ひいては局所的な変動性の尺度として機能します。

ボラティリティ予測

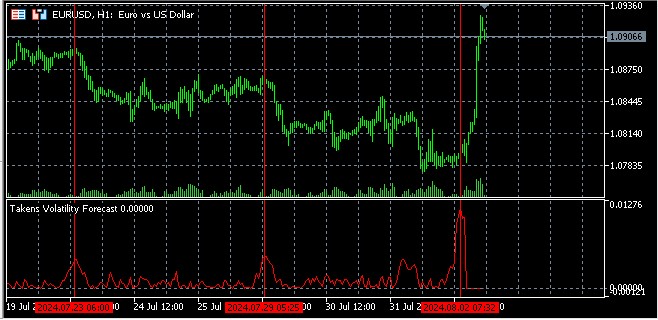
再構築された位相空間を使用してボラティリティを予測する基本的な考え方は、この空間内の近いポイントは近い将来に同様の動作をする可能性が高いというものです。

t+h時点のボラティリティを予測するには、次の操作をおこないます。

• 再構成された空間内の現在のx(t)点のk近傍点を見つける
• hステップ先のこれらの近隣の実際のボラティリティを計算する
• これらのボラティリティの平均を予測として使用します

数学的には次のように表現できます。

σ̂(t+h) = (1/k) Σ σ(ti+h)、ここで、tiはx(t)のk近傍点のインデックスです。

このアプローチの利点は、次のとおりです。

• 非線形の市場動向を考慮している
• 収益の分配に関する仮定を必要としない
• ボラティリティの複雑なパターンを捉えることができる

短所

• パラメータ（m、τ、k）の選択に敏感である。
• 大量のデータを扱う場合、計算コストが高くなる可能性がある

実装

このボラティリティ予測方法を実装するMQL5インジケーターを作成しましょう。

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ja/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

時間遅延と埋め込み次元を決定する方法

ターケンスの定理を使用して位相空間を再構築する場合、時間遅延(τ)と埋め込み次元(m)という2つの重要なパラメータを正しく選択することが重要です。これらのパラメータを誤って選択すると、再構築が不正確になり、結果として誤った結論につながる可能性があります。これらのパラメータを決定するための2つの主な方法を考えてみましょう。

時間遅延を決定するための自己相関関数(ACF)法

この方法は、自己相関関数が最初にゼロを横切るか、初期値の1/eなどの特定の低い値に達する時間遅延τを選択するという考えに基づいています。これにより、時系列の連続する値が互いに十分に独立する遅延を選択できます。

MQL5でのACFメソッドの実装は次のようになります。

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

この実装では、まず時系列の平均と分散を計算します。次に、1からmaxLagまでの各ラグについて、自己相関関数の値を計算します。ACF値が指定された閾値（デフォルトは0.1）以下になると、この遅延を最適な時間遅延として返します。

ACF法には長所と短所があります。実装が簡単で直感的である一方、データ内の非線形依存関係は考慮されません。これは、非線形動作を示すことが多い金融時系列を分析するときに大きな欠点となる可能性があります。

時間遅延を決定するための相互情報量(MI)法

この方法は情報理論に基づいており、データ内の非線形依存関係を考慮することができます。考え方としては、相互情報量関数の最初の局所最小値に対応する遅延τを選択することです。

MQL5での相互情報量法の実装は次のようになります。

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

この実装では、まず、指定されたラグに対する元のシリーズとそのシフトバージョン間の相互情報量を計算する CalculateMutualInformation関数を定義します。次に、FindOptimalLagMI関数で、さまざまなラグ値を反復処理して相互情報量の最初の局所最小値を検索します。

相互情報量法は、データ内の非線形依存性を考慮できるという点で、ACF法よりも優れています。これにより、複雑で非線形な動作を示すことが多い金融時系列の分析に適したものになります。ただし、この方法は実装が複雑で、より多くの計算が必要になります。

ACF法とMI法のどちらを選択するかは、特定のタスクと分析対象のデータの特性によって異なります。場合によっては、両方の方法を使用して結果を比較すると便利な場合があります。また、特に金融時系列の場合、最適な時間ラグは時間の経過とともに変化する可能性があることに留意することも重要です。そのため、このパラメータを定期的に再計算することをお勧めします。

最適な埋め込み次元を決定するための偽近傍(FNN: False Nearest Neighbor)アルゴリズム

最適な時間遅延が決定されたら、位相空間再構築における次の重要なステップは、適切な埋め込み次元を選択することです。この目的のための最も一般的な方法の1つは、偽近傍(FNN: False Nearest Neighbor)アルゴリズムです。

FNNアルゴリズムの考え方は、位相空間内のアトラクターの幾何学的構造が正しく再現されるような最小の埋め込み次元を見つけることです。このアルゴリズムは、正しく再構築された位相空間では、近い点は高次元空間に移動しても近いままであるという仮定に基づいています。

MQL5言語でのFNNアルゴリズムの実装を見てみましょう。

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

IsFalseNeighbor関数は、2点が偽近傍であるかどうかを判断します。現在の次元における2点間の距離と、次元を1つ増やした場合の距離を計算します。相対的な距離の変化が設定された閾値を超えた場合、その点は偽最近傍と見なされます。

メイン関数 FindOptimalEmbeddingDimensionは、1からmaxDimまでの次元を順に処理します。各次元において、時系列データの全ての点を走査します。各点に対して、現在の次元で最も近い近傍を探索し、その近傍がIsFalseNeighbor関数 によって偽であるかを判定します。すべての近傍点の数と偽最近傍の数をカウントし、偽最近傍の割合を計算します。もしこの割合が指定された許容閾値を下回った場合、その次元を最適な埋め込み次元として採用し、返します。

このアルゴリズムには、いくつかの重要なパラメータがあります。delayは、ACF（自己相関関数）または MI（相互情報量）法によって事前に決定された時間遅れです。maxDimは、考慮する最大の埋め込み次元を指定します。thresholdは、偽最近傍を判定するための閾値です。toleranceは、偽最近傍の割合の許容閾値を示します。これらのパラメータの選択は結果に大きな影響を与えるため、異なる値を試しながらデータの特性を考慮することが重要です。

FNNアルゴリズムには、いくつかの利点があります。この手法は、位相空間におけるデータの幾何学的構造を考慮できます。また、データ内のノイズに対して比較的頑健です。さらに、解析対象のシステムの性質について、事前の仮定を必要としません。

MQL5でカオス理論に基づく予測手法を実装する

位相空間を再構築するための最適なパラメータを決定したら、カオス理論に基づく予測手法の実装を開始できます。この手法は、位相空間内で近い状態にある点は、将来的にも類似した軌道をたどるという考え方に基づいています。

この方法の基本的なアイデアは以下の通りです。まず、現在の状態に最も近い過去のシステムの状態を探索 します。その後、それらの過去の状態がどのように推移したかを基に、現在の状態の将来の動きを予測します。このアプローチは、アナログ法または 最近傍法として知られています。

それでは、この手法を MetaTrader 5のインジケーターとして実装 してみましょう。このインジケーターは、以下の手順を実行します。

1. 時間遅れ法(Time Delay Method)を用いて位相空間を再構築する
2. 現在のシステムの状態に最も近いk個の近傍を探索する
3. 見つかった近傍の挙動をもとに、将来の値を予測する

以下に、この手法を実装したMQL5インジケーターのコードを示します。

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ja/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

このインジケーターは位相空間を再構築し、現在の状態に最も近い近傍を見つけ、その将来の値を使用して予測をおこないます。実際の値と予測値の両方をグラフ上に表示し、予測の品質を視覚的に評価できます。

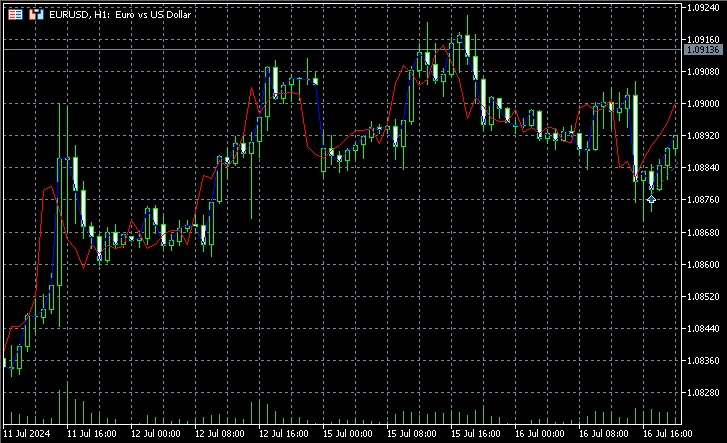
実装の重要な側面には、予測に加重平均を使用することが含まれます。加重平均では、各近傍の重みが現在の状態からの距離に反比例します。これにより、より近い近隣地域の方がより正確な予測を出す可能性が高いことを考慮に入れることができます。スクリーンショットから判断すると、このインジケーターは価格変動の方向を数バー先まで予測します。

概念EAの作成

最も興味深い部分に到達しました。以下は、カオス理論に基づいた完全に自動化された作業のコードです。

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

このコードは、カオス理論の概念を使用して金融市場の価格を予測する MetaTrader 5 EAです。EAは、再構築された位相空間で最近傍法に基づく予測方法を実装します。

EAには次の入力があります。

• InpEmbeddingDimension：位相空間再構成の埋め込み次元（デフォルト：3）
• InpTimeDelay：再構築の遅延時間（デフォルト：5）
• InpNeighbors：予測のための最近傍点の数（デフォルト：10）
• InpForecastHorizon：予測期間（デフォルト：10）
• InpLookback：分析のルックバック期間（デフォルト：1000）
• InpLotSize：取引のロットサイズ（デフォルト：0.1）

EAは以下のように動作します。

1. 新しいバーごとに、それぞれ自己相関関数(ACF)法と偽近傍法(FNN)アルゴリズムを使用して、optimalTimeDelayパラメータとoptimalEmbeddingDimensionパラメータを最適化します。
2. 次に、最近傍法を使用して、システムの現在の状態に基づいて価格予測をおこないます。
3. 価格予測が現在の価格よりも高い場合、EAはすべての売りポジションをクローズし、新しい買いポジションを開きます。価格予測が現在の価格よりも低い場合、EAはすべての買いポジションをクローズし、新しい売りポジションを開きます。

EAはPredictPrice関数を使用して、次をおこないます。

• 最適な埋め込み次元と時間遅延を使用して位相空間を再構築する
• システムの現在の状態とルックバック期間内のすべての状態間の距離を検出する
• 状態を距離の昇順に並べ替える
• InpNeighborsの最近傍点の将来の価格の加重平均を計算する（各近傍点の重みは現在の状態からの距離に反比例する）
• 価格予測として加重平均を返す

EAには、それぞれoptimalTimeDelayパラメータとoptimalEmbeddingDimensionパラメータを最適化するために使用される FindOptimalLagACF関数とFindOptimalEmbeddingDimension関数も含まれています。

全体として、EAはカオス理論の概念を使用して金融市場の価格を予測する革新的なアプローチを提供します。これにより、トレーダーはより情報に基づいた意思決定をおこなうことができ、これは投資収益の増加につながる可能性があります。

自動最適化によるテスト

いくつかの銘柄でのEAの動作を考えてみましょう。最初の通貨ペア、EURUSD、期間は2016年1月1日から：

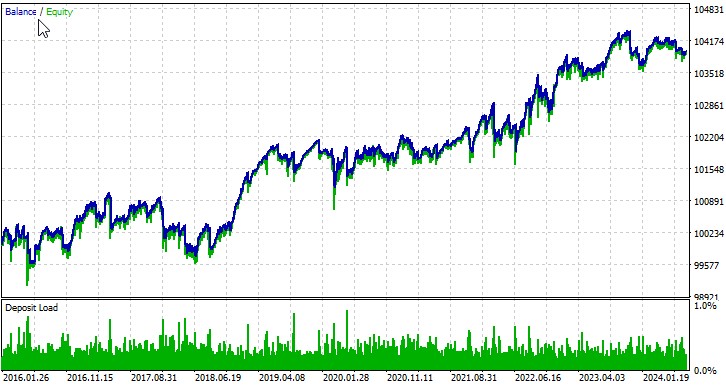
2番目のペア、AUD：

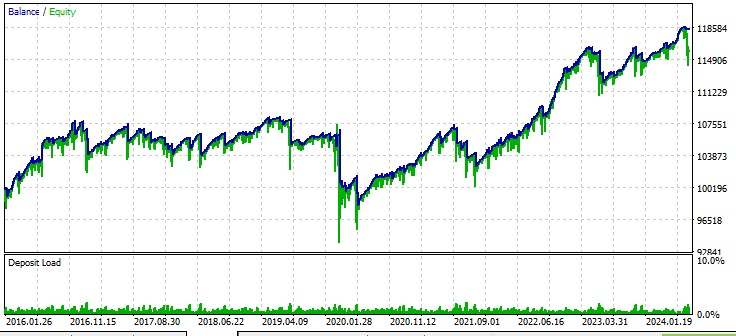
3番目のペア、GBPUSD：

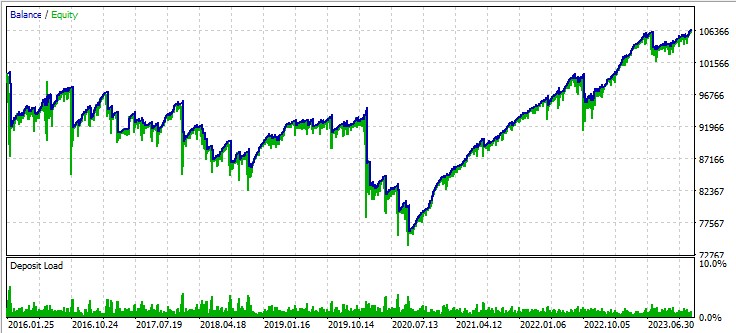
次のステップ

カオス理論に基づくEAのさらなる開発には、徹底的なテストと最適化が必要になります。さまざまな市場状況における効率性をよりよく理解するには、さまざまな時間枠と金融商品にわたる大規模なテストが必要です。機械学習手法を使用すると、EAパラメータを最適化し、変化する市場の現実への適応性を高めることができます。

リスク管理システムの改善には特に注意を払う必要があります。現在の市場のボラティリティと混沌としたボラティリティの予測を考慮した動的なポジション サイズ管理を実装すると、戦略の回復力が大幅に向上する可能性があります。

結論

この記事では、金融市場の分析と予測におけるカオス理論の応用について考察しました。具体的には、位相空間再構成、最適な埋め込み次元や時間遅延の決定、最近傍予測法など、重要な概念を検討しました。

私たちが開発したEAは、アルゴリズム取引におけるカオス理論の適用可能性を示しています。異なる通貨ペアでのテスト結果によれば、この戦略は利益を上げる可能性があるものの、その成功度合いは商品によって異なることが分かりました。

しかし、カオス理論を金融市場に適用するには、いくつかの課題が存在することも認識しておくことが重要です。金融市場は非常に複雑なシステムであり、多くの要因が影響を与えるため、モデルに組み込むことが困難、あるいは不可能な要素もあります。さらに、カオスシステムの特性から、長期的な予測は本質的に不可能であるということは、真剣な研究者の共通の認識です。

結論として、カオス理論は市場予測の「聖杯」ではありませんが、金融分析やアルゴリズム取引の分野における今後の研究開発において、有望な方向性を示しています。カオス理論の手法を機械学習やビッグデータ分析など、他のアプローチと組み合わせることで、新たな可能性が開かれることは明白です。