Teoria do caos no trading (Parte 2): Continuamos a imersão

Resumo da parte anterior do artigo

No primeiro artigo da série, apresentamos os conceitos básicos da teoria do caos e sua aplicação à análise dos mercados financeiros. Exploramos conceitos-chave, como atratores, fractais e o efeito borboleta, discutindo como eles se manifestam na dinâmica desses mercados. Destacamos as características dos sistemas caóticos no contexto financeiro e o conceito de volatilidade.

Também comparamos a teoria clássica do caos com a abordagem de Bill Williams, o que permitiu uma melhor compreensão das diferenças entre o uso científico e prático dessas ideias no trading. Uma parte importante do artigo foi a discussão sobre o expoente de Lyapunov como ferramenta de análise de séries temporais financeiras. Explicamos não apenas o significado teórico, mas também apresentamos a implementação prática do cálculo desse indicador em MQL5.

A parte final do artigo foi dedicada à análise estatística de reversões e continuações de tendência por meio do expoente de Lyapunov. Com base no par EURUSD e no timeframe horário, demonstramos como essa análise pode ser aplicada na prática e discutimos a interpretação dos resultados obtidos.

Este artigo lançou as bases para a compreensão da teoria do caos no contexto dos mercados financeiros e apresentou ferramentas práticas para sua aplicação no trading. Na segunda parte, aprofundaremos nosso entendimento sobre o tema, focando em aspectos mais complexos e suas aplicações práticas.

Continuamos a “desenterrar” a teoria do caos. E o primeiro tópico que abordaremos é a dimensão fractal como uma medida do grau de caos do mercado.

Dimensão fractal como uma medida do grau de caos do mercado

A dimensão fractal é um conceito fundamental na teoria do caos e na análise de sistemas complexos, incluindo os mercados financeiros. Ela fornece uma medida quantitativa de complexidade e autossimilaridade de um objeto ou processo, tornando-se especialmente útil para avaliar o grau de caos dos movimentos de mercado.

No contexto dos mercados financeiros, a dimensão fractal pode ser utilizada para medir a "rugosidade" dos gráficos de preços. Quanto maior a dimensão fractal, mais complexa e caótica é a estrutura de preços; quanto menor, mais suave e previsível é o movimento.

Existem vários métodos para calcular a dimensão fractal, sendo um dos mais populares o método de cobertura ou box-counting method. Ele consiste em cobrir o gráfico com uma grade de células de tamanhos variados e contar o número de células necessárias para cobrir o gráfico em diferentes escalas.

A fórmula para calcular a dimensão fractal D pelo método de cobertura é a seguinte:

D = -lim(ε→0) [log N(ε) / log(ε)]

onde N(ε) é o número de células de tamanho ε necessárias para cobrir o objeto.

A aplicação da dimensão fractal à análise dos mercados financeiros pode fornecer informações adicionais sobre a natureza dos movimentos de mercado para traders e analistas. Por exemplo:

• Identificação dos regimes de mercado: mudanças na dimensão fractal podem indicar transições entre diferentes estados de mercado, como tendências, movimentos laterais ou períodos caóticos.
• Avaliação da volatilidade: dimensões fractais elevadas frequentemente correspondem a períodos de alta volatilidade.
• Previsão: a análise das mudanças na dimensão fractal ao longo do tempo pode ajudar a prever os movimentos futuros do mercado.
• Otimização de estratégias de trading: compreender a estrutura fractal do mercado pode auxiliar no desenvolvimento e na otimização de algoritmos de trading.

Agora, veremos a implementação prática do cálculo da dimensão fractal no MQL5. Desenvolveremos um indicador que calculará a dimensão fractal de um gráfico de preços em tempo real.

Proponho a implementação de um indicador para calcular a dimensão fractal de um gráfico de preços em MQL5. Esse indicador usa o método de cobertura (box-counting method) para estimar a dimensão fractal.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

Este indicador calcula a dimensão fractal do gráfico de preços, utilizando o método de cobertura (box-counting method). A dimensão fractal é uma medida da "rugosidade" ou complexidade do gráfico e pode ser usada para avaliar o grau de caos do mercado.

Parâmetros de entrada:

• InpBoxSizesCount: quantidade de tamanhos diferentes de "caixas" para o cálculo
• InpMinBoxSize: tamanho mínimo da "caixa"
• InpMaxBoxSize: tamanho máximo da "caixa"
• InpDataLength: quantidade de candles usados para o cálculo

Algoritmo de funcionamento do indicador:

1. Para cada ponto do gráfico, o indicador calcula a dimensão fractal usando os dados dos últimos InpDataLength candles.
2. O método de cobertura é aplicado com diferentes tamanhos de "caixas", de InpMinBoxSize a InpMaxBoxSize.
3. Para cada tamanho de "caixa", calcula-se a quantidade necessária de "caixas" para cobrir o gráfico.
4. Um gráfico da relação entre o logaritmo da quantidade de "caixas" e o logaritmo do tamanho da "caixa" é construído.
5. Por meio de regressão linear, encontra-se a inclinação desse gráfico, que é a estimativa da dimensão fractal.

A interpretação dos resultados é que mudanças na dimensão fractal podem sinalizar uma mudança no regime de mercado.

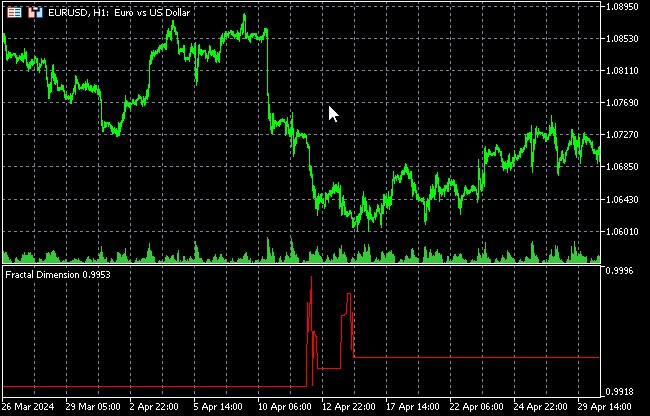
Análise recorrente para identificação de padrões ocultos nos movimentos de preços

A análise recorrente é um método poderoso de análise não linear de séries temporais, que pode ser aplicado com eficácia ao estudo da dinâmica dos mercados financeiros. Essa abordagem permite visualizar e quantificar padrões recorrentes em sistemas dinâmicos complexos, como os mercados financeiros.

O principal instrumento dessa análise é o diagrama de recorrência (recurrence plot). Ele representa visualmente os estados recorrentes de um sistema ao longo do tempo. No diagrama de recorrência, um ponto (i, j) é marcado se os estados nos momentos de tempo i e j forem semelhantes em certo sentido.

Para construir um diagrama de recorrência de uma série temporal financeira, seguem-se os seguintes passos:

1. Reconstrução do espaço de fases: utilizando o método de atrasos, transforma-se a série temporal unidimensional de preços em um espaço de fases multidimensional.
2. Definição do limite de similaridade: escolhe-se um critério pelo qual consideraremos dois estados como semelhantes.
3. Construção da matriz de recorrência: para cada par de momentos no tempo, determina-se se os estados correspondentes são semelhantes.
4. Visualização: representa-se a matriz de recorrência como uma imagem bidimensional, onde os estados semelhantes são marcados com pontos.

Os diagramas de recorrência permitem identificar diferentes tipos de dinâmica no sistema:

• Áreas homogêneas indicam períodos estacionários.
• Linhas diagonais sugerem dinâmica determinística.
• Estruturas verticais e horizontais podem sinalizar estados laminares.
• A ausência de estrutura é característica de processos aleatórios.

Para a análise quantitativa das estruturas nos diagramas de recorrência, utilizam-se diversas métricas de recorrência, como o percentual de recorrência, a entropia das linhas diagonais, o comprimento máximo de linha diagonal, entre outras.

A aplicação da análise recorrente às séries temporais financeiras pode ajudar a:

1. Identificar diferentes regimes de mercado (tendência, movimento lateral, estado caótico).
2. Detectar momentos de transição entre regimes.
3. Avaliar a previsibilidade do mercado em diferentes períodos.
4. Identificar padrões cíclicos ocultos.

Para implementar a análise recorrente no trading, pode-se desenvolver um indicador em MQL5 que construa o diagrama de recorrência e calcule as métricas de recorrência em tempo real. Esse indicador pode servir como uma ferramenta adicional para a tomada de decisões de trading, especialmente em combinação com outros métodos de análise técnica.

Na próxima parte do artigo, abordaremos uma implementação específica desse indicador e discutiremos como interpretar seus resultados no contexto de uma estratégia de trading.

Indicador de análise recorrente em MQL5

Este indicador implementa o método de análise recorrente para estudar a dinâmica dos mercados financeiros. Ele calcula três métricas-chave de recorrência: taxa de recorrência, determinismo e laminaridade.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Características principais do indicador:

O indicador é exibido em uma janela separada abaixo do gráfico de preços e o uso de três buffers para armazenar e exibir os dados. Ele calcula três medidas: Recurrence Rate (linha azul), que indica o nível geral de recorrência; Determinism (linha vermelha), que é uma medida da previsibilidade do sistema; e Laminarity (linha verde), que avalia a tendência do sistema de permanecer em um estado específico.

InpEmbeddingDimension (padrão: 3), que define a dimensão de inserção para a reconstrução do espaço de fases; InpTimeDelay (padrão: 1) para o atraso temporal na reconstrução; InpThreshold (padrão: 10) como o limite de similaridade dos estados em pontos; e InpWindowSize (padrão: 200) para definir o tamanho da janela de análise.

O algoritmo de funcionamento do indicador baseia-se no método de atrasos para reconstruir o espaço de fases a partir de uma série temporal unidimensional de preços. Para cada ponto na janela de análise, calcula-se sua "recorrência" em relação aos outros pontos. Com base na estrutura de recorrência obtida, são calculadas três métricas: Recurrence Rate, que determina a proporção de pontos recorrentes em relação ao total; Determinism, que indica a proporção de pontos recorrentes que formam linhas diagonais; e Laminarity, que avalia a proporção de pontos recorrentes que formam linhas verticais.

Aplicação do teorema de imersão de Takens na previsão de volatilidade

O teorema de imersão de Takens é um resultado fundamental na teoria de sistemas dinâmicos, com grande relevância para a análise de séries temporais, incluindo dados financeiros. Esse teorema afirma que um sistema dinâmico pode ser reconstruído a partir das observações de uma única variável usando o método de atrasos temporais.

No contexto dos mercados financeiros, o teorema de Takens permite reconstruir um espaço de fases multidimensional a partir de uma série temporal unidimensional de preços ou retornos. Isso é particularmente útil na análise da volatilidade, uma característica chave dos mercados financeiros.

Passos principais para aplicar o teorema de Takens na previsão de volatilidade:

1. Reconstrução do espaço de fases:
   • Escolher a dimensão de imersão (m)
   • Determinar o atraso temporal (τ)
   • Criar vetores m-dimensionais a partir da série temporal original
2. Análise do espaço reconstruído:
   • Identificar os vizinhos mais próximos para cada ponto
   • Estimar a densidade local dos pontos
3. Previsão de volatilidade:
   • Utilizar informações sobre a densidade local para estimar a volatilidade futura

Vamos detalhar esses passos:

Reconstrução do espaço de fases:

Dada uma série temporal de preços de fechamento {p(t)}, criamos vetores m-dimensionais da seguinte forma:

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

onde m é a dimensão de imersão, e τ é o atraso temporal.

A escolha adequada dos valores de m e τ é essencial para uma reconstrução bem-sucedida. Geralmente, τ é determinado por métodos de informação mútua ou função de autocorrelação, enquanto m é escolhido pelo método dos vizinhos falsos.

Análise do espaço reconstruído:

Após a reconstrução do espaço de fases, pode-se analisar a estrutura do atrator do sistema. Para a previsão de volatilidade, é especialmente importante a informação sobre a densidade local de pontos no espaço de fases.

Para cada ponto x(t), encontram-se seus k vizinhos mais próximos (geralmente, k varia entre 5 e 20) e calcula-se a distância média até esses vizinhos. Essa distância serve como uma medida de densidade local e, consequentemente, da volatilidade local.

Previsão de volatilidade:

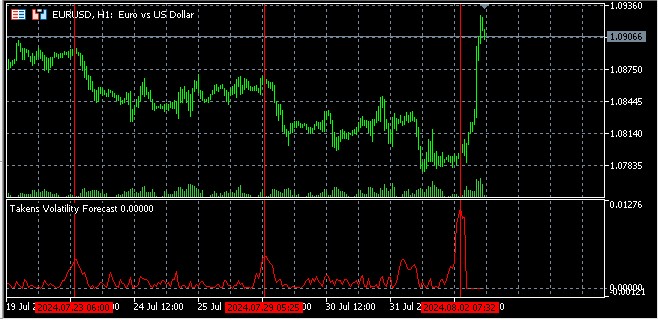
A ideia principal na previsão de volatilidade com o uso do espaço de fases reconstruído é que pontos próximos nesse espaço tendem a apresentar comportamentos semelhantes em breve.

Para prever a volatilidade no instante t+h, segue-se o seguinte:

• Encontrar os k vizinhos mais próximos do ponto atual x(t) no espaço reconstruído.
• Calcular a volatilidade real desses vizinhos h passos à frente.
• Utilizar a média dessas volatilidades como previsão.

Matematicamente, isso pode ser expresso como:

σ̂(t+h) = (1/k) Σ σ(ti+h), onde ti são os índices dos k vizinhos mais próximos de x(t).

Vantagens deste método:

• Considera a dinâmica não linear do mercado.
• Não exige suposições sobre a distribuição dos retornos.
• Pode capturar padrões complexos na volatilidade.

Desvantagens:

• Sensível à escolha dos parâmetros (m, τ, k).
• Pode ser computacionalmente custoso para grandes volumes de dados.

Implementação prática

Vamos criar um indicador em MQL5 que implementa este método de previsão de volatilidade:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Métodos para determinar o atraso temporal e a dimensão de imersão

Ao reconstruir o espaço de fases utilizando o teorema de Takens, é fundamental escolher corretamente dois parâmetros-chave: o atraso temporal (τ) e a dimensão de imersão (m). A escolha inadequada desses parâmetros pode resultar em uma reconstrução incorreta e, consequentemente, em conclusões errôneas. Vamos analisar dois métodos principais para determinar esses parâmetros.

Método da função de autocorrelação (ACF) para determinar o atraso temporal

O método da função de autocorrelação baseia-se na ideia de escolher um atraso temporal τ, no qual a função de autocorrelação cruza o zero pela primeira vez ou atinge um valor baixo específico, como 1/e do valor inicial. Isso permite selecionar um atraso no qual os valores consecutivos da série temporal se tornam suficientemente independentes entre si.

A implementação do método ACF em MQL5 pode ser descrita da seguinte forma:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

Nesta implementação, calculamos inicialmente a média e a variância da série temporal. Em seguida, para cada lag de 1 até maxLag, calculamos o valor da função de autocorrelação. Assim que o valor da ACF se torna menor ou igual a um limiar pré-definido (por padrão 0.1), retornamos este lag como o atraso temporal ideal.

O uso do método ACF possui vantagens e desvantagens. Por um lado, é simples de implementar e intuitivo. Por outro lado, ele não considera dependências não lineares nos dados, o que pode ser uma desvantagem significativa na análise de séries temporais financeiras, que frequentemente apresentam comportamento não linear.

Método da informação mútua (MI) para determinar o atraso temporal

Uma abordagem alternativa para determinar o atraso temporal ideal é o método da informação mútua. Este método baseia-se na teoria da informação e é capaz de considerar dependências não lineares nos dados. A ideia é escolher um atraso τ que corresponda ao primeiro mínimo local da função de informação mútua.

A implementação do método de informação mútua em MQL5 pode ser descrita da seguinte forma:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

Nesta implementação, definimos primeiro a função CalculateMutualInformation, que calcula a informação mútua entre a série original e sua versão deslocada para um lag especificado. Depois, na função FindOptimalLagMI, buscamos o primeiro mínimo local da informação mútua, testando vários valores de lag.

Comparado ao método ACF, o método de informação mútua apresenta a vantagem de capturar dependências não lineares nos dados. Isso o torna mais adequado para a análise de séries temporais financeiras, que frequentemente exibem comportamentos complexos e não lineares. No entanto, este método é mais complexo de implementar e exige maior esforço computacional.

A escolha entre o método ACF (função de autocorrelação) e o método MI (informação mútua) depende da tarefa específica e das características dos dados analisados. Em alguns casos, pode ser útil aplicar ambos os métodos e comparar os resultados. É importante lembrar que o atraso temporal ideal pode variar ao longo do tempo, especialmente em séries temporais financeiras. Portanto, pode ser necessário recalcular esse parâmetro periodicamente.

Algoritmo de vizinhos falsos próximos para determinar a dimensão de imersão ideal

Após determinar o atraso temporal ideal, o próximo passo crucial na reconstrução do espaço de fases é a escolha da dimensão de imersão mais apropriada. Um dos métodos mais populares para essa finalidade é o algoritmo de vizinhos falsos próximos (False Nearest Neighbors, FNN).

A ideia do algoritmo FNN é identificar a menor dimensão de imersão que reproduza corretamente a estrutura geométrica do atrator no espaço de fases. O algoritmo baseia-se no princípio de que, em um espaço de fases reconstruído adequadamente, pontos próximos devem permanecer próximos mesmo ao passar para uma dimensão superior.

Implementação do algoritmo FNN em MQL5

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

A função IsFalseNeighbor avalia se dois pontos são vizinhos falsos. Ela calcula a distância entre os pontos na dimensão atual e na dimensão imediatamente superior. Se a variação relativa da distância ultrapassar um limite predefinido, os pontos são considerados vizinhos falsos.

A função principal, FindOptimalEmbeddingDimension, explora dimensões de 1 até maxDim. Para cada dimensão, analisa todas as observações da série temporal. Para cada ponto, localiza o vizinho mais próximo na dimensão atual. Em seguida, verifica se o vizinho encontrado é falso, utilizando a função IsFalseNeighbor. O número total de vizinhos e de vizinhos falsos é contado, e calcula-se a proporção de vizinhos falsos. Caso essa proporção seja menor que o limite de tolerância especificado, a dimensão atual é considerada ótima e retornada.

Este algoritmo utiliza os seguintes parâmetros importantes: delay: o atraso temporal, previamente determinado pelos métodos ACF ou MI. maxDim: a dimensão máxima a ser avaliada. threshold: o limite para identificar vizinhos falsos. tolerance: o limite de tolerância para a proporção de vizinhos falsos. A escolha adequada desses parâmetros é essencial para obter resultados precisos. Recomenda-se experimentar diferentes valores e considerar as características específicas dos dados analisados.

O algoritmo FNN oferece várias vantagens. Ele considera a estrutura geométrica dos dados no espaço de fases. É robusto ao ruído nos dados. Não exige suposições prévias sobre a natureza do sistema analisado.

Implementação do método de previsão baseado na teoria do caos em MQL5

Após definir os parâmetros ideais para a reconstrução do espaço de fases, podemos implementar o método de previsão baseado na teoria do caos. A ideia central deste método é que estados próximos no espaço de fases tendem a apresentar evoluções semelhantes no futuro próximo.

A ideia principal do método é a seguinte: identificamos no histórico os estados do sistema mais próximos do estado atual e, com base no comportamento futuro desses estados, fazemos uma previsão para o estado atual. Esse enfoque é conhecido como método dos análogos ou método dos vizinhos mais próximos.

Vamos analisar a implementação desse método como um indicador para o MetaTrader 5. Nosso indicador executará os seguintes passos:

1. Reconstrução do espaço de fases usando o método de atrasos temporais.
2. Identificação dos k vizinhos mais próximos para o estado atual do sistema.
3. Previsão do valor futuro com base no comportamento dos vizinhos identificados.

Segue o código do indicador que implementa esse método:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

Este indicador reconstrói o espaço de fases, encontra os vizinhos mais próximos para o estado atual e utiliza os valores futuros desses vizinhos para gerar previsões. Ele exibe tanto os valores reais quanto os previstos no gráfico, permitindo uma avaliação visual da qualidade das previsões.

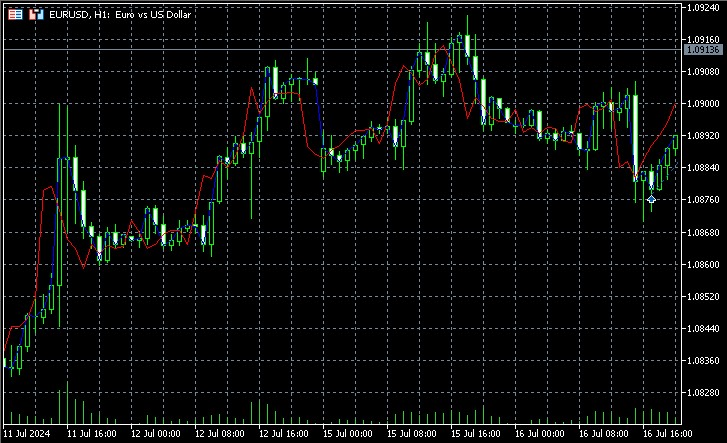
Os aspectos-chave da implementação incluem o uso de uma média ponderada para a previsão, onde o peso de cada vizinho é inversamente proporcional à sua distância em relação ao estado atual. Isso permite que vizinhos mais próximos contribuam de forma mais significativa, aumentando a precisão da previsão. Com base nos gráficos — o indicador consegue prever a direção do movimento de preços com antecedência de alguns candles.

Criação de um Expert Advisor com base na teoria do caos

Chegamos agora à parte mais interessante. Segue nosso código para um Expert Advisor completamente automatizado com base na teoria do caos:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Este código representa um Expert Advisor para o MetaTrader 5 que utiliza conceitos da teoria do caos para prever preços nos mercados financeiros. O EA implementa o método de previsão baseado em vizinhos mais próximos no espaço de fases reconstruído.

O Expert Advisor possui os seguintes parâmetros de entrada:

• InpEmbeddingDimension: dimensão de imersão para reconstrução do espaço de fases (padrão: 3)
• InpTimeDelay: atraso temporal para reconstrução (padrão: 5)
• InpNeighbors: número de vizinhos mais próximos para previsão (padrão: 10)
• InpForecastHorizon: horizonte de previsão (padrão: 10)
• InpLookback: período de análise retroativa (padrão: 1000)
• InpLotSize: tamanho do lote para negociações (padrão: 0.1)

Funcionamento do Expert Advisor:

1. A cada novo candle, o EA otimiza os parâmetros optimalTimeDelay e optimalEmbeddingDimension usando o método da função de autocorrelação (ACF) e o algoritmo de vizinhos falsos próximos (FNN), respectivamente.
2. Em seguida, realiza uma previsão de preços com base no estado atual do sistema, utilizando o método dos vizinhos mais próximos.
3. Se a previsão do preço for maior que o preço atual, o EA fecha todas as posições de venda abertas e abre uma nova posição de compra. Se a previsão for menor que o preço atual, o EA fecha todas as posições de compra abertas e abre uma nova posição de venda.

O Expert Advisor utiliza a função PredictPrice, que realiza os seguintes passos:

• Reconstrói o espaço de fases utilizando a dimensão de imersão e o atraso temporal ótimos.
• Calcula as distâncias entre o estado atual do sistema e todos os estados dentro do período de análise retroativa.
• Ordena os estados em ordem crescente de distância.
• Calcula a média ponderada dos preços futuros para os InpNeighbors vizinhos mais próximos, atribuindo pesos inversamente proporcionais às suas distâncias em relação ao estado atual.
• Retorna a média ponderada como previsão de preço.

O EA também inclui as funções FindOptimalLagACF e FindOptimalEmbeddingDimension, que otimizam os parâmetros optimalTimeDelay e optimalEmbeddingDimension, respectivamente.

De forma geral, esse Expert Advisor apresenta uma abordagem inovadora para a previsão de preços nos mercados financeiros, utilizando conceitos da teoria do caos. Ele pode ajudar os traders a tomarem decisões mais informadas e, potencialmente, aumentar a rentabilidade dos investimentos.

Testes com auto-otimização

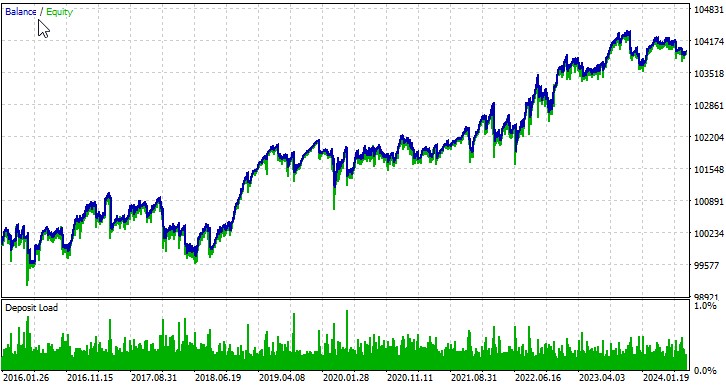
Vamos analisar o desempenho do nosso EA em vários ativos. Primeiro par de moedas, EURUSD, no período de 01/01/2016:

Segundo par, dólar australiano:

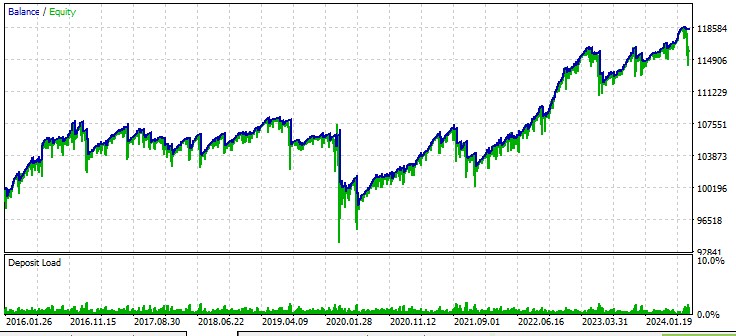
Terceiro par, libra - dólar:

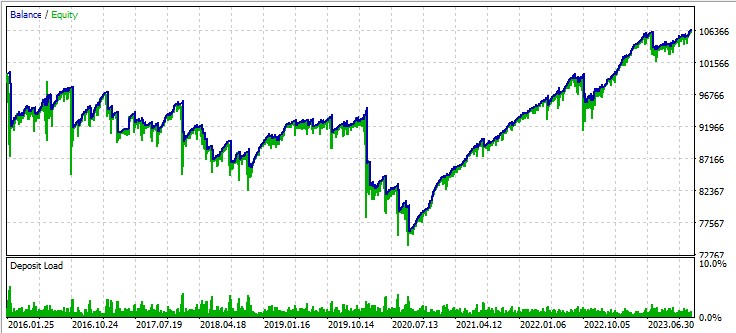
Próximos passos

O desenvolvimento contínuo deste Expert Advisor baseado na teoria do caos exigirá testes e otimizações aprofundadas. Testes abrangentes em diferentes intervalos de tempo e instrumentos financeiros são necessários para compreender melhor sua eficácia em diversas condições de mercado. A aplicação de técnicas de aprendizado de máquina pode contribuir significativamente para a otimização dos parâmetros do EA, aumentando sua capacidade de adaptação às mudanças nas condições de mercado.

A gestão de risco também merece atenção especial. A introdução de uma gestão dinâmica de posições, que considere a volatilidade atual do mercado e as previsões baseadas no caos, pode aumentar substancialmente a resiliência da estratégia.

Considerações finais

Neste artigo, exploramos a aplicação da teoria do caos na análise e previsão dos mercados financeiros. Abordamos conceitos fundamentais, como reconstrução do espaço de fases, determinação da dimensão de imersão e do atraso temporal ideais, além do método de previsão baseado em vizinhos mais próximos.

O Expert Advisor desenvolvido demonstra o potencial da teoria do caos na negociação algorítmica. Os testes em diferentes pares de moedas mostram que a estratégia pode gerar lucro, embora com diferentes graus de sucesso dependendo do instrumento.

No entanto, é importante reconhecer as limitações do uso da teoria do caos em finanças. Os mercados financeiros são sistemas extremamente complexos, influenciados por inúmeros fatores, muitos dos quais são difíceis ou impossíveis de modelar. Além disso, a natureza intrínseca dos sistemas caóticos torna o longo prazo imprevisível — um dos pilares fundamentais da pesquisa séria sobre o tema.

Por fim, embora a teoria do caos não seja o "Santo Graal" para a previsão dos mercados, ela representa uma abordagem promissora para estudos e desenvolvimentos futuros em análise financeira e negociação algorítmica. A combinação da teoria do caos com outras metodologias, como aprendizado de máquina e análise de big data, pode abrir novas possibilidades — algo tão evidente quanto a luz do dia.