Теория хаоса в трейдинге (Часть 2): Продолжаем погружение

Краткое изложение предыдущей части статьи

В первой статье цикла мы познакомились с основными концепциями теории хаоса и их применением к анализу финансовых рынков. Мы рассмотрели такие ключевые понятия, как аттракторы, фракталы и эффект бабочки, и обсудили, как они проявляются в динамике рынков. Особое внимание было уделено характеристикам хаотических систем в контексте финансов и понятию волатильности.

Мы также сравнили классическую теорию хаоса с подходом Билла Вильямса, что позволило лучше понять различия между научным и практическим применением этих концепций в трейдинге. Важной частью статьи стало обсуждение показателя Ляпунова как инструмента для анализа финансовых временных рядов. Мы не только объяснили его теоретическое значение, но и представили практическую реализацию расчета этого показателя на языке MQL5.

Завершающая часть статьи была посвящена статистическому анализу разворотов и продолжений тренда с использованием показателя Ляпунова. На примере пары EURUSD на часовом таймфрейме мы продемонстрировали, как этот анализ может быть применен на практике, и обсудили интерпретацию полученных результатов.

Эта статья заложила фундамент для понимания теории хаоса в контексте финансовых рынков и представила практические инструменты для ее применения в трейдинге. Во второй статье мы продолжим углублять наше понимание этой темы, фокусируясь на более сложных аспектах и их практическом применении.

Продолжаем «раскапывать» теорию хаоса. И первое, о чем мы поговорим — фрактальная размерность как мера хаотичности рынка

Фрактальная размерность как мера хаотичности рынка

Фрактальная размерность — это концепция, которая играет важную роль в теории хаоса и анализе сложных систем, включая финансовые рынки. Она предоставляет количественную меру сложности и самоподобия объекта или процесса, что делает ее особенно полезной для оценки степени хаотичности рыночных движений.

В контексте финансовых рынков фрактальная размерность может использоваться для измерения "изрезанности" ценовых графиков. Более высокая фрактальная размерность указывает на более сложную, хаотическую структуру цен, в то время как более низкая размерность может свидетельствовать о более гладком, предсказуемом движении.

Существует несколько методов расчета фрактальной размерности, но одним из наиболее популярных является метод покрытия или box-counting method. Этот метод заключается в покрытии графика сеткой с ячейками разного размера и подсчете количества ячеек, необходимых для покрытия графика при разных масштабах.

Формула для расчета фрактальной размерности D методом покрытия выглядит следующим образом:

D = -lim(ε→0) [log N(ε) / log(ε)]

где N(ε) - количество ячеек размера ε, необходимых для покрытия объекта.

Применение фрактальной размерности к анализу финансовых рынков может предоставить трейдерам и аналитикам дополнительную информацию о природе рыночных движений. Например:

• Идентификация рыночных режимов: Изменения в фрактальной размерности могут указывать на переходы между различными рыночными состояниями, такими как тренды, боковые движения или хаотические периоды.
• Оценка волатильности: Высокая фрактальная размерность часто соответствует периодам повышенной волатильности.
• Прогнозирование: Анализ изменений фрактальной размерности во времени может помочь в прогнозировании будущих движений рынка.
• Оптимизация торговых стратегий: Понимание фрактальной структуры рынка может помочь в разработке и оптимизации торговых алгоритмов.

Теперь давайте рассмотрим практическую реализацию расчета фрактальной размерности на языке MQL5. Мы разработаем индикатор, который будет вычислять фрактальную размерность ценового графика в режиме реального времени.

Предлагаю реализацию индикатора для расчета фрактальной размерности ценового графика на языке MQL5. Этот индикатор использует метод покрытия (box-counting method) для оценки фрактальной размерности.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ru/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

Этот индикатор вычисляет фрактальную размерность ценового графика, используя метод покрытия (box-counting method). Фрактальная размерность является мерой "изрезанности" или сложности графика и может использоваться для оценки степени хаотичности рынка.

Входные параметры:

• InpBoxSizesCount: количество различных размеров "коробок" для расчета
• InpMinBoxSize: минимальный размер "коробки"
• InpMaxBoxSize: максимальный размер "коробки"
• InpDataLength: количество свечей, используемых для расчета

Алгоритм работы индикатора:

1. Для каждой точки графика индикатор рассчитывает фрактальную размерность, используя данные за последние InpDataLength свечей.
2. Метод покрытия применяется с разными размерами "коробок" от InpMinBoxSize до InpMaxBoxSize.
3. Для каждого размера "коробки" вычисляется количество "коробок", необходимых для покрытия графика.
4. Строится график зависимости логарифма количества "коробок" от логарифма размера "коробки".
5. Методом линейной регрессии находится наклон этого графика, который и является оценкой фрактальной размерности.

Интерпретация результатов в том, что изменения фрактальной размерности могут сигнализировать о смене рыночного режима.

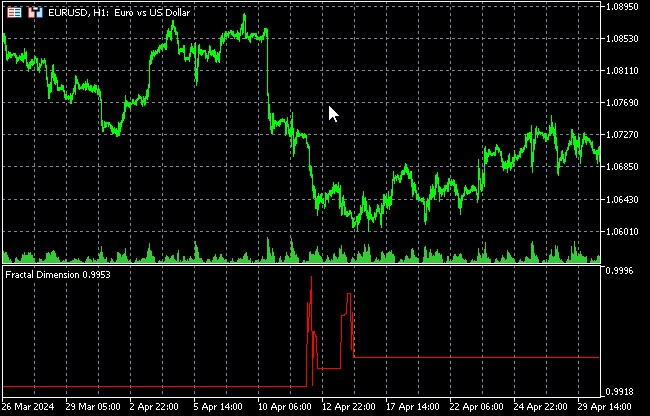
Рекуррентный анализ для выявления скрытых паттернов в ценовых движениях

Рекуррентный анализ — это мощный метод нелинейного анализа временных рядов, который может быть эффективно применен для изучения динамики финансовых рынков. Этот подход позволяет визуализировать и количественно оценить повторяющиеся паттерны в сложных динамических системах, к которым, несомненно, относятся и финансовые рынки.

Основным инструментом рекуррентного анализа является рекуррентная диаграмма (recurrence plot). Эта диаграмма представляет собой визуальное отображение повторяющихся состояний системы во времени. На рекуррентной диаграмме точка (i, j) закрашивается, если состояния в моменты времени i и j схожи в определенном смысле.

Для построения рекуррентной диаграммы финансового временного ряда следуют следующим шагам:

1. Реконструкция фазового пространства: Используя метод задержек, преобразуем одномерный временной ряд цен в многомерное фазовое пространство.
2. Определение порога сходства: Выбираем критерий, по которому будем считать два состояния схожими.
3. Построение матрицы рекуррентности: Для каждой пары моментов времени определяем, являются ли соответствующие состояния схожими.
4. Визуализация: Отображаем матрицу рекуррентности в виде двумерного изображения, где схожие состояния обозначаются точками.

Рекуррентные диаграммы позволяют выявить различные типы динамики в системе:

• Однородные участки указывают на стационарные периоды
• Диагональные линии свидетельствуют о детерминированной динамике
• Вертикальные и горизонтальные структуры могут указывать на ламинарные состояния
• Отсутствие структуры характерно для случайного процесса

Для количественной оценки структур на рекуррентной диаграмме используются различные меры рекуррентности, такие как процент рекуррентности, энтропия диагональных линий, максимальная длина диагональной линии и другие.

Применение рекуррентного анализа к финансовым временным рядам может помочь:

1. Идентифицировать различные рыночные режимы (тренд, боковое движение, хаотическое состояние)
2. Обнаруживать моменты смены режимов
3. Оценивать предсказуемость рынка в различные периоды
4. Выявлять скрытые циклические паттерны

Для практической реализации рекуррентного анализа в трейдинге можно разработать индикатор на языке MQL5, который будет строить рекуррентную диаграмму и вычислять меры рекуррентности в режиме реального времени. Такой индикатор может служить дополнительным инструментом для принятия торговых решений, особенно в сочетании с другими методами технического анализа.

В следующей части статьи мы рассмотрим конкретную реализацию такого индикатора и обсудим, как интерпретировать его показания в контексте торговой стратегии.

Индикатор реккурентного анализа на MQL5

Этот индикатор реализует метод рекуррентного анализа для изучения динамики финансовых рынков. Он вычисляет три ключевые меры рекуррентности: уровень рекуррентности, детерминизм и ламинарность.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ru/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Основные характеристики индикатора:

Основные характеристики индикатора заключаются в том, что он отображается в отдельном окне под графиком цены и использует три буфера для хранения и отображения данных. Индикатор рассчитывает три показателя: Recurrence Rate (синяя линия), который показывает общий уровень рекуррентности, Determinism (красная линия), представляющий собой меру предсказуемости системы, и Laminarity (зеленая линия), оценивающий тенденцию системы оставаться в определенном состоянии.

Входные параметры индикатора включают InpEmbeddingDimension (по умолчанию 3), который определяет размерность вложения для реконструкции фазового пространства, InpTimeDelay (по умолчанию 1) для временной задержки при реконструкции, InpThreshold (по умолчанию 10) как порог сходства состояний в пунктах, и InpWindowSize (по умолчанию 200) для задания размера окна анализа.

Алгоритм работы индикатора основывается на методе задержек для реконструкции фазового пространства из одномерного временного ряда цен. Для каждой точки в окне анализа вычисляется её "рекуррентность" по отношению к другим точкам. Затем на основе полученной рекуррентной структуры вычисляются три меры: Recurrence Rate, определяющий долю рекуррентных точек в общем количестве точек, Determinism, показывающий долю рекуррентных точек, формирующих диагональные линии, и Laminarity, оценивающий долю рекуррентных точек, формирующих вертикальные линии.

Применение теоремы вложения Такенса в прогнозировании волатильности

Теорема вложения Такенса - это фундаментальный результат в теории динамических систем, который имеет важное значение для анализа временных рядов, включая финансовые данные. Эта теорема утверждает, что динамическую систему можно реконструировать из наблюдений всего одной переменной, используя метод временных задержек.

В контексте финансовых рынков теорема Такенса позволяет нам реконструировать многомерное фазовое пространство из одномерного временного ряда цен или доходностей. Это особенно полезно при анализе волатильности, которая является ключевой характеристикой финансовых рынков.

Основные шаги применения теоремы Такенса для прогнозирования волатильности:

1. Реконструкция фазового пространства:
   • Выбор размерности вложения (m)
   • Выбор временной задержки (τ)
   • Создание m-мерных векторов из исходного временного ряда
2. Анализ реконструированного пространства:
   • Определение ближайших соседей для каждой точки
   • Оценка локальной плотности точек
3. Прогнозирование волатильности:
   • Использование информации о локальной плотности для оценки будущей волатильности

Рассмотрим эти шаги подробнее.

Реконструкция фазового пространства:

Пусть у нас есть временной ряд цен закрытия {p(t)}. Мы создаем m-мерные векторы следующим образом:

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

где m - размерность вложения, а τ - временная задержка.

Выбор правильных значений m и τ критически важен для успешной реконструкции. Обычно τ выбирается с использованием методов взаимной информации или автокорреляционной функции, а m - с помощью метода ложных ближайших соседей.

Анализ реконструированного пространства:

После реконструкции фазового пространства мы можем анализировать структуру аттрактора системы. Для прогнозирования волатильности особенно важна информация о локальной плотности точек в фазовом пространстве.

Для каждой точки x(t) мы находим её k ближайших соседей (обычно k выбирается в диапазоне от 5 до 20) и вычисляем среднее расстояние до этих соседей. Это расстояние служит мерой локальной плотности и, следовательно, локальной волатильности.

Прогнозирование волатильности

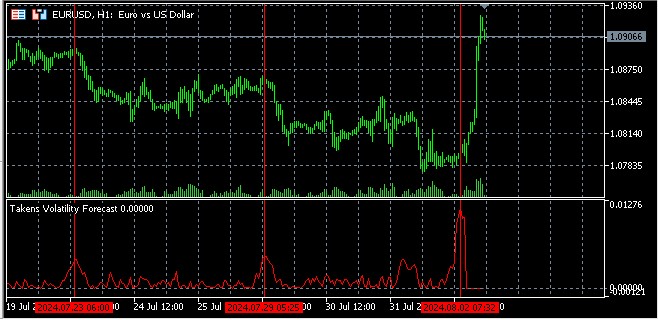
Основная идея прогнозирования волатильности с использованием реконструированного фазового пространства заключается в том, что точки, близкие в этом пространстве, вероятно, будут иметь схожее поведение в ближайшем будущем.

Для прогнозирования волатильности в момент времени t+h мы:

• Находим k ближайших соседей для текущей точки x(t) в реконструированном пространстве
• Вычисляем фактическую волатильность для этих соседей на h шагов вперед
• Используем среднее значение этих волатильностей как прогноз

Математически это можно выразить так:

σ̂(t+h) = (1/k) Σ σ(ti+h), где ti - индексы k ближайших соседей x(t)

Преимущества этого подхода:

• Учитывает нелинейную динамику рынка
• Не требует предположений о распределении доходностей
• Может уловить сложные паттерны в волатильности

Недостатки:

• Чувствителен к выбору параметров (m, τ, k)
• Может быть вычислительно затратным для больших объемов данных

Практическая реализация

Давайте создадим индикатор на MQL5, который будет реализовывать этот метод прогнозирования волатильности:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ru/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Предотвращаем выход за пределы массива
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Предотвращаем выход за пределы массива
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Предотвращаем выход за пределы массива
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Методы определения временной задержки и размерности вложения

При реконструкции фазового пространства с использованием теоремы Такенса критически важно правильно выбрать два ключевых параметра: временную задержку (τ) и размерность вложения (m). Неправильный выбор этих параметров может привести к некорректной реконструкции и, как следствие, к ошибочным выводам. Рассмотрим два основных метода определения этих параметров.

Метод автокорреляционной функции (ACF) для определения временной задержки

Метод автокорреляционной функции основан на идее выбора такой временной задержки τ, при которой автокорреляционная функция впервые пересекает ноль или достигает определенного низкого значения, например, 1/e от начального значения. Это позволяет выбрать задержку, при которой последовательные значения временного ряда становятся достаточно независимыми друг от друга.

Реализация метода ACF на MQL5 может выглядеть следующим образом:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

В этой реализации мы сначала вычисляем среднее значение и дисперсию временного ряда. Затем для каждого лага от 1 до maxLag мы вычисляем значение автокорреляционной функции. Как только значение ACF становится меньше или равно заданному порогу (по умолчанию 0.1), мы возвращаем этот лаг как оптимальную временную задержку.

Использование метода ACF имеет свои преимущества и недостатки. С одной стороны, он прост в реализации и интуитивно понятен. С другой стороны, он не учитывает нелинейные зависимости в данных, что может быть существенным недостатком при анализе финансовых временных рядов, которые часто демонстрируют нелинейное поведение.

Метод взаимной информации (MI) для определения временной задержки

Альтернативным подходом к определению оптимальной временной задержки является метод взаимной информации. Этот метод основан на теории информации и способен учитывать нелинейные зависимости в данных. Идея заключается в выборе такой задержки τ, которая соответствует первому локальному минимуму функции взаимной информации.

Реализация метода взаимной информации на MQL5 может выглядеть следующим образом:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

В этой реализации мы сначала определяем функцию CalculateMutualInformation, которая вычисляет взаимную информацию между исходным рядом и его сдвинутой версией для заданного лага. Затем в функции FindOptimalLagMI мы ищем первый локальный минимум взаимной информации, перебирая различные значения лага.

Метод взаимной информации имеет преимущество перед методом ACF в том, что он способен учитывать нелинейные зависимости в данных. Это делает его более подходящим для анализа финансовых временных рядов, которые часто демонстрируют сложное, нелинейное поведение. Однако этот метод более сложен в реализации и требует большего объема вычислений.

Выбор между методом ACF и методом MI зависит от конкретной задачи и характеристик анализируемых данных. В некоторых случаях может быть полезно применить оба метода и сравнить результаты. Важно также помнить, что оптимальная временная задержка может меняться со временем, особенно для финансовых временных рядов, поэтому может быть целесообразно периодически пересчитывать этот параметр.

Алгоритм ближайших ложных соседей для определения оптимальной размерности вложения

После определения оптимальной временной задержки следующим важным шагом в реконструкции фазового пространства является выбор подходящей размерности вложения. Одним из наиболее популярных методов для этой цели является алгоритм ближайших ложных соседей (False Nearest Neighbors, FNN).

Идея алгоритма FNN заключается в том, чтобы найти такую минимальную размерность вложения, при которой геометрическая структура аттрактора в фазовом пространстве будет корректно воспроизведена. Алгоритм основан на предположении, что в правильно реконструированном фазовом пространстве близкие точки должны оставаться близкими при переходе к пространству более высокой размерности.

Рассмотрим реализацию алгоритма FNN на языке MQL5:

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

Функция IsFalseNeighbor определяет, являются ли две точки ложными соседями. Она вычисляет расстояние между точками в текущей размерности и в размерности на единицу больше. Если относительное изменение расстояния превышает заданный порог, точки считаются ложными соседями.

Основная функция FindOptimalEmbeddingDimension перебирает размерности от 1 до maxDim. Для каждой размерности мы проходим по всем точкам временного ряда. Для каждой точки находим ближайшего соседа в текущей размерности. Затем проверяем, является ли найденный сосед ложным с помощью функции IsFalseNeighbor. Подсчитываем общее количество соседей и количество ложных соседей. После этого вычисляем долю ложных соседей. Если доля ложных соседей меньше заданного порога толерантности, считаем текущую размерность оптимальной и возвращаем ее.

Этот алгоритм имеет несколько важных параметров. delay — это временная задержка, определенная ранее методом ACF или MI. maxDim представляет максимальную рассматриваемую размерность вложения. threshold — это порог для определения ложных соседей. tolerance — порог толерантности для доли ложных соседей. Выбор этих параметров может существенно влиять на результат, поэтому важно экспериментировать с различными значениями и учитывать специфику анализируемых данных.

Алгоритм FNN имеет ряд преимуществ. Он учитывает геометрическую структуру данных в фазовом пространстве. Метод достаточно устойчив к шуму в данных. Он не требует предварительных предположений о природе изучаемой системы.

Реализация метода прогнозирования на основе теории хаоса в MQL5

После того как мы определили оптимальные параметры для реконструкции фазового пространства, мы можем приступить к реализации метода прогнозирования на основе теории хаоса. Этот метод основывается на идее, что близкие состояния в фазовом пространстве будут иметь схожую эволюцию в ближайшем будущем.

Основная идея метода заключается в следующем: мы находим в прошлом состояния системы, наиболее близкие к текущему состоянию, и на основе их будущего поведения делаем прогноз для текущего состояния. Этот подход известен как метод аналогов или метод ближайших соседей.

Давайте рассмотрим реализацию этого метода в виде индикатора для MetaTrader 5. Наш индикатор будет выполнять следующие шаги:

1. Реконструкция фазового пространства с использованием метода временных задержек.
2. Нахождение k ближайших соседей для текущего состояния системы.
3. Прогнозирование будущего значения на основе поведения найденных соседей.

Вот код индикатора, реализующего этот метод:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/ru/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Предотвращаем выход за пределы массива
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Предотвращаем выход за пределы массива
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Предотвращаем выход за пределы массива
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

Этот индикатор реконструирует фазовое пространство, находит ближайших соседей для текущего состояния и использует их будущие значения для прогнозирования. Он отображает как фактические, так и прогнозируемые значения на графике, позволяя визуально оценить качество прогноза.

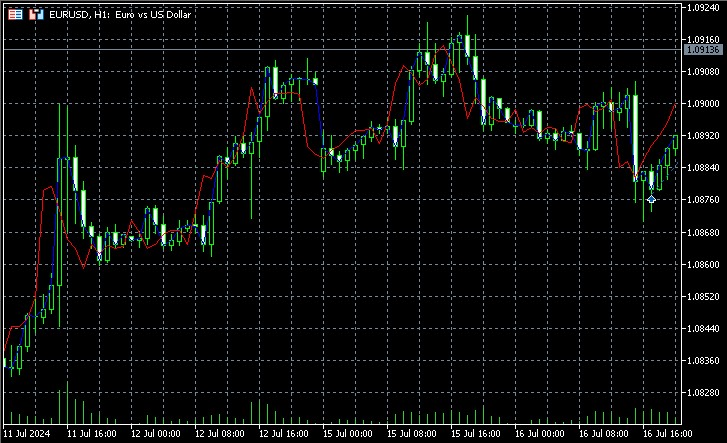
Ключевые аспекты реализации включают использование взвешенного среднего для прогнозирования, где вес каждого соседа обратно пропорционален его расстоянию от текущего состояния. Это позволяет учитывать, что более близкие соседи, вероятно, дадут более точный прогноз. Судя по скриншотам — индикатор заранее, за несколько баров, предсказывает направление движения цены.

Создание советника по концепции

Подошли вплотную к самому интересному. Вот наш код для полностью автоматической работы по теории хаоса:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Закрываем продажи
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Открываем покупку
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Закрываем покупки
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Открываем продажу
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Используем SortDoubleArray для сортировки по значениям массива distances
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Этот код представляет собой экспертного советника для MetaTrader 5, который использует концепции теории хаоса для прогнозирования цен на финансовых рынках. Советник реализует метод прогнозирования на основе метода ближайших соседей в реконструированном фазовом пространстве.

Советник имеет следующие входные параметры:

• InpEmbeddingDimension : размерность вложения для реконструкции фазового пространства (по умолчанию 3)
• InpTimeDelay : временная задержка для реконструкции (по умолчанию 5)
• InpNeighbors : количество ближайших соседей для прогнозирования (по умолчанию 10)
• InpForecastHorizon : горизонт прогнозирования (по умолчанию 10)
• InpLookback : период обратного просмотра для анализа (по умолчанию 1000)
• InpLotSize : размер лота для торговли (по умолчанию 0.1)

Советник работает следующим образом:

1. При каждом новом баре, он оптимизирует параметры  optimalTimeDelay  и  optimalEmbeddingDimension  с использованием метода автокорреляционной функции (ACF) и алгоритма ближайших ложных соседей (FNN) соответственно.
2. Затем он делает прогноз цены на основе текущего состояния системы, используя метод ближайших соседей.
3. Если прогноз цены выше текущей цены, советник закрывает все открытые продажи и открывает новую позицию на покупку. Если прогноз цены ниже текущей цены, советник закрывает все открытые покупки и открывает новую позицию на продажу.

Советник использует функцию PredictPrice, которая выполняет следующие шаги:

• Реконструирует фазовое пространство с использованием оптимальной размерности вложения и временной задержки.
• Находит расстояния между текущим состоянием системы и всеми состояниями в периоде обратного просмотра.
• Сортирует состояния по возрастанию расстояний.
• Вычисляет взвешенное среднее будущих цен для  InpNeighbors  ближайших соседей, где вес каждого соседа обратно пропорционален его расстоянию от текущего состояния.
• Возвращает взвешенное среднее в качестве прогноза цены.

Советник также включает функции FindOptimalLagACF и FindOptimalEmbeddingDimension, которые используются для оптимизации параметров optimalTimeDelay и optimalEmbeddingDimension соответственно.

В целом, этот советник предоставляет инновационный подход к прогнозированию цен на финансовых рынках, используя концепции теории хаоса. Он может помочь трейдерам сделать более информированные решения и потенциально увеличить доходность инвестиций.

Тестирование с авто-оптимизацией

Рассмотрим работу нашего советника на нескольких символах. Итак, первая валютная пара, EURUSD, период с 01.01.2016:

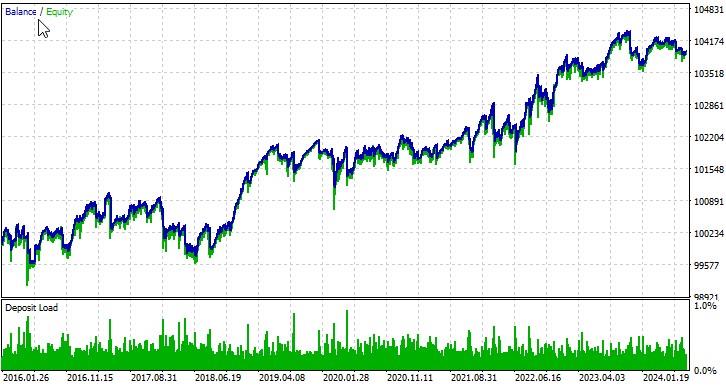
Вторая пара, австралийский доллар:

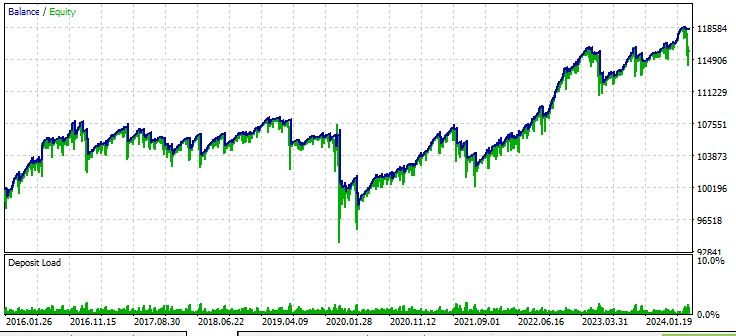
Третья пара, фунт - доллар:

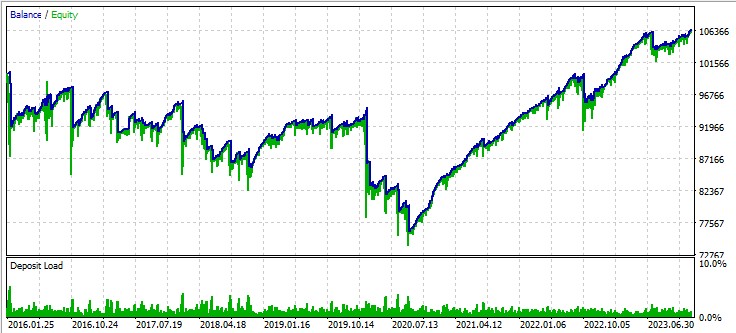
Дальнейшие шаги

Дальнейшее развитие нашего советника, основанного на теории хаоса, потребует углубленного тестирования и оптимизации. Необходимо провести масштабные испытания на различных временных интервалах и финансовых инструментах, чтобы лучше понять его эффективность в разных рыночных условиях. Применение методов машинного обучения может помочь в оптимизации параметров советника, повышая его адаптивность к изменяющимся рыночным реалиям.

Особое внимание следует уделить улучшению системы управления рисками. Внедрение динамического управления размером позиции, учитывающего текущую волатильность рынка и хаотический прогноз волатильности, может значительно повысить устойчивость стратегии.

Заключение

В данной статье мы рассмотрели применение теории хаоса для анализа и прогнозирования финансовых рынков. Мы изучили ключевые концепции, такие как реконструкция фазового пространства, определение оптимальной размерности вложения и временной задержки, а также метод прогнозирования на основе ближайших соседей.

Разработанный нами советник демонстрирует потенциал использования теории хаоса в алгоритмической торговле. Результаты тестирования на различных валютных парах показывают, что стратегия способна генерировать прибыль, хотя и с различной степенью успешности на разных инструментах.

Однако важно отметить, что применение теории хаоса в финансах сопряжено с рядом сложностей. Финансовые рынки являются крайне сложными системами, подверженными влиянию множества факторов, многие из которых трудно или вообще даже невозможно учесть в модели. Кроме того, сама природа хаотических систем делает долгосрочное прогнозирование принципиально невозможным — это один из основных постулатов серьезных исследователей.

В заключение, хотя теория хаоса и не является "Граалем" для прогнозирования рынков, она представляет собой перспективное направление для дальнейших исследований и разработок в области финансового анализа и алгоритмической торговли. Комбинирование методов теории хаоса с другими подходами, такими как машинное обучение и анализ больших данных, может открыть новые возможности, это ясно как день.