時間、価格、ボリュームに基づいた3Dバーの作成

はじめに

このプロジェクトを始めてから、すでに半年が経過しました。最初は愚かなアイデアだと思い、本格的に取り組むことはほとんどありませんでしたが、知り合いのトレーダーと話をすることはありました。 

すべては、単純な疑問から始まりました。なぜトレーダーは、2次元のチャートを見ながら3次元の市場を分析しようとするのでしょうか。プライスアクション、テクニカル分析、波動理論はいずれも、市場を平面に投影することで機能します。しかし、価格、ボリューム、時間の「本当の構造」を可視化した場合、何が見えるのでしょうか。

私のアルゴリズムシステムの研究において、従来の指標では価格とボリュームの重要な関係を見落とすことが多くありました。

3Dバーのアイデアはすぐに生まれたわけではありません。まず、市場深度の3D可視化を試み、次にボリュームと価格のクラスタの最初のスケッチを作成しました。そして時間軸を加え、最初の3Dバーを構築したとき、これは市場を見る全く新しい方法であることが明らかになりました。

本日は、この研究の成果を皆様に共有します。PythonとMetaTrader 5を用いてリアルタイムでボリュームバーを作成する方法を紹介し、計算の背後にある数学や、これらの情報を実際の取引でどのように活用できるかについても解説します。

3Dバーの特徴

2次元チャートで市場を見ている限り、最も重要なもの、すなわち市場の「本当の構造」を見落としてしまいます。従来のテクニカル分析は価格-時間やボリューム-時間の投影でおこなわれますが、これらの要素の相互作用全体を示すことはありません。

3D分析は根本的に異なり、市場全体の状態を一目で把握することを可能にします。ボリュームバーを構築する際には、市場の状態を文字通り「スナップショット」として作成しており、各次元には重要な情報が含まれます。

• バーの高さは価格変動の幅を示す
• バーの幅は時間のスケールを表す
• 奥行きはボリュームの分布を可視化する

これは重要な意味を持ちます。チャート上で同じように見える2つの価格変動を比較した場合、2次元では同一に見えても、ボリュームを加えると全く異なる構造が明らかになります。一方は大きなボリュームに支えられ、深く安定したバーを形成しますが、もう一方は最小限の取引しか伴わず、表面的な動きにすぎません。

3Dバーを用いた統合的アプローチは、テクニカル分析の古典的課題であるシグナルの遅延を解決します。バーのボリューム構造は最初のティックから形成が始まるため、通常のチャートに現れる前に強い動きの兆候を把握することが可能です。つまり、過去のパターンに依存せず、現在の取引の実際の動きに基づく予測分析が可能となります。

多変量データ分析は単なる美しい可視化ではなく、市場のマイクロ構造を理解するための全く新しい方法です。各3Dバーには次の情報が含まれています。

• 価格帯内のボリューム分布
• ポジション蓄積の速度
• 買い手と売り手の間の不均衡
• ミクロレベルのボラティリティ
• 動きの勢い

これらの要素は一つのメカニズムとして機能し、価格変動の本質を把握することを可能にします。従来のテクニカル分析では単なるキャンドルやバーしか見えませんが、3D分析は供給と需要の相互作用の複雑な構造を明らかにします。

主要指標を算出するための方程式、7Dバー構築の基本原理、異なる次元を統合するロジック

3Dバーの数学モデルは、実際の市場マイクロ構造の分析から生まれました。本システムにおける各バーは、三次元の立体として表現することができます。

class Bar3D:
    def __init__(self):
        self.price_range = None  # Price range
        self.time_period = None  # Time interval
        self.volume_profile = {} # Volume profile by prices
        self.direction = None    # Movement direction
        self.momentum = None     # Impulse
        self.volatility = None   # Volatility
        self.spread = None       # Average spread

ここでの重要なポイントは、バー内部のボリュームプロファイルの計算です。従来のバーとは異なり、本システムでは価格レベルごとのボリューム分布を詳細に分析します。

def calculate_volume_profile(self, ticks_data):
    volume_by_price = defaultdict(float)
    
    for tick in ticks_data:
        price_level = round(tick.price, 5)
        volume_by_price[price_level] += tick.volume
        
    # Normalize the profile
    total_volume = sum(volume_by_price.values())
    for price in volume_by_price:
        volume_by_price[price] /= total_volume
        
    return volume_by_price

モメンタムは価格とボリュームの変化率の組み合わせとして計算されます。

def calculate_momentum(self):
    price_velocity = (self.close - self.open) / self.time_period
    volume_intensity = self.total_volume / self.time_period
    self.momentum = price_velocity * volume_intensity * self.direction

特に注目すべきは、バー内部のボラティリティ分析です。本システムでは、価格変動のマイクロ構造を考慮した修正版ATR方程式を使用しています。

def calculate_volatility(self, tick_data):
    tick_changes = np.diff([tick.price for tick in tick_data])
    weighted_std = np.std(tick_changes * [tick.volume for tick in tick_data[1:]])
    time_factor = np.sqrt(self.time_period)
    self.volatility = weighted_std * time_factor

従来のバーとの根本的な違いは、すべての指標をリアルタイムで計算する点にあります。これにより、バーの構造が形成される過程をリアルタイムで観察することが可能です。

def update_bar(self, new_tick):
    self.update_price_range(new_tick.price)
    self.update_volume_profile(new_tick)
    self.recalculate_momentum()
    self.update_volatility(new_tick)
    
    # Recalculate the volumetric center of gravity
    self.volume_poc = self.calculate_poc()

すべての測定値は、特定の金融商品に合わせて調整された重み付け係数のシステムを通じて統合されます。

def calculate_bar_strength(self):
    return (self.momentum_weight * self.normalized_momentum +
            self.volatility_weight * self.normalized_volatility +
            self.volume_weight * self.normalized_volume_concentration +
            self.spread_weight * self.normalized_spread_factor)

実際の取引において、この数学モデルを用いることで、以下のような市場の側面を把握することができます。

• ボリューム蓄積の不均衡
• 価格形成速度の異常
• 保ち合いおよびブレイクアウトゾーン
• ボリューム特性によるトレンドの真の強さ

各3Dバーは、単なるチャート上の点ではなく、特定の瞬間における市場の状態を示す完全な指標です。

3Dバー作成アルゴリズムの詳細分析、MetaTrader 5での作業上の特徴、データ処理の特殊性

主要なアルゴリズムのデバッグを終え、ついに最も興味深い部分、つまり多次元バーのリアルタイム実装に取りかかりました。正直に言うと、当初は非常に困難な作業に思えました。MetaTrader 5は外部スクリプトに対してあまり親切ではなく、ドキュメントも十分に理解を助ける内容とは言えないことがありました。しかし、最終的にどのようにこの課題を克服したかをご説明します。

まず、データを格納するための基本的な構造から始めました。いくつかの試行を経て、以下のクラスが完成しました。

class Bar7D:
    def __init__(self):
        self.time = None
        self.open = None
        self.high = None
        self.low = None
        self.close = None
        self.tick_volume = 0
        self.volume_profile = {}
        self.direction = 0
        self.trend_count = 0
        self.volatility = 0
        self.momentum = 0

最も困難だったのは、ブロックサイズを正しく計算する方法を見つけることでした。多くの実験を経て、私は次の式に落ち着きました。

def calculate_brick_size(symbol_info, multiplier=45):
    spread = symbol_info.spread
    point = symbol_info.point
    min_price_brick = spread * multiplier * point
    
    # Adaptive adjustment for volatility
    atr = calculate_atr(symbol_info.name)
    if atr > min_price_brick * 2:
        min_price_brick = atr / 2
        
    return min_price_brick

ボリュームに関してもかなり苦労しました。当初は固定サイズのvolume_brickを使用しようと考えていましたが、すぐにそれではうまく機能しないことに気づきました。最終的に解決策として、適応型アルゴリズムを導入しました。

def adaptive_volume_threshold(tick_volume, history_volumes):
    median_volume = np.median(history_volumes)
    std_volume = np.std(history_volumes)
    
    if tick_volume > median_volume + 2 * std_volume:
        return median_volume + std_volume
    return max(tick_volume, median_volume / 2)

ただし、統計指標の計算は少し過剰だったと思います。

def calculate_stats(df):
    df['ma_5'] = df['close'].rolling(5).mean()
    df['ma_20'] = df['close'].rolling(20).mean()
    df['volume_ma_5'] = df['tick_volume'].rolling(5).mean()
    df['price_volatility'] = df['price_change'].rolling(10).std()
    df['volume_volatility'] = df['tick_volume'].rolling(10).std()
    df['trend_strength'] = df['trend_count'] * df['direction']
    
    # This is probably too much
    df['zscore_price'] = stats.zscore(df['close'], nan_policy='omit')
    df['zscore_volume'] = stats.zscore(df['tick_volume'], nan_policy='omit')
    return df

おかしなことですが、最も大変だったのはコードを書くことではなく、実際の市場環境でデバッグすることでした。 

以下は、3～9の範囲で正規化をおこなう関数の最終版です。なぜ3～9かというと、GannやTeslaはこの数字に何らかの「魔法」があると主張していたためです。また、ある有名なプラットフォーム上で、この数字を基に成功した反転スクリプトを作成したトレーダーを実際に見たこともあります。しかし、ここで陰謀論や神秘論に深入りするつもりはありません。代わりに、以下を試してみてください。

def create_true_3d_renko(symbol, timeframe, min_spread_multiplier=45, volume_brick=500, lookback=20000):
    """
    Creates 3D Renko bars with extended analytics
    """
    rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, lookback)
    if rates is None:
        print(f"Error getting data for {symbol}")
        return None, None
        
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    
    if df.isnull().any().any():
        print("Missing values detected, cleaning...")
        df = df.dropna()
        if len(df) == 0:
            print("No data for analysis after cleaning")
            return None, None
    
    symbol_info = mt5.symbol_info(symbol)
    if symbol_info is None:
        print(f"Failed to get symbol info for {symbol}")
        return None, None
    
    try:
        min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point
        if min_price_brick <= 0:
            print("Invalid block size")
            return None, None
    except AttributeError as e:
        print(f"Error getting symbol parameters: {e}")
        return None, None
    
    # Convert time to numeric and scale everything
    scaler = MinMaxScaler(feature_range=(3, 9))
    
    # Convert datetime to numeric (seconds from start)
    df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds()
    
    # Scale all numeric data together
    columns_to_scale = ['time_numeric', 'open', 'high', 'low', 'close', 'tick_volume']
    df[columns_to_scale] = scaler.fit_transform(df[columns_to_scale])
    
    renko_blocks = []
    current_price = float(df.iloc[0]['close'])
    current_tick_volume = 0
    current_time = df.iloc[0]['time']
    current_time_numeric = float(df.iloc[0]['time_numeric'])
    current_spread = float(symbol_info.spread)
    current_type = 0
    prev_direction = 0
    trend_count = 0
    
    try:
        for idx, row in df.iterrows():
            if pd.isna(row['tick_volume']) or pd.isna(row['close']):
                continue
                
            current_tick_volume += float(row['tick_volume'])
            volume_bricks = int(current_tick_volume / volume_brick)
            
            price_diff = float(row['close']) - current_price
            if pd.isna(price_diff) or pd.isna(min_price_brick):
                continue
                
            price_bricks = int(price_diff / min_price_brick)
            
            if volume_bricks > 0 or abs(price_bricks) > 0:
                direction = np.sign(price_bricks) if price_bricks != 0 else 1
                
                if direction == prev_direction:
                    trend_count += 1
                else:
                    trend_count = 1
                
                renko_block = {
                    'time': current_time,
                    'time_numeric': float(row['time_numeric']),
                    'open': float(row['open']),
                    'close': float(row['close']),
                    'high': float(row['high']),
                    'low': float(row['low']),
                    'tick_volume': float(row['tick_volume']),
                    'direction': float(direction),
                    'spread': float(current_spread),
                    'type': float(current_type),
                    'trend_count': trend_count,
                    'price_change': price_diff,
                    'volume_intensity': float(row['tick_volume']) / volume_brick,
                    'price_velocity': price_diff / (volume_bricks if volume_bricks > 0 else 1)
                }
                
                if volume_bricks > 0:
                    current_tick_volume = current_tick_volume % volume_brick
                if price_bricks != 0:
                    current_price += min_price_brick * price_bricks
                    
                prev_direction = direction
                renko_blocks.append(renko_block)
                
    except Exception as e:
        print(f"Error processing data: {e}")
        if len(renko_blocks) == 0:
            return None, None
    
    if len(renko_blocks) == 0:
        print("Failed to create any blocks")
        return None, None
        
    result_df = pd.DataFrame(renko_blocks)
    
    # Scale derived metrics to same range
    derived_metrics = ['price_change', 'volume_intensity', 'price_velocity', 'spread']
    result_df[derived_metrics] = scaler.fit_transform(result_df[derived_metrics])
    
    # Add analytical metrics using scaled data
    result_df['ma_5'] = result_df['close'].rolling(5).mean()
    result_df['ma_20'] = result_df['close'].rolling(20).mean()
    result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean()
    result_df['price_volatility'] = result_df['price_change'].rolling(10).std()
    result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std()
    result_df['trend_strength'] = result_df['trend_count'] * result_df['direction']
    
    # Scale moving averages and volatility
    ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength']
    result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns])
    
    # Add statistical metrics and scale them
    result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit')
    result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit')
    zscore_columns = ['zscore_price', 'zscore_volume']
    result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns])
    
    return result_df, min_price_brick

そして、単一スケールで得られたバーの系列はこのような形になります。あまり安定していないことがわかります。

統計分布

 

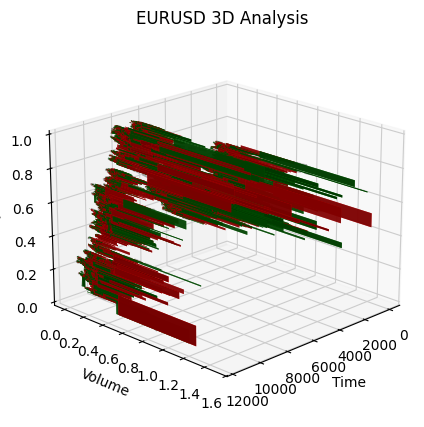
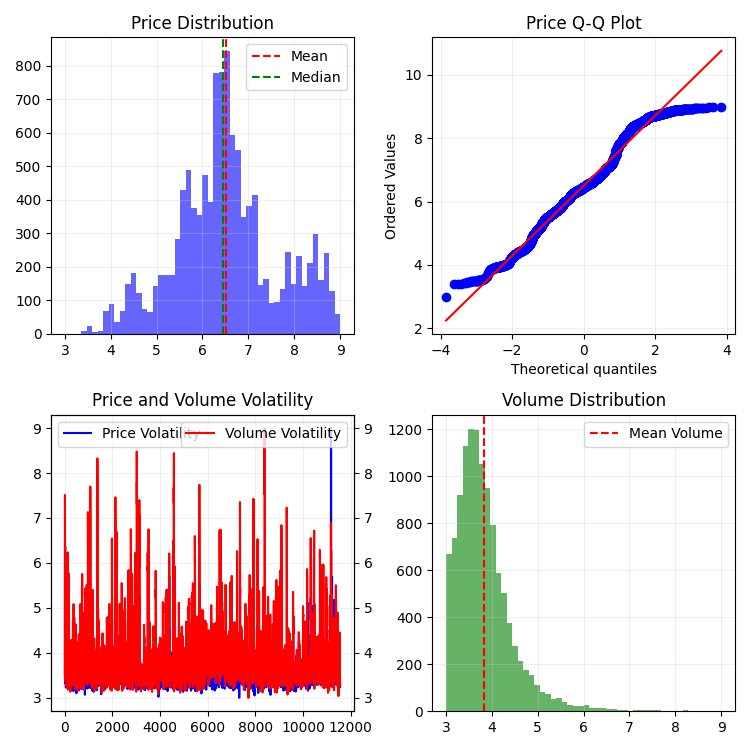
当然ながら、このようなバー系列には満足できませんでした。私の目標は、ある程度安定した系列、すなわち時間・ボリューム・価格が安定した系列を作成することでした。そこで次のような手法を導入しました。

ボラティリティ測定の導入 

create_stationary_4d_features関数を実装する際、私は根本的に異なるアプローチを取りました。従来の3Dバーでは単にデータを3～9の範囲にスケーリングするだけでしたが、ここでは真に安定した系列の作成に注力しました。

この関数の中心的な考え方は、安定した特徴量を用いて市場を四次元で表現することです。単なるスケーリングではなく、各次元は特別な方法で変換され、系列の安定性を実現しています。

1. 時間次元：時間は三角関数を用いて変換し、時刻を正弦波と余弦波に変換しました。具体的には「sin(2π * hour / 24)」と「cos(2π * hour / 24)」によって周期的特徴を作り、日次の季節性の問題を完全に排除しています。
2. 価格測定：絶対価格ではなく相対的な変化を使用します。コード上では、典型価格 (high + low + close)/3 を計算し、リターンとその加速度を求めることで実装しています。この手法により、価格水準に依存せず系列を安定化させることができます。
3. ボリューム測定：ここでの重要なポイントは、単なるボリューム変化ではなく、相対的な増分を取ることです。ボリュームはしばしば不均一に分布するため、この処理が重要です。コード上ではpct_change()とdiff()を連続して適用することで実装されています。
4. ボラティリティ測定：二段階の変換をおこなっています。まずリターンの標準偏差を用いて実行中ボラティリティを計算し、その後そのボラティリティの相対変化を計算します。結果として「ボラティリティのボラティリティ」を得ることができます。

各データブロックは20期間のスライディングウィンドウで形成されます。この20という数値は任意ではなく、データの局所的構造を保持しつつ、統計的に有意な計算をおこなうための妥協点として選ばれています。

すべての計算済み特徴量は最終的に3～9の範囲にスケーリングされますが、これは既に安定化された系列に対する二次的変換に過ぎません。これにより、3Dバーの従来の実装との互換性を保ちながら、データ前処理に根本的に異なるアプローチを適用できます。

特に重要なのは、移動平均、ボラティリティ、zスコアといった、元の関数から取得していた主要な指標をすべて保持することです。これにより、新しい実装は元の関数の直接的な置き換えとして使用でき、かつより高品質な安定化データを得ることができます。

結果として得られる特徴量セットは、統計的に安定しているだけでなく、市場構造に関する重要な情報をすべて保持しています。この手法により、データは機械学習や統計分析に適した形となり、同時に元の取引文脈との接続も維持されます。

関数は次のとおりです。 

def create_true_3d_renko(symbol, timeframe, min_spread_multiplier=45, volume_brick=500, lookback=20000):
    """
    Creates 4D stationary features with same interface as 3D Renko
    """
    rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, lookback)
    if rates is None:
        print(f"Error getting data for {symbol}")
        return None, None
        
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    
    if df.isnull().any().any():
        print("Missing values detected, cleaning...")
        df = df.dropna()
        if len(df) == 0:
            print("No data for analysis after cleaning")
            return None, None
    
    symbol_info = mt5.symbol_info(symbol)
    if symbol_info is None:
        print(f"Failed to get symbol info for {symbol}")
        return None, None
    
    try:
        min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point
        if min_price_brick <= 0:
            print("Invalid block size")
            return None, None
    except AttributeError as e:
        print(f"Error getting symbol parameters: {e}")
        return None, None
    
    scaler = MinMaxScaler(feature_range=(3, 9))
    df_blocks = []
    
    try:
        # Time dimension
        df['time_sin'] = np.sin(2 * np.pi * df['time'].dt.hour / 24)
        df['time_cos'] = np.cos(2 * np.pi * df['time'].dt.hour / 24)
        df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds()
        
        # Price dimension
        df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3
        df['price_return'] = df['typical_price'].pct_change()
        df['price_acceleration'] = df['price_return'].diff()
        
        # Volume dimension
        df['volume_change'] = df['tick_volume'].pct_change()
        df['volume_acceleration'] = df['volume_change'].diff()
        
        # Volatility dimension
        df['volatility'] = df['price_return'].rolling(20).std()
        df['volatility_change'] = df['volatility'].pct_change()
        
        for idx in range(20, len(df)):
            window = df.iloc[idx-20:idx+1]
            
            block = {
                'time': df.iloc[idx]['time'],
                'time_numeric': scaler.fit_transform([[float(df.iloc[idx]['time_numeric'])]]).item(),
                'open': float(window['price_return'].iloc[-1]),
                'high': float(window['price_acceleration'].iloc[-1]),
                'low': float(window['volume_change'].iloc[-1]),
                'close': float(window['volatility_change'].iloc[-1]),
                'tick_volume': float(window['volume_acceleration'].iloc[-1]),
                'direction': np.sign(window['price_return'].iloc[-1]),
                'spread': float(df.iloc[idx]['time_sin']),
                'type': float(df.iloc[idx]['time_cos']),
                'trend_count': len(window),
                'price_change': float(window['price_return'].mean()),
                'volume_intensity': float(window['volume_change'].mean()),
                'price_velocity': float(window['price_acceleration'].mean())
            }
            df_blocks.append(block)
                
    except Exception as e:
        print(f"Error processing data: {e}")
        if len(df_blocks) == 0:
            return None, None
    
    if len(df_blocks) == 0:
        print("Failed to create any blocks")
        return None, None
        
    result_df = pd.DataFrame(df_blocks)
    
    # Scale all features
    features_to_scale = [col for col in result_df.columns if col != 'time' and col != 'direction']
    result_df[features_to_scale] = scaler.fit_transform(result_df[features_to_scale])
    
    # Add same analytical metrics as in original function
    result_df['ma_5'] = result_df['close'].rolling(5).mean()
    result_df['ma_20'] = result_df['close'].rolling(20).mean()
    result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean()
    result_df['price_volatility'] = result_df['price_change'].rolling(10).std()
    result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std()
    result_df['trend_strength'] = result_df['trend_count'] * result_df['direction']
    
    # Scale moving averages and volatility
    ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength']
    result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns])
    
    # Add statistical metrics and scale them
    result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit')
    result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit')
    zscore_columns = ['zscore_price', 'zscore_volume']
    result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns])
    
    return result_df, min_price_brick

2Dで見ると次のようになります。

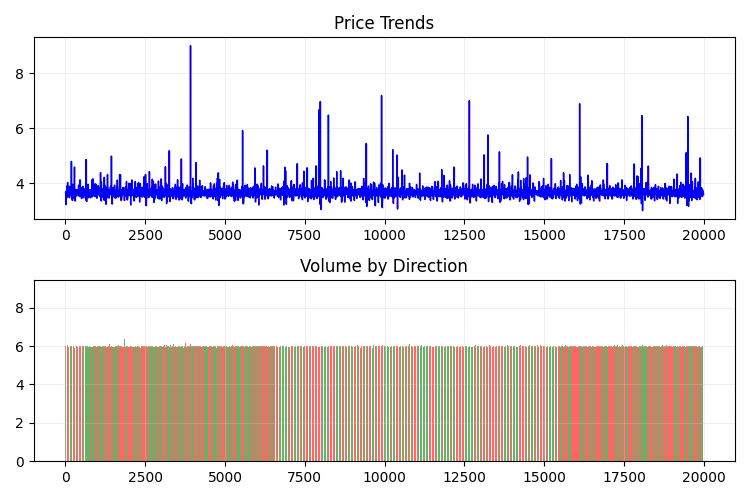
次に、Plotlyを用いて3D価格のインタラクティブモデルを作成してみましょう。従来の2次元チャートも隣に表示されるようにします。以下がそのコードです。

import plotly.graph_objects as go
from plotly.subplots import make_subplots


def create_interactive_3d(df, symbol, save_dir):
    """
    Creates interactive 3D visualization with smoothed data and original price chart
    """
    try:
        save_dir = Path(save_dir)
        
        # Smooth all series with MA(100)
        df_smooth = df.copy()
        smooth_columns = ['close', 'tick_volume', 'price_volatility', 'volume_volatility']
        
        for col in smooth_columns:
            df_smooth[f'{col}_smooth'] = df_smooth[col].rolling(window=100, min_periods=1).mean()
        
        # Create subplots: 3D view and original chart side by side
        fig = make_subplots(
            rows=1, cols=2,
            specs=[[{'type': 'scene'}, {'type': 'xy'}]],
            subplot_titles=(f'{symbol} 3D View (MA100)', f'{symbol} Original Price'),
            horizontal_spacing=0.05
        )
        
        # Add 3D scatter plot
        fig.add_trace(
            go.Scatter3d(
                x=np.arange(len(df_smooth)),
                y=df_smooth['tick_volume_smooth'],
                z=df_smooth['close_smooth'],
                mode='markers',
                marker=dict(
                    size=5,
                    color=df_smooth['price_volatility_smooth'],
                    colorscale='Viridis',
                    opacity=0.8,
                    showscale=True,
                    colorbar=dict(x=0.45)
                ),
                hovertemplate=
                "Time: %{x}<br>" +
                "Volume: %{y:.2f}<br>" +
                "Price: %{z:.5f}<br>" +
                "Volatility: %{marker.color:.5f}",
                name='3D View'
            ),
            row=1, col=1
        )
        
        # Add original price chart
        fig.add_trace(
            go.Candlestick(
                x=np.arange(len(df)),
                open=df['open'],
                high=df['high'],
                low=df['low'],
                close=df['close'],
                name='OHLC'
            ),
            row=1, col=2
        )
        
        # Add smoothed price line
        fig.add_trace(
            go.Scatter(
                x=np.arange(len(df_smooth)),
                y=df_smooth['close_smooth'],
                line=dict(color='blue', width=1),
                name='MA100'
            ),
            row=1, col=2
        )
        
        # Update 3D layout
        fig.update_scenes(
            xaxis_title='Time',
            yaxis_title='Volume',
            zaxis_title='Price',
            camera=dict(
                up=dict(x=0, y=0, z=1),
                center=dict(x=0, y=0, z=0),
                eye=dict(x=1.5, y=1.5, z=1.5)
            )
        )
        
        # Update 2D layout
        fig.update_xaxes(title_text="Time", row=1, col=2)
        fig.update_yaxes(title_text="Price", row=1, col=2)
        
        # Update overall layout
        fig.update_layout(
            width=1500,  # Double width to accommodate both plots
            height=750,
            showlegend=True,
            title_text=f"{symbol} Combined Analysis"
        )
        
        # Save interactive HTML
        fig.write_html(save_dir / f'{symbol}_combined_view.html')
        
        # Create additional plots with smoothed data (unchanged)
        fig2 = make_subplots(rows=2, cols=2, 
                            subplot_titles=('Smoothed Price', 'Smoothed Volume',
                                          'Smoothed Price Volatility', 'Smoothed Volume Volatility'))
        
        fig2.add_trace(
            go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['close_smooth'],
                      name='Price MA100'),
            row=1, col=1
        )
        
        fig2.add_trace(
            go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['tick_volume_smooth'],
                      name='Volume MA100'),
            row=1, col=2
        )
        
        fig2.add_trace(
            go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['price_volatility_smooth'],
                      name='Price Vol MA100'),
            row=2, col=1
        )
        
        fig2.add_trace(
            go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['volume_volatility_smooth'],
                      name='Volume Vol MA100'),
            row=2, col=2
        )
        
        fig2.update_layout(
            height=750,
            width=750,
            showlegend=True,
            title_text=f"{symbol} Smoothed Data Analysis"
        )
        
        fig2.write_html(save_dir / f'{symbol}_smoothed_analysis.html')
        
        print(f"Interactive visualizations saved in {save_dir}")
        
    except Exception as e:
        print(f"Error creating interactive visualization: {e}")
        raise

新しい価格帯は次のようになります。

全体として、非常に興味深い結果が得られます。時間ごとの価格のまとまりや、ボリュームごとの価格の外れ値のパターンが確認できます。このことから、市場が不安定で、大量のボリュームが流入し、ボラティリティが急上昇している場合には、統計を超えた危険な急変、いわゆるテールリスクに直面しているという感覚が生まれます。そして、この感覚はトップトレーダーの経験によっても裏付けられています。したがって、この座標上で価格の「異常な」動きを即座に検知することが可能です。このためだけでも多変量価格チャートというアイデアに感謝したいと思います。 

注意事項：

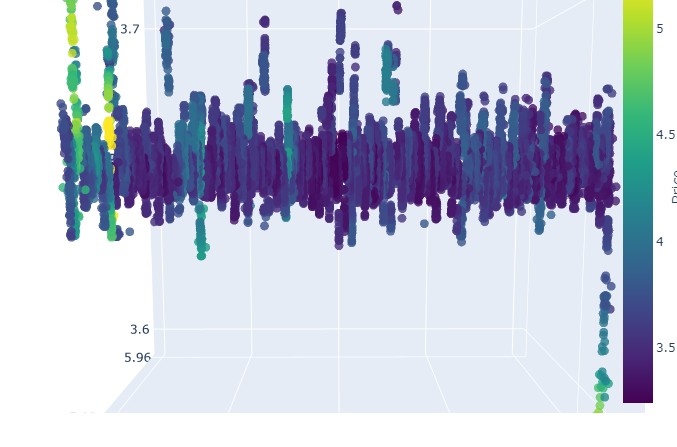
患者の診察（3Dグラフィック）

次に、可視化をおこないましょう。ただし、椰子の木の下での明るい未来ではなく、3D価格チャートです。状況を4つのクラスタに分けてみましょう。上昇トレンド、下降トレンド、上昇トレンドから下降トレンドへの反転、そして下降トレンドから上昇トレンドへの反転です。これをおこなうために、コードを少し変更する必要があります。バーのインデックスはもはや不要で、特定の日付のデータを読み込むようにします。実際には、これをおこなうにはmt5.copy_rates_rangeを使用すれば十分です。

def create_true_3d_renko(symbol, timeframe, start_date, end_date, min_spread_multiplier=45, volume_brick=500):
    """
    Creates 4D stationary features with same interface as 3D Renko
    """
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    if rates is None:
        print(f"Error getting data for {symbol}")
        return None, None
        
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    
    if df.isnull().any().any():
        print("Missing values detected, cleaning...")
        df = df.dropna()
        if len(df) == 0:
            print("No data for analysis after cleaning")
            return None, None
    
    symbol_info = mt5.symbol_info(symbol)
    if symbol_info is None:
        print(f"Failed to get symbol info for {symbol}")
        return None, None
    
    try:
        min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point
        if min_price_brick <= 0:
            print("Invalid block size")
            return None, None
    except AttributeError as e:
        print(f"Error getting symbol parameters: {e}")
        return None, None
    
    scaler = MinMaxScaler(feature_range=(3, 9))
    df_blocks = []
    
    try:
        # Time dimension
        df['time_sin'] = np.sin(2 * np.pi * df['time'].dt.hour / 24)
        df['time_cos'] = np.cos(2 * np.pi * df['time'].dt.hour / 24)
        df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds()
        
        # Price dimension
        df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3
        df['price_return'] = df['typical_price'].pct_change()
        df['price_acceleration'] = df['price_return'].diff()
        
        # Volume dimension
        df['volume_change'] = df['tick_volume'].pct_change()
        df['volume_acceleration'] = df['volume_change'].diff()
        
        # Volatility dimension
        df['volatility'] = df['price_return'].rolling(20).std()
        df['volatility_change'] = df['volatility'].pct_change()
        
        for idx in range(20, len(df)):
            window = df.iloc[idx-20:idx+1]
            
            block = {
                'time': df.iloc[idx]['time'],
                'time_numeric': scaler.fit_transform([[float(df.iloc[idx]['time_numeric'])]]).item(),
                'open': float(window['price_return'].iloc[-1]),
                'high': float(window['price_acceleration'].iloc[-1]),
                'low': float(window['volume_change'].iloc[-1]),
                'close': float(window['volatility_change'].iloc[-1]),
                'tick_volume': float(window['volume_acceleration'].iloc[-1]),
                'direction': np.sign(window['price_return'].iloc[-1]),
                'spread': float(df.iloc[idx]['time_sin']),
                'type': float(df.iloc[idx]['time_cos']),
                'trend_count': len(window),
                'price_change': float(window['price_return'].mean()),
                'volume_intensity': float(window['volume_change'].mean()),
                'price_velocity': float(window['price_acceleration'].mean())
            }
            df_blocks.append(block)
                
    except Exception as e:
        print(f"Error processing data: {e}")
        if len(df_blocks) == 0:
            return None, None
    
    if len(df_blocks) == 0:
        print("Failed to create any blocks")
        return None, None
        
    result_df = pd.DataFrame(df_blocks)
    
    # Scale all features
    features_to_scale = [col for col in result_df.columns if col != 'time' and col != 'direction']
    result_df[features_to_scale] = scaler.fit_transform(result_df[features_to_scale])
    
    # Add same analytical metrics as in original function
    result_df['ma_5'] = result_df['close'].rolling(5).mean()
    result_df['ma_20'] = result_df['close'].rolling(20).mean()
    result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean()
    result_df['price_volatility'] = result_df['price_change'].rolling(10).std()
    result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std()
    result_df['trend_strength'] = result_df['trend_count'] * result_df['direction']
    
    # Scale moving averages and volatility
    ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength']
    result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns])
    
    # Add statistical metrics and scale them
    result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit')
    result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit')
    zscore_columns = ['zscore_price', 'zscore_volume']
    result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns])
    
    return result_df, min_price_brick

変更後のコードは次のとおりです。

def main():
    try:
        # Initialize MT5
        if not mt5.initialize():
            print("MetaTrader5 initialization error")
            return

        # Analysis parameters
        symbols = ["EURUSD", "GBPUSD"]
        timeframes = {
            "M15": mt5.TIMEFRAME_M15
        }
        
        # 7D analysis parameters
        params = {
            "min_spread_multiplier": 45,
            "volume_brick": 500
        }

        # Date range for data fetching
        start_date = datetime(2017, 1, 1)
        end_date = datetime(2018, 2, 1)

        # Analysis for each symbol and timeframe
        for symbol in symbols:
            print(f"\nAnalyzing symbol {symbol}")
            
            # Create symbol directory
            symbol_dir = Path('charts') / symbol
            symbol_dir.mkdir(parents=True, exist_ok=True)
            
            # Get symbol info
            symbol_info = mt5.symbol_info(symbol)
            if symbol_info is None:
                print(f"Failed to get symbol info for {symbol}")
                continue

            print(f"Spread: {symbol_info.spread} points")
            print(f"Tick: {symbol_info.point}")
            
            # Analysis for each timeframe
            for tf_name, tf in timeframes.items():
                print(f"\nAnalyzing timeframe {tf_name}")
                
                # Create timeframe directory
                tf_dir = symbol_dir / tf_name
                tf_dir.mkdir(exist_ok=True)
                
                # Get and analyze data
                print("Getting data...")
                df, brick_size = create_true_3d_renko(
                    symbol=symbol,
                    timeframe=tf,
                    start_date=start_date,
                    end_date=end_date,
                    min_spread_multiplier=params["min_spread_multiplier"],
                    volume_brick=params["volume_brick"]
                )
                
                if df is not None and brick_size is not None:
                    print(f"Created {len(df)} 7D bars")
                    print(f"Block size: {brick_size}")
                    
                    # Basic statistics
                    print("\nBasic statistics:")
                    print(f"Average volume: {df['tick_volume'].mean():.2f}")
                    print(f"Average trend length: {df['trend_count'].mean():.2f}")
                    print(f"Max uptrend length: {df[df['direction'] > 0]['trend_count'].max()}")
                    print(f"Max downtrend length: {df[df['direction'] < 0]['trend_count'].max()}")
                    
                    # Create visualizations
                    print("\nCreating visualizations...")
                    create_visualizations(df, symbol, tf_dir)
                    
                    # Save data
                    csv_file = tf_dir / f"{symbol}_{tf_name}_7d_data.csv"
                    df.to_csv(csv_file)
                    print(f"Data saved to {csv_file}")
                    
                    # Results analysis
                    trend_ratio = len(df[df['direction'] > 0]) / len(df[df['direction'] < 0])
                    print(f"\nUp/Down bars ratio: {trend_ratio:.2f}")
                    
                    volume_corr = df['tick_volume'].corr(df['price_change'].abs())
                    print(f"Volume-Price change correlation: {volume_corr:.2f}")
                    
                    # Print warnings if anomalies detected
                    if df['price_volatility'].max() > df['price_volatility'].mean() * 3:
                        print("\nWARNING: High volatility periods detected!")
                        
                    if df['volume_volatility'].max() > df['volume_volatility'].mean() * 3:
                        print("WARNING: Abnormal volume spikes detected!")
                else:
                    print(f"Failed to create 3D bars for {symbol} on {tf_name}")
        
        print("\nAnalysis completed successfully!")
        
    except Exception as e:
        print(f"An error occurred: {e}")
        import traceback
        print(traceback.format_exc())
    finally:
        mt5.shutdown()

まず、最初のデータ区間を取り上げます。対象はEURUSDで、期間は2017年1月1日から2018年2月1日までです。実際、非常に強力な上昇トレンドとなっています。3Dバーでどのように見えるか、確認する準備はできていますか。

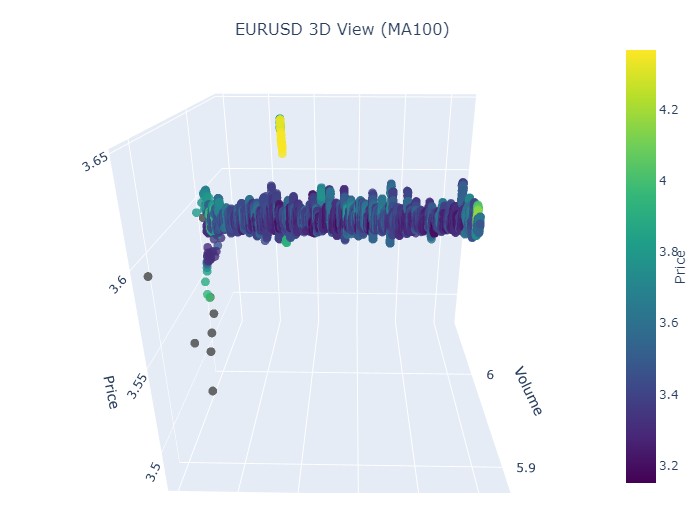
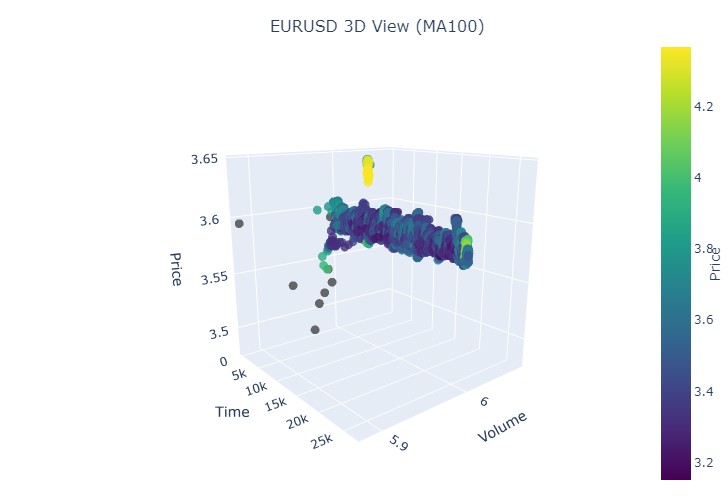
別の可視化は次のようになります。

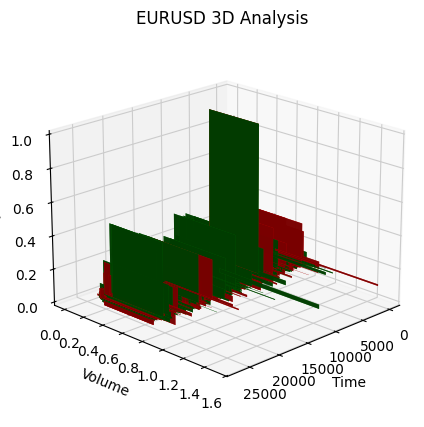
上昇トレンドの始まりに注目してみましょう。

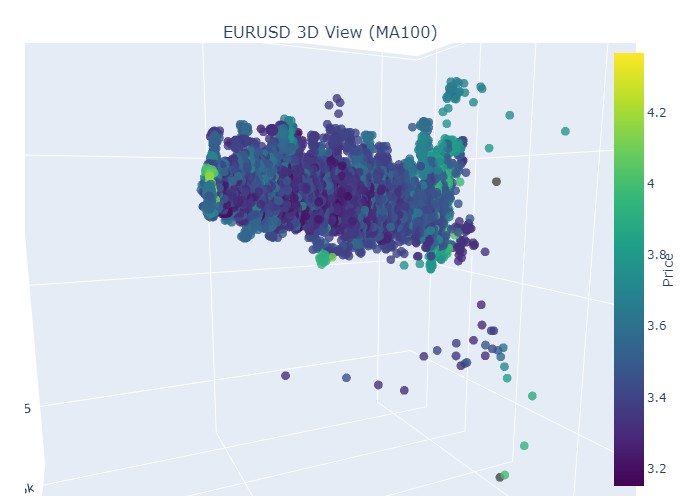
そしてこちらがトレンドの終わりです。

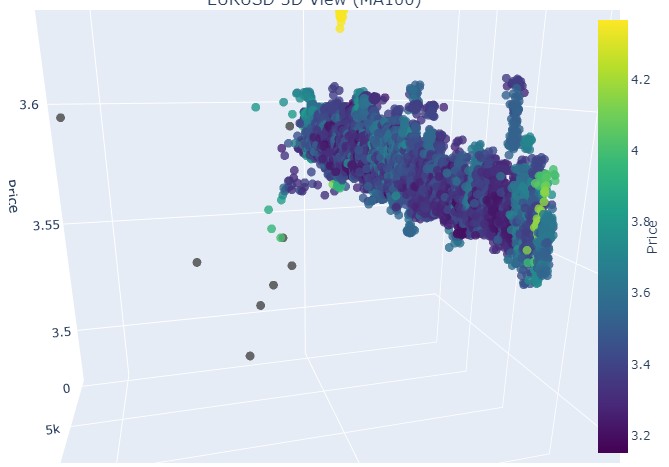
次に、下降トレンドを見てみましょう。2018年2月1日から2020年3月20日までです。

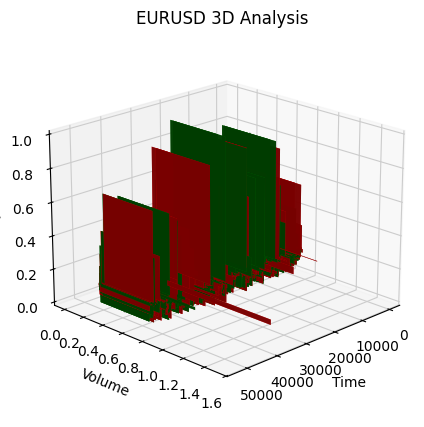
弱気トレンドの始まりは次のとおりです。

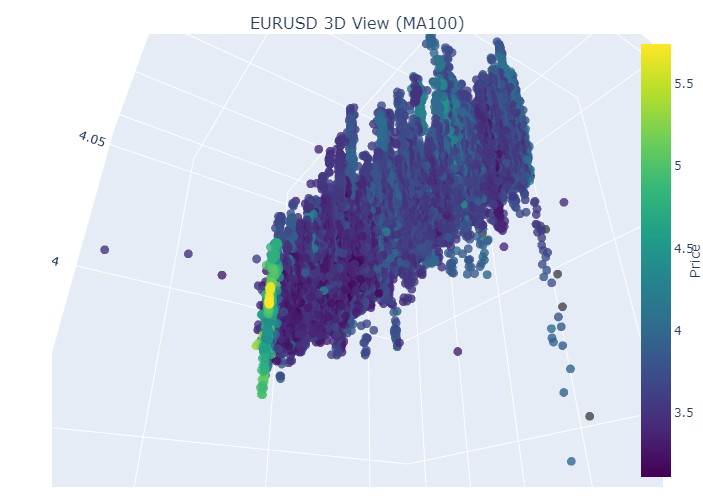
そしてこれが終わりです。

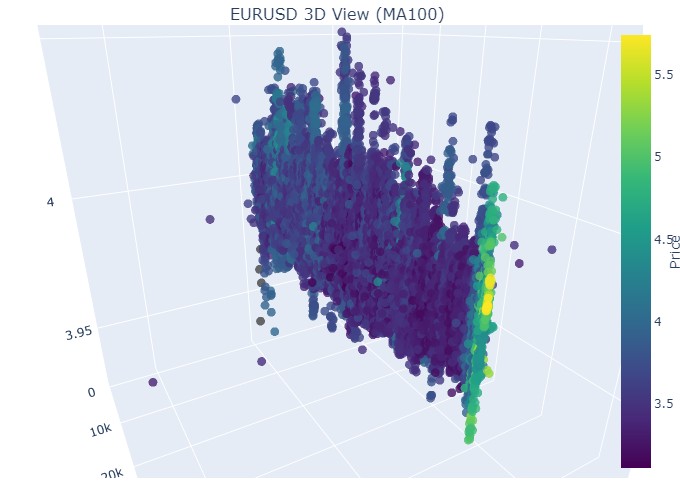
つまり、3D表現で見ると、どちらのトレンド（上昇トレンド、下降トレンド）も、最初は3Dドット密度の下に点が集まった領域として始まります。トレンドの終了は、いずれの場合も明るい黄色の色調で示されます。 

この現象、つまりEURUSDの価格が上昇トレンドおよび下降トレンドでどのように振る舞うかを記述するために、次の普遍的な方程式を用いることができます。

P(t) = P_0 + \int_{t_0}^{t} A \cdot e^{k(t-u)} \cdot V(u) \, du + N(t)

ここで

•  P(t)：特定の時点における通貨価格
•  P_0：特定の時点における初期価格
•  A：トレンドの振幅、価格変動の規模を表す
•  k：変化の速度を決定する係数（k>0は上昇トレンド、k<0は下降トレンドを意味する）
•  V(u)：特定の時点における取引量、市場の活動度に影響し、価格変動の重要度を高める可能性がある
•  N(t)：予測不可能な市場変動を反映したランダムノイズ

解説

この方程式は、複数の要因に基づいて通貨価格が時間とともにどのように変化するかを示しています。初期価格は出発点であり、その後の積分項はトレンドの振幅と変化速度の影響を考慮し、価格を指数的に上昇または下降させます。関数で表される取引量はもう一つの次元を加え、市場の活動度が価格変動に影響することを示しています。

このモデルにより、異なるトレンド下での価格変動を3D空間で可視化することが可能になります。時間軸、価格、ボリュームが組み合わさることで、市場活動の豊かな構造を描き出すことができます。また、このパターンにおける配色の明るさはトレンドの強さを示し、より明るい色は価格変動や取引量の微分値が高いことを示し、市場での強いボリュームの動きを知らせるシグナルとなります。

反転の表示

こちらは、11月14日から11月28日までの期間です。この期間のほぼ中央で、相場に反転が生じます。3D座標上ではどのように見えるのでしょうか。以下がその様子です。

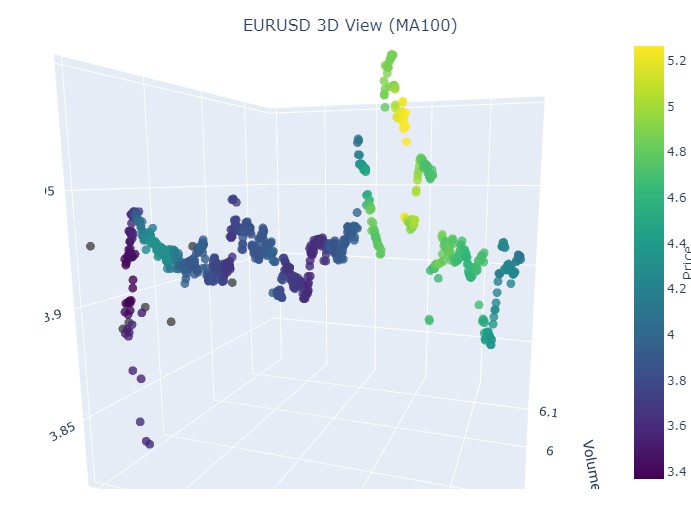
反転の瞬間には、すでにお馴染みの黄色が見られ、正規化された価格座標も上昇しています。次に、別のトレンド反転が起こった価格区間、2024年9月13日から同年10月10日までのデータを見てみましょう。

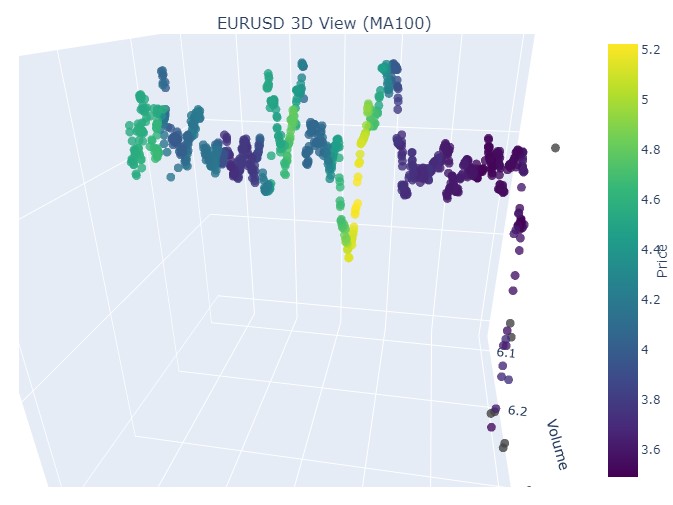
同じパターンが再び見られますが、黄色の色やその蓄積は今度は下側に位置しています。興味深い結果です。 

続いて、2024年8月19日から8月30日までの期間を見てみましょう。この日付範囲のほぼ中央で、トレンドの正確な反転が確認できます。座標を確認してみましょう。

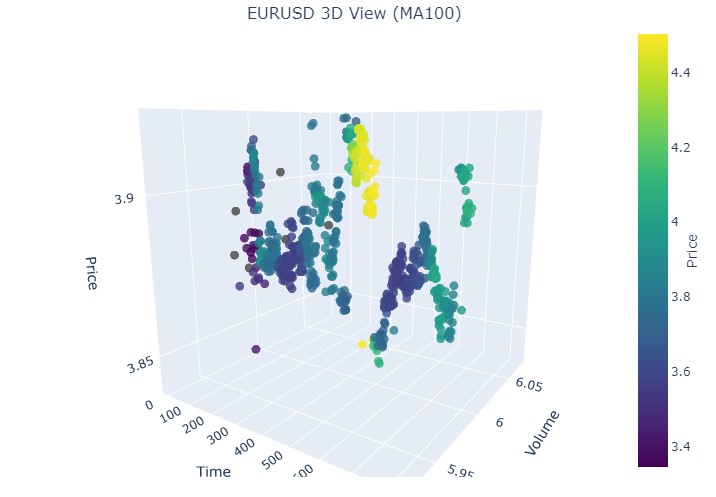
再び、まったく同じパターンが見られます。次に、2024年7月17日から8月8日までの期間を見てみましょう。この期間に、モデルは近いうちに反転の兆候を示すでしょうか。

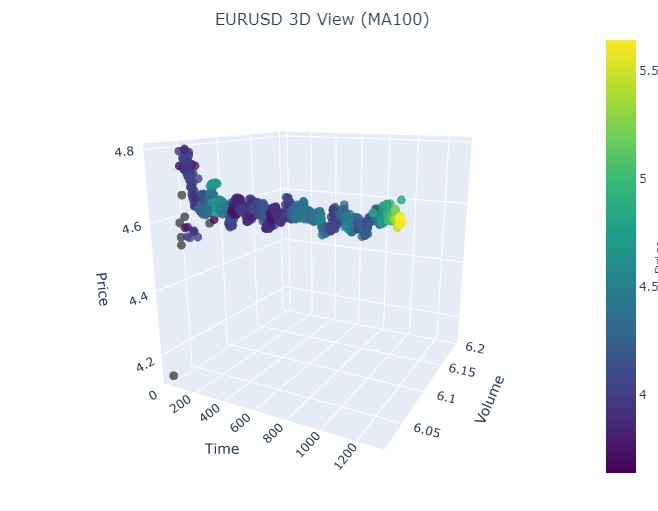
最終期間は2023年4月21日から8月10日までです。強気トレンドはそこで終了しました。

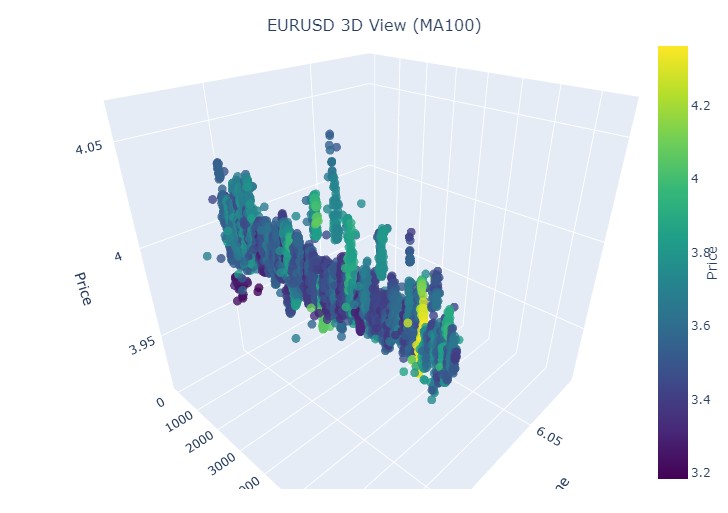
おなじみの黄色がまた見られます。

黄色のクラスタ

3Dバーを開発している際、非常に興味深い現象に出会いました。黄色のボリュームボラティリティクラスタです。そのチャート上での挙動にすっかり魅了されました。2022年から2024年までの膨大な過去データ（正確には40万本以上のバー）を解析したところ、驚くべきことが分かりました。

最初は目を疑いました。約10万本の黄色バーのうち、ほぼすべて（97％）が価格反転付近に位置していたのです。しかも、プラスマイナス3バーの範囲でこの法則は成り立ちました。興味深いことに、全反転のうち黄色バーを伴ったものは40％に過ぎませんでした（反転は約16.9万回ありました）。つまり、黄色バーが現れるとほぼ反転が保証されますが、反転は黄色バーなしでも発生し得ることになります。

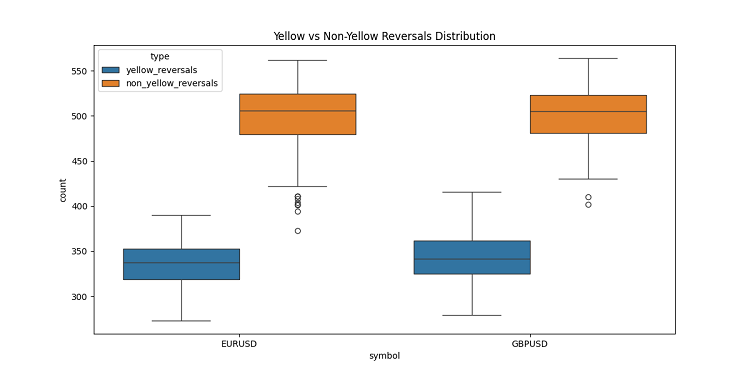
さらにトレンドを詳しく分析すると、明確なパターンが見えてきました。トレンドの初期や進行中は黄色バーはほとんど現れず、通常の3Dバーが密集したグループを形成しています。しかし、反転直前になると、黄色クラスタがチャート上で輝きます。

これは特に長期トレンドで顕著です。たとえば、EURUSDの2017年初めから2018年2月までの上昇トレンド、その後2020年3月までの下降トレンドを考えてみましょう。いずれの場合も、これら黄色クラスタは反転前に出現し、3D上の配置は文字通り価格の行方を示していました。

短期期間でも試してみました。2024年の2～3週間のセグメントをいくつか取り上げたところ、こちらも完全に機能しました。反転前には毎回黄色バーが出現し、「注意、トレンドが反転しようとしている」と警告しているかのようでした。

これは単なるインジケーターではありません。市場構造そのもの、つまりトレンド変化前のボリューム分布やボラティリティの変化に関する重要な知見に到達したと考えています。今では、3Dチャート上で黄色クラスタを見かけると、反転に備えるタイミングだと判断できます。

結論

3Dバーの探求を終えるにあたり、この取り組みが市場マイクロ構造の理解にどれほど深い変化をもたらしたかを改めて感じています。もともとは単なる可視化の実験に過ぎませんでしたが、結果として市場を理解するための根本的に新しい視点へと進化しました。

このプロジェクトを通して、従来の二次元的な価格表現にどれほど制約されていたかを痛感しました。三次元分析への移行は、価格・ボリューム・時間の関係性を理解する上で、まったく新しい地平を切り開きました。特に、重要な市場イベントに先行するパターンが三次元空間で非常に明瞭に現れることには強く感銘を受けました。

最も重要な発見は、潜在的なトレンド反転を早期に検知できる能力です。3D表現における特徴的なボリュームの蓄積やカラースキームの変化は、次のトレンド変化を示す非常に信頼性の高い指標であることが、多くの過去データで確認されました。これは単なる理論的観察ではありません。

今回開発した数学モデルは、単に可視化を行うだけでなく、市場動態を定量的に評価することも可能にします。最新の可視化技術やソフトウェアツールを統合することで、実際の取引にも応用できる方法となりました。私自身も日々これらのツールを活用しており、市場分析のアプローチに大きな変化をもたらしています。

しかし、これはあくまで旅の始まりに過ぎないと考えています。本プロジェクトは、多変量市場マイクロ構造分析の世界への扉を開きました。今後、この方向での研究はさらに多くの興味深い発見をもたらすと確信しています。次のステップとしては、3Dパターンを自動認識する機械学習の統合や、多変量分析に基づく新たな取引戦略の開発が考えられます。

最終的に、この研究の真価は、美しいチャートや複雑な方程式にあるのではなく、新たな市場洞察を提供する点にあります。研究者として、私は、テクニカル分析の未来は市場データを多変量的に解析するアプローチにあると強く信じています。