La teoría del caos en el trading (Parte 2): Continuamos la inmersión

Resumen de la parte anterior del artículo

En el primer artículo de la serie nos familiarizamos con los principales conceptos de la teoría del caos y su aplicación al análisis de los mercados financieros. Asimismo, examinamos conceptos clave como los atractores, los fractales y el efecto mariposa, y discutimos su aplicación a la dinámica del mercado. En el artículo prestamos especial atención a las características de los sistemas caóticos en el contexto de las finanzas y al concepto de volatilidad.

También comparamos la teoría clásica del caos con el enfoque de Bill Williams, lo cual nos permitió comprender mejor las diferencias entre la aplicación científica y práctica de estos conceptos en el trading. Una parte importante del artículo era un debate sobre el exponente de Lyapunov como herramienta para analizar series temporales financieras. No solo explicamos su significado teórico, sino que también presentamos la aplicación práctica del cálculo de este exponente en MQL5.

La última parte del artículo se dedicó al análisis estadístico de las inversiones y continuaciones de tendencia utilizando el exponente de Lyapunov. En el ejemplo del EURUSD en el marco temporal de horas demostramos cómo se puede aplicar este análisis en la práctica y discutimos la interpretación de los resultados obtenidos.

En dicho artículo sentamos las bases para entender la teoría del caos en el contexto de los mercados financieros y presentamos herramientas prácticas para aplicarla al trading. En el segundo artículo, seguiremos profundizando en este tema, centrándonos en aspectos más complejos y sus aplicaciones prácticas.

Vamos a seguir indagando en la teoría del caos. Y lo primero de lo que hablaremos es de la dimensionalidad fractal como medida de la aleatoriedad del mercado

La dimensionalidad fractal como medida de la aleatoriedad del mercado

La dimensionalidad fractal es un concepto que desempeña un papel importante en la teoría del caos y el análisis de sistemas complejos, incluidos los mercados financieros. Dado que ofrece una medida cuantitativa de la complejidad y autosimilitud de un objeto o proceso, resulta especialmente útil para evaluar el grado de aleatoriedad de los movimientos del mercado.

En el contexto de los mercados financieros, la dimensionalidad fractal puede utilizarse para medir la "rugosidad" de los gráficos de precio. Una dimensionalidad fractal más alta indicará una estructura de precios más compleja y caótica, mientras que una dimensionalidad más baja indicará un movimiento más suave y predecible.

Existen varios métodos para calcular la dimensionalidad fractal, pero uno de los más populares es el método de cobertura o de recuento de cajas (box-counting method). Este método consiste en cubrir el gráfico con una cuadrícula con celdas de diferentes tamaños y calcular el número de celdas necesarias para cubrir el gráfico a diferentes escalas.

La fórmula para calcular la dimensionalidad fractal D según el método de cobertura es la siguiente:

D = -lim(ε→0) [log N(ε) / log(ε)]

donde N(ε) será el número de celdas de tamaño ε necesarias para cubrir el objeto.

Aplicar la dimensionalidad fractal al análisis de los mercados financieros puede proporcionar a los tráders y analistas información adicional sobre la naturaleza de los movimientos del mercado. Por ejemplo:

• Identificación de los modos de mercado: Los cambios en la dimensionalidad fractal pueden indicar transiciones entre distintos estados del mercado, como tendencias, movimientos laterales o periodos caóticos.
• Estimación de la volatilidad: Una dimensionalidad fractal elevada suele corresponderse con periodos de mayor volatilidad.
• Predicción: Analizar los cambios de la dimensionalidad fractal a lo largo del tiempo puede ayudarnos a predecir futuros movimientos del mercado.
• Optimización de las estrategias comerciales: Comprender la estructura fractal del mercado puede ayudarnos a desarrollar y optimizar los algoritmos comerciales.

Veamos ahora la implementación práctica del cálculo de la dimensionalidad fractal en MQL5. Hoy desarrollaremos un indicador que calculará la dimensionalidad fractal de un gráfico de precio en tiempo real.

Le propongo implementar un indicador para calcular la dimensionalidad fractal de un gráfico de precio en MQL5. Este indicador usará el método de cobertura (box-counting method) para estimar la dimensionalidad fractal.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

Este indicador calculará la dimensionalidad fractal del gráfico de precio utilizando el método de cobertura. La dimensionalidad fractal es una medida de la "rugosidad" o complejidad de un gráfico y puede utilizarse para evaluar el grado de aleatoriedad del mercado.

Parámetros de entrada:

• InpBoxSizesCount: número de "cajas" de distintos tamaños que se calcularán
• InpMinBoxSize: tamaño mínimo de la "caja".
• InpMaxBoxSize: tamaño máximo de la "caja".
• InpDataLength: número de velas usadas para el cálculo

Algoritmo de funcionamiento del indicador:

1. Para cada punto del gráfico, el indicador calculará la dimensionalidad fractal utilizando los datos de las últimas velas InpDataLength.
2. El método de cobertura se aplica con diferentes tamaños de "caja" desde InpMinBoxSize hasta InpMaxBoxSize.
3. Para cada tamaño de "caja", se calculará el número de "cajas" necesarias para cubrir el gráfico.
4. El gráfico de dependencia del logaritmo del número de "cajas" se construirá partiendo del logaritmo del tamaño de la "caja".
5. El método de regresión lineal se usará para hallar la inclinación de este gráfico, que será una estimación de la dimensionalidad fractal.

La interpretación de los resultados se basará en el hecho de que los cambios en la dimensionalidad fractal pueden señalar un cambio en el modo de mercado.

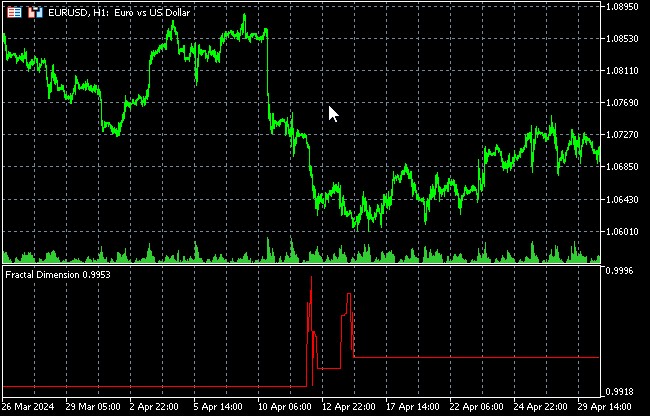
Análisis de recurrencia para identificar patrones ocultos en los movimientos de precio

El análisis de recurrencia es un potente método de análisis no lineal de series temporales que puede aplicarse eficazmente para estudiar la dinámica de los mercados financieros. Este enfoque nos permite visualizar y cuantificar patrones recurrentes en sistemas dinámicos complejos, entre los que sin duda se encuentran los mercados financieros.

La principal herramienta en el análisis de recurrencia es el gráfico de recurrencia. Este diagrama supone una representación visual de los estados recurrentes del sistema a lo largo del tiempo. En un diagrama de recurrencia, el punto (i, j) estará coloreado si los estados en los tiempos i y j son similares en algún sentido.

Para construir un diagrama de recurrencia de una serie temporal financiera, se seguirán los siguientes pasos:

1. Reconstrucción del espacio de fases: Usando el método del retardo, transformaremos las series temporales univariantes de precios en un espacio de fases multivariante.
2. Determinación del umbral de similitud: Elegiremos el criterio según el cual consideraremos que los dos estados son similares.
3. Construcción de una matriz de recurrencia: Para cada par de instantes temporales, determinaremos si los estados correspondientes son similares.
4. Visualización: Mostraremos la matriz de recurrencia como una imagen bidimensional, donde los estados similares se denotarán con puntos.

Los diagramas de recurrencia nos permiten identificar distintos tipos de dinámica en el sistema:

• Las zonas homogéneas indicarán periodos estacionarios
• Las líneas diagonales indicarán una dinámica determinista
• Las estructuras verticales y horizontales podrían indicar estados laminares
• La ausencia de estructura será característica de un proceso aleatorio

Para cuantificar las estructuras de un diagrama de recurrencia se usan diversas medidas de recurrencia, como el porcentaje de recurrencia, la entropía de las líneas diagonales, la longitud máxima de la línea diagonal y otras.

La aplicación del análisis de recurrencia a las series temporales financieras puede ayudarnos a:

1. Identificar diferentes modos de mercado (tendencia, movimiento lateral, estado caótico)
2. Detectar momentos de cambio de modo
3. Evaluar la previsibilidad del mercado en diferentes periodos
4. Identificar patrones cíclicos ocultos

Para la implementación práctica del análisis de recurrencia en el trading, podemos desarrollar un indicador en MQL5 que construirá un diagrama de recurrencia y calculará las medidas de recurrencia en tiempo real. Un indicador de este tipo podría servir como herramienta adicional para tomar decisiones comerciales, especialmente en combinación con otros métodos de análisis técnico.

En la siguiente parte del artículo, veremos una implementación específica de este indicador y discutiremos cómo interpretar sus lecturas en el contexto de una estrategia comercial.

Indicador de análisis de recurrencia en MQL5

Este indicador aplicará el método del análisis de recurrencia para estudiar la dinámica de los mercados financieros. Así, calculará tres medidas clave de recurrencia: el nivel de recurrencia, el determinismo y la laminaridad.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Principales características del indicador:

Las principales características del indicador son que se mostrará en una ventana independiente debajo del gráfico de precios y que utilizará tres búferes para almacenar y mostrar los datos. El indicador calculará tres indicadores: La tasa de recurrencia (línea azul), que mostrará el nivel global de recurrencia, el determinismo (línea roja), que supone una medida de la previsibilidad del sistema, y laminaridad (línea verde), que evaluará la tendencia del sistema a permanecer en un determinado estado.

Los parámetros de entrada del indicador incluirán InpEmbeddingDimension (por defecto 3), que define la dimensionalidad de incorporación para la reconstrucción del espacio de fases; InpTimeDelay (por defecto 1) para el retardo del tiempo de reconstrucción; InpThreshold (por defecto 10) como umbral para la similitud de estado en puntos, e InpWindowSize (por defecto 200) para especificar el tamaño de la ventana de análisis.

El algoritmo del indicador se basa en el método de retardo para la reconstrucción del espacio de fases a partir de una serie temporal de precios unidimensional. Para cada punto de la ventana de análisis, se calculará su "recurrencia" con respecto a otros puntos. A continuación, se calcularán tres medidas basadas en la estructura de recurrencia obtenida: La tasa de recurrencia, que determina la proporción de puntos de recurrencia en el número total de puntos, el determinismo, que muestra la proporción de puntos de recurrencia que forman líneas diagonales, y la laminaridad, que estima la proporción de puntos de recurrencia que forman líneas verticales.

Aplicación del teorema de incorporación de Takens a la previsión de la volatilidad

El teorema de incorporación de Takens supone un resultado fundamental de la teoría de sistemas dinámicos que tiene importantes implicaciones para el análisis de series temporales, incluidos los datos financieros. Este teorema afirma que un sistema dinámico puede reconstruirse partiendo de observaciones de una sola variable utilizando el método del retardo temporal.

En el contexto de los mercados financieros, el teorema de Takens nos permite reconstruir un espacio de fases multivariante a partir de una serie temporal univariante de precios o rendimientos. Esto resulta especialmente útil al analizar la volatilidad, que es una característica clave de los mercados financieros.

Pasos básicos de la aplicación del teorema de Takens a la previsión de la volatilidad:

1. Reconstrucción del espacio de fases:
   • Selección de la dimensionalidad de la incorporación (m)
   • Selección del retardo (τ)
   • Creación de vectores m-dimensionales a partir de la serie temporal original
2. Análisis del espacio reconstruido:
   • Determinación de los vecinos más próximos de cada punto
   • Estimación de la densidad puntual local
3. Previsión de la volatilidad:
   • Uso de la información sobre la densidad local para estimar la volatilidad futura

Veamos estos pasos con mayor detalle.

Reconstrucción del espacio de fases:

Vamos a imaginar que tenemos una serie temporal de precios de cierre {p(t)}. Crearemos vectores m-dimensionales de la siguiente manera:

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

donde m será la dimensionalidad de la incorporación y τ será el retardo temporal.

La elección de los valores correctos de m y τ resultará fundamental para el éxito de la reconstrucción. Por lo general, τ se selecciona utilizando métodos de información mutua o de función de autocorrelación, mientras que m se selecciona utilizando el método de los falsos vecinos más próximos.

Análisis del espacio reconstruido:

Tras la reconstrucción del espacio de fases, podremos analizar la estructura del atractor del sistema. La información sobre la densidad local de puntos en el espacio de fases será especialmente importante para prever la volatilidad.

Para cada punto x(t), hallaremos sus k vecinos más próximos (normalmente k se elige entre 5 y 20) y calcularemos la distancia media a estos vecinos. Esta distancia servirá como medida de la densidad local y, por tanto, de la volatilidad local.

Previsión de la volatilidad

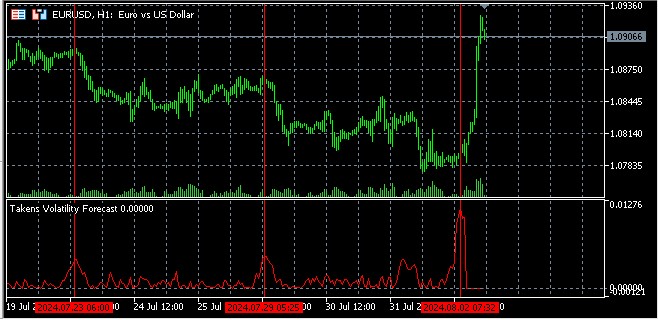
La idea básica en la previsión de la volatilidad con uso del espacio de fases reconstruido es que resulta probable que los puntos cercanos en este espacio tengan un comportamiento similar en un futuro próximo.

Para predecir la volatilidad en el momento t+h deberemos:

• Encontrar los k-vecinos más próximos del punto actual x(t) en el espacio reconstruido
• Calcular la volatilidad real de estos vecinos para h pasos por delante
• Utilizar la media de estas volatilidades como previsión

Matemáticamente, esto se puede expresar del siguiente modo:

σ̂(t+h) = (1/k) Σ σ(ti+h), donde ti son los índices de los k-vecinos más próximos de x(t)

Ventajas de este enfoque:

• Considera la dinámica no lineal del mercado
• No requiere suposiciones sobre la distribución del rendimiento
• Puede detectar patrones de volatilidad complejos

Desventajas:

• Resulta sensible a la elección de los parámetros (m, τ, k)
• Puede ser computacionalmente costoso para grandes cantidades de datos.

Implementación práctica

Vamos a crear un indicador en MQL5 que implementará este método de previsión de la volatilidad:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Métodos para determinar el retardo temporal y la dimensionalidad de la incorporación

Al reconstruir el espacio de fases usando el teorema de Takens, resulta fundamental elegir correctamente dos parámetros clave: el retardo temporal (τ) y la dimensionalidad de incorporación (m). Una elección incorrecta de estos parámetros podría provocar una reconstrucción errónea y, como consecuencia, conclusiones erróneas. Vamos a analizar dos métodos básicos para determinar estos parámetros.

Método de la función de autocorrelación (ACF) para determinar el retardo temporal

El método ACF se basa en la idea de seleccionar un retardo de tiempo τ en el que la función de autocorrelación cruza por primera vez cero o alcanza un cierto valor bajo, como 1/e del valor inicial. Esto permite elegir un retardo a partir del cual los valores sucesivos de la serie temporal se volverán suficientemente independientes entre sí.

La implementación del método ACF en MQL5 puede tener el aspecto que sigue:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

En esta aplicación, primero calcularemos la media y la varianza de la serie temporal. A continuación, para cada retardo de 1 a maxLag, calcularemos el valor de la función de autocorrelación. Una vez que el valor ACF sea menor o igual que el umbral especificado (por defecto 0,1), retornaremos este desfase como el desfase óptimo.

El método ACF presenta ventajas e inconvenientes. Por un lado, es intuitivo y resulta sencillo de aplicar. Por otra, no tiene en cuenta las dependencias no lineales de los datos, lo cual puede suponer un inconveniente importante al analizar series temporales financieras que a menudo presentan un comportamiento no lineal.

Método de información mutua (IM) para determinar el tiempo de retardo

Un enfoque alternativo para determinar el retardo óptimo sería el método de la información mutua. Este método se basa en la teoría de la información y es capaz de considerar las dependencias no lineales de los datos. La idea es elegir un retraso τ tal que se corresponda con el primer mínimo local de la función de información mutua.

La implementación del método de información mutua en MQL5 puede verse así:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

En esta implementación, primero definiremos la función CalculateMutualInformation, que calculará la información mutua entre la fila original y su versión desplazada para un retardo dado. A continuación, en la función FindOptimalLagMI, buscaremos el primer mínimo local de la información mutua buscando entre distintos valores de retardo.

El método de información mutua tiene la ventaja sobre el método ACF de que puede considerar las dependencias no lineales de los datos. Esto lo hace más adecuado para analizar series temporales financieras, que a menudo presentan un comportamiento complejo y no lineal. No obstante, este método resulta más difícil de aplicar y requiere más cálculos.

La elección entre el método ACF y el método MI dependerá de la tarea específica y de las características de los datos que vayamos a analizar. En algunos casos, podría resultar útil aplicar ambos métodos y comparar los resultados. También es importante recordar que el desfase óptimo puede cambiar con el tiempo, especialmente en el caso de las series temporales financieras, por lo que podría merecer la pena recalcular este parámetro periódicamente.

El algoritmo de falsos vecinos más próximos para determinar la dimensionalidad óptima de la incorporación

Tras determinar el retardo temporal óptimo, el siguiente paso importante en la reconstrucción del espacio de fases será elegir una dimensionalidad de incorporación adecuada. Uno de los métodos más populares para este fin será el algoritmo de falsos vecinos más próximos (FNN).

La idea del algoritmo FNN es encontrar una dimensionalidad de incorporación mínima en la que se reproduzca correctamente la estructura geométrica del atractor en el espacio de fases. El algoritmo se basa en el supuesto de que, en un espacio de fases reconstruido correctamente, los puntos cercanos deberán permanecer cercanos al pasar a un espacio de mayor dimensionalidad.

Vamos a analizar la implementación del algoritmo FNN en MQL5:

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

La función IsFalseNeighbor determina si dos puntos son falsos vecinos. Asimismo, calcula la distancia entre los puntos de la dimensionalidad actual y de una dimensionalidad una unidad mayor. Si el cambio relativo en la distancia supera un umbral determinado, los puntos se considerarán falsos vecinos.

La función principal FindOptimalEmbeddingDimension itera las dimensiones de 1 a maxDim. Para cada dimensionalidad, iteraremos todos los puntos de la serie temporal. Para cada punto encontraremos el vecino más cercano en la dimensionalidad actual. A continuación, comprobaremos si el vecino encontrado es falso usando la función IsFalseNeighbor. Luego contaremos el número total de vecinos y el número de falsos vecinos. A continuación, calcularemos la fracción de falsos vecinos. Si la fracción de falsos vecinos es inferior a un umbral de tolerancia específico, consideraremos la dimensionalidad actual como óptima y la retornaremos.

Este algoritmo tiene varios parámetros importantes. delay será el tiempo de retardo determinado previamente por el método ACF o MI. maxDim representará la dimensionalidad máxima de la incorporación considerada. threshold será el umbral de detección de falsos vecinos. tolerance será el umbral de tolerancia para la fracción de falsos vecinos. La elección de estos parámetros puede afectar significativamente al resultado, por lo que será importante experimentar con distintos valores y tener en cuenta las particularidades de los datos analizados.

El algoritmo FNN presenta una serie de ventajas. Considera la estructura geométrica de los datos en el espacio de fases. El método es bastante robusto frente al ruido en los datos. No requiere ninguna suposición previa sobre la naturaleza del sistema analizado.

Aplicación del método de previsión basado en la teoría del caos en MQL5

Una vez determinados los parámetros óptimos para la reconstrucción del espacio de fases, podremos proceder a aplicar un método de predicción basado en la teoría del caos. Este método se basa en la idea de que los estados cercanos en el espacio de fases tendrán una evolución semejante en un futuro próximo.

La idea básica del método es la siguiente: hallaremos los estados del sistema en el pasado que más se aproximen al estado actual y, basándonos en su comportamiento futuro, haremos una predicción para el estado actual. Este enfoque se conoce como método de los análogos o método del vecino más próximo.

Vamos a ver la implementación de este método en forma de indicador para MetaTrader 5. Nuestro indicador ejecutará los siguientes pasos:

1. Reconstrucción del espacio de fases usando el método del retardo temporal.
2. Búsqueda de los k-vecinos más próximos para el estado actual del sistema.
3. Predicción del valor futuro basada en el comportamiento de los vecinos hallados.

Aquí está el código del indicador que implementará este método:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

Este indicador reconstruirá el espacio de fases, encontrará los vecinos más próximos para el estado actual y utilizará sus valores futuros para la predicción. Mostrará tanto los valores reales como los previstos en un gráfico, lo que permitirá evaluar visualmente la calidad de la previsión.

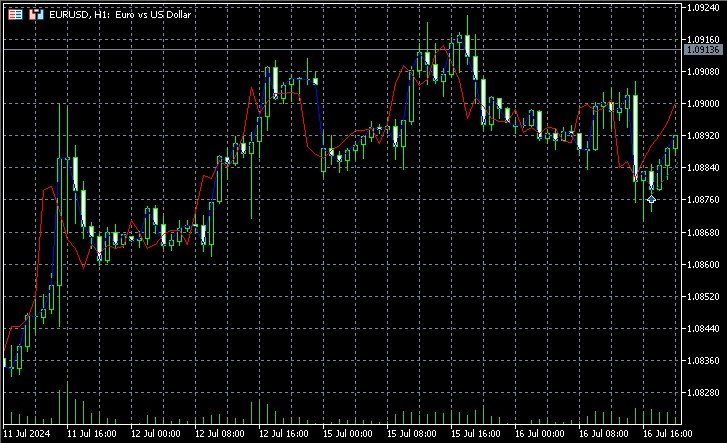
Los aspectos clave de la aplicación incluirán el uso de una media ponderada para la predicción en la que el peso de cada vecino será inversamente proporcional a su distancia del estado actual. Esto permitirá tener en cuenta que los vecinos más cercanos pueden dar una previsión más precisa. A juzgar por las capturas de pantalla, el indicador predice la dirección del movimiento del precio por adelantado, con varias barras de antelación.

Creando un asesor conceptual

Nos acercamos a la mejor parte. Aquí está nuestro código para un funcionamiento totalmente automático de la teoría del caos:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Este código es un asesor experto para MetaTrader 5 que utilizará los conceptos de la teoría del caos para predecir los precios en los mercados financieros. El EA aplicará un método de previsión basado en el método de los vecinos más próximos en el espacio de fases reconstruido.

El asesor experto tendrá los siguientes parámetros de entrada:

• InpEmbeddingDimension : dimensionalidad de la incorporación para la reconstrucción del espacio de fases (por defecto 3)
• InpTimeDelay : tiempo de retardo para la reconstrucción (por defecto 5)
• InpNeighbors : número de vecinos más próximos a predecir (por defecto 10)
• InpForecastHorizon : horizonte de previsión (por defecto 10)
• InpLookback : periodo de retrospectiva a analizar (por defecto 1000)
• InpLotSize : tamaño del lote para negociar (por defecto 0.1)

El asesor funcionará de la siguiente manera:

1. En cada nueva barra, optimizará los parámetros optimalTimeDelay y optimalEmbeddingDimension utilizando el método de la función de autocorrelación (ACF) y el algoritmo de los falsos vecinos más próximos (FNN), respectivamente.
2. A continuación, realizará una predicción de precios basada en el estado actual del sistema utilizando el método de vecinos más próximo.
3. Si el precio previsto es superior al precio actual, el asesor experto cerrará todas las ventas abiertas y abrirá una nueva posición de compra. Si el precio previsto es inferior al precio actual, el asesor experto cerrará todas las compras abiertas y abrirá una nueva posición de venta.

El asesor experto utilizará la función PredictPrice, que ejecuta los siguientes pasos:

• Reconstruye el espacio de fases usando la dimensionalidad de incorporación y el retardo de tiempo óptimos.
• Busca las distancias entre el estado actual del sistema y todos los estados en el periodo de retrospectiva.
• Ordena los estados en orden de distancia ascendente.
• Calcula la media ponderada de los precios futuros para InpNeighbors de los vecinos más próximos, donde el peso de cada vecino es inversamente proporcional a su distancia desde el estado actual.
• Retorna la media ponderada como previsión de precios.

El asesor experto también incluirá las funciones FindOptimalLagACF y FindOptimalEmbeddingDimension, que se utilizarán para optimizar los parámetros optimalTimeDelay y optimalEmbeddingDimension respectivamente.

En conjunto, este asesor ofrece un enfoque innovador de la previsión de precios en los mercados financieros utilizando conceptos de la teoría del caos. Asimismo, puede ayudar a los tráders a tomar decisiones más informadas y aumentar potencialmente el rendimiento de sus inversiones.

Pruebas con autooptimización

Vamos a considerar el trabajo de nuestro EA con varios símbolos. Bien, aquí tenemos el primer par de divisas, EURUSD, periodo de 01.01.2016:

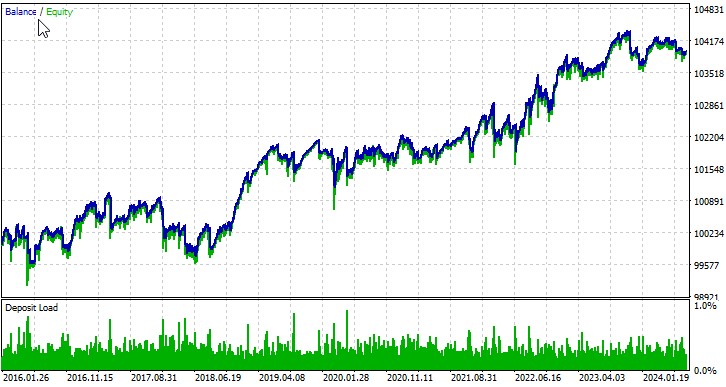
El segundo par, el dólar australiano:

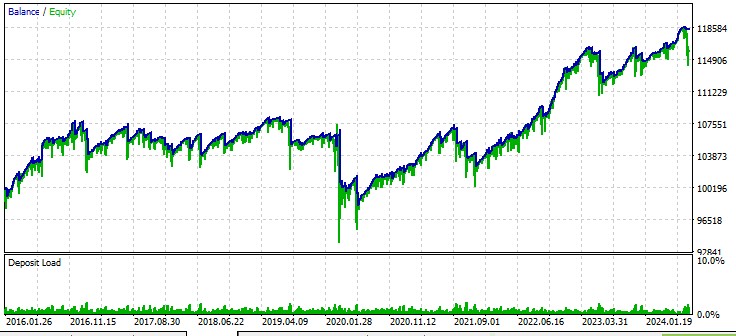
El tercer par, libra - dólar:

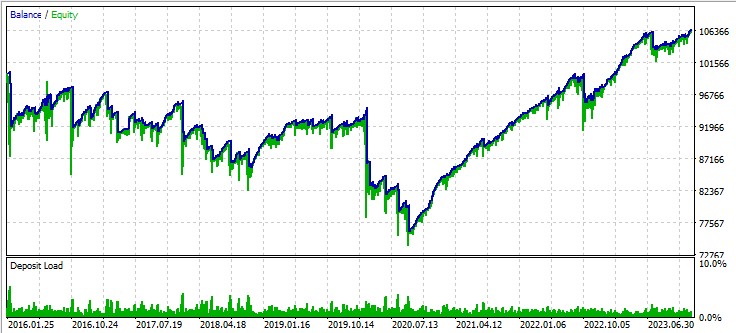
Próximos pasos

El desarrollo posterior de nuestro EA basado en la teoría del caos requerirá pruebas en profundidad y optimización. Por ello, deberemos realizar pruebas exhaustivas en diferentes intervalos temporales e instrumentos financieros para comprender mejor su eficacia en distintas condiciones de mercado. El uso de técnicas de aprendizaje automático puede ayudarnos a optimizar los parámetros de un asesor experto, aumentando su adaptabilidad a las cambiantes realidades del mercado.

Además, tendremos que prestar especial atención a la mejora del sistema de gestión de riesgos. La aplicación de una gestión dinámica del tamaño de las posiciones que considere la volatilidad actual del mercado y las previsiones de volatilidad caótica podría mejorar considerablemente la solidez de una estrategia.

Conclusión

En este artículo hemos examinado la aplicación de la teoría del caos al análisis y la previsión de los mercados financieros. Además, hemos explorado conceptos clave como la reconstrucción del espacio de fases, la determinación de la dimensionalidad de incorporación y el retardo de tiempo óptimos, y el método de predicción basado en el vecino más próximo.

El EA que hemos desarrollado demuestra el potencial del uso de la teoría del caos en el trading algorítmico. Los resultados de las pruebas realizadas con distintos pares de divisas muestran que la estrategia es capaz de generar beneficios, aunque con distintos niveles de éxito en los diferentes instrumentos.

No obstante, debemos señalar que la aplicación de la teoría del caos a las finanzas entraña una serie de complejidades. Los mercados financieros son sistemas muy complejos en los que influyen diversos factores, muchos de los cuales son difíciles o incluso imposibles de incorporar a un modelo. Además, la propia naturaleza de los sistemas caóticos hace que la previsión a largo plazo resulte fundamentalmente imposible: este es uno de los principales postulados de los investigadores serios.

En conclusión, aunque la teoría del caos no sea el "Grial" de la predicción de los mercados, supone una vía prometedora en la investigación y el desarrollo del análisis financiero y el trading algorítmico. La combinación de técnicas de la teoría del caos con otros enfoques, como el aprendizaje automático y la analítica de big data, puede abrir nuevas oportunidades, eso está más claro que el agua.