Chaostheorie im Handel (Teil 2): Tiefer tauchen

Zusammenfassung des vorherigen Artikels

Der erste Artikel befasste sich mit grundlegenden Konzepten der Chaostheorie und ihrer Anwendung auf die Analyse von Finanzmärkten. Wir haben uns mit Schlüsselkonzepten wie Attraktoren, Fraktalen und dem Schmetterlingseffekt beschäftigt und erörtert, wie sie sich in der Marktdynamik niederschlagen. Besonderes Augenmerk wurde auf die Eigenschaften chaotischer Systeme im Zusammenhang mit Finanzen und dem Konzept der Volatilität gelegt.

Außerdem haben wir die klassische Chaostheorie mit dem Ansatz von Bill Williams verglichen, um die Unterschiede zwischen der wissenschaftlichen und der praktischen Anwendung dieser Konzepte im Handel besser verstehen zu können. Der Lyapunov-Exponent als Instrument zur Analyse von Finanzzeitreihen stand im Mittelpunkt des Artikels. Wir haben sowohl seine theoretische Bedeutung als auch eine praktische Umsetzung seiner Berechnung in der Sprache MQL5 betrachtet.

Der letzte Teil des Artikels war der statistischen Analyse von Trendumkehrungen und -fortsetzungen unter Verwendung des Lyapunov-Exponenten gewidmet. Am Beispiel des EURUSD-Paares auf dem H1-Zeitrahmen haben wir gezeigt, wie diese Analyse in der Praxis angewendet werden kann, und die Interpretation der erzielten Ergebnisse diskutiert.

Der Artikel legte den Grundstein für das Verständnis der Chaostheorie im Kontext der Finanzmärkte und stellte praktische Instrumente für ihre Anwendung im Handel vor. Im zweiten Artikel werden wir unser Verständnis dieses Themas weiter vertiefen und uns auf komplexere Aspekte und deren praktische Anwendungen konzentrieren.

Als erstes werden wir über die fraktale Dimension als Maß für das Marktchaos sprechen.

Fraktale Dimension als Maß für das Marktchaos

Die fraktale Dimension ist ein Konzept, das in der Chaostheorie und bei der Analyse komplexer Systeme, einschließlich der Finanzmärkte, eine wichtige Rolle spielt. Sie bietet ein quantitatives Maß für die Komplexität und Selbstähnlichkeit eines Objekts oder Prozesses und ist daher besonders nützlich für die Bewertung des Grads der Zufälligkeit in Marktbewegungen.

Im Kontext der Finanzmärkte kann die fraktale Dimension zur Messung der „Zerklüftheit“ von Preischarten verwendet werden. Eine höhere fraktale Dimension deutet auf eine komplexere, chaotische Preisstruktur hin, während eine niedrigere Dimension auf eine gleichmäßigere, vorhersehbare Bewegung hinweisen kann.

Es gibt mehrere Methoden zur Berechnung der fraktalen Dimension. Eine der populärsten Methoden ist die Box-Counting-Methode. Bei dieser Methode wird das Chart mit einem Gitter aus Zellen unterschiedlicher Größe bedeckt und die Anzahl der Zellen gezählt, die benötigt werden, um das Chart in verschiedenen Maßstäben abzudecken.

Die Gleichung zur Berechnung der fraktalen Dimension D nach dieser Methode lautet wie folgt:

D = -lim(ε→0) [log N(ε) / log(ε)]

wobei N(ε) die Anzahl der Zellen der Größe ε ist, die zur Abdeckung des Objekts erforderlich sind.

Die Anwendung der fraktalen Dimension auf die Finanzmarktanalyse kann Händlern und Analysten zusätzliche Einblicke in die Natur der Marktbewegungen verschaffen. Zum Beispiel:

• Identifizierung von Marktmodi: Veränderungen in der fraktalen Dimension können auf Übergänge zwischen verschiedenen Marktzuständen wie Trends, flache Bewegungen oder chaotische Phasen hinweisen.
• Bewertung der Volatilität: Eine hohe fraktale Dimension geht häufig mit Zeiten erhöhter Volatilität einher.
• Vorhersage: Die Analyse der Veränderungen der fraktalen Dimension im Laufe der Zeit kann bei der Vorhersage künftiger Marktbewegungen helfen.
• Optimierung der Handelsstrategien: Das Verständnis der fraktalen Struktur des Marktes kann bei der Entwicklung und Optimierung von Handelsalgorithmen helfen.

Sehen wir uns nun die praktische Umsetzung der Berechnung der fraktalen Dimension in der Sprache MQL5 an. Wir werden einen Indikator entwickeln, der die fraktale Dimension des Preischarts in Echtzeit in MQL5 berechnet.

Der Indikator verwendet die Box-Counting-Methode zur Schätzung der fraktalen Dimension.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Fractal Dimension"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpBoxSizesCount = 5;    // Number of box sizes
input int    InpMinBoxSize    = 2;    // Minimum box size
input int    InpMaxBoxSize    = 100;  // Maximum box size
input int    InpDataLength    = 1000; // Data length for calculation

double FractalDimensionBuffer[];

int OnInit()
{
   SetIndexBuffer(0, FractalDimensionBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Fractal Dimension");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      FractalDimensionBuffer[i] = CalculateFractalDimension(close, i);
   }
   
   return(rates_total);
}

double CalculateFractalDimension(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double x[]; 
   double y[];
   ArrayResize(x, InpBoxSizesCount);
   ArrayResize(y, InpBoxSizesCount);
   
   for(int i = 0; i < InpBoxSizesCount; i++)
   {
      int boxSize = (int)MathRound(MathPow(10, MathLog10(InpMinBoxSize) + (MathLog10(InpMaxBoxSize) - MathLog10(InpMinBoxSize)) * i / (InpBoxSizesCount - 1)));
      x[i] = MathLog(1.0 / boxSize);
      y[i] = MathLog(CountBoxes(price, index, boxSize));
   }
   
   double a, b;
   CalculateLinearRegression(x, y, InpBoxSizesCount, a, b);
   
   return a; // The slope of the regression line is the estimate of the fractal dimension
}

int CountBoxes(const double &price[], int index, int boxSize)
{
   double min = price[index - InpDataLength];
   double max = min;
   
   for(int i = index - InpDataLength + 1; i <= index; i++)
   {
      if(price[i] < min) min = price[i];
      if(price[i] > max) max = price[i];
   }
   
   return (int)MathCeil((max - min) / (boxSize * _Point));
}

void CalculateLinearRegression(const double &x[], const double &y[], int count, double &a, double &b)
{
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   
   for(int i = 0; i < count; i++)
   {
      sumX += x[i];
      sumY += y[i];
      sumXY += x[i] * y[i];
      sumX2 += x[i] * x[i];
   }
   
   a = (count * sumXY - sumX * sumY) / (count * sumX2 - sumX * sumX);
   b = (sumY - a * sumX) / count;
}

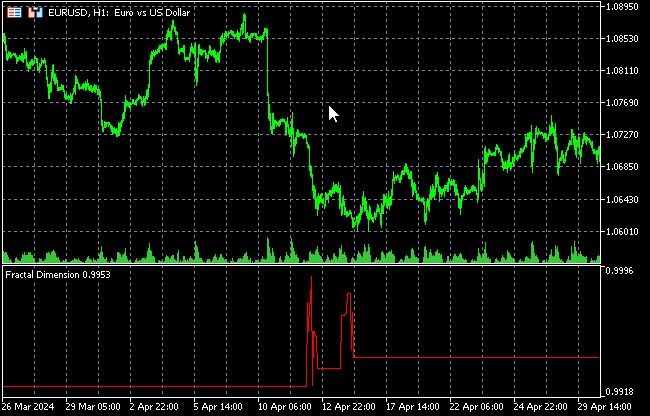
Der Indikator berechnet die fraktale Dimension eines Preischarts mit Hilfe der Box-Counting-Methode. Die fraktale Dimension ist ein Maß für die „Zerklüftheit“ oder Komplexität eines Charts und kann verwendet werden, um den Grad des Chaos auf dem Markt zu beurteilen.

Eingaben:

• InpBoxSizesCount - Anzahl der verschiedenen „Box“-Größen für die Berechnung
• InpMinBoxSize - minimale „Box“-Größe
• InpMaxBoxSize - maximale „Box“-Größe
• InpDataLength - Anzahl der für die Berechnung verwendeten Kerzen

Algorithmus für den Betrieb des Indikators:

1. Für jeden Punkt im Chart berechnet der Indikator die fraktale Dimension anhand der Daten für die letzten InpDataLength-Kerzen.
2. Die Box-Counting-Methode wird mit verschiedenen „Box“-Größen von InpMinBoxSize bis InpMaxBoxSize angewendet.
3. Die Anzahl der „Boxen“, die erforderlich ist, um die Chart abzudecken, wird für jede „Box“-Größe berechnet.
4. Es wird ein Abhängigkeitsdiagramm zwischen dem Logarithmus der Anzahl der „Boxen“ und dem Logarithmus der Größe der „Box“ erstellt.
5. Die Steigung der Kurve wird mit Hilfe der linearen Regressionsmethode berechnet, die eine Schätzung der fraktalen Dimension darstellt.

Änderungen in der fraktalen Dimension können eine Änderung des Marktmodus signalisieren.

Wiederholungsanalyse zur Aufdeckung verborgener Muster in Kursbewegungen

Die Rekursionsanalyse ist eine leistungsstarke Methode der nichtlinearen Zeitreihenanalyse, die effektiv zur Untersuchung der Dynamik von Finanzmärkten eingesetzt werden kann. Dieser Ansatz ermöglicht es uns, wiederkehrende Muster in komplexen dynamischen Systemen, zu denen die Finanzmärkte zweifellos gehören, zu visualisieren und zu quantifizieren.

Das wichtigste Instrument der Rekurrenzanalyse ist die Rekurrenzkurve. Dieses Diagramm ist eine visuelle Darstellung der sich wiederholenden Zustände eines Systems im Laufe der Zeit. In einem Rekursionsdiagramm wird ein Punkt (i, j) eingefärbt, wenn die Zustände zu den Zeitpunkten i und j in einem bestimmten Sinne ähnlich sind.

Gehen Sie folgendermaßen vor, um ein Rekursionsdiagramm für eine finanzielle Zeitreihe zu erstellen:

1. Rekonstruktion des Phasenraums: Mit Hilfe der Verzögerungsmethode transformieren wir die eindimensionale Preiszeitreihe in einen mehrdimensionalen Phasenraum.
2. Bestimmung der Ähnlichkeitsschwelle: Wir wählen ein Kriterium, nach dem wir zwei Zustände als ähnlich einstufen.
3. Konstruktion der Rekursionsmatrix: Für jedes Paar von Zeitpunkten bestimmen wir, ob die entsprechenden Zustände ähnlich sind.
4. Visualisierung: Wir stellen die Rekursionsmatrix als zweidimensionales Bild dar, wobei ähnliche Zustände durch Punkte gekennzeichnet sind.

Anhand von Rekursionsdiagrammen können wir verschiedene Arten von Dynamik in einem System erkennen:

• Homogene Regionen zeigen stationäre Perioden an.
• Diagonale Linien zeigen deterministische Dynamik an.
• Vertikale und horizontale Strukturen können auf laminare Bedingungen hinweisen.
• Das Fehlen einer Struktur ist charakteristisch für einen Zufallsprozess.

Um die Strukturen in einem Rekursionsdiagramm zu quantifizieren, werden verschiedene Rekursionsmaße verwendet, wie z. B. der prozentuale Anteil der Rekursion, die Entropie der Diagonalen, die maximale Länge einer Diagonalen und andere.

Die Anwendung der Rekursionsanalyse auf finanzielle Zeitreihen kann helfen:

1. Identifizierung verschiedener Marktzustände (Trend, Flaute, chaotischer Zustand).
2. Moduswechsel erkennen.
3. Bewertung der Vorhersagbarkeit des Marktes in verschiedenen Zeiträumen.
4. Verborgene zyklische Muster aufdecken.

Für die praktische Umsetzung der Rekursionsanalyse im Handel können wir einen Indikator in der Sprache MQL5 entwickeln, der ein Rekursionsdiagramm erstellt und Rekursionsmaße in Echtzeit berechnet. Ein solcher Indikator kann als zusätzliches Instrument für Handelsentscheidungen dienen, insbesondere wenn er mit anderen Methoden der technischen Analyse kombiniert wird.

Im nächsten Abschnitt werden wir uns eine spezifische Implementierung eines solchen Indikators ansehen und erörtern, wie seine Messwerte im Rahmen einer Handelsstrategie zu interpretieren sind.

Indikator für die Wiederholungsanalyse in MQL5

Der Indikator setzt die Methode der Rekursionsanalyse zur Untersuchung der Dynamik der Finanzmärkte um. Es berechnet drei Schlüsselmaße der Wiederholung: Wiederholungsgrad, Determinismus und Laminarität.

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 3
#property indicator_plots   3
#property indicator_label1  "Recurrence Rate"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Determinism"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_label3  "Laminarity"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrGreen

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 1;     // Time delay
input int    InpThreshold          = 10;    // Threshold (in points)
input int    InpWindowSize         = 200;   // Window size

double RecurrenceRateBuffer[];
double DeterminismBuffer[];
double LaminarityBuffer[];

int minRequiredBars;

int OnInit()
{
   SetIndexBuffer(0, RecurrenceRateBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, DeterminismBuffer, INDICATOR_DATA);
   SetIndexBuffer(2, LaminarityBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, 4);
   IndicatorSetString(INDICATOR_SHORTNAME, "Recurrence Analysis");
   
   minRequiredBars = InpWindowSize + (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   if(rates_total < minRequiredBars) return(0);
   
   int start = (prev_calculated > 0) ? MathMax(prev_calculated - 1, minRequiredBars - 1) : minRequiredBars - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      CalculateRecurrenceMeasures(close, rates_total, i, RecurrenceRateBuffer[i], DeterminismBuffer[i], LaminarityBuffer[i]);
   }
   
   return(rates_total);
}

void CalculateRecurrenceMeasures(const double &price[], int price_total, int index, double &recurrenceRate, double &determinism, double &laminarity)
{
   if(index < minRequiredBars - 1 || index >= price_total)
   {
      recurrenceRate = 0;
      determinism = 0;
      laminarity = 0;
      return;
   }

   int windowStart = index - InpWindowSize + 1;
   int matrixSize = InpWindowSize - (InpEmbeddingDimension - 1) * InpTimeDelay;
   
   int recurrenceCount = 0;
   int diagonalLines = 0;
   int verticalLines = 0;
   
   for(int i = 0; i < matrixSize; i++)
   {
      for(int j = 0; j < matrixSize; j++)
      {
         bool isRecurrent = IsRecurrent(price, price_total, windowStart + i, windowStart + j);
         if(isRecurrent)
         {
            recurrenceCount++;
            
            // Check for diagonal lines
            if(i > 0 && j > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j - 1))
               diagonalLines++;
            
            // Check for vertical lines
            if(i > 0 && IsRecurrent(price, price_total, windowStart + i - 1, windowStart + j))
               verticalLines++;
         }
      }
   }
   
   recurrenceRate = (double)recurrenceCount / (matrixSize * matrixSize);
   determinism = (recurrenceCount > 0) ? (double)diagonalLines / recurrenceCount : 0;
   laminarity = (recurrenceCount > 0) ? (double)verticalLines / recurrenceCount : 0;
}

bool IsRecurrent(const double &price[], int price_total, int i, int j)
{
   if(i < 0 || j < 0 || i >= price_total || j >= price_total) return false;

   double distance = 0;
   for(int d = 0; d < InpEmbeddingDimension; d++)
   {
      int offset = d * InpTimeDelay;
      if(i + offset >= price_total || j + offset >= price_total) return false;
      double diff = price[i + offset] - price[j + offset];
      distance += diff * diff;
   }
   distance = MathSqrt(distance);
   
   return (distance <= InpThreshold * _Point);
}

Hauptmerkmale des Indikators:

Der Indikator wird in einem separaten Fenster unterhalb des Kurscharts angezeigt und verwendet drei Puffer zum Speichern und Anzeigen von Daten. Der Indikator berechnet drei Metriken: Wiederholungsrate (blaue Linie), die den Gesamtgrad der Wiederholung anzeigt, Determinismus (rote Linie), der ein Maß für die Vorhersagbarkeit des Systems ist, und Laminarität (grüne Linie), die die Tendenz des Systems bewertet, in einem bestimmten Zustand zu bleiben.

Zu den Indikatoreingaben gehören InpEmbeddingDimension (Voreinstellung 3), die die Einbettungsdimension für die Phasenraumrekonstruktion festlegt, InpTimeDelay (Voreinstellung 1) für die Zeitverzögerung während der Rekonstruktion, InpThreshold (Voreinstellung 10) für die Zustandsähnlichkeitsschwelle in Punkten und InpWindowSize (Voreinstellung 200) für die Einstellung der Größe des Analysefensters.

Der Betriebsalgorithmus des Indikators basiert auf der Verzögerungsmethode zur Rekonstruktion des Phasenraums aus einer eindimensionalen Zeitreihe von Preisen. Für jeden Punkt im Analysefenster wird seine „Wiederholung“ im Verhältnis zu anderen Punkten berechnet. Anschließend werden auf der Grundlage der erhaltenen wiederkehrenden Struktur drei Maßnahmen berechnet: Wiederholungsrate, die den Anteil der Wiederholungspunkte an der Gesamtzahl der Punkte bestimmt, Determinismus, der den Anteil der Wiederholungspunkte angibt, die diagonale Linien bilden, und Laminarität, die den Anteil der Wiederholungspunkte schätzt, die vertikale Linien bilden.

Anwendung des Einbettungstheorems von Takens bei der Volatilitätsprognose

Das Einbettungstheorem von Takens ist ein grundlegendes Ergebnis in der Theorie dynamischer Systeme, das wichtige Auswirkungen auf die Analyse von Zeitreihen, einschließlich Finanzdaten, hat. Dieses Theorem besagt, dass ein dynamisches System aus den Beobachtungen nur einer Variablen mit Hilfe der Zeitverzögerungsmethode rekonstruiert werden kann.

Im Kontext der Finanzmärkte ermöglicht es das Theorem von Takens, einen mehrdimensionalen Phasenraum aus einer eindimensionalen Zeitreihe von Preisen oder Renditen zu rekonstruieren. Dies ist besonders nützlich bei der Analyse der Volatilität, die ein wesentliches Merkmal der Finanzmärkte ist.

Die grundlegenden Schritte bei der Anwendung des Theorems von Takens zur Prognose der Volatilität sind:

1. Rekonstruktion des Phasenraums:
   • Auswahl der Einbettungsdimension (m)
   • Auswahl der Zeitverzögerung (τ)
   • Erstellung m-dimensionaler Vektoren aus den ursprünglichen Zeitreihen
2. Analyse des rekonstruierten Raums:
   • Suche nach den nächsten Nachbarn für jeden Punkt
   • Schätzung der lokalen Punktdichte
3. Volatilitätsprognose:
   • Verwendung von Informationen über die lokale Dichte zur Schätzung der künftigen Volatilität

Schauen wir uns diese Schritte im Detail an.

Rekonstruktion des Phasenraums:

Wir haben eine Zeitreihe von Schlusskursen {p(t)}. Wir erstellen m-dimensionale Vektoren wie folgt:

x(t) = [p(t), p(t+τ), p(t+2τ), ..., p(t+(m-1)τ)]

wobei m eine Einbettungsdimension und τ eine Zeitverzögerung ist.

Die Wahl der richtigen Werte für m und τ ist entscheidend für eine erfolgreiche Rekonstruktion. In der Regel wird τ mit Hilfe der Methoden der gegenseitigen Information oder der Autokorrelationsfunktion und m mit Hilfe der Methode der falschen nächsten Nachbarn ausgewählt.

Analyse des rekonstruierten Raums:

Nachdem wir den Phasenraum rekonstruiert haben, können wir die Struktur des Systemattraktors analysieren. Für die Volatilitätsprognose sind Informationen über die lokale Dichte von Punkten im Phasenraum besonders wichtig.

Für jeden Punkt x(t) werden die k nächsten Nachbarn ermittelt (in der Regel wird k im Bereich von 5 bis 20 gewählt) und der durchschnittliche Abstand zu diesen Nachbarn berechnet. Dieser Abstand dient als Maß für die lokale Dichte und damit für die lokale Volatilität.

Prognose der Volatilität

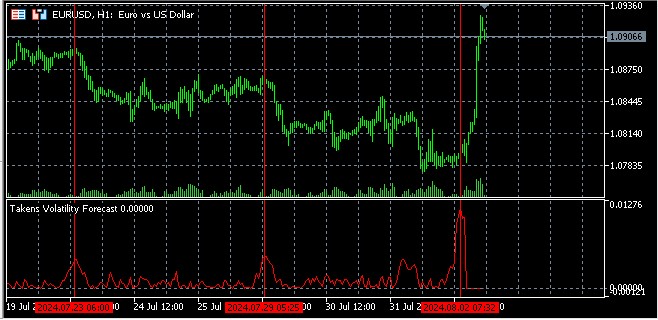
Der Grundgedanke der Volatilitätsprognose anhand des rekonstruierten Phasenraums ist, dass Punkte, die in diesem Raum nahe beieinander liegen, sich in naher Zukunft wahrscheinlich ähnlich verhalten werden.

Um die Volatilität zum Zeitpunkt t+h zu prognostizieren, gehen wir wie folgt vor:

• Wir ermitteln die k nächsten Nachbarn für den aktuellen Punkt x(t) im rekonstruierten Raum,
• berechnen die tatsächliche Volatilität für diese Nachbarn h Schritte voraus und
• verwenden den Durchschnitt dieser Volatilitäten als Prognose.

Mathematisch lässt sich dies wie folgt ausdrücken:

σ̂(t+h) = (1/k) Σ σ(ti+h), wobei ti die Indizes der k nächstgelegenen Nachbarn von x(t) sind.

Die Vorteile dieses Ansatzes:

• Sie berücksichtigt die nichtlineare Marktdynamik
• Sie erfordert keine Annahmen über die Verteilung der Erträge
• Wir sind in der Lage, komplexe Muster in der Volatilität zu erkennen

Nachteile

• Er ist empfindlich gegenüber der Wahl der Parameter (m, τ, k)
• Er kann bei großen Datenmengen sehr rechenintensiv sein.

Umsetzung

Erstellen wir einen MQL5-Indikator, der diese Methode der Volatilitätsprognose implementiert:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_label1  "Predicted Volatility"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double PredictedVolatilityBuffer[];

int OnInit()
{
   SetIndexBuffer(0, PredictedVolatilityBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Takens Volatility Forecast");
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedVolatilityBuffer[i] = PredictVolatility(close, i);
      }
   }
   
   return(rates_total);
}

double PredictVolatility(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }
   
   double distances[];
   ArrayResize(distances, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double sum = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         sum += diff * diff;
      }
      distances[i] = sqrt(sum);
   }
   
   int sortedIndices[];
   ArrayCopy(sortedIndices, distances);
   ArraySort(sortedIndices);
   
   double sumVolatility = 0;
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - sortedIndices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double futureReturn = (price[neighborIndex + InpForecastHorizon] - price[neighborIndex]) / price[neighborIndex];
      sumVolatility += MathAbs(futureReturn);
   }
   
   return sumVolatility / InpNeighbors;
}

Verfahren zur Bestimmung einer Zeitverzögerung und eines Einbettungsmaßes

Bei der Rekonstruktion des Phasenraums mit Hilfe des Takens'schen Theorems ist es entscheidend, zwei Schlüsselparameter richtig zu wählen: die Zeitverzögerung (τ) und die Einbettungsdimension (m). Eine falsche Wahl dieser Parameter kann zu einer fehlerhaften Rekonstruktion und in der Folge zu falschen Schlussfolgerungen führen. Es gibt zwei Hauptmethoden zur Bestimmung dieser Parameter.

Autokorrelationsfunktion (ACF) Methode zur Bestimmung der Zeitverzögerung

Die Methode beruht auf der Idee, eine Zeitverzögerung τ zu wählen, bei der die Autokorrelationsfunktion zum ersten Mal durch Null geht oder einen bestimmten niedrigen Wert erreicht, z. B. 1/e des Anfangswerts. So kann man eine Verzögerung wählen, bei der aufeinanderfolgende Werte der Zeitreihe ausreichend unabhängig voneinander werden.

Die Implementierung der ACF-Methode in MQL5 kann wie folgt aussehen:

int FindOptimalLagACF(const double &price[], int maxLag, double threshold = 0.1)
{
   int size = ArraySize(price);
   if(size <= maxLag) return 1;
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += price[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(price[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (price[i] - mean) * (price[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

Bei dieser Implementierung berechnen wir zunächst den Mittelwert und die Varianz der Zeitreihe. Anschließend wird für jede Verzögerung von 1 bis maxLag der Wert der Autokorrelationsfunktion berechnet. Sobald der ACF-Wert kleiner oder gleich einem bestimmten Schwellenwert (Standardwert 0,1) ist, wird diese Verzögerung als optimale Zeitverzögerung zurückgegeben.

Die ACF-Methode hat ihre Vor- und Nachteile. Einerseits ist es einfach und intuitiv zu implementieren. Andererseits werden nichtlineare Abhängigkeiten in den Daten nicht berücksichtigt, was bei der Analyse von Finanzzeitreihen, die häufig ein nichtlineares Verhalten aufweisen, ein erheblicher Nachteil sein kann.

Methode der gegenseitigen Information (MI) zur Bestimmung der Zeitverzögerung

Diese Methode basiert auf der Informationstheorie und ist in der Lage, nicht-lineare Abhängigkeiten in Daten zu berücksichtigen. Die Idee ist, eine Verzögerung τ zu wählen, die dem ersten lokalen Minimum der gegenseitigen Informationsfunktion entspricht.

Die Implementierung der Methode der gegenseitigen Information in MQL5 könnte wie folgt aussehen:

double CalculateMutualInformation(const double &price[], int lag, int bins = 20)
{
   int size = ArraySize(price);
   if(size <= lag) return 0;
   
   double minPrice = price[ArrayMinimum(price)];
   double maxPrice = price[ArrayMaximum(price)];
   double binSize = (maxPrice - minPrice) / bins;
   
   int histogram[];
   ArrayResize(histogram, bins * bins);
   ArrayInitialize(histogram, 0);
   
   int totalPoints = 0;
   
   for(int i = 0; i < size - lag; i++)
   {
      int bin1 = (int)((price[i] - minPrice) / binSize);
      int bin2 = (int)((price[i + lag] - minPrice) / binSize);
      if(bin1 >= 0 && bin1 < bins && bin2 >= 0 && bin2 < bins)
      {
         histogram[bin1 * bins + bin2]++;
         totalPoints++;
      }
   }
   
   double mutualInfo = 0;
   for(int i = 0; i < bins; i++)
   {
      for(int j = 0; j < bins; j++)
      {
         if(histogram[i * bins + j] > 0)
         {
            double pxy = (double)histogram[i * bins + j] / totalPoints;
            double px = 0, py = 0;
            for(int k = 0; k < bins; k++)
            {
               px += (double)histogram[i * bins + k] / totalPoints;
               py += (double)histogram[k * bins + j] / totalPoints;
            }
            mutualInfo += pxy * MathLog(pxy / (px * py));
         }
      }
   }
   
   return mutualInfo;
}

int FindOptimalLagMI(const double &price[], int maxLag)
{
   double minMI = DBL_MAX;
   int optimalLag = 1;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double mi = CalculateMutualInformation(price, lag);
      if(mi < minMI)
      {
         minMI = mi;
         optimalLag = lag;
      }
      else if(mi > minMI)
      {
         break;
      }
   }
   
   return optimalLag;
}

In dieser Implementierung definieren wir zunächst die Funktion CalculateMutualInformation, die die gegenseitige Information zwischen der ursprünglichen Reihe und ihrer verschobenen Version für eine bestimmte Verzögerung berechnet. Anschließend wird mit der Funktion FindOptimalLagMI das erste lokale Minimum der gegenseitigen Information gesucht, indem über verschiedene Werte für eine Verzögerung iteriert wird.

Die Methode der gegenseitigen Information hat gegenüber der ACF-Methode den Vorteil, dass sie in der Lage ist, nicht-lineare Abhängigkeiten in den Daten zu berücksichtigen. Dadurch eignet es sich besser für die Analyse von Finanzzeitreihen, die oft ein komplexes, nichtlineares Verhalten aufweisen. Diese Methode ist jedoch komplizierter zu implementieren und erfordert mehr Berechnungen.

Die Wahl zwischen der ACF- und der MI-Methode hängt von der spezifischen Aufgabe und den Merkmalen der zu analysierenden Daten ab. In manchen Fällen kann es sinnvoll sein, beide Methoden anzuwenden und die Ergebnisse zu vergleichen. Es ist auch wichtig, daran zu denken, dass sich die optimale Zeitverzögerung im Laufe der Zeit ändern kann, insbesondere bei finanziellen Zeitreihen, sodass es ratsam sein kann, diesen Parameter in regelmäßigen Abständen neu zu berechnen.

Algorithmus für falsche nächste Nachbarn zur Bestimmung der optimalen Einbettungsdimension

Sobald die optimale Zeitverzögerung bestimmt wurde, ist der nächste wichtige Schritt bei der Rekonstruktion des Phasenraums die Wahl einer geeigneten Einbettungsdimension. Eine der populärsten Methoden für diesen Zweck ist der Algorithmus der Falschen Nächsten Nachbarn (FNN).

Die Idee des FNN-Algorithmus ist es, eine solche minimale Einbettungsdimension zu finden, dass die geometrische Struktur des Attraktors im Phasenraum korrekt wiedergegeben wird. Der Algorithmus basiert auf der Annahme, dass in einem korrekt rekonstruierten Phasenraum nahe beieinander liegende Punkte auch dann nahe beieinander liegen sollten, wenn sie in einen höherdimensionalen Raum verschoben werden.

Schauen wir uns die Implementierung des FNN-Algorithmus in der Sprache MQL5 an:

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

int FindOptimalEmbeddingDimension(const double &price[], int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = ArraySize(price);
   int minRequiredSize = (maxDim - 1) * delay + 1;
   if(size < minRequiredSize) return 1;
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = price[i - k * delay] - price[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(price, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

Die Funktion IsFalseNeighbor bestimmt, ob zwei Punkte falsche Nachbarn sind. Sie berechnet den Abstand zwischen Punkten in der aktuellen Dimension und in der Dimension, die um eins größer ist. Wenn die relative Abstandsänderung einen bestimmten Schwellenwert überschreitet, werden die Punkte als falsche Nachbarn betrachtet.

Die Hauptfunktion FindOptimalEmbeddingDimension iteriert durch die Dimensionen von 1 bis maxDim. Für jede Dimension werden alle Punkte der Zeitreihe durchlaufen. Für jeden Punkt wird der nächstgelegene Nachbar in der aktuellen Dimension gesucht. Dann prüfen wir mit der Funktion IsFalseNeighbor, ob der gefundene Nachbar falsch ist. Wir zählen die Gesamtzahl der Nachbarn und die Anzahl der falschen Nachbarn. Anschließend berechnen wir den Anteil der falschen Nachbarn. Liegt der Anteil der falschen Nachbarn unter der angegebenen Toleranzschwelle, wird die aktuelle Dimension als optimal angesehen und zurückgegeben.

Der Algorithmus hat mehrere wichtige Parameter. delay — eine Zeitverzögerung, die zuvor durch die Methoden ACF oder MI bestimmt wurde. maxDim — maximale zu berücksichtigende Einbettungsdimension. threshold — Schwellenwert für die Erkennung falscher Nachbarn. tolerance — Toleranzschwelle für den Anteil der falschen Nachbarn. Die Wahl dieser Parameter kann das Ergebnis erheblich beeinflussen, daher ist es wichtig, mit verschiedenen Werten zu experimentieren und die Besonderheiten der zu analysierenden Daten zu berücksichtigen.

Der FNN-Algorithmus hat eine Reihe von Vorteilen. Dabei wird die geometrische Struktur der Daten im Phasenraum berücksichtigt. Die Methode ist recht robust gegenüber Rauschen in den Daten. Sie erfordert keine vorherigen Annahmen über die Art des untersuchten Systems.

Implementierung der auf der Chaostheorie basierenden Prognosemethode in MQL5

Sobald wir die optimalen Parameter für die Rekonstruktion des Phasenraums bestimmt haben, können wir mit der Umsetzung der auf der Chaostheorie basierenden Vorhersagemethode beginnen. Diese Methode beruht auf der Vorstellung, dass nahe gelegene Zustände im Phasenraum in naher Zukunft eine ähnliche Entwicklung nehmen werden.

Die Grundidee der Methode ist folgende: Wir finden die Zustände des Systems in der Vergangenheit, die dem aktuellen Zustand am nächsten kommen. Auf der Grundlage ihres zukünftigen Verhaltens erstellen wir eine Prognose für den aktuellen Zustand. Dieser Ansatz wird als analoge Methode oder Methode der nächsten Nachbarn bezeichnet.

Schauen wir uns die Implementierung dieser Methode als Indikator für MetaTrader 5 an. Der Indikator führt die folgenden Schritte aus:

1. Rekonstruktion des Phasenraums mit Hilfe der Zeitverzögerungsmethode.
2. Suche nach den k nächsten Nachbarn für den aktuellen Zustand des Systems.
3. Vorhersage des zukünftigen Wertes auf der Grundlage des Verhaltens der gefundenen Nachbarn.

Hier ist der Code des Indikators, der diese Methode implementiert:

#property copyright "Copyright 2024, Evgeniy Shtenco"
#property link      "https://www.mql5.com/en/users/koshtenko"
#property version   "1.00"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_plots   2
#property indicator_label1  "Actual"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_label2  "Predicted"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed

input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period

double ActualBuffer[];
double PredictedBuffer[];

int OnInit()
{
   SetIndexBuffer(0, ActualBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PredictedBuffer, INDICATOR_DATA);
   
   IndicatorSetInteger(INDICATOR_DIGITS, _Digits);
   IndicatorSetString(INDICATOR_SHORTNAME, "Chaos Theory Predictor");
   
   return(INIT_SUCCEEDED);
}

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start = MathMax(prev_calculated, InpLookback + InpEmbeddingDimension * InpTimeDelay + InpForecastHorizon);
   
   for(int i = start; i < rates_total; i++)
   {
      ActualBuffer[i] = close[i];
      if (i >= InpEmbeddingDimension * InpTimeDelay && i + InpForecastHorizon < rates_total)
      {
         PredictedBuffer[i] = PredictPrice(close, i);
      }
   }
   
   return(rates_total);
}

double PredictPrice(const double &price[], int index)
{
   int vectorSize = InpEmbeddingDimension;
   int dataSize = InpLookback;

   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      int priceIndex = index - i * InpTimeDelay;
      if (priceIndex < 0) return 0;  // Prevent getting out of array
      currentVector[i] = price[priceIndex];
   }

   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);

   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         int priceIndex = index - i - j * InpTimeDelay;
         if (priceIndex < 0) return 0;  // Prevent getting out of array
         double diff = currentVector[j] - price[priceIndex];
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }

   // Custom sort function for sorting distances and indices together
   SortDistancesWithIndices(distances, indices, dataSize);

   double prediction = 0;
   double weightSum = 0;

   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index - indices[i];
      if (neighborIndex + InpForecastHorizon >= ArraySize(price)) return 0;  // Prevent getting out of array
      double weight = 1.0 / (distances[i] + 0.0001);  // Avoid division by zero
      prediction += weight * price[neighborIndex + InpForecastHorizon];
      weightSum += weight;
   }

   return prediction / weightSum;
}

void SortDistancesWithIndices(double &distances[], int &indices[], int size)
{
   for(int i = 0; i < size - 1; i++)
   {
      for(int j = i + 1; j < size; j++)
      {
         if(distances[i] > distances[j])
         {
            double tempDist = distances[i];
            distances[i] = distances[j];
            distances[j] = tempDist;

            int tempIndex = indices[i];
            indices[i] = indices[j];
            indices[j] = tempIndex;
         }
      }
   }
}

Der Indikator rekonstruiert den Phasenraum, findet die nächstgelegenen Nachbarn für den aktuellen Zustand und verwendet deren zukünftige Werte, um Vorhersagen zu treffen. Es zeigt sowohl die tatsächlichen als auch die vorhergesagten Werte in einem Chart an, sodass wir die Qualität der Vorhersage visuell beurteilen können.

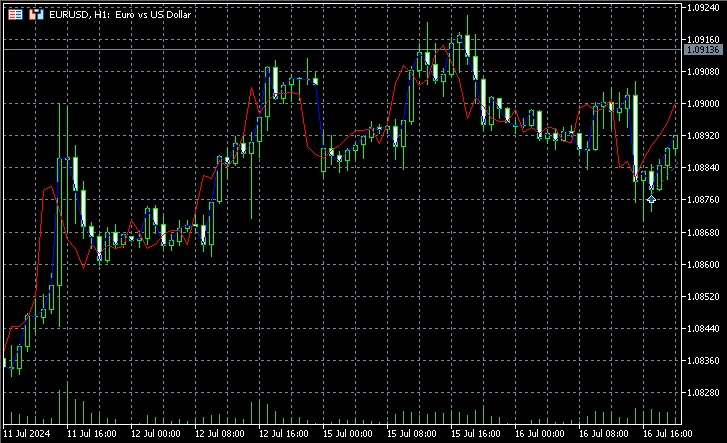
Zu den wichtigsten Aspekten der Implementierung gehört die Verwendung eines gewichteten Mittelwerts für die Vorhersage, wobei das Gewicht jedes Nachbarn umgekehrt proportional zu seiner Entfernung vom aktuellen Zustand ist. Auf diese Weise können wir berücksichtigen, dass näher gelegene Nachbarn wahrscheinlich eine genauere Prognose abgeben. Nach den Screenshots zu urteilen, sagt der Indikator die Richtung der Kursbewegung mehrere Balken im Voraus voraus.

Erstellung eines Konzepts EA

Wir haben den interessantesten Teil erreicht. Im Folgenden finden Sie den Code für eine vollautomatische Arbeit auf der Grundlage der Chaostheorie:

#property copyright "Copyright 2024, Author"
#property link      "https://www.example.com"
#property version   "1.00"
#property strict

#include <Arrays\ArrayObj.mqh>
#include <Trade\Trade.mqh>
CTrade Trade;
input int    InpEmbeddingDimension = 3;     // Embedding dimension
input int    InpTimeDelay          = 5;     // Time delay
input int    InpNeighbors          = 10;    // Number of neighbors
input int    InpForecastHorizon    = 10;    // Forecast horizon
input int    InpLookback           = 1000;  // Lookback period
input double InpLotSize            = 0.1;   // Lot size

ulong g_ticket = 0;
datetime g_last_bar_time = 0;
double optimalTimeDelay;
double optimalEmbeddingDimension;
int OnInit()
{
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
}

void OnTick()
{  
   OptimizeParameters();
   
   if(g_last_bar_time == iTime(_Symbol, PERIOD_CURRENT, 0)) return;
   g_last_bar_time = iTime(_Symbol, PERIOD_CURRENT, 0);
   
   double prediction = PredictPrice(iClose(_Symbol, PERIOD_CURRENT, 0), 0);
   Comment(prediction);
   
   if(prediction > iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close selling
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close SELL position: ", GetLastError());
         }
      }
      
      // Open buy
      double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
      ulong ticket = Trade.Buy(InpLotSize, _Symbol, ask, 0, 0, "ChaosBuy");
      if(ticket == 0)
         Print("Failed to open BUY position: ", GetLastError());
   }
   else if(prediction < iClose(_Symbol, PERIOD_CURRENT, 0))
   {
      // Close buying
      for(int i = PositionsTotal() - 1; i >= 0; i--)
      {
         if(PositionGetSymbol(i) == _Symbol && PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY)
         {
            ulong ticket = PositionGetInteger(POSITION_TICKET);
            if(!Trade.PositionClose(ticket))
               Print("Failed to close BUY position: ", GetLastError());
         }
      }
      
      // Open sell
      double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
      ulong ticket = Trade.Sell(InpLotSize, _Symbol, bid, 0, 0, "ChaosSell");
      if(ticket == 0)
         Print("Failed to open SELL position: ", GetLastError());
   }
}

double PredictPrice(double price, int index)
{
   int vectorSize = optimalEmbeddingDimension;
   int dataSize = InpLookback;
   
   double currentVector[];
   ArrayResize(currentVector, vectorSize);
   for(int i = 0; i < vectorSize; i++)
   {
      currentVector[i] = iClose(_Symbol, PERIOD_CURRENT, index + i * optimalTimeDelay);
   }
   
   double distances[];
   int indices[];
   ArrayResize(distances, dataSize);
   ArrayResize(indices, dataSize);
   
   for(int i = 0; i < dataSize; i++)
   {
      double dist = 0;
      for(int j = 0; j < vectorSize; j++)
      {
         double diff = currentVector[j] - iClose(_Symbol, PERIOD_CURRENT, index + i + j * optimalTimeDelay);
         dist += diff * diff;
      }
      distances[i] = MathSqrt(dist);
      indices[i] = i;
   }
   
   // Use SortDoubleArray to sort by 'distances' array values
   SortDoubleArray(distances, indices);
   
   double prediction = 0;
   double weightSum = 0;
   
   for(int i = 0; i < InpNeighbors; i++)
   {
      int neighborIndex = index + indices[i];
      double weight = 1.0 / (distances[i] + 0.0001);
      prediction += weight * iClose(_Symbol, PERIOD_CURRENT, neighborIndex + InpForecastHorizon);
      weightSum += weight;
   }
   
   return prediction / weightSum;
}

void SortDoubleArray(double &distances[], int &indices[])
{
    int size = ArraySize(distances);
    for(int i = 0; i < size - 1; i++)
    {
        for(int j = i + 1; j < size; j++)
        {
            if(distances[i] > distances[j])
            {
                // Swap distances
                double tempDist = distances[i];
                distances[i] = distances[j];
                distances[j] = tempDist;
                
                // Swap corresponding indices
                int tempIndex = indices[i];
                indices[i] = indices[j];
                indices[j] = tempIndex;
            }
        }
    }
}

int FindOptimalLagACF(int maxLag, double threshold = 0.1)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += series[i];
   mean /= size;
   
   double variance = 0;
   for(int i = 0; i < size; i++)
      variance += MathPow(series[i] - mean, 2);
   variance /= size;
   
   for(int lag = 1; lag <= maxLag; lag++)
   {
      double acf = 0;
      for(int i = 0; i < size - lag; i++)
         acf += (series[i] - mean) * (series[i + lag] - mean);
      acf /= (size - lag) * variance;
      
      if(MathAbs(acf) <= threshold)
         return lag;
   }
   
   return maxLag;
}

int FindOptimalEmbeddingDimension(int delay, int maxDim, double threshold = 0.1, double tolerance = 0.01)
{
   int size = InpLookback;
   double series[];
   ArraySetAsSeries(series, true);
   CopyClose(_Symbol, PERIOD_CURRENT, 0, size, series);
   
   for(int dim = 1; dim < maxDim; dim++)
   {
      int falseNeighbors = 0;
      int totalNeighbors = 0;
      
      for(int i = (dim + 1) * delay; i < size; i++)
      {
         int nearestNeighbor = -1;
         double minDist = DBL_MAX;
         
         for(int j = (dim + 1) * delay; j < size; j++)
         {
            if(i == j) continue;
            
            double dist = 0;
            for(int k = 0; k < dim; k++)
            {
               double diff = series[i - k * delay] - series[j - k * delay];
               dist += diff * diff;
            }
            
            if(dist < minDist)
            {
               minDist = dist;
               nearestNeighbor = j;
            }
         }
         
         if(nearestNeighbor != -1)
         {
            totalNeighbors++;
            if(IsFalseNeighbor(series, i, nearestNeighbor, dim, delay, threshold))
               falseNeighbors++;
         }
      }
      
      double fnnRatio = (double)falseNeighbors / totalNeighbors;
      if(fnnRatio < tolerance)
         return dim;
   }
   
   return maxDim;
}

bool IsFalseNeighbor(const double &price[], int index1, int index2, int dim, int delay, double threshold)
{
   double dist1 = 0, dist2 = 0;
   for(int i = 0; i < dim; i++)
   {
      double diff = price[index1 - i * delay] - price[index2 - i * delay];
      dist1 += diff * diff;
   }
   dist1 = MathSqrt(dist1);
   
   double diffNext = price[index1 - dim * delay] - price[index2 - dim * delay];
   dist2 = MathSqrt(dist1 * dist1 + diffNext * diffNext);
   
   return (MathAbs(dist2 - dist1) / dist1 > threshold);
}

void OptimizeParameters()
{
   double optimalTimeDelay = FindOptimalLagACF(50);
   double optimalEmbeddingDimension = FindOptimalEmbeddingDimension(optimalTimeDelay, 10);
   Print("Optimal Time Delay: ", optimalTimeDelay);
   Print("Optimal Embedding Dimension: ", optimalEmbeddingDimension);
}

Dieser Code ist ein EA für MetaTrader 5, der Konzepte der Chaostheorie nutzt, um Preise auf den Finanzmärkten zu prognostizieren. Der EA implementiert die Vorhersagemethode auf der Grundlage der Methode der nächsten Nachbarn im rekonstruierten Phasenraum.

Der EA verfügt über die folgenden Eingaben:

• InpEmbeddingDimension - Einbettungsdimension für die Phasenraumrekonstruktion (Standardwert - 3)
• InpTimeDelay - Zeitverzögerung für die Rekonstruktion (Standard - 5)
• InpNeighbors - Anzahl der nächsten Nachbarn für die Vorhersage (Standard - 10)
• InpForecastHorizon - Prognosehorizont (Standard - 10)
• InpLookback - Rückblickzeitraum für die Analyse (Standard - 1000)
• InpLotSize - Losgröße für den Handel (Standard - 0.1)

Der EA funktioniert folgendermaßen:

1. Bei jedem neuen Balken werden die Parameter optimalTimeDelay und optimalEmbeddingDimension mit der Methode der Autokorrelationsfunktion (ACF) bzw. dem Algorithmus der falschen nächsten Nachbarn (FNN) optimiert.
2. Anschließend wird eine Preisprognose auf der Grundlage des aktuellen Zustands des Systems unter Verwendung der Methode der nächsten Nachbarn erstellt.
3. Wenn die Preisprognose höher ist als der aktuelle Preis, schließt der EA alle offenen Verkaufspositionen und eröffnet eine neue Kaufposition. Wenn die Preisprognose niedriger ist als der aktuelle Preis, schließt der EA alle offenen Kaufpositionen und eröffnet eine neue Verkaufsposition.

Der EA verwendet die Funktion PredictPrice, die:

• den Phasenraum mit optimaler Einbettungsdimension und Zeitverzögerung rekonstruiert,
• die Abstände zwischen dem aktuellen Zustand des Systems und allen Zuständen im Rückblickszeitraum ermittelt,
• die Zustände nach zunehmender Entfernung sortiert.
• einen gewichteten Durchschnitt der künftigen Preise für die nächsten Nachbarn von InpNeighbors berechnet, wobei das Gewicht jedes Nachbarn umgekehrt proportional zu seiner Entfernung vom aktuellen Zustand ist und
• einen gewichteten Durchschnitt als Preisprognose zurückgibt.

Der EA enthält auch die Funktionen FindOptimalLagACF und FindOptimalEmbeddingDimension, die zur Optimierung der Parameter optimalTimeDelay bzw. optimalEmbeddingDimension verwendet werden.

Insgesamt bietet der EA einen innovativen Ansatz zur Vorhersage von Preisen auf den Finanzmärkten unter Verwendung der Konzepte der Chaostheorie. Sie kann den Händlern helfen, fundiertere Entscheidungen zu treffen und die Investitionserträge zu steigern.

Testen mit automatischer Optimierung

Betrachten wir die Arbeit unseres EA mit verschiedenen Symbolen. Das erste Währungspaar, EURUSD, Zeitraum vom 01.01.2016:

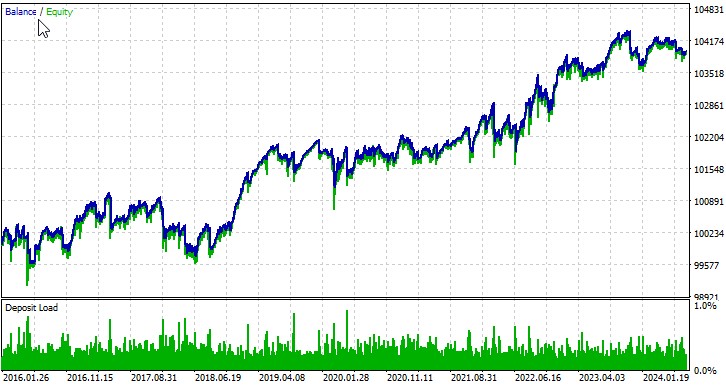
Zweites Paar, AUD:

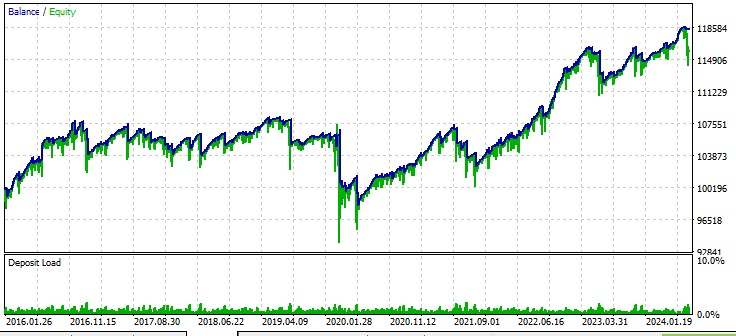
Drittes Paar: GBPUSD:

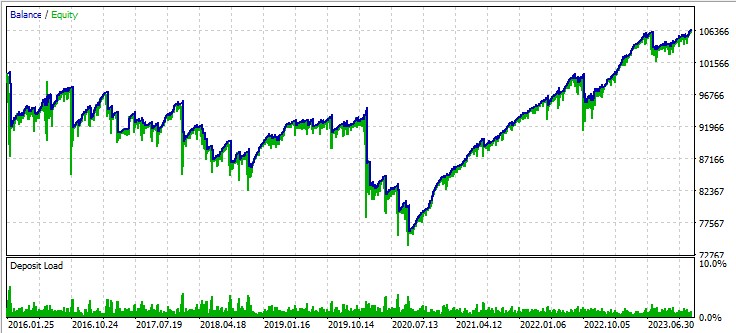
Nächste Schritte

Die weitere Entwicklung unseres auf der Chaostheorie basierenden EA erfordert eingehende Tests und Optimierungen. Um seine Effizienz unter verschiedenen Marktbedingungen besser zu verstehen, sind groß angelegte Tests mit unterschiedlichen Zeitrahmen und Finanzinstrumenten erforderlich. Der Einsatz von Methoden des maschinellen Lernens kann dazu beitragen, die EA-Parameter zu optimieren und ihre Anpassungsfähigkeit an sich ändernde Marktgegebenheiten zu erhöhen.

Besondere Aufmerksamkeit sollte der Verbesserung des Risikomanagementsystems gewidmet werden. Die Implementierung eines dynamischen Positionsgrößenmanagements, das die aktuelle Marktvolatilität und chaotische Volatilitätsprognosen berücksichtigt, kann die Widerstandsfähigkeit der Strategie erheblich verbessern.

Schlussfolgerung

In diesem Artikel haben wir uns mit der Anwendung der Chaostheorie auf die Analyse und Vorhersage der Finanzmärkte beschäftigt. Wir untersuchten Schlüsselkonzepte wie die Rekonstruktion des Phasenraums, die Bestimmung der optimalen Einbettungsdimension und Zeitverzögerung sowie die Methode der Vorhersage des nächsten Nachbarn.

Der von uns entwickelte EA demonstriert das Potenzial der Chaostheorie für den algorithmischen Handel. Die Testergebnisse für verschiedene Währungspaare zeigen, dass die Strategie in der Lage ist, Gewinne zu erzielen, wenn auch mit unterschiedlichem Erfolg für verschiedene Instrumente.

Die Anwendung der Chaostheorie auf das Finanzwesen ist jedoch mit einer Reihe von Herausforderungen verbunden. Die Finanzmärkte sind äußerst komplexe Systeme, die von vielen Faktoren beeinflusst werden, von denen viele nur schwer oder gar nicht in einem Modell berücksichtigt werden können. Außerdem macht die Natur chaotischer Systeme langfristige Vorhersagen grundsätzlich unmöglich - dies ist eines der Hauptpostulate seriöser Forscher.

Zusammenfassend lässt sich sagen, dass die Chaostheorie zwar nicht der Heilige Gral für Marktprognosen ist, aber eine vielversprechende Richtung für die weitere Forschung und Entwicklung im Bereich der Finanzanalyse und des algorithmischen Handels darstellt. Es liegt auf der Hand, dass die Kombination chaostheoretischer Methoden mit anderen Ansätzen wie maschinellem Lernen und Big-Data-Analytik neue Möglichkeiten eröffnen kann.