データサイエンスとML（第44回）：ベクトル自己回帰(VAR)を用いた外国為替OHLC時系列予測
131
0
内容
- ベクトル自己回帰(VAR)
- VARモデルの数学的背景
- VARモデルの前提
- PythonによるOHLC値へのVAR実装
- VARによるアウトオブサンプル予測
- VARを使用した自動売買ロボットの作成
- 最後に
ベクトル自己回帰(VAR)とは
VARは、複数の時系列変数の動的関係を分析するための伝統的かつ統計的な手法です。前回の記事で扱ったARIMAのような単変量自己回帰モデルは、1つの変数の過去値に基づいて予測をおこないますが、VARモデルは複数の変数間の相互関係を同時に扱います。
VARモデルでは、各変数を自分自身の過去の値だけでなく、システム内の他の変数の過去値の関数としてモデル化します。これにより、変数間の相互依存性を考慮した予測が可能となります。この記事では、VARの基礎と取引への応用について説明します。
起源
ベクトル自己回帰は、1960年代に経済学者クライヴ・グレンジャーによって初めて提案されました。グレンジャーの研究は、経済要因間の動的相互作用を理解しモデル化する基盤を築き、VARモデルは1970〜1980年代に計量経済学やマクロ経済学で急速に注目されました。
この手法は自己回帰(AR)モデルの多変量拡張です。従来のARモデル（ARIMAなど）が単一変数とそのラグ値の関係を分析するのに対し、VARは複数の変数を同時に扱います。VARモデルでは、各変数が自分自身のラグ値だけでなく、他の変数のラグ値にも回帰されます。
前回の記事ではARIMAを扱い、複数の変数を同時に学習や予測に取り入れることができないことを確認しました。本記事で扱うVARは、多変量の相互依存関係を考慮できるため、単変量予測に限定されるARIMAの課題を解決する手法と考えることができます。
このシンプルな手法（モデル）の理解を深めるため、まずはその数学的背景を見ていきましょう。
VARモデルの数学的背景
他の自己回帰モデル（AR、ARMA、ARIMA）とVARモデルの主な違いは、前者が単方向的であるのに対し（説明変数が目的変数に影響を与えるがその逆はない）、VARは双方向的である点です。
数学的には、ラグの次数をpとしたVAR(p)モデルは以下のように表されます。
ここで
- c = モデルの定数項（切片）
-
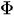= 時系列のラグiの係数 -
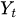= 時刻tにおける時系列の値 -
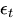= 時刻tにおける誤差項
K次元のVARモデル（変数がK個）で次数がPの場合、k=2のときは次のようになります。
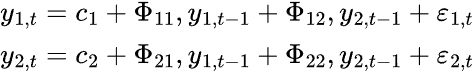
VARモデルでは複数の時系列変数が互いに影響し合うため、各時系列変数ごとに1つの方程式を持つ方程式系としてモデル化されます。以下は行列形式の式です。
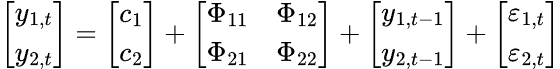
最終的にVARの方程式以下になります。
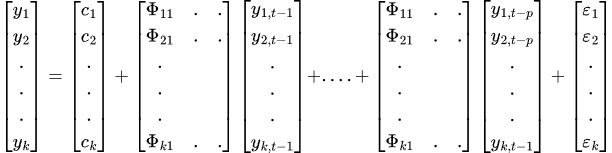
VARモデルから得られる結果の有効性と信頼性を確保するためには、いくつかの前提条件や要件を満たす必要があります。
VARモデルの前提
- 線形性
VARはその数式からも分かる通り、基本的には線形モデルです。そのため、モデルに投入するすべての変数は線形である必要があります（つまり、ラグ値の加重和として表現できること）。 - 定常性
VARモデルに使用するすべての変数は定常でなければなりません。具体的には、各時系列の平均、分散、共分散が時間とともに変化しないことを意味します。 データセットに非定常な特徴量が含まれている場合は、定常化処理をおこなう必要があります。 - 特徴量間に完全な多重共線性が存在しない
VARを効果的に機能させるためには、いずれの説明変数も他の変数の完全な線形結合であってはなりません。これはOLS推定で特異行列が発生するのを防ぐために重要です（行列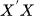
は正則（可逆）であることが必要です）。 冗長な特徴量は削除するか、正則化手法を用いて対応します。 - 残差の自己相関がない
残差は自己相関を持たない（ホワイトノイズである）ことが前提です。 残差に自己相関があると、標準誤差が歪み、統計的検定が無効になる可能性があります。 - 十分な観測値
VARモデルは、パラメータ推定のために十分なデータ量があることを前提としています。そのため、可能な限り多くの情報をモデルに与えることが、精度を高める上で重要です。
次に、PythonでこのVARモデルを実装する方法を見ていきましょう。
PythonによるOHLC値へのVAR実装
まず、Pythonで必要な依存パッケージをすべてインストールします。必要なパッケージは、添付ファイルのrequirements.txtに記載されています。
pip install -r requirements.txt
Import文
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import warnings # Suppress all warnings warnings.filterwarnings("ignore") sns.set_style("darkgrid")
まず、MetaTrader 5からOpen、High、Low、Close (OHLC)値をインポートします。
symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 if not mt5.symbol_select(symbol, True): print("Failed to select and add a symbol to the MarketWatch, Error = ",mt5.last_error) quit() rates = mt5.copy_rates_from_pos(symbol, timeframe, 1, 10000) df = pd.DataFrame(rates) # convert rates into a pandas dataframe df
以下が出力です。
| time | open | high | low | close | tick_volume | spread | real_volume | |
|---|---|---|---|---|---|---|---|---|
| 0 | 611280000 | 1.00780 | 1.01050 | 1.00630 | 1.00760 | 821 | 50 | 0 |
| 1 | 611366400 | 0.99620 | 1.00580 | 0.99100 | 0.99600 | 2941 | 50 | 0 |
| 2 | 611452800 | 0.99180 | 0.99440 | 0.98760 | 0.99190 | 1351 | 50 | 0 |
| 3 | 611539200 | 0.99330 | 0.99370 | 0.99310 | 0.99310 | 101 | 50 | 0 |
| 4 | 611798400 | 0.97360 | 0.97360 | 0.97320 | 0.97360 | 81 | 50 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 9995 | 1748390400 | 1.13239 | 1.13453 | 1.12838 | 1.12910 | 153191 | 0 | 0 |
| 9996 | 1748476800 | 1.12918 | 1.13849 | 1.12105 | 1.13659 | 191948 | 0 | 0 |
| 9997 | 1748563200 | 1.13630 | 1.13901 | 1.13127 | 1.13470 | 186924 | 0 | 0 |
| 9998 | 1748822400 | 1.13435 | 1.14500 | 1.13412 | 1.14436 | 168697 | 0 | 0 |
| 9999 | 1748908800 | 1.14385 | 1.14549 | 1.13642 | 1.13708 | 147424 | 0 | 0 |
日足データから1万本のバーを取得しました。モデルの前提条件に従うと、十分なデータ量が確保できていると言えます。
今回はOHLC値に対してモデルを適用したいため、その他の列は削除します。
ohlc_df = df.drop(columns=[ "time", "tick_volume", "spread", "real_volume" ]) ohlc_df
OHLC値のみを使用することにしたのは、これらの値の間には強い相関関係があり、モデルがその関係を捉える手助けになると考えたからです。加えて、これら4つの変数は金融商品の基本的な特徴量として抽出可能です。
ARは特徴量の定常性を前提とします。OHLC値は通常非定常なので、一階差分（前値との差分）を取って定常化します。
stationary_df = pd.DataFrame() for col in df.columns: stationary_df["Diff_"+col] = df[col].diff() stationary_df.dropna(inplace=True) stationary_df
以下が出力です。
| Diff_Open | Diff_High | Diff_Low | Diff_Close | |
|---|---|---|---|---|
| 1 | 0.00080 | 0.00180 | -0.01670 | -0.00950 |
| 2 | -0.00960 | -0.00840 | -0.01370 | -0.01880 |
| 3 | -0.01870 | -0.01930 | -0.00350 | -0.00190 |
| 4 | -0.00180 | -0.00210 | -0.00590 | -0.00870 |
| 5 | -0.00890 | -0.00310 | -0.01300 | -0.01200 |
| ... | ... | ... | ... | ... |
必要に応じて、新たに得られた変数が定常であるかどうかを確認することもできます。
from statsmodels.tsa.stattools import adfuller for col in stationary_df.columns: result = adfuller(stationary_df[col]) print(f'{col} p-value: {result[1]}')
以下が出力です。
Diff_Open p-value: 0.0 Diff_High p-value: 1.0471939301334604e-28 Diff_Low p-value: 1.1015540451195308e-23 Diff_Close p-value: 0.0
データを定常とみなすには、p-valueが0.05未満である必要があります。今回のデータではp-valueは0.05未満であるため、現時点では問題ありません。
また、VARの前提条件に従い、特徴量間に完全な多重共線性が存在しないことを確認する必要があります。
stationary_df.corr()
以下が出力です。
| Diff_Open | Diff_High | Diff_Low | Diff_Close | |
|---|---|---|---|---|
| Diff_Open | 1.000000 | 0.565829 | 0.563516 | 0.036347 |
| Diff_High | 0.565829 | 1.000000 | 0.452775 | 0.564026 |
| Diff_Low | 0.563516 | 0.452775 | 1.000000 | 0.557139 |
| Diff_Close | 0.036347 | 0.564026 | 0.557139 | 1.000000 |
特徴量間の相関行列を確認したところ問題はなさそうです。さらに、行列全体の平均絶対相関係数を確認し、|p| < 0.8であることを確認することもできます。
print("Mean absolute |p|:", np.abs(np.corrcoef(stationary_df, rowvar=False).mean()))
以下が出力です。
Mean absolute |p|: 0.5924538886295351 最適ラグ数の選択
先ほどの数式からも分かるように、VARモデルは過去の情報（ラグ）を用いて将来を予測します。そのため、どのラグ数を使用するのが最も適切かを決定する必要があります。幸い、statsmodelsのVAR関数には、いくつかの情報基準に基づいて最適なラグ数を推定する機能が備わっています。
今回は日足データを用いているため、30日分のラグを計算し、各情報基準の値を観察します。# Select optimal lag using AIC lag_order = model.select_order(maxlags=30) print(lag_order.summary())
以下が出力です。
VAR Order Selection (* highlights the minimums) ================================================== AIC BIC FPE HQIC -------------------------------------------------- 0 -41.87 -41.87 6.537e-19 -41.87 1 -45.15 -45.14 2.457e-20 -45.15 2 -45.63 -45.60 1.530e-20 -45.62 3 -45.85 -45.81 1.225e-20 -45.84 4 -45.99 -45.94 1.065e-20 -45.97 5 -46.18 -46.12 8.805e-21 -46.16 6 -46.24 -46.17 8.256e-21 -46.22 7 -46.28 -46.20 7.951e-21 -46.25 8 -46.31 -46.22 7.708e-21 -46.28 9 -46.34 -46.24 7.471e-21 -46.31 10 -46.36 -46.24 7.368e-21 -46.32 11 -46.41 -46.28 6.979e-21 -46.37 12 -46.42 -46.28 6.890e-21 -46.38 13 -46.44 -46.28 6.806e-21 -46.38 14 -46.45 -46.28 6.730e-21 -46.39 15 -46.45 -46.28 6.697e-21 -46.39 16 -46.46 -46.28 6.628e-21 -46.40 17 -46.49 -46.29* 6.460e-21 -46.42 18 -46.50 -46.28 6.419e-21 -46.42 19 -46.50 -46.28 6.383e-21 -46.43 20 -46.50 -46.27 6.358e-21 -46.43 21 -46.51 -46.27 6.306e-21 -46.43 22 -46.52 -46.26 6.292e-21 -46.43 23 -46.53 -46.26 6.216e-21 -46.44 24 -46.53 -46.25 6.185e-21 -46.44 25 -46.54 -46.24 6.162e-21 -46.44 26 -46.54 -46.24 6.113e-21 -46.44 27 -46.55 -46.23 6.092e-21 -46.44 28 -46.55 -46.22 6.086e-21 -46.44 29 -46.56* -46.22 6.031e-21* -46.44* 30 -46.56 -46.21 6.033e-21 -46.44 --------------------------------------------------
各行は異なるラグ次数に対応する値を示しており、アスタリスクが付いた値はその情報基準で最小値となるものです。これは、各基準に基づく「最適ラグ」を示しています。
ラグ選択の概要は以下の通りです。
- AIC：最適ラグは29（値：-46.56）
- BIC：最適ラグは17（値：-46.29）
- FPE：最適ラグは29（値：-6.031e-21）
- HQIC：最適ラグは29（値：-46.44）
一般的には、モデル選択にはAICとBICが用いられます。簡単に言うと、AICはより複雑なモデル（高いラグ数）を選びやすく、BICは複雑さに対してより強くペナルティを課すため、より単純なモデルを選びやすい傾向があります。
HQICはAICとBICの中間的な立場であり、FPEは予測誤差に焦点を当てています。
今回は、AIC基準に従って選ばれたラグ数を用いてモデルを適合させます。
# Fit the model with selected lag results = model.fit(lag_order.aic) print(results.summary())
以下が出力です。
Summary of Regression Results ================================== Model: VAR Method: OLS Date: Wed, 04, Jun, 2025 Time: 10:40:37 -------------------------------------------------------------------- No. of Equations: 4.00000 BIC: -46.2188 Nobs: 9970.00 HQIC: -46.4425 Log likelihood: 175968. FPE: 6.03280e-21 AIC: -46.5571 Det(Omega_mle): 5.75774e-21 -------------------------------------------------------------------- Results for equation diff_open ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const -0.000002 0.000013 -0.115 0.908 L1.diff_open -0.959329 0.010918 -87.867 0.000 L1.diff_high 0.009878 0.004957 1.993 0.046 L1.diff_low 0.006869 0.005010 1.371 0.170 L1.diff_close 0.995718 0.004583 217.244 0.000 L2.diff_open -0.935345 0.015071 -62.062 0.000 L2.diff_high 0.007118 0.006749 1.055 0.292 L2.diff_low 0.022288 0.006819 3.268 0.001 L2.diff_close 0.939861 0.011863 79.226 0.000 L3.diff_open -0.906595 0.018115 -50.045 0.000 L3.diff_high 0.003072 0.007954 0.386 0.699 L3.diff_low 0.018535 0.008097 2.289 0.022 L3.diff_close 0.910898 0.015703 58.006 0.000 L4.diff_open -0.898803 0.020501 -43.841 0.000 L4.diff_high 0.003670 0.008912 0.412 0.681 L4.diff_low 0.015668 0.009103 1.721 0.085 L4.diff_close 0.886824 0.018628 47.606 0.000 L5.diff_open -0.867308 0.022560 -38.445 0.000 L5.diff_high 0.001318 0.009676 0.136 0.892 L5.diff_low -0.000027 0.009942 -0.003 0.998 L5.diff_close 0.884632 0.020996 42.133 0.000 ... ... ... L29.diff_open -0.005922 0.004617 -1.283 0.200 L29.diff_high 0.007026 0.004956 1.418 0.156 L29.diff_low 0.004387 0.005005 0.876 0.381 L29.diff_close 0.035169 0.010568 3.328 0.001 ================================================================================= Results for equation diff_high ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000008 0.000048 0.165 0.869 L1.diff_open -0.010294 0.038697 -0.266 0.790 L1.diff_high -0.887555 0.017570 -50.515 0.000 L1.diff_low -0.020634 0.017757 -1.162 0.245 L1.diff_close 0.969305 0.016245 59.667 0.000 L2.diff_open 0.006028 0.053418 0.113 0.910 L2.diff_high -0.838250 0.023920 -35.043 0.000 L2.diff_low -0.057396 0.024169 -2.375 0.018 L2.diff_close 0.914246 0.042047 21.744 0.000 L3.diff_open -0.160354 0.064208 -2.497 0.013 L3.diff_high -0.807663 0.028191 -28.650 0.000 L3.diff_low -0.042960 0.028698 -1.497 0.134 L3.diff_close 0.869460 0.055659 15.621 0.000 L4.diff_open -0.168775 0.072664 -2.323 0.020 L4.diff_high -0.785399 0.031589 -24.863 0.000 L4.diff_low -0.054113 0.032265 -1.677 0.094 L4.diff_close 1.013851 0.066026 15.355 0.000 L5.diff_open -0.146275 0.079959 -1.829 0.067 L5.diff_high -0.746785 0.034295 -21.775 0.000 L5.diff_low -0.098885 0.035238 -2.806 0.005 L5.diff_close 1.012989 0.074419 13.612 0.000 ... ... ... L27.diff_open 0.020345 0.053645 0.379 0.705 L27.diff_high -0.153391 0.028136 -5.452 0.000 L27.diff_low -0.065690 0.028874 -2.275 0.023 L27.diff_close 0.251005 0.062004 4.048 0.000 L28.diff_open -0.005863 0.040235 -0.146 0.884 L28.diff_high -0.087603 0.023901 -3.665 0.000 L28.diff_low 0.008246 0.024229 0.340 0.734 L28.diff_close 0.134924 0.051754 2.607 0.009 L29.diff_open -0.000480 0.016364 -0.029 0.977 L29.diff_high -0.051136 0.017564 -2.911 0.004 L29.diff_low 0.035083 0.017741 1.977 0.048 L29.diff_close 0.054123 0.037457 1.445 0.148 ================================================================================= Results for equation diff_low ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000005 0.000047 0.101 0.920 L1.diff_open 0.024212 0.038141 0.635 0.526 L1.diff_high -0.058570 0.017317 -3.382 0.001 L1.diff_low -0.904567 0.017501 -51.686 0.000 L1.diff_close 0.976598 0.016012 60.993 0.000 L2.diff_open 0.067049 0.052650 1.274 0.203 L2.diff_high -0.084679 0.023576 -3.592 0.000 L2.diff_low -0.866233 0.023822 -36.363 0.000 L2.diff_close 0.937652 0.041442 22.626 0.000 L3.diff_open 0.065284 0.063284 1.032 0.302 L3.diff_high -0.108128 0.027785 -3.892 0.000 L3.diff_low -0.791679 0.028285 -27.989 0.000 L3.diff_close 0.844047 0.054858 15.386 0.000 L4.diff_open 0.018366 0.071619 0.256 0.798 L4.diff_high -0.116216 0.031134 -3.733 0.000 L4.diff_low -0.747223 0.031801 -23.497 0.000 L4.diff_close 0.816060 0.065076 12.540 0.000 L5.diff_open -0.040872 0.078809 -0.519 0.604 L5.diff_high -0.110998 0.033802 -3.284 0.001 L5.diff_low -0.731241 0.034731 -21.054 0.000 L5.diff_close 0.832344 0.073348 11.348 0.000 ... ... ... L29.diff_open 0.024357 0.016128 1.510 0.131 L29.diff_high 0.026179 0.017312 1.512 0.130 L29.diff_low -0.072592 0.017486 -4.151 0.000 L29.diff_close 0.051738 0.036919 1.401 0.161 ================================================================================= Results for equation diff_close ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000013 0.000071 0.185 0.853 L1.diff_open 0.037592 0.057827 0.650 0.516 L1.diff_high 0.007085 0.026256 0.270 0.787 L1.diff_low 0.011658 0.026535 0.439 0.660 L1.diff_close -0.020373 0.024276 -0.839 0.401 L2.diff_open 0.150341 0.079825 1.883 0.060 L2.diff_high -0.035345 0.035745 -0.989 0.323 L2.diff_low -0.041114 0.036117 -1.138 0.255 L2.diff_close -0.012920 0.062832 -0.206 0.837 L3.diff_open -0.000054 0.095949 -0.001 1.000 L3.diff_high -0.047439 0.042126 -1.126 0.260 L3.diff_low 0.028500 0.042884 0.665 0.506 L3.diff_close -0.113979 0.083173 -1.370 0.171 L4.diff_open -0.083562 0.108585 -0.770 0.442 L4.diff_high -0.083193 0.047204 -1.762 0.078 L4.diff_low 0.055907 0.048215 1.160 0.246 L4.diff_close 0.026375 0.098665 0.267 0.789 L5.diff_open -0.148622 0.119487 -1.244 0.214 L5.diff_high -0.065192 0.051248 -1.272 0.203 L5.diff_low 0.011819 0.052658 0.224 0.822 L5.diff_close 0.125327 0.111207 1.127 0.260 ... ... ... L29.diff_open 0.002852 0.024453 0.117 0.907 L29.diff_high -0.011652 0.026247 -0.444 0.657 L29.diff_low -0.004191 0.026511 -0.158 0.874 L29.diff_close 0.070689 0.055974 1.263 0.207 ================================================================================= Correlation matrix of residuals diff_open diff_high diff_low diff_close diff_open 1.000000 0.223818 0.241416 0.126479 diff_high 0.223818 1.000000 0.452061 0.770309 diff_low 0.241416 0.452061 1.000000 0.765777 diff_close 0.126479 0.770309 0.765777 1.000000
VARモデルは、他の統計的・従来型の時系列モデルと同様に、モデルの性能や特徴量に関する詳細な要約を提供します。この要約により、モデルの挙動を詳しく理解することができます。ここでは、上記モデルの要約を簡単に確認してみましょう。
回帰結果
-------------------------------------------------------------------- No. of Equations: 4.00000 BIC: -46.2188 Nobs: 9970.00 HQIC: -46.4425 Log likelihood: 175968. FPE: 6.03280e-21 AIC: -46.5571 Det(Omega_mle): 5.75774e-21
- No. of Equations:4、システム（モデル）が4つの内生変数、すなわちdiff_open、diff_high、diff_low、diff_closeを含んでいることを意味します。
- Nobs (Number of observations used)：今回はAIC基準を選択し、29ラグを使用したため、最初の29期間分のデータ（+1特徴量）は学習（推定）には含まれていません。これは、それ以前の値が初期ラグとして使用されるためです。
- AIC、BIC、HQIC、FPE：これらの値はすべて負の値となっており（通常の挙動です）、モデルの適合度が良好であることを示す良い指標です。
- Log Likelihood：高い正の値は、モデルの適合性が良好であることを示します。
各方程式の結果
各変数（diff_open、diff_high、diff_low、diff_close）について、次のように表示されます。
- Coefficientこれらの値は、それぞれのラグ変数（L1、L2など）が現在の値に与える影響を表しています。値が1に近いほど、その変数が現在の方程式の変数に与える正の影響が大きいことを意味し、逆に値が負の場合は負の影響があることを示します。
例：
Results for equation diff_open ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const -0.000002 0.000013 -0.115 0.908 L1.diff_open -0.959329 0.010918 -87.867 0.000
ここでの係数「-0.959329」は、昨日（ラグ1）のdiff_openが1単位増加した場合、他の変数を一定とすると本日の本日のdiff_openが0.959329単位減少することを意味します。 -
Std.Error
これらは係数推定値の精度を表します。 -
t-stat
これは統計的有意性を示す指標です。絶対値|t-stat|が大きいほど、その変数の有意性が高いことを意味します。絶対値が大きい（例：|t|>2）場合は統計的に有意と判断されます。
|(-87.867)| = +87.867と非常に大きな値であることから、ラグ1のdiff_open変数の影響は非常に有意であり、偶然によるものではないことがわかります。 -
prob
これは各係数のt値に対応するp値を示しています。特定のラグ変数が従属変数の現在の値に有意な影響を与えるかどうかを判断するために使います。
p値が0.05以下の場合、その変数は統計的に有意であるとみなされます。
残差相関行列
Correlation matrix of residuals diff_open diff_high diff_low diff_close diff_open 1.000000 0.223818 0.241416 0.126479 diff_high 0.223818 1.000000 0.452061 0.770309 diff_low 0.241416 0.452061 1.000000 0.765777 diff_close 0.126479 0.770309 0.765777 1.000000
これは各方程式間の予測誤差の相関を示しています。
diff_highとdiff_close(0.77)、およびdiff_lowとdiff_close（約0.766）の相関が高いことは、これらの変数ペアに共通する説明できない要因が影響していることを示唆しています。
VARによるアウトオブサンプル予測
前回の記事で扱ったARIMAモデルと同様に、VARを用いたアウトオブサンプル予測はやや難易度が高いです。機械学習モデルとは異なり、これらの従来型モデルは新しい情報に基づき定期的に更新する必要があります。
ここでは、この作業をおこなうための関数を作成してみましょう。
def forecast_next(model_res, symbol, timeframe): forecast = None # Get required lags for prediction rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, model_res.k_ar+1) # Get rates starting at the current bar to bars=lags used during training if rates is None or len(rates) < model_res.k_ar+1: print("Failed to get copy rates Error =", mt5.last_error()) return forecast, None # Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]].values stationary_input = np.diff(input_data, axis=0)[-model_res.k_ar:] # get the recent values equal to the number of lags used by the model try: forecast = model_res.forecast(stationary_input, steps=1) # predict the next price except Exception as e: print("Failed to forecast: ", str(e)) return forecast, None try: updated_data = np.vstack([model_res.endog, stationary_input[-1]]) # concatenate new/last datapoint to the data used during previous training updated_model = VAR(updated_data).fit(maxlags=model_res.k_ar) # Retrain the model with new data except Exception as e: print("Failed to update the model: ", str(e)) return forecast, None return forecast, updated_model
予測をおこなうには、まず初期学習済みモデルを用意し、各予測後にモデル変数を自身に再代入することで、新しい情報に基づいてモデルを更新する必要があります。
res_model = results # Initial model forecast, res_model = forecast_next(model_res=res_model, symbol=symbol, timeframe=timeframe) forecast_df = pd.DataFrame(forecast, columns=stationary_df.columns) print("next forecasted:\n", forecast_df)
以下が出力です。
next forecasted: diff_open diff_high diff_low diff_close 0 0.00435 0.003135 0.001032 -0.000655
これらすべてをクラスにラップすることで、学習と予測のプロセスを簡素化できます。
ファイル：VAR.py
import pandas as pd import numpy as np import MetaTrader5 as mt5 from statsmodels.tsa.api import VAR class VARForecaster: def __init__(self, symbol: str, timeframe: int): self.symbol = symbol self.timeframe = timeframe self.model = None def train(self, start_bar: int=1, total_bars: int=10000, max_lags: int=30): """Trains the VAR model using the collected OHLC from given bars from MetaTrader5 start_bar: int: The recent bar according to copyrates_from_pos total_bars: int: Total number of bars to use for training max_lags: int: The maximum number of lags to use """ self.max_lags = max_lags if not mt5.symbol_select(self.symbol, True): print("Failed to select and add a symbol to the MarketWatch, Error = ",mt5.last_error()) quit() rates = mt5.copy_rates_from_pos(self.symbol, self.timeframe, start_bar, total_bars) if rates is None: print("Failed to get copy rates Error =", mt5.last_error()) return if total_bars < max_lags: print(f"Failed to train, max_lags: {max_lags} must be > total_bars: {total_bars}") return train_df = pd.DataFrame(rates) # convert rates into a pandas dataframe train_df = train_df[["open", "high", "low", "close"]] stationary_df = np.diff(train_df, axis=0) # Convert OHLC values into stationary ones by differenciating them self.model = VAR(stationary_df) # Select optimal lag using AIC lag_order = self.model.select_order(maxlags=self.max_lags) print(lag_order.summary()) # Fit the model with selected lag self.model_results = self.model.fit(lag_order.aic) print(self.model_results.summary()) def forecast_next(self): """Gets recent OHLC from MetaTrader5 and predicts the next differentiated prices Returns: np.array: predicted values """ forecast = None # Get required lags for prediction rates = mt5.copy_rates_from_pos(self.symbol, self.timeframe, 0, self.model_results.k_ar+1) # Get rates starting at the current bar to bars=lags used during training if rates is None or len(rates) < self.model_results.k_ar+1: print("Failed to get copy rates Error =", mt5.last_error()) return forecast # Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]] stationary_input = np.diff(input_data, axis=0)[-self.model_results.k_ar:] # get the recent values equal to the number of lags used by the model try: forecast = self.model_results.forecast(stationary_input, steps=1) # predict the next price except Exception as e: print("Failed to forecast: ", str(e)) return forecast try: updated_data = np.vstack([self.model_results.endog, stationary_input[-1]]) # concatenate new/last datapoint to the data used during previous training updated_model = VAR(updated_data).fit(maxlags=self.model_results.k_ar) # Retrain the model with new data except Exception as e: print("Failed to update the model: ", str(e)) return forecast self.model = updated_model return forecast
これをPythonベースの自動売買ロボットにまとめてみましょう。
VARを使用した自動売買ロボットの作成
前述のクラスを用いると、次の値の予測やモデル学習が可能です。ここでは、その予測結果を取引戦略に組み込んでみましょう。
まず、前回の例では、現在の値から前の値を引いて定常化した値を使用しました。この方法でも機能しますが、実際の取引戦略に組み込むにはあまり実用的ではありません。
代わりに、始値と高値の差を計算して、ローソク足が始値からどれだけ上昇したかを把握し、始値と安値の差を計算して、ローソク足が始値からどれだけ下落したかを把握します。
これら2つの値を取得することで、1つはローソク足の上昇幅、もう1つは下降幅を追跡でき、予測結果をストップロスやテイクプロフィットの設定に活用できます。
次に、モデルで使用する特徴量を変更してみましょう。
# Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]] stationary_input = pd.DataFrame({ "high_open": input_data["high"] - input_data["open"], "open_low": input_data["open"] - input_data["low"] })
差分を取ることで得られた特徴量は、ほぼ定常変数であると考えられます（ここでは確認不要です）。
次に、メインのロボットファイル内で学習プロセスをスケジュールし、予測値を出力してみましょう。
ファイル名： VAR-TradingRobot.py
import MetaTrader5 as mt5 import schedule import time from VAR import VARForecaster symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 mt5_path = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # replace this with a desired MT5 path if not mt5.initialize(mt5_path): # initialize MetaTrader5 print("Failed to initialize MetaTrader5, error =", mt5.last_error()) quit() var_model = VARForecaster(symbol=symbol, timeframe=timeframe) var_model.train(start_bar=1, total_bars=10000, max_lags=30) # Train the VAR Model def get_next_forecast(): print(var_model.forecast_next()) schedule.every(1).minutes.do(get_next_forecast) while True: schedule.run_pending() time.sleep(60) else: mt5.shutdown()
以下が出力です。
[[0.00464001 0.00439884]]
これでhigh_openとopen_lowの2つの予測値が得られたので、次に単純移動平均(SMA)を使ったシンプルな取引戦略を作成してみましょう。
ファイル名： VAR-TradingRobot.py
import MetaTrader5 as mt5 import schedule import time import ta from VAR import VARForecaster from Trade.Trade import CTrade from Trade.SymbolInfo import CSymbolInfo from Trade.PositionInfo import CPositionInfo import numpy as np import pandas as pd symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 mt5_path = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # replace this with a desired MT5 path if not mt5.initialize(mt5_path): # initialize MetaTrader5 print("Failed to initialize MetaTrader5, error =", mt5.last_error()) quit() var_model = VARForecaster(symbol=symbol, timeframe=timeframe) var_model.train(start_bar=1, total_bars=10000, max_lags=30) # Train the VAR Model # Initlalize the trade classes MAGICNUMBER = 5062025 SLIPPAGE = 100 m_trade = CTrade(magic_number=MAGICNUMBER, filling_type_symbol=symbol, deviation_points=SLIPPAGE) m_symbol = CSymbolInfo(symbol=symbol) m_position = CPositionInfo() ##################################################### def pos_exists(pos_type: int, magic: int, symbol: str) -> bool: """Checks whether a position exists given a magic number, symbol, and the position type Returns: bool: True if a position is found otherwise False """ if mt5.positions_total() < 1: # no positions whatsoever return False positions = mt5.positions_get() for position in positions: if m_position.select_position(position): if m_position.magic() == magic and m_position.symbol() == symbol and m_position.position_type()==pos_type: return True return False def trading_strategy(): forecasts_arr = var_model.forecast_next().flatten() high_open = forecasts_arr[0] open_low = forecasts_arr[1] print(f"high_open: ",high_open, " open_low: ",open_low) # Get the information about the market rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, 50) # Get the last 50 bars information rates_df = pd.DataFrame(rates) if rates is None: print("Failed to get copy rates Error =", mt5.last_error()) return sma_buffer = ta.trend.sma_indicator(close=rates_df["close"], window=20) m_symbol.refresh_rates() if rates_df["close"].iloc[-1] > sma_buffer.iloc[-1]: # current closing price is above sma20 if pos_exists(pos_type=mt5.POSITION_TYPE_BUY, symbol=symbol, magic=MAGICNUMBER) is False: # If a buy position doesn't exist m_trade.buy(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.ask(), sl=m_symbol.ask()-open_low, tp=m_symbol.ask()+high_open) else: # if the closing price is below the moving average if pos_exists(pos_type=mt5.POSITION_TYPE_SELL, symbol=symbol, magic=MAGICNUMBER) is False: # If a buy position doesn't exist m_trade.sell(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.bid(), sl=m_symbol.bid()+high_open, tp=m_symbol.bid()-open_low) schedule.every(1).minutes.do(trading_strategy) while True: schedule.run_pending() time.sleep(60) else: mt5.shutdown()
この記事で紹介した取引クラスを用いて、同じ種類のポジションがすでに存在するかを確認します。存在しない場合に限り、同タイプのポジションを新たにオープンします。予測値high_openとopen_lowは、それぞれ買いポジションのテイクプロフィットとストップロスに使用され、売りポジションの場合は逆になります。
確認用のシグナルとして、期間20の単純移動平均(SMA)を使用します。現在の終値が移動平均を上回っていれば買いポジションを、下回っていれば売りポジションをオープンします。
以下が出力です。
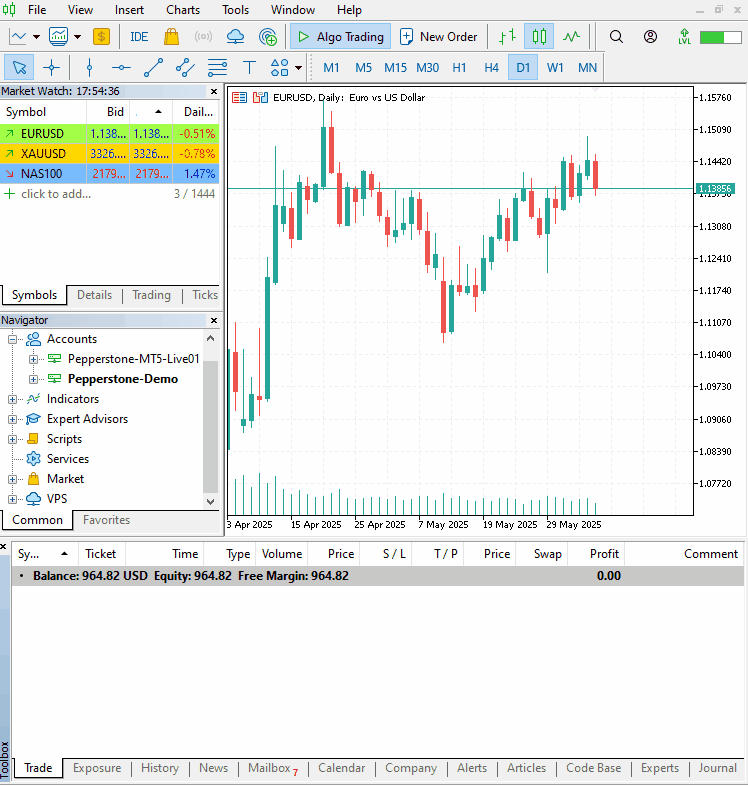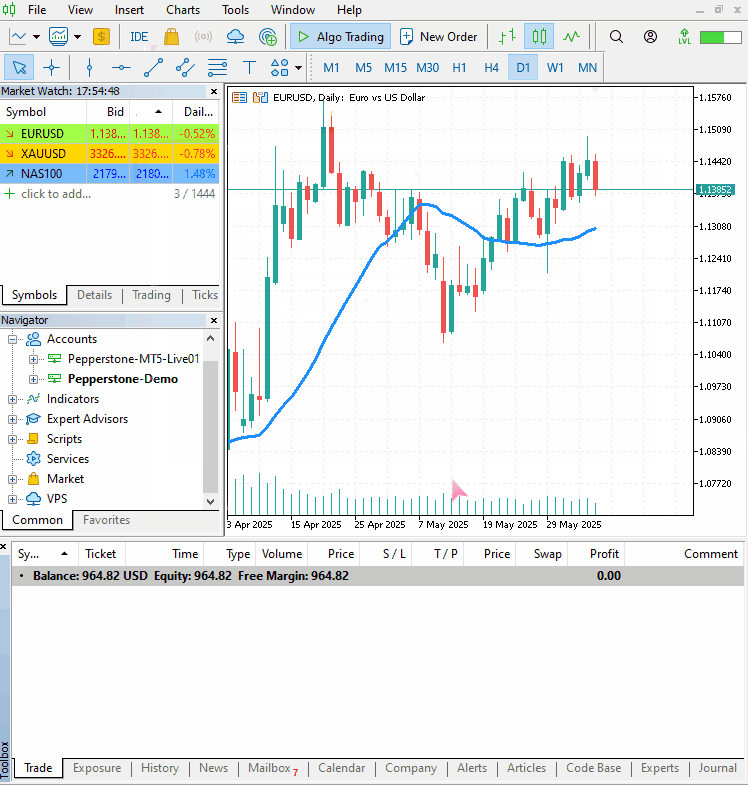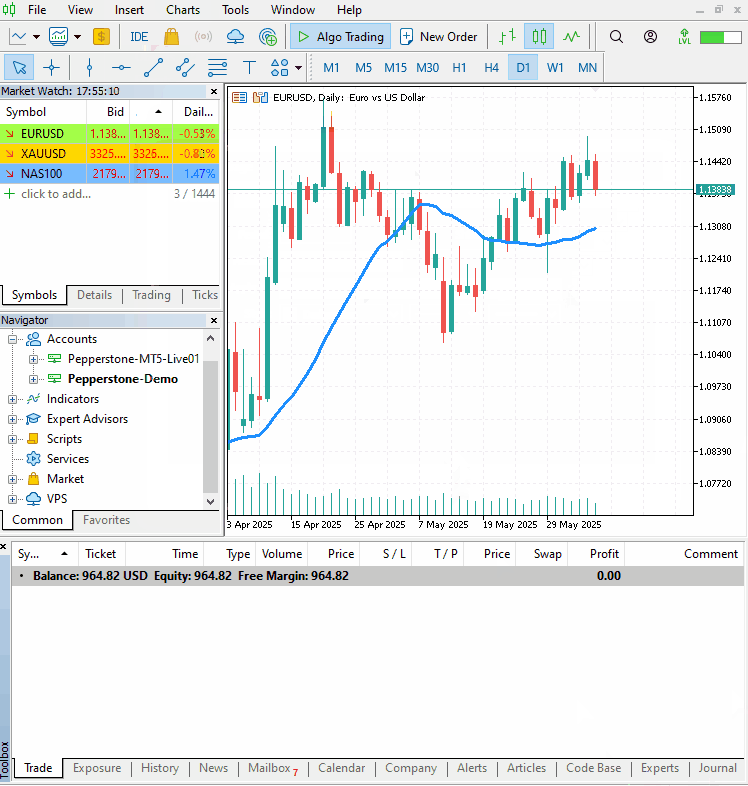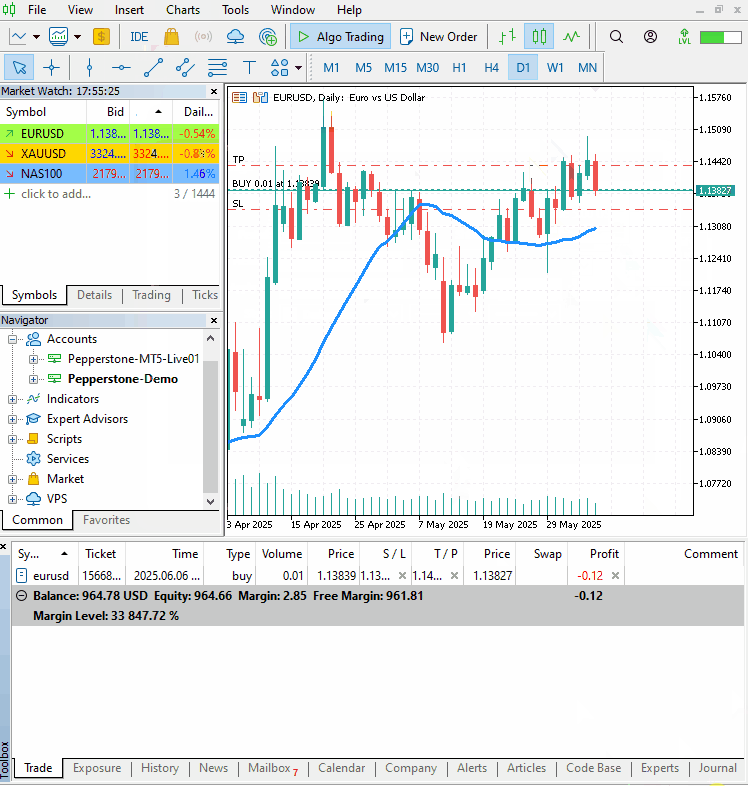
最後に
ベクトル自己回帰(VAR)は、複数の回帰変数を同時に予測できる古典的な時系列モデルとして優れた手法であり、この点は多くの機械学習モデルにはない特徴です。
このモデルの利点には以下が挙げられます。
- 柔軟なラグ構造により、変数ごとに異なるラグ長を設定できる
- 変数間の相互依存関係（動的関係）を捉えられる
- 従来の回帰モデルで必要とされる厳密な外生性の仮定が不要
一方、欠点としては以下が挙げられます。
- 定常変数に敏感で、定常データでのみ最良の性能を発揮する
- 変数とそのラグの間の線形関係を仮定しており、金融市場では必ずしも妥当とは限らない
- 多数の変数やラグを与えると過学習のリスクがある
本記事の目的は、このモデルの概要、構成、取引データへの応用方法についての理解を深めることであり、オンライン上では情報が少ないと感じたためまとめました。ご自身の用途に合わせて、さらに改良して活用してください。
ご一読、誠にありがとうございました。
今後の更新にもご注目ください。こちらのGitHubリポジトリで、MQL5言語向けの機械学習アルゴリズムの開発にぜひ貢献してください。
添付ファイルの表
| ファイル名 | 説明と使用方法 |
|---|---|
| Trade/* | Python言語でのMQL5のような取引クラス |
| error_description.py | MetaTrader 5のエラーコードの説明 |
| forex-ts-forecasting-using-var.ipynb | 学習目的の例を含むJupyter Notebook |
| VAR.py | 学習と予測をおこなうためにVARモデルを利用するクラスが |
| VAR-TradingRobot.py | VARモデルによる予測に基づいて売買取引を開始する自動売買ロボット |
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/18371
添付されたファイル |
Attachments.zip
(54.26 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
ディスカッションに移動
MQL5からDiscordへのメッセージの送信、Discord-MetaTrader 5ボットの作成
Telegramと同様に、Discordもその通信APIを使用してJSON形式の情報やメッセージを受信することができます。本記事では、MetaTrader5からDiscordの取引コミュニティに取引シグナルやアップデートを送信するためにDiscord APIをどのように利用できるかを探っていきます。
プライスアクション分析ツールキットの開発（第28回）：Opening Range Breakout Tool
各取引セッションの始まりでは、市場の方向性の偏りは、価格が初期価格幅（オープニングレンジ）を突破して初めて明確になります。本記事では、MQL5エキスパートアドバイザー(EA)を構築し、セッション開始直後の初期価格幅のブレイクアウトを自動的に検出して分析し、タイムリーでデータ駆動型のシグナルを提供して自信ある日中エントリーを可能にする方法を探ります。
MQL5で自己最適化エキスパートアドバイザーを構築する（第8回）：複数戦略分析(2)
次のフォローアップディスカッションにぜひご参加ください。今回は、これまでの2つの取引戦略を統合し、アンサンブル取引戦略（複合戦略）を作成する方法を解説します。複数の戦略を組み合わせる際のさまざまな手法を紹介するとともに、パラメータ空間の制御方法についても説明します。これにより、パラメータの数が増えても、効果的な最適化が可能な状態を保つことができます。
データサイエンスとML（第43回）：潜在ガウス混合モデル(LGMM)を用いた指標データにおける隠れパターン検出
チャートを見ていて、奇妙な感覚を覚えたことはありませんか。表面のすぐ下にパターンが隠されている気がして、もし解読できれば価格がどこに向かうか分かるかもしれない、そんな秘密のコードが存在するかもしれないという感覚です。ここで紹介するのがLGMM、マーケットの隠れたパターンを検出するモデルです。これは機械学習モデルで、隠れた市場のパターンを識別する手助けをします。
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索