インディケーター情報の測定

はじめに

機械学習は、学習データに基づき、市場の一般的な挙動を学習し、最終的にかなり正確な予測をおこないます。選択された学習アルゴリズムは、慎重に選択されたサンプルをかき分けて、意味のある情報を抽出する必要があります。このような高度なツールを使ってもうまくいかないのは、意味のある情報のほとんどがノイズの多いデータの中に隠されているからです。多くのストラテジー開発者にとって、自分たちが使っているデータセットがモデル学習に適していない可能性があることは明らかではないかもしれません。

インディケーターは、その対象となる価格系列に関する情報を提供するものと考えることができます。この前提に立つと、あるインディケーターがどれだけ情報を伝えているかを測るためにはエントロピーを使うことができます。Timothy Masters著「Testing and Tuning Market Trading Systems (TTMTS)」に記載されている手順とツールを使って、インディケーターデータの構造を評価する方法を紹介します。

インディケーターの情報を測定する理由

機械学習ツールを使ってストラテジーを練る場合、「何かが生まれるかもしれない」という期待から、あらゆる種類のデータをアルゴリズムに投げ込むことがよくあります。最終的に成功するかどうかは、モデルで使用される予測変数の品質に依存し、効果的な予測変数は通常、いくつかの特性を持ちます。そのひとつは、重要な情報コンテンツをたくさん含むということです。

モデル学習に用いる変数の情報量は重要であるが、効果的なモデル学習のための唯一の要件ではありません。そのため、情報量を測定することで、学習時にやみくもに使用していたインディケーターをスクリーニングすることができます。  ここで、エントロピーの概念が適用されます。

エントロピー

エントロピーについては すでに何回もMQL5.comで書かれています。読者の皆さんには申し訳ないのですが、もう1つ定義が必要です。ただし、これは概念の適用を理解するために不可欠であることをお約束します。これまでの記事で、エントロピー計算の歴史と導出方法を紹介しているので、ここでは簡潔にして、まず、その式から紹介することにします。

                                                        

H(X)はXのエントロピーを意味し、Xは任意の変数、例えばメッセージを表す離散変数です。メッセージの内容は、有限の値しか想定できません。式では小文字のxとなります。小文字xはメッセージの観測値であり、xの取りうるすべての値を列挙して集合Nにすることができます。

公平なサイコロの例を考えてみましょう。サイコロを振ると、ゲームの勝敗を決める情報が得られると認識できます。サイコロには1～6の数字が書かれた6つの面があります。表向きの数字のいずれかを観察できる確率は1/6です。

この例では、大文字のXはサイコロで、小文字のxはサイコロの側面に描かれた数字のどれかになります。これらはすべて集合N ={1,2,3,4,5,6} に配置されます。この式に当てはめると、このサイコロのエントロピーは0.7781となります。

                                                         

ここで、製造上の欠陥がある別のサイコロについて考えてみましょう。同じ数字が描かれた2面を持ちます。この欠陥のあるサイコロの場合、可能な値の集合Nは{1,1,3,4,5,6}となります。もう一度計算すると、平均エントロピーは0.6778となります。

                                                 

値を比較すると、情報量が減少していることがわかります。両方のサイコロを分析した結果、それぞれの値を観測する確率がすべて等しいとき、エントロピー方程式は最大値をとることがわかりました。したがって、エントロピーは、すべての可能な値の確率が等しいときに、その平均値が最大になります。

従来の実数を出力するインディケーターに欠陥のあるサイコロを与えたとしたら、大文字のXがインディケーターとなり、小文字のxはインディケーターの取り得る値の範囲となります。先に進む前に、エントロピー方程式が離散変数を厳密に扱っているため、問題があります。連続変数に変換することは可能ですが、その応用は難しいので、離散数の領域にこだわる方が簡単です。

インディケーターのエントロピーの計算

これは、値の範囲を同じ大きさの区間に分割し、それぞれの区間に入る値の数を数えることによっておこなわれます。この手法では、インディケーターのすべての値の最大範囲を列挙した元の集合は、それぞれが選択された区間である部分集合に置き換えられます。

連続変数を扱う場合、変数が取りうる値の確率の変動は、エントロピーをインディケーターに適用する際の重要な側面となるため、重要な意味を持ちます。

最初のサイコロの例に戻ります。それぞれの最終的なエントロピー値を、それぞれのnについてlog(N)で割ってみると。最初のサイコロは1、欠陥のあるサイコロは0.87という結果になりました。エントロピー値をその変数が取りうる値の数の対数で割ると、その変数の理論的な最大エントロピーに対する相対的な尺度が得られます。これは、比例エントロピーまたは相対エントロピーと呼ばれます。

この値は、インディケーターのエントロピーが理論上の最大平均値にどれだけ近いかを指し示すものであり、インディケーターを評価する上で有用なものです。最大値に近ければ近いほど良く、それ以外は機械学習には向かないインディケーターであることが示唆されます。 

                                  

上記の適用される最終式とそのコードは、以下でmql5スクリプトとして実装して記事の最後に添付してあるので、ダウンロードすることができます。このスクリプトを使えば、ほとんどのインディケーターを分析することができるようになります。

インディケーターのエントロピーを計算するスクリプト

このスクリプトは、ユーザーが調整可能な以下のパラメータを使用して起動されます。

• TimeFrame - インディケーター値を分析するために選択された時間枠です。
• IndicatorType - 分析用に組み込まれたインディケーターの1つを選択することができます。カスタムインディケーターを指定する場合は、Custom indicatorオプションを選択し、次のパラメータ値にインディケーター名を入力します。
  
• CustomIndicatorName - 事前のパラメータでCustom indicatorオプションが選択されている場合、ここに正しいインディケーター名を入力する必要があります。
  
• UseDefaults - trueに設定すると、インディケーターにハードコードされたデフォルトのユーザー入力が使用されます。
  
• IndicatorParameterTypes - インディケーターのデータ型を正しい順番で並べたカンマ区切りの文字列です。入力可能な例として、分析するインディケーターがそれぞれdouble、integer、integer、stringの4つの型の入力を受け付ける場合は単に「double, integer, integer, string」と入力すればよく、d= double, i=integer, s=string という短い形式の「d, i, i, s」もサポートされています。Enum値は，integer型にマッピングされます。
  
• IndicatorParameterValues - 前の入力と同様に、これもカンマで区切られた値のリストです。例えば、前の例では "0.5,4,5,string_value" となります。IndicatorParameterValuesとIndicatorParameterTypesのどちらかのパラメータの書式に誤りがある場合、解読できない特定の値や見つからない値は、インディケーターのデフォルト値が使用される結果となります。
  エラーメッセージは、[エキスパート]タブで確認します。なお、ここではインディケーターの名前を入れる必要はなく、カスタムインディケーターを検討している場合は、CustomIndicatorNameで指定する必要があります。
• IndicatorBuffer - 解析するインディケーターバッファです。
  
• HistoryStart - 履歴サンプルの開始日です。
  
• HistorySize - HistoryStartから相対的に分析するバーの数です。
  
• Intervals - 離散化処理に作成される区間の数です。TTMTSの著者は、数千のサンプルサイズに対して20の区間を指定し、2を絶対的な最小値として指定しています。  ここでは、サンプル数に応じて区間数を変化させることができるように実装することで、適切な値になるように自分なりに工夫しています（具体的には1000サンプルごとに51区間）。このオプションは、2より小さい値を入力した場合に利用できます。つまり、Intervalに2未満の任意の数値を設定し、分析する小節数に応じて使用するIntervalの数を変更することができます。
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

区間に選択された値についての注意点です。計算に使う区間の数を変えると、最終的なエントロピー値も変わってきます。分析をおこなう際には、使用する独立した入力の影響を最小化するために、ある程度の一貫性を持たせることが賢明でしょう。スクリプトでは、相対エントロピーの計算はEntropy.mqhファイルで定義された関数にカプセル化されています。

スクリプトは、結果のエントロピー値を[エキスパート]タブに表示するだけです。様々なビルトインおよびカスタムインディケーターに対してスクリプトを実行した結果、以下のような結果が得られました。ウィリアムパーセンテージレンジは、相対的なエントロピーが完璧に近いというのが興味深いです。市場円滑化指数のインディケーターと比較すると、散々な結果であることが分かります。

この結果をもとに、機械学習アルゴリズムに適したデータ処理をおこなうことができます。そのためには、インディケーターの統計的特性を厳密に分析する必要があります。インディケーター値の分布を調べると、偏りや外れ値などの問題が明らかになります。これらはすべて、モデルの学習を劣化させる可能性があります。

例として、上記で分析した2つのインディケーターについて、統計的な性質を調べてみます。

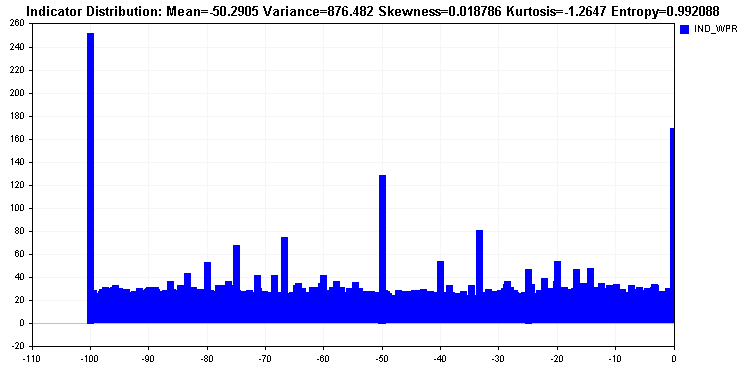
ウィリアムパーセンテージレンジの分布を見ると、ほとんどすべての値が全範囲に広がっており、マルチモーダルであることを除けば、分布はかなり均一であることがわかります。このような分布は理想的であり、エントロピー値にも反映されます。

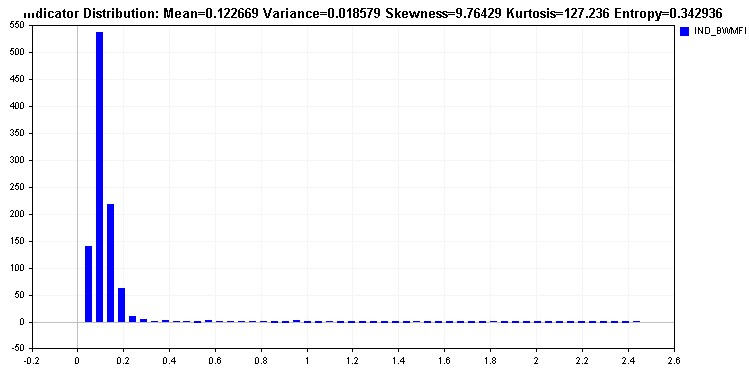
これは、マーケットファシリテーションインデックスの分布がロングテールであるのとは対照的です。このようなインディケーターは、ほとんどの学習アルゴリズムにとって問題があり、値の変換が必要です。値を変換することで、インディケーターの相対エントロピーを向上させることができるはずです。

インディケーターの情報量を向上させる

なお、インディケーターのエントロピーを増加させるような改造は、インディケーターのシグナルの精度を向上させるための手段とは見なさない方がよいです。エントロピーを高めても、役に立たないインディケーターを聖杯に変えることはできません。エントロピーを向上させることは、予測モデルに効果的に使用するためのインディケーターデータを処理することです。

このオプションは、エントロピー値が絶望的に悪く、0.5を大きく下回り、ゼロに近い場合に検討されるべきものです。上限の閾値は、純粋に任意です。許容できる最小値を選ぶのは、開発者次第です。要は、インディケーター値の分布ができるだけ均一に近いものを作るということです。変換を適用するかどうかの判断は、インディケーター値の大きさと代表的なサンプルに対しておこなわれた分析に基づいておこなわれるべきです。

適用される変換は、インディケーターの根本的な挙動を変更してはなりません。変換されたインディケーターは、生のインディケーターと同様の形状でなければなりません。例えば、谷とピークの位置は、両方の系列で類似している必要があります。そうでなければ、潜在的に有用な情報が失われる危険性があります。

テストデータの不完全性のさまざまな側面をターゲットにした変換方法が数多く存在します。ここでは、基本的な統計解析で明らかになった明らかな欠陥を修正するような、いくつかの簡単な変換を検討するのみです。前処理は、機械学習の広大な分野です。機械学習手法の応用を極めたいと考えている方には、この分野の知識を深めることをお勧めします。

いくつかの変換の効果を説明するために、様々な変換を適用するオプションがあり、また分析中のデータの分布を表示するスクリプトを紹介します。このスクリプトは、6つの変換関数の例を実装しています。

• 平方根関数変換は、過半数から大きく逸脱する時折のインディケーター値を押しつぶすのに適しています。

• 立方根変換は、負の値を持つインディケーターに最もよく適用されるもう1つ活性化関数です。

• 一方、対数変換は、先に述べた圧縮変換よりも大きな範囲で値を圧縮することができます。

• 双曲正接やロジスティック変換は、適切なスケールのデータ値に対して適用することで、無効な数値（ナンエラー）を生成する問題を回避することができます。

• 極端な変換はデータセットに極端な均一性をもたらします。類似の数値が非常に少なく、ほとんどがユニークな数値を出すインディケーターにのみ適用します。

変換されたインディケーター値を比較するスクリプト

先ほどのスクリプトと比較すると、分析するインディケーターを指定するためのユーザー入力が同じになっています。新しい入力は以下の通りです。

• DisplayTime - スクリプトは、インディケーターの分布のグラフィックを表示します。DisplayTimeは秒単位の整数値で、グラフィックが削除されるまでの表示時間です。

• ApplyTransfrom - スクリプトのモードを設定するブーリアン値です。falseの場合、スクリプトは分布を描き、サンプルの基本統計量と相対エントロピーを表示します。trueを設定すると、生のインディケーター値に変換を施し、変換前と変換後の相対エントロピー値を表示します。また、修正したサンプルの分布は、赤で曲線として描かれます。

• Select_transform - 前述の変換を列挙したもので、これを適用することでインディケーターのエントロピーを増大させることができます。

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

続けて、平方根と立方根の変換を適用した例を比較します。

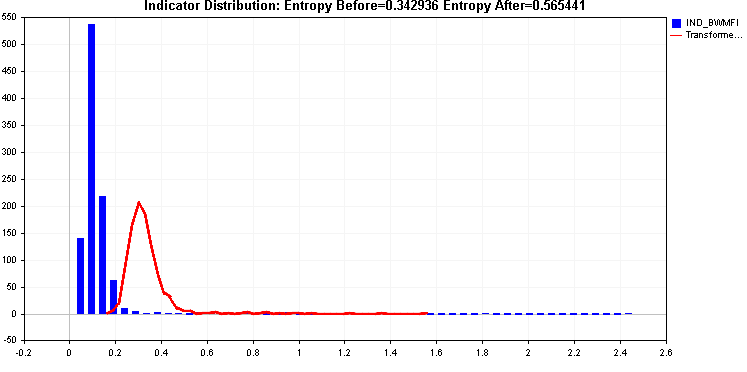
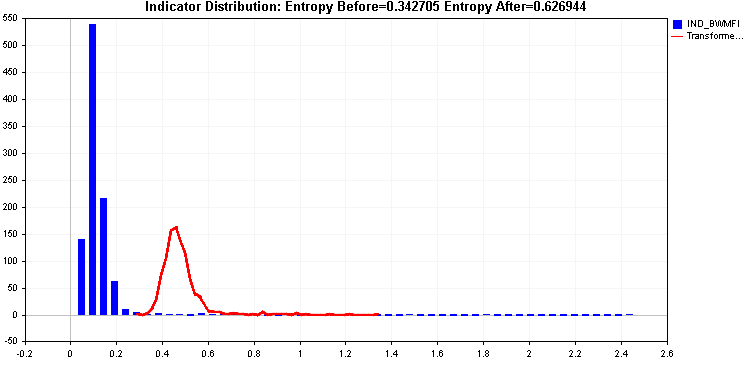
どちらもエントロピーを向上させますが、この右肩下がりが問題となり、これまで適用されてきた2つの変換では効果的に対処することができませんでした。

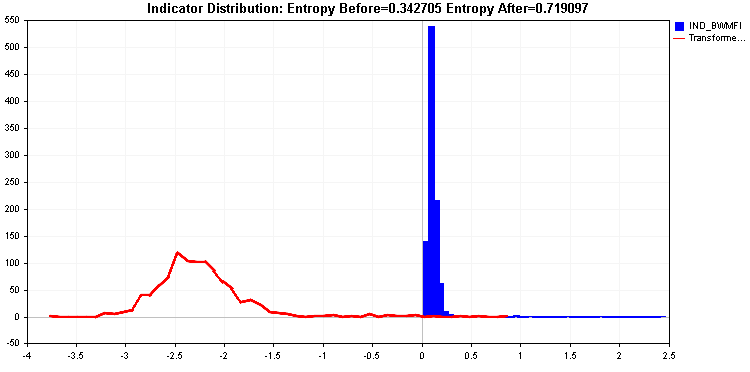
対数変換すると、さらに良いエントロピー値が得られます。それでもテールはかなり長いです。最後の手段として、極端な変換を適用することができます。

結論

予測モデルの学習に使用する前にインディケーター値を変換する必要性を評価するために、エントロピーの概念を検討した。

この概念は、2つのスクリプトで実装されました。すなわち、EntropyIndicatorAnalyisは、[エキスパート]タブにサンプルの相対エントロピーを表示します。もう1つのスクリプトであるIndicatorAnalysisは、さらに一歩進んで、生と変換後のインディケーター値の分布を描き、その前後の相対エントロピー値も表示します。

このツールは有用ですが、すべての種類のインディケーターに適用できるわけではないことに留意する必要があります。一般に、空の値を含む矢印ベースのインディケーターは、ここで説明したスクリプトには適していません。  そのような場合は、他の符号化技術が必要になります。

データ変換は、あらゆる種類の予測モデルを構築する際に考慮すべき前処理ステップのほんの一部に過ぎません。このような手法を用いることで、真にユニークな関係を抽出し、市場に打ち勝つための優位性を得ることができるのです。

ファイル名	詳細
Mql5/Include/Entropy.mqh	エントロピーを計算するための関数や、付属のスクリプトで使用するユーティリティ関数などの様々な定義が含まれるインクルードファイル
Mql5/Scripts/IndicatorAnalysis.mq5	インディケーター値の分布をエントロピーとともにグラフィック表示するスクリプト
Mql5/Scripts/EntropyIndicatorAnalysis	インディケーターのエントロピーを計算するのに使えるスクリプト