Medimos la informatividad de los indicadores

Introducción

El aprendizaje automático usa datos de entrenamiento como base para conocer el comportamiento general del mercado y, en última instancia, hacer predicciones precisas. El algoritmo de aprendizaje elegido debe pasar por una muestra cuidadosamente seleccionada para extraer información significativa. La razón por la que muchas personas no logran aplicar con éxito estas herramientas complejas es que gran parte de la información significativa se oculta entre datos ruidosos. Es posible que muchos estrategas no se den cuenta de que los conjuntos de datos usados pueden no resultar adecuados para el entrenamiento de modelos.

Los indicadores pueden considerarse proveedores de información sobre las series de precios subyacentes a las que se aplican. Partiendo de esta premisa, podemos usar la entropía para medir cuánta información transmite un indicador. Valiéndonos de los pasos y las herramientas descritos en el libro de Timothy Masters "Testing and Tuning Market Trading Systems" (TTMTS), demostraremos cómo se puede evaluar la estructura de datos de un indicador.

¿Por qué medir la informatividad de un indicador?

A menudo, al usar herramientas de aprendizaje automático para desarrollar una estrategia, en ocasiones, simplemente bombardeamos algoritmos con todo tipo de datos con la esperanza de que surja algo. En última instancia, el éxito dependerá de la calidad de los predictores usados en el modelo, y los predictores efectivos suelen tener ciertas características. Una de ellas es el contenido.

La cantidad de información en las variables usadas para entrenar el modelo es importante, pero no es el único requisito para un entrenamiento efectivo del modelo. Por ello, la medición del contenido informativo se puede utilizar para probar métricas que, de otro modo, se utilizarían a ciegas en el proceso de aprendizaje. Y aquí es donde entra en juego el concepto de entropía.

Entropía

La entropía ya ha sido tratada más de una vez en artículos en MQL5.com. Espero que el lector me permita una definición más, ya que resulta vital para comprender la aplicación del concepto. Los artículos anteriores han presentado la historia y la derivación del cálculo de la entropía, por lo que, para mayor brevedad, comenzaremos por la ecuación.

                                                        

H(X) significa la entropía de X. X es una variable discreta que representa una variable aleatoria, digamos un mensaje. El contenido del mensaje solo puede adoptar un número finito de valores. Esto se representa en la ecuación usando una x minúscula. Las x minúsculas son los valores del mensaje observados, como si todos los valores posibles de x estuvieran enumerados en el conjunto N.

Vamos a analizar un ejemplo de un dado "correcto". Podemos pensar que el dado lanzado ofrece información que determina el resultado del juego. Un dado tiene 6 caras, numeradas del 1 al 6: la probabilidad de ver cualquiera de los números es 1/6.

Usando este ejemplo, la X mayúscula sería el dado, mientras que la X minúscula podría ser cualquier número dibujado en las caras del mismo. Todos los números se ubican en el conjunto N ={ 1,2,3,4,5,6}. Aplicando la fórmula, encontramos que la entropía de este dado es 0.7781.

                                                         

Ahora vamos a considerar otro dado que tiene un defecto de fabricación. El mismo número se aplica a dos de sus caras. Para este dado defectuoso, el conjunto de N posibles valores será {1,1,3,4,5,6}. Usando nuevamente la fórmula, obtendremos una entropía promedio de 0.6778.

                                                 

Si comparamos los valores, notaremos que la informatividad ha disminuido. Al analizar ambos dados, cuando todas las probabilidades de observar cada valor posible resultan iguales, la ecuación de entropía ofrece el máximo valor posible. Por tanto, la entropía alcanza su valor medio máximo cuando las probabilidades de todos los valores posibles resultan iguales.

Si tiramos el dado defectuoso para un indicador que genera números reales tradicionales, X se convertirá en el indicador, mientras que la x minúscula será el rango de valores que puede adoptar el indicador. La ecuación de entropía trata rigurosamente con variables discretas. Podemos transformar la ecuación para que funcione con variables continuas, pero la implementación resultará complicada, por lo que será más fácil ceñirse a números discretos.

Calculando la entropía del indicador

Para aplicar la ecuación de entropía a variables continuas, deberemos discretizar los valores del indicador. Esto se logra dividiendo el rango de valores en intervalos del mismo tamaño y luego contando la cantidad de valores que caen dentro de cada intervalo. Al usar este método, el conjunto original que enumera el rango máximo de todos los valores del indicador es reemplazado por subconjuntos; cada uno de ellos representa los intervalos seleccionados.

Cuando se trata de variables continuas, la variación de las probabilidades de los posibles valores que puede asumir la variable cobra importancia, pues aporta una faceta importante a la aplicación de la entropía a los indicadores.

Regresemos al primer ejemplo con el dado de juego. Si dividimos los valores finales de entropía de cada uno por log(N) para cada uno de los respectivos n, el dado correcto dará 1, mientras que el defectuoso dará 0,87. Dividir el valor de la entropía por el logaritmo del número de valores que puede tomar una variable nos ofrece una medida relativa a la entropía máxima teórica de la variable, llamada entropía proporcional o relativa.

Es este valor el que sería útil en nuestra evaluación de los indicadores, ya que indicará lo cerca que se encuentra la entropía del indicador respecto a su valor promedio máximo teórico. Cuanto más cerca esté, mejor. De lo contrario, lo más probable es que el indicador no resulte adecuado para su uso en el aprendizaje automático. 

                                  

La ecuación final se muestra arriba, mientras que el código se implementa a continuación como un script MQL5 que se encuentra disponible para la descarga como archivo adjunto al final del artículo. Con la ayuda del script, podremos analizar la mayoría de los indicadores.

Script para calcular la entropía del indicador

El script se llama con los siguientes parámetros ajustables:

• TimeFrame - marco temporal seleccionado para analizar los valores del indicador.
• IndicatorType - aquí el usuario puede seleccionar uno de los indicadores incorporados para el análisis. Para especificar un indicador personalizado, seleccione "Indicador personalizado" e introduzca su nombre en el siguiente valor del parámetro.
  
• CustomIndicatorName - si se selecciona la opción "Indicador personalizado" para el parámetro anterior, aquí deberá introducir un nombre de indicador válido.
  
• UseDefaults - si es true, se utilizarán los parámetros de entrada personalizados por defecto, codificados rigurosamente en el indicador.
  
• IndicatorParameterTypes - se trata de una línea separada por comas que enumera los tipos de datos del indicador en el orden correcto. Por ejemplo, si el indicador que se analiza adopta cuatro parámetros de entrada del tipo double, integer, integer y string, simplemente introduzca "double, integer, integer, string". También se admite la forma abreviada "d, i, i, s". Los valores de enumeración se comparan con el tipo entero.
  
• IndicatorParameterValues - al igual que el parámetro anterior, esta también es una lista de valores separados por comas. Continuando con el ejemplo anterior, la línea se verá así: "0.5,4,5,string_value". Si hay algún error en la generación de parámetros, ya sea para IndicatorParameterValues o para IndicatorParameterTypes, esto hará que se usen valores de indicador predeterminados para cualquier valor particular que no se pueda decodificar o que falte.
  Consulte la pestaña de expertos para comprobar la existencia de mensajes de error. Tenga en cuenta que no aquí no será necesario especificar el nombre del indicador. Si estamos analizando un indicador personalizado, deberemos especificarlo en CustomIndicatorName.
• IndicatorBuffer - cuál de los búferes de indicador se va a analizar.
  
• HistoryStart - fecha de inicio de la muestra de la historia.
  
• HistorySize - número de barras para analizar en relación con HistoryStart.
  
• Intervals - número de intervalos para la muestra. El autor de TTMTS indica 20 intervalos para un tamaño de muestra de varios miles, siendo 2 el mínimo estricto. He añadido mi propio enfoque al valor apropiado al implementar la capacidad de variar el número de contenedores en relación con el tamaño de la muestra, específicamente 51 por cada 1000 muestras. Esta opción está disponible si el usuario introduce cualquier valor inferior a 2. Por lo tanto, al configurar el Intervalo en cualquier número inferior a 2, el número de intervalos usados cambiará según el número de barras analizadas.
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Tenga en cuenta el valor elegido para Intervals: el cambio en el número de intervalos utilizados en el cálculo modificará el valor de entropía final. Al realizar el análisis, sería recomendable seguir alguna secuencia para minimizar la influencia de los datos de entrada independientes. En el script, el cálculo de la entropía relativa se encapsula en una función definida en el archivo Entropy.mqh.

El script simplemente muestra el valor de entropía obtenido en la pestaña de expertos. La ejecución del script para varios indicadores integrados y personalizados da los resultados que se muestran a continuación. Resulta interesante destacar que el rango porcentual de Williams tiene una entropía relativa casi perfecta. Vamos a compararlo con Market Facilitation Index, que muestra un resultado decepcionante.

Con estos resultados, podemos tomar medidas adicionales para procesar los datos y adecuarlos a los algoritmos de aprendizaje automático. Esto implicará un análisis exhaustivo de las propiedades estadísticas del indicador. El análisis de la distribución de los valores de los indicadores revelará cualquier problema de desplazamiento, así como los valores atípicos que puedan degradar el entrenamiento del modelo.

Como ejemplo, veremos algunas de las propiedades estadísticas de los dos indicadores analizados anteriormente.

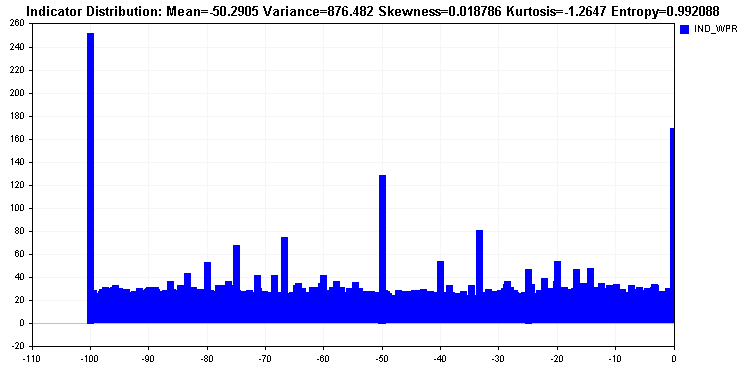
La distribución del rango de porcentaje de Williams muestra cómo casi todos los valores se distribuyen por todo el rango. Además de ser multimodal, la distribución resulta bastante uniforme. Esta distribución es ideal y se refleja en el valor de la entropía.

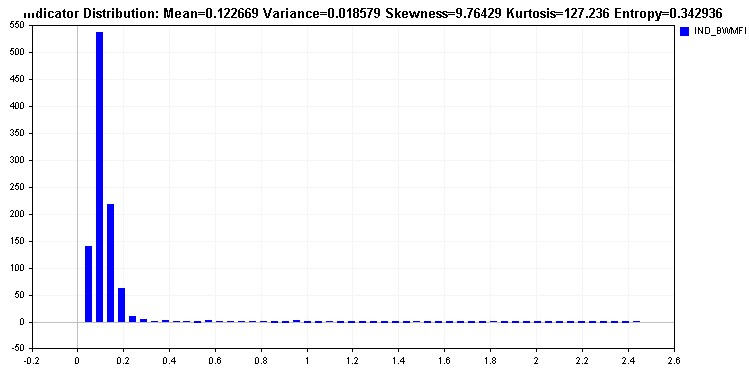
Esto es diferente de la distribución de Market Facilitation Index, que tiene una cola larga. Dicho indicador no resulta adecuado para la mayoría de los algoritmos de aprendizaje y requiere una transformación de sus valores. La transformación de los valores debería provocar una mejora en la entropía relativa del indicador.

Aumento de la informatividad del indicador

Debemos señalar que los cambios que aumentan la entropía del indicador no deben verse como una forma de mejorar la precisión de las señales proporcionadas por el mismo. El aumento de la entropía no convertirá un indicador inútil en el Santo Grial. La mejora de la entropía se relaciona con el procesamiento de los datos de los indicadores para un uso eficiente en modelos predictivos.

Esta opción debe considerarse cuando el valor de la entropía es irremediablemente malo, es decir, cualquier valor muy por debajo de 0,5 y más próximo a cero. Los umbrales superiores son puramente arbitrarios. Dependerá del desarrollador elegir un valor mínimo aceptable. El objetivo es aproximarse lo más posible a una distribución uniforme de los valores de los indicadores. La decisión de aplicar la transformación debe basarse en un análisis realizado sobre una muestra significativa y representativa de los valores del indicador.

La transformación aplicada no debe modificar el comportamiento del indicador. El indicador transformado debe tener la misma forma que el indicador sin transformar, por ejemplo, la ubicación de los valles y los picos debe ser la misma en ambas filas. Si este no fuera el caso, correríamos el riesgo de perder información potencialmente útil.

Hay muchos métodos de transformación que se focalizan en varios aspectos de las imperfecciones de los datos de prueba. Analizaremos solo unas pocas transformaciones simples destinadas a corregir defectos obvios encontrados usando análisis estadístico básico. El preprocesamiento es una rama muy amplia del aprendizaje automático. Recomendamos a cualquier persona que espere dominar la aplicación de métodos de aprendizaje automático adquirir más conocimientos en esta esfera.

Para ilustrar el efecto de algunas transformaciones, vamos a presentar un script que tiene la capacidad de aplicar varias transformaciones y también muestra la distribución de los datos analizados. El script implementa seis ejemplos de funciones de transformación:

• la transformación de la función de raíz cuadrada es adecuada para comprimir valores aleatorios de indicadores que se desvían significativamente de la mayoría.

• la transformación de raíz cúbica es otra función de compresión que funciona mejor para indicadores con valores negativos.

• mientras que la transformación logarítmica comprime los valores en mayor medida que las mencionadas anteriormente.

• La tangente hiperbólica y las transformaciones logísticas deben aplicarse a valores de datos de una escala adecuada para evitar la aparición de problemas con los números no válidos (errores nan).

• la transformación extrema provoca una uniformidad extrema en el conjunto de datos. Solo debe aplicarse a indicadores que producen en su mayoría valores únicos con muy pocos números similares.

Script para comparar valores de indicadores transformados

El script contiene los mismos datos personalizados que el anterior para especificar el indicador analizado. A continuación, describimos los nuevos parámetros de entrada:

• DisplayTime - el script muestra el gráfico de distribución del indicador. DisplayTime - valor entero en segundos que representa la cantidad de tiempo que se mostrará la imagen antes de eliminarse.

• ApplyTransfrom - valor booleano que especifica el modo de funcionamiento del script. Si es falso, el script dibujará la distribución y mostrará las estadísticas básicas de la muestra junto con la entropía relativa. Cuando es verdadero, aplicará la transformación a los valores del indicador sin procesar y mostrará los valores de entropía relativa antes y después de la transformación. La distribución de muestras modificadas se representará como una curva roja.

• select_transform - enumeración que proporciona las transformaciones descritas anteriormente, que se pueden aplicar para aumentar posiblemente la entropía del indicador.

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Vamos a continuar con los ejemplos, comparando la aplicación de las transformaciones de raíz cuadrada y raíz cúbica.

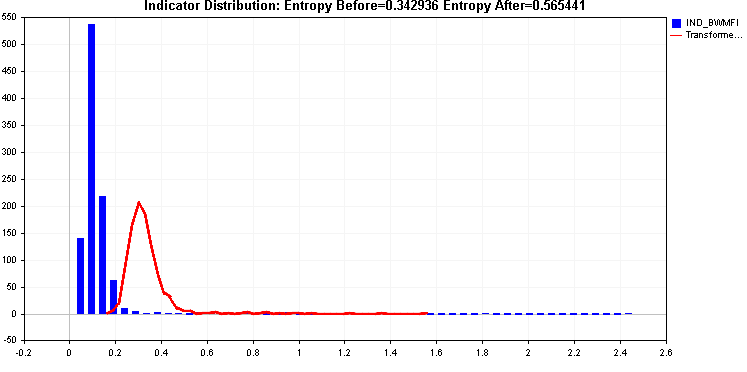
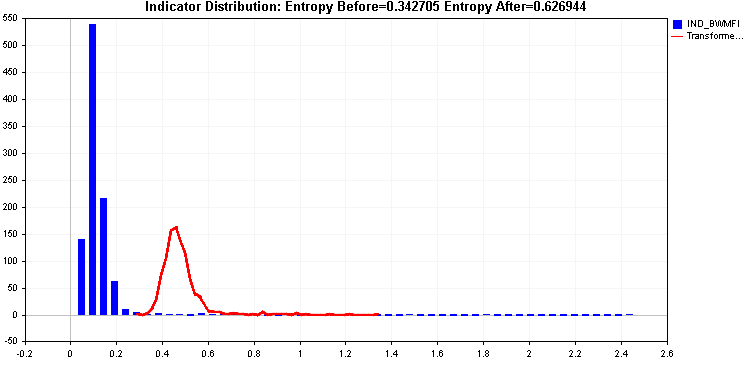
Ambos ofrecen una mejora de la entropía, pero esta cola derecha puede ser problemática. Las dos transformaciones aplicadas hasta ahora no han podido tratarla eficazmente.

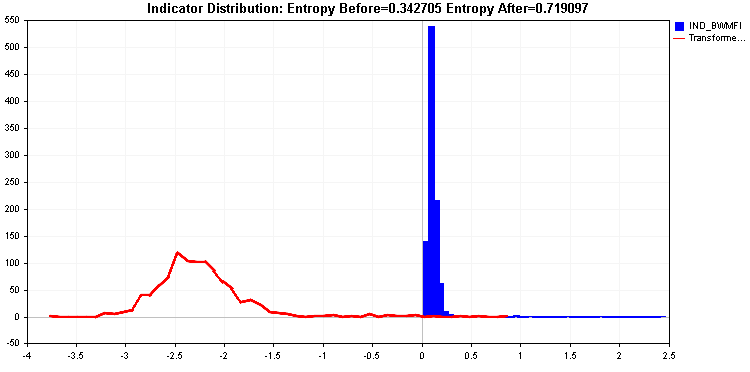
La transformación logarítmica ofrece un valor de entropía aún mejor. Pero las colas siguen resultando significativas. Como último recurso, podemos aplicar una transformación extrema.

Conclusión

Hoy hemos explorado el concepto de entropía para evaluar la necesidad de transformar los valores de los indicadores antes de usarlos en el entrenamiento de modelos predictivos.

El concepto se ha implementado en dos scripts. El primero, EntropyIndicatorAnalyis, muestra la entropía relativa de una muestra en la pestaña de expertos. El otro script, IndicatorAnalysis, va un paso más allá al dibujar la distribución de los valores del indicador sin procesar y convertidos, mostrando además los valores de entropía relativa antes y después.

Si bien las herramientas pueden ser útiles, no posible aplicarlas a todos los tipos de indicadores. Como regla general, los indicadores basados en flechas que contienen valores vacíos no resultan adecuados para los scripts descritos aquí. En dichos casos, se requerirán otros métodos de codificación.

El tema de la transformación de datos es solo uno de los posibles pasos del preprocesamiento que debemos considerar al construir cualquier modelo predictivo. El uso de estas técnicas nos ayudará a identificar relaciones verdaderamente únicas que pueden ofrecernos la ventaja necesaria para vencer a los mercados.

Nombre del archivo	Descripción
Mql5/Include/Entropy.mqh	archivo de inclusión que contiene varias definiciones de las funciones utilizadas para calcular la entropía, así como de las funciones de servicio usadas por los scripts adjuntos.
Mql5/Scripts/IndicatorAnalysis.mq5	script que representa un gráfico que muestra la distribución de los valores del indicador junto con su entropía.
Mql5/Scripts/EntropyIndicatorAnalysis	script que se puede utilizar para calcular la entropía del indicador