アンサンブル学習におけるゲーティングメカニズム

ゲーティング手法では、ゲート変数を用いてコンテキストに応じて各モデルの寄与度を動的に調整します。これらの変数は統制機構として機能し、モデル出力に戦略的な重みを与えることで、単一モデルよりも優れた予測性能を実現します。

従来のアンサンブル手法が平均、投票、スタッキングといったメカニズムに依存しているのに対し、ゲーティングはゲート変数を明示的に用いてモデル出力を統合します。このアプローチは、例えば経済動向がモデル精度に影響を及ぼす金融予測のような、モデル性能が変動しやすい場面で特に有効です。ゲート変数によってコンテキストに応じた重み付けをおこなうことで、複雑な環境における予測精度と適応性の向上が期待できます。

ゲーティング手法は一般的に、「ゲート変数に基づいて最も適した1つのモデルを選択する方法」と「すべてのモデルの出力をコンテキスト依存の重みで統合する方法」の2つに大別されます。後者は、複数のモデルの長所を活用し、より堅牢であることが多いです。以下では、両アプローチの具体例として「事前に定められた専門化」と「学習された専門化」を紹介します。

事前に定められた専門化

事前に定められた専門化は、ゲーティングの基本的な形態であり、1つの変数が複数の事前学習済み専門モデルの中から選択する際の決定要素として機能します。このアプローチは入力空間を効果的に分割し、ゲート変数の値に基づいてインスタンスを最適なモデルへと振り分けます。この概念を説明するために、変数AとBからなる2次元の特徴空間上の二値分類問題を考えてみましょう。この仮想的なシナリオでは、変数Bは2クラス間の識別にほとんど寄与しませんが、変数Aは中程度の予測力を持ち、一部のインスタンスでは正確に分類できる一方で、他では曖昧な結果となります。

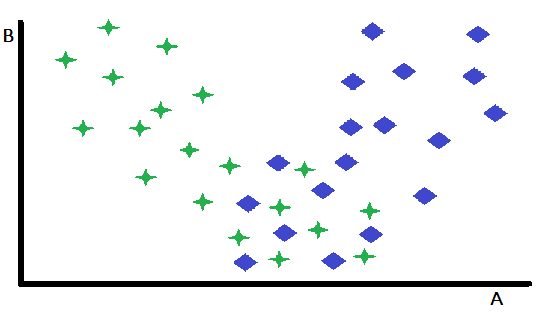
特徴の散布図を詳しく調べると、変数Bが、Aが堅牢に機能するインスタンスと、予測力が低下するインスタンスを効果的に区別していることがわかります。具体的には、Bの値が高いインスタンスは、Aを主な予測子として使用した場合に優れた分類精度を示します。この観察は、Bの閾値に基づいてデータセットを分割するという自然なパーティショニング戦略を示唆しています。この分割により、2つの異なる分類モデルの開発が可能になります。1つはB値が高いインスタンス向け、すなわちAが強力な予測子となる場合に最適化され、もう1つはB値が低いインスタンス向け、つまりAの信頼性が低くなる可能性がある場合に最適化されます。

この簡単な例はコアとなる原則を示していますが、分類が難しいインスタンスが残る場合、こうしたパーティショニングの効果は限定的になることに注意が必要です。このアプローチの主な利点は、より簡単に分類できるインスタンスを分離して効果的に対処できることです。この簡素化は、残りのより困難なデータのサブセットに対して、より高性能なモデルを開発するのにも役立ちます。ここで説明した例では概念を明確にするために1つの変数に焦点を当てていますが、実際のアプリケーションでは、適切なモデルの選択は複数の変数の値に依存する場合もあり、それらの変数は各モデルで用いられる主要な予測変数のセットに含まれることもあれば、含まれないこともあります。

学習された専門化

学習された専門化は、より高度なゲーティング手法を表します。最適な分割変数とそれに対応する閾値は事前に決定されるのではなく、データから直接学習されます。散布図を視覚的に検査することで潜在的な分割変数や閾値の予備的な洞察が得られることもありますが、このような直感的な手法は実用に耐えないことが多いです。

実際には、より体系的かつデータ駆動型のアプローチが必要です。通常は、幅広い候補となる分割変数とその閾値を探索する厳密な検索プロセスが含まれます。各候補分割変数と閾値について、データセットを分割し、そのサブセットごとにモデルを個別に学習させ、評価します。この探索と学習・評価の反復的なプロセスは、特に大規模なデータセットや複雑なモデルを扱う際に計算コストが高くなることがあります。しかし、モデル性能の向上がそのコスト増を正当化する場合が多いです。

さらに、最適な分割変数の探索は単一候補に限定すべきではありません。複数の潜在的な変数を包括的に評価し、最も効果的なゲーティング戦略を特定することが不可欠です。これには、データの各サブセットに最適なモデルを決定するうえで強力な予測力を持つ変数を見つけるため、特徴空間を体系的に探索する必要があります。最適なゲート変数の探索は、ニューラルネットワークやその他の学習アルゴリズムを用いて、入力と構成モデルとの関係を明らかにすることでおこなわれます。

モデル出力をゲート変数として用いた学習された専門化

学習された専門化の一変種として、すべての競合モデルが生成した予測を分析してモデル選択をおこなう独自のアプローチがあります。これは、事前に定義された変数によってモデルを選択する従来のゲーティング手法とは異なり、モデル自身の予測を意思決定要因として活用します。つまり、この学習された専門化の形式は、モデル出力のメタレベル分析を含みます。まず、競合するすべてのモデルが入力に対する予測を生成し、その後、これらの予測を分析して、その特定のインスタンスに最も信頼できるモデルを選択します。この方法では、モデル出力が動的なゲート変数として機能し、選択のプロセスを制御します。

二値分類問題を例に簡単に説明します。2つの競合モデルが同じクラスラベルに同意する場合、選択は容易です。一方、予測が異なる場合は、体系的な手法で対処する必要があります。

ひとつの原始的だが時折有効な方法として、学習データを分析して、予測が矛盾した際に最も信頼できる決定ルールを特定する方法があります。この分析では、インサンプルの性能データを用いて、特定の矛盾状況でどのモデルがより高精度かを判断します。たとえば、両モデルが異なる予測をした場合でも、あるモデルが一貫して優れているなら、そのモデルの予測を優先します。

このデータ駆動型アプローチにより、経験的証拠に基づくモデル出力の最適な組み合わせを決める一連の意思決定ルールを構築できます。

ただし、この単純な方法には明らかな限界もあります。学習サンプルが実際に遭遇する未知のデータを十分に代表していなければ、結果として得られるアンサンブルモデルの有効性は低くなります。より高度な手法（次節で解説）では、適用範囲が広く、実務上より良好な性能を発揮することが多いです。しかし、計算コストを抑え迅速に処理したい場合には、本手法も有効な選択肢となります。また、この簡略化されたアルゴリズムの詳細な解析は、より複雑な概念理解の良い基礎となります。

本手法の完全なソースコードは、この記事末尾に添付されたoracle.mqhファイルに収録されています。以下に示すのは、COracleクラスの宣言部分です。

//+------------------------------------------------------------------+
//| Tabulated combination of component model outputs                 |
//+------------------------------------------------------------------+
class COracle
  {
private:
   ulong             m_ncases;
   ulong             m_nin;
   ulong             m_ncats;
   uint              m_nmodels;
   matrix            m_thresh;
   ulong             m_tally[];
public:
                     COracle(void);
                    ~COracle(void);
   bool              fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats);
   double            predict(vector &inputs,IModel* &models[]);

  };

このクラスは、m_threshとm_tallyという2つのキーコンテナを定義します。m_thresh行列には、学習セットを均等なサイズのサブセットに分割する出力閾値が格納され、m_tally配列はこれらのサブセットごとに最適なモデルを識別します。fit()を呼び出すと、提供された学習データに基づいてモデルが構築されます。このメソッドの最初のセクションを以下に示します。

//+------------------------------------------------------------------+
//| fit an oracle                                                    |
//+------------------------------------------------------------------+
bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats)
  {
   if(predictors.Rows()!=targets.Size())
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return false;
     }

   m_ncases = predictors.Rows();
   m_nin = predictors.Cols();
   m_nmodels = models.Size();

   m_ncats = ncats;
   ulong nthresh = m_ncats - 1;
   ulong nbins = 1;

   nbins = (ulong)pow(m_ncats,m_nmodels);

   m_thresh = matrix::Zeros(m_nmodels,nthresh);

   ZeroMemory(m_tally);

   if(ArrayResize(m_tally,int(nbins))<0)
     {
      Print(__FUNCTION__," ", __LINE__," error ", GetLastError());
      return false;
     }

   matrix outputs(m_ncases,m_nmodels);
   matrix bins(nbins,m_nmodels);

   bins.Fill(0.0);

   vector inrow;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow=predictors.Row(icase);
      for(uint imodel =0; imodel<m_nmodels; imodel++)
         outputs[icase][imodel] = models[imodel].forecast(inrow);
     }

   double frac;
   for(uint imodel =0; imodel<m_nmodels; imodel++)
     {
      inrow = outputs.Col(imodel);
      qsortd(0,long(m_ncases-1),inrow);
      for(ulong i = 0; i<nthresh; i++)
        {
         frac = double(i+1)/double(ncats);
         m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))];
        }
     }

このメソッドは、出力行列内の各構成モデルの予測を収集することから始まります。bins行列は、各ビン内でどのモデルが最も優れていたかの回数をカウントするために使われます。次に、出力行列の各列について、ソートされた列ベクトルinrowの中から等間隔のエントリを見つけることで、閾値の数を決定します。fit()メソッドの次のセクションは以下のように続きます。

vector outrow;
   ulong ibin,index, klow, khigh, ibest, k;
   k = 0;
   double diff,best;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow = predictors.Row(icase);
      outrow = outputs.Row(icase);
      ibin = 0;
      index = 1;
      for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         if(outrow[imodel] <= m_thresh[imodel][0])
            k = 0;
         else
            if(outrow[imodel] > m_thresh[imodel][nthresh-1])
               k = nthresh;
            else
              {
               klow = 0;
               khigh = nthresh-1;
               while(true)
                 {
                  k = (klow+khigh)/2;
                  if(k == klow)
                    {
                     k = khigh;
                     break;
                    }
                  if(outrow[imodel]<=m_thresh[imodel][k])
                     khigh = k;
                  else
                     klow = k;
                 }
              }
         ibin += k * index;
         index *= ncats;
        }
      best = DBL_MAX;

学習データセット内の各サンプルについて、そのモデル予測に対応するビンが決定されます。次に、構成モデルの予測の中から真の値に最も近い予測を見つけます。該当するモデルとビンの組み合わせのカウントが増加されます。fit()メソッドの最後のセクションは、以下のコードで締めくくられます。

for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         diff = fabs(outrow[imodel] - targets[icase]);
         if(diff<best)
           {
            best = diff;
            k = imodel;
           }
        }
      bins[ibin][k]+=1.0;
     }

   for(ibin =0; ibin<nbins; ibin++)
     {
      k = 0;
      ibest = 0;
      for(uint imodel = 0; imodel<m_nmodels; imodel++)
        {
         if(bins[ibin][imodel] > double(ibest))
           {
            ibest = ulong(bins[ibin][imodel]);
            k = ulong(imodel);
           }
        }
      m_tally[ibin] = k;
     }

   return true;
  }

最後の手順では、bins行列を走査して、そのビンで最も頻繁に選択されたモデルを特定し、これらのモデルのインデックスをm_tallyに保存します。この分析で用いられるビニング処理は、複数のモデルの分類結果に基づいて学習サンプルを効率的に分類するために、行列構造を利用しています。この行列は、検討中のモデル数に対応する要素数を持つベクトルを格納しており、各ベクトルの要素は、ビンで表されるカテゴリの特定の組み合わせに対して、各モデルがターゲットに最も近いと判断された回数を記録しています。

たとえば、3つのモデルと4つのカテゴリがある場合を考えます。3軸それぞれがモデルを表し、各軸が4つのカテゴリに分割された3次元空間をイメージしてください。この場合、4×4×4の立方体が形成され、その中の各ポイントは3つのモデルのカテゴリ割り当ての組み合わせを表します。

ビニング処理では2つのインデックス変数を使用します。1つ目は行列内の特定のビン（行）を直接指定し、そのビンはサンプルのカテゴリの組み合わせに対応します。2つ目はスケーリング係数として機能し、多次元空間内で正しくインクリメントをおこなう役割を果たします。

このインデックス指定方法により、サンプルは正確に対応するビンに分類され、すべてのモデルにまたがるカテゴリの組み合わせを効率よく捉えることができます。

predict()メソッドでは、すべてのモデルを実行して各出力が属するビンを特定し、m_tally配列を参照して、そのサンプルに最も適したモデルを決定します。

//+------------------------------------------------------------------+
//| make a prediction                                                |
//+------------------------------------------------------------------+
double COracle::predict(vector &inputs,IModel* &models[])
  {
   ulong k, klow, khigh, ibin, index, nthresh ;
   nthresh = m_ncats -1;
   k = 0;
   ibin = 0;
   index = 1;
   vector otk(m_nmodels);

   for(uint imodel = 0; imodel<m_nmodels; imodel++)
     {
      otk[imodel] = models[imodel].forecast(inputs);

      if(otk[imodel]<m_thresh[imodel][0])
         k = 0;
      else
         if(otk[imodel]>m_thresh[imodel][nthresh-1])
            k = nthresh - 1;
         else
           {
            klow=0;
            khigh = nthresh -1 ;
            while(true)
              {
               k = (klow + khigh) / 2;
               if(k == klow)
                 {
                  k = khigh;
                  break;
                 }
               if(otk[imodel] <= m_thresh[imodel][k])
                  khigh = k;
               else
                  klow = k;
              }
           }
      ibin += k*index;
      index *= m_ncats;
     }

   return otk[ulong(m_tally[ibin])];
  }

コードの検証

スクリプト「Oracle_Demo.mq5」は、COracle クラスの機能を検証します。このプログラムでは、ユーザーが学習データセットのサイズ、ビンの数、モデルの数、および予測タスクの複雑さを調整するノイズレベルなど、さまざまなシミュレーションパラメータを設定できます。以下は、同等の予測性能を持つ3つのモデルを用いた複数のシナリオで得られた結果の一例です。

予測難易度：低、ビン数：2、学習データサイズ：10サンプル

PF      0       13:59:15.542    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10777835
MQ      0       13:59:15.542    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835

予測難易度：中、ビン数：2、学習データサイズ：10サンプル

FD      0       14:00:30.967    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38588979
KG      0       14:00:30.967    Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990

予測難易度：高、ビン数：2、学習データサイズ：10サンプル

ES      0       14:01:11.874    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16908710
ND      0       14:01:11.874    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689

予測難易度：低、ビン数：2、学習データサイズ：100サンプル

LQ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10706090
NJ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483

予測難易度：中、ビン数：2、学習データサイズ：100サンプル

LL      0       14:04:24.070    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36310507
JO      0       14:04:24.070    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485

予測難易度：高、ビン数：2、学習データサイズ：100サンプル

RJ      0       14:06:02.290    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12115161
PM      0       14:06:02.290    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456

予測難易度：低、ビン数：4、学習データサイズ：100サンプル

FI      0       14:08:24.445    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10681953
FR      0       14:08:24.445    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329

予測難易度：中、ビン数：4、学習データサイズ：100サンプル

KG      0       14:10:29.012    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36348921
LP      0       14:10:29.012    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647

予測難易度：高、ビン数：4、学習データサイズ：100サンプル

MR      0       14:12:16.225    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12231642
EE      0       14:12:16.225    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202

その後の実験では、情報を持たないモデルのシナリオをシミュレートするために、ランダムな予測を出力する第4のモデルが追加されました。以下に示す結果は、システムの挙動に大きな変化が生じたことを示しています。

予測難易度：低、ビン数：2、学習データサイズ：10サンプル

GH      0       14:13:47.886    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12971017
MS      0       14:13:47.886    Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652

予測難易度：中、ビン数：2、学習データサイズ：10サンプル

JN      0       14:14:16.985    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.40381512
MI      0       14:14:16.985    Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764

予測難易度：高、ビン数：2、学習データサイズ：10サンプル

ND      0       14:14:54.040    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16720001
OG      0       14:14:54.040    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663

予測難易度：低、ビン数：2、学習データサイズ：100サンプル

QJ      0       14:17:05.521    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12727773
HM      0       14:17:05.521    Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364

予測難易度：中、ビン数：2、学習データサイズ：100サンプル

QP      0       14:18:26.976    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38337835
CK      0       14:18:26.976    Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874

予測難易度：高、ビン数：2、学習データサイズ：100サンプル

IF      0       14:20:01.925    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13780482
IQ      0       14:20:01.925    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032

予測難易度：低、ビン数：4、学習データサイズ：100サンプル

HL      0       14:23:03.090    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12709947
QO      0       14:23:03.090    Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572

予測難易度：中、ビン数：4、学習データサイズ：100サンプル

CR      0       14:25:25.091    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38314408
CE      0       14:25:25.091    Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436

予測難易度：高、ビン数：4、学習データサイズ：100サンプル

GH      0       14:27:50.024    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13828093
CS      0       14:27:50.024    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816

両方の結果を分析すると、ノイズレベルが低いシナリオにおいては、この手法が非常に高い効果を発揮し、誤差分散の大幅な削減が確認されます。一方で、ノイズが多いシナリオでは、顕著な改善が見られないだけでなく、単一モデルを使用した場合よりも性能が劣化することも頻繁にあります。この現象は、すべての構成モデルが同等の予測力を持つ場合でも観察されますが、その際の性能差は比較的小さいものにとどまります。

また、2つのビンの代わりに4つのビンを使用した場合でも、性能差は一貫性がなく、ほとんど無視できる程度であることがテスト結果から明らかになりました。これは、すべてのモデルがほぼ同等の予測力を持っているか、あるいは1つのモデルが一貫して無意味な予測を行っている場合には当然の結果と言えます。現在の状況におけるこのアルゴリズムの主な役割は、情報価値のないモデルを識別し、排除することにあります。ただし、より多くのカテゴリ数が有効に働くようなシナリオが存在する可能性も考えられます。

ゲート付き一般回帰アンサンブル

このセクションでは、ゲーティング変数を用いたモデル結合の汎用的な手法を紹介します。この手法は、一般回帰ニューラルネットワーク(GRNN: General Regression Neural Networks)の概念に着想を得たもので、1つ以上の変数を動的なゲートとして用い、各構成モデルの影響度を調整します。従来のゲーティング手法が最終出力を生成するために単一のモデルを選択していたのに対し、本手法ではゲート変数に基づき、各モデルの出力に最適な重みを付けて統合します。ゲート変数には、各モデルの出力に加えて、外部の計測値などを含めることも可能です。この手法は「ゲート付き一般回帰法」と呼ばれます。

この手法を実装するには、少なくとも2つの学習済み構成モデルと、GRNNに着想を得たアンサンブルを学習させるための別個のデータセットが必要です。この学習データセットには、1つ以上のゲート変数、構成モデルの予測結果、および対応する目標値が含まれていなければなりません。特に、構成モデルの出力の一部をゲート変数として指定することもでき、この点において本手法は高い柔軟性を有しています。

GRNNは、連続値の予測を行う回帰タスク向けに設計された人工ニューラルネットワークの一種です。GRNNはカーネル密度推定の原理に基づいており、メモリベースの学習アプローチを採用しています。構造としては、入力層、パターン層、加算層、出力層の4層で構成されています。

入力層は予測変数を受け取り、それをパターン層へ送ります。パターン層では、各ニューロンが学習サンプルを表し、放射基底関数を用いて入力との類似度を計算します。加算層は、パターン層からの重み付き出力を集約し、出力層はその重みの合計を正規化することで最終的な予測値を生成します。

GRNNは学習時間が非常に短く、基礎となるデータ分布に自動的に適応できるため、非線形関係のモデリングに特に適しています。

本手法においては、テストサンプルと学習サンプル間の加重ユークリッド距離はゲート変数によって決定されます。具体的には、テストサンプルを評価する際に、GRNNゲートは、そのゲート変数がテストサンプルと類似している学習サンプルを優先的に考慮します。GRNNを用いてモデルの二乗誤差を予測する場合、各構成モデルに対する予測二乗誤差は、以下の式に従って計算されます。

構成モデルを組み合わせて共同予測を生成する方法は無数に存在しますが、最も基本的なアプローチは、最終的な予測を各モデルの出力の線形結合として表現する方法です。構成モデルが偏りのない予測という望ましい特性を備えている場合、この特性が保たれるのは、重みの総和が1になるという条件が満たされているときに限られます。たとえ予測が厳密に不偏でない場合でも、この条件は多くのケースで有利に働きます。不偏推定量の線形結合で平均二乗誤差(MSE)を最小化する場合、最適な重みは各推定量の分散の逆数に比例します。このとき、分散の代わりに予測された二乗誤差を用いることで、以下の式により重みを計算できます。

GRNNゲートによる予測を生成するには、まずカーネル幅(σ)に適切な値を設定し、特定のテストサンプルに対して各モデルの予測誤差を推定します。次に、これらの誤差に基づいて重みを計算し、テストサンプルに対して構成モデルを評価します。最後に、計算された重みを用いて各構成モデルの予測値を結合し、最終的な推定値を得ます。

カーネル幅(σ)の最適な値を決定する作業は容易ではなく、学習データに基づく推定が必要です。候補となるシグマベクトルの有効性を評価する最も効果的な方法は、交差検証です。この手法では、学習セットから1つのサンプルを取り出してテストケースとし、指定されたシグマベクトルを用いてこのサンプルに対するGRNNゲート予測を生成し、得られた予測値と実際の値を比較します。その後、サンプルを学習セットに戻し、この手順をデータセット内の全サンプルに対して繰り返します。これらの繰り返しから得られる平均二乗誤差が、候補シグマベクトルの品質を示す評価指標となります。

交差検証の誤差を最小化するカーネル幅(σ)のセットは、導関数を必要としない任意の最適化アルゴリズムを用いて求めることができます。中でも、差分進化法は堅牢性と幅広い適用性から高く評価されています。一方で、パウエル法計算効率に優れ、実際の応用の多くにおいて満足のいく性能を示します。複数の局所最適解が存在するような稀なケースでは、差分進化法が優位となることもありますが、本研究では効率性を重視してパウエル法を採用しています。

gatedreg.mqh ファイルには、ここで説明したGRNNに基づくゲート付きアンサンブル手法を実装する CGatedReg クラスのソースコードが含まれています。以下にそのクラス定義を示します。

//+------------------------------------------------------------------+
//|  GRNN gating model combination                                   |
//+------------------------------------------------------------------+
class CGatedReg:public CPowellsMethod
  {
private:
   ulong             m_nsamples;
   ulong             m_ngates;
   ulong             m_nmodels;
   matrix            m_tset;
   vector            m_sigma;
   vector            m_errvals;
   vector            m_params;

   double            criter(vector &params);
   double            trial(vector &gates, vector &contenders,long i_exclude,long n_exclude);
   virtual double    func(vector &p) {  return criter(p); }
public:
                     CGatedReg(void);
                    ~CGatedReg(void);
   bool              fit(matrix &gates, matrix &contenders,vector &targets);
   double            predict(vector &gates, vector &contenders);
  };

構成モデルからの予測値は、あらかじめ計算され、行列として保存されていることが前提となります。各モデルは、従属変数を予測できるよう事前に学習されている必要があります。ゲート変数（多くの場合は1つの変数）は、最終的な予測において各構成モデルの寄与度を個別に重み付けするために使用されます。fit()メソッドは、必要な学習データをコピーし、最適なカーネル幅(σ)を決定する役割を担います。このメソッドの実装については、次節で説明します。

//+------------------------------------------------------------------+
//| fit a gated grnn model                                           |
//+------------------------------------------------------------------+
bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets)
  {
   if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size()  || gates.Rows()!=targets.Size())
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid training data ");
      return false;
     }
   m_nsamples = gates.Rows();
   m_ngates = gates.Cols();
   m_nmodels = contenders.Cols();

   m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1);
   m_sigma = vector::Zeros(m_ngates);
   m_errvals = vector::Zeros(m_nmodels);

   for(ulong i = 0; i<m_nsamples; i++)
     {
      for(ulong j = 0; j<m_ngates; j++)
         m_tset[i][j] = gates[i][j];
      for(ulong k = 0; k<m_nmodels; k++)
         m_tset[i][m_ngates+k] = contenders[i][k];
      m_tset[i][m_ngates+m_nmodels] = targets[i];
     }

   m_params = vector::Zeros(m_ngates);

   double err =  criter(m_params);
   if(err > 0.0)
      Optimize(m_params);

   criter(m_params);

   return true;

  }

後続の予測では、各モデルの中間的な誤差予測に一般回帰法(GRNN)を用いる必要があるため、fit()メソッドに渡されたすべての入力（すなわち学習データ）を保持しておく必要があります。また、各予測の際にはm_errvalベクトルも使用されます。最適なカーネル幅(σ)を求めるために、パウエルの最適化手法が使用されます。最小化すべき目的関数は、privateメソッド「criter()」として定義されています。

//+------------------------------------------------------------------+
//|  function criterion                                              |
//+------------------------------------------------------------------+
double CGatedReg::criter(vector &params)
  {
   int i, ngates, nmodels, ncases;
   double  out, diff, error, penalty ;
   vector inputs1,inputs2,row;

   ngates = int(m_ngates); ;
   nmodels = int(m_nmodels) ;
   ncases = int(m_nsamples) ;

   penalty = 0.0 ;
   for(i=0 ; i<ngates ; i++)
     {
      if(params[i] > 8.0)
        {
         m_sigma[i] = exp(8.0) ;
         penalty += 10.0 * (params[i] - 8.0) ;
        }
      else
         if(params[i] < -8.0)
           {
            m_sigma[i] = exp(-8.0) ;
            penalty += 10.0 * (-params[i] - 8.0) ;
           }
         else
            m_sigma[i] = exp(params[i]) ;
     }

   error = 0.0 ;

   for(i=0 ; i<ncases ; i++)
     {
      row = m_tset.Row(i);
      inputs1 = np::sliceVector(row,0,m_ngates);
      inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels));
      out = trial(inputs1, inputs2, long(i), 0) ;
      diff = row[ngates+nmodels] - out ;
      error += diff * diff ;
     }

   return error / double(ncases) + penalty ;

  }

このメソッドでは、交差検証を用いて試行的なシグマベクトルの品質を評価します。各シグマを直接最適化するのではなく、シグマの対数を最適化することで、変動の影響を線形化し、安定性を高めています。これは、極端な値に対して平坦な特性を示すGRNNゲートの誤差面に起因する問題を軽減するためです。基準関数では、まずパラメータを指数関数的に変換しつつ、制限された範囲を設けています。また、極端なシグマ値を抑制するためにペナルティ項を導入しています。各学習サンプルに対して予測をおこない、その予測値と実際の値を比較して、二乗誤差を累積し、誤差基準として用います。

m_errvalsの各要素は、誤差計算式の分子を累積するためにゼロで初期化されます。この計算式の分母は、重みの正規化係数により打ち消されるため、明示的に計算する必要はありません。各項を合計に加える前に、テストサンプルと学習サンプルの連続的な近接性が確認されます。

このメソッドは、学習セット内のサンプルだけでなく、全く未知のサンプルに対しても予測に利用可能です。交差検証を実施する場合は、各学習サンプルのシーケンス番号「i_exclude」をtrial()ルーチンに渡します。距離制限パラメータn_excludeも渡し、通常はこれをゼロに設定して単一のサンプルのみを除外します。

なお、交差検証アルゴリズムは、時系列データに多い連続相関を持つ学習セットの扱いにおいて重大な制限があることに注意が必要です。この問題は、評価対象の学習サンプルに空間的に近接するサンプルを除外することで対処可能です。

//+------------------------------------------------------------------+
//| trial ( )                                                        |
//+------------------------------------------------------------------+
double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude)
  {
   int icase, ivar, idist, size, ncases;
   double psum, diff, dist, err, out ;

   m_errvals.Fill(0.0);
   int ngates = int(m_ngates);
   int nmodels = int(m_nmodels);
   size = ngates + nmodels + 1 ;
   ncases = int(m_nsamples);

   for(icase=0 ; icase<ncases ; icase++)
     {

      idist = (int)fabs(int(i_exclude) - icase) ;
      if(ncases - idist < idist)
         idist = ncases - idist ;

      if(idist <= int(n_exclude))
         continue ;

      dist = 0.0 ;

      for(ivar=0 ; ivar<ngates ; ivar++)
        {
         diff = gates[ivar] - m_tset[icase][ivar] ;
         diff /= m_sigma[ivar] ;
         dist += diff * diff ;
        }

      dist = exp(-dist) ;

      for(ivar=0 ; ivar<nmodels ; ivar++)
        {
         err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ;
         m_errvals[ivar] += dist * err * err ;
        }

     }

   psum = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
     {
      if(m_errvals[ivar] > 1.e-30)
         m_errvals[ivar] = 1.0 / m_errvals[ivar] ;
      else
         m_errvals[ivar] = 1.e30 ;
      psum += m_errvals[ivar] ;
     }

   for(ivar=0 ; ivar<nmodels ; ivar++)
      m_errvals[ivar] /= psum ;

   out = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
      out += m_errvals[ivar] * contenders[ivar] ;

   return out ;
  }

学習ケースが交差検証の除外テストに合格すると、2つのケース間の加重ユークリッド距離が計算されます。この距離は、各構成モデルの予測誤差を算出する際に用いるため指数関数で変換されます。続いて、各モデルの予測誤差が求められます。最後に、モデルの重み付け式を用いて、各候補モデルの出力をひとつの予測値に統合します。これが関数の戻り値となります。

//+------------------------------------------------------------------+
//|  infer                                                           |
//+------------------------------------------------------------------+
double CGatedReg::predict(vector &gates,vector &contenders)
  {
   return trial(gates,contenders,-1,0);
  }

ゲート付きGRNNアンサンブルのテスト

Gating_Demo.mqhスクリプトは、4つの異なるゲーティング戦略を包括的に比較します。各戦略は、モデル選択と組み合わせのさまざまな側面を示すことを目的としています。以下に 4 つの戦略の概要を示します。

• コンポーネント予測をゲーティング変数として利用する：この方法では、個々の構成モデルの予測をゲーティング変数として直接使用し、ベースラインメソッド（COracle クラス）と比較します。モデル選択において、モデル自身の出力を意思決定の要因として使う効果を検証します。

• 元の変数を使ったゲーティング：元の入力変数（構成モデルで使用されているもの）をゲーティング変数とします。これらは効果的なゲーティング信号として設計されていないため、無関係または不適切なゲーティング変数がモデル性能に与える影響を示します。

• ランダムゲーティング：ランダムに生成した数値をゲーティング変数として使用し、有益な情報がない状況を模擬します。完全に非情報的な信号を使った場合の性能低下を示す基準となります。

• 比率ベースのゲーティング：第1モデルと第2モデルの予測誤差比の対数をゲーティング変数として使います。実際の場面では非現実的（モデルの真の誤差は通常不明）ですが、2モデルの理想的シナリオとして機能します。複数モデルの場合も部分的に有用なゲーティング情報を提供します。

これら4つの戦略は、多様な性能条件下での評価を目的とし、アンサンブル学習におけるゲーティング手法の長所・短所を理解する助けとなります。スクリプトは、各ゲーティング戦略が全体の予測精度と誤差分散に与える影響を評価し、GRNNゲーティングの有効性を明らかにします。

モデル数：3、サンプル数：100、予測難易度：低

EK      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  1000    replications completed.
GL      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10790466
JP      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Component error = 0.10790458
DF      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Original error = 0.10790458
HM      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Random error = 0.10790458
DJ      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458

モデル数：3、サンプル数：100、予測難易度：高

GF      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12143040
FE      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Component error = 1.11991444
GQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Original error = 1.11991445
QI      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Random error = 1.11991443
EO      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443

モデル数：4、サンプル数：100、予測難易度：低

IO      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LK      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12792841
RS      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Component error = 0.11516554
MK      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Original error = 0.11516373
GR      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Random error = 0.11516595
GE      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Ratio error = 0.11516595

モデル数：4、サンプル数：100、予測難易度：高

QQ      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  1000    replications completed.
HE      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.14025014
EI      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Component error = 1.13144872
GM      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Original error = 1.13144863
QD      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Random error = 1.13144883
NL      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882

ランダムゲーティングによって達成された驚くべき性能向上は、GRNNゲーティングアルゴリズムの動作原理に起因します。一般的には、ランダムなゲーティング信号はノイズとなり、モデル選択に有益な情報を与えないため、性能を低下させると予想されます。しかし、GRNNの仕組みは学習サンプル間の加重ユークリッド距離に基づいており、テストサンプルがどれだけ学習サンプルに類似しているかで予測を調整します。

ゲーティング信号がランダムであっても、GRNNはデータおよびモデルの一般的な構造を用いて、各構成モデルの予測を加重平均します。ランダムなゲーティング値は特定モデルへの強い偏りを生じさせないため、アルゴリズムはデータの内在構造と、良好に学習した各モデルの性能により依存することになります。その結果、より堅牢なモデルの組み合わせが形成され、ランダムゲーティングはむしろ偏りを中和し、1つのモデルが意思決定を支配することを防ぐ役割を果たします。

たとえば、3つのモデルが高い予測精度を持ち、1つのモデルがランダムな予測を出す場合、ランダムゲーティングは無意識のうちにそのランダムモデルの影響力を減らす効果を持ちます。これにより、非情報的なモデルの寄与が抑えられ、アンサンブル全体の性能が著しく改善されます。。

このように、ランダムゲーティングは直感的には有益とは思えませんが、GRNNゲーティングはデータセットやモデル構造を活用し、特に予測が容易で各モデルの精度が高い問題において予想外の性能向上をもたらすことがあります。この挙動は、最適でない条件下でも複数モデルの潜在能力を活かして各モデルの寄与を効果的に調整するGRNNゲーティングの強力さを示しています。

また、このアルゴリズムは各モデルの予測誤差を的確に推定します。ランダム予測モデルのように常に大きな誤差を出すモデルは、一貫して高い誤差推定値を受けます。結果として、アンサンブル内でそのモデルには低い重みが割り当てられます。

この点はGRNNゲーティングの重要な利点を示しています。ゲーティング変数自体に十分な予測力がなくても、予測性能の悪いモデルを効果的に特定し重みを下げることができるのです。したがって、ゲーティング信号に意味のある情報がほとんどない場合でも、異なる予測精度のモデルを含むアンサンブルでは、GRNNゲーティングによって性能が大幅に改善されることがあります。

結論

本稿で紹介した技術は、学習アルゴリズムの予測性能および解釈可能性を高めるうえで、ゲーティングメカニズムが持つ柔軟性と適応力を明示するものです。使用する手法の選択は、タスクの複雑さ、データの性質、計算リソースなど、状況に応じて最適なものが異なります。多くの場合、最適化手法とドメイン知識を組み合わせることによって、最も効果的でかつ解釈しやすい結果を得ることができます。なお、本記事で言及したすべてのコードは巻末に添付してあります。以下の表では、各ソースファイルの内容について簡潔に説明しています。

ファイル名	説明
MQL5/include/gatedreg.mqh	ゲート付きGRNNアンサンブルを実装するCGatedRegクラスの定義
MQL5/include/imodel.mqh	学習済みモデルをカプセル化するインターフェイスの定義
MQL5/include/minimize.mqh	パウエル法を用いた関数最小化を実装するCPowellsMethodの定義
MQL5/include/multilayerperceptron.mqh	多層パーセプトロンの実装であるCMlpクラスの定義
MQL5/include/np.mqh	ベクトルと行列を操作するための汎用ヘルパー関数のコレクション
MQL5/include/oracle.mqh	専門的な構成モデルのセットからモデルを選択できるCOracleクラスの定義
MQL5/include/qsort.mqh	ベクトルをソートするためのシンプルな関数
Mql5/scripts/Gating_Demo.mq5	CGatedRegクラスの機能を示すスクリプト
Mql5/scripts/Oracle_Demo.mq5	COracleクラスの使用方法を示すスクリプト