측정 지표 정보

소개

머신 러닝은 학습 데이터를 통해 시장의 일반적인 행동을 학습합니다. 그리고 궁극적으로 상당히 정확한 예측을 내립니다. 선택한 학습 알고리즘은 의미 있는 정보를 추출하기 위해 신중하게 선택된 샘플을 사용합니다. 많은 사람들이 이러한 정교한 도구를 성공적으로 적용하지 못합니다. 그 이유는 대부분의 의미 있는 정보들이 노이즈가 많은 데이터에 숨겨져 있기 때문입니다. 많은 전략 개발자들은 자신들이 사용하는 데이터 세트가 모델 학습에 적합하지 않을 수 있다는 사실을 잘 모를 수 있습니다.

지표는 적용되는 기초 가격 계열에 대한 정보를 전달하는 전달자라고 볼 수 있습니다. 이 전제를 사용하면 엔트로피를 사용하여 지표가 전달한 정보의 양을 측정할 수 있습니다. 이제 티모시 마스터스가 쓴 '시장 트레이딩 시스템 테스트 및 튜닝(TTMTS)'에 설명된 단계와 도구를 사용해 지표 데이터의 구조를 평가하는 데 어떻게 사용할 수 있는지 보여드리겠습니다.

지표 정보를 측정하는 이유

전략 개발을 위해 머신러닝 도구를 사용할 때 우리는 종종 알고리즘에 모든 종류의 데이터를 던져놓고 무언가 결과가 나오기를 기대하는 방법에 의존합니다. 궁극적으로 그 성공 여부는 모델에 사용된 예측자의 품질에 따라 달라지며 효과적인 예측자는 일반적으로 어떠한 특성을 가지고 있습니다. 그 중 하나는 중요한 정보 콘텐츠로 가득 차 있습니다.

모델 학습에 사용되는 변수의 정보량은 중요하지만 정보량이 효과적인 모델 학습을 위한 유일한 요건은 아닙니다. 따라서 정보 콘텐츠를 측정하면 학습 과정에서 무턱대고 사용되는 지표를 골라내는 데 사용할 수 있습니다.  여기에 엔트로피의 개념이 적용됩니다.

엔트로피

엔트로피에 대한 글이 작성되었습니다: MQL5.com에서 이미 여러 번 소개한 바 있습니다. 독자들에게 죄송하지만 여러분이 또다른 정의를 이해해야 이 개념의 적용을 이해할수 있다는 점을 기억하세요. 앞에서 저는 엔트로피 계산의 역사와 영향에 대해 설명했습니다. 이제는 방정식부터 설명하겠습니다.

                                                        

H(X)는 X의 엔트로피를 의미하며 X는 메시지와 같은 임의의 변수를 나타내는 불연속 변수입니다. 메시지의 내용은 한정된 수의 값만 가정할 수 있습니다. 이는 방정식에서 작은 X로 표시됩니다. 작은 x는 메시지의 관찰된 값이며 가능한 모든 x 값을 집합으로 열거할 경우 N이 됩니다.

공정한 주사위의 예를 생각해 보세요. 주사위를 굴린다는 것은 게임의 결과를 결정하는 정보를 제공하는 것으로 인식될 수 있습니다. 주사위는 1~6번으로 번호가 매겨진 6개의 고유한 면이 있습니다. 숫자가 위로 향하는 사람이 관찰될 확률은 1/6입니다.

이 예에서 큰 X는 주사위, 작은 X는 주사위의 측면에 그려진 숫자가 될 수 있습니다. 모두 N ={ 1,2,3,4,5,6} 집합에 배치됩니다. 공식을 적용하면 이 주사위의 엔트로피는 0.7781입니다.

                                                         

이제 제조상의 결함이 있는 다른 주사위를 생각해 보세요. 양면에 같은 번호가 그려져 있습니다. 이 결함이 있는 주사위의 경우 가능한 값의 집합 N은 {1,1,3,4,5,6}입니다. 공식을 다시 사용하면 평균 엔트로피 값은 0.6778 이 됩니다.

                                                 

값을 비교해보면 정보 콘텐츠가 감소한 것을 알 수 있습니다. 두 주사위를 모두 분석하여 가능한 각 값을 관찰할 확률이 모두 같을 경우 엔트로피 방정식은 가능한 최대 값을 산출합니다. 따라서 엔트로피는 가능한 모든 값의 확률이 같을 때 최대 평균에 도달합니다.

기존 실수를 출력으로 생성하는 지표의 경우 결함이 있는 주사위를 버리면 됩니다. 그러면 X가 지표가 되고 작은 X는 지표가 가정할 수 있는 값의 범위가 됩니다. 그러나 엔트로피 방정식은 이산 변수를 엄격하게 다루기 때문에 문제가 있습니다. 연속형 변수로 작동하도록 방정식을 변환할 수는 있지만 적용이 어렵기 때문에 불연속형 숫자를 사용하는 것이 더 쉽습니다.

지표의 엔트로피 계산하기

엔트로피 방정식을 연속 변수에 적용하려면 지표의 값을 반드시 이산화해야 합니다. 이는 값의 범위를 동일한 크기의 간격으로 나눈 다음 각 간격에 속하는 값의 수를 세는 방식으로 수행됩니다. 이 방법을 사용하면 지표의 모든 값의 최대 범위를 열거한 원래 집합이 각각 선택한 간격인 하위 집합으로 대체됩니다.

연속형 변수를 다룰 때는 변수가 가정할 수 있는 가능한 값의 확률의 변화가 중요해집니다. 왜냐하면 이 변화가 지표에 엔트로피를 적용할 수 있는 통로를 제공하기 때문입니다.

주사위의 첫 번째 예로 돌아가 보겠습니다. 각각의 최종 엔트로피 값을 각각의 n에 대한 로그(N)로 나누면 다음과 같습니다. 첫 번째 주사위는 1을 산출하는 반면 결함이 있는 주사위는 0.87을 산출합니다. 엔트로피 값을 변수가 가정할 수 있는 값의 로그로 나누면 변수의 이론적 최대 엔트로피와 관련된 측정값이 생성됩니다. 이를 비례 엔트로피 또는 상대 엔트로피라고도 하며

이 값은 지표의 엔트로피가 이론적 최대 평균에 얼마나 가까운지를 나타내는 것이므로 지표 평가에 유용할 수 있습니다. 최대값인 1에 가까울수록 좋으며 그 반대편에 있는 것은 머신 러닝에 사용하기에 좋지 않은 지표임을 나타낼 수 있습니다. 

                                  

위에 표시된 최종 적용 방정식과 코드는 아래에 mql5 스크립트로 구현되어 있으며 첨부 파일에서 다운로드할 수 있습니다. 스크립트를 사용하면 대부분의 지표를 분석할 수 있습니다.

지표의 엔트로피를 계산하는 스크립트

스크립트는 다음과 같은 사용자가 조정 가능한 매개변수를 사용하여 호출됩니다:

• TimeFrame - 지표 값을 분석할 시간 프레임을 선택합니다.
• IndicatorType - 여기에서 사용자는 분석을 위해 기본으로 제공되는 내장 지표 중 하나를 선택할 수 있습니다. 사용자 지정 지표를 지정하려면 사용자 지정 지표 옵션을 선택하고 다음 매개변수 값에 지표의 이름을 입력합니다.
  
• CustomIndicatorName - 이전 매개변수에 사용자 지정 지표 옵션을 선택한 경우 사용자는 여기에 올바른 지표 이름을 입력해야 합니다.
  
• UseDefaults - true로 설정하면 지표에 하드 코딩된 기본 사용자 입력이 사용됩니다.
  
• IndicatorParameterTypes - 지표의 데이터 유형을 올바른 순서로 나열하는 쉼표로 구분된 문자열입니다. - 가능한 입력의 예로, 분석할 지표가 각각 더블 , 정수, 정수, 문자열 유형의 4개 입력을 받는다고 가정할 때 사용자는 "double , integer, integer, string "을 입력하면 되며 d= double , i=integer, s=string인 축약형 숏폼으로 "d , i, i, s" 도 지원됩니다. 열거형(Enum) 값은 정수 유형에 매핑됩니다.
  
• IndicatorParameterValues - 이전 입력과 마찬가지로 쉼표로 구분된 값의 목록입니다(예: "0.5,4,5,string_value"). IndicatorParameterValues 혹은 IndicatorParameterTypes의 유형 중 매개변수 형식에 오류가 있는 경우 해독할 수 없거나 누락된 특정 값에는 지표의 기본값을 사용하게 됩니다.
  EA 탭에서 오류 메시지를 확인하세요. 여기에 지표 이름을 포함할 필요는 없으며 사용자 지정 지표를 고려 중인 경우 CustomIndicatorName으로 지정해야 합니다.
• IndicatorBuffer - 분석할 지표 버퍼를 지정할 수 있습니다.
  
• HistoryStart - 히스토리 샘플의 시작 날짜입니다.
  
• HistorySize - HistoryStart와 관련하여 기준으로 분석할 바의 개수입니다.
  
• Intervals - 이 매개변수는 디스크리트화 프로세스를 위해 생성될 숫자 간격을 나타내는 데 사용됩니다. TTMTS의 작성자는 샘플 크기가 수천 개일 경우 20개의 간격을 지정하고 2개를 최소값으로 규정했습니다.  샘플 크기에 따라 간격의 수를 변경할 수 있는 기능을 구현하여 사용하기에 적절한 값에 저만의 스핀을 추가했습니다(예: 샘플 1000개당 51개). 이 옵션은 사용자가 2보다 작은 값을 입력하는 경우에 사용할 수 있습니다. 따라서 간격을 2보다 작은 숫자로 설정하면 분석 중인 바의 수에 따라 사용되는 간격의 수가 변경됩니다.
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

간격에 대해 선택한 값이 무엇인지 메모합니다. 계산에 사용되는 간격 수를 변경하면 최종 엔트로피 값이 달라집니다. 분석시에는 사용된 독립적인 입력의 영향을 최소화할 수 있도록 어느 정도 일관성을 유지하는 것이 좋습니다. 스크립트에서 상대 엔트로피 계산은 Entropy.mqh 파일에 정의된 함수에 캡슐화 되어 있습니다.

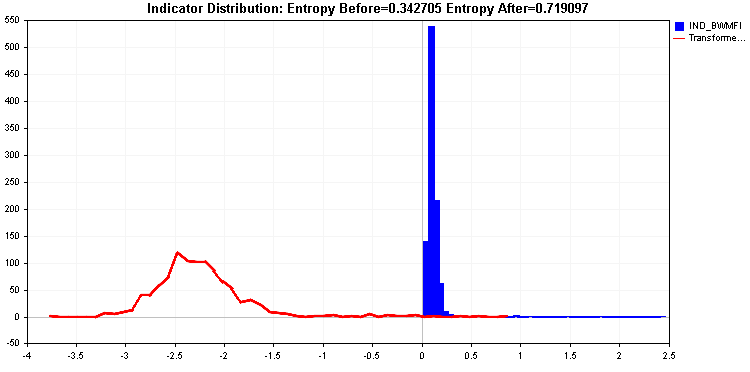
스크립트는 결과 엔트로피 값을 EA 탭에 출력합니다. 다양한 기본 제공 및 사용자 지정 지표에 대해 스크립트를 실행하면 아래와 같은 결과가 나타납니다. 윌리엄의 퍼센트 범위는 완벽에 가까운 상대 엔트로피를 가지고 있다는 점이 흥미롭습니다. 실망스러운 결과를 보여주는 시장 촉진 지수 지표와 비교해 보세요.

이러한 결과를 바탕으로 머신러닝 알고리즘에 적합하도록 데이터를 처리하는 추가적인 단계를 수행할 수 있습니다. 여기에는 지표의 통계적 속성을 엄격하게 분석하는 작업이 필요합니다. 지표 값의 분포를 연구하면 왜곡 및 이상값과 관련된 문제를 파악할 수 있습니다. 이 모든 것이 모델 학습을 저하시킬 수 있습니다.

예를 들어 위에서 분석한 두 지표의 통계적 속성을 살펴봅니다.

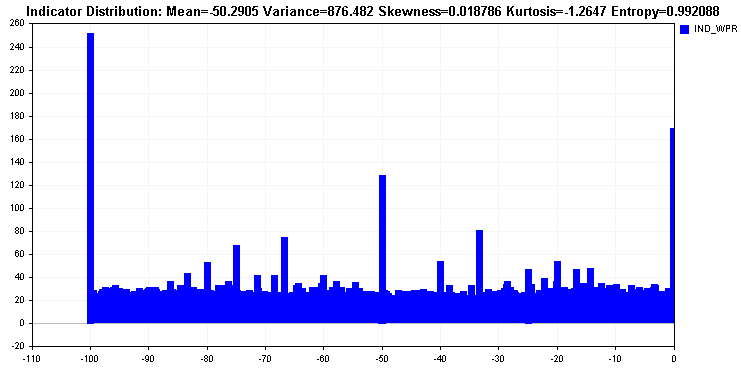
윌리엄의 퍼센트 범위의 분포를 보면 거의 모든 값이 전체 범위에 걸쳐 분포되어 있으며 다중 모달을 제외하고는 상당히 균일하게 분포되어 있음을 알 수 있습니다. 이러한 분포는 이상적이며 엔트로피 값에 반영됩니다.

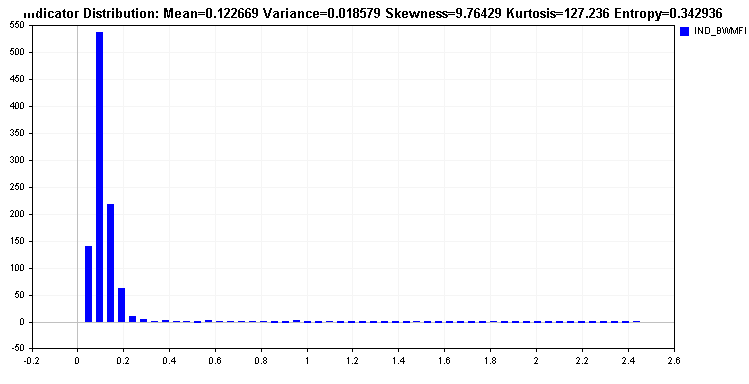
이는 긴 꼬리를 가진 시장 촉진 지수 분포와 대조적입니다. 이러한 지표는 대부분의 학습 알고리즘에서 문제가 될 수 있으며 값을 변환해야 하는 것이 필요합니다. 값을 변환하면 지표의 상대 엔트로피가 개선될 것입니다.

지표의 정보 콘텐츠 개선하기

지표의 엔트로피를 높이는 변경은 지표가 제공하는 신호의 정확도를 개선하는 방법으로 간주되어서는 안 된다는 점을 명시해야 합니다. 엔트로피를 높인다고 해서 쓸모없는 지표가 정답이 되지는 않습니다. 엔트로피를 개선하는 작업은 예측 모델에서 효과적으로 사용할 수 있도록 지표 데이터를 처리하는 것을 의미합니다.

이 옵션은 엔트로피 값이 0.5보다 훨씬 낮고 0에 가까운, 절망적으로 나쁜 경우에 고려해야 합니다. 상한 임계값은 순전히 임의적인 것입니다. 허용 가능한 최소값을 선택하는 것은 개발자의 몫입니다. 요점은 가능한 한 균일하게 지표 값의 분포를 생성하는 것입니다. 변환을 적용할지 여부를 결정할 때는 지표 값 중 대표성이 있는 대규모 샘플을 대상으로 수행한 분석을 기반으로 해야 합니다.

적용된 변환으로 인해 지표의 기본적인 동작이 변경되어서는 안 됩니다. 변환된 지표는 원시 지표와 비슷한 모양을 가져야 합니다(예: 최저점과 최고점의 위치가 두 시리즈에서 비슷해야 함). 그렇지 않은 경우 잠재적으로 유용한 정보가 손실될 위험이 있습니다.

다양한 종류의 테스트 데이터 불완전성에 따라 다양한 변환 방법이 있습니다. 우리는 기본적인 통계 분석을 통해 드러난 명백한 결함을 수정하기 위한 몇 가지 간단한 변환만 고려할 것입니다. 전처리는 머신 러닝의 방대한 분야입니다. 머신 러닝적 적용을 마스터하고 싶은 사람은 이 분야에 대한 더 많은 지식을 습득하는 것이 좋습니다.

일부 변환의 효과를 설명하기 위해 다양한 변환을 적용하고 분석 중인 데이터의 분포를 표시하는 옵션이 있는 스크립트를 사용할 것입니다. 이 스크립트에는 6가지 변환 함수 예제가 구현되어 있습니다:

• 제곱근 함수 변환은 대다수에서 상당히 벗어난 지표 값을 가끔씩 스쿼싱하는 데 적합합니다.

• 큐브 루트 변환은 음수 값을 가진 지표에 가장 잘 적용되는 또 다른 스쿼싱 함수입니다.

• 로그 변환은 앞서 언급한 압축 변환보다 더 큰 범위로 값을 압축하고

• 쌍곡선 탄젠트 및 로지스틱 변환을 적절한 규모의 데이터 값에 적용하여 잘못된 숫자(nan 오차)가 생성되는 문제를 방지해야 합니다.

• 극단적인 변환은 데이터 세트에서 극단적인 균일성을 유도합니다. 변환은 유사한 수치가 거의 없고 대부분 고유한 값을 생성하는 지표에만 적용해야 합니다.

변환된 지표 값을 비교하는 스크립트

이전 스크립트와 비교하기 위해 동일한 사용자 입력이 포함되어 있습니다. 새로운 입력 항목은 아래에 설명되어 있습니다:

• DisplayTime - 지표 분포의 그래픽을 표시합니다. DisplayTime은 그래픽이 제거되기 전까지 표시되는 시간(초)을 나타내는 정수 값입니다.

• ApplyTransfrom - 스크립트의 모드를 설정하는 부울 값입니다. false인 경우 스크립트는 분포를 그리고 상대 엔트로피와 함께 샘플의 기본 통계를 표시합니다. true로 설정하면 원시 지표 값에 변환을 적용하고 변환 전후의 상대 엔트로피 값을 표시합니다. 수정된 샘플의 분포 역시빨간색 곡선으로 그려집니다.

• Select_transform - 지표의 엔트로피를 높이기 위해 적용할 수 있는, 앞서 설명한 변환을 제공하는 열거형입니다.

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

예제를 계속 진행하면서 제곱근과 큐브근 변환의 적용을 비교해 보겠습니다.

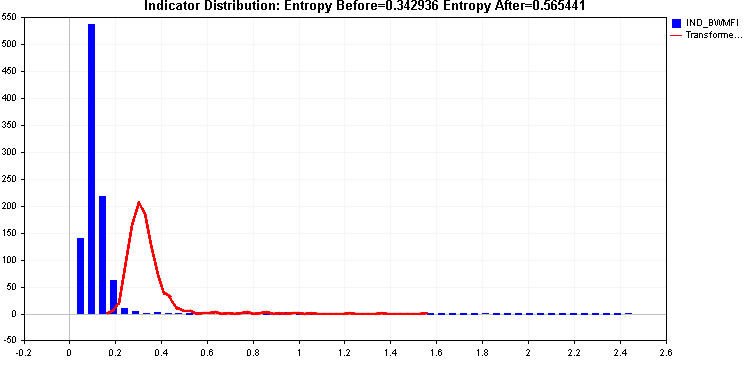
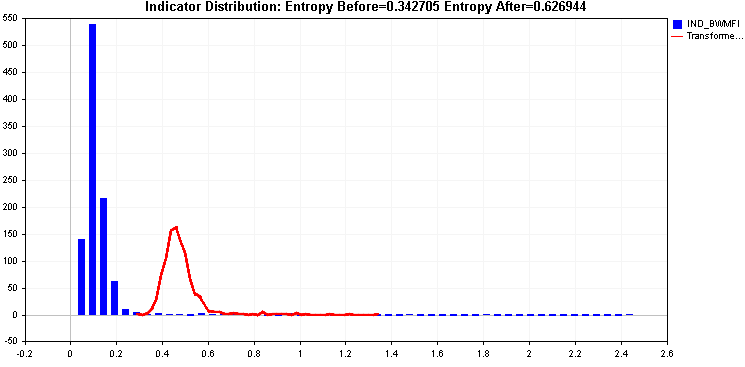
둘 다 엔트로피를 개선하지만 오른쪽 꼬리가 문제가 될 수 있습니다. 지금까지 적용된 두 가지 변환은 이를 효과적으로 처리하지 못했습니다.

로그 변환은 더 나은 엔트로피 값을 생성합니다. 여전히 꼬리는 상당히 중요합니다. 최후의 수단으로 극단적인 변환을 적용할 수 있습니다.

결론

우리는 예측 모델 학습에 사용하기 전에 지표 값을 변환해야 할 필요성을 평가하기 위해 엔트로피의 개념을 살펴봤습니다.

이 개념은 두 개의 스크립트로 구현되었습니다. EA 탭에서 샘플의 상대 엔트로피를 인쇄하는 EntropyIndicatorAnalyis. 다른 스크립트인 IndicatorAnalysis는 한 단계 더 나아가 원시 및 변환된 지표 값의 분포를 그리면서 상대 엔트로피 값의 전후를 표시합니다.

이 도구는 유용하지만 모든 종류의 지표에 적용될 수는 없다는 점에 유의해야 합니다. 일반적으로 빈 값을 포함하는 화살표 기반의 지표는 여기에 설명된 스크립트에 적합하지 않으며 이러한 경우 다른 인코딩 기술이 필요합니다.

데이터 변환이라는 주제는 모든 종류의 예측 모델을 구축할 때 고려되어야 하는 가능한 전처리 단계의 일부에 불과합니다. 이러한 기법을 사용하면 시장을 이기는 데 필요한 진정으로 독특한 관계를 추출하는 데 도움이 됩니다.

파일 이름	설명
Mql5/Include/Entropy.mqh	엔트로피 계산에 사용되는 함수에 대한 다양한 정의가 포함된 파일과 첨부된 스크립트에서 사용하는 유틸리티 함수가 포함된 파일을 포함합니다.
Mql5/Scripts/IndicatorAnalysis.mq5	지표 값의 분포를 엔트로피와 함께 그래픽으로 표시하는 스크립트입니다.
Mql5/Scripts/EntropyIndicatorAnalysis	지표의 엔트로피를 계산하는 데 사용할 수 있는 스크립트입니다.