Messen der Information von Indikatoren

Einführung

Das maschinelle Lernen stützt sich auf Trainingsdaten, um das allgemeine Verhalten des Marktes zu erlernen und letztendlich ziemlich genaue Vorhersagen zu treffen. Der gewählte Lernalgorithmus muss sich durch eine sorgfältig ausgewählte Stichprobe wühlen, um aussagekräftige Informationen zu gewinnen. Der Grund, warum viele diese hochentwickelten Tools nicht erfolgreich anwenden können, ist, dass die meisten aussagekräftigen Informationen in verrauschten Daten verborgen sind. Vielen Strategieentwicklern ist vielleicht nicht klar, dass die von uns verwendeten Datensätze für das Modelltraining nicht geeignet sind.

Indikatoren können als Überbringer von Informationen über die zugrunde liegenden Preisreihen betrachtet werden, auf die sie angewendet werden. Unter dieser Prämisse kann die Entropie dazu verwendet werden, zu messen, wie viel Information ein Indikator übermittelt. Anhand der Schritte und Werkzeuge, die im Buch Testing and Tuning Market Trading Systems (TTMTS) von Timothy Masters dokumentiert sind, werden wir demonstrieren, wie diese zur Bewertung der Struktur von Indikatordaten verwendet werden können.

Warum die Information der Indikatoren messen?

Bei der Verwendung von Tools für maschinelles Lernen zur Strategieentwicklung greifen wir oft darauf zurück, einfach alle möglichen Daten auf die Algorithmen zu werfen, in der Hoffnung, dass etwas dabei herauskommt. Letztlich hängt der Erfolg von der Qualität der im Modell verwendeten Prädiktoren ab, und wirksame Prädiktoren haben in der Regel bestimmte Merkmale. Eine davon ist mit einem hohen Informationsgehalt ausgestattet.

Die Menge an Informationen in den für das Modelltraining verwendeten Variablen ist wichtig, aber nicht die einzige Voraussetzung für ein effektives Modelltraining. Daher kann die Messung des Informationsgehalts dazu verwendet werden, Indikatoren zu überprüfen, die ansonsten während des Ausbildungsprozesses blind verwendet würden.  Hier kommt das Konzept der Entropie zum Tragen.

Entropie

Über die Entropy wurde bereits mehrfach, auch auf MQL5.com, geschrieben. Ich entschuldige mich bei den Lesern, dass sie eine weitere Definition über sich ergehen lassen müssen, aber ich verspreche, dass dies für das Verständnis der Anwendung des Konzepts wesentlich ist. In früheren Artikeln wurden die Geschichte und die Herleitung der Entropieberechnung erläutert, sodass wir der Kürze halber gleich mit der Gleichung beginnen werden.

                                                        

H(X) ist die Entropie von X. X ist eine diskrete Variable, die eine beliebige Variable, beispielsweise eine Nachricht, darstellt. Der Inhalt der Nachricht kann nur eine endliche Anzahl von Werten annehmen. Dies wird in der Gleichung als kleines x dargestellt. Kleine x sind die beobachteten Werte der Meldungen, sodass, wenn alle möglichen Werte von x in einer Menge N aufgezählt würden.

Nehmen wir zum Beispiel einen fairen Würfel. Die Würfel, wenn sie gewürfelt werden, können als Informationen wahrgenommen werden, die den Ausgang eines Spiels bestimmen. Der Würfel hat 6 individuelle Seiten, die von 1 bis 6 nummeriert sind. Die Wahrscheinlichkeit, dass eine der Zahlen nach oben zeigt, beträgt 1/6.

In diesem Beispiel wäre das große X der Würfel und das kleine x könnte eine der Zahlen sein, die auf die Seiten des Würfels gemalt sind. Diese werden alle in die Menge N ={ 1,2,3,4,5,6} eingeordnet. Nach dieser Formel beträgt die Entropie dieses Würfels 0,7781.

                                                         

Betrachten wir nun einen anderen Würfel, der einen Fabrikationsfehler hat. Es hat 2 Seiten mit der gleichen Nummer. Für diesen defekten Würfel ist die Menge N der möglichen Werte {1,1,3,4,5,6}. Wenn wir die Formel erneut anwenden, erhalten wir einen durchschnittlichen Entropiewert von 0,6778.

                                                 

Vergleicht man die Werte, so stellt man fest, dass der Informationsgehalt gesunken ist. Analysiert man beide Würfel, so ergibt die Entropiegleichung ihren größtmöglichen Wert, wenn die Wahrscheinlichkeiten für die Beobachtung jedes möglichen Wertes gleich sind. Daher erreicht die Entropie ihren maximalen Mittelwert, wenn die Wahrscheinlichkeiten aller möglichen Werte gleich sind.

Wenn wir die defekten Würfel für einen Indikator verwerfen, der traditionelle reelle Zahlen als Ausgabe produziert. Dann wird X zum Indikator und die kleinen x sind die Werte des Wertebereichs, die der Indikator annehmen kann. Bevor wir fortfahren, haben wir ein Problem, denn die Entropiegleichung befasst sich ausschließlich mit diskreten Variablen. Eine Umformung der Gleichung, um mit kontinuierlichen Variablen zu arbeiten, ist möglich, aber die Anwendung wäre schwierig, sodass es einfacher ist, im Bereich der diskreten Zahlen zu bleiben.

Berechnung der Entropie eines Indikators

Um die Entropiegleichung auf kontinuierliche Variablen anzuwenden, müssen wir die Werte des Indikators diskretisieren, indem wir den Wertebereich in gleich große Intervalle unterteilen und dann die Anzahl der Werte zählen, die in jedes Intervall fallen. Bei dieser Methode wird die ursprüngliche Menge, die den maximalen Bereich aller Werte des Indikators aufzählt, durch Teilmengen ersetzt, die jeweils die ausgewählten Intervalle darstellen.

Bei kontinuierlichen Variablen ist die Variation der Wahrscheinlichkeiten der möglichen Werte, die die Variable annehmen kann, von Bedeutung, da sie eine wichtige Facette bei der Anwendung der Entropie auf Indikatoren darstellt.

Um auf das erste Beispiel des Würfels zurückzukommen. Wenn wir die endgültigen Entropiewerte jedes einzelnen durch log(N) für das jeweilige n dividieren. Der erste Würfel ergibt 1, während der fehlerhafte Würfel 0,87 ergibt. Dividiert man den Entropiewert durch den Logarithmus der Anzahl der Werte, die die Variable annehmen kann, erhält man ein Maß, das sich auf die theoretische maximale Entropie der Variablen bezieht. Das wird auch als proportionale oder relative Entropie bezeichnet.

Dieser Wert ist für die Indikatorbewertung von Nutzen, da er angibt, wie nahe die Entropie des Indikators an seinem theoretischen Höchstwert liegt. Je näher er an einem Maximalwert liegt, desto besser, und alles, was am anderen Ende liegt, kann auf einen Indikator hindeuten, der für die Verwendung in maschinellen Lernverfahren ungeeignet ist. 

                                  

Die endgültige Gleichung, die oben gezeigt wird, und der Code sind unten als mql5-Skript implementiert, das als Anhang am Ende des Artikels zum Download zur Verfügung steht. Mit diesem Skript können wir die meisten Indikatoren analysieren.

Ein Skript zur Berechnung der Entropie eines Indikators

Das Skript wird mit den folgenden vom Nutzer einstellbaren Parametern aufgerufen:

• TimeFrame - ausgewählter Zeitrahmen für die Analyse der Indikatorwerte.
• IndicatorType - hier kann der Nutzer einen der integrierten Indikatoren für die Analyse auswählen. Um einen nutzerdefinierten Indikator festzulegen, wählen Sie die Option Custom Indikator und geben Sie den Namen des Indikators in den nächsten Parameterwert ein.
  
• CustomIndicatorName - wenn die Option CustomIndicator für den vorherigen Parameter ausgewählt wurde, muss der Nutzer hier den richtigen Namen des Indikators eingeben.
  
• UseDefaults - wenn diese Option auf true gesetzt ist, werden die im Indikator fest kodierten Standard-Nutzereingaben verwendet.
  
• IndicatorParameterTypes - dies ist eine durch Komma getrennte Zeichenkette, die die Datentypen des Indikators in der richtigen Reihenfolge auflistet, ein Beispiel für eine mögliche Eingabe: Angenommen, der zu analysierende Indikator akzeptiert 4 Eingaben des Typs double, integer, integer bzw. string, dann muss der Nutzer einfach „double, integer, integer, string“ eingeben; die Kurzform „d, i, i, s“ wird ebenfalls unterstützt, wobei d= double, i=integer und s=string. Enum-Werte werden auf den Typ Integer abgebildet.
  
• IndicatorParameterValues - wie bei der vorherigen Eingabe handelt es sich auch hier um eine durch Kommata getrennte Liste von Werten, z. B. „0.5,4,5,string_value“, wie im vorherigen Beispiel. Liegt ein Fehler in der Formatierung der Parameter für IndicatorParameterValues oder IndicatorParameterTypes vor, werden die Standardwerte des Indikators für nicht auflösbare oder fehlende Werte verwendet.
  Überprüfen Sie die Registerkarte Experten auf Fehlermeldungen. Beachten Sie, dass der Name des Indikators hier nicht angegeben werden muss. Wenn es sich um einen nutzerdefinierten Indikator handelt, muss dieser durch CustomIndicatorName angegeben werden.
• IndicatorBuffer - der Nutzer kann festlegen, welcher der Indikatorpuffer analysiert werden soll.
  
• HistoryStart - das Startdatum der Stichprobe der Kurshistorie.
  
• HistorySize - dies ist die Anzahl der zu analysierenden Balken relativ zu HistoryStart.
  
• Intervals - dieser Parameter wird verwendet, um die Anzahl der Intervalle anzugeben, die für den Deskretisierungsprozess erstellt werden. Der Autor von TTMTS gibt 20 Intervalle für einen Stichprobenumfang von mehreren Tausend an, wobei 2 als harter Mindestwert festgelegt wurde.  Ich habe hier einen eigenen Ansatz für einen geeigneten Wert entwickelt, indem ich die Möglichkeit eingebaut habe, die Anzahl der Intervalle in Abhängigkeit vom Stichprobenumfang zu variieren, und zwar 51 für jeweils 1000 Stichproben. Diese Option ist verfügbar, wenn ein Nutzer einen Wert kleiner als 2 eingibt. Wenn Sie also Intervall auf eine beliebige Zahl kleiner als 2 einstellen, ändert sich die Anzahl der verwendeten Intervalle je nach der Anzahl der analysierten Takte.
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Noch ein Hinweis zu dem für Intervalle gewählten Wert: Wenn Sie die Anzahl der in der Berechnung verwendeten Intervalle ändern, ändert sich der endgültige Entropiewert. Bei der Durchführung von Analysen wäre es ratsam, eine gewisse Konsistenz zu wahren, um die Auswirkungen des verwendeten unabhängigen Inputs zu minimieren. Im Skript ist die Berechnung der relativen Entropie in einer Funktion gekapselt, die in der Datei Entropy.mqh definiert ist.

Das Skript gibt einfach den resultierenden Entropiewert in der Registerkarte „Experten“ aus. Wenn Sie das Skript für verschiedene integrierte und nutzerdefinierte Indikatoren ausführen, erhalten Sie die unten aufgeführten Ergebnisse. Es ist interessant festzustellen, dass William's Percent Range eine relative Entropie nahe der Perfektion aufweist. Vergleichen Sie dies mit dem Market Facilitation Index, der ein enttäuschendes Ergebnis zeigt.

Mit diesen Ergebnissen können wir weitere Schritte unternehmen, um die Daten so zu verarbeiten, dass sie für maschinelle Lernalgorithmen geeignet sind. Dazu ist eine strenge Analyse der statistischen Eigenschaften des Indikators erforderlich. Durch die Untersuchung der Verteilung der Indikatorwerte lassen sich Probleme mit Schieflage und Ausreißern erkennen. All dies kann die Modellbildung beeinträchtigen.

Als Beispiel untersuchen wir einige statistische Eigenschaften von zwei oben analysierten Indikatoren.

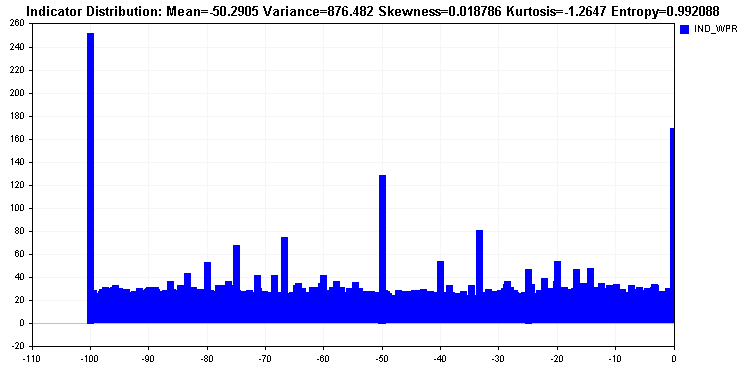
Die Verteilung der prozentualen Spanne von Williams zeigt, dass fast alle Werte über die gesamte Spanne verteilt sind; abgesehen davon, dass die Verteilung multimodal ist, ist sie ziemlich gleichmäßig. Eine solche Verteilung ist ideal und spiegelt sich im Entropiewert wider.

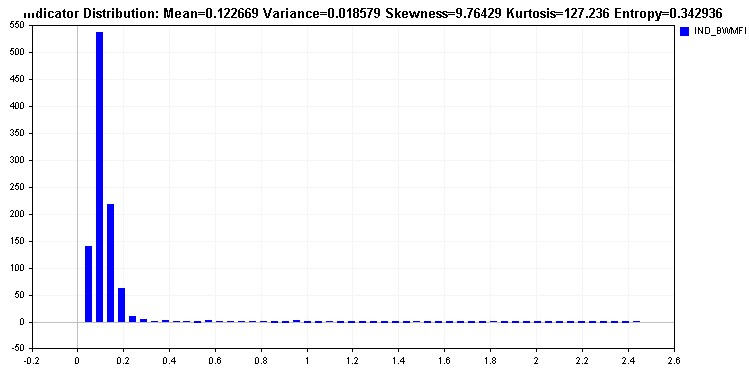
Dies steht im Gegensatz zur Verteilung des Market Facilitation Index, der einen langen „Rattenschwanz“ von Werten aufweist. Ein solcher Indikator wäre für die meisten Lernalgorithmen problematisch und erfordert eine Transformation der Werte. Die Umwandlung der Werte sollte zu einer Verbesserung der relativen Entropie des Indikators führen.

Verbesserung des Informationsgehalts eines Indikators

Es sollte darauf hingewiesen werden, dass Änderungen, die die Entropie des Indikators erhöhen, nicht als eine Möglichkeit zur Verbesserung der Genauigkeit der vom Indikator gelieferten Signale angesehen werden sollten. Durch die Erhöhung der Entropie wird ein nutzloser Indikator nicht zum heiligen Gral. Bei der Verbesserung der Entropie geht es um die Verarbeitung der Indikatordaten für eine effektive Nutzung in Vorhersagemodellen.

Diese Option sollte in Betracht gezogen werden, wenn der Entropiewert hoffnungslos schlecht ist, d. h. weit unter 0,5 und näher an Null liegt. Obere Schwellenwerte sind rein willkürlich. Es ist Sache des Entwicklers, einen akzeptierten Mindestwert zu wählen. Das Ziel ist es, eine möglichst gleichmäßige Verteilung der Indikatorwerte zu erreichen. Die Entscheidung, eine Transformation anzuwenden, sollte auf einer Analyse beruhen, die an einer umfangreichen und repräsentativen Stichprobe von Indikatorwerten durchgeführt wurde.

Die angewandte Transformation sollte das eigentliche Verhalten des Indikators nicht verändern. Der transformierte Indikator sollte eine ähnliche Form wie der Rohindikator haben, d. h. die Lage der Tiefpunkte und Spitzenwerte sollte in beiden Reihen ähnlich sein. Wenn dies nicht der Fall ist, besteht die Gefahr, dass potenziell nützliche Informationen verloren gehen.

Es gibt zahlreiche Transformationsmethoden, die auf verschiedene Aspekte der Unzulänglichkeiten von Testdaten abzielen. Wir werden nur einige einfache Transformationen betrachten, die darauf abzielen, offensichtliche Mängel zu beheben, die durch grundlegende statistische Analysen aufgedeckt werden. Die Vorverarbeitung ist ein weites Feld des maschinellen Lernens. Jeder, der die Anwendung von Methoden des maschinellen Lernens beherrschen möchte, sollte sich mehr Wissen auf diesem Gebiet aneignen.

Um die Auswirkungen einiger Transformationen zu veranschaulichen, stellen wir ein Skript vor, das die Möglichkeit bietet, verschiedene Transformationen anzuwenden und auch die Verteilung der analysierten Daten anzuzeigen. Das Skript implementiert 6 Beispiele für Transformationsfunktionen:

• Die Transformation mit der Quadratwurzel ist geeignet, um gelegentlich auftretende Indikatorwerte, die erheblich von der Mehrheit abweichen, zu unterdrücken.

• Die Transformation mit der Kubikwurzel ist eine weitere Funktion zur Quadratur, die am besten für Indikatoren mit negativen Werten geeignet ist.

• Die Transformation mit der Log-Funktion komprimiert die Werte hingegen in größerem Umfang als die zuvor genannten komprimierenden Transformationen.

• Die hyperbolischen Tangens und die logistischen Transformationen sollten auf Datenwerte einer geeigneten Skala angewendet werden, um Probleme mit der Erzeugung ungültiger Zahlen (Nan-Fehler) zu vermeiden.

• Die extreme Transformation führt zu extremer Gleichförmigkeit in einem Datensatz. Sie sollte nur auf Indikatoren angewandt werden, die überwiegend eindeutige Werte mit sehr wenigen ähnlichen Zahlen liefern.

Ein Skript zum Vergleich transformierter Indikatorwerte

Im Vergleich zum früheren Skript enthält es die gleichen Nutzereingaben zur Angabe des zu analysierenden Indikators. Die neuen Eingaben werden im Folgenden beschrieben:

• DisplayTime - das Skript zeigt eine Grafik der Verteilung des Indikators an. DisplayTime ist ein ganzzahliger Wert in Sekunden, der die Zeit angibt, die die Grafik sichtbar ist, bevor sie entfernt wird.

• ApplyTransfrom - ist ein boolescher Wert, der den Modus für das Skript festlegt. Bei false zeichnet das Skript die Verteilung und zeigt grundlegende Statistiken der Stichprobe zusammen mit der relativen Entropie an. Wenn true gesetzt ist, wird eine Transformation auf die rohen Indikatorwerte angewendet und die relativen Entropiewerte vor und nach der Transformation angezeigt. Die Verteilung der veränderten Proben kann auch als Kurve in Rot eingezeichnet werden.

• Select_transform - ist eine Aufzählung mit den zuvor beschriebenen Transformationen, die angewendet werden können, um die Entropie des Indikators zu erhöhen.

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Wir fahren mit den Beispielen fort und vergleichen die Anwendung von Quadratwurzel- und Kubikwurzeltransformationen.

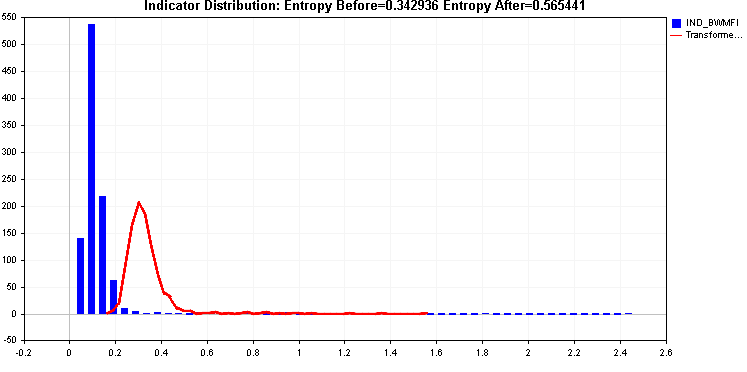
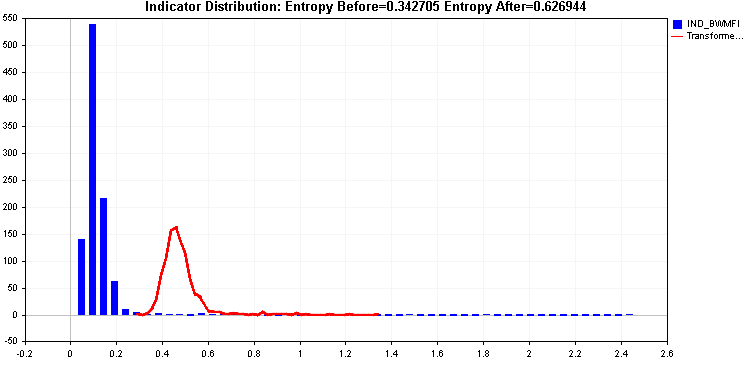
Beide bieten eine Verbesserung der Entropie, aber die restlichen Werte auf der rechten Seite könnten problematisch sein, da die beiden bisher angewandten Transformationen nicht in der Lage waren, ihn effektiv zu bewältigen.

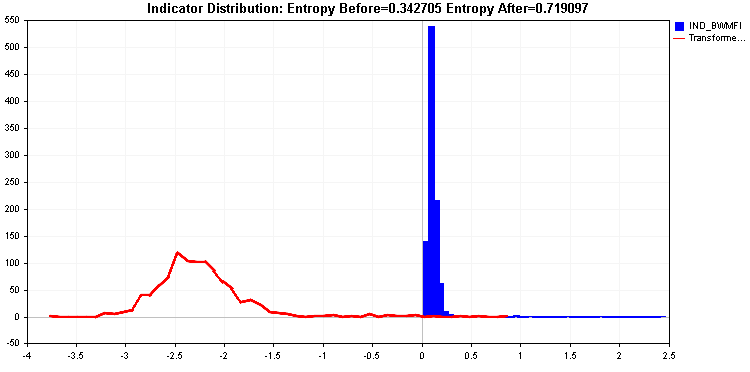
Die Log-Transformation ergibt einen noch besseren Entropiewert. Dennoch sind die Reste ziemlich signifikant. Als letzten Ausweg können wir die Extremtransformation anwenden.

Schlussfolgerung

Wir haben das Konzept der Entropie untersucht, um die Notwendigkeit einer Transformation der Indikatorwerte vor der Verwendung beim Training des Vorhersagemodells zu bewerten.

Das Konzept wurde in zwei Skripten umgesetzt. EntropyIndicatorAnalyis gibt die relative Entropie einer Probe auf der Registerkarte Experten aus. Das andere Skript IndicatorAnalysis geht noch einen Schritt weiter, indem es die Verteilung der rohen und transformierten Indikatorwerte zeichnet und die relativen Entropiewerte davor und danach anzeigt.

Die Tools können zwar nützlich sein, sind aber nicht auf alle Arten von Indikatoren anwendbar: Pfeilbasierte Indikatoren, die leere Werte enthalten, sind für die hier beschriebenen Skripte nicht geeignet.  In solchen Fällen wären andere Kodierungstechniken erforderlich.

Das Thema Datentransformation ist nur eine Teilmenge der möglichen Vorverarbeitungsschritte, die bei der Erstellung jeglicher Art von Vorhersagemodellen berücksichtigt werden sollten. Der Einsatz solcher Techniken wird dazu beitragen, wirklich einzigartige Beziehungen zu finden, die den nötigen Vorsprung bieten, um die Märkte zu schlagen.

Dateiname	Beschreibung
Mql5/Include/Entropie.mqh	Include-Datei, die verschiedene Definitionen für Funktionen zur Berechnung der Entropie und für Hilfsfunktionen enthält, die von den beigefügten Skripten verwendet werden.
Mql5/Skripte/IndikatorAnalyse.mq5	ein Skript, das eine Grafik anzeigt, die die Verteilung der Indikatorwerte zusammen mit ihrer Entropie darstellt.
Mql5/Scripts/EntropyIndicatorAnalysis	ein Skript, das zur Berechnung der Entropie eines Indikators verwendet werden kann.