Измерение информативности индикатора

Введение

Машинное обучение опирается на обучающие данные, чтобы изучить общее поведение рынка и в конечном итоге делать точные прогнозы. Выбранный алгоритм обучения должен пройти через тщательно отобранную выборку для извлечения значимой информации. Причина, по которой многим не удается успешно применить эти сложные инструменты, заключается в том, что большая часть значимой информации скрыта в зашумленных данных. Многие разработчики стратегий могут не осознавать, что используемые наборы данных могут не подходить для обучения модели.

Индикаторы можно рассматривать как поставщиков информации об основных ценовых рядах, к которым они применяются. Используя эту предпосылку, энтропию можно использовать для измерения того, сколько информации передается индикатором. Используя шаги и инструменты, описанные в книге Тимоти Мастерса "Тестирование и настройка систем рыночной торговли" (TTMTS), написанной Тимоти Мастерсом, мы продемонстрируем, как можно оценить структуру данных индикатора.

Зачем измерять информативность индикатора?

Часто при использовании инструментов машинного обучения для разработки стратегии мы прибегаем к тому, чтобы просто забрасывать алгоритмы всевозможными данными в надежде, что из этого что-то получится. В конечном итоге успех будет зависеть от качества предикторов, используемых в модели, а эффективные предикторы обычно обладают определенными характеристиками. Одна из них - информационное наполнение.

Количество информации в переменных, используемых для обучения модели, важно, но это не единственное требование для эффективного обучения модели. Таким образом, измерение информационного содержания можно использовать для проверки показателей, которые в противном случае использовались бы вслепую в процессе обучения. Здесь как раз и применяется понятие энтропии.

Энтропия

Об энтропии уже неоднократно писали на MQL5.com. Я надеюсь, читатель простит мне еще одно определение, так как это важно для понимания применения концепции. В предыдущих статьях была представлена история и вывод расчета энтропии, поэтому для краткости мы начнем с уравнения.

                                                        

H(X) означает энтропию X. X — дискретная переменная, представляющая произвольную переменную, скажем, сообщение. Содержимое сообщения может принимать только конечное число значений. Это представлено в уравнении как малый x. Малые х — это наблюдаемые значения сообщений, как если бы все возможные значения х были перечислены в наборе N.

Рассмотрим пример "правильной" кости. Брошенную кость можно воспринимать как предоставление информации, которая определяет исход игры. У игральной кости 6 граней, пронумерованных от 1 до 6. Вероятность увидеть любое из чисел равна 1/6.

Используя этот пример, большой X будет игральной костью, а малый x может быть любым числом, нарисованным на гранях игральной кости. Все числа помещены в множество N ={ 1,2,3,4,5,6}. Применив формулу, мы узнаем, что энтропия этой кости равна 0,7781.

                                                         

Теперь рассмотрим другую игральную кость, имеющую производственный брак. На две ее грани нанесено одно и то же число. Для этой дефектной кости набор N возможных значений равен {1,1,3,4,5,6}. Снова используя формулу, мы получаем среднее значение энтропии 0,6778.

                                                 

Сравнивая значения, мы замечаем, что информативность уменьшилась. При анализе обеих костей, когда все вероятности наблюдения каждого возможного значения равны, уравнение энтропии дает максимально возможное значение. Следовательно, энтропия достигает своего максимального среднего значения, когда вероятности всех возможных значений равны.

Если мы отбросим дефектную кость для индикатора, который выдает на выходе традиционные действительные числа, X становится индикатором, а маленький x будет диапазоном значений, которые может принимать индикатор. Уравнение энтропии имеет дело строго с дискретными переменными. Преобразование уравнения для работы с непрерывными переменными возможно, но реализация будет затруднена, поэтому проще придерживаться дискретных чисел.

Расчет энтропии индикатора

Чтобы применить уравнение энтропии к непрерывным переменным, мы должны дискретизировать значения индикатора. Это делается путем деления диапазона значений на интервалы одинакового размера, а затем подсчета количества значений, попадающих в каждый интервал. При использовании этого метода исходное множество, перечисляющее максимальный диапазон всех значений индикатора, заменяется подмножествами, каждое из которых представляет собой выбранные интервалы.

При работе с непрерывными переменными вариации вероятностей возможных значений, которые может принять переменная, становятся значительными, поскольку они обеспечивают важный аспект применения энтропии к индикаторам.

Вернемся к первому примеру с игральной костью. Если мы разделим конечные значения энтропии каждого на log(N) для каждого из соответствующих n, правильная кость даст 1, а дефектная - 0.87. Деление значения энтропии на логарифм числа значений, которые может принимать переменная, дает меру, которая является относительной теоретической максимальной энтропии переменной, называемой пропорциональной, или относительной энтропией.

Именно это значение было бы полезно при нашей оценке индикаторов, поскольку оно укажет, насколько энтропия индикатора близка к его теоретическому максимальному среднему значению. Чем ближе, тем лучше. В противном случае индикатор, скорее всего, непригоден для использования в машинном обучении. 

                                  

Окончательное уравнение показано выше, а код реализован ниже в виде MQL5-скрипта, который доступен для скачивания в виде вложения в конце статьи. С помощью скрипта мы сможем анализировать большинство индикаторов.

Скрипт для расчета энтропии индикатора

Скрипт вызывается со следующими настраиваемыми параметрами:

• TimeFrame - выбранный таймфрейм для анализа значений индикатора.
• IndicatorType - здесь пользователь может выбрать один из встроенных индикаторов для анализа. Чтобы указать пользовательский индикатор, выберите "Пользовательский индикатор" и введите его имя в следующем значении параметра.
  
• CustomIndicatorName - если для предыдущего параметра выбрана опция "Пользовательский индикатор", здесь необходимо ввести правильное имя индикатора.
  
• UseDefaults - при true будут использоваться пользовательские входные параметры по умолчанию, жестко закодированные в индикаторе.
  
• IndicatorParameterTypes - строка с разделителями-запятыми, в которой перечислены типы данных индикатора в правильном порядке. Например, если анализируемый индикатор принимает четыре входных параметра типа double, integer, integer и string, просто вводим "double, integer, integer, string". Также поддерживается короткая форма "d, i, i, s". Значения перечисления сопоставляются с целочисленным типом.
  
• IndicatorParameterValues - как и предыдущий параметр, это также список значений, разделенных запятыми. Продолжая предыдущий пример, строка будет выглядеть так: "0.5,4,5,string_value". Если есть какая-либо ошибка в формировании параметров либо для IndicatorParameterValues, либо для IndicatorParameterTypes, это приведет к тому, что значения индикатора по умолчанию будут использоваться для любых конкретных значений, которые не могут быть расшифрованы или отсутствуют.
  Проверьте вкладку экспертов на наличие сообщений об ошибках. Обратите внимание, что нет необходимости указывать здесь имя индикатора. Если рассматривается пользовательский индикатор, он должен быть указан в CustomIndicatorName.
• IndicatorBuffer - какой из индикаторных буферов анализировать.
  
• HistoryStart - дата начала выборки истории.
  
• HistorySize - количество баров для анализа относительно HistoryStart.
  
• Intervals - количество интервалов для дискретизации. Автор TTMTS указывает 20 интервалов для размера выборки в несколько тысяч, причем 2 являются жестким минимальным значением. Я добавил свой собственный подход к подходящему значению, реализовав возможность варьировать количество интервалов относительно размера выборки, в частности, 51 на каждые 1000 выборок. Эта опция доступна, если пользователь вводит любое значение меньше 2. Таким образом при установке Interval на любое число меньше 2 количество используемых интервалов будет меняться в зависимости от количества анализируемых баров.
  

//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_BEARS;
input string   CustomIndicatorName="";
input bool     UseDefaults=true;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';
input int HistorySize=50000;
input int      Intervals=0;

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(Symbol(),Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   Print("Entropy of ",(IndicatorType==IND_CUSTOM)?CustomIndicatorName:EnumToString(IndicatorType)," is ",relativeEntroy(Intervals,buffer));
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

//if(!p_size)
//  return true;

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Обратите внимание на значение, выбранное для Intervals: изменение количества интервалов, используемых в расчете, изменит конечное значение энтропии. При проведении анализа было бы целесообразно соблюдать некоторую последовательность, чтобы свести к минимуму влияние независимых входных данных. В скрипте расчет относительной энтропии инкапсулирован в функцию, определенную в файле Entropy.mqh.

Скрипт просто выводит полученное значение энтропии на вкладке экспертов. Запуск скрипта для различных встроенных и пользовательских индикаторов дает результаты, показанные ниже. Интересно отметить, что процентный диапазон Уильямса имеет относительную энтропию, близкую к совершенству. Сравним его с индикатором Market Facilitation Index, который показывает неутешительный результат.

С этими результатами мы можем предпринять дальнейшие шаги для обработки данных, чтобы сделать их пригодными для алгоритмов машинного обучения. Это предполагает проведение тщательного анализа статистических свойств индикатора. Изучение распределения значений индикатора выявит любые проблемы с перекосом и выбросами, которые могут ухудшить обучение модели.

В качестве примера рассмотрим некоторые статистические свойства двух проанализированных выше индикаторов.

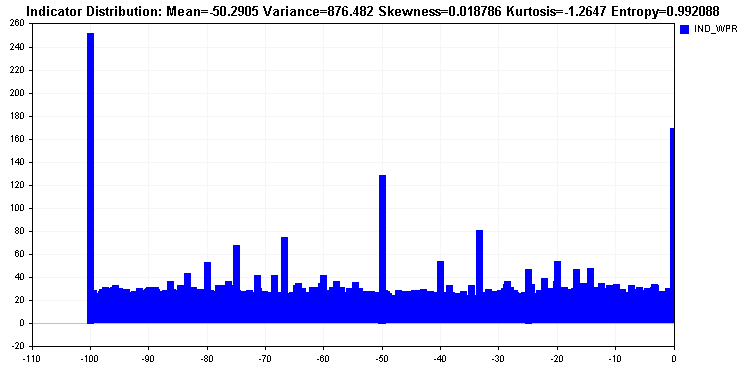
Распределение процентного диапазона Уильямса показывает, как почти все значения распределены по всему диапазону. Помимо мультимодальности, распределение является довольно равномерным. Такое распределение является идеальным и отражается на значении энтропии.

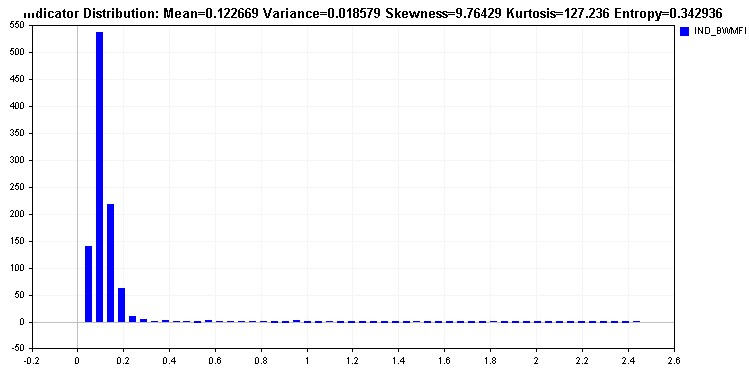
Это отличается от распределения Market Facilitation Index, который имеет длинный хвост. Такой индикатор не подходит для большинства алгоритмов обучения и требует преобразования значений. Преобразование значений должно привести к улучшению относительной энтропии индикатора.

Повышение информативности индикатора

Следует отметить, что изменения, повышающие энтропию индикатора, не следует рассматривать как способ повысить точность сигналов, предоставляемых индикатором. Повышение энтропии не превратит бесполезный индикатор в грааль. Улучшение энтропии связано с обработкой данных индикатора для эффективного использования в прогностических моделях.

Этот вариант следует рассматривать, когда значение энтропии безнадежно плохое - все, что значительно ниже 0,5 и ближе к нулю. Верхние пороги являются чисто произвольными. Разработчик должен самостоятельно выбрать приемлемое минимальное значение. Весь смысл в том, чтобы получить максимально близкое к равномерному распределение значений индикатора. Решение о применении преобразования должно основываться на анализе, проведенном на значительной и репрезентативной выборке значений показателей.

Применяемое преобразование не должно изменять поведение индикатора. Преобразованный индикатор должен иметь ту же форму, что и необработанный индикатор, например, расположение впадин и пиков должно быть одинаковым в обоих рядах. Если это не так, мы рискуем потерять потенциально полезную информацию.

Существует множество методов преобразования, нацеленных на различные аспекты несовершенства тестовых данных. Мы рассмотрим лишь несколько простых преобразований, направленных на исправление очевидных дефектов, обнаруженных с помощью базового статистического анализа. Предварительная обработка — обширная ветвь машинного обучения. Всем, кто надеется освоить применение методов машинного обучения, рекомендуется получить больше знаний в этой области.

Чтобы проиллюстрировать эффект некоторых преобразований, мы представляем скрипт, который имеет возможность применять различные преобразования, а также отображает распределение анализируемых данных. Скрипт реализует шесть примеров функций трансформации:

• преобразование функции квадратного корня подходит для сжатия случайных значений индикатора, которые значительно отклоняются от большинства.

• преобразование кубического корня — еще одна функция сжатия, которая лучше всего подходит для индикаторов с отрицательными значениями.

• в то время как логарифмическое преобразование сжимает значения в большей степени, чем упомянутые ранее.

• гиперболический тангенс и логистические преобразования должны применяться к значениям данных подходящего масштаба, чтобы избежать проблем с получением недопустимых чисел (ошибки nan).

• экстремальное преобразование вызывает экстремальную однородность в наборе данных. Его следует применять только к индикаторам, которые дают в основном уникальные значения с очень небольшим количеством похожих цифр.

Скрипт для сравнения преобразованных значений индикатора

Скрипт содержит те же пользовательские данные для указания анализируемого индикатора, что и предыдущий. Новые входные параметры описаны ниже:

• DisplayTime - скрипт отображает график распределения индикатора. DisplayTime — целочисленное значение в секундах, которое представляет собой время, в течение которого изображение будет отображаться перед удалением.

• ApplyTransfrom — логическое значение, задающее режим работы скрипта. При false скрипт рисует распределение и отображает базовую статистику выборки вместе с относительной энтропией. При true он применяет преобразование к необработанным значениям индикатора и отображает относительные значения энтропии до и после преобразования. Распределение модифицированных образцов изображается в виде кривой красного цвета.

• Select_transform - перечисление, предоставляющее описанные ранее преобразования, которые можно применить для возможного увеличения энтропии индикатора.

//+------------------------------------------------------------------+
//|                                            IndicatorAnalysis.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Entropy.mqh>
//--- input parameters
input ENUM_TIMEFRAMES Timeframe=0;
input ENUM_INDICATOR  IndicatorType=IND_CUSTOM;
input string   CustomIndicatorName="";
input bool     UseDefaults=false;
input string   IndicatorParameterTypes="";
input string   IndicatorParameterValues="";
input int      IndicatorBuffer=0;
input datetime HistoryStart=D'2023.02.01 04:00';;
input int HistorySize=50000;
input int DisplayTime=30;//secs to keep graphic visible
input bool ApplyTransform=true;
input ENUM_TRANSFORM Select_transform=TRANSFORM_LOG;//Select function transform

int handle=INVALID_HANDLE;
double buffer[];
MqlParam b_params[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!processParameters(UseDefaults,b_params))
      return;

   int y=10;
   while(handle==INVALID_HANDLE && y>=0)
     {
      y--;
      handle=IndicatorCreate(_Symbol,Timeframe,IndicatorType,ArraySize(b_params),b_params);
     }
//---
   if(handle==INVALID_HANDLE)
     {
      Print("Invalid indicator handle, error code: ",GetLastError());
      return;
     }

   ResetLastError();
//---
   if(CopyBuffer(handle,IndicatorBuffer,HistoryStart,HistorySize,buffer)<0)
     {
      Print("error copying to buffer, returned error is ",GetLastError());
      IndicatorRelease(handle);
      return;
     }
//---
   DrawIndicatorDistribution(DisplayTime,ApplyTransform,Select_transform,IndicatorType==IND_CUSTOM?CustomIndicatorName:EnumToString(IndicatorType),buffer);
//---
   IndicatorRelease(handle);
  }
//+------------------------------------------------------------------+
bool processParameters(bool use_defaults,MqlParam &params[])
  {

   bool custom=(IndicatorType==IND_CUSTOM);

   string ind_v[],ind_t[];

   int types,values;

   if(use_defaults)
      types=values=0;
   else
     {
      types=StringSplit(IndicatorParameterTypes,StringGetCharacter(",",0),ind_t);
      values=StringSplit(IndicatorParameterValues,StringGetCharacter(",",0),ind_v);
     }

   int p_size=MathMin(types,values);

   int values_to_input=ArrayResize(params,(custom)?p_size+1:p_size);

   if(custom)
     {
      params[0].type=TYPE_STRING;
      params[0].string_value=CustomIndicatorName;
     }

   if(use_defaults)
      return true;

   int i,z;
   int max=(custom)?values_to_input-1:values_to_input;

   for(i=0,z=(custom)?i+1:i; i<max; i++,z++)
     {
      if(ind_t[i]=="" || ind_v[i]=="")
        {
         Print("Warning: Encountered empty string value, avoid adding comma at end of string parameters");
         break;
        }

      params[z].type=EnumType(ind_t[i]);

      switch(params[z].type)
        {
         case TYPE_INT:
            params[z].integer_value=StringToInteger(ind_v[i]);
            break;
         case TYPE_DOUBLE:
            params[z].double_value=StringToDouble(ind_v[i]);
            break;
         case TYPE_STRING:
            params[z].string_value=ind_v[i];
            break;
         default:
            Print("Error: Unknown specified parameter type");
            break;
        }
     }

   return true;

  }


//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_DATATYPE EnumType(string type)
  {
   StringToLower(type);
   const ushort firstletter=StringGetCharacter(type,0);

   switch(firstletter)
     {
      case 105:
         return TYPE_INT;
      case 100:
         return TYPE_DOUBLE;
      case 115:
         return TYPE_STRING;
      default:
         Print("Error: could not parse string to match data type");
         return ENUM_DATATYPE(-1);
     }

   return ENUM_DATATYPE(-1);
  }
//+------------------------------------------------------------------+

Продолжая примеры, мы сравниваем применение преобразований квадратного корня и кубического корня.

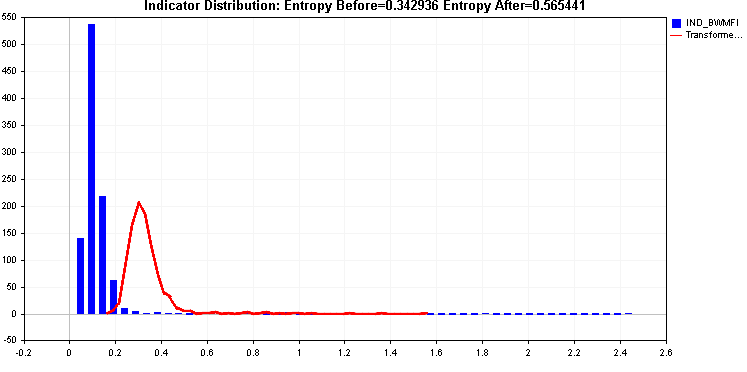
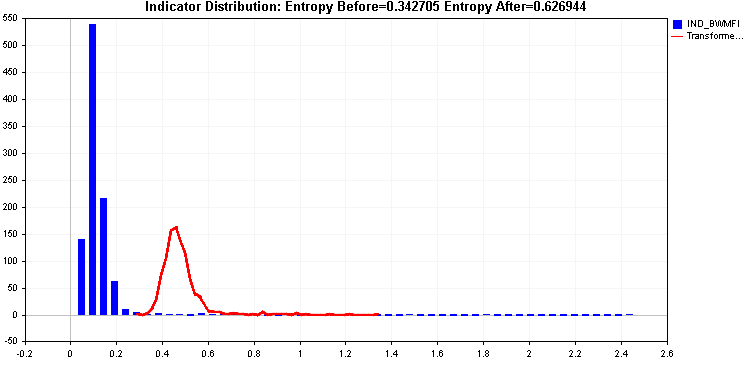
Оба обеспечивают улучшение энтропии, но этот правый хвост может быть проблематичным. Два примененных преобразования не смогли эффективно с ним справиться.

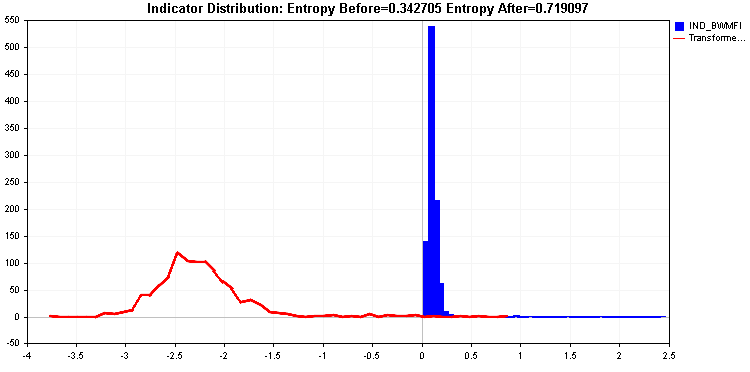
Логарифмическое преобразование дает еще лучшее значение энтропии. Но хвосты по-прежнему значительны. В крайнем случае мы можем применить экстремальное преобразование.

Заключение

Мы исследовали концепцию энтропии, чтобы оценить необходимость преобразования значений индикатора перед их использованием в обучении прогнозной модели.

Концепция была реализована в двух скриптах. В частности, EntropyIndicatorAnalyis, который отображает относительную энтропию образца на вкладке экспертов. Другой скрипт IndicatorAnalysis делает еще один шаг вперед, рисуя распределение необработанных и преобразованных значений индикатора, а также отображая значения относительной энтропии до и после.

Хотя инструменты могут быть полезными, они не могут быть применены ко всем типам индикаторов. Как правило, индикаторы на основе стрелок, которые содержат пустые значения, не подходят для описанных здесь скриптов. В таких случаях потребуются другие методы кодирования.

Тема преобразования данных — это лишь часть возможных шагов предварительной обработки, которые следует учитывать при построении любой прогностической модели. Использование таких методов поможет выявить действительно уникальные отношения, которые могут обеспечить преимущество, необходимое для победы над рынками.

Имя файла	Описание
Mql5/Include/Entropy.mqh	include-файл, который содержит различные определения функций, используемых для вычисления энтропии, а также служебные функции, используемые прилагаемыми скриптами.
Mql5/Scripts/IndicatorAnalysis.mq5	скрипт, отображающий график, показывающий распределение значений индикатора вместе с его энтропией.
Mql5/Scripts/EntropyIndicatorAnalysis	скрипт, который можно использовать для расчета энтропии индикатора