MetaTrader 5 / 統計と分析
English Русский Deutsch
preview
段階的特徴量選択の基準としての相互情報量

段階的特徴量選択の基準としての相互情報量

MetaTrader 5 — 統計と分析 | 3 4月 2025, 09:26
129 0
Francis Dube
Francis Dube

はじめに

相互情報量は、特に複雑で非線形な関係を扱う際に、効果的な予測変数を特定するための強力なツールです。他の手法では見落とされがちな依存関係を明らかにできるため、このような複雑な関係を活用できるモデルにとって特に有用です。この記事では、Hanchuan Peng、Fuhui Long、Chris Dingによる研究論文「Feature Selection Based on Mutual Information:Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy」で提案されたアルゴリズムに着目し、特徴量選択における相互情報量の応用について考察します。

まず、連続変数における相互情報量の推定方法を説明し、その後、特徴量選択のプロセスについて詳しく解説します。最後に、合成データセットと実データセットの両方を用いた例を通じて、本アルゴリズムの有効性を示します。


連続変数の相互情報量の推定

相互情報量(I(X;Y))は、2つのランダム変数XとYが共有する情報の量を定量化する指標です。離散変数の場合、その計算は比較的容易で、結合確率と周辺確率を用いた総和によって求められます。

離散相互情報量

しかし、連続変数は、その値の範囲が無限であるため、大きな課題を伴います。この問題に対処する一般的な方法として、連続変数をビンに分割し、離散型の相互情報量の計算式を適用する手法があります。しかし、この方法の精度はビンの幅やビンの数に大きく依存するため、推定される相互情報量に大きなばらつきが生じる可能性があります。

連続相互情報量

連続変数の相互情報量を計算するには、離散和から連続積分へと移行する必要があります。この計算には、結合確率密度関数(PDF)および周辺確率密度関数の情報が必要ですが、データが限られている場合、それらを直接得ることは難しいのが一般的です。この問題を解決する方法の一つにParzenウィンドウ法 があります。ここの手法では、データ上にウィンドウ関数を適用し、ウィンドウ内のデータ点に重みを付けた総和を計算することで、確率密度関数を推定します。各データ点に割り当てられる重みは、ウィンドウの中心からの距離が大きくなるにつれて減少します。ウィンドウをデータ空間内で移動しながら加重総和を計算することで、確率密度関数の推定値を構築できます。

Parzen密度近似

この手法は、基礎となる分布が不明または複雑な場合に特に有効です。ウィンドウの形状とサイズを調整することで、密度推定の滑らかさと精度を調整できます。しかし、ウィンドウパラメータの選択が推定結果の品質に大きく影響することに注意することが重要です。Parzen密度推定の有効性は、適切な重み付け関数の選択に依存します。この重み付け関数は、理想的には1に統合され、引数がゼロから離れるにつれて急速に減衰するべきです。この重み付け関数の一般的な選択肢として、スケールパラメータσ（シグマ）を特徴とするガウス関数があります。

ガウス重み関数

ただし、シグマの最適値を決定することは困難であり、推定される密度に大きなばらつきが生じることがよくあります。シグマの選択に対するこの敏感さは、Parzenウィンドウ法の大きな欠点であり、正確な密度推定が求められる予測変数候補の評価などのタスクには理想的とは言えません。

連続変数間の相互情報量を推定するためのParzenウィンドウ法の代替手法は、適応型分割です。適応型分割は、固定ビニングの単純な方法に比べて大きな改善をもたらします。情報量が多い領域を繰り返し細分化することで、適応型分割は計算リソースをデータ空間の最も重要な領域に集中させることができます。このターゲットを絞ったアプローチにより、特に複雑で不均一な分布を扱う場合に、相互情報量の推定がより正確になります。適応型分割の主な強みは、データ構造体に応じて動的に適応できる点です。再帰的な分割プロセスにより、依存関係が大きい領域がさらに細分化され、情報量が少ない領域はそのまま残ります。この動的なアプローチによって、データを過度に平滑化したり、過剰適合させたりするリスクがある固定ビニングの問題を回避できます。

さらに、適応型分割には統計的テストが組み込まれており、分割プロセスをガイドします。潜在的な分割の統計的有意性を評価することで、真の情報とランダムなノイズを区別できます。これにより、相互情報量の推定値が過大になるリスクがある過剰適合を防ぐことができます。ナイーブな方法の主な問題点は、事例がほとんどないか全くない二変量領域に過度に焦点を当て、情報が密集している領域を無視する可能性があることです。 

適応型分割

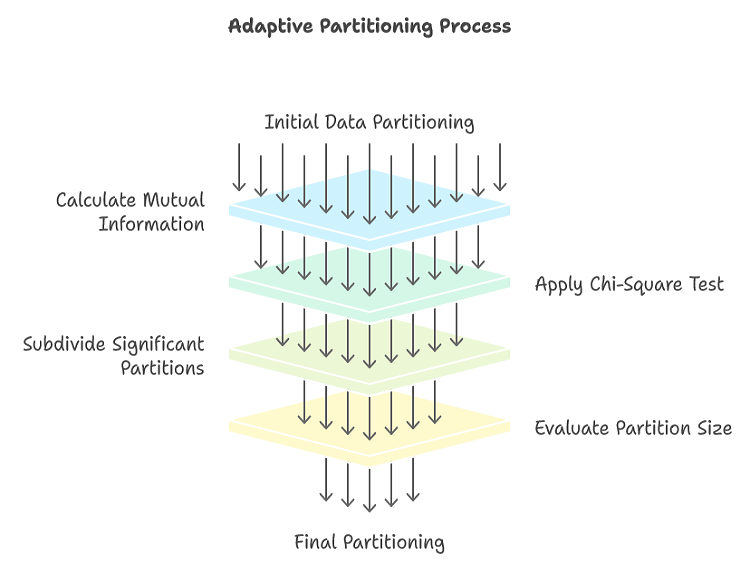
適応型分割は、データ空間の粗粒度の分割から始まります。各パーティションごとに、変数間の相互情報量が計算されます。この値が事前に定められた閾値を超えると、パーティションはさらに小さなサブパーティションに分割されます。この再帰的な分割プロセスは、停止基準が満たされるまで続きます。分割プロセスが早期に停止すると、結果として得られる分割が粗すぎて、詳細が失われ、推定される相互情報量に下方バイアスが生じる可能性があります。逆に、分割プロセスが長すぎると、分割が過度に細かくなり、過剰適合が発生し、ノイズによって相互情報量の推定値が膨らむ可能性があります。

パーティションをさらに細分化する必要があるかどうかを判断するには、カイ二乗検定を用います。このテストは、パーティション内の2つの変数間の独立性を評価します。パーティションは4つのサブパーティションに分割され、2x2の分割表が作成されます。4つのサブパーティションのそれぞれに含まれるデータポイントの数がカウントされます。2つの変数間の独立性という帰無仮説の下で、各サブパーティション内のデータポイントの予想数は、限界合計に基づいて計算されます。計算されたカイ二乗統計量は、自由度1のカイ二乗分布の臨界値と比較されます。計算値が臨界値を超える場合、独立性の帰無仮説は棄却され、パーティション内の2つの変数間に有意な関係があることを示します。

.カイ二乗検定が有意な場合、パーティションはさらに小さく分割されます。このプロセスは、パーティションが十分に均質になるまで、または停止基準が満たされるまで再帰的に続きます。カイ二乗検定が有意でない場合、パーティションは均質であるとみなされ、それ以上の細分化は行いません。

単純な2x2分割では見逃される可能性のある、パーティション内のより複雑な関係に対処するために、アルゴリズムには追加のチェックが組み込まれています。2x2カイ二乗検定で有意な関係が検出されなかったが、パーティションが比較的大きいままである場合、より精密な4x4分割が実行されます。次に、この4x4パーティションにカイ二乗検定を適用して、非ランダム分布の存在を評価します。4x4テストでも有意な関係が検出されない場合、パーティションは同質であると見なされ、全体的な相互情報量への寄与が計算されます。この場合、それ以上の細分化はおこないません。

2x2または4x4カイ二乗検定のいずれかでパーティション内の分布が均一でないことが示された場合、パーティションは4つの小さなサブパーティションに分割されます。これらのサブパーティションは、サイズをチェックすることによって異なる方法で処理されます。サブパーティションが小さすぎる場合は、終端と見なされます。全体的な相互情報量への寄与が計算され、パーティションはそれ以上の細分化の対象ではなくなります。それ以外の場合、サブパーティションが十分に大きい場合は、将来の細分化の候補としてフラグが付けられます。

標準的な2x2カイ二乗検定統計量は、以下の式で示されます。

2x2カイ二乗検定統計量


MQL5における適応型分割

mutualinfo.mqhにあるCapmクラスは、連続変数の相互情報量を推定するための適応型分割アルゴリズムを実装します。再帰的な分割プロセスを管理するために、カスタム構造体IntStackを利用します。この構造体には、パーティションとそれに含まれるサブパーティションに関する情報が保持されます。この構造体には6つのメンバーがあり、詳細は以下のとおりです。

  • XstartとXstop：現在の囲みパーティション内の1つの変数のインデックスの範囲を定義します。
  • YstartとYstop：現在の囲みパーティション内の2番目の変数のインデックスの範囲を定義します。
  • DataStartとDataStop：これらは、囲みパーティション内のデータポイントの開始インデックスと終了インデックスを指定し、サブパーティションをマークします。
//+------------------------------------------------------------------+
//| int type stack structure                                         |
//+------------------------------------------------------------------+
struct IntStack
  {
   int Xstart ;     // X value (rank) at which this rectangle starts
   int Xstop ;      // And stops
   int Ystart ;     // Ditto for Y
   int Ystop ;
   int DataStart ;  // Starting index into indices for the cases in this
   int DataStop ;   // rectangle, and the (inclusive) ending index
  };

Capmコンストラクタは3つの引数を取ります。

  • no_split：ほぼ等しい値を処理する方法を決定するブールフラグ。trueに設定すると、アルゴリズムによって、そのような値がパーティション分割中にグループ化され、異なるパーティションに分割されることが防止されます。
  • dep_vals：分析する変数の1つの値を含むベクトル。この変数は通常、他の多数の変数に対して相互情報量が計算される変数です。
  • chi_critical_value：分割プロセスで使用されるカイ二乗検定の閾値。この値はテストの有意水準を決定し、パーティションの深さに影響します。一般的には4.0から8.0までの値が適切ですが、普遍的な有用性から6.0が一般的な選択肢となります。
//+------------------------------------------------------------------+
//|  constructor                                                     |
//+------------------------------------------------------------------+
Capm::Capm(bool no_split,vector &dep_vals, double chi_critical_value = 6.0)
  {
   m_no_split = no_split;
   m_size = int(dep_vals.Size()) ;
   m_chi_crit = chi_critical_value;

   if(ArrayResize(m_indices,m_size)<0 || !m_tempvals.Resize(m_size) || ArrayResize(m_ranks,m_size)<0
      || (m_no_split && ArrayResize(m_tied_ranks,m_size)<0))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return;
     }

   for(int i=0 ; i<m_size ; i++)
     {
      m_tempvals[i] = dep_vals[i] ;
      m_indices[i] = i ;
     }

   qsortdsi(0, m_size-1, m_tempvals, m_indices) ;

   for(int i=0 ; i<m_size ; i++)
     {
      m_ranks[m_indices[i]] = i ;
      if(! m_no_split)
         continue ;
      if(i < m_size-1  &&
         m_tempvals[i+1] - m_tempvals[i] < 1.e-12 * (1.0+fabs(m_tempvals[i])+fabs(m_tempvals[i+1])))
         m_tied_ranks[i] = 1 ;
      else
         m_tied_ranks[i] = 0 ;
     }
  }

Capmクラスのコンストラクタは、データ内の同点を考慮するかどうかを決定するno_splitフラグと、変数間の有意な関係を識別するために使用されるカイ二乗検定の閾値を設定するchi_critical_valueを設定することから始まります。次に、コンストラクタは、データ、ランク、および同点値を格納するための配列にメモリを割り当てます。変数の値を一時ベクトルにコピーし、ソートします。データポイントの元のインデックスは、m_indices配列に保存されます。最後に、コンストラクタはソートされたデータポイントにランクを割り当て、同点の値を識別し、no_splitフラグが設定されている場合は、それらをm_tied_ranks配列にマークします。

//+------------------------------------------------------------------+
//| Mutual information using the Adaptive partitioning method        |
//+------------------------------------------------------------------+
class Capm
  {

public:
                     Capm(bool no_split,vector &dep_vals, double chi_critical_value = 6.0) ;
                    ~Capm(void) ;
   double            fit(vector &raw) ;

private:
   bool               m_no_split;  // respect ties
   int m_size ;                        // Number of cases
   int m_ranks[] ;                     // 'Dependent' variable ranks
   int m_tied_ranks[] ;                // tied[i] != 0 if case with rank i == case with rank i+1
   double m_chi_crit ;                 // Chi-square test criterion
   int               m_indices[];      // indices
   vector            m_tempvals;       // temp values
  } ;

Capmクラスのfit()メソッドは、1つの変数（コンストラクタに提供）と引数として指定された別の変数間の相互情報量を推定するように設計されています。2番目の変数の値を表す単一のベクトルを入力として受け取ります。このベクトルは、コンストラクタに提供されたベクトルと同じ次元を持つ必要があります。異なるベクトルでfit()メソッドを複数回呼び出すことで、1つの変数とさまざまな変数間の相互情報量を効率的に計算できます。

//+------------------------------------------------------------------+
//|  mutual information for continuous variables                     |
//+------------------------------------------------------------------+
double Capm::fit(vector &raw)
  {
   int i, k, ix, iy, nstack, splittable ;
   int current_indices[], x[], fullXstart, fullXstop, fullYstart, fullYstop, ipos ;
   int trialXstart[4], trialXstop[4], trialYstart[4], trialYstop[4] ;
   int ipx, ipy, xcut[4], ycut[4], iSubRec, x_tied[], ioff ;
   int X_AllTied, Y_AllTied ;
   int centerX, centerY, currentDataStart, currentDataStop ;
   int actual[4], actual44[16] ;
   vector expected(16), xfrac(4), yfrac(4) ;
   double diff, testval;
   double px, py, pxy, MI ;

   IntStack stack[];

   if(ArrayResize(stack,1,256)<0)
     {
      Print(__FUNCTION__," arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   if(ArrayResize(current_indices,m_size)<0 || ArrayResize(x,m_size)<0
      || (m_no_split && ArrayResize(x_tied,m_size)<0))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   for(i=0 ; i<m_size ; i++)
     {
      m_tempvals[i] = raw[i] ;
      m_indices[i] = i ;
     }

   if(!qsortdsi(0, m_size-1, m_tempvals, m_indices))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   for(i=0 ; i<m_size ; i++)
     {
      x[m_indices[i]] = i ;
      if(! m_no_split)
         continue ;
      if(i < m_size-1  &&
         m_tempvals[i+1] - m_tempvals[i] < 1.e-12 * (1.0+fabs(m_tempvals[i])+fabs(m_tempvals[i+1])))
         x_tied[i] = 1 ;
      else
         x_tied[i] = 0 ;
     }

   for(i=0 ; i<m_size ; i++)
     {
      m_indices[i] = i ;
     }

   stack[0].Xstart = 0 ;
   stack[0].Xstop = m_size-1 ;
   stack[0].Ystart = 0 ;
   stack[0].Ystop = m_size-1 ;
   stack[0].DataStart = 0 ;
   stack[0].DataStop = m_size-1 ;
   nstack = 1 ;

   MI = 0.0 ;
   while(nstack > 0)
     {

      --nstack ;
      fullXstart = stack[nstack].Xstart ;
      fullXstop = stack[nstack].Xstop ;
      fullYstart = stack[nstack].Ystart ;
      fullYstop = stack[nstack].Ystop ;
      currentDataStart = stack[nstack].DataStart ;
      currentDataStop = stack[nstack].DataStop ;


      centerX = (fullXstart + fullXstop) / 2 ;
      X_AllTied = (x_tied.Size())  && (x_tied[centerX] != 0) ;
      if(X_AllTied)
        {
         for(ioff=1 ; centerX-ioff >= fullXstart ; ioff++)
           {
            if(! x_tied[centerX-ioff])
              {
               X_AllTied = 0 ;
               centerX -= ioff ;
               break ;
              }
            if(centerX + ioff == fullXstop)
               break ;
            if(! x_tied[centerX+ioff])
              {
               X_AllTied = 0 ;
               centerX += ioff ;
               break ;
              }
           }
        }

      centerY = (fullYstart + fullYstop) / 2 ;
      Y_AllTied = (m_tied_ranks.Size())  && (m_tied_ranks[centerY] != 0) ;
      if(Y_AllTied)
        {
         for(ioff=1 ; centerY-ioff >= fullYstart ; ioff++)
           {
            if(! m_tied_ranks[centerY-ioff])
              {
               Y_AllTied = 0 ;
               centerY -= ioff ;
               break ;
              }
            if(centerY + ioff == fullYstop)
               break ;
            if(! m_tied_ranks[centerY+ioff])
              {
               Y_AllTied = 0 ;
               centerY += ioff ;
               break ;
              }
           }
        }

      if(X_AllTied  ||  Y_AllTied)
         splittable = 0 ;
      else
        {
         trialXstart[0] = trialXstart[1] = fullXstart ;
         trialXstop[0] = trialXstop[1] = centerX ;
         trialXstart[2] = trialXstart[3] = centerX+1 ;
         trialXstop[2] = trialXstop[3] = fullXstop ;
         trialYstart[0] = trialYstart[2] = fullYstart ;
         trialYstop[0] = trialYstop[2] = centerY ;
         trialYstart[1] = trialYstart[3] = centerY+1 ;
         trialYstop[1] = trialYstop[3] = fullYstop ;

         for(i=0 ; i<4 ; i++)
            expected[i] = (currentDataStop - currentDataStart + 1) *
                          (trialXstop[i]-trialXstart[i]+1.0) / (fullXstop-fullXstart+1.0) *
                          (trialYstop[i]-trialYstart[i]+1.0) / (fullYstop-fullYstart+1.0) ;

         actual[0] = actual[1] = actual[2] = actual[3] = 0 ;
         for(i=currentDataStart ; i<=currentDataStop ; i++)
           {
            k = m_indices[i] ;
            if(x[k] <= centerX)
              {
               if(m_ranks[k] <= centerY)
                  ++actual[0] ;
               else
                  ++actual[1] ;
              }
            else
              {
               if(m_ranks[k] <= centerY)
                  ++actual[2] ;
               else
                  ++actual[3] ;
              }
           }

         testval = 0.0 ;
         for(i=0 ; i<4 ; i++)
           {
            diff = fabs(actual[i] - expected[i]) - 0.5 ;
            testval += diff * diff / expected[i] ;
           }

         splittable = (testval > m_chi_crit)  ?  1 : 0 ;

このメソッドは、パーティション分割プロセスを管理するためのスタックを初期化することから始まります。データセット全体が最初にルートパーティションとしてスタックにプッシュされます。その後、アルゴリズムはスタックからパーティションを繰り返しポップし、その均質性を評価します。パーティション内の変数間の潜在的な関係の統計的有意性を評価するために、カイ二乗検定が適用されます。テストで有意な関係が示された場合、パーティションは4つのサブパーティションに分割され、各サブパーティションはさらなる検討のためにスタックに戻されます。このプロセスは、すべてのパーティションが停止基準を満たすか、均質になるまで継続されます。

if(! splittable && fullXstop-fullXstart > 30 && fullYstop-fullYstart > 30)
           {
            ipx = fullXstart - 1 ;
            ipy = fullYstart - 1 ;
            for(i=0 ; i<4 ; i++)
              {
               xcut[i] = (fullXstop - fullXstart + 1) * (i+1) / 4 + fullXstart - 1 ;
               xfrac[i] = (xcut[i] - ipx) / (fullXstop - fullXstart + 1.0) ;
               ipx = xcut[i] ;
               ycut[i] = (fullYstop - fullYstart + 1) * (i+1) / 4 + fullYstart - 1 ;
               yfrac[i] = (ycut[i] - ipy) / (fullYstop - fullYstart + 1.0) ;
               ipy = ycut[i] ;
              }
            for(ix=0 ; ix<4 ; ix++)
              {
               for(iy=0 ; iy<4 ; iy++)
                 {
                  expected[ix*4+iy] = xfrac[ix] * yfrac[iy] *
                                      (currentDataStop - currentDataStart + 1) ;
                  actual44[ix*4+iy] = 0 ;
                 }
              }
            for(i=currentDataStart ; i<=currentDataStop ; i++)
              {
               k = m_indices[i] ;
               for(ix=0 ; ix<3 ; ix++)
                 {
                  if(x[k] <= xcut[ix])
                     break ;
                 }
               for(iy=0 ; iy<3 ; iy++)
                 {
                  if(m_ranks[k] <= ycut[iy])
                     break ;
                 }
               ++actual44[ix*4+iy] ;
              }
            testval = 0.0 ;
            for(ix=0 ; ix<4 ; ix++)
              {
               for(iy=0 ; iy<4 ; iy++)
                 {
                  diff = fabs(actual44[ix*4+iy] - expected[ix*4+iy]) - 0.5 ;
                  testval += diff * diff / expected[ix*4+iy] ;
                 }
              }
            splittable = (testval > 3 * m_chi_crit)  ?  1 : 0 ;
           }
        }

      if(splittable)
        {

         for(i=currentDataStart ; i<=currentDataStop ; i++)
            current_indices[i] = m_indices[i] ;

         ipos = currentDataStart ;
         for(iSubRec=0 ; iSubRec<4 ; iSubRec++)
           {

            if(actual[iSubRec] >= 3)
              {
               stack[nstack].Xstart = trialXstart[iSubRec] ;
               stack[nstack].Xstop = trialXstop[iSubRec] ;
               stack[nstack].Ystart = trialYstart[iSubRec] ;
               stack[nstack].Ystop = trialYstop[iSubRec] ;
               stack[nstack].DataStart = ipos ;
               stack[nstack].DataStop = ipos + actual[iSubRec] - 1 ;
               ++nstack ;
               if(ArrayResize(stack,nstack+1,256)<0)
                 {
                   Print(__FUNCTION__," arrayresize error ", GetLastError());
                   return EMPTY_VALUE;
                 }

               if(iSubRec == 0)
                 {
                  for(i=currentDataStart ; i<=currentDataStop ; i++)
                    {
                     k = current_indices[i] ;
                     if(x[k] <= centerX  &&  m_ranks[k] <= centerY)
                        m_indices[ipos++] = current_indices[i] ;
                    }
                 }
               else
                  if(iSubRec == 1)
                    {
                     for(i=currentDataStart ; i<=currentDataStop ; i++)
                       {
                        k = current_indices[i] ;
                        if(x[k] <= centerX  &&  m_ranks[k] > centerY)
                           m_indices[ipos++] = current_indices[i] ;
                       }
                    }
                  else
                     if(iSubRec == 2)
                       {
                        for(i=currentDataStart ; i<=currentDataStop ; i++)
                          {
                           k = current_indices[i] ;
                           if(x[k] > centerX  &&  m_ranks[k] <= centerY)
                              m_indices[ipos++] = current_indices[i] ;
                          }
                       }
                     else
                       {
                        for(i=currentDataStart ; i<=currentDataStop ; i++)
                          {
                           k = current_indices[i] ;
                           if(x[k] > centerX  &&  m_ranks[k] > centerY)
                              m_indices[ipos++] = current_indices[i] ;
                          }
                       }
              }

            else
              {
               if(actual[iSubRec] > 0)
                 {
                  px = (trialXstop[iSubRec] - trialXstart[iSubRec] + 1.0) / m_size ;
                  py = (trialYstop[iSubRec] - trialYstart[iSubRec] + 1.0) / m_size ;
                  pxy = (double) actual[iSubRec] / m_size ;
                  MI += pxy * log(pxy / (px * py)) ;
                 }
              }
           }
        }
      else
        {
         px = (fullXstop - fullXstart + 1.0) / m_size ;
         py = (fullYstop - fullYstart + 1.0) / m_size ;
         pxy = (currentDataStop - currentDataStart + 1.0) / m_size ;
         MI += pxy * log(pxy / (px * py)) ;
        }
     }

   return MI;

カイ二乗検定で有意でなかったり、データポイントの数が最小であったりして均質であると判断されるパーティションについては、相互情報量が計算されます。この計算では、パーティション内の結合確率分布と周辺確率分布を推定し、以下の式を適用します。

相互情報貢献

このプロセスは再帰的に継続され、それ以上の大きな分割が不可能になるまでパーティションが分割され、評価されます。相互情報量の最終的な推定値は、すべての端末パーティションからの寄与を合計することによって得られ、データ構造体に基づいた包括的な推定値を提供します。メソッドでエラーが発生した場合、MQL5の組み込みEMPTY_VALUE定数と同等の値を返します。次のセクションでは、段階的な特徴量選択アルゴリズムの実装にCapmクラスを使用します。


相互情報量を用いた予測変数の選択

相互情報量を特徴量選択のタスクに適用する場合の目標は、目的変数との結合依存性を最大化する、候補予測変数の大きなセットから予測変数のサブセットを識別することです。この結合依存性は相互情報量の一般化であり、1つの量が単一の変数ではなく、変数の集合である点が特徴です。予測変数のより大きなサブセットに対して結合依存性を計算することは、次元の呪いにより計算上困難になります。これは、データの多次元分割が必要となり、特に次元数（予測変数）が増加するにつれて、非常にスパースなセルが生成されるためです。

さらに、特徴量の組み合わせの数が膨大であるため、たとえ中規模な特徴量セットであっても、その計算量は圧倒的です。この組み合わせ爆発により、すべての可能なサブセットを網羅的に検索することは非現実的となり、効率的な検索戦略が必要になります。

特徴量選択の一般的なアプローチとして、前向きステップワイズ選択があります。この方法は、空のモデルから開始し、選択した基準に基づいてモデルの性能を最も向上させる特徴量を反復的に追加します。このアプローチは効率的ですが、貪欲法に依存しているため、最適な特徴量の組み合わせを見逃す可能性があります。たとえば、2つの特徴量を組み合わせると、それぞれ単独で使用する場合よりも予測力が大幅に向上することがありますが、アルゴリズムは各ステップでの段階的な改善に焦点を当てるため、特徴量間の相乗効果を見逃してしまうことがあります。

他の手法として高次法や後方選択なども存在しますが、前向きステップワイズ選択は計算効率が高いため、特に大規模なデータセットや限られた計算リソースを扱う場合に最も実用的な選択肢です。さらに、結合依存性に特化したコンテキストで前向きステップワイズ選択を適用すると、驚くべき特性が現れます。結合依存性を明示的に最適化しなくても、最適な特徴量サブセットを効果的に近似することができるのです。

Peng、Long、Dingは、最大関連性・最小冗長性(MRMR)基準として知られる相互情報量に基づく特徴量選択アルゴリズムを提案しました。このアルゴリズムは、計算上困難な結合依存性を明示的に計算することなく、最適な特徴量サブセットを効率的に近似します。MRMR基準は、関連性と冗長性の概念に基づいており、特徴量セットSと目的変数Yの関連性は、YとS内の各特徴量との平均相互情報量として定義されます。

関連性

ここで、∣S∣はS内の特徴量の数であり、I(Xi, Y)は特徴量XiとY間の相互情報量です。

関連性を最大化することは直感的ですが、冗長性によって最適でない特徴量サブセットにつながる可能性があります。目的変数に対する個々の関連性に基づいて特徴量を単純に選択すると、追加の情報をほとんど提供しない、相関の高い特徴量のセットを選んでしまう可能性があります。この問題に対処するためには、特徴量の関連性だけでなく、既に選択された特徴量との冗長性も考慮する必要があります。

予測変数候補Xiの冗長性は、 既に選択された特徴セットSに関して、XiとS内の各特徴量との間の平均相互情報量として 定義されます。

冗長性

ここで、I(Xi,Xj)は候補特徴量XiとSにすでに存在する特徴量Xjとの間の相互情報量です。

冗長性の数学的表現は、関連性の表現と同一であることに注意することが重要です。唯一の違いは、その解釈にあります。候補特徴量と目的変数との相互情報量を計算する際、それは「関連性」と呼ばれます。しかし、候補特徴と、すでに選択された特徴量セット内にある特徴量との相互情報量を計算する際、それは「冗長性」と呼ばれます。

本質的には、どちらの概念も2つの変数間で共有される情報の量を測定することですが、その解釈は文脈によって異なります。関連性では、特徴量と目的変数との関係に注目し、冗長性では、候補特徴とすでに選択された特徴量との間にどれだけの重複があるかに注目します。

要約すると、MRMRアルゴリズムは次のように動作します。

  1. 目的変数Yとの相互情報量が最も高い特徴量が最初に選ばれます。
  2. その後の各ステップでは、アルゴリズムは次の基準を最大化する特徴量を選択します。

MRMR基準

この基準は、目的変数Y（すなわち I(X_i, Y)）に対する特徴量の関連性と、既に選択された特徴量との冗長性のバランスを取ります。MRMRアルゴリズムの注目すべき点は、結合依存性を直接最適化することが計算上困難であるにもかかわらず、最適な特徴量サブセットを効果的に近似できることです。この結果は直感的には明らかではないものの、元の論文において数学的に証明されています。

選択された特徴量の統計的有意性を評価するために、次の2つのモンテカルロ順列 (MCP)テストを採用できます。

  • 個々の特徴量の有意性：このテストでは、各特徴の目的変数との関連性を、順列によって得られたヌル分布と比較することで、その有意性を評価します。具体的には、特徴量の値をランダムに並べ替えることで、「その特徴量が目的変数と無関係である」ことを仮定したヌル分布を作成します。観測された関連性がこのヌル分布の値よりも有意に高い場合、その特徴量は真に情報量の多い（有益な）特徴量である可能性が高いと判断できます。
  • 全体的なモデルの有意性：このテストでは、選択された特徴量セット全体の有意性を評価します。個々の特徴量の関連性の累積和を、順列によって得られたヌル分布と比較することで検証をおこないます。具体的には、目的変数の値をランダムに並べ替え、「特徴と目的変数が無関係である」ことを仮定したヌル分布を作成します。観測された累積関連性がこのヌル分布の値よりも有意に高い場合、選択された特徴量セットは目的変数を予測する上で有効であると判断できます。


相互情報量に基づく段階的選択のMQL5実装

mutualinfo.mqhのCmrmrクラスはMRMRアルゴリズムを実装し、コンストラクタで次のパラメータを受け取ります。
  • num_reps：モンテカルロ順列検定の複製回数。これを1以下の値に設定すると、テストは無効になります。
  • max_preds：選択する特徴量の最大数。
  • chisquare_thresh：相互情報量を推定するために使用される適応型分割法のカイ二乗検定閾値。
  • m_verbose：アルゴリズムの実行中に詳細な出力を表示するかどうかを制御するブールフラグ。
//+-----------------------------------------------------------------------+
//|Relevance minus redundancy for building an optimal subset of predictors|
//+-----------------------------------------------------------------------+
class Cmrmr
  {
private:
   int               m_max_preds;
   int               m_reps;
   bool              m_verbose;
   int               m_samples;
   int               m_vars;
   matrix            m_preds;
   vector            m_target;
   vector            m_crits;
   double            m_chisquare_thresh;
   ulong             m_selected_vars[];
   matrix            m_critical_values;
   vector            mutualinfo(int which_size,int &which[],vector &targs);
public:
                     Cmrmr(int num_reps,int max_preds, double chisquare_thresh,bool verbose);
                    ~Cmrmr(void);
   bool              StepWise(matrix &predictors, vector &targets);
   matrix            GetCriticalValues(void);
   bool              GetSelectedVars(ulong &output[]);
  };

Cmrmrクラスを使用して特徴量選択プロセスを開始するには、このクラスのオブジェクトをインスタンス化し、そのStepWise()メソッドを呼び出す必要があります。StepWise()メソッドは、2つの主要な入力を受け取ります。

  • 候補予測変数の行列：この行列には、実務者が考慮したいすべての潜在的な特徴量のデータが含まれている必要があります。
  • 目的変数のベクトル：このベクトルには目的変数の値が含まれている必要があります。

このメソッドは、特徴量選択プロセスの成功または失敗を示すブール値を返します。CmrmrクラスのStepWise()メソッドは、必要なデータ構造を初期化し、MCPテストループに進みます。MCPテストが要求されていない場合（num_repsが1以下）、ループは1回だけ実行されます。ループ内で、メソッドはCapmクラスのインスタンスを使用して、各候補予測変数と目的変数間の相互情報量を計算します。

//+------------------------------------------------------------------+
//|  Stepwise feature selection based on mutual information          |
//+------------------------------------------------------------------+
bool Cmrmr::StepWise(matrix &predictors,vector &targets)
  {
   if(m_selected_vars.Size())
      ArrayFree(m_selected_vars);

   m_preds = predictors;
   m_samples = int(m_preds.Rows());
   m_vars = int(m_preds.Cols());
   m_max_preds = m_max_preds>=m_vars?m_vars:m_max_preds;
   m_target = targets;
   
   
   int i, j, k, ivar, irep;
   int index[], stepwise_mcpt_count[], solo_mcpt_count[], stepwise_ivar[], which_preds[],original_stepwise_ivar[] ;

   int nkept,best_ivar;
   vector casework(m_samples), sorted(m_samples), mutual(m_vars);
   vector crit(m_vars), relevance(m_vars), original_relevance(m_vars), current_crits(m_vars), sorted_crits(m_vars);
   double best_crit, dtemp, group_pvalue,solo_pvalue;
   vector stepwise_crit(m_vars), original_stepwise_crit(m_vars);
   double sum_relevance;
   vector original_sum_relevance(m_vars), sum_redundancy(m_vars);
   vector target = m_target;

   best_crit = -DBL_MAX;
   best_ivar = -1;
   nkept = m_max_preds;

   if(ArrayResize(index,m_vars)<0 || ArrayResize(stepwise_mcpt_count,m_vars)<0 ||
      ArrayResize(solo_mcpt_count,m_vars)<0 || ArrayResize(which_preds,m_vars)<0 || ArrayResize(stepwise_ivar,m_vars)<0 ||
      ArrayResize(original_stepwise_ivar,m_vars)<0)
     {
      Print(__FUNCTION__," array resize error ", GetLastError());
      return false;
     }

   int unif_error;
   for(irep=0 ; irep<m_reps ; irep++)
     {
      if(irep)
        {
         i = m_samples ;
         while(i > 1)
           {
            j = (int)(MathRandomUniform(0.0,1.0,unif_error) * i);
            if(unif_error)
              {
               Print(__FUNCTION__," Mathrandomuniform error ", GetLastError());
               return false;
              }
            if(j >= i)
               j = i - 1 ;
            dtemp = target[--i] ;
            target[i] = target[j] ;
            target[j] = dtemp ;
           }
        }

      for(i=0 ; i<m_vars ; i++)
         which_preds[i] = i ;

      crit = mutualinfo(m_vars,which_preds,target);

      for(ivar=0 ; ivar<m_vars ; ivar++)
        {
         relevance[ivar] = crit[ivar] ;
         if(ivar == 0  ||  crit[ivar] > best_crit)
           {
            best_crit = crit[ivar] ;
            best_ivar = ivar ;
           }
        }

      stepwise_crit[0] = best_crit ;
      stepwise_ivar[0] = best_ivar ;
      sum_relevance = best_crit ;
      if(irep == 0)
        {

         original_stepwise_crit[0] = best_crit ;
         original_stepwise_ivar[0] = best_ivar ;
         original_sum_relevance[0] = sum_relevance ;
         stepwise_mcpt_count[0] = 1 ;

         for(ivar=0 ; ivar<m_vars ; ivar++)
           {
            index[ivar] = ivar ;
            original_relevance[ivar] = sorted_crits[ivar] = current_crits[ivar] = crit[ivar] ;
            solo_mcpt_count[ivar] = 1 ;
           }

         if(!qsortdsi(0, m_vars-1, sorted_crits, index))
           {
            Print(__FUNCTION__, " failed qsort ");
            return false;
           }

         if(m_verbose)
            Print("       Variable         MI") ;

         for(i=m_vars-1 ; i>=0 ; i--)
           {
            k = index[i] ;

            if(m_verbose)
               PrintFormat("%15s %12.4lf",string(k), current_crits[k]) ;
           }
        }

      else
        {
         if(sum_relevance >= original_sum_relevance[0])
            ++stepwise_mcpt_count[0] ;
         for(ivar=0 ; ivar<m_vars ; ivar++)
           {
            if(relevance[ivar] >= original_relevance[ivar])
               ++solo_mcpt_count[ivar] ;
           }
        }

      for(i=0 ; i<m_vars ; i++)
         sum_redundancy[i] = 0.0 ;

      for(nkept=1 ; nkept<m_max_preds ; nkept++)
        {

         if(irep == 0 && m_verbose)
           {
            Print("Predictors so far   Relevance   Redundancy   Criterion") ;
            for(i=0 ; i<nkept ; i++)
              {
               k = stepwise_ivar[i] ;
               PrintFormat("%15s %12.4lf %12.4lf %12.4lf",string(k), relevance[k], relevance[k] - stepwise_crit[i], stepwise_crit[i]) ;
              }
           }

         k = 0 ;
         for(i=0 ; i<m_vars ; i++)
           {
            for(j=0 ; j<nkept ; j++)
              {
               if(stepwise_ivar[j] == i)
                  break ;
              }
            if(j == nkept)
               which_preds[k++] = i ;
           }
         if(k != (m_vars - nkept))
           {
            Print(__FUNCTION__, " failed assertion ", __LINE__);
            return false;
           }

         k = stepwise_ivar[nkept-1] ;

         casework = m_preds.Col(k);

         crit = mutualinfo(m_vars-nkept,which_preds,casework);

         for(i=0 ; i<(m_vars-nkept) ; i++)
           {
            k = which_preds[i] ;
            sum_redundancy[k] += crit[i] ;
            index[i] = k ;
            sorted_crits[i] = current_crits[i] = ((relevance[k] - sum_redundancy[k]) / double(nkept)) ;
            if(i == 0  ||  current_crits[i] > best_crit)
              {
               best_crit = current_crits[i] ;
               best_ivar = k ;
              }
           }

         stepwise_crit[nkept] = best_crit ;
         stepwise_ivar[nkept] = best_ivar ;
         sum_relevance += relevance[best_ivar] ;

         if(irep == 0)
           {
            original_stepwise_crit[nkept] = best_crit ;
            original_stepwise_ivar[nkept] = best_ivar ;
            original_sum_relevance[nkept] = sum_relevance ;
            stepwise_mcpt_count[nkept] = 1 ;

            if(!qsortdsi(0, m_vars-nkept-1, sorted_crits, index))
              {
               Print(__FUNCTION__, " failed qsort ");
               return false;
              }

            if(m_verbose)
              {
               Print("Additional candidates, in order of decreasing relevance minus redundancy") ;
               Print("       Variable     Relevance   Redundancy   Criterion") ;

               for(i=m_vars-nkept-1 ; i>=0 ; i--)
                 {
                  k = index[i] ;
                  PrintFormat("%15s %12.4lf %12.4lf %12.4lf",
                              string(k), relevance[k], sum_redundancy[k] / nkept,
                              relevance[k] - sum_redundancy[k] / nkept) ;
                 }
              }
           }

         else
           {
            if(sum_relevance >= original_sum_relevance[nkept])
               ++stepwise_mcpt_count[nkept] ;
           }

        }

     }
//---
   m_critical_values = matrix::Zeros(nkept,m_reps>1?5:3);
//---
   if(ArrayResize(m_selected_vars,nkept)<0)
     {
      Print(__FUNCTION__, " failed array resize ", GetLastError());
      return false;
     }
//---
   if(m_verbose)
     {
      if(m_reps > 1)
         Print("Final predictors ||  Relevance ||  Redundancy || Criterion  ||  Solo pval || Group pval") ;
      else
         Print("Final predictors  ||  Relevance ||  Redundancy ||  Criterion") ;
     }
//---
   for(i=0 ; i<nkept ; i++)
     {
      k = original_stepwise_ivar[i] ;
      m_selected_vars[i] = ulong(k);

      m_critical_values[i][0] = original_relevance[k];
      m_critical_values[i][1] = original_relevance[k] - original_stepwise_crit[i];
      m_critical_values[i][2] = original_stepwise_crit[i];

      if(m_critical_values.Cols()>3)
        {
         group_pvalue = (double) stepwise_mcpt_count[i] / (double) m_reps;
         solo_pvalue = (double) solo_mcpt_count[k] / (double) m_reps;
         m_critical_values[i][3] = solo_pvalue;
         m_critical_values[i][4] = group_pvalue;
        }

      if(m_verbose)
        {
         if(m_reps > 1)
            PrintFormat("%15s %12.4lf %12.4lf %12.4lf    %8.3lf    %8.3lf",string(k), m_critical_values[i][0], m_critical_values[i][1], m_critical_values[i][2],solo_pvalue,group_pvalue) ;
         else
            PrintFormat("%15s %12.4lf %12.4lf %12.4lf",string(k), m_critical_values[i][0], m_critical_values[i][1], m_critical_values[i][2]);
        }
     }

   return true;

  }

Cmrmrクラス内のprivateメソッドであるmutualinfo()メソッドは、適応型分割法を使用して、指定された予測変数と目的変数間の相互情報量を推定する役割を担います。mutualinfo()の列インデックスとして指定された選択された予測変数の相互情報量近似のベクトルを返します。

//+------------------------------------------------------------------+
//| continuous mutual infomation                                     |
//+------------------------------------------------------------------+
vector Cmrmr::mutualinfo(int which_size,int &which[],vector &targs)
  {
   vector res = vector::Zeros(m_vars);

   res.Fill(-DBL_MAX);

   vector vars;

   Capm mia(true,targs,m_chisquare_thresh);

   for(int i = 0; i<which_size; i++)
     {
      vars = m_preds.Col(which[i]);
      res[i] = mia.fit(vars);
     }

   return res;

  }

StepWise()メソッドは、計算された相互情報値をrelevanceベクトルに保存します。これらの値は、冗長性項を計算する後続の反復で必要になるためです。相互情報量が最も高い特徴が最初の特徴量として選択され、その情報はstepwise_crit変数とstepwise_ivar変数に格納されます。さらに、選択された特徴量の累積的な関連性を追跡するためにsum_relevance変数が初期化され、後でMCPテストに使用されます。

初期の、順序が入れ替わっていない複製の場合、アルゴリズムは最初に選択された特徴量の関連性と基準の元の値を保存します。また、全体的なモデルの重要性テストと個々の特徴量の重要性テストのカウンターも初期化します。さらに、各候補特徴と目的変数の相互情報量を表示する表が出力され、初期特徴ランキングに関する洞察が提供されます。この表は、初期選択プロセスを視覚化するのに役立ち、有意性検定フェーズ中に並べ替えられた値と比較するための参照として機能します。

初期の順序変更されていない複製ではない場合、アルゴリズムは、MRMRアルゴリズムによって選択された特徴セットの統計的有意性を評価するように設計された2つのMCPテストの実行に進みます。選択されたセットに新しい特徴量が追加されるときに進化する冗長性を効率的に管理するために、アルゴリズムはsum_redundancy配列を使用します。配列はゼロで初期化されます。この配列は、すでに選択されている特徴量に対する各候補特徴量の累積冗長性を格納するために使用されます。

最初は、特徴が選択されていないため、この配列内のすべての値はゼロに設定されます。選択したセットに新しい特徴量が追加されると、残りの候補特徴量のそれぞれとの冗長性を更新する必要があります。選択セットの増加に関する特徴量の冗長性は、候補の特徴量とすでに選択されている特徴量の間での平均相互情報量として定義されます。新しい特徴量と残りの候補特徴量のそれぞれとの間の相互情報量が計算されます。これにより、新しい特徴量が選択した各特徴量とどの程度の情報を共有するかが定量化されます。残りの各特徴量の冗長性値は、新しく追加された特徴量と既存の特徴量の間での相互情報値を加算することによって更新されます。

冗長性の値を更新した後、アルゴリズムは残りの候補特徴量ごとにMRMR（最大関連性、最小冗長性）基準を計算します。MRMR基準は、各特徴量の平均冗長性をその関連性から減算することによって計算されます。残りのすべての候補特徴量に対してMRMR基準が計算されると、MRMRスコアが最も高い特徴量が選択されます。アルゴリズムはこのプロセスを反復的に繰り返し、新しい特徴量が追加されるたびにsum_redundancy配列を更新し、MRMR基準を再計算します。より多くの特徴量が選択されると、選択されたセットの残りの特徴量の冗長性が継続的に更新され、特徴量選択プロセスで特徴量間の関係の変化が考慮されるようになります。

これが初期の、順序が入れ替わっていない複製である場合、これらの量の元の値は、後で順序のテスト中に比較するために保存されます。それ以外の場合は、「グループ」および「ソロ」順列テストのカウンタが増加します。必要な回数の反復を完了すると、アルゴリズムは、選択された特徴、その関連性、および順列テストからのp値をまとめた表を表示して終了します。StepWise()が呼び出され、正常に実行された後、GetCriticalValues()を呼び出して、詳細モードで表示される値の表の行列を取得できます。一方、GetSelectedVars()は、クラスのm_max_predsプロパティに対応する選択された変数(列)のインデックスを取得します。

//+------------------------------------------------------------------+
//| get the matrix of decision variables                             |
//| matrix rows arranged in terms of descending relevance of each    |
//| candidate predictor. Most relevant predictors critical values are|
//| in the first row, etc.                                           |
//| Column 0 is the calculated relevance                             |
//| Column 1 is the calculated redundancy                            |
//| Column 2 is the calculated Stepwise Mutual information           |
//| Column 3 and 4 will exist only if MCP test is specified          |
//| Column 3 is the Solo probability value                           |
//| Column 4 are the Group probability values                        |
//+------------------------------------------------------------------+
matrix Cmrmr::GetCriticalValues(void)
{
  return m_critical_values;
}
//+--------------------------------------------------------------------------+
//|get the indices of the most relevant predictors as determined by algorithm|
//+--------------------------------------------------------------------------+
bool Cmrmr::GetSelectedVars(ulong &output[])
{
 return (ArrayCopy(output,m_selected_vars)>0);
}

次のセクションでは、合成データセットと実際のデータセットを使用してCmrmrクラスがどのように適用されるかを見ていきます。


関連性と冗長性を排除した例

MRMRアルゴリズムの適用を効果的に示すために、まず合成データセットに適用します。データセットは、100個のサンプルと10個の潜在的な予測変数（特徴量）で構成されています。目的変数Yは、行列の最初の4列を合計することによって構築されるため、目的変数と予測変数の関係はこれらの列に対して決定論的になります。ただし、列4から7は目的に関する実際の情報を提供しないため、無関係な特徴量として機能します。列8と9の変数は、それぞれ列インデックス{1,3}と{0,2}の変数の組み合わせです。

//---
   MathSrand(125);

   matrix rdata(100,10);

   rdata.Random(0.0,1.0);

   vector dep = rdata.Col(0) + rdata.Col(1) + rdata.Col(2) + rdata.Col(3);

   vector sum02 = rdata.Col(0) + rdata.Col(2);

   vector sum13 = rdata.Col(1) + rdata.Col(3);

   if(!rdata.Col(sum13,8) || !rdata.Col(sum02,9))
     {
      Print(" Failed column insertion ", GetLastError());
      return;
     }

目的は、MRMRアルゴリズムを使用して、列を最も関連性の高い予測変数として識別することです。この実験は、RelevanceMinusRedundancy.mq5スクリプトで実装されており、モンテカルロ順列の数や選択する特徴の最大数など、さまざまなハイパーパラメータをカスタマイズできます。スクリプトは詳細モードで実行するように構成されており、特徴量選択プロセス中に詳細な出力を提供します。

//inputs
input int NumReplications = 100;
input int MaxPredictors = 10;
input double ChiSquareThreshold = 6.0;

RelevanceMinusRedundancy.mq5スクリプトの初期出力は、各候補予測変数と目的変数間の個々の相互情報値です。相互情報量の降順に並べられているため、最も関連性の高い特徴を簡単に識別できます。

Variable         MI
      9       0.2675
      8       0.1696
      0       0.1662
      3       0.1336
      2       0.0823
      1       0.0645
      6       0.0000
      7       0.0000
      4       0.0000
      5       0.0000

予想どおり、MRMRアルゴリズムによって選択される最初の特徴は、目的変数との個々の相互情報量が最も高い特徴です。この場合は、列インデックス9のものです。

Predictors so far   Relevance   Redundancy   Criterion
            9       0.2675       0.0000       0.2675

2番目に選択される特徴量は、列インデックス8の変数です。分析の結果を見ると、この変数は関連性が高く、最初に選択された変数との冗長性も最小限であることがわかります。

Predictors so far   Relevance   Redundancy   Criterion
            9       0.2675       0.0000       0.2675
            8       0.1696       0.0000       0.1696

選択された3番目の特徴量は、冗長性が選択プロセスにどのように影響するかを示しています。列 0、1、2、3の特徴量は目的変数に直接関連していますが、すでに選択されている特徴（列8と9）との冗長性が高いため、全体的なMRMR基準が低下します。したがって、アルゴリズムは、既存のセットとの冗長性が低い、直接的に関連が少ない特徴量を選択します。いくつかの関連のない特徴量を選択した後にのみ、アルゴリズムは、選択されたセットとの冗長性が低下するため、列0、1、2、および3の特徴量を優先し始めます。

Additional candidates, in order of decreasing relevance minus redundancy
Variable     Relevance   Redundancy   Criterion
    5       0.0000       0.0000       0.0000
    4       0.0000       0.0000       0.0000
    7       0.0000       0.0000       0.0000
    6       0.0000       0.0000       0.0000
    1       0.0645       0.0600       0.0044
    0       0.1662       0.1351       0.0311
    2       0.0823       0.1426      -0.0603
    3       0.1336       0.1781      -0.0445

この合成例では無関係な変数の関連性はゼロでしたが、実際のシナリオでは、無関係な特徴が目的変数とある程度の関係を示し、ゼロではない冗長性につながる可能性があることに注意することが重要です。このような場合、MRMRアルゴリズムは関連性と冗長性を効果的にバランスさせ、固有の情報を提供する特徴量を優先します。

Final predictors ||  Relevance ||  Redundancy || Criterion  || Solo pval|| Group pval
9                     0.2675        0.0000       0.2675       0.010       0.010
8                     0.1696        0.0000       0.1696       0.010       0.010
4                     0.0000        0.0000       0.0000       1.000       0.010
5                     0.0000        0.0000       0.0000       1.000       0.010
6                     0.0000        0.0000       0.0000       1.000       0.010
7                     0.0000        0.0000       0.0000       1.000       0.010
1                     0.0645        0.0738      -0.0093       0.010       0.010
0                     0.1662        0.1811      -0.0149       0.010       0.010
2                     0.0823        0.1077      -0.0254       0.010       0.010
3                     0.1336        0.1584      -0.0247       0.010       0.010

モンテカルロ順列検定から得られたp値は、選択された特徴の統計的有意性に関する貴重な洞察を提供します。p値が低いほど、その特徴量が偶然によるものではなく、本当に有益であるという強い証拠を示します。統計的有意性を判断するために、通常、p値の閾値0.05が使用されます。

次は、より現実的なデータセットでのアルゴリズムのデモンストレーションです。StepWiseFeatureSelectionByMutualInformation.mq5スクリプトは、金融データに対するMRMRアルゴリズムの実用的なアプリケーションを提供します。これは、一連のテクニカル指標を使用して特定の銘柄の将来の収益を予測するという前提に基づいています。スクリプトは、さまざまなルックバック期間を持つマネーフロー指数(MFI)、移動平均(MA)、ベアーズパワー、ブルズパワーの4つのインジケーターを計算します。これらのインジケーターは、特徴量選択プロセスの候補特徴量として機能します。MRMRアルゴリズムを適用することにより、スクリプトは将来のリターンを効果的に予測できる最も有益なインジケーターの組み合わせを特定することを目指します。これには、選択した他の特徴量との冗長性を最小限に抑えながら、目的変数（将来のリターン）に関連する特徴量を選択することが含まれます。

//+------------------------------------------------------------------+
//|                  StepWiseFeatureSelectionByMutualInformation.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#resource "\\Indicators\\LogReturns.ex5"
#include<mutualinfo.mqh>
#include<ErrorDescription.mqh>
//+------------------------------------------------------------------+
//|indicator type                                                    |
//+------------------------------------------------------------------+
enum SELECT_INDICATOR
  {
   MFI=0,//MFI
   MA,//MA
   BEARS,//BEARS
   BULLS//BULLS
  };
//--- input parameters
input int NumReplications = 100;
input int MaxPredictors = 10;
input double ChiSquareThreshold = 6.0;
input bool VerboseOutPut = false;
input uint     period_inc=2;//lookback increment
input uint     max_lookback=6;
input ENUM_MA_METHOD         AppliedMA = MODE_SMA;
input ENUM_APPLIED_PRICE     AppliedPrice = PRICE_CLOSE;
input datetime SampleStartDate=D'2019.12.31';
input datetime SampleStopDate=D'2022.12.31';
input string   SetSymbol="BTCUSD";
input ENUM_TIMEFRAMES SetTF = PERIOD_D1;
//----
string predictor_names[];                      // variable names
int size_sample,                      //training set size
    size_observations,                //size of of both training and testing sets combined
    maxperiod,                        //maximum lookback
    indicator_handle=INVALID_HANDLE;  //long moving average indicator handle
//---
vector indicator[];                   //indicator indicator values;
//---
matrix feature_matrix;          //full matrix of features;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---get relative shift of sample set
   int samplestart,samplestop,num_features;
   samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate);
   samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate);
   num_features = int((max_lookback/period_inc)*4);
//---check for errors from ibarshift calls
   if(samplestart<0 || samplestop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(samplestart - samplestop) + 1 ;
   maxperiod=int(max_lookback);
//---check for input errors
   if(size_observations<=0 || maxperiod<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---allocate memory
   if(ArrayResize(indicator,num_features+1)<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//----get the full collection of indicator values
   int period_len;
   int k=0;
//---
   for(SELECT_INDICATOR select_indicator = 0; select_indicator<4; select_indicator++)
     {
      for(int iperiod=0; iperiod<int((indicator.Size()-1)/4); iperiod++)
        {
         period_len=int((iperiod+1) * period_inc);
         int try
               =10;
         predictor_names.Push(EnumToString(select_indicator)+"_"+string(period_len));
         while(try)
           {
            switch(select_indicator)
              {
               case MFI:
                  indicator_handle=iMFI(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len,VOLUME_TICK);
                  break;
               case MA:
                  indicator_handle=iMA(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len,0,AppliedMA,AppliedPrice);
                  break;
               case BEARS:
                  indicator_handle=iBearsPower(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len);
                  break;
               case BULLS:
                  indicator_handle=iBullsPower(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len);
                  break;
              }

            if(indicator_handle==INVALID_HANDLE)
               try
                  --;
            else
               break;
           }

         if(indicator_handle==INVALID_HANDLE)
           {
            Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError());
            return;
           }

         Comment("copying data to buffer for indicator ",period_len);
         try
               = 0;
         while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try
                  <10)
              {
               try
                  ++;
               Sleep(5000);
              }

         if(try
               <10)
               ++k;
         else
           {
            Print("error copying to indicator buffers ",GetLastError());
            Comment("");
            return;
           }

         if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle))
            indicator_handle=INVALID_HANDLE;
        }
     }

//---resize matrix
   if(!feature_matrix.Resize(size_observations,indicator.Size()-1))
     {
      Print(__LINE__);
      Print(ErrorDescription(GetLastError()));
      Comment("");
      return;
     }
//---copy collected data to matrix
   for(ulong i = 0; i<feature_matrix.Cols(); i++)
      if(!feature_matrix.Col(indicator[i],i))
        {
         Print(__LINE__);
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
//---
   int try
         = 10;
   while(try
            >-1 && indicator_handle == INVALID_HANDLE)
        {
         indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\LogReturns",0,1,1);
         try
            --;
        }
//---
   if(try
         <0)
        {
         Print("Could not initialize returns indicator ");
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
   else
     {
      try
            = 10;
     }
//---
   while(try
            >-1 && !indicator[indicator.Size()-1].CopyIndicatorBuffer(indicator_handle,0,samplestop-1,size_observations))
        {
         Sleep(2000);
         try
            --;
        }
//---
   if(try
         <0)
        {
         Print("Could not collect returns indicator info ");
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
   else
     {
      IndicatorRelease(indicator_handle);
      Comment("");
     }
//--- display the dataset
   string console;
   for(uint i = 0; i<predictor_names.Size(); i++)
      console+=StringFormat(" %12s ",predictor_names[i]);
   console+=" NextBar Returns (Target) ";
   Print(console);
   for(ulong i = 0; i<feature_matrix.Rows(); i++)
     {
      console = "";
      for(ulong j = 0; j<feature_matrix.Cols(); j++)
         console += StringFormat(" %12.6lf ",feature_matrix[i][j]);
      console+=StringFormat(" %12.6lf ",indicator[indicator.Size()-1][i]);
      Print(console);
     }
//---
   Cmrmr mstep(NumReplications,MaxPredictors,ChiSquareThreshold,VerboseOutPut);
//---
   if(!mstep.StepWise(feature_matrix,indicator[indicator.Size()-1]))
      return;
//---
   Print(" Final predictor labels ");
   ulong variables[];
   if(mstep.GetSelectedVars(variables))
     {
      for(uint i = 0; i<variables.Size(); i++)
         Print(predictor_names[variables[i]]);
     }
   return;
  }
//+------------------------------------------------------------------+
以下は、MetaTrader 5端末から収集されたインジケーターのデータセットの一部と、最後の列の目的変数です。全部で12個の候補予測変数（インジケーター）があります。
MFI_2         MFI_4         MFI_6          MA_2          MA_4          MA_6       BEARS_2       BEARS_4       BEARS_6       BULLS_2       BULLS_4       BULLS_6  NextBar Returns(Target)
0.000000     53.151442     46.921608   7213.654000   7279.552750   7260.007333    -76.371267   -101.867797   -107.113146     87.265733     61.769203     56.523854     -0.003564
0.000000     26.316595     34.451328   7180.962000   7244.558000   7255.420333    -41.795089    -70.889078    -83.462247     42.344911     13.250922      0.677753     -0.032447
0.000000      0.000000     36.720977   7053.740000   7133.697000   7204.281833   -127.731696   -210.813447   -251.244462    153.948304     70.866553     30.435538      0.054562

以下は、スクリプトのデフォルトパラメータを使用した予測分析の結果です。まず、相互情報量の表を見てみましょう。ここで、いくつかのインジケーターは目的との相互情報量がゼロであることがわかります。期間の長さが6の移動平均インジケーターは、目的に対する相互情報が最も高くなります。
PS          Variable         MI
ND                 5       0.0308
LG                 4       0.0293
MJ                 3       0.0279
GM                 6       0.0227
JP                 9       0.0182
IS                 1       0.0165
MF                 8       0.0135
JI                 7       0.0126
HL                 0       0.0000
JO                 2       0.0000
GS                10       0.0000
HD                11       0.0000

当然、アルゴリズムによって最初に選択されるのはMA_6です。最初の選択がおこなわれたので、それと情報を共有する他の候補予測変数があるかどうかを確認するのは興味深いでしょう(MA_6)。これは、以下の冗長性の値を調べることで推測できます。

ME   Predictors so far   Relevance   Redundancy   Criterion
GH                 5       0.0308       0.0000       0.0308
II   Additional candidates, in order of decreasing relevance minus redundancy
FE          Variable     Relevance   Redundancy   Criterion
LE                 0       0.0000       0.0095      -0.0095
ED                 1       0.0165       0.0869      -0.0704
FD                 2       0.0000       0.1149      -0.1149
PE                11       0.0000       0.2768      -0.2768
ID                 8       0.0135       0.3251      -0.3116
NS                 7       0.0126       0.3492      -0.3366
CR                10       0.0000       0.3484      -0.3484
ES                 6       0.0227       0.4030      -0.3802
IS                 9       0.0182       0.4285      -0.4103
CR                 3       0.0279       2.5363      -2.5084
DR                 4       0.0293       3.0096      -2.9803
MFI_2は、目的変数との関連性がゼロであるにもかかわらず、残りのすべての候補予測変数の中で冗長性が最も少ないため、アルゴリズムの次の選択になります。また、列インデックス3と4（それぞれMA_2とMA_4）の予測変数がMA_6との冗長性のレベルが最も高いことにも注意してください。これらは、より短い期間で計算された同じインジケーターであるため、これは理にかなっています。以下は、さらに2つの選択をおこなった後の予測変数セットです。どちらも目的変数との関連性はゼロです。注目すべきは、選ばれなかった候補者セットのトップ予測変数です。アルゴリズムは、最後の2つの選択が選択された予測変数にグループとして与えた希薄化効果により、関連する予測変数を考慮し始めます。
PQ   Predictors so far   Relevance   Redundancy   Criterion
FL                 5       0.0308       0.0000       0.0308
JK                 0       0.0000       0.0095      -0.0095
DK                 2       0.0000       0.1796      -0.1796
EE  Additional candidates, in order of decreasing relevance minus redundancy
JH         Variable     Relevance   Redundancy   Criterion
CH                6       0.0227       0.1469      -0.1241
PH                9       0.0182       0.1465      -0.1283
GI               10       0.0000       0.2024      -0.2024
PG                7       0.0126       0.2133      -0.2007
PF               11       0.0000       0.2308      -0.2308
GG                8       0.0135       0.2664      -0.2529
QG                1       0.0165       0.4679      -0.4514
KF                3       0.0279       0.8840      -0.8561
LF                4       0.0293       1.0372      -1.0079
結果についての解説を締めくくるにあたり、先に進んで、アルゴリズムによって選択された最終的な予測変数のセットを示します。
OQ  Final predictors ||  Relevance ||  Redundancy || Criterion  ||  Solo pval || Group pval
HN                5       0.0308       0.0000       0.0308       0.010       0.010
DJ                0       0.0000       0.0095      -0.0095       1.000       0.010
JG                2       0.0000       0.1796      -0.1796       1.000       0.010
HD                6       0.0227       0.1620      -0.1393       0.010       0.010
FQ                9       0.0182       0.2023      -0.1842       0.010       0.010
DL               11       0.0000       0.2798      -0.2798       1.000       0.010
KJ                1       0.0165       0.2932      -0.2767       0.010       0.010
OG                7       0.0126       0.3298      -0.3172       0.010       0.010
OE               10       0.0000       0.4151      -0.4151       1.000       0.010
JP                8       0.0135       0.4585      -0.4450       0.010       0.010
RN   Final predictor labels
NO  MA_6
DE  MFI_2
NN  MFI_6
KP  BEARS_2
DJ  BULLS_2
FL  BULLS_6
PQ  MFI_4
MK  BEARS_4
FM  BULLS_4
OF  BEARS_6


結論

この記事では、Peng、Long、Dingによって提案されたMRMR (Max-Dependency, Max-Relevance, Min-Redundancy)アルゴリズムに焦点を当てて、特徴量選択における相互情報量の応用について検討しました。まず、連続変数に対する相互情報量の推定について説明し、特徴と目的変数の間にある複雑で非線形な依存関係を捉える能力 を強調しました。その後、MRMRアルゴリズムを通じて、目的変数への関連性を最大化しつつ、すでに選択された特徴量との冗長性を最小限に抑えるという競合する目標を、どのように効果的にバランスさせるかを示しました。

さらに、本アルゴリズムがMRMRスコアに基づいて特徴を反復的に追加し、モンテカルロ順列テストを用いて統計的有意性を評価することで、選択された特徴量セットが最も情報価値の高い予測変数となることを保証する仕組みを説明しました。また、合成データと実データを用いた例を通じて、MRMRアルゴリズムの実用性を示しました。MRMR アルゴリズムは、関係のない特徴量や多重共線性による影響を受けることが多い実世界のデータにおいても、その有効性を発揮することを確認しました。MRMR アルゴリズムは、目的変数との関連性を最大化しながら冗長性を抑えることで、変数間の関係が複雑で非線形な場合でも、最適な特徴量セットを選択するための有力な手法であることが分かりました。

記事で参照されているすべてのコードは以下に添付されています。次の表では、この記事に付随するすべてのソースコードファイルについて説明します。

ファイル名
詳細
MQL5/include/np.mqh
 行列およびベクトルユーティリティ関数のヘッダーファイル
MQL5/include/mutualinfo.mqh
 連続変数の相互情報量を推定するための適応型分割法を実装するCapmクラスの定義を含むヘッダーファイルと、相互情報量に基づいて段階的な特徴量選択を実装するCmrmrクラスの定義
MQL5/scripts/RelevanceMinusRedundancy.mq5
 合成データを使用してCmrmrクラスを使用する方法を示すスクリプト
MQL5/scripts/StepWiseFeatureSelectionByMutualInformation.mq5
 より現実的なデータセットでのCmrmrクラスの適用を示す別のスクリプト

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/16416

添付されたファイル |
ZIPをダウンロード
np.mqh (74.16 KB)
mutualinfo.mqh (26.74 KB)
RelevanceMinusRedundancy.mq5 (1.69 KB)
StepWiseFeatureSelectionByMutualInformation.mq5 (7.39 KB)
Mql5.zip (19.35 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
プライスアクション分析ツールキットの開発（第3回）：Analytics Master EA プライスアクション分析ツールキットの開発（第3回）：Analytics Master EA
シンプルな取引スクリプトから完全に機能するエキスパートアドバイザー(EA)に移行することで、取引エクスペリエンスが大幅に向上します。チャートを自動で監視し、バックグラウンドで重要な計算を実行し、さらに2時間ごとに定期的な更新を提供するシステムを想像してみてください。このEAは、的確な取引判断を下すために不可欠な主要指標を分析し、常に最新の情報を取得して戦略を効果的に調整できるようにします。
データサイエンスとML（第32回）：AIモデルを最新の状態に保つ、オンライン学習 データサイエンスとML（第32回）：AIモデルを最新の状態に保つ、オンライン学習
常に変化する取引の世界では、市場の変動に適応することは選択肢ではなく、必要不可欠です。新たなパターンやトレンドが日々生まれる中で、最先端の機械学習モデルでさえ、進化する環境に対応し続けることが困難になっています。本記事では、モデルを自動的に再訓練することで、その有効性を維持し、新しい市場データに柔軟に適応させる方法を解説します。
MQL5で取引管理者パネルを作成する（第6回）：取引管理パネル(II) MQL5で取引管理者パネルを作成する（第6回）：取引管理パネル(II)
この記事では、多機能管理パネルの取引管理パネル(Trade Management Panel)を強化します。コードを簡素化し、読みやすさ、保守性、効率性を向上させる強力なヘルパー関数を導入します。また、追加のボタンをシームレスに統合し、インターフェイスを強化して、より幅広い取引タスクを処理する方法も紹介します。ポジションの管理、注文の調整、ユーザーとのやり取りの簡素化など、このガイドは、堅牢でユーザーフレンドリーな取引管理パネルの開発に役立ちます。
MQL5経済指標カレンダーを使った取引（第3回）：通貨、重要度、時間フィルターの追加 MQL5経済指標カレンダーを使った取引（第3回）：通貨、重要度、時間フィルターの追加
この記事では、MQL5経済カレンダーダッシュボードにフィルターを実装し、通貨、重要度、時間ごとにニュースイベントの表示を絞り込みます。まず、各カテゴリのフィルター基準を設定し、それをダッシュボードに組み込むことで、関連するイベントのみが表示されるようにします。最後に、各フィルターが動的に更新され、トレーダーにとって必要な、焦点を絞ったリアルタイムの経済情報が提供されるようにします。