Características del Wizard MQL5 que debe conocer (Parte 55): SAC con Prioritized Experience Replay (PER)

La creciente complejidad de los modelos de redes neuronales viene impulsada por nuestra capacidad para procesar grandes cantidades de datos. El aprendizaje automático tradicional tiene problemas de eficiencia, mientras que las redes neuronales, ejemplificadas por plataformas como DeepSeek, Grok y ChatGPT, ofrecen soluciones potentes.

Sin embargo, el entrenamiento de estos modelos presenta desafíos, especialmente con datos históricos limitados. El sobreajuste es un problema importante, ya que los modelos corren el riesgo de aprender ruido en lugar de patrones significativos. El entrenamiento tradicional suele dar prioridad a minimizar las funciones de pérdida, lo que puede conducir a una generalización deficiente.

El aprendizaje por refuerzo (Reinforcement Learning, RL) aborda esto equilibrando la explotación (optimización de pesos) y la exploración (prueba de alternativas). Técnicas como la reproducción priorizada de experiencias (Prioritized Experience Replay, PER) mejoran la eficiencia del aprendizaje y mitigan los problemas de escasez de datos que se observan en campos como el comercio, donde los datos económicos mensuales son limitados.

Las consideraciones clave del RL incluyen el diseño de una función de recompensa eficaz, la selección del algoritmo adecuado y la elección entre métodos basados en el valor (por ejemplo, Q-Learning, DQN) y métodos basados en políticas (por ejemplo, PPO, TRPO). Los enfoques actor-crítico (por ejemplo, A3C, SAC) equilibran la estabilidad y la eficiencia. Los métodos basados en políticas (PPO, A3C) garantizan un aprendizaje estable, mientras que los métodos no basados en políticas (DQN, SAC) maximizan la eficiencia de los datos.

La adaptabilidad de RL lo convierte en una valiosa incorporación a los procesos de aprendizaje automático, complementando los enfoques tradicionales. Cuando se entrenan modelos complejos con datos limitados, dar prioridad a las actualizaciones de peso sobre la minimización de pérdidas fomenta una mejor generalización y robustez.

Prioritized Experience Replay (PER)

Los búferes de reproducción de experiencias priorizadas (Prioritized Experience Replay, PER) y los búferes de reproducción típicos (para muestreo aleatorio) se utilizan en RL con algoritmos fuera de política como DQN y SAC, ya que permiten almacenar y muestrear experiencias pasadas. PER se diferencia de un búfer de reproducción típico en la forma en que se priorizan y muestrean las experiencias pasadas. 

Con el búfer de reproducción típico, las experiencias se muestrean de manera uniforme y aleatoria, lo que significa que cualquiera de las experiencias pasadas tiene la misma probabilidad de ser seleccionada, independientemente de su importancia o relevancia para el proceso de aprendizaje. Con PER, las experiencias pasadas se muestrean en función de su «prioridad». Propiedad que a menudo se cuantifica mediante la magnitud del error de diferencia temporal. Este error sirve como indicador del potencial de aprendizaje. A cada experiencia se le asigna un valor de este error y las experiencias con valores altos se muestrean con mayor frecuencia. Esta priorización puede implementarse utilizando un enfoque proporcional o basado en rangos.

Los búferes de reproducción típicos tampoco introducen ni utilizan sesgos. PER lo hace y esto podría sesgar injustamente el proceso de aprendizaje, por lo que, para corregirlo, PER utiliza ponderaciones de muestreo por importancia para ajustar el impacto de cada experiencia muestreada. Por lo tanto, los búferes de reproducción típicos son más eficientes en cuanto a muestras, ya que realizan muchas menos tareas en segundo plano que los PER. Por otro lado, PER ofrece un aprendizaje más centrado y constructivo, algo que los amortiguadores típicos no hacen.

Por lo tanto, no hace falta decir que implementar un PER sería más complejo que un búfer de reproducción típico; sin embargo, la razón por la que se hace hincapié en esto aquí es porque el PER requiere una clase adicional para mantener la cola de prioridades, a menudo denominada «árbol de sumas». Esta estructura de datos permite un muestreo más eficiente de las experiencias en función de su prioridad. El PER tiende a conducir a una convergencia más rápida y a un mejor rendimiento, ya que se centra en experiencias que son más informativas o desafiantes para el agente.

Implementación en el modelo

Nuestra clase PER, en Python, utiliza una inicialización que valida los parámetros de su constructor, concretamente el parámetro mode. Podría estar equivocado, pero creo que esto es algo que no se puede hacer de forma inmediata con C/ MQL5. Declaramos esta función __init__ de la siguiente manera:

        def __init__(self, capacity, alpha=0.6, beta=0.4, beta_increment=0.001, mode='proportional'):
                self.capacity = capacity
                self.alpha = alpha
                self.beta = beta
                self.beta_increment = beta_increment
                self.mode = mode

                if mode == 'proportional':
                        self.tree = SumTree(capacity)
                elif mode == 'rank':
                        self.priorities = []
                        self.data = []
                else:
                        raise ValueError("Invalid mode. Choose 'proportional' or 'rank'.")

Una vez declarada la clase, una de las funciones importantes que debe incluir es un método para añadir experiencias al búfer. Lo implementamos de la siguiente manera: 

    def add(self, error, sample):
        p = self._get_priority(error)
        if self.mode == 'proportional':
            self.tree.add(p, sample)
        elif self.mode == 'rank':
            heapq.heappush(self.priorities, -p)
            if len(self.data) < self.capacity:
                self.data.append(sample)
            else:
                heapq.heappop(self.priorities)
                heapq.heappush(self.data, sample)

Tenga en cuenta que, en esta adición de experiencias, el modo de muestreo es clave, ya que si seleccionamos experiencias basándonos en la proporción del error, simplemente las añadimos al árbol de sumas, pero si elegimos basándonos en la clasificación de la magnitud del error, utilizamos un módulo importado heapq que actualizamos con esta muestra como se ha indicado anteriormente. Por lo tanto, en el muestreo de proporción se utiliza la clase de árbol de suma y no el de rango. Así es como se implementa:

class SumTree:
    def __init__(self, capacity):
        self.capacity = capacity
        self.tree = np.zeros(2 * capacity - 1)
        self.data = np.zeros(capacity, dtype=object)
        self.write = 0
        self.n_entries = 0

    def _propagate(self, idx, change):
        parent = (idx - 1) // 2
        self.tree[parent] += change
        if parent != 0:
            self._propagate(parent, change)

    def _retrieve(self, idx, s):
        left = 2 * idx + 1
        right = left + 1

        if left >= len(self.tree):
            return idx

        if s <= self.tree[left]:
            return self._retrieve(left, s)
        else:
            return self._retrieve(right, s - self.tree[left])

    def total(self):
        return self.tree[0]

    def add(self, p, data):
        idx = self.write + self.capacity - 1

        self.data[self.write] = data
        self.update(idx, p)

        self.write += 1
        if self.write >= self.capacity:
            self.write = 0

        if self.n_entries < self.capacity:
            self.n_entries += 1

    def update(self, idx, p):
        change = p - self.tree[idx]
        self.tree[idx] = p
        self._propagate(idx, change)

    def get(self, s):
        idx = self._retrieve(0, s)
        data_idx = idx - self.capacity + 1
        return (idx, self.tree[idx], self.data[data_idx])

Con esta clase clave definida, el otro componente crucial de esto es la función de muestra en sí, que es parte de la clase PER. 

def sample(self, batch_size):
        batch = []
        idxs = []
        segment = self.tree.total() / batch_size if self.mode == 'proportional' else len(self.data) / batch_size
        priorities = []

        self.beta = np.min([1., self.beta + self.beta_increment])

        for i in range(batch_size):
            a = segment * i
            b = segment * (i + 1)

            if self.mode == 'proportional':
                s = random.uniform(a, b)
                (idx, p, data) = self.tree.get(s)
                priorities.append(p)
                batch.append(data)
                idxs.append(idx)
            elif self.mode == 'rank':
                idx = random.randint(0, len(self.data) - 1)
                priorities.append(-self.priorities[idx])
                batch.append(self.data[idx])
                idxs.append(idx)

        sampling_probabilities = np.array(priorities) / self.tree.total() if self.mode == 'proportional' else np.array(priorities) / sum(self.priorities)
        is_weights = np.power(len(self.data) * sampling_probabilities, -self.beta)
        is_weights /= is_weights.max()

        return batch, idxs, is_weights

Una vez más, el modo de muestreo, ya sea proporcional o basado en rangos, es una consideración clave aquí. Estos dos enfoques asignan las prioridades de cada experiencia, considerando el error TD, con una diferencia matizada. Magnitud del error TD y rango del error TD. El error TD es efectivamente la diferencia entre el resultado de una experiencia y el valor real u objetivo. Nunca se utiliza en su estado bruto para ponderar las experiencias, sino que se convierte en un valor de prioridad como se muestra en este listado:

def _get_priority(self, error):
        return (error + 1e-5) ** self.alpha

Es este valor de prioridad cuya magnitud (para el muestreo de proporción) o rango (para el muestreo por rango) se utiliza para seleccionar experiencias para entrenar el modelo. PER fue introducido por Tom Schaul et al. en 2015. Las experiencias con mayor prioridad se muestrean con más frecuencia, lo que mejora la eficiencia del muestreo y acelera el aprendizaje por refuerzo. Las prioridades se actualizan después del aprendizaje. Los pesos de muestreo por importancia se utilizan para corregir el sesgo introducido por el muestreo no uniforme basado en prioridades. Esto se indica en la función de muestra de la clase PER anterior. Profundicemos en estos dos modos de muestreo.

Priorización proporcional

Como se ha mencionado anteriormente, las prioridades son directamente proporcionales al error de diferencia temporal (∣δ∣). Por lo tanto, la prioridad para una experiencia se calcularía de la siguiente manera:

pi=∣δi∣+ϵ

Donde ϵ, que es mayor que cero, es una pequeña constante que garantiza que todas las experiencias no tengan una prioridad cero. Por lo tanto, la probabilidad de muestreo para la experiencia sería:

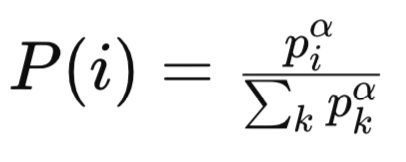
Donde:

• pi es la prioridad de la i-ésima experiencia en el búfer de reproducción. La prioridad se basa normalmente en la magnitud del error de diferencia temporal (TD) para esa experiencia. Las experiencias con errores TD más grandes se consideran más importantes y se les asigna una prioridad más alta.

• α es un hiperparámetro que controla el grado de priorización. Cuando (α = 0), todas las experiencias se muestrean de manera uniforme (sin priorización). Cuando (α = 1), el muestreo se basa completamente en las prioridades.

• Sigma/suma de todas las prioridades k es el término de normalización, que garantiza que las probabilidades sumen 1. Suma las prioridades de todas las experiencias en el búfer de reproducción, elevadas a la potencia de (α).

• P(i) es la probabilidad de muestrear la experiencia (i)-ésima. Es proporcional a la prioridad de la experiencia (Piα), normalizada por la suma de todas las prioridades elevadas a la potencia de (α).

A continuación, se puede utilizar un árbol de suma o una estructura de datos de forma similar para muestrear de manera eficiente las experiencias I. proporcional a piα. La distribución muestral con priorización proporcional es continua y está directamente relacionada con la magnitud de los errores TD. Las experiencias con errores TD elevados suelen tener prioridades significativamente altas, lo que da lugar a una distribución con una cola pesada.

Esto podría dar lugar a que algunas experiencias se muestren con demasiada frecuencia (lo cual sería muy preocupante si sus errores TD fueran valores atípicos) y otras se muestren muy raramente debido a que sus errores son pequeños. La sensibilidad a los errores de entrenamiento puede variar entre las tareas de las fases de entrenamiento, pero existe una vulnerabilidad a la priorización proporcional de los valores atípicos en los errores de TD, ya que los valores grandes pueden dominar la distribución muestral.

Por ejemplo, consideremos un escenario en el que una experiencia tenía una diferencia entre el resultado y el objetivo de 1000, mientras que las demás tenían una diferencia de 1. Es evidente que este valor tan elevado se muestreará con frecuencia de forma desproporcionada. Esta característica puede conducir a un sobreajuste a experiencias ruidosas o atípicas, especialmente en entornos de datos con una alta varianza en las recompensas o los valores Q. Una posible medida de mitigación para esto podría ser el recorte o la normalización del error TD. Por ejemplo:

pi=min⁡(∣δi∣,δmax)+ϵ

Donde, en esencia, la prioridad de una experiencia se establece en el mínimo entre su propio error de TD y el error de TD más alto de todas las experiencias dentro del segmento muestreado más un pequeño valor distinto de cero, épsilon. Las complejidades del tiempo operativo al tratar con un árbol de suma son sencillas cuando se calcula la prioridad para cada experiencia, ya que llegan a O(1) por experiencia. El muestreo y actualización de prioridades llega a O(log n) por operación, donde n es el tamaño del búfer. Sin sobrecarga adicional para ordenar y clasificar, esto hace que sea computacionalmente eficiente para las actualizaciones.

La priorización proporcional (PP) puede fomentar un entrenamiento inestable en los casos en que los errores de TD varían significativamente entre las fases de entrenamiento, ya que la distribución del muestreo cambiaría rápidamente. También es sensible a los hiperparámetros, por lo que las elecciones de alfa y épsilon deben hacerse con cuidado para equilibrar la exploración y la explotación. El PP puede converger más rápido en tareas con errores "de buen comportamiento", lo que es indicativo del valor del aprendizaje, pero es probable que presente dificultades en entornos ruidosos y no estacionarios.

PP es adecuado para tareas en las que los errores de TD se comportan bien y son directamente indicativos del potencial/valor del aprendizaje. Es muy eficaz en entornos con poco ruido y valores Q estables donde los errores de TD son directamente proporcionales a experiencias importantes. Ejemplos de ello son los juegos de Atari con estructuras de recompensa estables y tareas de control continuo con funciones de valor fluidas.

Los pesos de muestreo de importancia de PP tienden a variar debido a la distribución de muestreo de cola pesada. Experiencias con pesos de prioridad bajos y, por lo tanto, valores P(i) bajos (es decir, probabilidad de muestreo de la experiencia i) y esto conduce a pesos wi grandes (pesos de ajuste destinados a corregir el sesgo). Esta configuración tiene el potencial de tener una consecuencia no deseada: amplificar los gradientes y desestabilizar el entrenamiento. Esto significa, por tanto, que la beta también debe ajustarse cuidadosamente para lograr un equilibrio entre la corrección del sesgo y la estabilidad.

En resumen, PP es adecuado cuando los errores de TD se comportan bien y se correlacionan con el valor de aprendizaje; el entorno de datos tiene poco ruido y valores Q estables; y la eficiencia computacional es crítica, lo que significa que los costos generales de clasificación y ordenamiento no son aceptables. El ajuste fino de los hiperparámetros alfa, beta y épsilon puede ayudar a manejar valores atípicos y gestionar la inestabilidad.

Priorización basada en rangos

Con este modo, las prioridades se basan en los valores del índice de clasificación del error TD en la lista ordenada de errores TD. El rango de una experiencia i se establece ordenando todas las experiencias por la magnitud del error de diferencia temporal en orden descendente. ¿Por qué orden descendente? Porque intuitivamente dicha lista interpreta la importancia de una experiencia. Cuanto más arriba en la lista, más importante es una experiencia. En segundo lugar, desde un punto de vista computacional, tiene sentido tener las experiencias a las que se hará más referencia en los índices más bajos dentro de un montón, ya que el algoritmo no tiene que recorrer todo el montón para llegar a las experiencias destinadas a realizar la mayor parte del entrenamiento. La prioridad de la experiencia i normalmente se calcula como:

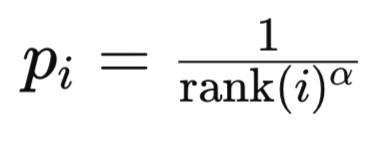
Donde:

- rank(i) es el rango de la i-ésima experiencia.

- alfa es un hiperparámetro que controla la fuerza de la priorización.

La probabilidad de muestreo para la experiencia utiliza una fórmula similar a la que ya hemos cubierto anteriormente en priorización proporcional.

Con la priorización basada en rangos (Rank-Based Prioritization, RP), la distribución del muestreo es discreta y se basa en rangos. Esto tiende a hacerlo menos sensible a la escala absoluta de errores de TD. Las experiencias se eligen en función de su rango en lugar de la magnitud del error. Esto conduce a una distribución más uniforme al momento del muestreo dado que la diferencia en priorización entre las experiencias está casi “estandarizada” ya que está controlada por el ranking respectivo de las experiencias. e. 1/1, ½, ⅓, etc..). Además, RP es menos propenso a sobreajustar valores atípicos ya que la prioridad más alta asignada a cualquier experiencia se fija en 1/1 independientemente de su magnitud de error TD. Sin embargo, esta robustez se ve eclipsada por un muestreo insuficiente de experiencias con errores de TD muy elevados si la función de prioridad basada en rango decae demasiado rápido.

Sin embargo, además del riesgo de no muestrear las experiencias clave, el principal inconveniente de la RP sigue siendo la complejidad computacional. Ordenar un búfer completo para determinar los rangos es una complejidad computacional operativa de magnitud O(nlogn) para un búfer completo de tamaño n. En la práctica, esta clasificación se puede evitar manteniendo una estructura de datos ordenada (como un árbol de búsqueda binario o un montón) para los errores de TD, pero las actualizaciones aún requieren O(logn) cálculos operativos por experiencia. El muestreo y la actualización se mantienen en O(logn), al igual que el guardado con el muestreo basado en proporciones. En resumen, RP tiene una sobrecarga computacional significativamente mayor en comparación con PP.

Cuando el entrenamiento RP es más estable ya que la distribución de muestreo es menos sensible a los cambios en las magnitudes de error de TD. También tiende a proporcionar probabilidades de muestreo consistentes a lo largo del tiempo dado que los rangos son relativos y se ven menos afectados por el ruido y los valores atípicos. Puede converger más lentamente para tareas donde los errores de TD absolutos son cruciales/altamente informativos para el proceso de entrenamiento, ya que no prioriza errores de alta magnitud de manera tan agresiva. También es un poco más fácil de ajustar (ajustando hiperparámetros) porque la función de prioridad basada en rango es menos sensible a la escala.

RP es adecuado en entornos de recompensas escasas o para tareas que tienen recompensas retrasadas o una alta variación de recompensa. RP es un modo preferido donde la estabilidad y el muestreo equilibrado son críticos incluso si la convergencia puede ser lenta.

Tanto PP como RP introducen un sesgo debido a sus métodos de muestreo no uniformes y como ya se mencionó y se muestra en el método de muestreo en la fuente anterior. La fórmula básica para esto es:

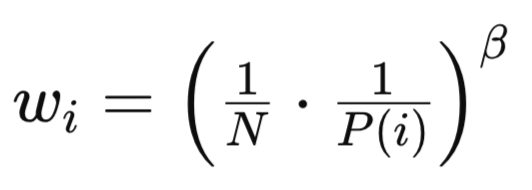
Donde:

- N es el número total de experiencias en el búfer de reproducción.

- P(i) es la probabilidad de muestrear la i-ésima experiencia.

- beta (β∈[0,1]) es un hiperparámetro que controla la fuerza de la corrección de muestreo de importancia.

A pesar de tener fórmulas similares, los pesos RP y PP difieren en aspectos clave. En el caso de RP, los pesos de muestreo de importancia son más uniformes dado que la distribución es menos sesgada. Esta menor variación en los valores de wi conduce a un entrenamiento más estable y a una menor sensibilidad a beta. Además, la corrección del sesgo es más fácil de gestionar ya que la distribución basada en rangos es inherentemente más equilibrada.

Prueba de clase de señal

Si usamos el código listado arriba y modificamos el código del modelo SAC del último artículo al tener un PER en lugar de un buffer de reproducción típico/simple, estaríamos en condiciones de entrenar el modelo y exportar una red con sus pesos como un archivo ONNX. En el último artículo explicamos cómo se puede gestionar esta exportación, y aquí hay notas orientativas sobre cómo exportar también un modelo ONNX desde Python. MQL5 utiliza los modelos ONNX integrándolos como recursos durante la compilación. 

En el lado MQL5 del IDE, nuestra clase de señal personalizada, que en sentido estricto no difiere de la que teníamos en el último artículo sobre SAC, debe ser ensamblada por el asistente MQL5. Para los nuevos lectores, hay guías aquí y aquí sobre cómo hacerlo. Las pruebas no validadas cruzadas para el USD JPY en el marco temporal diario para el año 2023 nos presentan el siguiente informe:

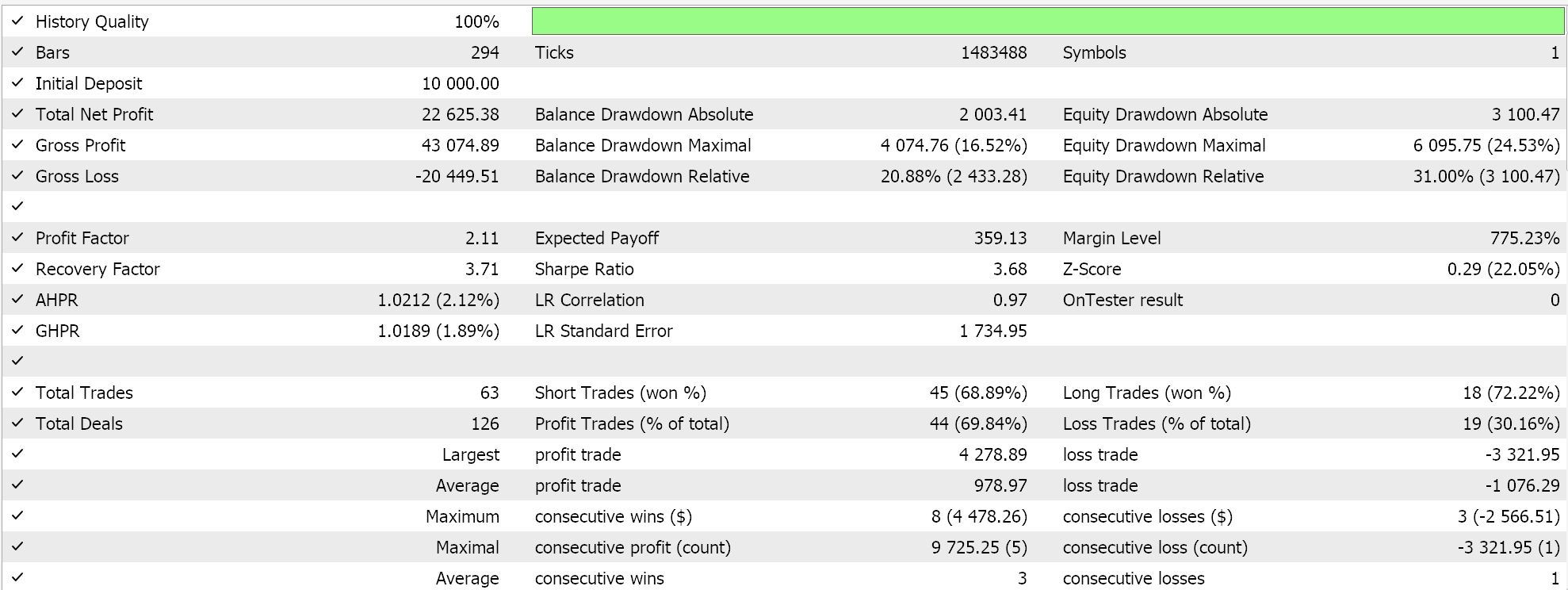
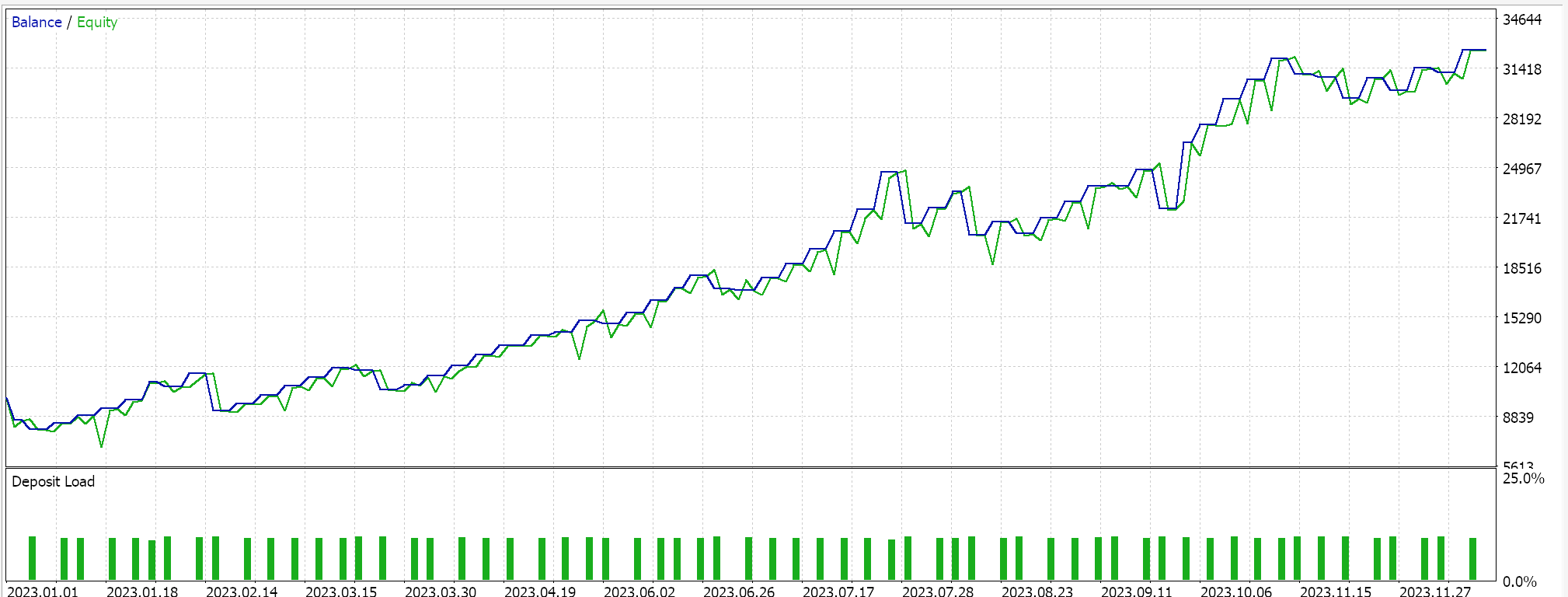
Sin embargo, en el futuro, la validación cruzada con modelos en Python se puede realizar de manera muy eficiente, por lo que tal vez sea algo que comience a incorporar en estos artículos en el futuro. Sin embargo, como siempre, el rendimiento pasado no garantiza resultados futuros y se invita al lector a realizar su propia diligencia adicional antes de decidir utilizar o implementar cualquiera de los sistemas que se comparten aquí.

Conclusión

Hemos revisado el caso del aprendizaje por refuerzo reiterando por qué, en el contexto actual de modelos complejos y datos históricos de prueba limitados, es muy importante dar prioridad al proceso de llegar a los pesos adecuados de la red por encima de las puntuaciones teóricas de la función de baja pérdida. El proceso importa. Y para terminar, hemos destacado un búfer de reproducción alternativo para el aprendizaje por refuerzo, el búfer de reproducción de experiencias priorizadas, como un búfer que no solo mantiene a mano las experiencias recientes para su muestreo durante el entrenamiento, sino que también toma muestras de este búfer en proporción a su relevancia o a lo que la red tiene que aprender de la experiencia muestreada.

Archivo	Descripción
wz_55.mq5	Asesor experto con encabezado que muestra los archivos utilizados.
SignlWZ_55.mqh	Archivo de clase de señal personalizada.
USDJPY.onnx	Archivo ONNX de la red.