
Algoritmos Genéticos: ¡Es fácil!
Introducción
Con "algoritmo genético" (GA, por sus siglas en inglés) nos referimos al algoritmo heurístico (EA), que facilita una solución aceptable al problema en la mayoría de casos relevantes. No obstante, la corrección de las decisiones no está probada matemáticamente, y se utiliza frecuentemente para problemas cuya solución analítica es muy difícil, o incluso imposible.
Un ejemplo clásico de problema de esta clase (clase NP) es un "problema de vendedor ambulante" (uno de los problemas de optimización más famosos). (El reto principal es encontrar la ruta más ventajosa que pase por todas las ciudades disponibles al menos una vez, volviendo al final a la ciudad inicial.) Pero no hay nada en contra de usarlos para tareas, lo que lleva a una formalización.
Los EA se usan generalmente para resolver problemas de alta complejidad computacional, en lugar de pasar por todas las opciones. Esto llevaría una cantidad de tiempo significativa. Se utilizan en los campos de inteligencia artificial, tales como reconocimiento de patrones, softwares de antivirus, ingeniería, juegos de ordenador y otras áreas.
Se debería mencionar que MetaQuotes Software Corp. usa GA en sus productos de software de MetaTrader4 / 5. Todos conocemos el Probador de Estrategias y sabemos cuánto tiempo y esfuerzo se puede ahorrar usando un optimizador de estrategia incorporado, en el que, al igual que con la enumeración, es posible optimizar con el uso de un GA. Además, el probador de MetaTrader 5 permite el uso de criterios de optimización de usuario. Quizás, el lector tenga interés en leer los artículos sobre el GA y sus ventajas, facilitadas por el EA, en contraste con la enumeración directa.
1. Un poco de historia
Hace poco más de un año, necesitaba un algoritmo de optimización para entrenar redes neuronales. Tras familiarizarme rápidamente con los algoritmos varios, elegí el GA. Como resultado de mi búsqueda de implementaciones ya hechas, encontré que las que estaban abiertas para el acceso público o bien tenían limitaciones funcionales, como el número de parámetros que se podían optimizar, o estaban "demasiado afinadas".
Necesitaba un instrumento universalmente flexible no solo para entrenar todo tipo de redes neuronales, sino también para solucionar de forma general cualquier problema de optimización. Tras un largo estudio de "creaciones genéticas" extranjeras, seguí siendo incapaz de entender cómo funcionaban. Esto era a causa de un estilo de código muy elaborado, o por mi falta de experiencia en programación, o seguramente por ambas razones.
Las principales dificultades surgían al codificar genes en un código binario, y después trabajar con ellos en esta forma. En cualquier caso, decidí escribir un algoritmo genético de cero, centrándome en su escalabilidad y fácil modificación en el futuro.
No quise encargarme de la transformación binaria, y decidí trabajar con los genes directamente, es decir, representar el cromosoma con un conjunto de genes en forma de números reales. Así es como surgió el código para mi algoritmo genético, con una representación de cromosomas con números reales. Más adelante, aprendí que no había descubierto nada nuevo, y que ya existían otros algoritmos genéticos análogos (llamados GA de código real) desde hacía más de 15 años, que es cuando surgieron las primeras publicaciones sobre ellos.
Dejaré que el propio lector juzgue mi visión de enfoque de la implementación y principios del funcionamiento del GA, puesto que se basa en la experiencia personal de su uso en problemas prácticos.
2. Descripción del GA
El GA contiene principios tomados de la naturaleza misma. Estos son los principios de herencia y variabilidad. La herencia es la capacidad de los organismos de transferir sus cualidades y características evolucionarias a sus descendientes. Gracias a esta capacidad, todos los seres vivos dejan detrás las características de sus especies en su descendencia.
La variabilidad de genes en organismos vivos asegura la diversidad genética de la población, y es fortuita: la naturaleza no tiene forma de saber de antemano qué cualidades se preferirán en el futuro (cambio climático, aumento/disminución de alimentos, emergencia de especies competidoras, etc). Esta variabilidad permite la aparición de criaturas con nuevas cualidades, que pueden sobrevivir y dejar detrás sus descendientes en las nuevas condiciones alteradas de su hábitat.
En biología, la variabilidad que surgió a causa de la emergencia de mutaciones se llama mutacional, y la variabilidad que surgió a causa de la combinación cruzada de genes a través de la reproducción se llama combinacional. Ambos tipos de variaciones se implementan en el GA. Además, hay una implementación de mutagénesis que imita el mecanismo natural de las mutaciones (cambios en la secuencia de nucleótidos del ADN): la natural (espontánea) y la artificial (inducida).
La unidad más sencilla de transferencia de información en el criterio del algoritmo es el gen : unidad estructural y funcional de herencia que controla el desarrollo de una cualidad o propiedad particular. Llamaremos a una variable de la función el gen. El gen se representa con un número real. El conjunto de variables de gen de la función estudiada es la cualidad característica del cromosoma.
Aceptemos representar el cromosoma en forma de columna. A continuación, el cromosoma para la función f (x) = x ^ 2 tendrá este aspecto:
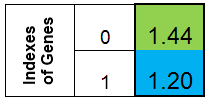
Figura 1. Cromosoma para la función f (x) = x ^ 2
en la que el valor del índice 0 de la función f (x) llamó a la adaptación de los organismos (llamaremos a esta función la función fitness - FF, y el valor de la función - VFF ). Es conveniente almacenar el cromosoma en un array monodimensional. Este es el array double Chromosome [].
Todos los especímenes de la misma era evolucionaria se combinan en una población. Además, la población se divide arbitrariamente en dos colonias iguales - la colonia progenitora y la descendiente. Como resultado de cruzar las especies progenitoras, que se seleccionan de entre la población entera, y otros operadores del GA, hay una colonia de nuevos descendientes igual a la mitad del tamaño de la población, que reemplaza la colonia de descendientes en la población.
La población total de organismos durante una búsqueda para el mínimo de la función f (x) = x ^ 2 puede tener el siguiente aspecto:
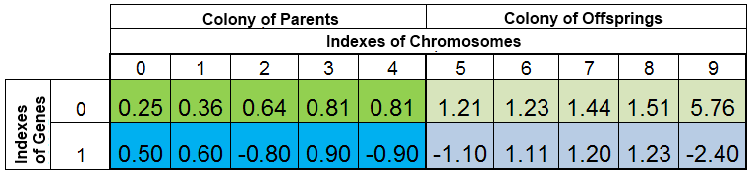
Figura 2. Población total de organismos
La población distribuida según VFF. Aquí, el índice 0 del cromosoma se toma por el espécimen con el FF más pequeño. La nueva descendencia sustituye completamente solo a los organismos en la colonia de descendientes, mientras que la colonia progenitora permanece intacta. Sin embargo, la colonia progenitora puede no está siempre completa, puesto que los especímenes duplicados se destruyen, y luego los nuevos descendientes llenan los espacios vacantes en la colonia progenitora. El resto se coloca en la colonia de descendientes.
En otras palabras, el tamaño de la población rara vez se mantiene constante, y varía de era en era, casi de la misma forma que sucede en la naturaleza. Por ejemplo, la población antes del engendramiento y después del engendramiento podría tener el siguiente aspecto:
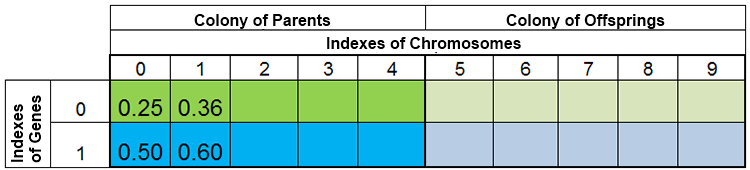
Figura 3. La población antes del engendramiento
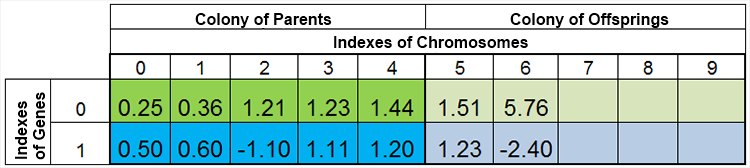
Figura 4. La población después del engendramiento
El mecanismo descrito del "semi-reemplazo" de la población por los descendientes, así como la destrucción de duplicados y la prohibición de engendramientos cruzados de organismos consigo mismos tiene un claro objetivo: evitar el efecto "cuello de botella" (un término de biología que se refiere a la reducción de la reserva genética de la población como resultado de una reducción crítica a causa de diversas razones, que puede llevar a la completa extinción de una especie. GA se enfrenta al fin de las apariciones de cromosomas únicos y se "queda atascado" en uno de los extremos locales).
3. Descripción de la función UGAlib
Algoritmo GA:- Crear una proto-población. Los genes se generan de forma fortuita dentro de un margen concreto.
- Determinar el fitness de cada organismo, o en otras palabras, el cálculo del VFF.
- Preparar la población para la reproducción tras eliminar los cromosomas duplicados.
- Aislamiento y mantenimiento del cromosoma de referencia (con el mejor VFF).
- Operadores de UGA (selección, reproducción, mutación). Para cada reproducción y mutación se seleccionan nuevos progenitores. Preparar la población para la siguiente era.
- Comparación de genes de la mejor descendencia con los genes del cromosoma de referencia. Si el cromosoma de la mejor descendencia es mejor que el cromosoma de referencia, entonces el primero sustituirá al segundo.
Continúe a partir del quinto párrafo hasta que dejen de aparecer cromosomas mejores que el de referencia para un número específico de eras.
3.1. Global variables. Variables globales
Se anunciaron las siguientes variables a nivel global:
//----------------------Global variables----------------------------- double Chromosome[]; //A set of optimized arguments of the function - genes //(for example: the weight of the neuron network, etc.)- of the chromosome int ChromosomeCount =0; //Maximum possible amount of chromosomes in a colony int TotalOfChromosomesInHistory=0;//Total number of chromosomes in the history int ChrCountInHistory =0; //Number of unique chromosomes in the base chromosome int GeneCount =0; //Number of genes in the chromosome double RangeMinimum =0.0;//Minimum search range double RangeMaximum =0.0;//Maximum search range double Precision =0.0;//Search step int OptimizeMethod =0; //1-minimum, any other - maximum int FFNormalizeDigits =0; //Number of symbols after the comma in the fitness value int GeneNormalizeDigits =0; //Number of symbols after the comma in the genes value double Population [][1000]; //Population double Colony [][500]; //Offspring colony int PopulChromosCount =0; //The current number of chromosomes in a population int Epoch =0; //Number of epochs without progress int AmountStartsFF=0; //Number of launches of the fitness function //————————————————————————————————————————————————————————————————————————
3.2. UGA. La función principal del GA
En realidad es la principal función del GA, llamada desde el cuerpo del programa para realizar los pasos alistados arriba. Por tanto, no la describiremos en detalle.
Tras completar el algoritmo, se grabó la siguiente información en el registro:
- Cuántas épocas habían en total (generaciones).
- Cuántas faltas en total.
- El número de cromosomas únicos.
- El número total de lanzamientos de FF.
- El número total de cromosomas en el historial.
- Porcentaje de duplicados en el número total de cromosomas en el historial.
- Mejor resultado.
"El número de cromosomas únicos" y el "número total de lanzamientos de FF": tienen el mismo tamaño, pero se calculan de forma diferente. Uso para control.
//———————————————————————————————————————————————————————————————————————— //Basic function UGA void UGA ( double ReplicationPortion, // Proportion of replication. double NMutationPortion, // Proportion of natural mutations. double ArtificialMutation, // Proportion of artificial mutations. double GenoMergingPortion, // Proportion of borrowed genes. double CrossingOverPortion, // Proportion of cross -over. //--- double ReplicationOffset, // Coefficient of displacement of interval borders double NMutationProbability // Probability of mutation of each gene in% ) { //generator reset takes place only once MathSrand((int)TimeLocal()); //-----------------------Variables------------------------------------- int chromos=0, gene =0;//indexes of chromosomes and genes int resetCounterFF =0;//counter of resets of "Epochs without progress" int currentEpoch =1;//number of the current epoch int SumOfCurrentEpoch=0;//sum of "Epochs without progress" int MinOfCurrentEpoch=Epoch;//minimum of "epochs without progress" int MaxOfCurrentEpoch=0;//maximum of "Epochs without progress" int epochGlob =0;//total number of epochs // Colony [number of traits(genes)][number of individuals in a colony] ArrayResize(Population,GeneCount+1); ArrayInitialize(Population,0.0); // Colony of offspring [number of traits(genes)][number of individuals in a colony] ArrayResize(Colony,GeneCount+1); ArrayInitialize(Colony,0.0); // Chromosome bank // [number of traits (genes)][number of chromosomes in the bank] double historyHromosomes[][100000]; ArrayResize(historyHromosomes,GeneCount+1); ArrayInitialize(historyHromosomes,0.0); //---------------------------------------------------------------------- //--------------Verification of the correctness of incoming parameters---------------- //...the number of chromosomes mus be less than 2 if(ChromosomeCount<=1) ChromosomeCount=2; if(ChromosomeCount>500) ChromosomeCount=500; //---------------------------------------------------------------------- //====================================================================== // 1) Create a proto- population —————1) ProtopopulationBuilding(); //====================================================================== // 2) Determine the fitness of each individual —————2) //For the 1st colony for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=0;chromos<ChromosomeCount;chromos++) Population[0][chromos]=Colony[0][chromos]; //For the 2nd colony for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos-ChromosomeCount]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) Population[0][chromos]=Colony[0][chromos-ChromosomeCount]; //====================================================================== // 3) Prepare the population for reproduction ————3) RemovalDuplicates(); //====================================================================== // 4) Extract the reference chromosome —————4) for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; //====================================================================== ServiceFunction(); //The main cycle The main cycle of the genetic algorithm from 5 to 6 while(currentEpoch<=Epoch) { //==================================================================== // 5) Operators of UGA —————5) CycleOfOperators ( historyHromosomes, //--- ReplicationPortion, //Proportion of replication. NMutationPortion, //Proportion of natural mutation. ArtificialMutation, //Proportion of artificial mutation. GenoMergingPortion, //Proportion of borrowed genes. CrossingOverPortion,//Proportion of cross- over. //--- ReplicationOffset, //Coefficient of displacement of interval borders NMutationProbability//Probability of mutation of each gene in % ); //==================================================================== // 6) Compare the genes of the best offspring with the genes of the reference chromosome. // If the chromosome of the best offspring is better that the reference chromosome, // replace the reference. —————6) //If the optimization mode is - minimization if(OptimizeMethod==1) { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]<Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Rest the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //If the optimization mode is - minimization else { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]>Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Reset the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //==================================================================== //Another epoch went by.... epochGlob++; } Print("Epochs went by=",epochGlob," Number of resets=",resetCounterFF); Print("MinOfCurrentEpoch",MinOfCurrentEpoch, " AverageOfCurrentEpoch",NormalizeDouble((double)SumOfCurrentEpoch/(double)resetCounterFF,2), " MaxOfCurrentEpoch",MaxOfCurrentEpoch); Print(ChrCountInHistory," - Unique chromosome"); Print(AmountStartsFF," - Total number of launches of FF"); Print(TotalOfChromosomesInHistory," - Total number of chromosomes in the history"); Print(NormalizeDouble(100.0-((double)ChrCountInHistory*100.0/(double)TotalOfChromosomesInHistory),2),"% of duplicates"); Print(Chromosome[0]," - best result"); } //————————————————————————————————————————————————————————————————————————
3.3. Creating a Proto- population. Crear una proto-población.
Puesto que en la mayoría de los problemas de optimización no hay forma de saber de antemano dónde se encuentran los argumentos de la función en el número de línea, la mejor opción es la generación fortuita dentro de un margen concreto.
//———————————————————————————————————————————————————————————————————————— //Creating a proto- population void ProtopopulationBuilding() { PopulChromosCount=ChromosomeCount*2; //Fill up the population with chromosomes with random //...genes in the range between RangeMinimum...RangeMaximum for(int chromos=0;chromos<PopulChromosCount;chromos++) { //beginning with the 1st indexes (the 0 index is reserved for VFF) for(int gene=1;gene<=GeneCount;gene++) Population[gene][chromos]= NormalizeDouble(SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); TotalOfChromosomesInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.4. GetFitness. Obtener el fitness
Realiza la función optimizada para cada cromosoma en orden.
//------------------------------------------------ ------------------------ // Getting the fitness for each individual. void GetFitness ( double &historyHromosomes[][100000] ) { for(int chromos=0;chromos<ChromosomeCount;chromos++) CheckHistoryChromosomes(chromos,historyHromosomes); } //————————————————————————————————————————————————————————————————————————
3.5. CheckHistoryChromosomes. Verificación del cromosoma a través de la base del cromosoma
El cromosoma de cada organismo se verifica a través de la base si se ha calculado el FF para ello, y en caso de que asi sea, entonces el VFF listo se toma de la base; si no, el FF se llama para ello. Por tanto, el recurso que se repite, los cálculos intensivos de FF, se excluyen.
//———————————————————————————————————————————————————————————————————————— //Verification of chromosome through the chromosome base. void CheckHistoryChromosomes ( int chromos, double &historyHromosomes[][100000] ) { //-----------------------Variables------------------------------------- int Ch1=0; //Index of the chromosome from the base int Ge =0; //Index of the gene int cnt=0; //Counter of unique genes. If at least one gene is different //- the chromosome is acknowledged unique //---------------------------------------------------------------------- //If at least one chromosome is stored in the base if(ChrCountInHistory>0) { //Enumerate the chromosomes in the base to find an identical one for(Ch1=0;Ch1<ChrCountInHistory && cnt<GeneCount;Ch1++) { cnt=0; //Compare the genes, while the gene index is less than the number of genes and while there are identical genes for(Ge=1;Ge<=GeneCount;Ge++) { if(Colony[Ge][chromos]!=historyHromosomes[Ge][Ch1]) break; cnt++; } } //If there are enough identical genes then we can use a ready- made solution from the base if(cnt==GeneCount) Colony[0][chromos]=historyHromosomes[0][Ch1-1]; //If there is no such chromosome, then we calculate the FF for it... else { FitnessFunction(chromos); //.. and if there is space in the base, then save it if(ChrCountInHistory<100000) { for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } } //If the base is empty, calculate the FF for it and save it in the base else { FitnessFunction(chromos); for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.6. CycleOfOperators. Ciclo de Operaciones en UGA
Ahora, el destino de una época entera de vida artificial se decide literalmente: una nueva generación nace y muere. Esto ocurre de la siguiente manera: dos progenitores se eligen para procrear, o uno para realizar un acto de mutación sobre sí mismo. Para cada operador de GA se determina un parámetro apropiado. Como resultado, obtenemos una descendencia. Esto se repite una y otra vez, hasta que la colonia de descendientes se llena completamente. Entonces, la colonia de descendientes se libera en el hábitat, para que cada uno de ellos demuestre de lo que es capaz, y nosotros calculamos el VFF.
Tras ponerse a prueba con "fuego, agua y tuberías de cobre", la colonia de descendientes se adapta a la población. El siguiente paso en evolución artificial será el asesinato sagrado de clones para prevenir el agotamiento de "sangre" en generaciones futuras y la subsiguiente clasificación de la población renovada por grados de fitness.
//———————————————————————————————————————————————————————————————————————— //Cycle of operators of UGA void CycleOfOperators ( double &historyHromosomes[][100000], //--- double ReplicationPortion, //Proportion of replications. double NMutationPortion, //Proportion of natural mutations. double ArtificialMutation, //Proportion of artificial mutations. double GenoMergingPortion, //Portion of borrowed genes. double CrossingOverPortion,//Proportion of cross-over. //--- double ReplicationOffset, //Coefficient of displacement of interval borders double NMutationProbability//Probability of mutation of each gene in % ) { //-----------------------Variables------------------------------------- double child[]; ArrayResize (child,GeneCount+1); ArrayInitialize(child,0.0); int gene=0,chromos=0, border=0; int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,6); ArrayInitialize(fit,0.0); //Counter of planting spots in a new population. int T=0; //---------------------------------------------------------------------- //Set a portion of operators of UGA double portion[6]; portion[0]=ReplicationPortion; //Proportion of replications. portion[1]=NMutationPortion; //Proportion of natural mutations. portion[2]=ArtificialMutation; //Proportion of artificial mutations. portion[3]=GenoMergingPortion; //Proportion of borrowed genes. portion[4]=CrossingOverPortion;//Proportion of cross- overs. portion[5]=0.0; //------------------------Cycle of operators of UGA--------- //Fill up the new colony with offspring while(T<ChromosomeCount) { //============================ for(i=0;i<6;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(portion[i]-portion[5]); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[4][1]); for(u=0;u<5;u++) { if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; } //============================ switch(u) { //--------------------- case 0: //------------------------Replication-------------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { Replication(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 1: //---------------------Natural mutation------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { NaturalMutation(child,NMutationProbability); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 2: //----------------------Artificial mutation----------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { ArtificialMutation(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast-forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 3: //-------------The creation of an individual with borrowed genes----------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { GenoMerging(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One space is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- default: //---------------------------Crossing-Over--------------------------- //If there is place in the new colony, create a new individual if(T<ChromosomeCount) { CrossingOver(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- } }//End of the cycle operators of UGA-- //Determine the fitness of each individual in the colony of offspring GetFitness(historyHromosomes); //Settle the offspring into the main population if(PopulChromosCount>=ChromosomeCount) { border=ChromosomeCount; PopulChromosCount=ChromosomeCount*2; } else { border=PopulChromosCount; PopulChromosCount+=ChromosomeCount; } for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=0;gene<=GeneCount;gene++) Population[gene][chromos+border]=Colony[gene][chromos]; //Prepare the population for the next reproduction RemovalDuplicates(); }//the end of the function //————————————————————————————————————————————————————————————————————————
3.7. Replication. Replicación
El operador es lo más cercano al fenómeno natural conocido en biología como "replicación de ADN", aunque, en esencia, no es lo mismo. Aún así, preferí mantener este título al no encontrar ningún equivalente más cercano en la naturaleza.
La replicación es el operador genético más importante, que genera nuevos genes mientras transmite las cualidades de los cromosomas progenitores. Es el operador principal, que asegura la convergencia del algoritmo. El GA solo puede funcionar con ello sin el uso de otros operadores, pero en este caso el número de lanzamientos de FF sería mucho mayor.
Considere el principio del operador de Replicación. Usamos dos cromosomas progenitores. El nuevo gen de descendencia es un número aleatorio del intervalo
[C1-((C2-C1)*ReplicationOffset),C2+((C2-C1)*ReplicationOffset)],
en el que los genes progenitores C1 y C2 ReplicationOffset - Coeficiente de desplazamiento de los bordes de intervalo [C1, C2] .
Por ejemplo, del organismo paterno (azul) y del materno (rosa), se puede crear un vástago (verde):
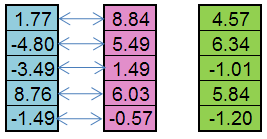
Figura 5. El principio del operador Replicación funciona
La probabilidad del gen de descendencia se puede resumir gráficamente:
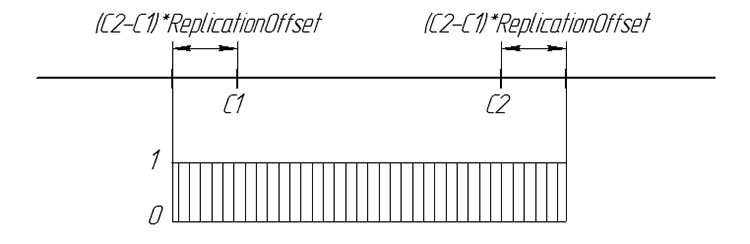
Figura 6. La probabilidad de la aparición del gen de descendencia en una línea de número
Los otros genes de descendencia se generan de la misma forma.
//------------------------------------------------ ------------------------ // Replication void Replication ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- SelectTwoParents(address_mama,address_papa); //-------------------Cycle of gene enumeration-------------------------------- for(int i=1;i<=GeneCount;i++) { //----figure out where the father and mother came from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search had not gone over the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if we С1>C2, swi if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of the created gene Minimum = C1-((C2-C1)*ReplicationOffset); Maximum = C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search has not gone over the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- temp=RNDfromCI(Minimum,Maximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } //————————————————————————————————————————————————————————————————————————3.8. NaturalMutation. Mutación natural
Las mutaciones ocurren constantemente a través del curso de los procesos que se dan en células vivas, y sirve como material para la selección natural. Surgen de forma espontánea a través de la vida entera del organismo en sus condiciones de hábitat normales, con una frecuencia de una vez por cada 10 ^ 10 generaciones de célula.
Nosotros, los curiosos investigadores, no tenemos por qué ceñirnos al orden natural, y esperamos lo justo para la siguiente mutación del gen. El parámetro NMutationProbability , que se expresa como un porcentaje y determina la probabilidad de mutación de cada gen en el cromosoma, nos ayudará a ello.
En el operador NaturalMutation , la mutación consiste en la generación de un gen aleatorio en el intervalo [RangeMinimum, RangeMaximum] . NMutationProbability = 100% significaría una mutación del 100% en todos los genes del cromosoma, y NMutationProbability = 0% significaría la total ausencia de mutaciones. La última opción no es apropiada para ser usada en problemas prácticos.
//------------------------------------------------ ------------------------ // The natural mutation. void NaturalMutation ( double &child[], double NMutationProbability ) { //-----------------------Variables------------------------------------- int address=0; double prob=0.0; //---------------------------------------------------------------------- if(NMutationProbability<0.0) prob=0.0; if(NMutationProbability>100.0) prob=100.0; //-----------------Parent selection------------------------ SelectOneParent(address); //--------------------------------------- for(int i=1;i<=GeneCount;i++) if(RNDfromCI(0.0,100.0)<prob) child[i]=NormalizeDouble( SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits ); } //————————————————————————————————————————————————————————————————————————
3.9. ArtificialMutation. Mutación artificial
La principal tarea de este operador es la generación de sangre "fresca". Usamos dos progenitores, y los genes de la descendencia se seleccionan de los espacios en el número de línea no asignados por los genes progenitores. Protege el GA de atascarse en uno de los extremos locales. En una proporción mayor, comparado con otros operadores, acelera la convergencia o la ralentiza, aumentando el número de lanzamientos de FF.
Al igual que Replication, usamos dos cromosomas progenitores. Pero la tarea del operador ArtificialMutation no es pasar las cualidades de los progenitores a la descendencia, sino hacer el vástago diferente a ellos. Por tanto, es algo completamente opuesto: se usa el mismo coeficiente de borde intervalo de desplazamiento, pero los genes se generan fuera del intervalo que ya habría sido tomado por Replication. El nuevo gen de la descendencia es un número aleatorio de los intervalos [RangeMinimum, C1-(C2-C1) * ReplicationOffset] y [C2 + (C2-C1) * ReplicationOffset, RangeMaximum]
La probabilidad de un gen en la descendencia ReplicationOffset = 0.25 se puede representar gráficamente de la siguiente manera:
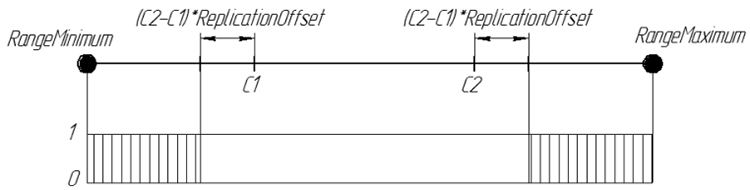
Figura 7. La probabilidad de un gen en la descendencia ReplicationOffset = 0.25 en la línea real de intervalo [RangeMinimum; RangeMaximum]
//———————————————————————————————————————————————————————————————————————— //Artificial mutation. void ArtificialMutation ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0,p=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //-------------------Cycle of genes enumeration------------------------------ for(int i=1;i<=GeneCount;i++) { //----determine where the mother and father are from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search doesn't go beyond the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if С1>C2, we change their places if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of creating the new gene Minimum=C1-((C2-C1)*ReplicationOffset); Maximum=C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search doesn't go beyond the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- p=MathRand(); if(p<16383.5) { temp=RNDfromCI(RangeMinimum,Minimum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } else { temp=RNDfromCI(Maximum,RangeMaximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } } //————————————————————————————————————————————————————————————————————————
3.10 GenoMerging. Tomar genes prestados
El operador GA dado no tiene un equivalente natural. De hecho, es difícil imaginarse cómo este maravilloso mecanismo funcionaría en organismos vivos. No obstante, tiene la extraordinaria capacidad de transferir genes de un número de progenitores (el número de progenitores es igual al número de genes) a la descendencia. El operador no genera nuevos genes, y es un mecanismo de búsqueda combinable.
Funciona del siguiente modo: se selecciona un progenitor para el primer gen de descendencia, y el primer gen se toma de él. Para el segundo gen se selecciona un segundo progenitor, y el gen se toma de él. Así sucesivamente. Se recomienda aplicar esto si el número de genes es mayor a uno. De lo contrario, se debería desactivar, puesto que el operador generará duplicaciones de los cromosomas.
//———————————————————————————————————————————————————————————————————————— //Borrowing genes. void GenoMerging ( double &child[] ) { //-----------------------Variables------------------------------------- int address=0; //---------------------------------------------------------------------- for(int i=1;i<=GeneCount;i++) { //-----------------Selecting parents------------------------ SelectOneParent(address); //-------------------------------------------------------- child[i]=Population[i][address]; } } //————————————————————————————————————————————————————————————————————————
3.11. CrossingOver. Cruzar
El concepto que en biología se conoce como "cruzar" es el fenómeno de intercambiar secciones de cromosomas. Al igual que en el caso de GenoMerging, este es un mecanismo de búsqueda combinable.
Se seleccionan dos cromosomas progenitores. Ambos se "cortan" en un lugar aleatorio. El cromosoma de la descendencia constará de partes de los cromosomas progenitores.
Es más fácil ilustrar este mecanismo con una imagen:
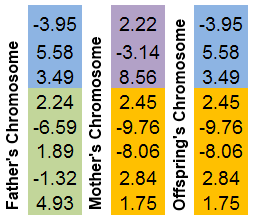
Figura 8. El mecanismo de intercambio de partes de cromosomas
Se recomienda aplicar esto si el número de genes es mayor a uno. De lo contrario, se debería desactivar, puesto que el operador generará duplicaciones de los cromosomas.
//———————————————————————————————————————————————————————————————————————— //Crossing-over. void CrossingOver ( double &child[] ) { //-----------------------Variables------------------------------------- int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //Determine the breakage point int address_of_gene=(int)MathFloor((GeneCount-1)*(MathRand()/32767.5)); for(int i=1;i<=GeneCount;i++) { //----copy the mother's genes-------- if(i<=address_of_gene+1) child[i]=Population[i][address_mama]; //----copy the father's genes-------- else child[i]=Population[i][address_papa]; } } //————————————————————————————————————————————————————————————————————————
3.12. SelectTwoParents. La selección de dos progenitores
Para prevenir el agotamiento de la reserva genética, existe una prohibición de cruce reproductor con uno mismo. Se realizan diez intentos para encontrar progenitores diferentes, y si no logramos encontrar un par apropiado, permitiremos el cruce reproductor con uno mismo. Básicamente, con ello obtenemos una copia del mismo espécimen.
Por una parte, la probabilidad de clonar organismos se reduce; por otra, se previene la circularidad de la búsqueda, puesto que puede surgir una situación en la que sería prácticamente imposible hacer esto (elegir diferentes progenitores) en un número de pasos razonable.
Se usa en los operadores Replication, ArtificialMutation, y CrossingOver.
//———————————————————————————————————————————————————————————————————————— //Selection of two parents. void SelectTwoParents ( int &address_mama, int &address_papa ) { //-----------------------Variables------------------------------------- int cnt=1; address_mama=0;//address of the mother individual in a population address_papa=0;//address of the father individual in a population //---------------------------------------------------------------------- //----------------------------Selection of parents-------------------------- //Ten attempts to chose different parents. while(cnt<=10) { //For the mother individual address_mama=NaturalSelection(); //For the father individual address_papa=NaturalSelection(); if(address_mama!=address_papa) break; } //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.13. SelectOneParent. La selección de un progenitor
Aquí, todo es más sencillo: se selecciona un progenitor de la población.
Se usa en los operadores NaturalMutation y GenoMerging.
//———————————————————————————————————————————————————————————————————————— //Selection of one parent. void SelectOneParent ( int &address//address of the parent individual in the population ) { //-----------------------Variables------------------------------------- address=0; //---------------------------------------------------------------------- //----------------------------Selecting a parent-------------------------- address=NaturalSelection(); //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.14. NaturalSelection. Selección natural
Selección natural: el proceso que lleva a la supervivencia y reproducción preferencial de seres mejor adaptados a las condiciones de su entorno con sus cualidades hereditarias.
El operador es similar al operador tradicional "Roulette" (Selección de ruleta: selección de organismos con x "lanzamientos" de la ruleta. La ruleta contiene un sector para cada miembro de la población. El tamaño del sector x es proporcional al valor correspondiente de fitness), pero tiene diferencias significativas. Tiene en cuenta la posición de organismos según los más y menos adecuados. Además, incluso un organismo que tiene los peores genes tiene una posibilidad de dejar detrás de sí una descendencia. Esto es justo, ¿no? A pesar de ello, no se trata de una cuestión de justicia, sino del hecho de que en la naturaleza todos los organismos tienen la oportunidad de dejar detrás de sí una descendencia.
Por ejemplo, tomemos 10 organismos con los siguientes VFF en el problema de maximización: 256, 128, 64, 32, 16, 8, 4, 2, 0, -1 - los valores más altos se corresponden con un mejor fitness. Este ejemplo se toma para que podamos ver que la "distancia" entre organismos vecinos es 2 veces mayor que entre los dos organismos anteriores. No obstante, en el gráfico circular, la probabilidad de que cada organismo deje descendencia se muestra así:
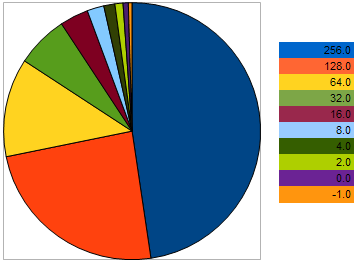
Figura 9. El gráfico de probabilidad de seleccionar los organismos progenitores
demuestra que cuanto peor son los genes de los organismos, menores son sus probabilidades. Del mismo modo, cuanto más se acerque un organismo al mejor espécimen, mayores son sus probabilidades de reproducción.

Figura 10. El gráfico de probabilidad de seleccionar los organismos progenitores
//———————————————————————————————————————————————————————————————————————— //Natural selection. int NaturalSelection() { //-----------------------Variables------------------------------------- int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,PopulChromosCount); ArrayInitialize(fit,0.0); double delta=(Population[0][0]-Population[0][PopulChromosCount-1])*0.01-Population[0][PopulChromosCount-1]; //---------------------------------------------------------------------- for(i=0;i<PopulChromosCount;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(Population[0][i]+delta); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[PopulChromosCount-1][1]); for(u=0;u<PopulChromosCount;u++) if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; return(u); } //————————————————————————————————————————————————————————————————————————
3.15. RemovalDuplicates. Eliminación de duplicados
Esta función elimina cromosomas duplicados en la población, y los cromosomas únicos restantes (únicos para la población de la época actual) se distribuyen en orden por el VFF, determinado por el tipo de optimización (creciente o decreciente).
//———————————————————————————————————————————————————————————————————————— //Removing duplicates sorted by VFF void RemovalDuplicates() { //-----------------------Variables------------------------------------- int chromosomeUnique[1000];//Array stores the unique trait //of each chromosome: 0-duplicate, 1-unique ArrayInitialize(chromosomeUnique,1); //Assume that there are no duplicates double PopulationTemp[][1000]; ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Ge =0; //Index of the gene int Ch =0; //Index of the chromosome int Ch2=0; //Index of the second chromosome int cnt=0; //Counter //---------------------------------------------------------------------- //----------------------Remove duplicates---------------------------1 //Chose the first from the pair for comparison... for(Ch=0;Ch<PopulChromosCount;Ch++) { //If it's not a duplicate... if(chromosomeUnique[Ch]!=0) { //Chose the second from the pair... for(Ch2=0;Ch2<PopulChromosCount;Ch2++) { if(Ch!=Ch2 && chromosomeUnique[Ch2]!=0) { //Zeroize the counter of identical genes cnt=0; //Compare the genes. while there are identical genes present for(Ge=1;Ge<=GeneCount;Ge++) { if(Population[Ge][Ch]!=Population[Ge][Ch2]) break; else cnt++; } //If there are the same amount of identical genes as total genes //..the chromosome is considered a duplicate if(cnt==GeneCount) chromosomeUnique[Ch2]=0; } } } } //The counter calculates the number of unique chromosomes cnt=0; //Copy the unique chromosomes into a temporary array for(Ch=0;Ch<PopulChromosCount;Ch++) { //If the chromosome is unique, copy it, if not, go to the next if(chromosomeUnique[Ch]==1) { for(Ge=0;Ge<=GeneCount;Ge++) PopulationTemp[Ge][cnt]=Population[Ge][Ch]; cnt++; } } //Assigning the variable "All chromosomes" the value of counter of unique chromosomes PopulChromosCount=cnt; //Return unique chromosomes back to the array for temporary storage //..of combined populations for(Ch=0;Ch<PopulChromosCount;Ch++) for(Ge=0;Ge<=GeneCount;Ge++) Population[Ge][Ch]=PopulationTemp[Ge][Ch]; //=================================================================1 //----------------Ranking the population---------------------------2 PopulationRanking(); //=================================================================2 } //————————————————————————————————————————————————————————————————————————
3.16. PopulationRanking. Clasificar la población
La clasificación la hace el VFF. El método es similar a "bubbly" (el algoritmo consta de pasajes repetidos a través del array ordenado. Por cada pase, los elementos se comparan sucesivamente por parejas, y si el orden de una pareja es incorrecto, se lleva a cabo un intercambio de elementos. Los pasajes a través del array se repiten hasta que uno de los pasajes muestra que ya no se necesitan más intercambios, lo que significa que el array se ha ordenado con éxito.
Al pasar a través del algoritmo, si hay un elemento que destaca, este "sale a la superficie" hasta alcanzar la posición deseada, igual que una burbuja en agua; de ahí el nombre del algoritmo). No obstante, hay una diferencia: solo se ordenan los índices del array, no sus contenidos. Este método es más rápido y se lleva a cabo a una velocidad ligeramente diferente al proceso de copiar un array a otro. Y cuanto más grande sea el array ordenado, más pequeña será la diferencia.
//———————————————————————————————————————————————————————————————————————— //Population ranking. void PopulationRanking() { //-----------------------Variables------------------------------------- int cnt=1, i = 0, u = 0; double PopulationTemp[][1000]; //Temporary population ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Indexes[]; //Indexes of chromosomes ArrayResize (Indexes,PopulChromosCount); ArrayInitialize(Indexes,0); int t0=0; double ValueOnIndexes[]; //VFF of corresponding //..chromosome indexes ArrayResize (ValueOnIndexes,PopulChromosCount); ArrayInitialize(ValueOnIndexes,0.0); double t1=0.0; //---------------------------------------------------------------------- //Fill in the indexes in the temporary array temp2 and //...copy the first line from the sorted array for(i=0;i<PopulChromosCount;i++) { Indexes[i] = i; ValueOnIndexes[i] = Population[0][i]; } if(OptimizeMethod==1) { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]>ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } else { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]<ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } //Create a sorted-out array based on the obtained indexes for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) PopulationTemp[i][u]=Population[i][Indexes[u]]; //Copy the sorted-out array back for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) Population[i][u]=PopulationTemp[i][u]; } //————————————————————————————————————————————————————————————————————————
3.17. RNDfromCustomInterval. El generador de números aleatorios de un intervalo concreto
Simplemente, una herramienta útil. Es muy práctica en UGA.
//———————————————————————————————————————————————————————————————————————— //Generator of random numbers from the selected interval. double RNDfromCI(double RangeMinimum,double RangeMaximum) { return(RangeMinimum+((RangeMaximum-RangeMinimum)*MathRand()/32767.5));} //————————————————————————————————————————————————————————————————————————
3.18. SelectInDiscreteSpace. La selección en espacio discreto
Se usa para reducir el espacio de búsqueda. Con el parámetro step = 0.0, la búsqueda se lleva a cabo en un espacio continuo (limitado a las limitaciones del lenguaje; en el caso de MQL, el 15º símbolo significativo inclusive). Para usar el algoritmo GA con mayor precisión, deberá escribir una biblioteca adicional para trabajar con cifras largas.
El trabajo de la función en RoundMode = 1 se ilustra en la siguiente figura:
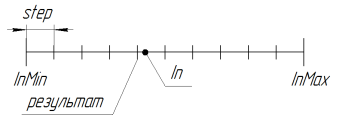
Figura 11. el trabajo de la función SelectInDiscreteSpace en RoundMode = 1
//———————————————————————————————————————————————————————————————————————— //Selection in discrete space. //Modes: //1-closest below //2-closest above //any closest double SelectInDiscreteSpace ( double In, double InMin, double InMax, double step, int RoundMode ) { if(step==0.0) return(In); // secure the correctness of borders if( InMax < InMin ) { double temp = InMax; InMax = InMin; InMin = temp; } // during a breach - return the breached border if( In < InMin ) return( InMin ); if( In > InMax ) return( InMax ); if( InMax == InMin || step <= 0.0 ) return( InMin ); // bring to the specified scale step = (InMax - InMin) / MathCeil ( (InMax - InMin) / step ); switch( RoundMode ) { case 1: return( InMin + step * MathFloor ( ( In - InMin ) / step ) ); case 2: return( InMin + step * MathCeil ( ( In - InMin ) / step ) ); default: return( InMin + step * MathRound ( ( In - InMin ) / step ) ); } } //————————————————————————————————————————————————————————————————————————
3.19. FitnessFunction. Función de fitness
No es parte del GA. La función recibe el índice del cromosoma en la población para el que se calculará el VFF. El VFF se escribe en el índice cero del cromosoma transmitido. El código de esta función es único para cada tarea.
3.20. ServiceFunction. Función de servicio
No es parte del GA. El código en esta función es único para cada tarea específica. Se puede usar para implementar control sobre épocas. Por ejemplo, para mostrar el mejor VFF para la época actual.
4. Ejemplos del UGA en funcionamiento
Todos los problemas de optimización se solucionan por medio del EA, y se dividen en dos tipos:
- El genotipo consta de un fenotipo. Los valores de los genes de cromosoma se nombran directamente por los argumentos de una función de optimización. Ejemplo 1.
- El genotipo no se corresponde con el fenotipo. Se requiere la interpretación del significado de los genes de cromosoma para calcular la función optimizada. Ejemplo 2.
4.1. Ejemplo 1
Plantéese el problema con una respuesta que ya sepa para asegurarse de que el algoritmo funciona, y después proceda a resolver el problema. La solución de este será de gran interés para muchos traders.
Problema: encontrar la función mínima y máxima "Skin":
en el segmento [-5, 5].
Respuesta: fmin (3.07021,3.315935) = -4.3182, fmax (-3.315699; -3.072485) = 14.0606.
Figura 12. El gráfico de "Skin" en el segmento [-5, 5]
Para resolver el problema, escribimos el siguiente script:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" #include "Skin.mqh"//testing function //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Gene pool parameter----"; input int ChromosomeCount_P = 50; //Number of chromosomes in a colony input int GeneCount_P = 2; //Number of genes input int FFNormalizeDigits_P = 4; //Number of fitness symbols input int GeneNormalizeDigits_P = 4; //Number of genes input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Operator parameters----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing-over. //--- input double ReplicationOffset_P = 0.5; //Coefficient of interval borders displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = -5.0; //Minimum range search input double RangeMaximum_P = 5.0; //Maximum range search input double Precision_P = 0.0001;//The required accuracy input int OptimizeMethod_P = 1; //Optim.:1-Min,other-Max //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double ERROR=0.0;//Average error in gen //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparing global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum range search RangeMaximum =RangeMaximum_P; //Maximum range search Precision =Precision_P; //Search step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of symbols in fitness GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//Proportion of crossing-over. //--- ReplicationOffset_P, //Coefficient of interval border replacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," mc - Time of implementation"); //---------------------------------- return(0); } //————————————————————————————————————————————————————————————————————————
Aquí está el código entero del script para resolver el problema. Ejecútelo y obtenga la información facilitada por la función Comment ():
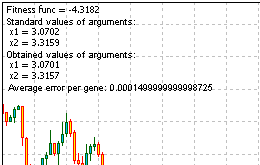
Figura 13. El resultado de la solución del problema
En los resultados podemos ver que el algoritmo funciona.
4.3. Ejemplo 2
Comúnmente se cree que el indicador ZZ muestra las salidas ideales de un sistema de trading anulado. El indicador es muy popular entre los seguidores de la "teoría de la onda" y aquellos que la usan para determinar el tamaño de las "figuras".
Problema: determinar si hay algún punto de entrada para un sistema de trading anulado en datos del historial, diferente de los vértices ZZ, dando en total más puntos de ganancia teórica.
Para el experimento, seleccionaremos una pareja GBPJPY para 100 barras M1. Acepte el diferencial de 0 puntos (cuotas de cinco dígitos). Para empezar, debe determinar los mejores parámetros ZZ. Para ello, usaremos una enumeración simple para encontrar el mejor valor del parámetro ExtDepth usando un script sencillo:
#property script_show_inputs //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input int History=100; input double Spred =80.0; input int Depth =5; //For "one-time" use input bool loop =true;//Use enumeration or not //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- void OnStart() { //-----------------------Variables------------------------------------- double ZigzagBuffer [];//For storing the buffer of the ZZ indicator double PeaksOfZigzag[];//for storing the values of the ZZ extremum int Zigzag_handle; //Indicator marker ArraySetAsSeries(ZigzagBuffer,true); ArrayResize(PeaksOfZigzag,History); int depth=3; double PipsSum=0.0; int PeaksCount=0; bool flag=true; //---------------------------------------------------------------------- if(loop==true) { while(depth<200 && flag==true) { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",depth); //--- reset the code error ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<100;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Could not copy the indicator buffer. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- PipsSum=0.0; PeaksCount=0; for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; //----------------------------------------------------------- if(PeaksCount<=2) flag=false; else { Print(depth," ",PeaksCount," ",PipsSum); depth+=1; } //----------------------------------------------------------- } } else { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",Depth); //--- reser the error code ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<History;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Was not able to copy the buffer indicator. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; } Print(Depth," ",PeaksCount," ",PipsSum); //----------------------------------------------------------- } } //————————————————————————————————————————————————————————————————————————
Ejecutando el script, obtenemos 4077 puntos en ExtDepth = 3. 19 vértices de indicador "entran" en 100 barras. Con el aumento de ExtDepth, el número de vértices ZZ se reduce, y también la rentabilidad.
Ahora podemos encontrar los vértices en el ZZ alternativo, usando UGA. Los vértices ZZ pueden tener tres posiciones para cada barra: 1) High (Alto), 2) Low (Bajo), 3) No vertex (Sin vértice). La presencia y posición del vértice la llevará cada gen para cada barra. Por tanto, el tamaño del cromosoma será de 100 genes.
Según mis cálculos (y las autoridades matemáticas pueden corregirme si me equivoco), en 100 barras puede construir 3 ^ 100, o 5.15378e47 opciones alternativas "zigzags" . Este es el número exacto de opciones que se deben considerar usando una enumeración directa. Durante el cálculo a una velocidad de 100000000 opciones por segundo, ¡necesitaremos 1,6e32 años! Esto es más que la edad del universo. Aquí es cuando empecé a tener dudas sobre la capacidad de encontrar una solución a este problema.
Pero comencemos.
Puesto que UGA usa la representación del cromosoma con números reales, necesitamos codificar de alguna forma la posición de los vértices. Este es precisamente el caso cuando el genotipo del cromosoma no se corresponde con el fenotipo. Asigne un intervalo de búsqueda para los genes [0, 5]. Aceptemos que el intervalo [0, 1] se corresponde con el vértice de ZZ en Alto, el intervalo [4, 5] se corresponde con el vértice en Bajo, y el intervalo (1, 4) se corresponde con la ausencia de vértice.
Es necesario considerar un punto importante. Puesto que la proto-población se genera aleatoriamente con genes en el intervalo especificado, el primer espécimen tendrá muy malos resultados, posiblemente incluso con unos cuantos cientos de puntos negativos. Tras unas cuantas generaciones (aunque puede darse el caso de que suceda en la primera generación), veremos la aparición de un espécimen cuyos genes serán consistentes con la ausencia de vértices en general. Esto significaría la ausencia de comercio y el pago del inevitable diferencial.
Según algunos extraders: "La mejor estrategia para comerciar es no hacerlo". Este organismo será el vértice de la evolución artificial. Para hacer que esta evolución "artificial" dé a luz a organismos de trading, es decir, hacer que establezca los vértices del ZZ alternativo, asignaremos al fitness de los organismos sin vértices el valor de "-10000000.0", colocándolo deliberadamente en la posición más baja de la evolución en comparación con cualquier otro organismo.
Aquí está el código de script que usa UGA para encontrar los vértices del ZZ alternativo:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Parameters of the gene pool----"; input int ChromosomeCount_P = 100; //Number of chromosomes in the colony input int GeneCount_P = 100; //Number of genes input int FFNormalizeDigits_P = 0; //Number of fitness symbols input int GeneNormalizeDigits_P= 0; //Number of gene symbols input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Parameters of operators----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing - over. input double ReplicationOffset_P = 0.5; //Coefficient of interval border displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = 0.0; //Minimum search range input double RangeMaximum_P = 5.0; //Maximum search range input double Precision_P = 1.0; //Required accuracy input int OptimizeMethod_P = 2; //Optim.:1-Min,other -Max input string Other = "----Other----"; input double Spred = 80.0; input bool Show = true; //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double Hight []; double Low []; datetime Time []; datetime Ti []; double Peaks []; bool show; //———————————————————————————————————————————————————————————————————————— //--------------------------Body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparation of global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum search range RangeMaximum =RangeMaximum_P; //Maximum search range Precision =Precision_P; //Searching step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of fitness symbols GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Preparation of global variables ArraySetAsSeries(Hight,true); CopyHigh (NULL,0,0,GeneCount+1,Hight); ArraySetAsSeries(Low,true); CopyLow (NULL,0,0,GeneCount+1,Low); ArraySetAsSeries(Time,true); CopyTime (NULL,0,0,GeneCount+1,Time); ArrayResize (Ti,GeneCount+1);ArrayInitialize(Ti,0); ArrayResize(Peaks,GeneCount+1);ArrayInitialize(Peaks,0.0); show=Show; //---------------------------------------------------------------------- //local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Очистим экран ObjectsDeleteAll(0,-1,-1); ChartRedraw(0); //launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of replication of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//proportion of crossing- over. //--- ReplicationOffset_P, //Coefficient of interval border displacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- //Display the last result on the screen show=true; ServiceFunction(); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," мс - time of execution"); //---------------------------------- return(0); } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Service function. Called up from UGA. | | //If there is no need for it, leave the function empty, like this: | // void ServiceFunction() | // { | // } | //-----------------------------------------------------------------------+ void ServiceFunction() { if(show==true) { //-----------------------Variables----------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //-------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Chromosome[u]; if(temp<=1.0 ) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } } ObjectsDeleteAll(0,-1,-1); for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; ObjectCreate (0,"BoxBackName"+(string)V,OBJ_TREND,0,Ti[V],Peaks[V],Ti[V+1],Peaks[V+1]); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_COLOR,Black); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_SELECTABLE,true); } ChartRedraw(0); Comment(PipsSum); } //---------------------------------------------------------------------- else return; } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Function of determining the fitness of the individual. Called up from UGA. | //-----------------------------------------------------------------------+ void FitnessFunction(int chromos) { //-----------------------Variables------------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //---------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Colony[u][chromos]; if(temp<=1.0) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); PeaksCount++; } } if(PeaksCount>1) { for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; Colony[0][chromos]=PipsSum; } else Colony[0][chromos]=-10000000.0; AmountStartsFF++; } //————————————————————————————————————————————————————————————————————————
Cuando ejecutamos el script, obtenemos los vértices con un beneficio total de 4.939 puntos. Además, solo nos llevó 17.929 veces el contar todos los puntos, en comparación con los 3 ^ 100 necesarios con la enumeración directa. ¡En mi ordenador, esto llevó 21,7 segundos, en lugar de 1,6e32 años!
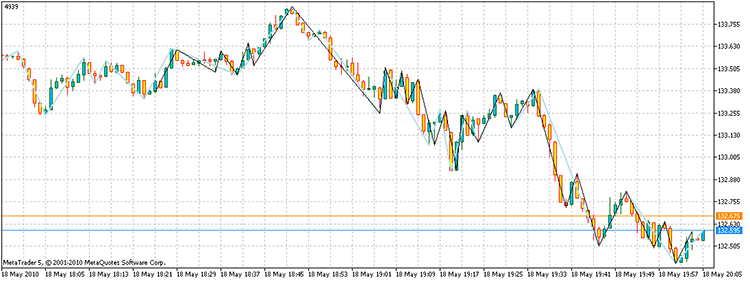
Figura 14. El resultado de la solución del problema. Los segmentos de color negro - un ZZ alternativo en azul cielo - indicador ZZ
Por tanto, la respuesta a la pregunta es: "Sí existe".
5. Recomendaciones para trabajar con UGA
- Intente establecer las condiciones calculadas correctamente en FF para poder obtener un resultado preciso del algoritmo. Piense de nuevo en el ejemplo 2. Quizás esta sea mi principal recomendación.
- No use valores demasiado pequeños para el parámetro de Precisión. Aunque el algoritmo sea capaz de trabajar con un paso 0, debería exigir una precisión razonable de la solución. Este parámetro está diseñado para reducir la dimensión del problema.
- Varíe el tamaño de la población y el valor umbral del número de épocas. Una buena solución sería asignar un parámetro Época dos veces mayor del que se muestra con MaxOfCurrentEpoch. No elija valores demasiado grandes, porque esto no acelerará el proceso de encontrar una solución al problema.
- Experimente con los parámetros de operadores genéticos. No hay parámetros universales, y debería asignarlos según las condiciones de la tarea que debe llevar a cabo.
Descubrimientos
Además de un poderoso Probador de Estrategias, el lenguaje MQL5 le permite crear una herramienta igual de práctica para el trader, permitiéndole resolver problemas verdaderamente complejos. Obtendremos un algoritmo de optimización muy flexible y escalable. Y me siendo tremendamente orgulloso de este descubrimiento, a pesar de que no fui el primero en realizarlo.
El lector podrá contribuir fácilmente al desarrollo de la evolución "artificial", porque el UGA se diseñó inicialmente de manera que se puede modificar y extender fácilmente con operadores adicionales y bloques de cálculo.
Le deseo éxito al lector a la hora de encontrar soluciones óptimas. Espero haberle podido ayudar a ello. ¡Buena suerte!
Nota. Este artículo usó el indicador ZigZag. Todos los códigos fuente de UGA se pueden encontrar adjuntos.
Licencia: Los códigos fuente adjuntos al artículo (código UGA) se pueden distribuir bajo las condiciones de licencia BSD.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/55
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Un Ejemplo de Estrategia de Trading Basada en Diferencias de Zona Horaria en Continentes Distintos
Un Ejemplo de Estrategia de Trading Basada en Diferencias de Zona Horaria en Continentes Distintos
 MQL para "Dummies": Cómo Diseñar y Construir Clases de Objetos
MQL para "Dummies": Cómo Diseñar y Construir Clases de Objetos
 Crear y Publicar Informes de Trading y Notificaciones SMS
Crear y Publicar Informes de Trading y Notificaciones SMS
 Crear un Indicador con Buffers de Indicador Múltiples para Principiantes
Crear un Indicador con Buffers de Indicador Múltiples para Principiantes
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Por favor muéstrame la lista de errores. El código es muy viejo, pero no hay nada que rompa incluso después 14 años.
el problema es con la variable "ArtificialMutation" y la función. He cambiado la función a ArtificialMutationP y funciona.
Los problemas con el error ServiceFunction y FitnessFunction están bien, entiendo lo que está pasando allí. He adjuntado capturas de pantalla.
Cuando trato de compilar UGA_script o UGA_the_alternative_ZigZag directamente después de la extracción desde el ZIP me da errores que provienen de la UGAlib.
Una vez que cambié el nombre de la función (y su llamada en el caso 2) a ArtificialMutationP compiló y funcionó.
Todavía estoy trabajando a través de su buen trabajo para entender completamente. Gracias
Pregunta.
los datos históricos (el número de barras) es el recuento de genes, ¿es correcto?
el problema es con la variable "ArtificialMutation" y la función. He cambiado la función a ArtificialMutationP y funciona.
Los problemas con el error ServiceFunction y FitnessFunction están bien, entiendo lo que está pasando allí. He adjuntado capturas de pantalla.
Cuando trato de compilar UGA_script o UGA_the_alternative_ZigZag directamente después de la extracción desde el ZIP me da errores que provienen de la UGAlib.
Una vez que cambié el nombre de la función (y su llamada en el caso 2) a ArtificialMutationP compiló y funcionó.
Todavía estoy trabajando a través de su buen trabajo para entender completamente. Gracias
Prueba estearchivo
Gracias por sus amables palabras .