Redes neuronales en el trading: Modelos bidimensionales del espacio de enlaces (Quimera)

MetaTrader 5 — Sistemas comerciales | 27 octubre 2025, 14:21

323

Dmitriy Gizlyk

Introducción

La modelización de series temporales es una tarea compleja con una amplia gama de aplicaciones en diversos campos, como la medicina, los mercados financieros y la energía. Las principales dificultades para desarrollar modelos universales de series temporales se relacionan con:

La necesidad de considerar las dependencias multiescala, incluidas las autocorrelaciones a corto plazo, la estacionalidad y las tendencias a largo plazo. Esto requiere el uso de arquitecturas flexibles y potentes.
El procesamiento adaptativo de series temporales multivariantes en las que la relación entre las variables analizadas puede ser dinámica y no lineal. Para ello se deben desarrollar mecanismos que tengan en cuenta las interacciones dependientes del contexto.
La minimización de la necesidad de preprocesamiento manual de datos mediante la identificación automática de patrones estructurales sin necesidad de ajustar parámetros complejos.
La eficiencia computacional, especialmente cuando se trata de secuencias largas, lo cual requiere optimizar la arquitectura del modelo para utilizar eficazmente los recursos computacionales y reducir los costes de formación.

Los métodos estadísticos clásicos requieren un preprocesamiento significativo de los datos de origen y no siempre captan adecuadamente las dependencias no lineales complejas. Las arquitecturas de redes neuronales profundas han demostrado una gran expresividad, pero la complejidad computacional cuadrática de los modelos basados en la arquitectura de Transformer dificulta su aplicación a series temporales multivariantes con un gran número de características analizadas. Además, estos modelos no suelen distinguir entre componentes estacionales y a largo plazo, o usan supuestos rígidos a priori, lo que reduce su adaptabilidad en diferentes escenarios de aplicación.

Una de las soluciones a los problemas anteriores se propuso en el artículo "Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models". El framework Quimera es un modelo bidimensional de espacio de estados (2D-SSM) que utiliza transformaciones lineales a lo largo de los ejes de tiempo y variables. El framework Quimera incluye tres componentes principales: los modelos de espacio de estados a lo largo de la dimensión temporal, a lo largo de las variables a analizar, y las transiciones transversales entre estas dimensiones. La parametrización de Chimera se basa en matrices diagonales compactas, por lo que es capaz de recuperar tanto los métodos estadísticos clásicos como las arquitecturas SSM modernas.

Además, Chimera utiliza la discretización adaptativa para considerar los patrones estacionales y las características de los sistemas dinámicos.

En su trabajo, los autores de Chimera analizan el rendimiento del framework propuesto en varias tareas de series temporales multivariantes (clasificación, predicción y detección de anomalías). Los resultados experimentales presentados muestran que Chimera logra una precisión comparable o superior a la de los métodos más avanzados, con una reducción global del coste computacional.

El algoritmo de Chimera

Los modelos de espacio de estados (SSM) ocupan un lugar importante en los métodos de análisis de series temporales gracias a su sencillez, así como a sus capacidades expresivas para modelizar relaciones complejas, incluidas las autorregresivas. Estos modelos se usan para representar sistemas en los que el estado en el momento actual depende del estado anterior del entorno analizado. Sin embargo, tradicionalmente, los SSM describen sistemas en los que el estado depende de una única variable (por ejemplo, el tiempo). Esto limita su aplicación cuando se requiere una modelización multivariante de series temporales, pues resulta necesario captar las dependencias tanto en el contexto temporal como en el contexto de las variables analizadas.

Las series temporales multivariantes son estructuras más complejas que requieren métodos capaces de tener en cuenta las interdependencias entre varias variables simultáneamente. Los modelos clásicos de espacio de estados bidimensionales (2D-SSM) utilizados para describir dichas estructuras adolecen de una serie de limitaciones, lo que restringe su eficacia en comparación con los métodos de aprendizaje profundo más avanzados. Aquí cabe destacar las siguientes desventajas:

La restricción a las dependencias lineales. Los 2D-SSM clásicos solo pueden modelizar relaciones lineales, lo que se convierte en una limitación importante al intentar describir las relaciones no lineales más complejas, características de las series temporales multivariantes reales.
Discreción del modelo. Estos modelos suelen tener una resolución predeterminada y no pueden ajustarse de forma automática a las características cambiantes de los datos. Esto los hace ineficaces para modelizar patrones estacionales o de otro tipo que tengan una resolución variable.
Dificultades para procesar grandes conjuntos de datos. En aplicaciones prácticas, los 2D-SSM suelen ser ineficaces para procesar grandes cantidades de datos, lo que limita su uso en tareas del mundo real.
Estaticidad de los parámetros de actualización. Los métodos clásicos de actualización de los parámetros del modelo son fijos, lo que no permite considerar adecuadamente la dinámica de las dependencias que pueden cambiar con el tiempo. Se trata de una limitación importante en aplicaciones en las que los datos evolucionan y demandan enfoques adaptativos.

Por otra parte, los métodos de aprendizaje profundo, que se han desarrollado activamente en los últimos años, ofrecen la posibilidad de superar varias de estas limitaciones. Pueden usarse para modelizar dependencias no lineales más complejas y considerar la dinámica de las series temporales, lo que las hace prometedoras para su aplicación en tareas de análisis de datos multivariantes.

El framework Chimera utiliza 2D-SSM para modelizar series temporales multivariantes, donde el primer eje corresponde a la dimensión temporal y el segundo a las variables. Por lo tanto, cada estado supone una función tanto temporal como de variables. El primer paso consiste en convertir la forma continua 2D-SSM en una discreta, considerando el tamaño de paso Δ1 y Δ2, que representan la resolución de la señal original en cuanto al eje. Utilizando el método Zero-Order Hold (ZOH), podemos discretizar los datos de origen como:

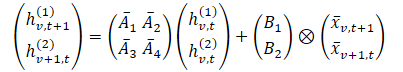
Donde t y v se usan para indicar el índice en las dimensiones de tiempo y de variables analizadas, respectivamente. Esta expresión puede representarse de forma más sencilla.

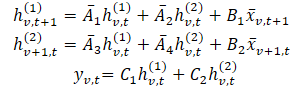
En esta formulación, intuitivamente, hv,t(1) es un estado oculto que transporta información a través del tiempo (cada estado depende de su marca de tiempo anterior, pero dentro de la misma característica), donde A1 y A2 controlan el énfasis en la información temporal y variacional cruzada transmitida, respectivamente. Del mismo modo, hv,t(2) es un estado oculto que contiene información sobre las variaciones cruzadas (cada estado depende de otras variables pero con la misma marca temporal).

Los datos de las series temporales suelen seleccionarse partiendo de un proceso continuo subyacente. En estos casos, la variable Δ1 de discretización del eje temporal puede interpretarse como la resolución o la frecuencia de discretización de los datos continuos subyacentes. Sin embargo, la discretización a lo largo del eje variable, que es discreto por naturaleza, supone un proceso no intuitivo y plantea dudas sobre su significado. El paso de discretización en 1D-SSM tiene profundas conexiones con los mecanismos de puerta RNN, proporcionando automáticamente la normalización del modelo, y conduce a las propiedades deseables como la invariancia de resolución.

El SSM discreto bidimensional presentado por los parámetros ({Ai}, {Bi}, {Ci}, kΔ1, ℓΔ2) se desarrolla con una velocidad k mayor que el SSM 2D discreto con parámetros ({Ai}, {Bi}, {Ci}, Δ1ℓΔ2), y ℓ más rápido ({Ai}, {Bi}, {Ci}, kΔ1, Δ2). En consecuencia, los parámetros Δ1 pueden verse como un controlador de la longitud de las dependencias que capta el modelo. Es decir, basándonos en la descripción anterior, vemos la discretización en el eje temporal como el establecimiento de la resolución o la frecuencia de discretización. Un Δ1 pequeño puede captar el progreso a largo plazo, mientras que un Δ1 mayor captará los patrones estacionales.

La discretización a lo largo del eje de las variables analizadas puede verse como un mecanismo similar a las puertas de los modelos RNN, donde Δ2 controla la longitud del contexto del modelo. Valores de Δ2 mayores significarán una ventana de contexto más pequeña, ignorando otras variables, mientras que valores de Δ2 menores significarán más énfasis en las dependencias entre las variables analizadas.

Para mejorar la expresividad y la capacidad de recuperar los procesos autorregresivos del modelo, los estados ocultos hv,t(1) deberán llevar información sobre las marcas temporales pasadas. Para ello, en la dimensión temporal, los autores del framework restringen las matrices A1 y A2 para que tengan una estructura asociada. Además, para A3 y A4, incluso la estructura de matriz diagonal más simple resulta eficaz para fusionar la información sobre la dimensionalidad de las variables analizadas.

La naturaleza causal de 2D-SSM provoca un flujo de información limitado a lo largo de la dimensionalidad de las variables, ya que no están ordenadas. Para resolver este problema, se usan dos módulos diferentes para la medición de las características de pasada directa e inversa.

De forma similar al eficiente 1D-SSM, la formulación independiente de los datos puede verse como una convolución con el núcleo K. Esta formulación no solo conduce a un aprendizaje más rápido permitiendo el procesamiento en paralelo, sino que también vincula Chimera a las investigaciones más recientes sobre la arquitectura moderna basada en la convolución para series temporales.

Como ya hemos comentado, los parámetros A1 y A2 controlan el énfasis en la información temporal y variacional cruzada pasada. Del mismo modo, los parámetros Δ1 y B1 controlan el énfasis en los datos de referencia actuales e históricos. Como estos parámetros son independientes de los datos, pueden interpretarse como una característica global del sistema. Sin embargo, en los sistemas complejos, el énfasis depende de la señal de la señal original. Por ello, será necesario que estos parámetros sean una función de los datos de origen. La dependencia de los parámetros analizados permite al modelo seleccionar la información relevante y filtrar la irrelevante para cada conjunto de datos de origen, ofreciendo un mecanismo similar al del Transformer. Además, según los datos, el modelo deberá aprender de forma adaptativa una mezcla útil de información sobre variaciones. Hacer que los parámetros dependan de los datos de origen resuelve aún más este problema y permite al modelo mezclar parámetros relevantes y filtrar los irrelevantes para modelar la variable de interés. Una de las contribuciones técnicas principales de Chimera es la construcción de Bi, Ci y Δi mediante una función a partir de los datos de origen 𝐱v,t.

El framework Chimera utiliza una pila 2D-SSM con una no linealidad intermedia. Para mejorar la expresividad y la capacidad de los 2D-SSM mencionados, de forma similar a los modelos SSM profundos, se permite el entrenamiento de todos los parámetros y se usan múltiples 2D-SSM en cada capa, cada uno con su propia responsabilidad.

Chimera sigue la descomposición común de las series temporales y las descompone en componentes de tendencia y patrones estacionales. Sin embargo, usa las características especiales de 2D-SSM para captar estos términos.

La visualización del framework Chimera por parte del autor se presenta a continuación.

Visualización del autor del framework Quimera

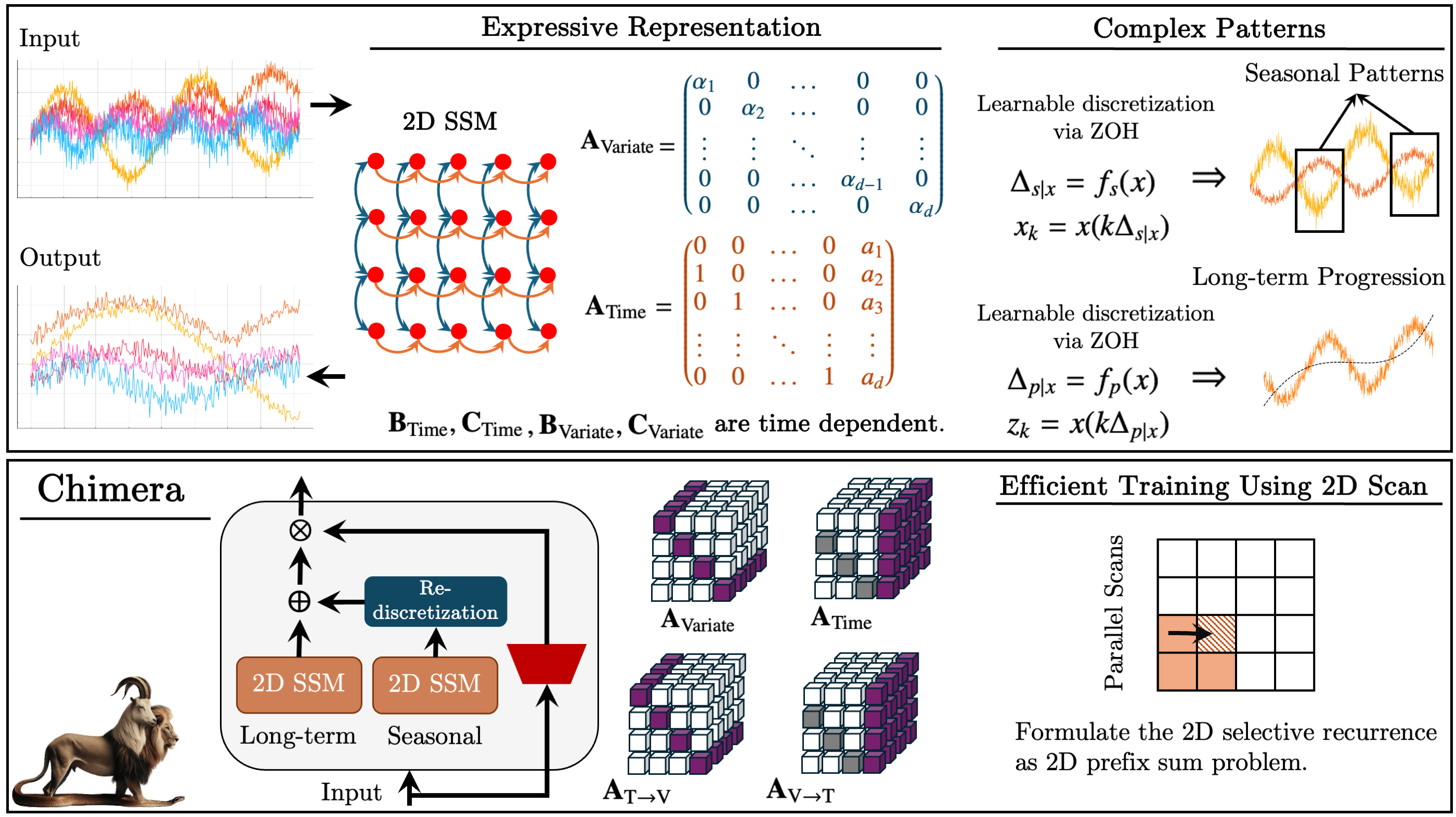
Implementación con MQL5

Tras repasar los aspectos teóricos del framework Quimera, abordaremos la aplicación práctica de nuestra propia visión de los planteamientos propuestos. En esta sección, analizaremos la interpretación del concepto propuesto utilizando las capacidades del lenguaje de programación MQL5. Sin embargo, antes de proceder a la implantación del software, la arquitectura del modelo deberá diseñarse cuidadosamente para garantizar que sea flexible, eficiente y adaptable a distintos tipos de datos.

Soluciones arquitectónicas

Uno de los componentes clave del framework Quimera son las matrices de acento de estado oculto A{1,…,4}. Los autores del framework proponen utilizar matrices diagonales con aumento, lo cual reduce el número de parámetros a entrenar y disminuye la complejidad computacional. Este enfoque reduce sustancialmente el consumo de recursos y acelera el proceso de formación de modelos.

Sin embargo, esta solución tiene sus desventajas. El uso de matrices diagonales impone limitaciones significativas al modelo, ya que solo puede analizar las dependencias locales entre los elementos subsiguientes de la secuencia. Esto limita su expresividad y su capacidad para revelar patrones complejos. A este respecto, en nuestra interpretación usaremos matrices totalmente entrenadas. Este enfoque aumentará el número de parámetros, pero ampliará enormemente la adaptabilidad del modelo, permitiendo dependencias más complejas en los datos analizados.

Al mismo tiempo, nuestras matrices variantes conservarán el concepto clave de la solución original: no dependerán directamente de los datos de origen y serán entrenadas. Esto permite que el modelo sea más versátil, lo cual resulta especialmente importante para resolver diversos problemas de análisis de secuencias temporales multivariantes.

Otro aspecto importante es la integración de estas matrices en el proceso computacional. Como se muestra en la parte teórica, las matrices de acento se multiplican por los estados latentes del modelo, lo cual se corresponde con los principios de las capas neuronales. Ante esto, proponemos implementarlos como una capa convolucional de la red neuronal, donde la matriz de acento será un tensor de parámetros entrenable. La integración en arquitecturas de redes neuronales estándar permitirá utilizar algoritmos de optimización previamente implementados.

Además, para poder organizar el proceso de cálculo paralelo de cuatro matrices de acento a la vez, hemos decidido combinarlas en un único tensor concatenado, lo que, a su vez, requiere combinar dos matrices de estados ocultos en un único tensor.

A pesar de todas las ventajas de este enfoque, resulta que no es lo suficientemente versátil como para trabajar con otras matrices paramétricas en 2D-SSM. Una de las limitaciones es que la estructura de las matrices es fija, lo cual reduce la flexibilidad del modelo a la hora de procesar datos multivariantes complejos. En este sentido, para mejorar la capacidad expresiva del modelo, usaremos las matrices dependientes del contexto Bi, Ci y Δi, que son capaces de adaptarse dinámicamente a los datos de origen, proporcionando un análisis más profundo de las dependencias temporales.

Las matrices dependientes del contexto se forman a partir de la información obtenida de los datos de origen, lo cual permite considerar su estructura y variar los parámetros del modelo según las características de la secuencia analizada. Este enfoque permite al modelo analizar no solo las relaciones locales, sino también tener en cuenta las tendencias globales, lo que resulta especialmente importante para las tareas de previsión y el trabajo con series temporales.

Siguiendo las recomendaciones de los autores del framework, implementaremos estas matrices mediante capas neuronales especializadas encargadas de adaptar los parámetros según el contexto.

En el siguiente paso, una tarea importante será organizar el proceso de interacción de datos complejos dentro del modelo 2D-SSM. Esto requiere una gestión eficiente de los recursos informáticos, ya que las complejas estructuras de datos multidimensionales necesitan de un enfoque de procesamiento optimizado. Considerando los requisitos de eficiencia computacional y rendimiento del sistema, hemos decidido colocar este bloque de operaciones en un kernel independiente que se ejecuta junto al programa OpenCL.

Este planteamiento presenta varias ventajas significativas. En primer lugar, permite reducir significativamente la latencia en el procesamiento de datos gracias a la ejecución en paralelo de las operaciones en el procesador gráfico. Esto resulta fundamental a la hora de analizar grandes cantidades de información, ya que el procesamiento secuencial puede acarrear importantes costes de tiempo. En segundo lugar, gracias a la aceleración por hardware OpenCL es posible paralelizar los cálculos de forma eficaz, lo que permite procesar series temporales complejas en tiempo real.

Incorporación del programa OpenCL

Tras el diseño detallado de la arquitectura de los enfoques implementados, el siguiente paso será implementarlo en código. En primer lugar, deberemos introducir cambios en el programa OpenCL para optimizar la ejecución de las operaciones de cálculo y garantizar una interacción eficaz con los principales componentes del modelo. Así, crearemos un algoritmo para la compleja interacción entre los parámetros 2D-SSM entrenados y los datos de origen en el kernel SSM2D_FeedForward.

En los parámetros del método, transmitiremos los punteros a los búferes de datos que contienen todos los parámetros necesarios del modelo y las proyecciones de los datos de origen en el contexto del tiempo y las variables analizadas.

__kernel void SSM2D_FeedForward(__global const float *ah,
                                __global const float *b_time,
                                __global const float *b_var,
                                __global const float *px_time,
                                __global const float *px_var,
                                __global const float *c_time,
                                __global const float *c_var,
                                __global const float *delta_time,
                                __global const float *delta_var,
                                __global       float *hidden,
                                __global       float *y
                               )
  {
   const size_t n = get_local_id(0);
   const size_t d = get_global_id(1);
   const size_t n_total = get_local_size(0);
   const size_t d_total = get_global_size(1);

En el cuerpo del kernel, como de costumbre, primero identificaremos el flujo actual en el espacio de tareas bidimensional. La primera dimensión corresponde al número de elementos de la secuencia y la segunda a la dimensionalidad de las características. En este caso, combinaremos todos los elementos de secuencia de la misma característica en grupos de trabajo.

Aquí cabe señalar que las proyecciones de los parámetros entrenados y de los datos de origen en el contexto del tiempo y de los indicadores analizados deben llevarse a una forma comparable en la fase de preparación de los datos antes de su transmisión al kernel.

A continuación, determinaremos el estado oculto en ambos contextos dada la información actualizada. Luego guardaremos los valores resultantes en el búfer de datos correspondiente.

//--- Hidden state
   for(int h = 0; h < 2; h++)
     {
      float new_h = ah[(2 * n + h) * d_total + d] + ah[(2 * n_total + 2 * n + h) * d_total + d];
      if(h == 0)
         new_h += b_time[n] * px_time[n * d_total + d];
      else
         new_h += b_var[n] * px_var[n * d_total + d];
      hidden[(h * n_total + n)*d_total + d] = IsNaNOrInf(new_h, 0);
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Después de realizar las operaciones, deberemos sincronizar los hilos del grupo de trabajo, ya que necesitaremos los resultados de todo el grupo de trabajo para realizar más operaciones.

En el siguiente paso, definiremos el resultado del modelo. Para ello, deberemos multiplicar las matrices de contexto y discretización por el estado oculto calculado anteriormente. Para realizar esta operación, organizaremos un ciclo, en cuyo cuerpo multiplicaremos los elementos matriciales correspondientes en el contexto del tiempo y de las variables analizadas. Luego sumaremos los resultados de las operaciones de ambos contextos.

//--- Output
   uint shift_c = n;
   uint shift_h1 = d;
   uint shift_h2 = shift_h1 + n_total * d_total;
   float value = 0;
   for(int i = 0; i < n_total; i++)
     {
      value += IsNaNOrInf(c_time[shift_c] * delta_time[shift_c] * hidden[shift_h1], 0);
      value += IsNaNOrInf(c_var[shift_c] * delta_var[shift_c] * hidden[shift_h2], 0);
      shift_c += n_total;
      shift_h1 += d_total;
      shift_h2 += d_total;
     }

Ahora deberemos transferir el valor obtenido al elemento correspondiente del búfer de resultados global y finalizar el trabajo del kernel.

//---
   y[n * d_total + d] = IsNaNOrInf(value, 0);
  }

A continuación tendremos que organizar los algoritmos de pasada inversa. Después optimizaremos los parámetros mediante las capas neuronales correspondientes. Pero para distribuir el gradiente de error entre ellas, crearemos el kernel SSM2D_CalcHiddenGradient, en cuyo cuerpo construiremos un algoritmo inverso al anterior.

En los parámetros del kernel, transmitiremos los punteros al mismo conjunto de matrices, complementándolo con gradientes de error. Para evitar confusiones en un gran número de búferes, utilizaremos el prefijo grad_ para los búferes de los gradientes de error correspondientes.

__kernel void SSM2D_CalcHiddenGradient(__global const float *ah,
                                       __global       float *grad_ah,
                                       __global const float *b_time,
                                       __global       float *grad_b_time,
                                       __global const float *b_var,
                                       __global       float *grad_b_var,
                                       __global const float *px_time,
                                       __global       float *grad_px_time,
                                       __global const float *px_var,
                                       __global       float *grad_px_var,
                                       __global const float *c_time,
                                       __global       float *grad_c_time,
                                       __global const float *c_var,
                                       __global       float *grad_c_var,
                                       __global const float *delta_time,
                                       __global       float *grad_delta_time,
                                       __global const float *delta_var,
                                       __global       float *grad_delta_var,
                                       __global const float *hidden,
                                       __global const float *grad_y
                                      )
  {
//---
   const size_t n = get_global_id(0);
   const size_t d = get_local_id(1);
   const size_t n_total = get_global_size(0);
   const size_t d_total = get_local_size(1);

Está previsto que este kernel se ejecute en el mismo espacio de tareas que el kernel de pasa directa. Sin embargo, en este caso, combinaremos los flujos en grupos de trabajo basados en el espacio de características.

Antes de empezar, inicializaremos una serie de variables locales en las que almacenaremos los valores intermedios y los desplazamientos en los búferes de datos.

//--- Initialize indices for data access
   uint shift_c = n;
   uint shift_h1 = d;
   uint shift_h2 = shift_h1 + n_total * d_total;
   float grad_hidden1 = 0;
   float grad_hidden2 = 0;

A continuación, organizaremos un ciclo de distribución del gradiente de error desde el búfer de resultados hasta el estado oculto, así como las matrices de contexto y de discretización, según su influencia en el resultado final del modelo. Asimismo, distribuiremos simultáneamente el gradiente de error en los contextos del tiempo y de las variables analizadas.

//--- Backpropagation: compute hidden gradients from y
   for(int i = 0; i < n_total; i++)
     {
      float grad = grad_y[i * d_total + d];
      float c_t = c_time[shift_c];
      float c_v = c_var[shift_c];
      float delta_t = delta_time[shift_c];
      float delta_v = delta_var[shift_c];
      float h1 = hidden[shift_h1];
      float h2 = hidden[shift_h2];
      //-- Accumulate gradients for hidden states
      grad_hidden1 += IsNaNOrInf(grad * c_t * delta_t, 0);
      grad_hidden2 += IsNaNOrInf(grad * c_v * delta_v, 0);
      //--- Compute gradients for c_time, c_var, delta_time, delta_var
      grad_c_time[shift_c] += grad * delta_t * h1;
      grad_c_var[shift_c]  += grad * delta_v * h2;
      grad_delta_time[shift_c] += grad * c_t * h1;
      grad_delta_var[shift_c]  += grad * c_v * h2;
      //--- Update indices for the next element
      shift_c += n_total;
      shift_h1 += d_total;
      shift_h2 += d_total;
     }

Luego distribuiremos el gradiente de error en las matrices de acento.

//--- Backpropagate through hidden -> ah, b_time, px_time
   for(int h = 0; h < 2; h++)
     {
      float grad_h = (h == 0) ? grad_hidden1 : grad_hidden2;
      //--- Store gradients in ah (considering its influence on two elements)
      grad_ah[(2 * n + h) * d_total + d] = grad_h;
      grad_ah[(2 * (n_total + n) + h) * d_total + d] = grad_h;
     }

Y pasaremos a las proyecciones de los datos de origen.

//--- Backpropagate through px_time and px_var (influenced by b_time and b_var)
   grad_px_time[n * d_total + d] = grad_hidden1 * b_time[n];
   grad_px_var[n * d_total + d] = grad_hidden2 * b_var[n];

El gradiente de error sobre la matriz Bi, entre tanto, deberemos recopilarlo en todas las dimensiones. Por ello, primero pondremos a cero el valor del búfer de gradiente de error correspondiente y sincronizaremos los hilos del grupo de trabajo.

   if(d == 0)
     {
      grad_b_time[n] = 0;
      grad_b_var[n] = 0;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Y, a continuación, resumiremos los valores de los flujos individuales de los grupos de trabajo.

//--- Sum gradients over all d for b_time and b_var
   grad_b_time[n] += grad_hidden1 * px_time[n * d_total + d];
   grad_b_var[n] += grad_hidden2 * px_var[n * d_total + d];
  }

Transferiremos los resultados de las operaciones a los búferes de datos globales correspondientes y finalizaremos el kernel.

Con esto daremos por completo el trabajo en el lado del programa OpenCL. Podrá ver su código completo en el archivo adjunto.

Objeto 2D-SSM

Una vez finalizado el trabajo en el lado de OpenCL, el siguiente paso consistirá en construir la estructura 2D-SSM en el lado del programa principal. Para ello, crearemos la clase CNeuron2DSSMOCL, dentro de la cual implementaremos los algoritmos necesarios. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuron2DSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindowOut;
   uint                 iUnitsOut;
   CNeuronBaseOCL       cHiddenStates;
   CLayer               cProjectionX_Time;
   CLayer               cProjectionX_Variable;
   CNeuronConvOCL       cA;
   CNeuronConvOCL       cB_Time;
   CNeuronConvOCL       cB_Variable;
   CNeuronConvOCL       cC_Time;
   CNeuronConvOCL       cC_Variable;
   CNeuronConvOCL       cDelta_Time;
   CNeuronConvOCL       cDelta_Variable;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForwardSSM2D(void);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradientsSSM2D(void);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuron2DSSMOCL(void)  {};
                    ~CNeuron2DSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuron2DSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

En la estructura de objetos presentada vemos el ya familiar conjunto de métodos virtuales redefinidos y un número bastante grande de objetos internos. Creo que el número de objetos no resulta inesperado, lo dicta la arquitectura del modelo. Y en parte, la finalidad de los objetos se adivina por su nombre. Presentaremos una descripción más detallada de la funcionalidad de cada objeto durante la implementación de los algoritmos de construcción de los métodos de nuestra clase.

Todos los objetos internos se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor de la clase, Ya hemos hablado muchas veces de las ventajas de este enfoque. Y la inicialización de todos los objetos declarados y heredados se realizará en el método Init.

bool CNeuron2DSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window_in, uint window_out, uint units_in, uint units_out,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_out,
                                                       optimization_type, batch))
      return false;
   SetActivationFunction(None);

En los parámetros del método obtenemos una serie de constantes que nos permitirán definir de forma inequívoca la arquitectura del objeto a crear. Entre ellas, destacan las dimensionalidades de los datos de origen y el resultado esperado ({units_in, window_in} y {units_out, window_out}, respectivamente).

En el cuerpo del método, como es habitual, llamaremos primero al método homónimo de la clase padre, al que pasaremos las dimensiones del resultado esperado. El método de la clase padre ya implementa el bloque de control y los algoritmos necesarios para inicializar los objetos e interfaces heredados. Por lo tanto, después de ejecutar con éxito las operaciones del método de la clase padre, almacenaremos de forma segura las dimensionalidades del tensor resultante en las variables internas.

   iWindowOut = window_out;
   iUnitsOut = units_out;

Como hemos mencionado anteriormente, al construir los kernels en el lado del programa OpenCL, las proyecciones de los datos de origen de ambos contextos deberán tener una apariencia comparable. En nuestra aplicación, los convertiremos a la dimensionalidad del tensor de resultados. En primer lugar, crearemos un modelo de proyección de los datos de origen en el contexto del tiempo.

Para preservar la información de las secuencias unitarias de las series temporales multidimensionales, primero realizaremos una proyección independiente de las secuencias univariantes a un tamaño determinado. Y aquí deberemos recordar que en la entrada recibimos los datos como una matriz cuyas filas corresponden a los pasos temporales. En consecuencia, para trabajar cómodamente con secuencias unitarias necesitaremos transponer primero la matriz de datos iniciales obtenida.

//---
   int index = 0;
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeOCL *transp = NULL;
//--- Projection Time
   cProjectionX_Time.Clear();
   cProjectionX_Time.SetOpenCL(OpenCL);
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) ||
      !cProjectionX_Time.Add(transp))
     {
      delete transp;
      return false;
     }

Y solo entonces podremos usar las facilidades de la capa de convolución para cambiar la dimensionalidad de las secuencias unitarias.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, iUnitsOut, window_in, 1,
                                                       optimization, iBatch) ||
      !cProjectionX_Time.Add(conv))
     {
      delete conv;
      return false;
     }

A continuación, deberemos realizar una proyección de los datos de medición de las características. Para ello, realizaremos la transposición inversa de los datos.

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, window_in, iUnitsOut, optimization, iBatch) ||
      !cProjectionX_Time.Add(transp))
     {
      delete transp;
      return false;
     }

Y efectuaremos la proyección de datos utilizando la capa de convolución.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, iWindowOut, iUnitsOut, 1,
                                                          optimization, iBatch) ||
      !cProjectionX_Time.Add(conv))
     {
      delete conv;
      return false;
     }

Del mismo modo, realizaremos la proyección de datos en el contexto de las características. Solo que esta vez, primero haremos la proyección sobre el eje variable y luego transpondremos los datos y haremos la proyección sobre el eje temporal.

//--- Projection Variables
   cProjectionX_Variable.Clear();
   cProjectionX_Variable.SetOpenCL(OpenCL);
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, iUnitsOut, units_in, 1,
                                                        optimization, iBatch) ||
      !cProjectionX_Variable.Add(conv))
     {
      delete conv;
      return false;
     }

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, iUnitsOut, optimization, iBatch) ||
      !cProjectionX_Variable.Add(transp))
     {
      delete transp;
      return false;
     }

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, iWindowOut, iUnitsOut, 1,
                                                        optimization, iBatch) ||
      !cProjectionX_Variable.Add(conv))
     {
      delete conv;
      return false;
     }

Tras inicializar los modelos de proyección de los datos de origen, pasaremos a trabajar con otros objetos internos. Aquí inicializaremos primero el objeto de estado oculto. Este objeto solo se utilizará para almacenar datos y no contendrá parámetros de aprendizaje. Sin embargo, deberá tener un tamaño suficiente para almacenar los datos de estado oculto de ambos contextos.

//--- HiddenState
   index++;
   if(!cHiddenStates.Init(0, index, OpenCL, 2 * iUnitsOut * iWindowOut, optimization, iBatch))
      return false;

A continuación, pasaremos a las matrices de acento del estado latente. Como ya hemos mencionado, implementaremos las 4 matrices en una única capa convolucional. Esto nos permitirá llevar a cabo su trabajo en paralelo.

Aquí deberemos considerar que en la salida de esta capa esperamos obtener multiplicaciones del estado oculto por 4 matrices independientes. En este caso, dos de ellas trabajarán con el contexto temporal y las otras dos con el contexto de características. Para obtener el efecto deseado, declararemos una capa de convolución con un número de filtros igual a 2 veces la ventana de datos de origen, lo que se corresponderá con dos matrices de acento. Y especificaremos el funcionamiento de la capa convolucional con dos secuencias independientes que corresponderán a los contextos de tiempo y características. Recordemos que la capa de convolución usa diferentes matrices de filtrado para secuencias independientes. De esta forma obtendremos 4 matrices de acentos que trabajarán con diferentes contextos por parejas.

//--- A*H
   index++;
   if(!cA.Init(0, index, OpenCL, iWindowOut, iWindowOut, 2 * iWindowOut, iUnitsOut, 2,
                                                                optimization, iBatch))
      return false;

Aquí cabe señalar que unos parámetros de acento elevados pueden provocar un efecto de explosión de los gradientes de error. Por ello, reduciremos los parámetros en un factor de 10 después de la inicialización aleatoria.

if(!SumAndNormilize(cA.GetWeightsConv(), cA.GetWeightsConv(), cA.GetWeightsConv(),
                                               iWindowOut, false, 0, 0, 0, 0.05f))
   return false;

En el siguiente paso, generaremos matrices adaptativas dependientes del contexto Bi, Ci y Δi, que en nuestra aplicación serán funciones de los datos de origen. Para generarlas, utilizaremos capas de convolución que tomarán como entrada las proyecciones de los datos de origen del contexto correspondiente, y generarán como salida la matriz necesaria.

//--- B
   index++;
   if(!cB_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, 
                                                         optimization, iBatch))
      return false;
   cB_Time.SetActivationFunction(TANH);
   index++;
   if(!cB_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, 
                                                            optimization, iBatch))
      return false;
   cB_Variable.SetActivationFunction(TANH);

El enfoque propuesto será similar a las puertas de RNN. Y utilizaremos la tangente hiperbólica como funciones de activación para las matrices Bi y Ci, destacando la posibilidad de dependencia positiva y negativa.

//--- C
   index++;
   if(!cC_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                optimization, iBatch))
      return false;
   cC_Time.SetActivationFunction(TANH);
   index++;
   if(!cC_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                    optimization, iBatch))
      return false;
   cC_Variable.SetActivationFunction(TANH);

La matriz Δi realizará las funciones de la discretización entrenada y no podrá contener valores negativos. Para ello, utilizaremos SoftPlus como función de activación, que es un análogo suave de ReLU.

//--- Delta
   index++;
   if(!cDelta_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                    optimization, iBatch))
      return false;
   cDelta_Time.SetActivationFunction(SoftPlus);
   index++;
   if(!cDelta_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                        optimization, iBatch))
      return false;
   cDelta_Variable.SetActivationFunction(SoftPlus);
//---
   return true;
  }

Tras inicializar todos los objetos internos, solo deberemos devolver el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método.

Hoy hemos hecho un buen trabajo, pero aún no hemos terminado. Le sugiero que nos tomemos un breve descanso y continuemos en el próximo artículo. En él, completaremos la construcción de los objetos necesarios, los integraremos en el modelo y comprobaremos la eficacia de los enfoques aplicados sobre datos históricos reales.

Conclusión

En este artículo, hemos presentado el framework del modelo bidimensional de espacio de estados Chimera, que ofrece nuevos enfoques para modelar series temporales multivariantes teniendo en cuenta las dependencias en el contexto del tiempo y las características. Chimera usa modelos de espacio de estados bidimensionales (2D-SSM), lo que le permite modelizar eficazmente tanto las progresiones a largo plazo como los patrones estacionales.

En la parte práctica, hemos empezado a trabajar en la implementación de nuestra propia visión de los enfoques propuestos mediante MQL5. Sin embargo, los trabajos iniciados aún no han concluido. En el próximo artículo seguiremos construyendo los enfoques propuestos y probaremos definitivamente la eficacia de las soluciones implementadas usando datos históricos reales.

Enlaces

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto de recopilación con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17210

Archivos adjuntos |

Descargar ZIP

MQL5.zip (2458.91 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Simulación de mercado (Parte 07): Sockets (I)

Sockets. ¿Sabes para qué sirven o cómo usarlos en MetaTrader 5? Si la respuesta es no, comencemos aprendiendo un poco sobre ellos. Este artículo trata de lo más básico. Pero, como existen diversas maneras de hacer lo mismo, y lo que realmente nos interesa es siempre el resultado, quiero mostrar que sí, existe una forma sencilla de pasar datos desde MetaTrader 5 hacia otros programas, como, por ejemplo, Excel. Sin embargo, la idea principal no es transferir datos de MetaTrader 5 a Excel, sino hacer lo contrario. Es decir, transferir datos desde Excel, o desde cualquier otro programa, hacia MetaTrader 5.

Kit de herramientas de negociación MQL5 (Parte 7): Ampliación de la libreria EX5 de gestión del historial con las funciones de última orden pendiente cancelada

Aprenda a completar la creación del módulo final en la librería History Manager EX5, centrándose en las funciones responsables de gestionar la orden pendiente cancelada más recientemente. Esto le proporcionará las herramientas necesarias para recuperar y almacenar de manera eficiente los detalles clave relacionados con las órdenes pendientes canceladas con MQL5.

Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 9): Flujo externo

Este artículo explora una nueva dimensión del análisis utilizando librerías externas diseñadas específicamente para análisis avanzados. Estas librerías, como pandas, proporcionan potentes herramientas para procesar e interpretar datos complejos, lo que permite a los operadores obtener una visión más profunda de la dinámica del mercado. Al integrar estas tecnologías, podemos salvar la brecha entre los datos brutos y las estrategias viables. Únase a nosotros para sentar las bases de este enfoque innovador y liberar el potencial de combinar la tecnología con la experiencia en el comercio.

Desarrollamos un asesor experto multidivisas (Parte 22): Inicio de la transición a la sustitución dinámica de ajustes

Si hemos empezado a automatizar la optimización periódica, también deberíamos ocuparnos de la actualización automática de los ajustes de los asesores expertos que ya están trabajando en la cuenta comercial. También deberíamos permitirle ejecutar un asesor experto en el simulador de estrategias y cambiar su configuración en una sola pasada.