Redes neuronales en el trading: Detección adaptativa de anomalías del mercado (Final)

Introducción

En el artículo anterior, aprendimos los aspectos teóricos del framework DADA(Adaptive Bottlenecks and Dual Adversarial Decoders), diseñado para detectar anomalías en series temporales mediante técnicas de aprendizaje profundo. Esta herramienta ayuda a analizar los datos y poner de relieve las condiciones anormales del mercado, lo que resulta especialmente importante en entornos de alta volatilidad. El uso de métodos adaptativos de procesamiento de la información permite al modelo ajustarse con flexibilidad a entornos del mercado en cambio constante, lo cual lo convierte en una herramienta universal para analizar diversas series temporales.

La arquitectura del framework DADA se basa en tres componentes clave, cada uno de los cuales cumple una tarea específica. El primero es el módulo de cuellos de botella adaptativos (Adaptive Bottlenecks), capaz de modificar dinámicamente el grado de compresión de los datos analizados. Este enfoque ayuda a conservar las características más relevantes de los datos de mercado y a minimizar la pérdida de información que podría afectar a la calidad del análisis. A diferencia de los modelos tradicionales, en los que los parámetros de compresión son fijos, aquí todo se ajusta en tiempo real según la situación del mercado.

El segundo elemento importante es un sistema con dos descodificadores adversarios. El primer descodificador reconstruye los estados normales del mercado, lo cual permite al modelo comprender mejor las pautas típicas de comportamiento del mercado. El segundo descodificador se centra en los datos anómalos, ayudando a distinguir claramente entre situaciones estándar y aquellas que se desvían de la norma. Este enfoque reduce la probabilidad de falsas activaciones y hace que el modelo resulte más fiable.

El tercer componente clave es el mecanismo de parcheo y enmascaramiento, que desempeña un papel importante en el procesamiento de las series temporales. Este mecanismo permite resaltar dinámicamente las partes críticas de los datos, ocultar los componentes de ruido y mejorar la calidad de la presentación de la información. El parcheado se usa para dividir los datos en pequeños segmentos, lo cual permite al modelo analizar las características locales de la serie temporal. El enmascaramiento aleatorio favorece un mejor aprendizaje de los modelos. Al recuperar las zonas enmascaradas, el modelo se ve obligado a considerar las dependencias ocultas en los datos, lo que mejora su capacidad para detectar pautas y regularidades complejas. En combinación, ambos métodos mejoran la precisión de la detección de anomalías y hacen que el modelo sea más robusto frente a las fluctuaciones del mercado. El enmascaramiento también mejora la generalizabilidad del modelo al evitar el sobreentrenamiento en partes concretas de los datos del mercado.

Una de las principales ventajas del framework DADA es su adaptabilidad. A diferencia de los algoritmos tradicionales, que requieren un reaprendizaje cuando cambian las condiciones del mercado, el DADA puede ajustar automáticamente sus parámetros. Esto resulta especialmente importante en el trading de alta frecuencia, donde las decisiones se toman en fracciones de segundo. El ajuste dinámico permite que el modelo funcione eficazmente en un amplio abanico de situaciones de mercado, desde tendencias estables hasta bruscos picos de volatilidad.

A continuación le mostramos la visualización del framework DADA por parte del autor.

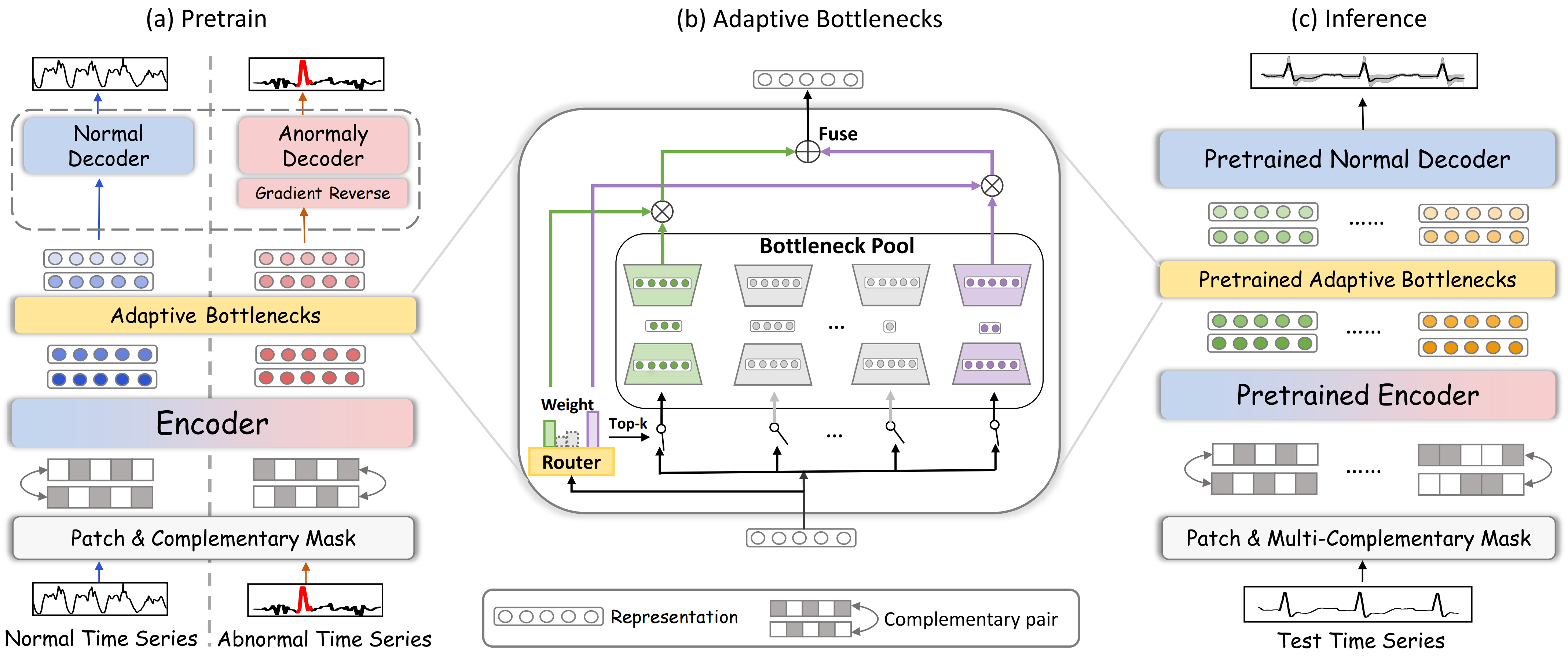
En la parte práctica del artículo anterior, construimos el objeto de capa convolucional multiventana CNeuronMultiWindowsConvOCL. Debemos decir que la creación de un objeto de este tipo no se desprende directamente de la descripción que hace el autor de la arquitectura del framework DADA. Sin embargo, en nuestra aplicación, cumplirá una de las funciones clave del módulo Adaptive Bottlenecks. Su uso nos permitirá modificar dinámicamente el grado de compresión de los datos analizados.

El módulo Adaptive Bottlenecks

El siguiente paso importante de nuestro trabajo será la construcción directa del módulo de cuellos de botella adaptativos (Adaptive Bottlenecks). Este módulo supone una potente herramienta de procesamiento dinámico de datos de origen que permite analizar eficazmente series temporales complejas e identificar anomalías en su comportamiento.

Ya hemos mencionado su similitud conceptual con el módulo Mixture of Experts (MoE), que implementamos anteriormente como parte del objeto CNeuronMoE. Ambos módulos explotan el enfoque de funcionamiento en paralelo de múltiples minimodelos que realizan análisis sobre los datos de origen. El módulo selecciona dinámicamente los k minimodelos más adecuados para procesar el segmento analizado, usando como base el análisis de su contexto. Este enfoque aumenta la adaptabilidad y precisión del modelo global al permitirle centrarse en los patrones más relevantes.

Una característica clave de Adaptive Bottlenecks es el uso de un conjunto de autocodificadores como minimodelos, cada uno con un grado diferente de compresión de la información analizada en el espacio latente. Esto permite al modelo adaptarse con mayor flexibilidad a las condiciones cambiantes y ajustar el nivel de detalle de la representación inicial de los datos según las características identificadas de las series temporales. Con esta arquitectura, Adaptive Bottlenecks reducen eficazmente la redundancia de datos, minimizan el impacto del ruido y mejoran la detección de patrones anómalos.

Construiremos nuestra visión del módulo Adaptive Bottlenecks dentro del objeto CNeuronAdaBN. Como podemos adivinar, se utiliza CNeuronMoE como clase padre. Esta decisión obedece al deseo de reutilizar mecanismos clave de Mixture of Experts, como el equilibrio dinámico de la carga entre minimodelos y la selección adaptativa de los expertos más relevantes. Al fin y al cabo, cumplen plenamente el concepto Adaptive Bottlenecks. Esto también se refleja en la estructura del nuevo objeto, que se resume a continuación.

class CNeuronAdaBN   :  public CNeuronMoE
  {
public:
                     CNeuronAdaBN(void) {};
                    ~CNeuronAdaBN(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint &bottlenecks[], uint top_k, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronAdaBN; }
  };

Como podemos ver, planeamos sobrescribir solo el método de inicialización del objeto, sin crear ningún objeto interno adicional.

Aquí cabe recordar que la clase padre CNeuronMoE incluye un objeto de selección de k expertos más relevantes (cGates) y un array dinámico (cExperts) que contiene punteros a objetos sucesivos del modelo interno. A primera vista, el concepto de expertos paralelos puede parecer poco compatible con la visión tradicional de los modelos secuenciales. Sin embargo, usamos una secuencia de capas convolucionales capaces de analizar secuencias unitarias de forma independiente. Esto ha permitido crear mini MLP especializados que funcionan en paralelo. Al mismo tiempo, cada minimodelo tiene sus propios parámetros entrenables.

Esta solución arquitectónica aumenta significativamente la adaptabilidad del sistema, ya que cada experto se entrena en su subtarea específica, lo cual permite una mejor identificación de patrones complejos en las series temporales. Además, el sistema dinámico de selección de expertos óptimos garantiza que durante análisis solo se utilicen los modelos más pertinentes, lo que aumenta la precisión de las previsiones.

class CNeuronMoE  :  public CNeuronBaseOCL
  {
protected:
   CNeuronTopKGates     cGates;
   CLayer               cExperts;
   //---
   ..........
   ..........
   ..........
  };

El mecanismo de selección de k expertos más relevantes heredado de la clase padre cumple plenamente los requisitos del módulo CNeuronAdaBN. Así que usaremos la funcionalidad heredada. Además, bastará con rellenar el array dinámico heredado con una nueva secuencia de objetos según la tarea a resolver, y su mantenimiento podrá realizarse por los medios existentes en la clase padre. Esto también se aplica a la organización de los procesos de pasada directa e inversa.

La secuencia de los objetos internos se establece en el método Init, que redefiniremos.

bool CNeuronAdaBN::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                        uint window, uint window_out, uint units_count,
                        uint &bottlenecks[], uint top_k, uint variables,
                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables,
                                                                 optimization_type, batch))
      return false;

En los parámetros del método, como es habitual, obtenemos una serie de constantes que nos permiten interpretar sin ambigüedades la arquitectura de la clase. Entre otros parámetros que conocemos por la clase padre, destaca el array bottlenecks, que contiene los tamaños de los estados latentes de los autocodificadores creados.

En el cuerpo del método llamamos directamente al método homónimo de la clase básica de la capa neuronal completamente conectada. Recordemos que este objeto en particular es el padre común de todos los objetos de capas neuronales de nuestra biblioteca. En este caso, no usamos el método de inicialización directa de la clase padre porque no queremos inicializar el conjunto de expertos del objeto padre. Sin embargo, esta solución provoca la necesidad de construir un proceso para inicializar todos los objetos heredados.

Una vez inicializadas con éxito las interfaces básicas, procederemos a inicializar los objetos heredados de la clase padre. Primero inicializaremos el módulo de selección adaptativa de k expertos más relevantes. Aquí determinaremos el número total de expertos según el tamaño del array bottlenecks. Como demás parámetros utilizaremos las constantes obtenidas de un programa externo.

   int index = 0;
   if(!cGates.Init(0, index, OpenCL, window, units_count * variables, bottlenecks.Size(), top_k, optimization, iBatch))
      return false;

A continuación, prepararemos un array dinámico y las variables locales para el almacenamiento temporal de los punteros a los objetos internos del módulo Adaptive Bottlenecks a crear.

   cExperts.Clear();
   cExperts.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronMultiWindowsConvOCL *mwconv = NULL;
   CNeuronTransposeRCDOCL *transp = NULL;

Aquí organizaremos un ciclo y calcularemos el tamaño total de todos los estados latentes de los autocodificadores creados.

   uint bn_size = 0;
   for(uint i = 0; i < bottlenecks.Size(); i++)
      bn_size += bottlenecks[i];

Con esto completaremos la fase preparatoria y procederemos a crear la secuencia de objetos de nuestros autocodificadores.

Sorprendentemente, primero crearemos la capa convolucional estándar. A primera vista, esto puede no parecer una elección obvia, especialmente dada la complejidad de la arquitectura del módulo Adaptive Bottlenecks. Sin embargo, este paso desempeñará un papel importante en el procesamiento posterior de los datos.

El punto clave es que al crear la capa convolucionales, especificaremos un número de filtros igual a la suma de todos los estados latentes de los autocodificadores. Esta decisión se debe a que cada autocodificador trabaja con el mismo conjunto de datos de entrada. Y el nivel de detalle de los datos comprimidos depende del tamaño del estado latente. En este caso, cada filtro de capa convolucional funcionará independientemente de los demás y generará el valor de su propio elemento en el búfer de resultados. En esencia, puede compararse a un gran número de minimodelos que comprimen los datos analizados en un único elemento. Y ahora podemos combinarlos en el número de grupos requerido con el número de elementos que necesitamos en cada uno. Al mismo tiempo, el número de elementos de cada grupo puede ser distinto. Lo único necesario será que se mantenga el número total de elementos.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, bn_size, units_count, variables, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

Esa es la propiedad que usaremos. A continuación declaramos una capa convolucional multiventana. Cada ventana convolucional tomará su propio grupo de elementos, que constituirán el estado latente del autocodificador individual. Y luego restaurará los datos al tamaño indicado.

   index++;
   mwconv = new CNeuronMultiWindowsConvOCL();
   if(!mwconv ||
      !mwconv.Init(0, index, OpenCL, bottlenecks, window_out, units_count, variables, optimization, iBatch) ||
      !cExperts.Add(mwconv))
     {
      delete conv;
      return false;
     }
   mwconv.SetActivationFunction(SoftPlus);

A continuación, tenemos previsto añadir otra capa al descodificador de los autocodificadores creados. Al mismo tiempo, cada autocodificador deberá tener su propia capa con parámetros entrenables únicos. Pero aquí deberemos tener en cuenta que el resultado de la capa convolucional multiventana que se ha inicializado en último lugar, puede representarse como un tensor de 4 dimensiones [Variable, Units, Autoencoder, Dimension]. Usando simplemente una capa convolucional, no podremos proporcionar parámetros únicos a los autocodificadores. No obstante, esto se logrará fácilmente si ponemos en primer plano la dimensionalidad del autoencoder. Por ello, a continuación declararemos una capa de transposición de datos.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_count * variables, bottlenecks.Size(), window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Detrás añadiremos una capa convolucional especificando en el parámetro variables el número de autocodificadores, lo que indicará al objeto inicializado la necesidad de crear arrays de pesos únicos.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_out, window_out, window, units_count * variables, bottlenecks.Size(),
                                                                                       optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Y luego, añadiremos un objeto de transposición de datos que devolverá los resultados de las operaciones a la representación original.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, bottlenecks.Size(), units_count * variables, window, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

En este punto finalizaremos el método, retornando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

Al mismo tiempo, concluimos el análisis de los algoritmos para construir los métodos de nuestra visión de la organización del módulo Adaptive Bottlenecks. Como hemos mencionado anteriormente, las operaciones de pasada directa y inversa se realizan por los medios heredados de la clase padre. Encontrará el código completo de este objeto y todos sus métodos en el archivo adjunto.

Arquitectura de los modelos

Hoy hemos decidido no combinar todo el framework DADA en un único objeto. En su lugar, tomaremos soluciones ya probadas de nuestra biblioteca, les añadiremos el módulo Adaptive Bottlenecks creado anteriormente, y construiremos la arquitectura lineal flexible del modelo entrenado a partir de todo esto.

Este enfoque nos ofrecerá mucha más libertad. En primer lugar, hace que el sistema sea más flexible: podemos sustituir u optimizar fácilmente módulos individuales sin reescribir todo el código. En segundo lugar, nos "dejará las manos libres" en cuanto a la elección de la arquitectura del codificador y el descodificador. Ahora no tendremos límites estrictos y podremos experimentar, adaptar el modelo a tareas específicas y buscar configuraciones óptimas.

Sí, esta modularidad hace que el proceso de descripción del modelo resulte un poco más complicado, pero es un precio razonable a pagar por la flexibilidad y adaptabilidad del modelo.

En este experimento, entrenaremos tres modelos a la vez, cada uno de los cuales desempeñará un papel clave en el marco general de análisis y toma de decisiones. Este planteamiento permitirá crear un sistema inteligente multinivel capaz de analizar datos, adaptarse a los cambios en la dinámica del mercado, prever nuevos movimientos de precios y ajustar la estrategia basándose en un complejo análisis de datos.

El primer modelo será un Codificador del estado del entorno construido sobre la arquitectura del framework DADA con un decodificador de estado normal. Su entrenamiento se basará en los principios de un autoencoder clásico, cuya principal tarea consistirá en recuperar los datos de origen del espacio latente con una pérdida mínima. Esto nos permitirá entrenar al sistema para que encuentre la compresión de datos más informativa que conserve todas las características significativas del entorno. Dicho mecanismo permitirá no solo reducir la cantidad de información, sino también revelar dependencias ocultas en los datos analizados, lo que resulta sumamente importante para construir un modelo analítico de gran precisión.

El segundo componente clave del sistema será el Actor, que sustituirá al descodificador de anomalías presente en la arquitectura original del framework DADA. Este módulo desempeñará la función de interacción activa con el entorno del mercado, ya que su objetivo principal consistirá en identificar tendencias estables, reconocer puntos de posible inversión de la tendencia y tomar decisiones encaminadas a optimizar la estrategia comercial.

El Actor analizará los datos de origen multidimensionales, reconocerá los patrones recurrentes y la dinámica de los estados cambiantes del mercado y, a continuación, generará señales comerciales basadas en los patrones identificados. Esto hace que el sistema no sea solo analítico, sino adaptativo, capaz de analizar los datos y adaptarse a los cambios, encontrando los momentos óptimos para entrar o salir del mercado.

Sin embargo, incluso con un potente mecanismo de análisis y generación de señales, la cuestión de la precisión de las previsiones sigue resultando importante. Y aquí es donde entra en juego el tercer modelo, cuya principal tarea consistirá en estimar la dirección más probable del movimiento ulterior de los precios. Este componente del sistema complementa la labor del Actor y actuará como un filtro adicional para las soluciones comerciales.

La arquitectura de todos los modelos se describe en el método CreateDescriptions. En los parámetros de este método transmitiremos los 3 punteros a los búferes de datos dinámicos en los que formaremos la descripción de la solución arquitectónica de los modelos entrenados.

bool CreateDescriptions(CArrayObj *&encoder, CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

En el cuerpo del método comprobaremos directamente la relevancia de los punteros obtenidos y, si es necesario, crearemos nuevas instancias de objetos.

En el primer paso, formaremos una descripción de la arquitectura del Codificador de estados del entorno. Como no resulta difícil adivinar, este modelo recibirá como entrada una descripción tensorial del estado analizado del entorno. Para registrar los datos iniciales, crearemos una capa totalmente conectada de tamaño suficiente.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

En la entrada del modelo, tenemos previsto introducir los datos de origen "brutos" recibidos del terminal. Obviamente, las distintas variables de la descripción multimodal del estado del entorno pertenecen a distribuciones diferentes. Y esto dificulta en gran medida su análisis. A continuación vendrá la capa de normalización por lotes, que normalizará los datos en una forma comparable.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Luego los autores del framework DADA sugieren utilizar el módulo de parcheo y enmascaramiento. Para enmascarar aleatoriamente el 20% de los datos analizados usaremos una capa Dropout.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDropoutOCL;
   descr.count = prev_count;
   descr.probability = 0.2f;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Los autores del framework DADA realizan el parcheado de datos dentro de secuencias unitarias. En nuestro caso, para crear las condiciones óptimas para procesar secuencias unitarias, deberemos transponer los datos.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.window = BarDescr;
   prev_count = descr.count = HistoryBars;
   descr.activation = SoftPlus;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y ahora solo tendremos que utilizar la capa convolucional para realizar el procesamiento independiente de segmentos de un tamaño determinado. En este caso, utilizaremos 2 capas convolucionales consecutivas que realizarán la codificación paralela de segmentos no solapados y actuarán simultáneamente como codificador de nuestro modelo de codificación del estado del entorno.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.window = HistoryBars / Segments;
   prev_count = descr.count = (HistoryBars + descr.window - 1) / descr.window;
   descr.step = descr.window;
   descr.layers = BarDescr;
   descr.activation = SoftPlus;
   int prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize;
   descr.layers = BarDescr;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A esto le seguirá el módulo Adaptive Bottlenecks, en el que creamos 15 pequeños autocodificadores con un estado latente múltiplo de 8. Para codificar los datos de cada segmento, utilizaremos los 3 autocodificadores que mejor encajen.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAdaBN;
   descr.window = prev_wout;
   descr.count = prev_count;
   descr.window_out = 256;
   descr.step = 3; // Top K
   descr.layers = BarDescr; // Variables
     {
      int temp[15];
      for(uint i = 0; i < temp.Size(); i++)
         temp[i] = int(i + 1) * 8;
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Para recuperar los datos de los segmentos analizados, utilizaremos un decodificador cuyo papel será desempeñado por 2 capas convolucionales consecutivas, de forma similar al codificador del modelo.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize / 2;
   descr.activation = SoftPlus;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = HistoryBars / Segments;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Obsérvese que estamos usando la tangente hiperbólica como función de activación en la salida del descodificador. Y esto no es casualidad. Después de todo, el modelo, tras la capa de normalización por lotes, trabajará con datos normalizados cuya varianza se aproximará a "1" con media cero. Usando la regla de los 3 sigmas, algo más del 68% de los datos distribuidos normalmente se sitúan dentro del intervalo ± una desviación típica de la media. Con una desviación típica igual a "1", obtendremos un intervalo de [-1, 1]. En este rango se encuentra el rango de valores de la tangente hiperbólica. Así, a la salida del descodificador obtendremos los valores en el rango más probable, excluyendo los valores atípicos.

A continuación, para comprobar la calidad de la recuperación de los datos analizados, tendremos que comparar los resultados del descodificador con los datos analizados. Sin embargo, conviene recordar que, para procesar con mayor comodidad las secuencias unitarias, hemos transpuesto los datos. Así que los devolveremos a la representación original por transposición inversa.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y retornaremos los valores obtenidos a la distribución de los datos de origen.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = HistoryBars * BarDescr;
   descr.layers = 1;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

El rendimiento de los otros dos modelos se basa en el análisis del estado latente de nuestro codificador de estados del entorno generado a la salida del módulo Adaptive Bottlenecks. Por consiguiente, almacenaremos los parámetros de este módulo en una variable local.

//--- Latent
   CLayerDescription *latent = encoder.At(LatentLayer);
   if(!latent)
      return false;

El siguiente paso consistirá en crear la descripción de la arquitectura del Actor. Se espera que el Actor analice el entorno en el contexto del balance actual y las posiciones abiertas y, a continuación, genere la operación más óptima. Para organizar este proceso, prevemos introducir en la entrada del modelo un vector de descripción del estado de la cuenta. Para escribir los datos, crearemos una capa totalmente conectada de tamaño suficiente.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

También someteremos los datos obtenidos a normalización.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Luego aplicaremos una capa de concatenación que combinará dos grupos de datos: la información del estado de la cuenta y una representación concatenada del entorno derivada del estado latente del Codificador. Esto permitirá al modelo considerar tanto los resultados financieros como las características generalizadas del entorno a la hora de tomar decisiones.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = latent.count * latent.window * latent.layers;
   descr.batch = 1e4;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Le seguirá un módulo de toma de decisiones compuesto por 3 capas totalmente conectadas. Este módulo procesará los datos fusionados, extrayendo patrones clave y generando la solución final del modelo.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SIGMOID;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Este último modelo de predicción de las probabilidades de los próximos movimientos de precios ha sido dotado de la arquitectura más sencilla. Dentro de este modelo está previsto analizar solo una representación concisa del estado del entorno. Para obtener los datos de origen, crearemos una capa completamente conectada a partir de los datos de estado latente del Codificador.

   probability.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = latent.count * latent.window * latent.layers;
   descr.activation = latent.activation;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación vendrá un módulo de decisión de 3 capas totalmente conectadas.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions / 3;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

Los resultados del análisis se trasladarán al área de valores de probabilidad mediante la función SoftMax.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   prev_count = descr.count = prev_count;
   descr.step = 1;
   descr.activation = None;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

En el apéndice del artículo se ofrece una descripción completa de la arquitectura de los modelos.

Entrenamiento de los modelos

Tras describir la arquitectura de los modelos, pasaremos a la siguiente etapa, su entrenamiento, cuyo algoritmo se implementará en el asesor experto "...\DADA\Study.mq5". Deberemos implementar el entrenamiento paralelo de 3 modelos a la vez, lo cual requiere algunas modificaciones en el algoritmo de este asesor experto. En el marco de este artículo, no nos detendremos en una revisión detallada del código de todo el EA. Analizaremos únicamente el método de entrenamiento directo de los modelos Train.

En el cuerpo del método, primero haremos un poco de trabajo preparatorio, concretamente, declararemos algunas variables locales.

void Train(void)
  {
//---
   vector<float> probability = vector<float>::Full(Buffer.Size(), 1.0f / Buffer.Size());
//---
   vector<float> result, target, state;
   matrix<float> fstate = matrix<float>::Zeros(1, NForecast * BarDescr);
   bool Stop = false;
//---
   uint ticks = GetTickCount();

El entrenamiento directo de los modelos se realizará dentro del sistema de ciclos. El ciclo exterior iterará los paquetes de entrenamiento. Aquí, para cada paquete, mostraremos aleatoriamente una trayectoria del búfer de reproducción de experiencias, así como el estado de inicio del entrenamiento en la trayectoria seleccionada.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch)
     {
      int tr = SampleTrajectory(probability);
      int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - Batch));
      if(start <= 0)
        {
         iter -= Batch;
         continue;
        }
      if(!Encoder.Clear() ||
         !Actor.Clear())
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }
      result = vector<float>::Zeros(NActions);

Y como parte del ciclo anidado, el entrenamiento del modelo se realizará en estados sucesivos de un solo paquete.

Aquí cabe señalar que los modelos desarrollados en el marco de este artículo no contienen bloques de recurrencia. Normalmente, estos modelos se entrenan con estados completamente aleatorios extraídos del búfer de reproducción de experiencias. No obstante, en este caso, el aprendizaje tendrá lugar en trayectorias "casi perfectas" cuyas acciones son generadas directamente por el algoritmo de este EA basándose en la información disponible sobre los estados de los entornos posteriores. Al fin y al cabo, a diferencia del entrenamiento de modelos en tiempo real, cuando trabajamos con el búfer de reproducción de experiencias disponemos de datos sobre los estados de los entornos posteriores para todas las entradas guardadas excepto las más recientes. Esto nos permitirá guiar con mayor precisión el proceso de aprendizaje.

Pero también existe la otra "cara de la moneda". En este caso, no tendremos información sobre las posiciones abiertas. Y es importante que entrenemos el modelo no solo para abrir posiciones, sino también para acompañarlas con la búsqueda del punto de salida óptimo. Por consiguiente, formaremos pequeños paquetes de entrenamiento con la formación de posiciones "óptimas" durante entrenamiento.

      for(int i = start; i < MathMin(Buffer[tr].Total, start + Batch); i++)
        {
         if(!state.Assign(Buffer[tr].States[i].state) ||
            MathAbs(state).Sum() == 0 ||
            !bState.AssignArray(state))
           {
            iter -= Batch + start - i;
            break;
           }
         //---
         bTime.Clear();
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bTime.GetIndex() >= 0)
            bTime.BufferWrite();
         //--- Account
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
         float profit = float(bState[0] / _Point * (result[0] - result[3]));
         bAccount.Clear();
         bAccount.Add(1);
         bAccount.Add((PrevEquity + profit) / PrevEquity);
         bAccount.Add(profit / PrevEquity);
         bAccount.Add(MathMax(result[0] - result[3], 0));
         bAccount.Add(MathMax(result[3] - result[0], 0));
         bAccount.Add((bAccount[3] > 0 ? profit / PrevEquity : 0));
         bAccount.Add((bAccount[4] > 0 ? profit / PrevEquity : 0));
         bAccount.Add(0);
         bAccount.AddArray(GetPointer(bTime));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

En el cuerpo del ciclo, primero recuperaremos la información del búfer de reproducción de datos y generaremos los objetos de datos de origen para los modelos entrenados. Después, llamaremos a los métodos de pasada directa del Codificador del estado del entorno.

         //--- Feed Forward
         if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Y después, llamaremos a métodos similares de los otros dos modelos, pasándoles como entrada el puntero al objeto de Coficador del estado del entrono.

         if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }
         if(!Probability.feedForward(GetPointer(Encoder), LatentLayer, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

A continuación vendrá el proceso de entrenamiento de la "operación comercial óptima". Este proceso se trasladó íntegramente del artículo sobre el aprendizaje multitarea. Su descripción detallada puede encontrarse en el enlace, y la omitiremos aquí.

Tras preparar los valores objetivo, procederemos a optimizar los parámetros de los modelos para minimizar las desviaciones respecto a los valores objetivo. El primero que se entrenará es el Codificador del entorno. Como tensor de valores objetivo, le pasaremos el vector de descripción del estado del entorno analizado, que también se ha utilizado en la pasada directa.

         //--- State Encoder
         if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL, NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

En segundo lugar, entrenaremos al Actor minimizando la desviación de la "operación comercial óptima".

         //--- Actor Policy
         if(!Actor.backProp(GetPointer(bActions), (CNet*)GetPointer(Encoder), LatentLayer)
            || !Encoder.backPropGradient((CBufferFloat*)NULL, (CBufferFloat*)NULL, LatentLayer, true)
            )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Para entrenar el tercer modelo, determinaremos la dirección del próximo movimiento del precio según el color de la siguiente barra.

         target = vector<float>::Zeros(NActions / 3);
         if(fstate[0, 0] > 0)
            target[0] = 1;
         else
            if(fstate[0, 0] < 0)
               target[1] = 1;
         if(!Result.AssignArray(target) ||
            !Probability.backProp(Result, (CBufferFloat*)NULL)
            || !Encoder.backPropGradient((CBufferFloat*)NULL, (CBufferFloat*)NULL, LatentLayer)
           )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Ahora solo quedará informar al usuario del progreso del proceso de aprendizaje y pasar a la siguiente iteración del sistema de ciclos.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + i - start) * 100.0 / (Iterations);
            string str = StringFormat("%-13s %6.2f%% -> Error %15.8f\n", "Encoder",
                                         percent, Encoder.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent,
                                                     Actor.getRecentAverageError());
            str += StringFormat("%-13s %6.2f%% -> Error %15.8f\n", "Probability", 
                                      percent, Probability.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Una vez completadas con éxito todas las iteraciones de entrenamiento del modelo, registraremos los resultados e iniciaremos el proceso de finalización del EA.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Probability", Probability.getRecentAverageError());
   ExpertRemove();
//---
  }

El código completo de este asesor experto se presenta en el archivo adjunto y estará disponible para el autoaprendizaje. Además, en el anexo se presentan los programas de interacción con el entorno y de prueba de los modelos entrenados.

Simulación

Tras un extenso trabajo de aplicación de los enfoques propuestos por los autores del framework DADA usando herramientas MQL5 y su integración en modelos entrenados, llega la fase clave: la comprobación de la eficacia de las soluciones aplicadas con datos históricos reales. Esto nos permitirá evaluar la viabilidad de su uso en condiciones reales de mercado.

Para entrenar el modelo, generaremos una muestra de pasadas aleatorias en el simulador de estrategias de MetaTrader 5 con los datos históricos del par de divisas EURUSD y el marco temporal M1 para todo el año 2024. Los datos históricos se recopilarán utilizando parámetros de indicadores normalizados, lo que garantizará la pureza del experimento y excluirá la influencia de factores extraños.

Los modelos entrenados se probarán con los datos históricos de enero-febrero de 2025. Al mismo tiempo, todos los parámetros del experimento se mantendrán sin cambios, lo que nos permitirá obtener una evaluación objetiva de la política de comportamiento del Actor entrenado. La comprobación del rendimiento del modelo con los datos que no se han utilizado durante entrenamiento supone un paso importante en su validación, ya que esto demuestra la calidad del rendimiento del modelo en condiciones cercanas al mundo real.

Ahora le presentamos los resultados de las pruebas.

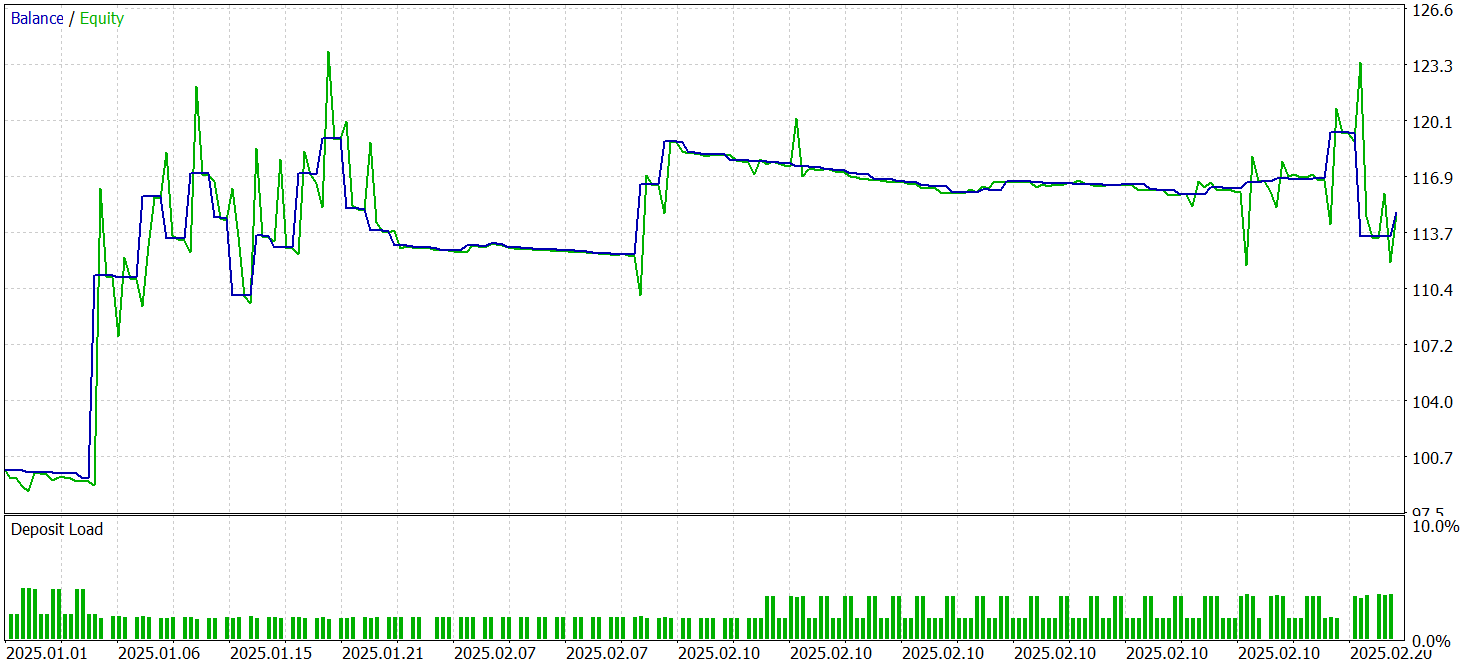
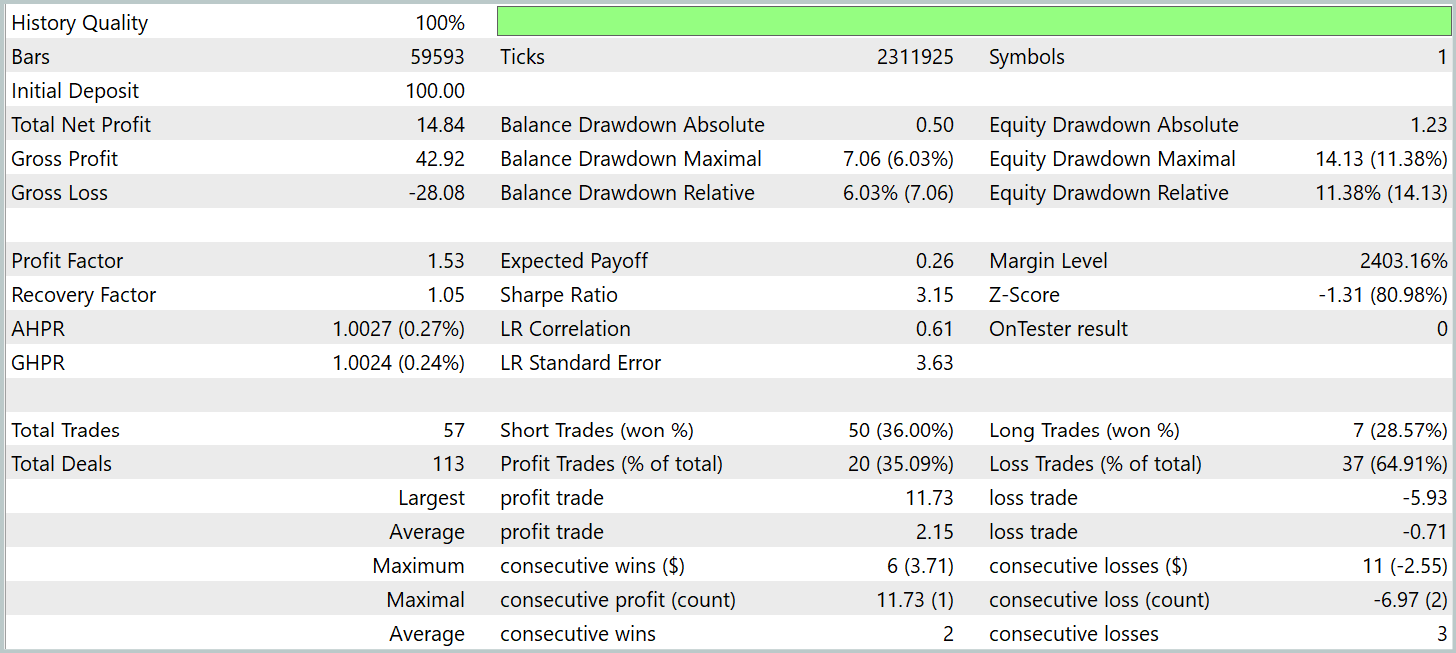
Durante el periodo de prueba, el modelo ha realizado 57 transacciones comerciales, más del 35% de las cuales se han cerrado con beneficios. No obstante, el hecho de que de la posición media rentable supere en tres veces el indicador similar de las transacciones deficitarias ha permitido al modelo obtener beneficios durante el periodo de prueba y fijar el factor de beneficio al nivel de 1,53.

Sin embargo, debemos considerar que el beneficio se obtiene en la primera quincena de enero. Durante el resto del periodo, el gráfico de balance ha fluctuado en un margen estrecho. Esto puede indicar la necesidad de explorar opciones para optimizar el rendimiento del modelo.

Aquí cabe señalar que durante la implementación hemos realizado una serie de cambios de diseño en la arquitectura del framework DADA. Por consiguiente, los resultados obtenidos solo resultan relevantes para esta aplicación.

Conclusión

En este artículo nos hemos familiarizado con el framework DADA, que ofrece un enfoque innovador combinando un mecanismo de cuello de botella adaptativo y dos descodificadores paralelos para un análisis más preciso de las series temporales. Una ventaja clave de este método es su capacidad para adaptarse dinámicamente a diferentes estructuras de datos sin necesidad de adaptación previa.

Hemos trabajado mucho para implementar usando MQL5 nuestra propia visión de los enfoques propuestos por los autores del framework. Luego hemos integrado las soluciones aplicadas en los modelos, tras lo cual hemos realizado el entrenamiento con datos históricos reales. Durante las pruebas, los modelos entrenados han sido capaces de mostrar rentabilidad. Sin embargo, el gráfico del balance no ha mostrado una tendencia al alza sostenida, lo cual indica la necesidad de seguir optimizando la estrategia.

Enlaces

• Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL