Redes neuronales en el trading: Clusterización doble de series temporales (DUET)

Introducción

Las series temporales multivariantes suponen secuencias de datos en las que cada marcador temporal contiene varias variables interrelacionadas que caracterizan procesos complejos. Se usan ampliamente en el análisis económico, la gestión de riesgos y otras áreas que requieren la predicción de datos multivariantes. A diferencia de las series temporales univariantes, las series temporales multivariantes permiten considerar las correlaciones entre variables, lo que hace posible realizar previsiones más precisas.

En los mercados financieros, el análisis multivariante de series temporales se usa para predecir los precios de los activos, estimar la volatilidad, identificar tendencias y desarrollar estrategias comerciales. Por ejemplo, a la hora de predecir las cotizaciones bursátiles se consideran factores como el volumen comercial, los tipos de interés, los indicadores macroeconómicos y las noticias. Todos estos parámetros están interrelacionados, y analizarlos conjuntamente puede revelar patrones que no están disponibles al considerar cada variable por separado.

Un reto clave en el procesamiento multivariante de series temporales es la construcción de métodos capaces de detectar dependencias temporales y entre canales. No obstante, en la práctica surgen dificultades debido a la variabilidad de los datos. Durante los periodos de crisis económica, las estructuras de correlación entre activos cambian, lo cual dificulta el uso de los modelos tradicionales.

Los métodos de procesamiento de datos existentes pueden dividirse en tres categorías. El primer enfoque consiste en analizar independientemente cada canal, pero ignora las interrelaciones entre variables. El segundo consiste en combinar todos los canales, pero esto puede dar lugar a la inclusión de información innecesaria y reducir la precisión. El tercero es la clusterización de variables, pero esta limita la flexibilidad del modelo.

Para abordar los problemas anteriores, los autores del artículo "DUET: Dual Clustering Enhanced Multivariate Time Series Forecasting" proponen el método DUET que combina dos tipos de clusterización: temporal y por canales. La clusterización temporal (TCM) agrupa los datos en función de características similares y permite a los modelos adaptarse a los cambios a lo largo del tiempo. A la hora de analizar los mercados financieros, permite considerar las distintas fases de los ciclos económicos. La clusterización de canales (CCM) identifica las variables clave, eliminando el ruido y mejorando la precisión de la predicción. Así, identifica las relaciones estables entre activos, lo que resulta especialmente importante para construir carteras de inversión diversificadas.

Después, los resultados se combinan mediante el módulo de fusión Fusion Module (FM), que sincroniza la información sobre patrones temporales y las dependencias entre canales. Este planteamiento permite predecir con mayor exactitud el comportamiento de sistemas complejos como los mercados financieros. Los experimentos realizados por los autores del framework han demostrado que DUET supera a los métodos existentes, ofreciendo predicciones más precisas. Este tiene en cuenta los patrones temporales heterogéneos y la dinámica entre canales adaptándose a la variabilidad de los datos.

El algoritmo DUET

La arquitectura del framework DUET supone un enfoque innovador en la previsión de series temporales multivariantes que utiliza la clusterización dual de datos de origen en las dimensiones temporal y de canal. Esto mejora la calidad del rendimiento del modelo y hace que sus resultados resulten más interpretables. El planteamiento puede compararse con el trabajo de un analista experimentado que descompone un sistema de datos complejo en bloques individuales, analizándolos primero de forma individual y luego colectivamente para obtener una visión más detallada. El framework DUET incluye varios módulos clave, cada uno con una función especializada en el proceso de análisis de datos:

1. Normalización de datos de origen (Instance Normalization).
2. Módulo de clusterización temporal (Temporal Clustering Module — TCM).
3. Módulo de clusterización de canales (Channel Clustering Module — CCM).
4. Módulo de fusión de información (Fusion Module — FM).
5. Módulo de predicción (Prediction Module).

La normalización de los datos de origen elimina los valores atípicos y suaviza las fluctuaciones bruscas, lo que hace que el modelo resulte más robusto frente a las diferencias entre las muestras de entrenamiento y de prueba. Esto es especialmente importante en el análisis de datos financieros, donde el ruido de alta frecuencia puede ocultar tendencias significativas. La normalización también ayuda a igualar las características estadísticas de las secuencias temporales unitarias procedentes de distintas fuentes, reduciendo así la influencia de los valores anómalos.

El módulo de clusterización temporal Temporal Clustering Module (TCM) analiza las dependencias temporales y agrupa las secuencias en clústeres, de forma similar a como los analistas financieros clasifican los activos en función de su volatilidad, liquidez y características históricas. El MTC se basa en una arquitectura de múltiples codificadores paralelos (Mixture of Experts — MoE), que permite seleccionar dinámicamente el más apropiado para cada segmento analizado según la clusterización previamente realizada de las series temporales. De este modo se logra una representación precisa de las secuencias temporales, ya que los distintos grupos de datos pueden requerir métodos de procesamiento únicos. La MoE cambia adaptativamente entre codificadores, lo que permite al modelo manejar con eficacia series temporales de distinta naturaleza, incluidos datos bursátiles de alta frecuencia.

Los codificadores analizan series temporales representadas como características latentes que se descomponen en tendencias a largo y corto plazo. Esto permite identificar patrones ocultos que mejoran la previsión de futuras variaciones de precio en los mercados financieros.

El módulo de clusterización de canales Channel Clustering Module (CCM) realiza la clusterización de canales utilizando las características de frecuencia de las señales. Este módulo estima las correlaciones entre canales, identificando las dependencias clave y excluyendo los componentes redundantes o insignificantes. Al igual que un analista financiero que selecciona indicadores macroeconómicos y técnicos significativos para excluir las fluctuaciones aleatorias del mercado, el CCM ayuda a destacar las señales más informativas.

El análisis de la distancia entre los vectores de amplitud de las características frecuenciales de los canales permite determinar las señales correlacionadas y excluir los fenómenos de ruido. Esto resulta especialmente útil en los mercados financieros, donde las dependencias ocultas entre activos pueden utilizarse para construir estrategias de arbitraje o identificar riesgos sistemáticos.

El módulo de fusión Fusion Module (FM) combina representaciones temporales y de canal mediante un mecanismo de atención enmascarada. Este proceso es similar al análisis de las complejas relaciones entre los distintos factores del mercado, en el que el analista sintetiza la información procedente de distintas fuentes para obtener una imagen holística y global. El FM identifica los clústeres más significativos y filtra las señales irrelevantes, mejorando la precisión de la predicción. El uso del mecanismo de atención enmascarada nos permite cambiar dinámicamente la importancia de los distintos componentes de los datos, lo cual hace que el procesamiento sea más adaptativo. Esto resulta fundamental en las aplicaciones financieras, donde la estructura de las dependencias entre activos puede cambiar debido a los eventos macroeconómicos.

En el último paso, el módulo de predicción utiliza las características agregadas para pronosticar los valores futuros de las series temporales. Este proceso puede compararse con el trabajo de un inversor profesional que realiza predicciones fundadas sobre los movimientos futuros de los precios basándose en datos históricos del mercado. El módulo de predicción usa técnicas de redes neuronales para tener en cuenta dependencias no lineales complejas y adaptarse a posibles cambios estructurales en los datos. Las predicciones finales se someten a una normalización inversa, lo que permite interpretarlas a la escala de los datos de origen.

Mediante la aplicación de técnicas avanzadas de aprendizaje automático como el mecanismo de atención enmascarada, el análisis de características de frecuencia y la clusterización de rasgos latentes, DUET ofrece predicciones muy precisas e interpretables. El algoritmo, ayuda a encontrar patrones ocultos en secuencias temporales complejas y a aplicar estos conocimientos para optimizar las estrategias comerciales cuando los enfoques tradicionales no son suficientemente eficaces. Frente a los métodos tradicionales, que requieren un importante ajuste manual y la intervención de expertos, DUET detecta automáticamente a las características estructurales de los datos en tiempo real, adaptándose a ellas. Esto lo hace especialmente útil para analizar series temporales de alta frecuencia y trabajar en un entorno de mercado que muda rápidamente.

A continuación le mostramos la visualización del framework DUET realizada por el autor.

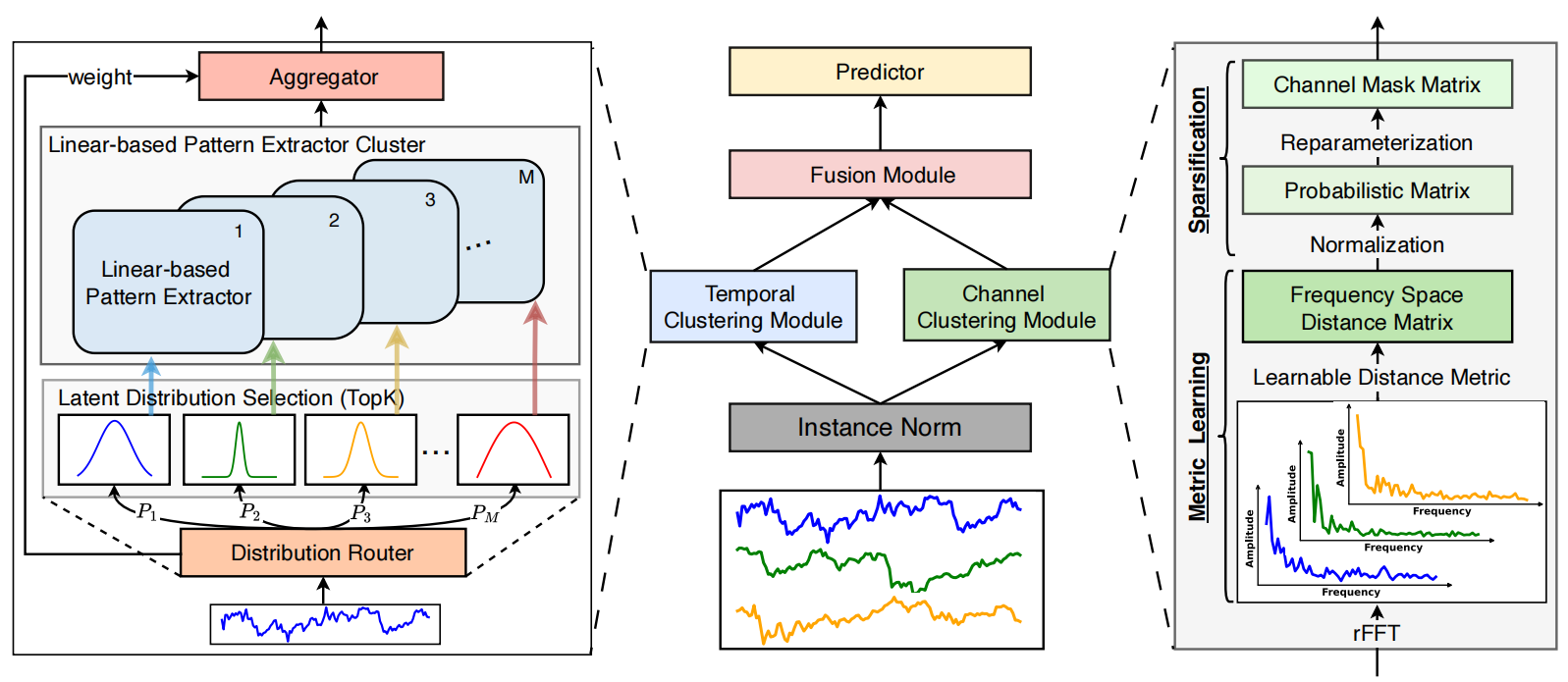
Aplicación usando las propiedades MQL5

Tras una revisión detallada de los aspectos teóricos del framework DUET, pasaremos a la parte práctica de nuestro trabajo, en la que implementaremos nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5.

La arquitectura modular de DUET facilita el desarrollo paso a paso: cada bloque funcional puede analizar como un elemento independiente del sistema. La separación en módulos autónomos simplifica la depuración, las pruebas y la posterior optimización. Y comenzaremos nuestro trabajo con la construcción del módulo de clusterización temporal.

Módulo de clusterización temporal

Como ya hemos mencionado, el módulo de clusterización temporal incluye varios codificadores que funcionan en paralelo. Como parte de este artículo, crearemos la arquitectura de codificador más simple posible a partir de dos capas consecutivas completamente conectadas con la creación de no linealidad entre ellas mediante una función de activación. Sin embargo, debemos considerar que cada codificador procesa segmentos separados e independientes utilizando sus propios parámetros entrenados. Y para organizar este tipo de trabajo utilizaremos capas de convolución. Suministrándole una secuencia completa de datos de entrada, fijaremos el tamaño de la ventana analizada y un paso igual al tamaño del segmento. Como resultado, los parámetros de la capa convolucional actuarán como una capa codificadora completamente conectada, garantizando que todos los segmentos de la secuencia se procesen en paralelo. Y para aumentar el número de codificadores que trabajan en paralelo, bastará con multiplicar el número de filtros de la capa convolucional.

Nos hemos decidido por la organización del funcionamiento en paralelo de los codificadores. Sin embargo, tenga en cuenta que los autores del framework DUET sugieren utilizar solo los codificadores más relevantes. Se supone que las series temporales siguen una distribución normal latente. Como ya sabrá, una distribución normal se caracteriza por la media y la varianza. Para seleccionar las k distribuciones latentes más probables, los autores del framework usan el método "Noisy Gating", que puede representarse como:

La adición de ruido con una distribución (ε) normal estabiliza el entrenamiento, mientras que Softplus mantiene la varianza positiva.

A continuación, elegimos las k distribuciones latentes más probables y calculamos sus pesos usando la función SoftMax. Así, las series temporales pertenecientes a las mismas k distribuciones latentes más probables son procesadas por un grupo común de codificadores. Multiplicando la máscara resultante por los resultados del codificador se obtendrá un resultado ponderado y se eliminará la influencia de los filtros que sean irrelevantes.

Una vez decidida la solución arquitectónica, podemos ponernos manos a la obra. Y primero implementamos el algoritmo para seleccionar los k codificadores más relevantes. Para ello, organizaremos la parametrización de los parámetros de distribución de los segmentos individuales mediante una capa convolucional. Pero el algoritmo para seleccionar los k codificadores más relevantes se implementará en el lado del contexto OpenCL. Para ello, crearemos el kernel TopKgates.

__kernel void TopKgates(__global const float *inputs,
                        __global const float *noises,
                        __global float *gates,
                        const uint k)
  {
   size_t idx = get_local_id(0);
   size_t var = get_global_id(1);
   size_t window = get_local_size(0);
   size_t vars = get_global_size(1);

En los parámetros del kernel obtendremos los punteros a 3 búferes de datos (datos de origen, ruido, resultados) y el número de elementos a muestrear.

En el cuerpo del kernel, primero identificaremos el flujo actual en el espacio de tareas, como es habitual. En este caso, utilizaremos un espacio de tareas bidimensional con agrupación local en la primera dimensión, que combinará flujos pertenecientes al mismo segmento y se corresponderá con el número de codificadores utilizados por el modelo.

A continuación, determinaremos el desplazamiento en los búferes de datos locales.

   const int shift_logit = var * 2 * window + idx;
   const int shift_std = shift_logit + window;
   const int shift_gate = var * window + idx;

Y cargaremos los datos de origen correspondientes.

   float logit = IsNaNOrInf(inputs[shift_logit], MIN_VALUE);
   float noise = IsNaNOrInf(noises[shift_gate], 0);
   if(noise != 0)
     {
      noise *= Activation(inputs[shift_std], 3);
      logit += IsNaNOrInf(noise, 0);
     }

Si el ruido no es "0", ajustaremos el valor de la variable logit para tener en cuenta la varianza y el ruido.

A continuación, tendremos que determinar los k valores logit máximos dentro de un mismo grupo de trabajo. Para ello, crearemos un array en memoria local como medio de intercambio de datos entre los flujos del grupo de trabajo y declararemos las variables locales auxiliares.

   __local float temp[LOCAL_ARRAY_SIZE];
//---
   const uint ls = min((uint)window, (uint)LOCAL_ARRAY_SIZE);
   uint bigger = 0;
   float max_logit = logit;

A continuación, declararemos un ciclo para enumerar los elementos del grupo de trabajo con un paso igual al tamaño del array local.

//--- Top K
#pragma unroll
   for(int i = 0; i < window; i += ls)
     {
      if(idx >= i && idx < (i + ls))
         temp[idx % ls] = logit;
      barrier(CLK_LOCAL_MEM_FENCE);

En el cuerpo del ciclo, los elementos de la ventana actual guardan sus valores en un array local con sincronización posterior obligatoria de los flujos del grupo de trabajo.

A continuación, crearemos un ciclo anidado, dentro de cuyas iteraciones cada flujo contará cuántos elementos del array local son mayores que el logit del flujo actual.

      for(int i1 = 0; (i1 < min((int)ls,(int)(window-i)) && bigger <= k); i1++)
        {
         if(temp[i1] > logit)
            bigger++;
         if(temp[i1] > max_logit)
            max_logit = temp[i1];
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Paralelamente, buscaremos el valor máximo dentro de un grupo local.

Una vez ejecutadas todas las iteraciones del ciclo anidado, sincronizaremos de nuevo los flujos del grupo de trabajo y solo entonces pasaremos a la siguiente iteración del ciclo exterior.

Creo que es obvio que solo k flujos con valores logit máximos no han alcanzado el umbral de superación de elementos. Guardaremos sus valores en el búfer de resultados.

   if(bigger <= k)
      gates[shift_gate] = logit - max_logit;
   else
      gates[shift_gate] = MIN_VALUE;
  }

En el resto de casos, escribiremos la constante del valor mínimo en el búfer de resultados, lo que dará un coeficiente de influencia cero en el proceso de aplicación de la función SoftMax.

El kernel presentado anteriormente organizará la pasada directa del proceso de selección de los k codificadores más relevantes en cada caso. Sin embargo, para construir un modelo verdaderamente adaptativo, necesitaremos organizar el proceso de entrenamiento de la selección del codificador. Por supuesto, no utilizaremos los parámetros entrenados dentro del kernel presentado anteriormente. No obstante, se aplicarán para generar los datos de origen utilizados. Por lo tanto, solo tendremos que pasar el gradiente de error a la capa de datos de origen. Este proceso se organizará en el kernel TopKgatesGrad, en cuya estructura de parámetros añadiremos los punteros a los búferes de gradientes de error correspondientes.

__kernel void TopKgatesGrad(__global const float *inputs,
                            __global float *grad_inputs,
                            __global const float *noises,
                            __global const float *gates,
                            __global float *grad_gates)
  {
   size_t idx = get_global_id(0);
   size_t var = get_global_id(1);
   size_t window = get_global_size(0);
   size_t vars = get_global_size(1);

En el cuerpo del kernel, identificaremos el flujo actual de operaciones en el espacio bidimensional de tareas. La estructura del espacio de tareas se tomará prestada del kernel de pasada directa, solo que ahora no agruparemos los flujos en grupos de trabajo.

A continuación, determinaremos el desplazamiento en los búferes de datos globales, de forma similar al algoritmo de pasada directa.

   const int shift_logit = var * 2 * window + idx;
   const int shift_std = shift_logit + window;
   const int shift_gate = var * window + idx;

Y lo primero que haremos es cargar el resultado de la pasada directa del flujo correspondiente.

   const float gate = IsNaNOrInf(gates[shift_gate], MIN_VALUE);
   if(gate <= MIN_VALUE)
     {
      grad_inputs[shift_logit] = 0;
      grad_inputs[shift_std] = 0;
      return;
     }

Como no resulta difícil de adivinar, si el valor obtenido es igual a la constante mínima, podremos guardar directamente los valores nulos en el búfer de gradiente de los datos de origen. Este valor equivaldrá a excluir el codificador de otras operaciones.

En caso contrario, cargaremos el valor del gradiente de error en el nivel de resultado y lo pasaremos inmediatamente al elemento correspondiente del búfer de gradiente de datos de origen (logit de margen de error).

   float grad = IsNaNOrInf(grad_gates[shift_gate], 0);
   grad_inputs[shift_logit] = grad;

Obviamente, no asignaremos un gradiente de error al nivel de ruido. Sin embargo, nos quedará por determinar el valor del error en el nivel de varianza. Como ya sabrá, durante la pasada directa la varianza se ha multiplicado por el ruido, así que el siguiente paso consistirá en extraer el valor del ruido.

   float noise = IsNaNOrInf(noises[shift_gate], 0);
   if(noise == 0)
     {
      grad_inputs[shift_std] = 0;
      return;
     }

Claro está, cuando el ruido sea "0", la varianza no participará en las operaciones de pasada directa. Por consiguiente, en tal caso, simplemente almacenaremos el gradiente cero sin realizar ninguna otra operación.

Bien, en el último caso, ajustaremos el valor del gradiente de error según el coeficiente de ruido y la derivada de la función de activación.

   grad *= noise;
   grad_inputs[shift_std] = Deactivation(grad, Activation(inputs[shift_std], 3), 3);
  }

Luego guardaremos el resultado obtenido en el búfer de datos global y finalizaremos el kernel.

Encontrará el código completo de los dos kernels anteriores en el artículo adjunto.

La próxima etapa de nuestro trabajo consistirá en organizar este proceso al margen del programa principal. En primer lugar, crearemos el objeto CNeuronTopKGates en el que construiremos un algoritmo para seleccionar los k codificadores más relevantes. Más abajo sumaremos la estructura del nuevo objeto.

class CNeuronTopKGates  :  public CNeuronSoftMaxOCL
  {
protected:
   int               iK;
   CBufferFloat      cbNoise;
   CNeuronConvOCL    cProjection;
   CNeuronBaseOCL    cGates;
   //---
   virtual bool      TopKgates(void);
   virtual bool      TopKgatesGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTopKGates(void) {};
                    ~CNeuronTopKGates(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint gates, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronTopKGates; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual uint      GetGates(void) const { return cProjection.GetFilters() / 2; }
   virtual uint      GetUnits(void) const { return cProjection.GetUnits(); }
  };

En la estructura presentada, vemos que TopKgates y TopKgatesGradient se añaden al conjunto habitual de métodos virtuales redefinidos. Se trata de los métodos-envoltorios de los kernels descritos anteriormente creados en el lado del programa OpenCL. Para crearlos hemos utilizado un algoritmo que ya conocemos, y hoy no nos detendremos en él.

Los pocos objetos internos se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor de la clase. Y la inicialización de todos los objetos declarados y heredados se realizará en el método Init, en cuyos parámetros obtendremos las constantes que nos permitirán interpretar inequívocamente la arquitectura del objeto que se está creando.

bool CNeuronTopKGates::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint units_count, uint gates, uint top_k, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, gates * units_count,
                                                        optimization_type, batch))
      return false;
   SetHeads(units_count);

Las operaciones del método de inicialización comenzarán con una llamada al método homónimo de la clase padre, en el que ya se dispondrá del control mínimo necesario y la inicialización de los objetos heredados.

Tenga en cuenta que en este caso estaremos utilizando el objeto de función SoftMax como clase padre. Esto nos permitirá convertir los resultados de la selección de los k codificadores más relevantes a una representación probabilística sin crear un objeto interno adicional. Para ello, bastará con utilizar la funcionalidad de la clase padre.

Una vez ejecutadas con éxito las operaciones de los métodos de la clase padre, procederemos a la construcción del algoritmo de inicialización de los objetos recién declarados. Aquí inicializaremos primero la capa convolucional de la proyección de los parámetros de distribución de datos de los segmentos analizados.

   if(!cProjection.Init(0, 0, OpenCL, window, window, 2 * gates, units_count, 1, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(None);

En la salida de esta capa, esperamos obtener los valores medios y la varianza de cada uno de los codificadores de nuestro modelo. Como consecuencia, el número de filtros de la capa convolucional será 2 veces el número especificado de codificadores.

Aquí es donde añadiremos un búfer de datos en el que generaremos el ruido.

   if(!cbNoise.BufferInit(Neurons(), 0) ||
      !cbNoise.BufferCreate(OpenCL))
      return false;

Y al final de las operaciones del método, inicializaremos una capa totalmente conectada para registrar los resultados del kernel de pasada directa TopKgates creado anteriormente.

   if(!cGates.Init(0, 1, OpenCL, Neurons(), optimization, iBatch))
      return false;
   cGates.SetActivationFunction(None);
//---
   return true;
  }

A continuación, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Nótese que en este caso no estaremos creando objetos para registrar la distribución de probabilidad de los codificadores Top K. Tenemos previsto convertir los valores logit absolutos al espacio de probabilidad mediante la clase padre. En consecuencia, todos los objetos que sirven a este proceso ya habrán sido creados e inicializados en la clase padre.

El siguiente paso en nuestro trabajo consistirá en construir un método de pasada directa del objeto de selección de los k codificadores más relevantes CNeuronTopKGates::feedForward. En los parámetros de este método, como es habitual, obtendremos el puntero al objeto de los datos de origen, que pasaremos inmediatamente al método homónimo del objeto de generación de indicadores estadísticos de la distribución de los segmentos analizados.

bool CNeuronTopKGates::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cProjection.FeedForward(NeuronOCL))
      return false;

A continuación, observe que los autores del framework DUET sugieren añadir ruido a los valores logit solo durante el entrenamiento. Por lo tanto, comprobaremos el modo del modelo y generaremos ruido si es necesario.

   if(bTrain)
     {
      double random[];
      if(!Math::MathRandomNormal(0, 1, Neurons(), random))
         return false;
      if(!cbNoise.AssignArray(random))
         return false;
      if(!cbNoise.BufferWrite())
         return false;
     }
   else
      if(!cbNoise.Fill(0))
         return false;

De lo contrario, llenaremos el búfer de ruido con valores cero.

Y luego llamaremos al método-envoltorio de selección de los k codificadores más relevantes.

   if(!TopKgates())
      return false;
//---
   return CNeuronSoftMaxOCL::feedForward(cGates.AsObject());
  }

Pasaremos los resultados obtenidos al método homónimo de la clase padre, que nos permitirá convertir los valores absolutos al espacio de probabilidad.

Después retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Como ya habrá notado, el método de pasada directa tiene un algoritmo lineal. En consecuencia, obtendremos el mismo algoritmo lineal para los métodos de pasada inversa. Por lo tanto, le sugiero que los estudie por su cuenta. Encontrará el código completo de este objeto y todos sus métodos en el archivo adjunto al artículo.

En esta fase, construiremos los algoritmos para seleccionar los k codificadores más relevantes tanto en el lado del programa principal como en el contexto OpenCL. Ahora ya podemos construir la arquitectura Mixture of Experts, que estamos implementando como parte del objeto CNeuronMoE. Más abajo sumaremos la estructura del nuevo objeto.

class CNeuronMoE  :  public CNeuronBaseOCL
  {
protected:
   CNeuronTopKGates     cGates;
   CLayer               cExperts;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMoE(void) {};
                    ~CNeuronMoE(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint experts, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMoE; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      TrainMode(bool flag)
     {  bTrain = flag;  cGates.TrainMode(bTrain); }
  };

En la estructura presentada, solo veremos 2 objetos internos. Uno es el objeto creado anteriormente para seleccionar los k codificadores más relevantes, mientras que el segundo será un array dinámico para escribir los punteros a nuestros objetos codificadores. Ambos objetos se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor de la clase. Todo el trabajo de inicialización de los objetos especificados se organizará en el método Init.

En los parámetros del método de inicialización se transmitirán las constantes que dan una idea inequívoca de la arquitectura del objeto creado. En este caso, es posible cambiar la dimensionalidad de los datos a la salida del objeto.

bool CNeuronMoE::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                      uint window, uint window_out, uint units_count,
                      uint experts, uint top_k,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_count, optimization_type, batch))
      return false;

El algoritmo comienza llamando al método homónimo de la clase padre, en el que ya está organizado el proceso de inicialización de los objetos heredados y el punto de control de los datos iniciales.

A continuación, inicializaremos el objeto para seleccionar los codificadores más relevantes.

   int index = 0;
   if(!cGates.Init(0, index, OpenCL, window, units_count, experts, top_k, optimization, iBatch))
      return false;

Y pasaremos a la inicialización directa de los objetos codificadores. En primer lugar, prepararemos un array dinámico y variables locales para almacenar temporalmente punteros a los objetos.

   cExperts.Clear();
   cExperts.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeRCDOCL *transp = NULL;

La primera capa que se creará es la capa convolucional, que actuará como primera capa codificadora. Tenemos previsto alimentar la entrada de este objeto con un tensor de datos fuente relevante para todos los codificadores. El número de filtros de esta capa será igual al producto del tamaño del tensor de resultados de un codificador por su número en el modelo. Este enfoque nos permitirá realizar el cálculo paralelo de los valores de todos los codificadores a la vez.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, window_out * experts, units_count, 1, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

Para crear no linealidad entre las capas del codificador, utilizaremos SoftPlus como función de activación.

A continuación, tendremos que añadir una segunda capa de codificadores. Y, como comprenderá, cada codificador deberá tener su propio conjunto de parámetros. Esa es la oportunidad que tenemos. También podemos usar una capa convolucional. Bastará con especificar el número de codificadores en el parámetro del número de secuencias independientes que se van a analizar. Sin embargo, deberemos considerar que a la salida de la primera capa obtendremos un tensor de dimensionalidad tridimensional { Units, Encoders, Dimension }. Esto no se corresponderá con el algoritmo de la capa convolucional que hemos creado antes.

Para organizar el proceso correcto tendremos que intercambiar las 2 primeras dimensiones. Este trabajo lo realizará la capa de transposición de datos.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_count, experts, window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Ahora podremos inicializar la capa convolucional, que actuará como la segunda capa de nuestros codificadores independientes.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_out, window_out, window_out, units_count, experts, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Y añadiremos una capa de transposición inversa de datos.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, experts, units_count, window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Con esto completaremos el algoritmo de inicialización de los objetos internos. Después devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Una vez finalizado el trabajo de inicialización de objetos, construiremos el algoritmo de pasada directa dentro del método CNeuronMoE::feedForward.

bool CNeuronMoE::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cGates.FeedForward(NeuronOCL))
      return false;

En los parámetros del método obtendremos el puntero al objeto de datos de origen, que pasaremos inmediatamente al método homónimo del objeto de selección de los codificadores más relevantes.

A continuación, trabajaremos con los codificadores. Observe que usan como datos de entrada el mismo objeto que obtuvimos en los parámetros del método. Primero almacenaremos el puntero resultante en una variable local.

   CNeuronBaseOCL *prev = NeuronOCL;
   int total = cExperts.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *neuron = cExperts[i];
      if(!neuron ||
         !neuron.FeedForward(prev))
         return false;
      prev = neuron;
     }

Y organizaremos un ciclo de iteración secuencial de capas codificadoras con llamada a sus métodos de pasada directa.

Una vez ejecutadas todas las iteraciones del ciclo, obtendremos un conjunto completo de resultados de todos los codificadores. Recordemos que previamente hemos obtenido una máscara probabilística de los codificadores más relevantes para cada segmento de los datos de origen. Y ahora, para obtener la suma ponderada para cada segmento de los datos de origen analizados, solo tendremos que multiplicar el vector-cadena de distribución de la probabilidad de la relevancia de los codificadores para un segmento por la matriz de resultados del trabajo de los codificadores con él.

   if(!MatMul(cGates.getOutput(), prev.getOutput(), getOutput(),
              1, cGates.GetGates(), Neurons() / cGates.GetUnits(), cGates.GetUnits()))
      return false;
//---
   return true;
  }

Guardaremos los valores obtenidos en el búfer de resultados de nuestro objeto. Después finalizaremos el método, retornando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluirá nuestra revisión de los algoritmos utilizados en la construcción de los métodos del objeto de conjuntos de codificadores. Le propongo dejar los métodos de pasada inversa de este objeto para un estudio independiente. El código completo de este objeto y todos sus métodos estará disponible, como siempre, en el archivo adjunto del artículo.

Hoy hemos tenido un día estupendo, pero hemos agotado prácticamente la extensión del artículo. Eso sí, nuestro trabajo aún no ha concluido. Haremos una breve pausa y seguiremos haciendo realidad nuestra propia visión de los planteamientos propuestos por los autores del framework DUET en el próximo artículo.

Conclusión

Hoy hemos presentado el framework DUET, que combina la clusterización temporal (TCM) y de canales (CCM) de series temporales multivariantes para lograr un análisis y pronóstico más precisos de las mismas. El TCM adapta los modelos a los cambios a lo largo del tiempo, mientras que el CCM destaca las variables clave, reduciendo el ruido.

En la parte práctica del artículo, hemos presentado la implementación del módulo de clusterización temporal (TCM). En el próximo artículo, continuaremos con la aplicación iniciada. Asimismo, presentaremos nuestra propia visión de los planteamientos propuestos por los autores del framework y llevaremos el trabajo a su conclusión lógica probando el modelo con datos históricos reales.

Enlaces

• DUET: Dual Clustering Enhanced Multivariate Time Series Forecasting
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL