Redes neuronales en el trading: Detección adaptativa de anomalías del mercado (DADA)

Introducción

Con el desarrollo de la tecnología y la automatización de los procesos, las series temporales se han convertido en una parte integrante del análisis de los mercados financieros. La detección eficaz de anomalías en los datos de mercado permite identificar a tiempo posibles amenazas, como fluctuaciones bruscas de los precios, manipulación de activos y cambios en la liquidez. Esto resulta especialmente importante en el trading algorítmico, la gestión de riesgos y la evaluación de la resistencia de los sistemas financieros. Los picos repentinos de volatilidad, las desviaciones en los volúmenes comerciales o las correlaciones inusuales entre activos pueden ser señal de perturbaciones, actividad especulativa o incluso crisis de mercado.

Los métodos actuales de detección de anomalías basados en el aprendizaje profundo han logrado avances significativos, pero muestran ciertas limitaciones. En la mayoría de los casos, estos enfoques requieren un entrenamiento independiente para cada nuevo conjunto de datos, lo cual dificulta su aplicación en el mundo real. Los datos financieros cambian constantemente y sus patrones históricos no siempre se repiten.

Uno de los principales retos es la diferente estructura de los datos en los distintos mercados. Los algoritmos modernos suelen utilizar autocodificadores para "recordar" el comportamiento normal del mercado, ya que las anomalías resultan poco frecuentes. Sin embargo, si el modelo retiene demasiada información, empieza a considerar el ruido del mercado y la precisión de la detección de anomalías disminuye. Por el contrario, una compresión excesiva de los datos puede provocar la omisión de patrones importantes. La mayoría de los enfoques usan un grado de compresión fijo, lo que limita la adaptación de los modelos a las distintas condiciones del mercado.

Otra dificultad es la variedad de las anomalías. Muchos modelos se entrenan solo con datos normales, pero sin un conocimiento de las propias anomalías, estas son difíciles de detectar. Por ejemplo, una subida de precios puede suponer una anomalía en un mercado, pero ser normal en otro. En algunos activos, las anomalías se asocian a explosiones de liquidez repentinas, mientras que en otros, a correlaciones inesperadas. Por ello, el modelo puede omitir señales importantes o generar señales falsas con demasiada frecuencia.

Para abordar estos problemas, los autores del artículo "Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders" proponen el nuevo framework DADA que utiliza la compresión adaptativa de la información y dos descodificadores independientes. A diferencia de los métodos tradicionales, el DADA es flexible para adaptarse a distintos datos. En lugar de un nivel de compresión fijo, usa múltiples opciones y elige la más adecuada para cada caso. Esto ayuda a reconocer mejor las especificidades de los datos de mercado y a conservar patrones importantes.

En la salida del modelo se usan dos descodificadores. Uno se encarga de los datos normales, y el otro se ocupa de los anormales. El primer descodificador aprende a reconstruir la serie temporal, mientras que el segundo descodificador aprende ejemplos de las anomalías. Esto ayuda a distinguir claramente entre normal y anormal, reduciendo la probabilidad de señales falsas.

El algoritmo DADA

Las series temporales son secuencias de datos que cambian con el tiempo. Cualquier desviación respecto al comportamiento normal de los datos puede ser señal de crisis, fallos o actividad fraudulenta. Para detectar eficazmente estas anomalías, el framework DADA (Detector with Adaptive Bottlenecks and Dual Adversarial Decoders) utiliza métodos de aprendizaje profundo de análisis adaptativo de series temporales y detección de patrones anormales. Una característica clave del DADA es su versatilidad. No requiere adaptación previa a un tema específico y puede trabajar con una amplia gama de datos de entrada.

El framework DADA se basa en la idea de reconstrucción de datos mediante enmascaramiento, lo que lo convierte en una herramienta eficaz para analizar dependencias temporales y detectar valores atípicos. Este método permite que el modelo no solo recuerde patrones en los datos, sino que aprenda a comprender su estructura reconstruyendo las secciones faltantes o distorsionadas.

El proceso de aprendizaje implica trabajar con dos tipos de secuencias: normales y anormales. A diferencia de los enfoques tradicionales, que requieren una partición previa manual de los datos anormales, los autores del framework DADA utilizaron un enfoque generativo: añadir ruido artificial a la serie temporal original. Este enfoque no solo simplifica la preparación de los datos al eliminar el trabajo manual, sino que también hace que el modelo resulte más versátil. Al fin y al cabo, está entrenado para detectar desviaciones de distinta naturaleza: saltos, valores atípicos, cambios de tendencia, cambios de volatilidad y otros patrones.

En el primer paso, los datos de origen se dividen en segmentos (parches) a los que se aplica un enmascaramiento aleatorio. Así se garantiza que el modelo está entrenado para recuperar los datos faltantes. Esto aumenta su capacidad para identificar anomalías y patrones ocultos.

A continuación, los segmentos se introducen en el codificador, donde se convierten en una representación latente compacta. El codificador se entrena para encontrar las características clave de la serie temporal, ignorando el ruido y los detalles irrelevantes. Este enfoque permite al modelo resumir mejor la información y trabajar con datos de distinta naturaleza, ya sean gráficos de precios en los mercados financieros, series temporales de volúmenes comerciales u otros indicadores.

Uno de los componentes clave del modelo es un mecanismo de cuello de botella adaptativo que ajusta el grado de compresión de la información según la estructura y la calidad de los datos. Cuando los datos contienen una señal significativa, el modelo retiene más detalles, y si la información resulta redundante o muy ruidosa, se mejora la compresión, lo que ayuda a minimizar el impacto del ruido y mejora la detección de anomalías.

El módulo de cuello de botella adaptativo (AdaBN) modifica dinámicamente el grado de compresión de los datos. Este mecanismo consta de un conjunto de pequeños modelos parecidos a autocodificadores. Cada uno tiene una representación latente de un tamaño diferente:

donde DownNeti(•) ejecuta la compresión de los datos, y UpNeti(•) ejecuta la recuperación.

El enrutador adaptativo selecciona la ruta óptima basándose en el análisis de los datos de entrada:

donde Wrouter, Wnoise son las matrices a entrenar.

Las k rutas mejor ajustadas con el valor máximo de R(z) se utilizan para comprimir cada segmento.

Tras la codificación, las representaciones ocultas se envían a dos descodificadores paralelos. Uno está diseñado para reconstruir datos normales y se entrena para minimizar el error de reconstrucción mientras que el segundo sirve para detectar anomalías, creando la máxima discrepancia entre los valores recuperados y los originales. Este proceso competitivo permite al modelo distinguir eficazmente entre patrones estándar y desviaciones inesperadas.

Durante las pruebas y la explotación, el descodificador anormal se desconecta y la evaluación se realiza únicamente en el descodificador normal. Si el modelo recupera los datos con gran precisión, la serie temporal responde a un comportamiento normal. No obstante, si la reconstrucción va acompañada de errores significativos, esto indica una posible anomalía.

A continuación le mostramos la visualización del framework DADA realizada por el autor.

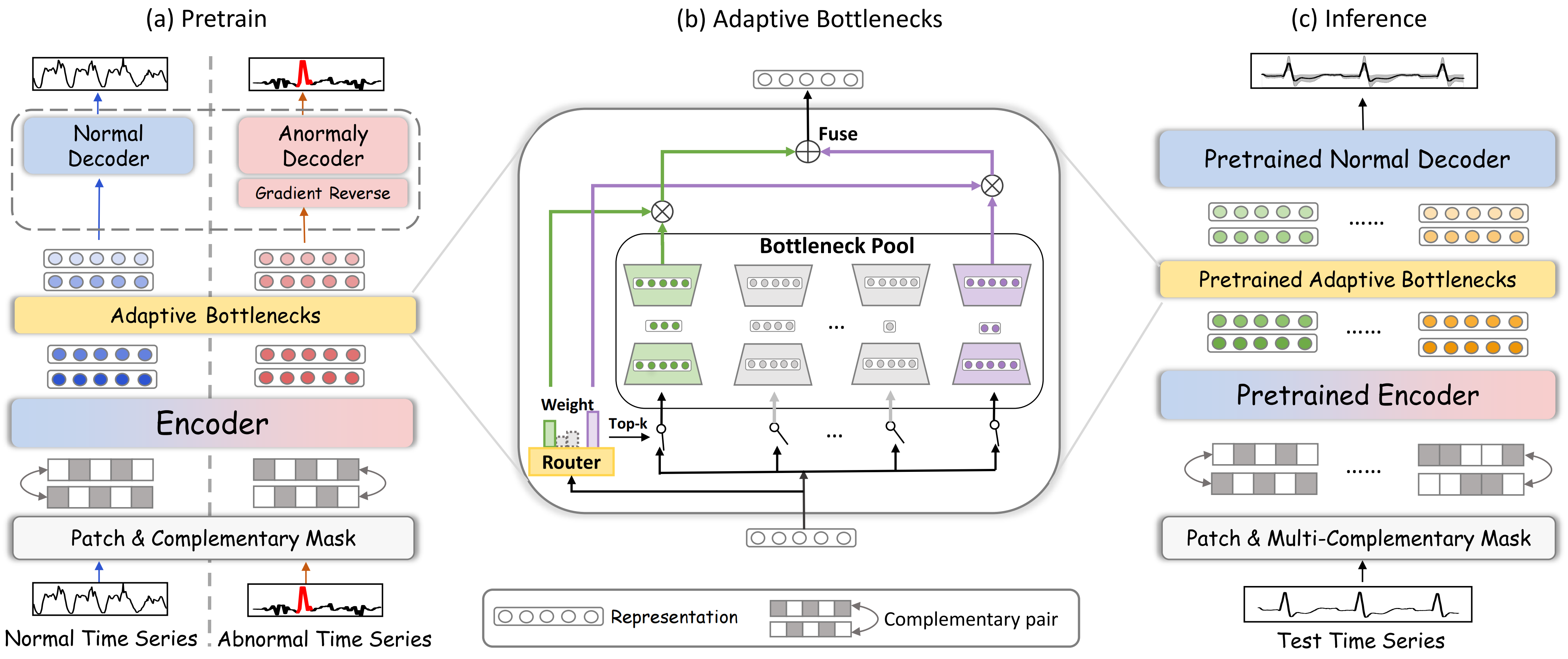
Implementación con MQL5

Tras considerar los aspectos teóricos del framework DADA, abordaremos la parte práctica de nuestro trabajo, en la que analizaremos la variante de implementación de nuestra propia visión de los enfoques propuestos mediante MQL5. Un elemento clave de este framework es el módulo de cuello de botella adaptativo. Comenzaremos nuestro trabajo analizando su construcción.

Creo que no soy el único que ha notado su similitud con el módulo Mixture of Experts que ya implementamos antes. Pero hay una diferencia importante. El objeto CNeuronMoE que construimos antes presupone el uso de minimodelos de la misma arquitectura. Sin embargo, en este caso necesitaremos variar el tamaño de la capa de estado latente para cada modelo, adaptándolo a las diferentes características de los datos. Ya no podemos realizar dicha variante con la ayuda de objetos de capa convolucional, como se hacía antes. Obviamente, podemos crear cada modelo por separado y pasar los datos por ellos secuencialmente. Pero esto se traducirá en una menor utilización de los equipos y mayores costes de formación y funcionamiento del modelo.

Para eliminar los problemas anteriores, hemos decidido desarrollar un nuevo objeto de capa convolucional multiventana. Este se basa en la idea de utilizar simultáneamente múltiples variantes de la dimensionalidad de la ventana convolucional. Esto permitirá al modelo analizar los datos a distintos niveles de detalle en flujos computacionales paralelos. Este planteamiento flexibiliza la arquitectura, mejora la calidad del procesamiento de los datos de origen y permite un uso más eficiente de la potencia de cálculo. Como resultado, el modelo puede adaptarse mejor a las diferentes estructuras temporales de los datos de entrada, garantizando una gran precisión y rapidez.

Creación de algoritmos en el lado del programa OpenCL

Como siempre, situaremos el grueso de las operaciones matemáticas en el contexto de OpenCL. Aquí creamos el kernel FeedForwardMultWinConv, dentro del cual organizamos el proceso de pasada directa de nuestra nueva capa.

__kernel void FeedForwardMultWinConv(__global const float *matrix_w,
                                     __global const float *matrix_i,
                                     __global float *matrix_o,
                                     __global const int *windows_in,
                                     const int inputs,
                                     const int windows_total,
                                     const int window_out,
                                     const int activation
                                    )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t outputs = get_global_size(0);

En los parámetros del kernel obtenemos los punteros a los 4 búferes de datos y las 4 constantes que definen la estructura de los datos iniciales y los resultados.

Observe que uno de los búferes globales (windows_in) contiene valores enteros. En él se transmiten las dimensiones de las ventanas convolucionales. Se supone que hay una secuencia de segmentos en el búfer de datos de origen (matrix_i). Dentro de cada segmento, se secuencian los datos de cada ventana convolucional.

Tenemos previsto llamar este kernel en un espacio de tareas bidimensional. La dimensionalidad de la primera dimensión indica el número de valores en el búfer de resultados para cada secuencia unitaria, mientras que la segunda dimensión indicará el número de dichas secuencias unitarias.

Aquí conviene aclarar que la primera dimensión indica exactamente el número de valores de el búfer de resultados, no el número de elementos de la secuencia unitaria. En otras palabras, el tamaño de la primera dimensión es igual al producto del número de segmentos analizados en la secuencia unitaria por el número de filtros y ventanas convolucionales usados. Cada elemento usa el mismo número de filtros, independientemente del tamaño de la ventana convolucional. Esto se debe a la necesidad de obtener la unidad de los formatos de datos recuperados a partir de la representación comprimida.

En el cuerpo del kernel, primero identificamos el flujo actual en el espacio de tareas bidimensional en cada dimensión.

A continuación, debemos determinar el desplazamiento en los búferes de datos globales hasta los elementos deseados. Obviamente, el identificador de flujo de la primera dimensión apuntará a un elemento de el búfer de resultados dentro de la secuencia unitaria analizada. Pero para determinar el desplazamiento en los otros búferes de datos, tendremos que trabajar un poco.

En primer lugar, debemos determinar la posición del elemento dentro del segmento analizado. Para ello, tomamos el resto de la división del ID de la primera dimensión por el número total de elementos del búfer de resultados para un segmento.

   const int id = i % (window_out * windows_total);

Luego preparamos algunas variables locales para el almacenamiento temporal de valores intermedios.

   int step = 0;
   int shift_in = 0;
   int shift_weight = 0;
   int window_in = 0;
   int window = 0;

Y organizamos un ciclo de iteración de todos los valores del búfer de las ventanas convolucionales.

#pragma unroll
   for(int w = 0; w < windows_total; w++)
     {
      int win = windows_in[w];
      step += win;

En el cuerpo del ciclo, calculamos la suma de todas las ventanas convolucionales, lo que nos dará el tamaño de un segmento en el búfer de datos de origen. Además, dentro de este ciclo, determinamos el desplazamiento dentro del segmento actual hasta la ventana convolucional deseada (shift_in), el tamaño de la ventana convolucional que se va a analizar (window_in) y el desplazamiento en el búfer de parámetros entrenados hasta el comienzo de los elementos de la matriz de la ventana convolucional deseada (shift_weight).

      if((w * window_out) < id)
        {
         shift_in = step;
         window_in = win;
         shift_weight += (win + 1) * window_out;
        }
     }

A continuación, determinamos el número de segmentos completos hasta el elemento actual en el búfer de resultados (steps) y añadimos el desplazamiento correspondiente en el búfer de datos de origen hasta el segmento deseado.

   int steps = (int)(i / (window_out * windows_total));
   shift_in += steps * step + v * inputs;

Al desplazamiento en el búfer de los parámetros entrenados le añadimos una corrección para el filtro correcto. Para ello, tomaremos el resto obtenido de la división de la posición del elemento analizado en el segmento actual del búfer de resultados, lo que nos dará el número de elemento dentro de los resultados de la ventana convolucional actual. Básicamente, el valor resultante indica el filtro que queremos. El número de parámetros entrenados en cada filtro es igual al tamaño de la ventana convolucional más el elemento bias. Así, multiplicando el número de filtros por el número de parámetros a entrenar, obtenemos el desplazamiento deseado.   

shift_weight += (id % window_out) * (window_in+1);

Tras completar el trabajo preparatorio, vamos a organizar un ciclo para calcular el valor del elemento actual en una variable local.

   float sum = matrix_w[shift_weight + window_in];
#pragma unroll
   for(int w = 0; w < window_in; w++)
      if((shift_in + w) < inputs)
         sum += IsNaNOrInf(matrix_i[shift_in + w], 0) * matrix_w[shift_weight + w];

Luego corregimos el valor obtenido por la función de activación y lo almacenamos en el elemento correspondiente del búfer de resultados global.

 matrix_o[v * outputs + i] = Activation(sum, activation);
}

Tras construir el algoritmo de pasada directa, procedemos a organizar los procesos de pasada inversa. Aquí, primero creamos un kernel con la distribución del gradiente de error al nivel de datos de origen CalcHiddenGradientMultWinConv. La estructura de los parámetros de esta unidad de extracción de kernels se basa en gran medida en la unidad de extracción de kernels de pasada directa, solo que añadiremos los punteros a los búferes de los gradientes de error correspondientes.

__kernel void CalcHiddenGradientMultWinConv(__global const float *matrix_w,
                                            __global const float *matrix_i,
                                            __global float *matrix_ig,
                                            __global const float *matrix_og,
                                            __global const int *windows_in,
                                            const int outputs,
                                            const int windows_total,
                                            const int window_out,
                                            const int activation
                                           )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t inputs = get_global_size(0);

El funcionamiento de este kernel también se construye en el espacio bidimensional, solo que esta vez, la primera medición indicará un desplazamiento en el búfer de datos de origen. Al fin y al cabo, es en el nivel de datos de origen donde debemos recopilar los valores de los gradientes de error de todos los filtros.

En el cuerpo del kernel, como siempre, primero identificamos el flujo en todas las dimensiones del espacio de tareas. Y después, organizamos un ciclo de suma de toda la ventana convolucional, para determinar el tamaño del segmento en el búfer de datos de origen.

   int step = 0;
#pragma unroll
   for(int w = 0; w < windows_total; w++)
      step += windows_in[w];

Esto nos permitirá determinar el número de secuencia del segmento del elemento analizado y el desplazamiento dentro de dicho segmento.

int steps = (int)(i / step);
int id = i % step;

A continuación, declaramos varias variables locales para el almacenamiento temporal de datos y organizamos otro ciclo, dentro del cual definimos el tamaño de la ventana convolucional que se va a analizar (window_in), el número de serie de la ventana convolucional (window) y el desplazamiento dentro del segmento actual hasta el comienzo de la ventana convolucional actual (before).

   int window = 0;
   int before = 0;
   int window_in = 0;
#pragma unroll
   for(int w = 0; w < windows_total; w++)
     {
      window_in = windows_in[w];
      if((before + window_in) >= id)
         break;
      window = w + 1;
      before += window_in;
     }

Los valores resultantes nos permitirán determinar el desplazamiento en el búfer de resultados (shift_out) y el tensor de parámetros (shift_weight).

int shift_weight = (before + window) * window_out + id - before;
int shift_out = (steps * windows_total + window) * window_out + v * outputs;

Con esto concluye el trabajo preparatorio: ya disponemos de información suficiente para sumar los gradientes de error. Así que vamos a organizar otro ciclo en el que recopilaremos los valores de los gradientes de error de todos los filtros con los coeficientes de peso correspondientes.

   float sum = 0;
#pragma unroll
   for(int w = 0; w < window_out; w++)
      sum += IsNaNOrInf(matrix_og[shift_out + w], 0) * matrix_w[shift_weight + w * (window_in + 1)];

Luego corregiremos el valor obtenido mediante la derivada de la función de activación de la capa de datos original, y almacenaremos el resultado en el elemento correspondiente del búfer de gradiente de error global.

 matrix_ig[v * inputs + i] = Deactivation(sum, matrix_i[v * inputs + i], activation);
}

El tercer paso de nuestro trabajo consistirá en construir el proceso de distribución del gradiente de error al nivel de los coeficientes de peso y ajustarlos para minimizar el error global del rendimiento del modelo. Como parte de este trabajo, implementaremos un algoritmo para optimizar los parámetros de Adam en el kernel UpdateWeightsMultWinConvAdam.

Para construir correctamente el algoritmo anterior, ampliaremos el número de parámetros del kernel, añadiremos ciertas constantes específicas y 2 búferes de momentos globales.

__kernel void UpdateWeightsMultWinConvAdam(__global float *matrix_w,
                                           __global const float *matrix_og,
                                           __global const float *matrix_i,
                                           __global float *matrix_m,
                                           __global float *matrix_v,
                                           __global const int *windows_in,
                                           const int windows_total,
                                           const int window_out,
                                           const int inputs,
                                           const int outputs,
                                           const float l,
                                           const float b1,
                                           const float b2
                                          )
  {
   const size_t i = get_global_id(0);  // weight shift
   const size_t v = get_local_id(1);   // variable
   const size_t variables = get_local_size(1);

También tenemos previsto usar este kernel en un espacio de tareas bidimensional. Y esta vez la primera dimensión apuntará al elemento optimizado en el búfer global de parámetros entrenados. Sin embargo, en este caso existe un matiz a considerar. Cuando se trata de series temporales multivariantes, cada secuencia unitaria se analiza usando parámetros comunes entrenados. Por lo tanto, en esta etapa tendremos que recopilar los gradientes de error de todas las secuencias unitarias. Para organizar el funcionamiento en paralelo de las secuencias unitarias individuales, las distribuiremos a lo largo de la segunda dimensión del espacio de tareas. No obstante, ponerlas en grupos de trabajo nos permitirá organizar el proceso de intercambio de datos. Con el fin de compartir los datos dentro de un grupo de trabajo, crearemos un array en la memoria local del contexto OpenCL.

__local float temp[LOCAL_ARRAY_SIZE];

A continuación procederemos al trabajo preparatorio, en el que deberemos determinar los desplazamientos en los búferes de datos. Probablemente lo más sencillo que podemos hacer es definir un paso en el búfer de resultados (step_out). Este será igual al producto del número de ventanas convolucionales de un segmento por el número de filtros.

int step_out = window_out * windows_total;

Para conseguir el resto de parámetros, tendremos que trabajar. En primer lugar, declararemos las variables locales en las que guardaremos los resultados intermedios.

int step_in = 0;
int shift_in = 0;
int shift_out = 0;
int window = 0;
int number_w = 0;

Y organizaremos un ciclo de iteración de valores en el búfer global de tamaños de ventanas convolucionales.

#pragma unroll
   for(int w = 0; w < windows_total; w++)
     {
      int win = windows_in[w];
      if((step_in + w)*window_out <= i &&
         (step_in + win + w + 1)*window_out > i)
        {
         shift_in = step_in;
         shift_out = (step_in + w + 1) * window_out;
         window = win;
         number_w = w;
        }
      step_in += win;
     }

En el cuerpo del ciclo definiremos el desplazamiento hasta la ventana convolucional requerida en los búferes de origen (shift_in) y de resultados (shift_out), el tamaño de la ventana convolucional (window) y su número de secuencia en el búfer (number_w). Además, calcularemos la suma de todas las ventanas convolucionales (step_in), que nos indicará el tamaño del segmento. Este es el mismo valor que utilizaremos como paso del búfer de datos de origen.

Aquí cabe señalar que no todos los parámetros entrenados están asociados a el búfer de datos de origen. Al fin y al cabo, existe el elemento bias. Y además introduciremos una bandera para detectar dicho elemento.

bool bias = ((i - (shift_in + number_w) * window_out) % (window + 1) == window);

A continuación, corregiremos el desplazamiento hasta el elemento deseado en el búfer de resultados.

int t = (i - (shift_in + number_w) * window_out) / (window + 1);
shift_out += t + v * outputs;

Y realizaremos una operación similar para el desplazamiento en el búfer global de datos de origen.

   shift_in += (i - (shift_in + number_w) * window_out) % (window + 1) + v * inputs;

Con esto finalizaremos la etapa de los trabajos preparatorios y pasaremos directamente a la determinación del gradiente de error del parámetro analizado. Para ello, organizaremos un ciclo para recopilar el gradiente de error de todos los elementos del búfer de resultados, cuyos valores se han calculado utilizando el parámetro optimizado en este flujo.

   float grad = 0;
   int total = (inputs + step_in - 1) / step_in;
#pragma unroll
   for(int t = 0; t < total; t++)
     {
      int sh_out = t * step_out + shift_out;
      if(bias && sh_out < outputs)
        {
         grad += IsNaNOrInf(matrix_og[sh_out], 0);
         continue;
        }

Para los elementos de bias, simplemente resumiremos los valores del gradiente de error y ajustaremos los demás al elemento correspondiente de los datos de origen.

 int sh_in = t * step_in + shift_in;
 if(sh_in >= inputs)
    break;
 grad += IsNaNOrInf(matrix_og[sh_out] * matrix_i[sh_in], 0);
}

Obsérvese aquí que en este ciclo solo hemos recopilado valores de error dentro de una única secuencia unitaria. Pero, como ya hemos mencionado, el parámetro optimizado ha sido utilizado por todas las secuencias de las series temporales multivariantes. Por ello, deberemos recopilar los valores de todas las secuencias unitarias que se han calculado en el grupo de trabajo antes de iniciar el trabajo de optimización de los parámetros. Para ello, en el primer paso, sumaremos los valores individuales de los elementos del array local.

//--- sum
   const uint ls = min((uint)variables, (uint)LOCAL_ARRAY_SIZE);
#pragma unroll
   for(int s = 0; s < (int)variables; s += ls)
     {
      if(v >= s && v < (s + ls))
         temp[v % ls] = (i == 0 ? 0 : temp[v % ls]) + grad;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Y luego sumaremos los valores acumulados en los elementos del array local.

   uint count = ls;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if(v < ls)
         temp[v] += (v < count && (v + count) < ls ? temp[v + count] : 0);
      if(v + count < ls)
         temp[v + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Una vez obtenido el gradiente de error total de todos los flujos del grupo de trabajo, podremos actualizar el valor del parámetro analizado. Y para eso, nos bastará con un flujo.

   if(v == 0)
     {
      grad = temp[0];
      float mt = IsNaNOrInf(clamp(b1 * matrix_m[i] + (1 - b1) * grad, -1.0e5f, 1.0e5f), 0);
      float vt = IsNaNOrInf(clamp(b2 * matrix_v[i] + (1 - b2) * pow(grad, 2), 1.0e-6f, 1.0e6f), 1.0e-6f);
      float weight = clamp(matrix_w[i] + IsNaNOrInf(l * mt / sqrt(vt), 0), -MAX_WEIGHT, MAX_WEIGHT);
      matrix_w[i] = weight;
      matrix_m[i] = mt;
      matrix_v[i] = vt;
     }
  }

Según los resultados de las operaciones, en los búferes de datos globales corregiremos el valor del parámetro analizado y los momentos correspondientes.

Con esto concluirá la construcción de los algoritmos de capas convolucionales multiventana en nuestro programa OpenCL. Encontrará su código completo en los anexos.

Objeto de capa convolucional multiventana

La siguiente fase de nuestro trabajo consistirá en integrar en el programa principal los algoritmos de capas convolucionales multiventana construidos anteriormente. Para ello, crearemos un nuevo objeto CNeuronMultiWindowsConvOCL, en el que organizaremos los procesos de servicio de los kernels creados en el lado del contexto OpenCL. Más abajo resumiremos la estructura del nuevo objeto.

class CNeuronMultiWindowsConvOCL    :  public CNeuronConvOCL
  {
protected:
   int               aiWindows[];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronMultiWindowsConvOCL(void) {  activation = SoftPlus;  iWindow = -1; }
                    ~CNeuronMultiWindowsConvOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint &windows[], uint window_out, uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMultiWindowsConvOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

En esencia, nuestro nuevo objeto CNeuronMultiWindowsConvOCL será una versión modificada de la capa convolucional estándar. Por lo tanto, resultará lógico utilizarla como clase padre. Esto nos permitirá heredar la lógica básica del trabajo con convoluciones y evitar la duplicación de código.

En la estructura presentada, podemos ver el conjunto habitual de métodos virtuales redefinidos. Sin embargo, la principal diferencia del nuevo objeto consistirá en trabajar con varias variantes de la dimensionalidad de las ventanas convolucionales al mismo tiempo. Esto requerirá la creación de elementos adicionales de almacenamiento de datos e interfaces para pasarlos al contexto OpenCL. Para ello, declararemos un array adicional aiWindows y modificaremos los parámetros del método de inicialización del objeto Init.

bool CNeuronMultiWindowsConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                      uint &windows[], uint window_out, uint units_count,
                                      uint variables, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(windows.Size() <= 0 || ArrayCopy(aiWindows, windows) < int(windows.Size()))
      return false;

Aquí es importante destacar que, a pesar de todos los cambios realizados en el algoritmo CNeuronMultiWindowsConvOCL, hemos intentado preservar en la medida de lo posible la lógica y las capacidades de la clase padre. Esto no solo simplificará la integración de un nuevo objeto en una arquitectura existente, sino que también permitirá reutilizar mecanismos ya depurados.

El algoritmo del método de inicialización de objetos comenzará con la comprobación del tamaño del array de la ventana convolucional obtenida en los parámetros y el copiado de sus valores en un array interno especialmente creado.

A continuación, determinaremos la suma de todas las ventanas convolucionales añadiendo un elemento bias a cada una.

int window = 0;
for(uint i = 0; i < aiWindows.Size(); i++)
   window += aiWindows[i] + 1;

Es una operación poco obvia, pero necesaria. La cuestión es que para cada ventana convolucional tenemos que generar una matriz de pesos de tamaño (Windowi + 1) * Filters Así, el tamaño total del búfer de parámetros será:

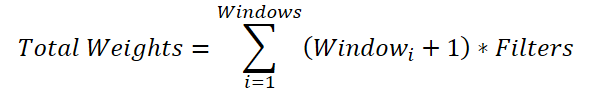
Podemos tomar la variable total del número de filtros más allá del signo de suma:

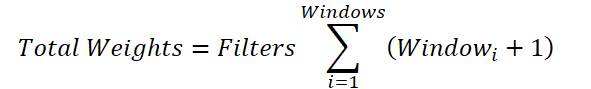
Si sustituimos la suma de las ventanas por un valor común, llegaremos a una fórmula para determinar el número de parámetros entrenados para una única ventana convolucional. Solo en nuestra clase padre se prevé la adición de un único elemento bias, y no según el número de ventanas convolucionales que necesitamos. Por ello, añadiremos al total un elemento de compensación para cada ventana. Y después, reduciremos el valor obtenido en 1 y los transmitiremos como ventana convolucional y paso al método de inicialización de la clase padre.

window--;
if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, window, window_out,
                         units_count * aiWindows.Size()*variables, 1, ADAM, batch))
   return false;

Como tenemos previsto utilizar los mismos parámetros para todas las secuencias unitarias, indicaremos el número de dichos parámetros como "1". Al mismo tiempo, aumentaremos el número de elementos de la secuencia multiplicando por el número de ventanas convolucionales y secuencias unitarias.

Este enfoque nos ha permitido inicializar todos los búferes de datos heredados con el tamaño adecuado, incluida la inicialización del búfer de parámetros entrenados con valores aleatorios.

Ahora solo nos quedará crear un búfer de datos global para transmitir el array de ventanas convolucionales al contexto OpenCL. Como comprenderá, rellenaremos los valores de este búfer al inicializar el objeto y no los cambiaremos durante el entrenamiento y el funcionamiento del modelo. Por lo tanto, crearemos un búfer de datos solo en el contexto OpenCL, y almacenaremos en nuestro objeto solo el puntero a él.

   iVariables = variables;
   iWindow = OpenCL.AddBufferFromArray(aiWindows, 0, aiWindows.Size(), CL_MEM_READ_ONLY);
   if(iWindow < 0)
      return false;
//---
   return true;
  }

Luego comprobaremos si el búfer de datos global se ha creado correctamente mediante el manejador devuelto y finalizaremos el método de inicialización de un nuevo objeto, devolviendo previamente el resultado lógico de las operaciones al programa que realiza la llamada.

Después de inicializar el nuevo objeto, sobrescribiremos el método de pasada directa CNeuronMultiWindowsConvOCL::feedForward. Como ya habrá adivinado, aquí es donde el kernel FeedForwardMultWinConv creado previamente se pone en la cola para su ejecución. Sin embargo, a pesar del uso de un algoritmo común para estos casos, hay un par de matices sobre los que nos gustaría llamar la atención.

bool CNeuronMultiWindowsConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;

En los parámetros del método obtendremos un puntero al objeto de datos de origen, cuya relevancia comprobaremos inmediatamente.

Después de pasar con éxito el bloque de control, inicializaremos los arrays del espacio de tareas.

uint global_work_offset[2] = {0, 0};
uint global_work_size[2] = {Neurons() / iVariables, iVariables};

Como hemos mencionado anteriormente, al describir el algoritmo de dicho kernel, la segunda dimensión indicará el número de secuencias unitarias en los datos de origen. Pero el número de flujos en la primera dimensión vendrá determinado por la relación entre el número total de elementos del búfer de resultados de nuestro objeto y el número de secuencias unitarias.

A continuación, transferiremos los datos a los parámetros del kernel.

   ResetLastError();
   int kernel = def_k_FeedForwardMultWinConv;
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_matrix_i, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_matrix_o, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_matrix_w, WeightsConv.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_windows_in, iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Aquí vale la pena señalar que transmitiremos un manejador previamente guardado como el búfer de dimensionalidad de las ventanas convolucionales, mientras que la dimensionalidad de la secuencia de datos de origen se determinará dividiendo el tamaño del búfer de datos de origen por el número de secuencias unitarias.

   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_inputs, NeuronOCL.Neurons() / iVariables))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_window_out, iWindowOut))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_windows_total, (int)aiWindows.Size()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_activation, (int)activation))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.Execute(kernel, 2, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Tras pasar con éxito todos los parámetros, pondremos en la cola el kernel y finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.

Del mismo modo, se llevará a cabo la cola de ejecución de los kernels de la organización de los procesos de pasada inversa, solo que en la distribución de gradientes de error, especificaremos la función de activación de la capa de datos de origen. Y para las operaciones de optimización de los parámetros del modelo, no olvidaremos crear grupos de trabajo dentro de la segunda dimensión del espacio de tareas.

bool CNeuronMultiWindowsConvOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;
//---
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2] = {WeightsConv.Total(), iVariables};
   uint local_work_size[2] = {1, iVariables};
//---
.........
.........
.........
//---
   if(!OpenCL.Execute(kernel, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Con esto concluiremos nuestra consideración de los algoritmos para construir una capa convolucional multiventana. En el archivo adjunto incluimos el código completo del objeto CNeuronMultiWindowsConvOCL y todos sus métodos.

El artículo casi ha finalizado, pero aún no hemos terminado nuestro trabajo. Así que haremos una breve pausa y continuaremos implementando nuestra propia visión de los planteamientos propuestos por los autores del framework DADA en el siguiente artículo....

Conclusión

Los mercados financieros actuales se caracterizan no solo por una enorme cantidad de datos, sino también por una gran volatilidad. Esto hace que la tarea de detección de anomalías resulte especialmente difícil. El framework DADA ofrece un enfoque fundamentalmente nuevo que combina cuellos de botella adaptativos y dos descodificadores paralelos para realizar un análisis más preciso de las series temporales. Su principal ventaja es su capacidad para ajustarse dinámicamente a distintas estructuras de datos sin necesidad de adaptación previa, lo que la convierte en una herramienta versátil.

En la parte práctica del artículo, hemos empezado a aplicar nuestra propia visión de los enfoques propuestos por los autores del framework usando herramientas MQL5. Sin embargo, nuestro trabajo aún no ha terminado, así que lo continuaremos en el próximo artículo.

Enlaces

• Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL