Modelos polinómicos en el trading

Introducción

La eficacia de la negociación depende en gran parte de los métodos de análisis de los datos del mercado. Uno de estos métodos son los polinomios ortogonales. Estos polinomios suponen funciones matemáticas que pueden utilizarse para resolver una serie de problemas relacionados con el comercio.

Los polinomios ortogonales más conocidos son los de Legendre, Chebyshev, Laguerre y Hermite. Cada uno de estos polinomios tiene propiedades únicas que permiten usarlos para resolver distintos problemas. He aquí algunas de las principales formas en que pueden utilizarse:

• Modelización de series temporales. Los polinomios ortogonales pueden usarse para describir series temporales. Su uso puede ayudar a identificar tendencias y otros patrones.
• Regresión. Los polinomios ortogonales pueden aplicarse en el análisis de regresión. Su uso mejora la calidad del modelo, haciéndolo más interpretable.
• Predicción. Los polinomios ortogonales pueden utilizarse para realizar predicciones: cuál será el precio si se mantienen las tendencias actuales.

Veamos cómo podemos aplicar los polinomios ortogonales en la práctica.

Polinomios ortogonales e indicadores

La esencia total del análisis técnico se reduce a identificar patrones en los movimientos de los precios. Pero las series temporales financieras suelen contener ruido que ocultan estos patrones. Veamos cómo podemos aplicar los polinomios ortogonales en condiciones de mercado.

La idea básica reside en que estos polinomios pueden utilizarse para descomponer señales complejas en componentes más simples. Dicha descomposición permite filtrar el ruido e identificar tendencias.

A modo de ejemplo, tomaremos los polinomios de Legendre y crearemos un indicador de suavización basado en ellos. La fórmula general de estos polinomios y su área de definición vienen dadas por las siguientes expresiones:

Utilizaremos polinomios de hasta 9º grado. Para el suavizado resulta suficiente; el uso de polinomios de grados superiores puede añadir ruido y ocultar las principales tendencias del movimiento de los precios. Las fórmulas de los polinomios que utilizaremos figuran en la tabla.

n	Polinomios de Legendre
0	1
1	x
2	(3*x^2-1)/2
3	(5*x^3-3*x)/2
4	(35*x^4-30*x^2+3)/8
5	(63*x^5-70*x^3+15*x)/8
6	(231*x^6-315*x^4+105*x^2-5)/16
7	(429*x^7-693*x^5+315*x^3-35*x)/16
8	(6435*x^8-12012*x^6+6930*x^4-1260*x^2+35)/128
9	(12155*x^9-25740*x^7+18018*x^5-4620*x^3+315*x)/128

En primer lugar, debemos convertir los índices de precios al dominio de definición de estos polinomios. Para ello, aplicaremos a cada índice i una función de desplazamiento:

Después, calcularemos los valores de todos los polinomios de interés para cada valor de x[i]. Para poner un ejemplo, vamos a calcular el valor de un polinomio de 2º grado con periodo igual a 3:

Ahora deberemos introducir una corrección para la naturaleza discreta de los datos. La suma de los valores polinómicos de grados 1 y superiores deberá ser igual a cero. Para cumplir esta condición necesitaremos calcular la corrección:

Usaremos esta corrección para ajustar los valores del polinomio:

Ahora viene la parte divertida. Cualquier serie temporal puede descomponerse en una suma de polinomios tomados con un peso determinado:

Las propias ponderaciones pueden calcularse de la forma que sigue:

Parece confuso, e incluso da un poco de miedo. Pero en realidad es muy sencillo. Vamos a tomar un polinomio de grado 0 con periodo N. Sus valores en todos los puntos serán iguales a 1. Y su peso será:

Es la fórmula de la SMA. Los pesos de polinomios de grados superiores equivalen a algunos osciladores con coeficientes especialmente seleccionados. Por tanto, se podría decir que los polinomios ortogonales son SMA con algunas adiciones calculadas inteligentemente. Los polinomios de Legendre son muy resistentes al ruido y destacan en tareas de filtrado. Por ejemplo, un polinomio de Legendre de grado 1 tendrá este aspecto.

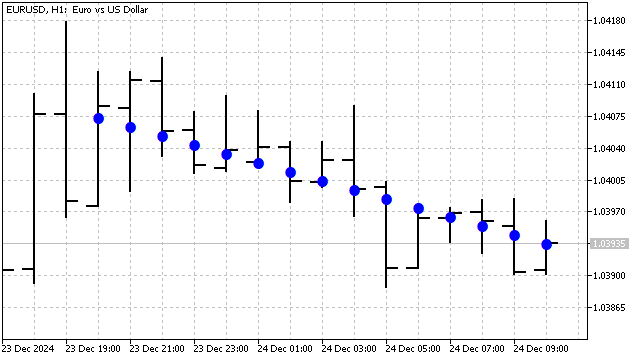
Además de los polinomios de Legendre, para la extracción de tendencias y el suavizado, se pueden utilizar los polinomios de Chebyshev. Existen dos tipos de polinomios. Estos se diferencian entre sí por su comportamiento en los bordes. La principal ventaja de estos polinomios reside en su sensibilidad a los cambios bruscos de precio. La fórmula de estos polinomios es muy sencilla:

n	polinomios de 1º tipo	polinomios de 2º tipo
0	1	1
1	x	2*x
2	2*x^2-1	4*x^2-1
3	4*x^3-3*x	8*x^3-4*x
4	8*x^4-8*x^2+1	16*x^4-12*x^2+1
5	16*x^5-20*x^3+5*x	32*x^5-32*x^3+6*x
6	32*x^6-48*x^4+18*x^2-1	64*x^6-80*x^4+24*x^2-1
7	64*x^7-112*x^5+56*x^3-7*x	128*x^7-192*x^5+80*x^3-8*x
8	128*x^8-256*x^6+160*x^4-32*x^2+1	256*x^8-448*x^6+240*x^4-40*x^2+1
9	256*x^9-576*x^7+432*x^5-120*x^3+9*x	512*x^9-1024*x^7+672*x^5-160*x^3+10*x

Y así es como se ve el suavizado con un polinomio Chebyshev de 3er grado.

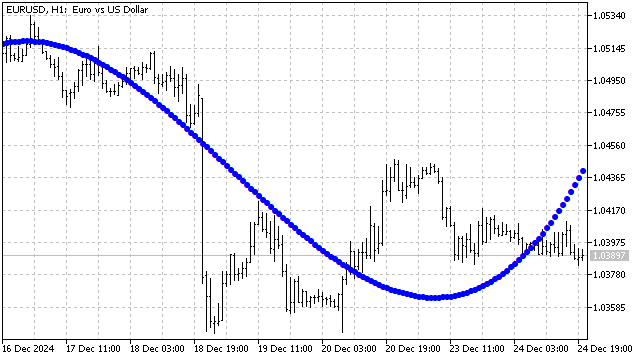
Hasta ahora hemos analizado polinomios con dominio de definición +/-1, pero existen polinomios con otros dominios de definición. Por ejemplo, el polinomio de Laguerre se define para todos los valores no negativos del argumento. Su fórmula tiene el aspecto que sigue:

n	Polinomios de Laguerre
0	1
1	-x+1
2	(x^2-4*x+2)/2
3	(-x^3+9*x^2-18*x+6)/6
4	(x^4-16*x^3+72*x^2-96*x+24)/24
5	(-x^5+25*x^4-200*x^3+600*x^2-600*x+120)/120
6	(x^6-36*x^5+450*x^4-2400*x^3+5400*x^2-4320*x+720)/720
7	(-x^7+49*x^6-882*x^5+7350*x^4-29400*x^3+52920*x^2-35280*x+5040)/5040
8	(x^8-64*x^7+1568*x^6-18816*x^5+117600*x^4-376320*x^3+564480*x^2-322560*x+40320)/40320
9	(-x^9+81*x^8-2592*x^7+42336*x^6-381024*x^5+1905120*x^4-5080320*x^3+6531840*x^2-3265920*x+362880)/362880

Y la función shift para su argumento tendrá este aspecto:

Este cambio provocará que el comportamiento del polinomio de Laguerre no solo depende del grado, sino también de su periodo. Este polinomio es sensible a las variaciones recientes de los precios. Por ejemplo, este será el aspecto de un polinomio de Laguerre de grado 5 en un gráfico:

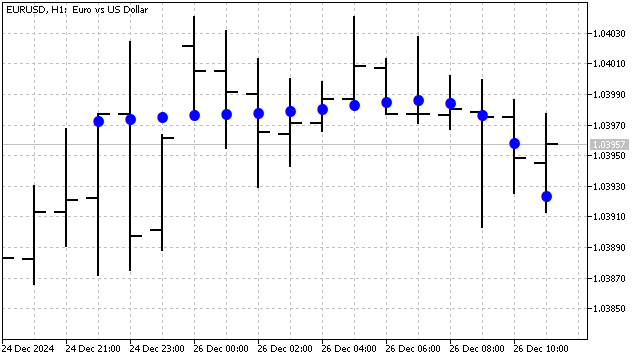
Otro ejemplo interesante de ortogonalidad son los polinomios de Hermite Estos polinomios se usan en muchas áreas de las matemáticas y la física, y se definen para cualquier valor del argumento. Su fórmula tendrá el siguiente aspecto:

n	Polinomios de Hermite
0	1
1	x
2	x^2-1
3	x^3-3*x
4	x^4-6*x^2+3
5	x^5-10*x^3+15*x
6	x^6-15*x^4+45*x^2-15
7	x^7-21*x^5+105*x^3-105*x
8	x^8-28*x^6+210*x^4-420*x^2+105
9	x^9-36*x^7+378*x^5-1260*x^3+945*x

La función de desplazamiento centra los valores de los precios:

Como resultado, hemos obtenido un filtro de suavizado cuya eficacia dependerá del grado del polinomio y su periodo.

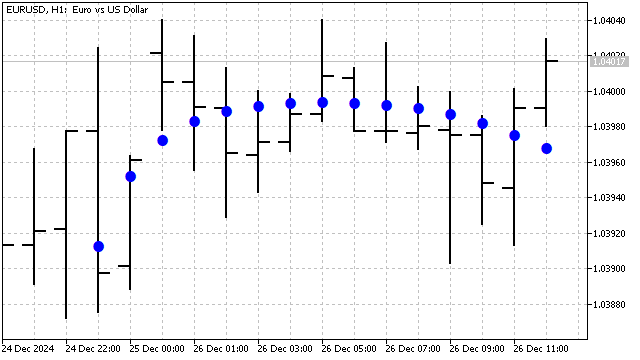
Ya hemos considerado los polinomios ortogonales clásicos básicos, pero podemos crear perfectamente nuestra propia variante de dichos polinomios. Por ejemplo, un polinomio que combine las ventajas de los polinomios de Chebyshev y Hermite vendrá dado por la fórmula:

n	Polinomios de Chebyshev-Hermite
0	1
1	2*x
2	4*x^2-2
3	8*x^3-12*x
4	16*x^4-48*x^2+12
5	32*x^5-160*x^3+120*x
6	64*x^6-480*x^4+720*x^2-120
7	128*x^7-1344*x^5+3360*x^3-1680*x
8	256*x^8-3584*x^6+13440*x^4-13440*x^2+1680
9	512*x^9-9216*x^7+48384*x^5-80640*x^3+30240*x

Este polinomio resultará sensible a las tendencias no lineales: cuadráticas, cúbicas, etc. Así se verá en el gráfico el polinomio Chebyshev-Hermite de grado 9:

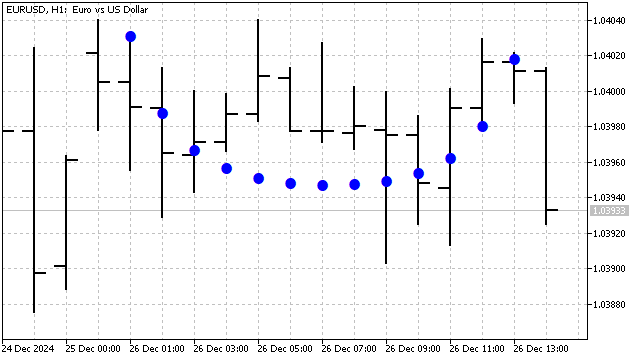
El uso de polinomios ortogonales tiene varias ventajas.

• Estabilidad y eliminación de la correlación. La ortogonalidad de los polinomios garantiza su robustez frente a cambios en los parámetros del modelo. Cada polinomio es independiente de los demás, lo cual permite modelizar y estudiar por separado cada componente de la serie temporal.
• Interpretabilidad. Cada polinomio ortogonal se corresponde con un patrón diferente de comportamiento de los precios. Los coeficientes de peso polinómicos nos permiten destacar los modelos más importantes y centrarnos en ellos.
• Adaptabilidad y eficacia. Los polinomios ortogonales se ajustan a valores concretos de las series temporales. La aparición de nuevos precios provoca cambios en los pesos, debido a lo cual el modelo polinómico se adapta al estado actual del mercado, mientras que el uso de polinomios no lineales hace que esta adaptación resulte eficiente.

La única característica de los polinomios ortogonales que puede considerarse una desventaja es que estos polinomios procesan todos los precios dentro del polinomio. Dicho de otro modo, el indicador construido a partir de tales polinomios "dibuja". Desde mi punto de vista, esta característica no supone una desventaja: simplemente el indicador encuentra la mejor aproximación cuando llegan nuevos datos.

La aplicación de polinomios ortogonales impone algunas limitaciones. El periodo del indicador deberá ser mayor que el grado del polinomio. A efectos prácticos, podemos limitarnos al 3er grado del polinomio. Este indicador combina la SMA, la tendencia lineal y dos parábolas: cuadrática y cúbica. Eso bastará para suavizar algunas situaciones bastante difíciles. Pero, al aumentar el periodo del indicador, también puede aumentar el grado del polinomio.

Veamos ahora algunos ejemplos de aplicación de los polinomios ortogonales en el trading.

Estrategias comerciales

Basándose en polinomios ortogonales, los tráders pueden crear diferentes estrategias comerciales. Por ejemplo, usando la regresión polinómica basada en polinomios ortogonales, los tráders no solo pueden analizar los movimientos de precios pasados, sino también crear un modelo que pueda adaptarse a los cambios actuales del mercado.

A modo de ejemplo, veamos algunas estrategias comerciales basadas en las desviaciones de la media.

Tomaremos la estrategia más simple: la apertura de posiciones se producirá cuando el precio cruza la SMA. La media móvil la sustituiremos por un polinomio ortogonal, y dejaremos inalteradas las reglas de apertura y cierre de posiciones:

• Si el precio cruza el polinomio de abajo a arriba: abrimos una posición Buy, cerramos una posición Sell.
• Si el precio cruza el polinomio de arriba a abajo: abrimos una posición Sell, cerramos una posición Buy.

A pesar de su simplicidad, esta estrategia resulta bastante viable.

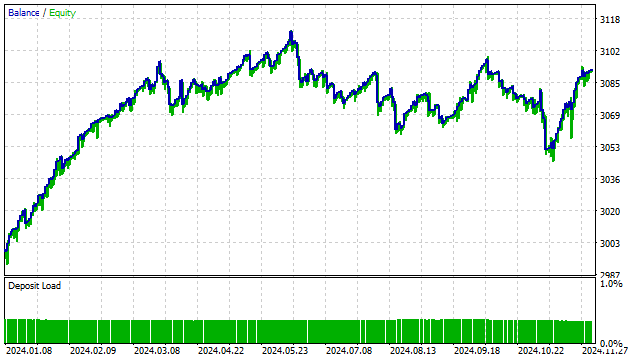
Vamos a complicar un poco esta estrategia y a sustituir el precio por el valor de algún polinomio. Es decir, tendremos un análogo de la estrategia con el cruce de dos SMA. El resultado es previsible: de todas las opciones posibles, el optimizador de estrategias ha preferido los polinomios ortogonales.

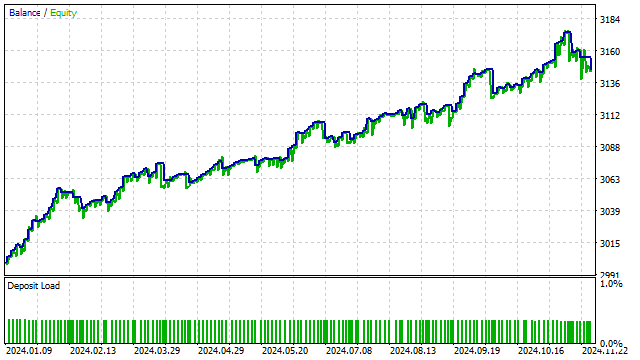
Los modelos polinómicos también pueden usarse en estrategias más complejas. Si la estrategia usa indicadores, podemos intentar sustituirlos por polinomios ortogonales. Esta sustitución podría mejorar la estrategia.

Tomaremos como ejemplo el indicador Commodity channel index (CCI). La fórmula clásica de este indicador es la siguiente:

Vamos a hacer algunos cambios menores en este indicador. Como hemos dicho: La SMA es un polinomio de grado 0. En lugar de SMA, utilizaremos un polinomio ortogonal de cualquier grado. En consecuencia, calcularemos la desviación media absoluta con respecto a este polinomio. El indicador ha resultado así:

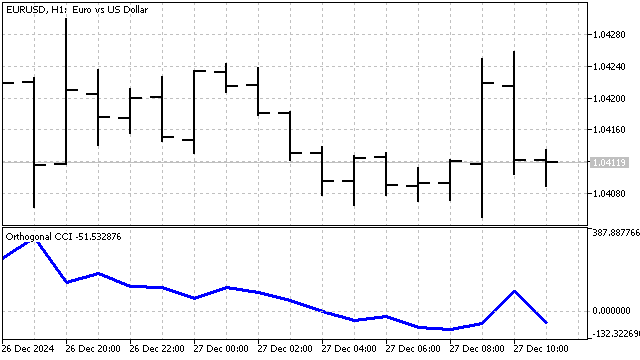
La estrategia comercial será similar a la estrategia clásica:

• abrir una posición Buy si el indicador está por debajo del nivel establecido y sigue bajando;
• abrir una posición Sell si el indicador supera el nivel establecido y sigue aumentando;
• posiciones de cierre según la señal contraria.

Aquí tenemos el resultado de la prueba de dicha estrategia con un polinomio de 3er grado:

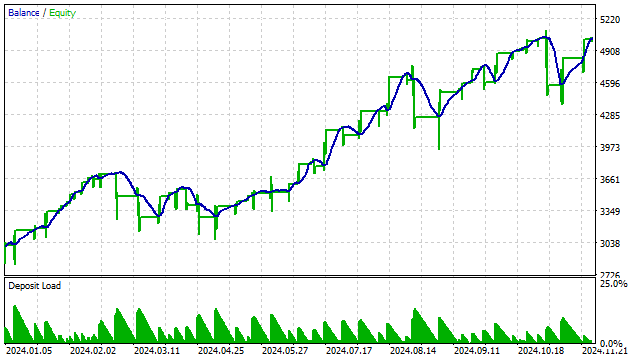
Otros indicadores pueden construirse a partir de polinomios ortogonales. Por ejemplo, he decidido construir un análogo de RSI. La idea es sencilla: primero construimos un polinomio y luego calculamos cuántos precios se han ubicado por encima de ese polinomio. Usando este número como base, sacaremos conclusiones sobre el estado de sobrecompra/sobreventa.

Luego creamos una estrategia simple basada en este indicador:

• abrir una posición si el indicador ha alcanzado un nivel de sobrecompra o sobreventa;
• cerrar las posiciones si el indicador está en el centro.

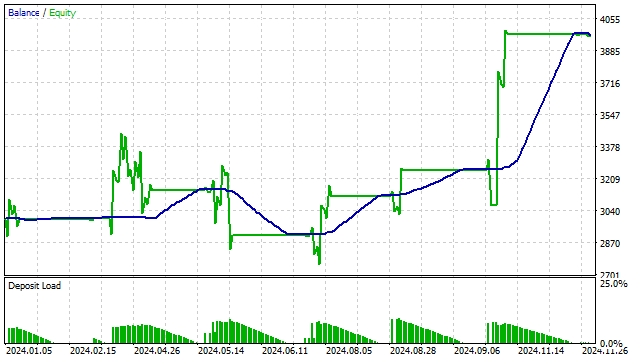
Además, los polinomios ortogonales pueden integrarse en diversos algoritmos de aprendizaje automático. La flexibilidad de las funciones polinómicas permite a los algoritmos de máquina identificar dependencias complejas en los datos. 

Por ejemplo, podemos utilizar polinomios para generar nuevas características a partir de los datos de origen. Los polinomios ortogonales ofrecen estimaciones independientes de los distintos componentes de una serie temporal. Gracias a esta propiedad, podemos reducir el sobreentrenamiento. Esto puede mejorar la calidad de los datos de entrenamiento y el rendimiento de los modelos.

Vamos a tomar cualquier red neuronal y a suministrar a la entrada los valores de los coeficientes de peso de los polinomios ortogonales. Pero en este caso necesitaremos construir un sistema de polinomios completo: empezando con un polinomio de grado 1, y terminando con N-1, donde N será el número de precios a procesar.

Conclusión

Los polinomios ortogonales suponen una potente herramienta para analizar series temporales financieras: ofrecen una amplia serie de ventajas y permiten evaluar los cambios en el mercado. El uso de polinomios ortogonales en las estrategias comerciales puede aumentar su eficacia y mejorar los resultados de las transacciones.

En la redacción de este artículo hemos utilizado los siguientes programas.

Nombre	Tipo	Descripción
Orthogonal polynomials	indicador	modela polinomios ortogonales en el gráfico Type - tipo del polinomio iPeriod - periodo del polinomio (no inferior a 2) N - grado del polinomio, valores permitidos 0 - 9 Shift - desplazamiento del indicador
EA Orthogonal polynomials	asesor	aplica una estrategia comercial basada en la intersección del precio y el polinomio
EA Orthogonal polynomials 2	asesor	aplica una estrategia de intersección de dos polinomios
Orthogonal CCI	indicador	CCI en la que pueden usarse polinomios ortogonales en lugar de SMA
EA Orthogonal CCI	asesor	aplica una estrategia basada en la variante ortogonal de la CCI
Orthogonal RSI	indicador	determina el estado de sobrecompra/sobreventa mediante polinomios ortogonales
EA Orthogonal RSI	asesor	aplica una estrategia basada en la variante ortogonal de RSI