
Estudiamos la clase CCanvas. Suavizado y sombras
Índice
- Introducción
- 1. Coordenadas y canvas
- 2. Algoritmo de suavizado
- 3. Sombra del objeto
- 4. Ejemplo de algoritmo de difuminación de Gauss
- 5. Clase de dibujado de la sombra
- Conclusión
Introducción
Creo que una de las tareas que se pueden resolver dibujando con la ayuda de CCanvas es la representación de diferentes efectos dinámicos. Por ejemplo, la implementación de construcciones gráficas con uso del suavizado: estas construcciones suavizadas adquieren un aspecto más atractivo. O el dibujado de un nuevo estilo de representación de la línea del indicador, llamado spline. E incluso puede dibujar un indicador dinámico en una ventana aparte, algo parecido al dibujado de una característica de frecuencia en un oscilador. En cualquier caso, el dibujado abre nuevos horizontes de aplicación en sus desarrollos.
1. Coordenadas y canvas
El canvas se construye en las coordenadas del gráfico. El tamaño del gráfico en este caso se mide en píxeles. La esquina superior izquierda del gráfico son las coordenadas (0,0).
Al dibujar en el canvas conviene tener en cuenta que las coordenadas de los primitivos y primitivos coloreados se definen exclusivamente en int. Pero al dibujar los primitivos usando el suavizado con el método PixelSetAA las coordenadas se establecen en double, en el método CircleAA las coordenadas se establecen en int, y el tamaño del entorno, en double.
| Método | Coordenadas | Tamaño |
|---|---|---|
| PixelSetAA | double | - |
| LineAA | int | - |
| PolylineAA | int | - |
| PolygonAA | int | - |
| TriangleAA | int | - |
| CircleAA | int | double |
Es decir, al definir las coordenadas para el método PixelSetAA las coordenadas del punto pueden ser del tipo: (120.3, 25.56). El script PixelSetAA.mq5 dibuja dos columnas de once puntos. En la columna de la izquierda para cada punto en el eje X constituye 0.1, y el incremento en el eje Y, 3.0. En la columna de la derecha para cada punto en el eje X constituye 0.1, y el incremento en el eje Y, 3.1.
Para que sea posible ver de qué forma se dibujarán estos puntos, hemos aumentado varias veces el resultado del funcionamiento del script PixelSetAA.mq5:
![]()
Fig. 1. Funcionamiento del método PixelSetAA
Para que el funcionamiento del script sea más visual, he añadido los límites en los que tiene lugar el suavizado, así como un texto con las coordenadas para el dibujado:
![]()
Fig. 2. Funcionamiento visual de PixelSetAA
Como puede ver, solo en las coordenadas sin parte fraccionaria el píxel se colorea con el color indicado. Si una de las coordenadas de un punto se establece con una parte fraccionaria, entonces ese punto se dibujará con dos píxeles con diferente saturación cromática (columna izquierda).
Cuando ambas coordenadas de un punto se establecen con una parte fraccionaria, entonces ese punto se dibujará ya con tres píxeles con diferente saturación cromática (columna derecha). Precisamente este dibujado con tres píxeles, pero con diferente saturación cromática permite obtener el efecto de suavizado.
2. Algoritmo de suavizado
Los métodos de la clase CCanvas que dibujan primitivos mediante el suavizado para representarlas en la pantalla, usan el método común de cálculo de color del punto PixelSetAA.
| Método | Método final de cálculo de la imagen |
|---|---|
| PixelSetAA | PixelSetAA |
| LineAA | PixelSetAA |
| PolylineAA | LineAA -> PixelSetAA |
| PolygonAA | LineAA -> PixelSetAA |
| TriangleAA | LineAA -> PixelSetAA |
| CircleAA | PixelSetAA |
La demostración del método de dibujado con suavizado PixelSetAA se ve en la fig. 1.
Resulta que al dibujar con suavizado, el método PixelSetAA es la base de la clase CCanvas. Por eso, pienso que será interesante descubrir cómo se implementa precisamente el algoritmo de suavizado.
Recordemos que las coordenadas X e Y del método PixelSetAA tienen el tipo double, de esta forma, el método PixelSetAA puede adoptar las coordenadas del punto ubicado entre los píxeles:
//+------------------------------------------------------------------+ //| Draw pixel with antialiasing | //+------------------------------------------------------------------+ void CCanvas::PixelSetAA(const double x,const double y,const uint clr) {
A continuación, declaramos tres matrices. La matriz rr[] es una matriz auxiliar para calcular cuánto cubre un píxel virtual (píxel que queremos dibujar) a los píxeles físicos de la pantalla. Las matrices xx[] y yy[] son las matrices de las coordenadas con las que se dibujarán los píxeles para transmitir a la imagen el efecto de suavizado.
void CCanvas::PixelSetAA(const double x,const double y,const uint clr) { static double rr[4]; static int xx[4]; static int yy[4];
La figura que se encuentraa más abajo demostrará la conexión entre un píxel virtual y la capa de píxeles físicos:
![]()
Fig. 3. Capa de píxeles físicos
Es decir, un píxel virtual (un píxel cuyas coordenadas hemos obtenido mediante cálculos) siempre tiene coordenadas fragmentarias y puede cubrir simultáneamente de forma parcial cuatro píxeles físicos. En este caso, el algoritmo de suavizado debe ejecutar su tarea principal, colorear estos cuatro píxeles físicos con el color del píxel virtual, pero con intensidad diferente. De esta forma se engaña a nuestra mente, el ojo verá una imagen un poco difuminada, pero sin transiciones cromáticas bruscas y con límites suaves.
El siguiente bloque incluye los cálculos preliminares. Obtenemos las coordenadas de entrada redondeadas hasta el número entero más próximo:
static int yy[4]; //--- preliminary calculations int ix=(int)MathRound(x); int iy=(int)MathRound(y);
Para enteder cómo funciona la función matemática MathRound (hacia qué lado se dará el redondeo, si la cifra tiene ".5") es mejor iniciar este código:
void OnStart() { Print("MathRound(3.2)=",DoubleToString(MathRound(3.2),8),"; (int)MathRound(3.2)=",IntegerToString((int)MathRound(3.2))); Print("MathRound(3.5)=",DoubleToString(MathRound(3.5),8),"; (int)MathRound(3.5)=",IntegerToString((int)MathRound(3.5))); Print("MathRound(3.8)=",DoubleToString(MathRound(3.8),8),"; (int)MathRound(3.8)=",IntegerToString((int)MathRound(3.8))); } //+------------------------------------------------------------------+
y el resultado de la ejecución:
MathRound(3.8)=4.00000000; (int)MathRound(3.8)=4 MathRound(3.5)=4.00000000; (int)MathRound(3.5)=4 MathRound(3.2)=3.00000000; (int)MathRound(3.2)=3
A continuación viene el cálculo de delta dx y dy y de la diferencia entre las coordenadas de entrada x e y y los valores redondeados ix y iy:
int iy=(int)MathRound(y); double rrr=0; double k; double dx=x-ix; double dy=y-iy;
Ahora comprobamos: si tanto delta dx, como dy son iguales a cero, entonces abandonamos el método PixelSetAA.
double dy=y-iy; uchar a,r,g,b; uint c; //--- no need for anti-aliasing if(dx==0.0 && dy==0.0) { PixelSet(ix,iy,clr); return; }
Si los deltas no han resultado iguales a cero, pasamos a la preparación de la matriz de píxeles:
PixelSet(ix,iy,clr); return; } //--- prepare array of pixels xx[0]=xx[2]=ix; yy[0]=yy[1]=iy; if(dx<0.0) xx[1]=xx[3]=ix-1; if(dx==0.0) xx[1]=xx[3]=ix; if(dx>0.0) xx[1]=xx[3]=ix+1; if(dy<0.0) yy[2]=yy[2]=iy-1; if(dy==0.0) yy[2]=yy[2]=iy; if(dy>0.0) yy[2]=yy[2]=iy+1;
Precisamente este bloque crea la base para generar la ilusión de una imagen suavizada.
Para visualizar el funcionamiento de este bloque, he escrito el script PrepareArrayPixels.mq5, que mostramos aquí junto con un vídeo del funcionamiento del mismo:
Vídeo 1. Funcionamiento del script PrepareArrayPixels.mq5
Después de rellenar la matriz de píxeles, hay que calcular los "pesos", es decir, el grado en el que el píxel virtual cubre a los píxeles reales:
yy[2]=yy[2]=iy+1; //--- calculate radii and sum of their squares for(int i=0;i<4;i++) { dx=xx[i]-x; dy=yy[i]-y; rr[i]=1/(dx*dx+dy*dy); rrr+=rr[i]; }
Y la etapa final, dibujar el suavizado:
rrr+=rr[i];
}
//--- draw pixels
for(int i=0;i<4;i++)
{
k=rr[i]/rrr;
c=PixelGet(xx[i],yy[i]);
a=(uchar)(k*GETRGBA(clr)+(1-k)*GETRGBA(c));
r=(uchar)(k*GETRGBR(clr)+(1-k)*GETRGBR(c));
g=(uchar)(k*GETRGBG(clr)+(1-k)*GETRGBG(c));
b=(uchar)(k*GETRGBB(clr)+(1-k)*GETRGBB(c));
PixelSet(xx[i],yy[i],ARGB(a,r,g,b));
}
3. Sombra del objeto
Dibujando la sombra, damos a los objetos gráficos un trazado de contornos más suave. Además, aparece un pequeño efecto de volumen: los objetos gráficos visualmente dejan de ser planos. Además, las sombras poseen una propiedad muy útil e interesante: las sombras de los objetos, normalmente, son semitransparentes, y al superponer gráficos con las sombras, se crea un efecto adicional de volumen.
Más abajo se muestran los tipos de sombra más extendidos:
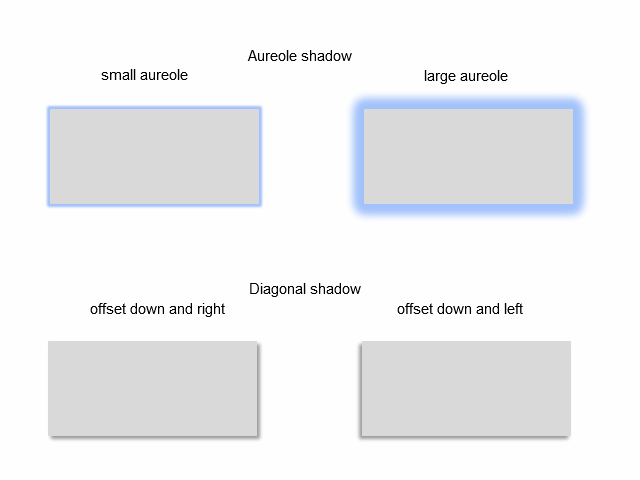
Fig. 4. Tipos de sombra
La sombra del tipo "aureola" puede tener un ajuste llamado amplitud de la aureola. La sombra del tipo "diagonal externa" tiene un ajuste para establecer el ángulo en el que se desplaza la sombra. Ambos tipos de sombra tienen un ajuste para elegir el color de la sombra.
¿Para elegir un algoritmo de dibujado conveniente necesitamos ver de qué consta la sombra? En esto nos ayudará un zoom profundo. Este es el aspecto que tienen las sombras del dibujo 4 con un aumento intenso:
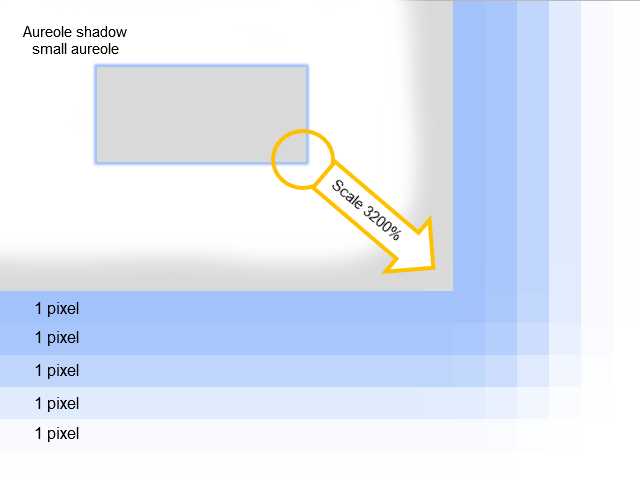
Fig. 5. De qué está formada la sombra.
Como ahora se ve, la sombra de la "aureola" consta de varios contornos con un grosor de 1 píxel. En estos contornos cambia suavemente la saturación de color.
3.2. Obteniendo una distribución normal
Para conseguir una transición suave al dibujar la sombra, usaremos el filtro gráfico más extendido, el difuminación de Gauss (más abajo se hablará sobre el algoritmo de difuminación de Gauss). Este filtro usa distribución normal al calcular las transformaciones aplicadas a cada píxel de la imagen. El cálculo de la difuminación de cada píxel de la imagen depende del radio de difuminación (este parámetro se establece antes de comenzar a aplicar el filtro) y debe realizarse teniendo en cuenta todos los píxeles de alrededor.
Aunque se hable de radio de difuminación, en realidad en los cálculos se aplica una cuadrícula de píxeles con un tamaño de N x N:
![]()
donde Radius es el radio de difuminación.
En el dibujo de más abajo se muestra un ejemplo de una cuadrícula de píxeles para un radio de difminación igual a 3.
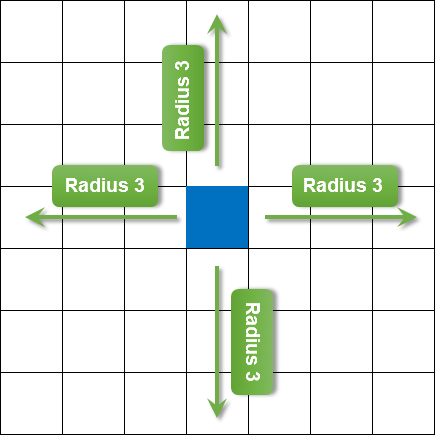
Fig. 6. Radio de difuminación
En este punto, voy a omitir la teoría de la aceleración de cálculos de este filtro, solo diré que utilizaremos la propiedad de separabilidad del filtro de Gauss: primero aplicamos la difuminación en el eje X, y después la aplicamos en el eje Y. En este caso, los cálculos ven aumentada su velocidad, sin que por ello sufra su calidad.
La influencia de los píxeles colindantes en el píxel calculado no es unívoca y se calcula por distribución normal. Cuanto más lejos se encuentre el píxel del que calculamos, menor será su influencia en el píxel calculado. Para calcular la distribución normal de Gauss vamos a usar la la biblioteca de análisis numérico ALGLIB. El script GQGenerateRecToExel.mq5 nos ayudará a mostrar de forma visual el modelado de una distribución normal. Este script obtiene con la ayuda de la biblioteca ALGLIB la matriz de los coeficientes de peso de la distribución normal y muestra estos valores en el archivo <catálogo de datos>\MQL5\Files\GQGenerateRecToExel.csv. Y este es el aspecto del gráfico que hemos construido basándonos en el archivo GQGenerateRecToExel.csv:
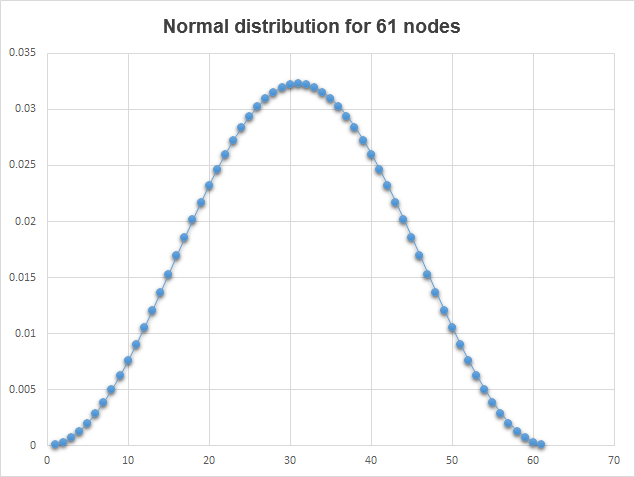
Fig. 7. Distribución normal
Usando como ejemplo el script GQGenerateRecToExel.mq5, veremos un ejemplo de cómo obtener la matriz de los coeficientes de peso de una distribución normal. Aquí y en lo sucesivo, en los scripts se usará la misma función GetQuadratureWeights:
//+------------------------------------------------------------------+ //| Gets array of quadrature weights | //+------------------------------------------------------------------+ bool GetQuadratureWeights(const double mu0,const int n,double &w[]) { CAlglib alglib; // static member of class CAlglib double alp[]; // array alpha coefficients double bet[]; // array beta coefficients ArrayResize(alp,n); ArrayResize(bet,n); ArrayInitialize(alp,1.0); // initializes a numeric array alpha ArrayInitialize(bet,1.0); // initializes a numeric array beta double out_x[]; int inf=0; //| Info - error code: | //| * -3 internal eigenproblem solver hasn't | //| converged | //| * -2 Beta[i]<=0 | //| * -1 incorrect N was passed | //| * 1 OK | alglib.GQGenerateRec(alp,bet,mu0,n,inf,out_x,w); if(inf!=1) { Print("Call error in CGaussQ::GQGenerateRec"); return(false); } return(true); }
Esta función rellena la matriz w[] con los coeficientes de peso de la distribución normal, y también comprueba el resultado de la llamada de la función de la biblioteca ALGLIB a través del análisis de la variable inf.
Al dibujar la sombra en el canvas se usan operaciones con recursos ResourceReadImage, como la lectura de los datos del recurso gráfico y el rellanado de la matriz con estos datos.
Al trabajar con los recursos conviene recordar que las matrices de los píxeles se guardan en el formato uint (más información: representación de color ARGB). Asimismo, hay que saber cómo se transforma una imagen bidimensional, que tiene altura y anchura, en una matriz unidimensional. El algoritmo de transformación es el siguiente: se pegan consecutivamente las imágenes en una gran línea. En el dibujo se muestran dos imágenes con dimensiones de 4 x 3 píxeles y 3 x 4 píxeles, que se transforman en una matriz unidmiensional:
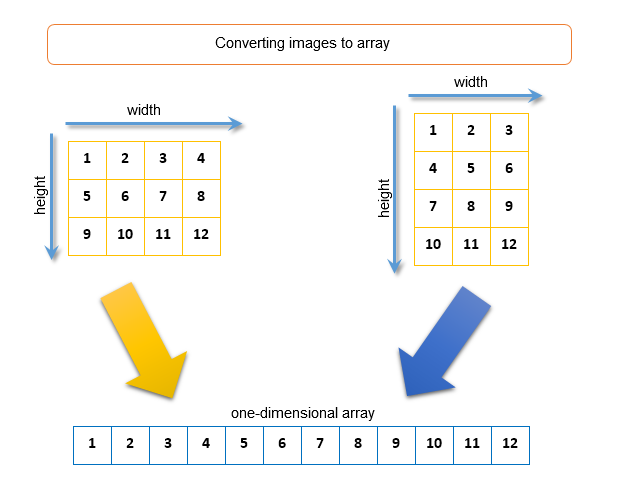
Fig. 8. Transformación de una imagen en una matriz unidimensional
4. Ejemplo de algoritmo de difuminación de Gauss
La difuminación de Gauss la veremos tomando como ejemplo el algoritmo de ShadowTwoLayers.mq5. Para trabajar, necesitamos dos archivos a conectar: Canvas.mqh y la biblioteca de análisis numérico ALGLIB:
#property script_show_inputs #include <Canvas\Canvas.mqh> #include <Math\Alglib\alglib.mqh>
Parámetros de entrada:
//--- input input uint radius=4; // radius blur input color clrShadow=clrBlack; // shadow color input uchar ShadowTransparence=160; // transparency shadows input int ShadowShift=3; // shadow shift input color clrDraw=clrBlue; // shadow color input uchar DrawwTransparence=255; // transparency draws //---
Para trabajar, crearemos dos canvas. El canvas inferior coumplirá la función de capa en la que se dibuja la sombra, y el canvas superior cumplirá la función de capa de trabajo, en ella se dibujarán las figuras gráficas. El tamaño de ambos canvas es igual al tamaño del gráfico (no describiré las funciones de obtención de la altura y anchura del gráfico en píxeles, puesto que estos ejemplos existen en la documentación, en el apartado Ejemplos de trabajo con el gráfico):
//--- create canvas CCanvas CanvasShadow; CCanvas CanvasDraw; if(!CanvasShadow.CreateBitmapLabel("ShadowLayer",0,0,ChartWidth, ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return; } if(!CanvasDraw.CreateBitmapLabel("DrawLayer",0,0,ChartWidth ,ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return; }
Ahora vamos a dibujar un poco el canvas. Primero dibujamos en el canvas inferior las piezas de trabajo de la figuras de sombra (por defecto, las sombras se dibujan transparentes), y después dibujamos un rectángulo en el canvas superior.
//--- draw on canvas CanvasShadow.Erase(ColorToARGB(clrNONE,0)); CanvasShadow.FillRectangle(ChartWidth/10,ChartHeight/10, ChartWidth/2-ChartWidth/10,ChartHeight/10*9,ColorToARGB(clrShadow,ShadowTransparence)); CanvasShadow.FillRectangle(ChartWidth/2,ChartHeight/12,ChartWidth/3*2, ChartHeight/2,ColorToARGB(clrShadow,ShadowTransparence)); CanvasShadow.Update(); CanvasDraw.Erase(ColorToARGB(clrNONE,0)); CanvasDraw.FillRectangle(ChartWidth/10-ShadowShift,ChartHeight/10-ShadowShift,ChartWidth/2-ChartWidth/10-ShadowShift, ChartHeight/10*9-ShadowShift,ColorToARGB(clrDraw,DrawwTransparence)); CanvasDraw.Update();
Nos debe salir un dibujo así (preste atención: los rectángulos de la "sombra" aún no están difuminados):
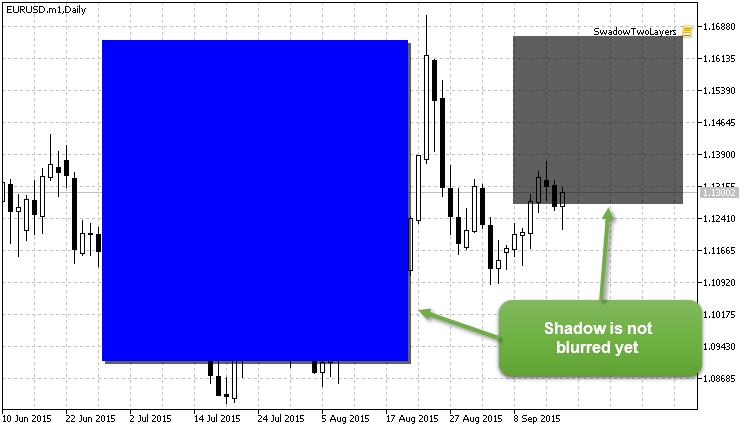
Fig. 9. Las sombras aún no están difuminadas
La difuminación se realizará en el canvas inferior (CanvasShadow). Para ello, hay que leer los datos (ResourceReadImage) del recurso gráfico del canvas inferior (CanvasShadow.ResourceName()) y rellenar con estos datos la matriz unidimensional (res_data):
//+------------------------------------------------------------------+ //| reads data from the graphical resource | //+------------------------------------------------------------------+ ResetLastError(); if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height)) { Print("Error reading data from the graphical resource ",GetLastError()); Print("attempt number two"); //--- attempt number two: now the picture width and height are known ResetLastError(); if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height)) { Print("Error reading data from the graphical resource ",GetLastError()); return; } }
El siguiente paso es obtener la matriz de los coeficientes de peso de la distribución normal a través de la llamada de la función GetQuadratureWeights y la descomposición de la matriz unidimensional en cuatro matrices: Alfa, Red, Green, Blue (canal alfa, rojo, verde, azul). La descomposición en colores es imprescindible porque los efectos gráficos se deben aplicar para cada componente del color.
//+------------------------------------------------------------------+ //| decomposition of pictures on the components r, g, b | //+------------------------------------------------------------------+ ... if(!GetQuadratureWeights(1,NNodes,weights)) return; for(int i=0;i<size;i++) { clr_temp=res_data[i]; a_data[i]=GETRGBA(clr_temp); r_data[i]=GETRGBR(clr_temp); g_data[i]=GETRGBG(clr_temp); b_data[i]=GETRGBB(clr_temp); }
El siguiente fragmento de código es el responsable de la "magia": la difuminación. Primero difuminamos la imagen conforme al eje X, y después hacemos lo mismo con el eje de la Y. Este enfoque surge de la propiedad de la separabilidad del filtro de Gauss, logrando, además, una aceleración en los cálculos, sin que por ello se vea afectada su calidad. Veamos un ejemplo de cómo se forma la difuminación conforme a este eje de la imagen, el eje X:
//+------------------------------------------------------------------+ //| blur horizontal (axis X) | //+------------------------------------------------------------------+ uint XY; // pixel coordinate in the array double a_temp=0.0,r_temp=0.0,g_temp=0.0,b_temp=0.0; int coef=0; int j=(int)radius; for(uint Y=0;Y<res_height;Y++) // cycle on image width { for(uint X=radius;X<res_width-radius;X++) // cycle on image height { XY=Y*res_width+X; a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0; coef=0; for(int i=-1*j;i<j+1;i=i+1) { a_temp+=a_data[XY+i]*weights[coef]; r_temp+=r_data[XY+i]*weights[coef]; g_temp+=g_data[XY+i]*weights[coef]; b_temp+=b_data[XY+i]*weights[coef]; coef++; } a_data[XY]=(uchar)MathRound(a_temp); r_data[XY]=(uchar)MathRound(r_temp); g_data[XY]=(uchar)MathRound(g_temp); b_data[XY]=(uchar)MathRound(b_temp); } //--- remove artifacts on the left for(uint x=0;x<radius;x++) { XY=Y*res_width+x; a_data[XY]=a_data[Y*res_width+radius]; r_data[XY]=r_data[Y*res_width+radius]; g_data[XY]=g_data[Y*res_width+radius]; b_data[XY]=b_data[Y*res_width+radius]; } //--- remove artifacts on the right for(uint x=res_width-radius;x<res_width;x++) { XY=Y*res_width+x; a_data[XY]=a_data[(Y+1)*res_width-radius-1]; r_data[XY]=r_data[(Y+1)*res_width-radius-1]; g_data[XY]=g_data[(Y+1)*res_width-radius-1]; b_data[XY]=b_data[(Y+1)*res_width-radius-1]; } }
Bien, vemos dos ciclos incorporados:
for(uint Y=0;Y<res_height;Y++) // cycle on image width { for(uint X=radius;X<res_width-radius;X++) // cycle on image height { ... } }
Esta inclusión posibilita el paso por cada píxel de la imagen:
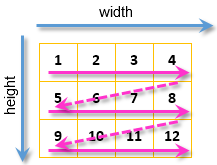
Fig. 10. Paso por cada píxel de la imagen
El ciclo incorporado posibilita el cálculo de la difuminación conforme al eje X para cada píxel:
for(uint X=radius;X<res_width-radius;X++) // cycle on image height { XY=Y*res_width+X; a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0; coef=0; for(int i=-1*j;i<j+1;i=i+1) { a_temp+=a_data[XY+i]*weights[coef]; r_temp+=r_data[XY+i]*weights[coef]; g_temp+=g_data[XY+i]*weights[coef]; b_temp+=b_data[XY+i]*weights[coef]; coef++; } a_data[XY]=(uchar)MathRound(a_temp); r_data[XY]=(uchar)MathRound(r_temp); g_data[XY]=(uchar)MathRound(g_temp); b_data[XY]=(uchar)MathRound(b_temp); }
Para cada píxel a la izquierda y la derecha se escoge un número de píxeles adyacentes igual al radio de difuminación. Recordemos que ya hemos obtenido anteriormente la matriz de los coeficientes de peso de la distribución normal a través de la función GetQuadratureWeights. Resulta la siguiente compatibilidad: número de píxeles adyacentes de la izquierda + píxel para el que se calcula la difuminación + número de píxeles adyacentes de la derecha = número de elementos de la matriz de los coeficientes de peso. De esta forma, cada píxel adyacente se corresponde con un valor determinado en la matriz de los coeficientes de peso.
La difuminación del color se calcula así: cada píxel adyacente se multiplica por el coeficiente de peso que le corresponde, luego los valores obtenidos se suman. Más abajo mostramos un ejemplo de cálculo de la difuminación de una imagen en color rojo, con un radio establecido igual a 4:
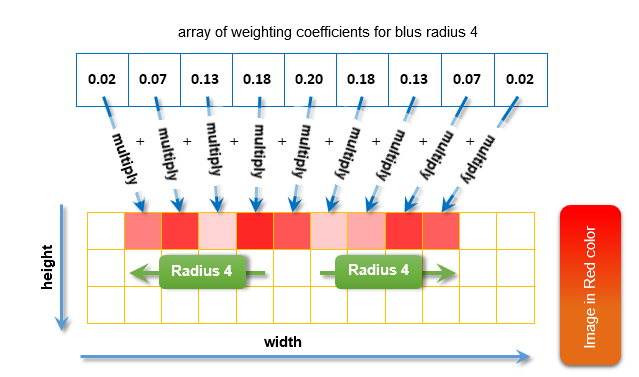
Fig. 11. Cálculo de la difuminación
Con este algoritmo de difuminación nos quedan artefactos en los bordes de la imagen: franjas de píxeles sin difuminar. La anchura de estas franjas es igual al radio de difuminación. Cuanto mayor sea el radio de difuminación, más anchas serán las franjas de los píxeles no difuminados. En esta algoritmo, estos artefactos se eliminan copiando píxeles difuminados:
//--- remove artifacts on the left for(uint x=0;x<radius;x++) { XY=Y*res_width+x; a_data[XY]=a_data[Y*res_width+radius]; r_data[XY]=r_data[Y*res_width+radius]; g_data[XY]=g_data[Y*res_width+radius]; b_data[XY]=b_data[Y*res_width+radius]; } //--- remove artifacts on the right for(uint x=res_width-radius;x<res_width;x++) { XY=Y*res_width+x; a_data[XY]=a_data[(Y+1)*res_width-radius-1]; r_data[XY]=r_data[(Y+1)*res_width-radius-1]; g_data[XY]=g_data[(Y+1)*res_width-radius-1]; b_data[XY]=b_data[(Y+1)*res_width-radius-1]; }
Se realizarán operaciones análogas de difminación para el eje Y. Como resultado obtenemos cuatro matrices a1_data[], r1_data[], g1_data[], b1_data[], en las que se guardan los valores difuminados para el canal alfa, rojo, verde, azul, respectivamente. Solo queda tomar el color para cada píxel de estos cuatro componentes y aplicarlo al canvas CanvasShadow:
//--- for(int i=0;i<size;i++) { clr_temp=ARGB(a1_data[i],r1_data[i],g1_data[i],b1_data[i]); res_data[i]=clr_temp; } for(uint X=0;X<res_width;X++) { for(uint Y=radius;Y<res_height-radius;Y++) { XY=Y*res_width+X; CanvasShadow.PixelSet(X,Y,res_data[XY]); } } CanvasShadow.Update(); CanvasDraw.Update(); Sleep(21000);
Resultado de la difuminación de la capa con sombras:
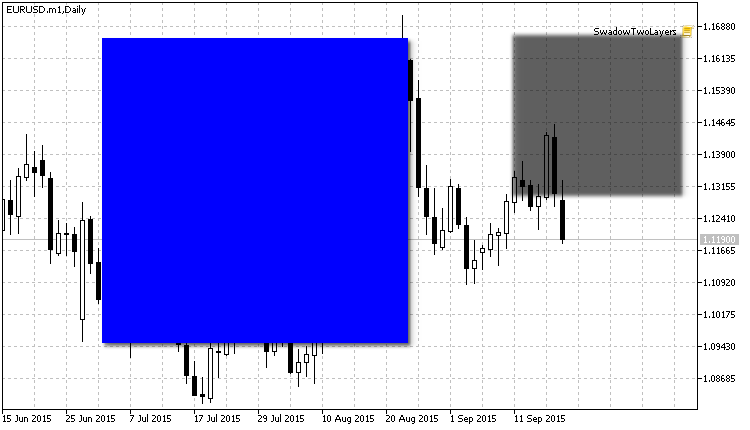
Fig. 12. Las sombras ahora están difuminadas
5. Clase de dibujado de la sombra
Implementaremos en la clase CGauss un ejemplo del dibujado en el canvas. La clase CGauss permite dibujar dichos primitivos con sombra:
| Primitivos | Descripción |
|---|---|
| LineVertical | Dibuja una línea vertical con sombra |
| LineHorizontal | Dibuja una línea horizontal con sombra |
| Line | Dibuja una línea arbitraria con sombra |
| Polyline | Dibuja una polilínea con sombra |
| Polygon | Dibuja un polígono con sombra |
| Rectangle | Dibuja un rectángulo con sombra |
| Circle | Dibuja un círculo con sombra |
| FillRectangle | Dibuja un rectángulo coloreado con sombra |
| FillTriangle | Dibuja un triángulo coloreado con sombra |
| FillPolygon | Dibuja un polígono coloreado con sombra |
| FillCircle | Dibuja un círculo coloreado con sombra |
| FillEllipse | Dibuja una elipse coloreada con sombra |
| Fill | Colorea un área con sombra |
| TextOut | Muestra el texto con sombra |
Vídeo demostrativo del funcionamiento del script Blur.mq5, que dibuja primitivos con sombras:
Vídeo 2. Dibujado de primitivos con sombras
En la clase CGauss se usa la biblioteca de análisis numérico ALGLIB para calcular el color de la sombra. En esta clase se ha implementado un tipo de sombra, la sombra dibujada como diagonal externa hacia abajo y la derecha con desplazamineto (mirar fig. 4.)
Idea general de la clase CGauss: creamos dos canvas. El canvas inferior coumplirá la función de capa en la que se dibuja la sombra, y el canvas superior cumplirá la función de capa de trabajo, en ella se dibujarán las figuras gráficas. Los tamaños de ambos canvas son iguales al tamaño del gráfico. Además, el canvas inferior al ser creado se traslada en horizontal y vertical en una magnitud igual al desplazamiento de la sombra, de esta forma se facilita el cálculo de las coordenadas de dibujado de las sombras.
El algoritmo de dibujado funciona según el siguiente principio: en el canvas inferior se dibuja consecutivamente un número de objetos igual al radio de difuminación. El color de cada objeto se calcula según el algoritmo de Gauss, logrando una transición suave del color establecido para la sombra hasta la transparencia total.
Conclusión
En el artículo se han analizado los algoritmos de formación del suavizado en la clase CCanvas, diversos ejemplos de cálculo y dibujado de la difuminación y las sombras de los objetos. En los cálculos de formación de la difuminación y las sombras se aplica la biblioteca de análisis numérico ALGLIB.
En base a los ejemplos de implementación de la difuminación se ha escrito la clase CGauss, que dibuja los primitivos gráficos con sombras.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1612
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Asesor experto multiplataforma: Introducción
Asesor experto multiplataforma: Introducción
 Interfaces gráficas IX: Control "Paleta para seleccionar el color" (Capítulo 1)
Interfaces gráficas IX: Control "Paleta para seleccionar el color" (Capítulo 1)
 Interfaces gráficas IX: Elementos "Indicador de progreso" y "Gráfico lineal" (Capítulo 2)
Interfaces gráficas IX: Elementos "Indicador de progreso" y "Gráfico lineal" (Capítulo 2)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Lo probé junto con otras variantes hace aproximadamente un año - sólo Photoshop funcionó con mis fotos originales, de todas las variantes.
Es personal, no te preocupes )
No me gusta mucho el estilo de narración de Vladimir, es un poco aburrido.
Pero aquí es bastante vívido.
¿Qué aplicación práctica pueden tener los gráficos en el trading?
Mucha gente habla incluso de la poca practicidad de las líneas de tendencia, por no hablar de los gráficos de líneas o sombras.
Y lo más cercano a la práctica es comprar y vender, y se pueden hacer botones para ellos. Así que pueden ser más bonitos con la ayuda de sombras ;)
¡ahí tienes, que está cerca de mi pregunta )
¿funcionará con trazo de texto ?!
aquí está mi ejemplo:
(este marcado se hace en Canvas)
el punto es que SI usted hace N copias de texto y colocarlo "en un círculo" alrededor del texto principal, a continuación, con un tamaño de fuente grande (más de 50 puntos ... y tengo ^ 150 puntos) y la inscripción de varias líneas, 5-7 líneas (registros en la pantalla),
entonces al crear OBJETOS - el ordenador portátil puede y colgar ..... Tuve que reiniciar el terminal ... ¡¡¡¡y en kanvas - el portátil está en silencio, pero el tiempo para crear una etiqueta de texto multilínea tales = 5 minutos !!!!
... optimizado el código, ahora en kanvas crea 7 líneas de registro en 101 segundos (un poco más de un minuto).
¡esto sigue siendo muy largo !
¡¡¿Hay alguna manera o método para crear un trazo de texto más rápido ?!!
¡...sigo interesado en las opiniones de los expertos sobre este tema !
¡Gracias !
¡Ahí lo tienes, que está cerca de mi pregunta )
¿funcionará esto con trazo de texto?!
aquí está mi ejemplo:
(este marcado se hace en Canvas)
el punto es que SI usted hace N copias de texto y colocarlo "en un círculo" alrededor del texto principal, a continuación, con un tamaño de fuente grande (más de 50 puntos ... y tengo ^ 150 puntos) y la inscripción de varias líneas, 5-7 líneas (registros en la pantalla),
entonces al crear OBJETOS - el ordenador portátil puede y colgar ..... ¡¡¡¡Tuve que reiniciar el terminal ... y en kanvas - el portátil está en silencio, pero el tiempo para crear una etiqueta de texto multilínea tales = 5 minutos !!!!
... optimizado el código, ahora en kanvas crea 7 líneas de registro en 101 segundos (un poco más de un minuto).
¡esto sigue siendo muy largo !
¡¡¿Hay alguna manera o método para crear un trazo de texto más rápido ?!!
¡...sigo interesado en las opiniones de los expertos sobre este tema !
¡Gracias !
¡Ahí lo tienes, que está cerca de mi pregunta también )
¿funcionará con trazo de texto ?!
aquí está mi ejemplo:
(este marcado se realiza en Canvas)
el punto es que si usted hace N copias de texto y colocarlo "en un círculo" alrededor del texto principal, a continuación, con un tamaño de fuente grande (más de 50 puntos ... y tengo ^ 150 puntos) y la inscripción de varias líneas, 5-7 líneas (registros en la pantalla),
entonces al crear OBJETOS - el ordenador portátil puede y colgar ..... Tuve que reiniciar el terminal ... ¡¡¡¡y en kanvas - el portátil está en silencio, pero el tiempo para crear una etiqueta de texto multilínea tales = 5 minutos !!!!
... optimizado el código, ahora en kanvas crea 7 líneas de registro durante 101 segundos (un poco más de un minuto).
¡eso sigue siendo mucho tiempo !
¡¿Hay alguna forma o método para crear un trazo de texto más rápido?!
¡...sigo interesado en las opiniones de los expertos sobre este tema !
¡Gracias !