MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
研究 CCanvas 类。抗锯齿和阴影

研究 CCanvas 类。抗锯齿和阴影

MetaTrader 5 — 示例 | 15 九月 2016, 10:49
1 812 0
Vladimir Karputov
Vladimir Karputov

目录

 

概论

我相信, 利用 CCanvas 类能够在绘图时解决显示动态效果的问题。例如, 通过抗锯齿算法实现图形构造可令它们具有更吸引人的外观。或者在显示指标线时绘制称之为花键的新样式。或许在单独窗口里绘制动态指标, 某种程度上类似于在示波器上绘制频率特性。在任何情况下, 绘图为个人发展开辟了新的应用领域。

 

1. 坐标和画布

画布内建于图表的坐标系。在此情况下图表的大小以像素度量。图表左上角的坐标为 (0,0)。

请留意, 当在画布上绘图时坐标和彩色需要以 int 基本类型给定。以及, 用于抗锯齿方法 PixelSetAA 作图时的基本类型, 坐标要以 double 给定, 方法 CircleAA 使用的坐标要以 int 给定, 圆形的尺寸 — 要以 double 给定。

方法 坐标 大小
PixelSetAA double -
LineAA int -
PolylineAA int -
PolygonAA int -
TriangleAA int -
CircleAA int double

 

也就是说, 当为 PixelSetAA 方法给定坐标时, 点坐标可能类似于: (120.3, 25.56)。脚本 PixelSetAA.mq5 绘制两纵列, 每列十一点共。在左列, 每一点沿 X 轴增加 0.1, 且沿 Y 轴增加 3.0。在右列, 每一点沿 X 轴增加 0.1, 且沿 Y 轴增加 3.1。

为便于观察这些点如何绘制, PixelSetAA.mq5 脚本的操作结果被放大了若干倍:

图例. 1. 方法 PixelSetAA 的操作

图例. 1. 方法 PixelSetAA 的操作

为了更好的观察, 我添加了抗锯齿边框以及绘图坐标的文本。

图例. 2. 方法 PixelSetAA 的直观操作

图例. 2. 方法 PixelSetAA 的直观操作

如您所见, 只有不带分数的像素坐标按照给定颜色着色。不过, 如果点的坐标之一带分数, 则该点将会使用两种不同的饱和度着色 (左列)。

点的两个坐标均含分数的情况下, 则每个点用三个不同饱和度的像素绘制 (右列)。这种采用各种饱和度特别绘制的三个像素可以达到平滑的效果。

 

2. 抗锯齿算法

类 CCanvas 所含的抗锯齿绘图基础方法, 使用通用点颜色计算方法 PixelSetAA 用于屏幕显示。

方法 图像计算的最终方法
PixelSetAA PixelSetAA
LineAA PixelSetAA
PolylineAA LineAA -> PixelSetAA
PolygonAA LineAA -> PixelSetAA
TriangleAA LineAA -> PixelSetAA
CircleAA PixelSetAA

抗锯齿绘图方法 PixelSetAA 的展示如图例. 1 所示。

结果发现当绘制抗锯齿时, 方法 PixelSetAA 充当 CCanvas 类的基础。因此, 我相信挖掘抗锯齿算法是如何准确实施的, 这一定很有趣。

让我提醒你, PixelSetAA 方法的 X 和 Y 坐标有一个 double 类型, 因此, 方法 PixelSetAA 可以得到 位于像素之间 的点坐标:

//+------------------------------------------------------------------+
//| 绘制抗锯齿像素                                                    |
//+------------------------------------------------------------------+
void CCanvas::PixelSetAA(const double x,const double y,const uint clr)
  {

下一步, 我们将声明三个数组。数组 rr[] 是一个辅助数组, 用于计算一个虚拟像素 (可绘制) 覆盖多少个屏幕上的物理像素。数组 xx[] 和 yy[] 是坐标数组, 用于绘制增加图像平滑效果的像素。

void CCanvas::PixelSetAA(const double x,const double y,const uint clr)
  {
   static double rr[4];
   static int    xx[4];
   static int    yy[4];

下图展示了一个虚拟像素及其覆盖的物理像素之间的连接:

图例. 3. 物理像素的覆盖面

图例. 3. 物理像素的覆盖面

这意味着一个 虚拟像素 (计算出的坐标) 经常含有分数坐标， 且能够同时覆盖 四个物理像素。在这种情况下, 抗锯齿算法需要执行它的主要职责 — 用一个虚拟像素的颜色为四个物理像素着色, 但使用不同的迭代。如此, 它将会蒙骗我们的视觉 — 眼睛会看到一个温和色彩混合且边界柔和的略微模糊的图像。

下一个模块包含初步计算。我们获取传入坐标值, 并舍入为最接近的整数:

static int    yy[4];
//--- 初步计算
   int    ix=(int)MathRound(x);
   int    iy=(int)MathRound(y);

为了更好地理解一个数学函数 MathRound 如何工作 (如果数字含有分数 ".5", 向上舍入或向下舍入), 建议运行以下代码:

void OnStart()
  {
   Print("MathRound(3.2)=",DoubleToString(MathRound(3.2),8),"; (int)MathRound(3.2)=",IntegerToString((int)MathRound(3.2)));
   Print("MathRound(3.5)=",DoubleToString(MathRound(3.5),8),"; (int)MathRound(3.5)=",IntegerToString((int)MathRound(3.5)));
   Print("MathRound(3.8)=",DoubleToString(MathRound(3.8),8),"; (int)MathRound(3.8)=",IntegerToString((int)MathRound(3.8)));
  }
//+------------------------------------------------------------------+

及执行结果

MathRound(3.8)=4.00000000; (int)MathRound(3.8)=4
MathRound(3.5)=4.00000000; (int)MathRound(3.5)=4
MathRound(3.2)=3.00000000; (int)MathRound(3.2)=3

紧接着计算 dx 和 dy 的增量 — 传入坐标 x 和 y 之间的差值, 以及它们的舍入值 ix 和 iy:

int    iy=(int)MathRound(y);
   double rrr=0;
   double k;
   double dx=x-ix;
   double dy=y-iy;

现在, 我们必须检查: 若 dx 和 dy 两者均等于零, 则我们退出 PixelSetAA 方法。

double dy=y-iy;
   uchar  a,r,g,b;
   uint   c;
//--- 对于抗锯齿没必要
   if(dx==0.0 && dy==0.0)
     {
      PixelSet(ix,iy,clr);
      return;
     }

如果增量不等于零, 那么我们用准备的像素数组继续处理:

PixelSet(ix,iy,clr);
      return;
     }
//--- 准备像素数组
   xx[0]=xx[2]=ix;
   yy[0]=yy[1]=iy;
   if(dx<0.0)
      xx[1]=xx[3]=ix-1;
   if(dx==0.0)
      xx[1]=xx[3]=ix;
   if(dx>0.0)
      xx[1]=xx[3]=ix+1;
   if(dy<0.0)
      yy[2]=yy[2]=iy-1;
   if(dy==0.0)
      yy[2]=yy[2]=iy;
   if(dy>0.0)
      yy[2]=yy[2]=iy+1;

此模块专门创建了一个基础, 用于平滑图像错觉。

为了此模块的直观操作, 我编写了一段 PrepareArrayPixels.mq5 脚本, 并录制了它如何工作的视频:

视频 1。脚本 PrepareArrayPixels.mq5 的操作

当像素数组填满之后, 计算 "权重", 看看一个虚拟像素如何做到覆盖真实像素:

yy[2]=yy[2]=iy+1;
//--- 计算半径及其平方和
   for(int i=0;i<4;i++)
     {
      dx=xx[i]-x;
      dy=yy[i]-y;
      rr[i]=1/(dx*dx+dy*dy);
      rrr+=rr[i];
     }

还有最后的步骤 — 绘制模糊:

rrr+=rr[i];
     }
//--- 绘制像素
   for(int i=0;i<4;i++)
     {
      k=rr[i]/rrr;
      c=PixelGet(xx[i],yy[i]);
      a=(uchar)(k*GETRGBA(clr)+(1-k)*GETRGBA(c));
      r=(uchar)(k*GETRGBR(clr)+(1-k)*GETRGBR(c));
      g=(uchar)(k*GETRGBG(clr)+(1-k)*GETRGBG(c));
      b=(uchar)(k*GETRGBB(clr)+(1-k)*GETRGBB(c));
      PixelSet(xx[i],yy[i],ARGB(a,r,g,b));
     }

 

3. 对象阴影

绘制阴影为图形对象添加了一个柔和的外轮廓, 从而创造了一点立体效果, 所以图形对象不再看起来很平。此外, 阴影还有一个很有趣、有益的属性: 物体的阴影通常是透明的, 在其上叠加带阴影的图形可创建立体感觉。


3.1. 阴影类型

最常见的阴影类型如下所示:

图例. 4. 阴影类型

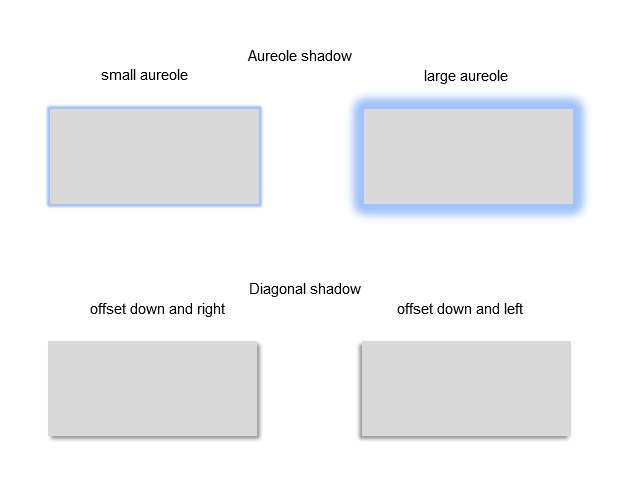
图例. 4. 阴影类型

"光环" 阴影也许可以设置光环宽度。"外部对角线" 阴影也许可以设置阴影透视的角度。这两种类型的阴影均可选择设置颜色。

若要选择绘制阴影的相关算法, 我们必须观察阴影要包括什么。在图像的这些地方灵活地缩放。参看下图, 从图像 4中近距离观察阴影如何形成

图例. 5. 阴影包括什么

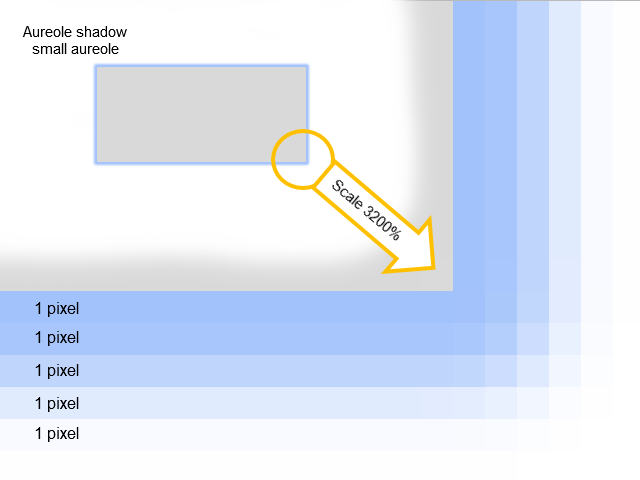
图例. 5. 阴影包括什么

现在已经清楚了 "光环" 阴影是由若干 1 像素宽度的轮廓构成。这些轮廓的色彩饱和度逐级变化。


3.2. 获取正态分布

当绘制阴影时为了得到平稳过渡, 我们将使用最常见的图形滤波器 — 高斯模糊 (有关高斯模糊算法的信息在下面提供)。当计算应用到图像每一个像素的变换时, 滤波器使用正态分布。图像中每个像素的模糊计算取决于模糊半径 (使用滤波器之前的给定参数), 并且对于所有周围像素必须小心执行。

尽管提到的是模糊半径, 实际上是用一个 N × N 的像素网格用于计算:

网格公式

此处 Radius 是模糊半径。

下面的插图显示了一个模糊半径等于 3 的像素网格的例子。

图例. 6. 模糊半径

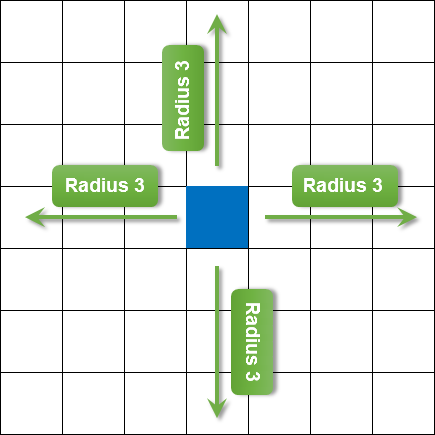
图例. 6. 模糊半径

我不打算涉及此滤波器的快速计算理论, 只会略微提到一些高斯滤波器将会用到的可分离性属性: 首先我们沿 X 轴进行模糊化, 然后在 Y 轴上进行处理。这有助于计算速度更快, 而不影响质量。

相邻像素的影响对于像素计算是不均匀的, 可用正态分布计算。进一步, 来自计算的像素, 影响更小。通过高斯算法计算正态分布, 我们将使用 数值分析库 ALGLIB。脚本 GQGenerateRecToExel.mq5 将帮助我们清晰地展示一个正态分布模型。该脚本使用 ALGLIB 库 接收一个正态分布的权重系数数组, 并显示在文件 <data catalogue>\MQL5\Files\GQGenerateRecToExel.csv 里的这些数值。这是在 GQGenerateRecToExel.csv 文件数据基础上构建的图表外观:

图例. 7. 正态分布

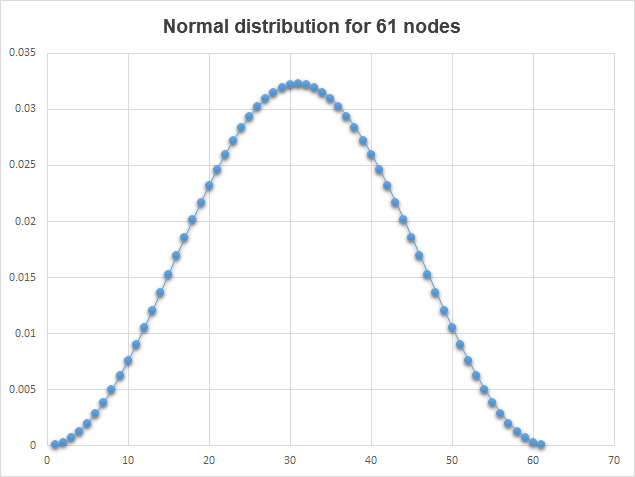
图例. 7. 正态分布

使用 GQGenerateRecToExel.mq5 脚本作为示例, 我们将检查获取正态分布权重系数数组的示例。脚本里将同样使用 GetQuadratureWeights 函数:

//+------------------------------------------------------------------+
//| 获取积分权重数组                                                  |
//+------------------------------------------------------------------+
bool GetQuadratureWeights(const double mu0,const int n,double &w[])
  {
   CAlglib alglib;            // 类 CAlglib 的静态成员
   double      alp[];         // α 系数数组 
   double      bet[];         // β 系数数组
   ArrayResize(alp,n);
   ArrayResize(bet,n);
   ArrayInitialize(alp,1.0);  // 初始化 α 数组数值
   ArrayInitialize(bet,1.0);  // 初始化 β 数组数值

   double      out_x[];
   int         inf=0;
//| 错误代码:                                                        |
//|                 * -3    内部特征问题求解器尚未                    |
//|                         融合                                     |
//|                 * -2    Beta[i]<=0                               |
//|                 * -1    传递的 N 不正确                           |
//|                 *  1    OK                                       |
   alglib.GQGenerateRec(alp,bet,mu0,n,inf,out_x,w);
   if(inf!=1)
     {
      Print("调用 CGaussQ::GQGenerateRec 错误");
      return(false);
     }
   return(true);
  }

此函数用正态分布的权重系数填充 w[] 数组, 并通过分析 inf 变量来检查调用 ALGLIB 库 函数的结果。


3.3. 资源

当在画布上绘制阴影时, 使用 (ResourceReadImage) 操纵资源, 例如, 从图形资源里读取数据, 并用此数据填充数组。

当操纵资源时您应留意像素数组被保存为 uint 格式 (更多参阅: ARGB 色彩呈现)。您还应该知道如何将具有宽度和高度的 2D 图像转换为一维数组。用于转换的算法如下: 按顺序将图像的每一行转成一长溜。以下插图显示了两幅大小为 4 x 3 像素和 3 x 4 像素的图像, 将它们转化为一维数组:

图例. 8. 转换图像为一维数组

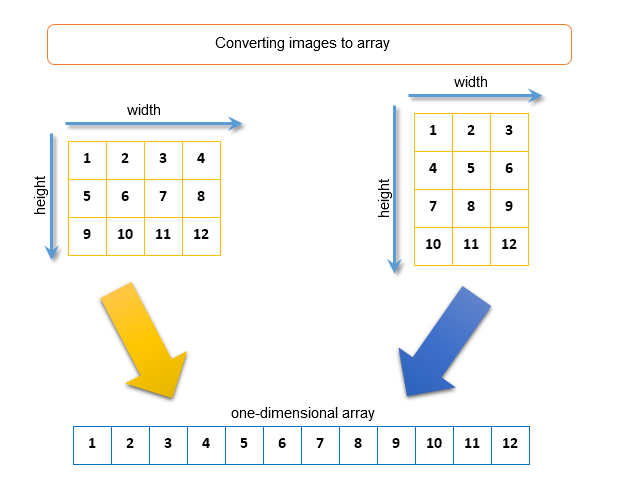
图例. 8. 转换图像为一维数组

 

4. 高斯模糊算法的示例

高斯模糊将会考虑应用 ShadowTwoLayers.mq5 算法。脚本操作需要两个包含文件 Canvas.mqh 和 数值分析库 ALGLIB:

#property script_show_inputs
#include <Canvas\Canvas.mqh>
#include <Math\Alglib\alglib.mqh>

输入参数:

//--- 输入
input uint  radius=4;               // 模糊半径
input color clrShadow=clrBlack;     // 阴影颜色
input uchar ShadowTransparence=160; // 透明度
input int   ShadowShift=3;          // 阴影偏移
input color clrDraw=clrBlue;        // 阴影颜色
input uchar DrawwTransparence=255;  // 透明度
//---

我们将创建两块画布。底层画布将执行绘制阴影的功能, 上层画布将作为工作层用来绘制图形说明。两块画布的大小等于图表大小 (获取图表高度和宽度的函数描述在此未给出, 因为这些例程在演示版块 操纵图表示例 里提供):

//--- 创建画布
   CCanvas CanvasShadow;
   CCanvas CanvasDraw;
   if(!CanvasShadow.CreateBitmapLabel("ShadowLayer",0,0,ChartWidth,
      ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE))
     {
      Print("创建画布错误: ",GetLastError());
      return;
     }
   if(!CanvasDraw.CreateBitmapLabel("DrawLayer",0,0,ChartWidth
      ,ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE))
     {
      Print("创建画布错误: ",GetLastError());
      return;
     }

现在我们在画布上涂一点。首先, 我们将在底层画布上绘制一片阴影 (阴影绘制省缺为透明), 然后在上层画布上绘制矩形。

//--- 在画布上绘图
   CanvasShadow.Erase(ColorToARGB(clrNONE,0));
   CanvasShadow.FillRectangle(ChartWidth/10,ChartHeight/10,
                              ChartWidth/2-ChartWidth/10,ChartHeight/10*9,ColorToARGB(clrShadow,ShadowTransparence));
   CanvasShadow.FillRectangle(ChartWidth/2,ChartHeight/12,ChartWidth/3*2,
                              ChartHeight/2,ColorToARGB(clrShadow,ShadowTransparence));
   CanvasShadow.Update();

   CanvasDraw.Erase(ColorToARGB(clrNONE,0));
   CanvasDraw.FillRectangle(ChartWidth/10-ShadowShift,ChartHeight/10-ShadowShift,ChartWidth/2-ChartWidth/10-ShadowShift,
                            ChartHeight/10*9-ShadowShift,ColorToARGB(clrDraw,DrawwTransparence));
   CanvasDraw.Update();

我们应得到如下图像 (注意: 长方形 "阴影" 尚未模糊化):

图例. 9. 阴影尚未模糊化

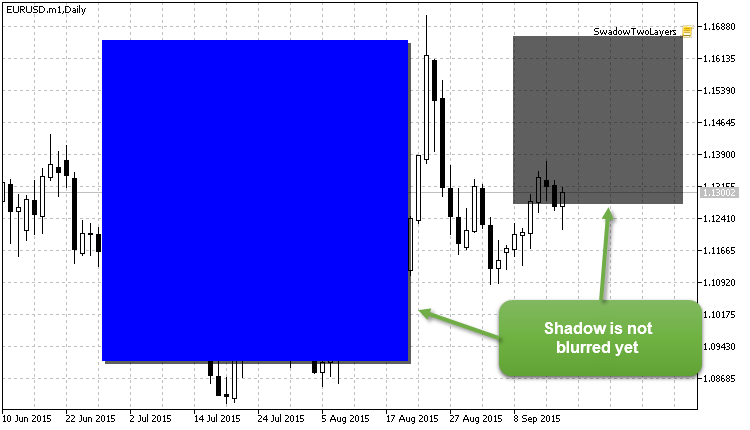
图例. 9. 阴影尚未模糊化

模糊化将在底层画布上执行 (CanvasShadow)。为此目的您必须从图形资源底层画布 (CanvasShadow.ResourceName()) 上读取数据 (ResourceReadImage), 并将此数据填充到一维数组 (res_data):

//+------------------------------------------------------------------+
//| 从图形资源里读取数据                                              |
//+------------------------------------------------------------------+
   ResetLastError();
   if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height))
     {
      Print("从图形资源里读取数据错误 ",GetLastError());
      Print("尝试第二次");
      //--- 尝试第二次: 现在图片宽度和长度已知
      ResetLastError();
      if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height))
        {
         Print("从图形资源里读取数据错误 ",GetLastError());
         return;
        }
     }

下一步通过 GetQuadratureWeights 函数获得正态分布的权重系数数组, 并将一维数组分解为四个数组: Alfa, Red, Green 和 Blue。颜色分解的主要需求是因为图形效果必须应用于每个色彩分量。

//+------------------------------------------------------------------+
//| 图片分解为组件 r, g, b                                            |
//+------------------------------------------------------------------+
...
   if(!GetQuadratureWeights(1,NNodes,weights))
      return;

   for(int i=0;i<size;i++)
     {
      clr_temp=res_data[i];
      a_data[i]=GETRGBA(clr_temp);
      r_data[i]=GETRGBR(clr_temp);
      g_data[i]=GETRGBG(clr_temp);
      b_data[i]=GETRGBB(clr_temp);
     }

以下代码片段负责模糊 "魔法"。首先, 图像将被沿着 X 轴模糊化, 随后沿 Y 轴进行相同处理。这种方法来自高斯滤波器的可分离属性, 可加速计算而无需压缩品质。让我们来看看图像沿 X 轴模糊化的示例:

//+------------------------------------------------------------------+
//| 水平模糊 (轴 X)                                                   |
//+------------------------------------------------------------------+
   uint XY;             // 数组中的像素坐标
   double   a_temp=0.0,r_temp=0.0,g_temp=0.0,b_temp=0.0;
   int      coef=0;
   int      j=(int)radius;
   for(uint Y=0;Y<res_height;Y++)                  // 圈定图像宽度
     {
      for(uint X=radius;X<res_width-radius;X++)    // 圈定图像高度
        {
         XY=Y*res_width+X;
         a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0;
         coef=0;
         for(int i=-1*j;i<j+1;i=i+1)
           {
            a_temp+=a_data[XY+i]*weights[coef];
            r_temp+=r_data[XY+i]*weights[coef];
            g_temp+=g_data[XY+i]*weights[coef];
            b_temp+=b_data[XY+i]*weights[coef];
            coef++;
           }
         a_data[XY]=(uchar)MathRound(a_temp);
         r_data[XY]=(uchar)MathRound(r_temp);
         g_data[XY]=(uchar)MathRound(g_temp);
         b_data[XY]=(uchar)MathRound(b_temp);
        }
      //--- 删除左侧工件
      for(uint x=0;x<radius;x++)
        {
         XY=Y*res_width+x;
         a_data[XY]=a_data[Y*res_width+radius];
         r_data[XY]=r_data[Y*res_width+radius];
         g_data[XY]=g_data[Y*res_width+radius];
         b_data[XY]=b_data[Y*res_width+radius];
        }
      //--- 删除右侧工件
      for(uint x=res_width-radius;x<res_width;x++)
        {
         XY=Y*res_width+x;
         a_data[XY]=a_data[(Y+1)*res_width-radius-1];
         r_data[XY]=r_data[(Y+1)*res_width-radius-1];
         g_data[XY]=g_data[(Y+1)*res_width-radius-1];
         b_data[XY]=b_data[(Y+1)*res_width-radius-1];
        }
     }

所以, 我们看到两个嵌套循环:

for(uint Y=0;Y<res_height;Y++)                  // 圈定图像宽度
     {
      for(uint X=radius;X<res_width-radius;X++)    // 圈定图像高度
        {
         ...
        }
     }

这种嵌套确保了遍历该图像的每个像素:

图例. 10. 遍历图像的每个像素

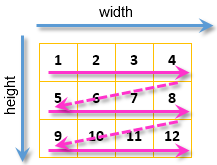
图例. 10. 遍历图像的每个像素

嵌套循环确保沿 X 轴, 每个像素均经过模糊计算:

for(uint X=radius;X<res_width-radius;X++)    // 圈定图像高度
        {
         XY=Y*res_width+X;
         a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0;
         coef=0;
         for(int i=-1*j;i<j+1;i=i+1)
           {
            a_temp+=a_data[XY+i]*weights[coef];
            r_temp+=r_data[XY+i]*weights[coef];
            g_temp+=g_data[XY+i]*weights[coef];
            b_temp+=b_data[XY+i]*weights[coef];
            coef++;
           }
         a_data[XY]=(uchar)MathRound(a_temp);
         r_data[XY]=(uchar)MathRound(r_temp);
         g_data[XY]=(uchar)MathRound(g_temp);
         b_data[XY]=(uchar)MathRound(b_temp);
        }

每个像素左侧和右侧的叠加像素数量等于选择的模糊半径。我提醒您, 以前我们使用 GetQuadratureWeights 函数来获取正态分布的权重系数数组。得到以下兼容: 左侧叠加像素数量 + 执行模糊的计算像素 + 右侧叠加像素数量 = 权重系数元素的数组数量。如此, 每个相邻像素对应于权重系数数组里的特别数值。

这是如何计算每种颜色的模糊: 每相邻像素由对应于它的权重系数相乘, 并将获得的值进行累加。下例是模糊半径等于 4 时, 图像中红色模糊化:

图例. 11. 模糊化计算

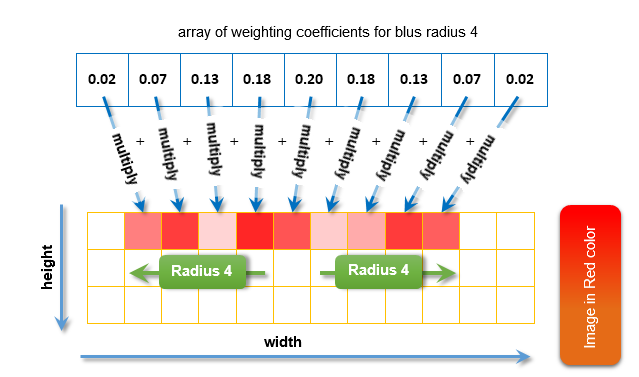
图例. 11. 模糊化计算

工件, 是尚未模糊化的像素条纹, 当应用模糊算法时沿图像边缘的残留部分。这些条纹的宽度等于模糊半径。模糊半径越大, 像素条纹未能模糊的部分越宽 。在算法中, 这些工件是通过复制像素模糊删除:

//--- 删除左侧工件
      for(uint x=0;x<radius;x++)
        {
         XY=Y*res_width+x;
         a_data[XY]=a_data[Y*res_width+radius];
         r_data[XY]=r_data[Y*res_width+radius];
         g_data[XY]=g_data[Y*res_width+radius];
         b_data[XY]=b_data[Y*res_width+radius];
        }
      //--- 删除右侧工件
      for(uint x=res_width-radius;x<res_width;x++)
        {
         XY=Y*res_width+x;
         a_data[XY]=a_data[(Y+1)*res_width-radius-1];
         r_data[XY]=r_data[(Y+1)*res_width-radius-1];
         g_data[XY]=g_data[(Y+1)*res_width-radius-1];
         b_data[XY]=b_data[(Y+1)*res_width-radius-1];
        }

类似的模糊操作也在 Y 轴执行。作为结果, 我们得到四个数组 a1_data[], r1_data[], g1_data[], b1_data[], 它们分别含有 Alpha, red, green 和 blue 的模糊值。它还从四个组件里收集每个像素的颜色, 并将其应用到 CanvasShadow 画布:

//---
   for(int i=0;i<size;i++)
     {
      clr_temp=ARGB(a1_data[i],r1_data[i],g1_data[i],b1_data[i]);
      res_data[i]=clr_temp;
     }
   for(uint X=0;X<res_width;X++)
     {
      for(uint Y=radius;Y<res_height-radius;Y++)
        {
         XY=Y*res_width+X;
         CanvasShadow.PixelSet(X,Y,res_data[XY]);
        }
     }
   CanvasShadow.Update();
   CanvasDraw.Update();
   Sleep(21000);

阴影图层的模糊结果:

图例. 12. 阴影现已模糊化

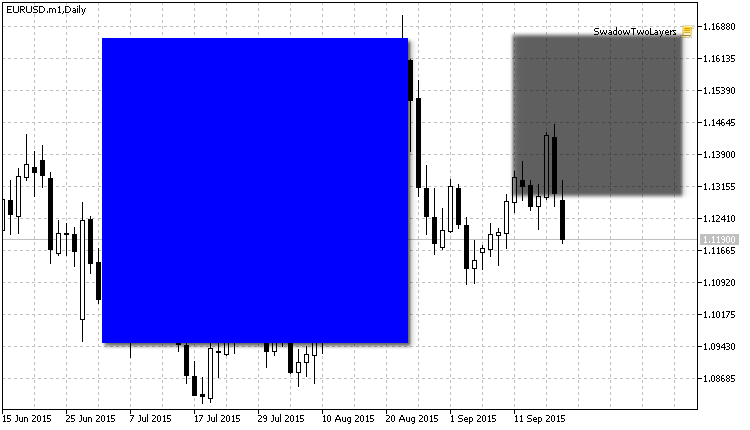
图例. 12. 阴影现已模糊化

 

5. 用于绘制阴影的类

在画布上绘制的例子在 CGauss 类中实现。类 CGauss 可以绘制这些基本阴影:

图元 描述
LineVertical 绘制带阴影的垂直线
LineHorizontal 绘制带阴影的水平线
Line 随意绘制带阴影的线条
Polyline 绘制带阴影的折线
Polygon 绘制带阴影的多边形
Rectangle 绘制带阴影的长方形
Circle 绘制带阴影的圆形
FillRectangle 绘制带阴影的实心长方形
FillTriangle 绘制带阴影的实心三角形
FillPolygon 绘制带阴影的实心多边形
FillCircle 绘制带阴影的实心圆形
FillEllipse 绘制带阴影的实心椭圆型
Fill 填充阴影区域
TextOut 显示带阴影文本

 

脚本 Blur.mq5 的展示视频绘制基本阴影:

视频 2. 绘制基本阴影

数值分析库 ALGLIB 用于在 CGauss 类中计算阴影颜色。在该类中实现了一种阴影类型 — 在右边斜下侧绘制阴影 (参见图例. 4)。

CGauss 的一般思路是创建两块画布。底层画布将执行绘制阴影的功能, 上层画布将作为工作层用来绘制图形说明。两块画布的尺寸等于图表的大小。其中底层画布在创建时, 按照阴影位移大小在水平和垂直方向平移 — 这种计算阴影绘制坐标的方式变得十分容易。

阴影绘制算法遵照以下原理操作: 物体数量等于随后在底层画布上绘制的模糊半径。每个对象的颜色通过高斯算法计算, 从而得到自给定阴影颜色到完全透明的渐变梯度。

 

结论

在此文中, 我已经在 CCanvas 类中涵盖了抗锯齿算法, 附带了为物体计算和绘制模糊化与阴影的示例。由此, 数值分析库 ALGLIB 已应用到形成模糊和色调的计算之中。

除此之外, 还基于各种例程编写了绘制图形基本阴影的 CGauss 类。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/1612

附加的文件 |
下载ZIP
blur.mq5 (5.93 KB)
gqgeneraterectoexel.mq5 (3.68 KB)
pixelsetaa.mq5 (3.99 KB)
preparearraypixels.mq5 (4.98 KB)
shadowtwolayers.mq5 (13.28 KB)
gauss.mqh (24.33 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
如何使用 EA 遵照您的规则拷贝信号? 如何使用 EA 遵照您的规则拷贝信号?
当您订阅了一个信号, 也许会发生这样的情形: 您的交易账户杠杆为 1:100, 而提供者的杠杆为 1:500, 且使用最小手数, 而您的账户余额大约相等 — 但拷贝比率只有 10% 到 15%。本文介绍在这种情况下如何增加拷贝比率。
图形界面 VII: 表格控件 (第一章) 图形界面 VII: 表格控件 (第一章)
MetaTrader 图形界面系列的第七部分处理的是三种表格类型：文本标签型，编辑框型，以及绘制型。另一种重要并且常用的控件是页面，它使您可以显示/隐藏成组的其他控件并且在您的MQL应用程序中开发有效利用空间的界面。
图形界面 VII: 页面控件 (第二章) 图形界面 VII: 页面控件 (第二章)
第七部分的第一章介绍了用于创建三种表格控件的类: 文字标签型表格(CLabelsTable), 编辑框型表格(CTable) 以及绘制型表格(CCanvasTable)。在本文中(第二章)我们将讨论页面(Tabs)控件。
交易机器人的虚假触发保护 交易机器人的虚假触发保护
交易系统的盈利能力不仅由逻辑和金融工具的动态分析精度, 而且还要由逻辑算法的性能品质来定义。虚假触发就是交易机器人主要逻辑品质低的典型。在本文里研究这个特别问题的解决方式。