Kennenlernen der CCanvas Klasse. Kantenglättung (Antialiasing) und Schatten
860
0
Inhaltsverzeichnis
- Einführung
- 1. Koordinaten und Leinwand
- 2. Algorithmus der Kantenglättung
- 3. Der Schatten von Objekten
- 4. Beispiel für den Gaußschen Unschärfealgorithmus
- 5. Klasse für das Zeichnen von Schatten
- Schlussfolgerung
Einführung
Ich glaube, dass die Darstellung verschiedener, dynamischer Effekte mittels der Klasse CCanvas problemlos gelöst werden kann. So könnte zum Beispiel eine Kantenglättung graphischen Objekten ein attraktiveres Aussehen verleihen. Oder das Zeichnen von Indikatorlinien in einem neuen Stil - Splines. Oder vielleicht wird die Darstellung eines dynamischen Indikators in einem separaten Fenster irgendwie ähnlich der Darstellung einer Frequenz in einem Oszilloskop. In jedem Fall öffnen sich neue Horizonte für die eigenen Anwendungen.
1. Koordinaten und Leinwand
Die Leinwand ist auf den Koordinaten des Chart aufgebaut. Es wird die Größe des Chart in Pixel gemessen. Die Ecke des Charts links oben hat die Koordinaten (0,0).
Beachten Sie bitte, zum Zeichnen von Primitives und farbigen Primitives werden deren Koordinaten ausschließlich als int übergeben. Aber für das Zeichnen von Primitives unter Verwendung der Methode zur Kantenglättung PixelSetAA, werden die Koordinaten als double übergeben, die Koordinaten für die Methode CircleAA als int, und die Größe des Kreises — als double.
| Methoden | Koordinaten | Größe |
|---|---|---|
| PixelSetAA | double | - |
| LineAA | int | - |
| PolylineAA | int | - |
| PolygonAA | int | - |
| TriangleAA | int | - |
| CircleAA | int | double |
Das heißt, die Koordinaten für die Methode PixelSetAA eines Punktes könnten so aussehen: (120.3, 25.56). Das Skript PixelSetAA.mq5 zeichnet zwei Spalten mit elf Punkten. In der linken Spalte ist der Zuwachs je Punkt auf der X-Achse 0.1 und der Zuwachs auf der Y-Achse ist 3.0. In der rechten Spalte beträgt der Zuwachs für jeden Punkt auf der X-Achse 0.1 und auf der Y-Achse 3.1.
Um zu sehen, wie die Punkte gezeichnet werden, vergrößern wir die Ergebnisse des Skripts PixelSetAA.mq5 mehrmals:
Fig. 1. Die Arbeitsweise der Methode von PixelSetAA
Zum besseren Verständnis habe ich die Grenzen der Kantenglättung und Koordinatenwerte der Zeichnung ergänzt:
Fig. 2. Optische Arbeitsweise der Methode von PixelSetAA
Wie man sieht, werden nur die Pixel mit Koordinaten ohne Nachkommaanteil in der gegebenen Farbe gezeichnet gefärbt. Hat ein Punkt aber eine Koordinate mit Nachkommaanteil, wird er durch zwei Pixel (linke Spalte) mit unterschiedlicher Farbsättigung gezeichnet.
Wenn aber beide Koordinaten eines Punktes Nachkommaanteile enthalten, werden die Punkte durch drei Pixel unterschiedlicher Farbsättigung gezeichnet (reche Spalte). Diese besondere Art des Zeichnens durch drei Pixel mit unterschiedlicher Farbsättigung erzielt den Glättungseffekt.
2. Algorithmus der Kantenglättung
Die Methoden der CCanvas Klasse, die die 'Primitives' der Kantenglättung zeichnen, verwenden im Allgemeinen zur Berechnung der Farbe der Punkte die Methode PixelSetAA für die Darstellung auf dem Schirm.
| Methoden | Endgültige Methode zur Bildberechnung |
|---|---|
| PixelSetAA | PixelSetAA |
| LineAA | PixelSetAA |
| PolylineAA | LineAA -> PixelSetAA |
| PolygonAA | LineAA -> PixelSetAA |
| TriangleAA | LineAA -> PixelSetAA |
| CircleAA | PixelSetAA |
Wie die Kantenglättung durch die Methode PixelSetAA arbeitet, ist in Fig. 1 zu sehen.
Es zeigt sich, dass bei einer Darstellung mit Kantenglättung, die Methode PixelSetAA als Basis der CCanvas Klasse agiert. Daher glaube ich, es ist interessant herauszufinden, wie denn der Algorithmus der Kantenglättung umgesetzt wurde.
Erinnern wir uns, die Koordinaten X und Y der Methode PixelSetAA sind vom Typ double, daher kann PixelSetAA mit Punktkoordinaten arbeiten, die zwischen den Pixel liegen:
//+------------------------------------------------------------------+ //| Draw pixel with antialiasing | //+------------------------------------------------------------------+ void CCanvas::PixelSetAA(const double x,const double y,const uint clr) {
Als nächstes deklarieren wir drei Arrays. Der Array rr[] ist ein Hilfsarray zur Berechnung wie viel ein virtueller Pixel (der gezeichnet werden kann) den tatsächlichen Pixel auf dem Schirm überdeckt. Die Arrays xx[] und yy[] enthalten die Koordinaten, die für das Zeichnen der Pixel mit dem Glättungseffekten im Bild verwendet werden.
void CCanvas::PixelSetAA(const double x,const double y,const uint clr) { static double rr[4]; static int xx[4]; static int yy[4];
Die folgende Abbildung zeigt die Verbindung zwischen einem virtuellen Pixel und die Überdeckung der physikalischen Pixel:
Fig. 3. Überdeckung der tatsächlichen Pixel
Das bedeutet, ein virtueller Pixel (mit berechneten Koordinaten) hat manchmal Koordinaten mit einem Nachkommaanteil und überdeckt vier reale Pixel gleichzeitig. In diesem Fall muss der Algorithmus der Kantenglättung seine Hauptaufgabe erfüllen — das Färben der vier realen Pixel mit einer virtuellen Pixelfarbe, wenn auch mit unterschiedlichen Abstufungen. So täuschen wir unsere Augen — sie sehen ein leicht verschwommenes Bild mit milden Farbübergängen und weichen Rändern.
Der nächste Block enthält vorläufige Berechnungen. Wir erhalten die Werte der eingehenden Koordinaten, gerundet auf die nächste Ganzzahl:
static int yy[4]; //--- preliminary calculations int ix=(int)MathRound(x); int iy=(int)MathRound(y);
Zum besseren Verständnis, wie die Funktion MathRound arbeitet (auf- oder abrunden beim Dezimalanteil von ".5"), empfiehlt es sich, diesen Code laufen zu lassen:
void OnStart() { Print("MathRound(3.2)=",DoubleToString(MathRound(3.2),8),"; (int)MathRound(3.2)=",IntegerToString((int)MathRound(3.2))); Print("MathRound(3.5)=",DoubleToString(MathRound(3.5),8),"; (int)MathRound(3.5)=",IntegerToString((int)MathRound(3.5))); Print("MathRound(3.8)=",DoubleToString(MathRound(3.8),8),"; (int)MathRound(3.8)=",IntegerToString((int)MathRound(3.8))); } //+------------------------------------------------------------------+
und erhält:
MathRound(3.8)=4.00000000; (int)MathRound(3.8)=4 MathRound(3.5)=4.00000000; (int)MathRound(3.5)=4 MathRound(3.2)=3.00000000; (int)MathRound(3.2)=3
Gefolgt von der Berechnung von delta von dx und dy — der Differenz zwischen eingehenden Koordinaten x y und deren gerundete Werte ix und iy:
int iy=(int)MathRound(y); double rrr=0; double k; double dx=x-ix; double dy=y-iy;
Jetzt müssen wir prüfen: sind beide dx und dy gleich Null, verlassen wir die Methode PixelSetAA.
double dy=y-iy; uchar a,r,g,b; uint c; //--- no need for anti-aliasing if(dx==0.0 && dy==0.0) { PixelSet(ix,iy,clr); return; }
Sind die deltas ungleich Null, bereiten wir den Pixelarray vor:
PixelSet(ix,iy,clr); return; } //--- prepare array of pixels xx[0]=xx[2]=ix; yy[0]=yy[1]=iy; if(dx<0.0) xx[1]=xx[3]=ix-1; if(dx==0.0) xx[1]=xx[3]=ix; if(dx>0.0) xx[1]=xx[3]=ix+1; if(dy<0.0) yy[2]=yy[2]=iy-1; if(dy==0.0) yy[2]=yy[2]=iy; if(dy>0.0) yy[2]=yy[2]=iy+1;
Dieser Block erstellt eine Grundlage für die Illusion geglätteter Bilder.
Um die Arbeitsweise sichtbar zu machen, schrieb ich das Skript PrepareArrayPixels.mq5 und erstellte das Video, das sie erklärt:
Video 1. Arbeitsweise des Skripts PrepareArrayPixels.mq5
Nachdem das Pixelarray gefüllt wurde, werden die "Wichtungen" berechnet, um zu sehen, wie ein virtueller Pixel die realen Pixel überdeckt:
yy[2]=yy[2]=iy+1; //--- calculate radii and sum of their squares for(int i=0;i<4;i++) { dx=xx[i]-x; dy=yy[i]-y; rr[i]=1/(dx*dx+dy*dy); rrr+=rr[i]; }
Und jetzt die letzte Stufe - Zeichnung der Unschärfe:
rrr+=rr[i];
}
//--- draw pixels
for(int i=0;i<4;i++)
{
k=rr[i]/rrr;
c=PixelGet(xx[i],yy[i]);
a=(uchar)(k*GETRGBA(clr)+(1-k)*GETRGBA(c));
r=(uchar)(k*GETRGBR(clr)+(1-k)*GETRGBR(c));
g=(uchar)(k*GETRGBG(clr)+(1-k)*GETRGBG(c));
b=(uchar)(k*GETRGBB(clr)+(1-k)*GETRGBB(c));
PixelSet(xx[i],yy[i],ARGB(a,r,g,b));
}
3. Der Schatten von Objekten
Das Zeichnen von Schatten gibt graphischen Objekten weichere Konturen und gibt ihnen etwas Volumen, sie scheinen nicht mehr flach zu sein. Schatten haben außerdem eine sehr interessante und vorteilhafte Eigenschaft: Die Schatten der Objekte sind normalerweise transparent, und bei der Überlagerung von Grafiken mit Schatten erzeugen sie zusätzlich Volumen.
Die häufigsten Arten von Schatten sind unten gezeigt:
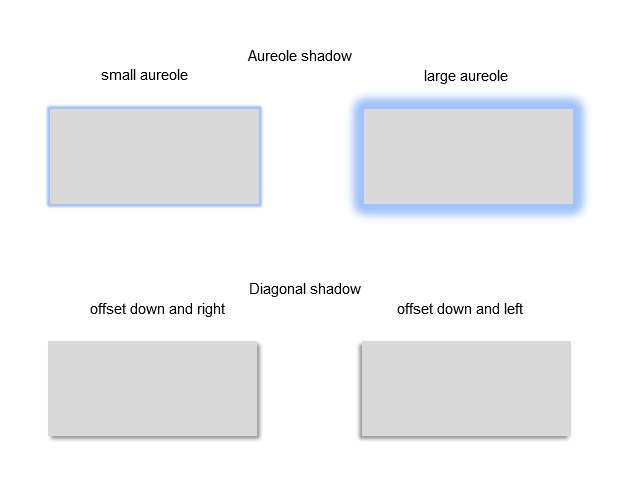
Fig. 4. Arten von Schatten
Ein "Aureole-Schatten" kann eine Wert für dessen Breite haben. Ein "außerhalb diagonal" Schatten könnte einen Wert für den Winkel haben, in dessen Richtung er verschoben wurde. Beide Schattentypen besitzen Einstellungen zur Farbe.
Für die Wahl des richtigen Algorithmus' eines Schattens müssen wir wissen, woraus der Schatten besteht. Vergrößern wir dazu einfach das Bild. Unten sehen wir den Schatten aus dem Bild 4 stark vergrößert:
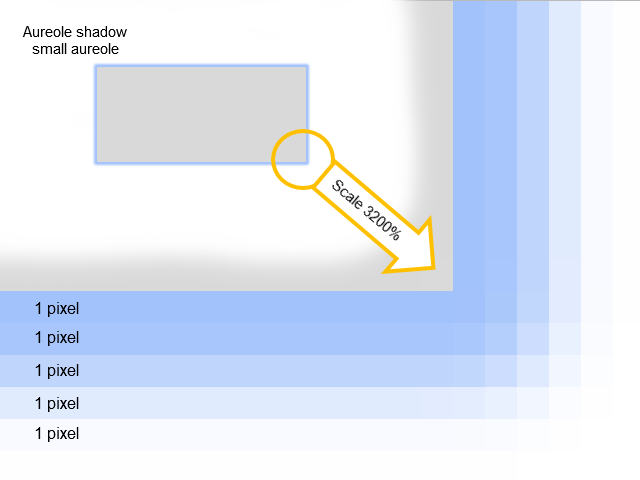
Fig. 5. Woraus ein Schatten besteht
Es wird klar, ein "Aureole-Schatten" ist aus mehreren 1-Pixel starken Umrissen aufgebaut. Diese Umrisse haben eine schrittweise Änderung der Farbsättigung.
3.2. Berechnung mit der Normalverteilung
Für einen weichen Übergang beim Zeichnen der Schatten verwenden wir den häufigsten graphischen Filter — die Gaußsche Unschärfe (Informationen über die Gaußsche Unschärfe finden Sie unten). Dieser Filter verwendet die Normalverteilung, um die Transformation für jeden Pixel des Bildes zu berechnen. Die Berechnung der Unschärfe jedes Pixels des Bildes hängt vom Radius der Unschärfe ab (der Parameter wird vor der Verwendung übergeben) und muss unter Berücksichtigung der umgebenden Pixel erfolgen.
Obwohl vom Radius der Unschärfe gesprochen wurde, wird für die Berechnung tatsächlich ein N x N Gitter verwendet:
wobei Radius ein Radius der Unschärfe ist.
Das Bild unten zeigt das Beispiel eines Pixelgitters für einen Radius der Unschärfe von 3.
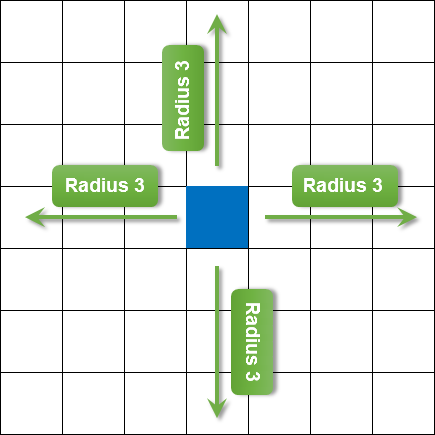
Fig. 6. Unschärferadius
Ich werde die Theorie einer schnellen Berechnung dieses Filters übergehen und nur kurz erwähnen, dass eine Trenneigenschaft des Gaußschen Filters verwendet wird: Zuerst 'verwischen' wir entlang der X-Achse und erst dann entlang der Y-Achse. Das beschleunigt die Berechnung, ohne die Qualität zu beeinflussen.
Der Einfluss benachbarter Pixel auf die berechneten Pixel ist unterschiedlich und verwendet die Normalverteilung zur Berechnung. Je weiter der Pixel vom berechneten Pixel entfernt ist, desto geringer ist seine Auswirkung. Zur Berechnung der Normalverteilung durch den Gaußschen Algorithmus verwenden wir die Numerik-Bibliothek ALGLIB. Das Skript GQGenerateRecToExel.mq5 demonstriert uns eine Normalverteilung. Von der Bibliothek ALGLIB library erhält das Skript einen Array mit Wichtungskoeffizienten der Normalverteilung und schreibt diese Werte in die Datei <data catalogue>\MQL5\Files\GQGenerateRecToExel.csv. Und so sieht der Chart aus, der mit Hilfe der Daten aus GQGenerateRecToExel.csv erstellt wurde:
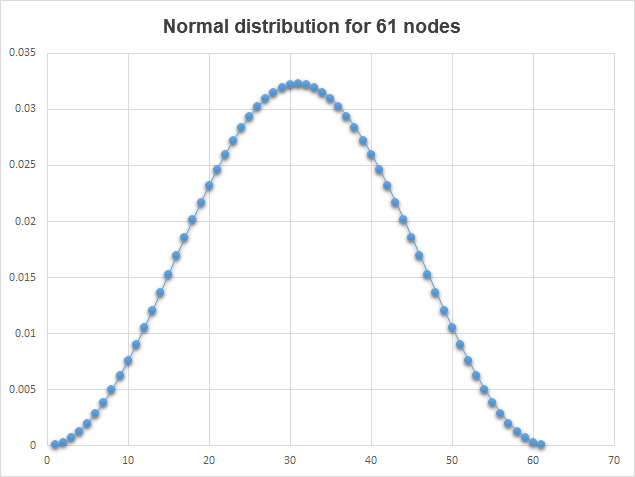
Fig. 7. Normalverteilung
Am Beispiel des Skripts GQGenerateRecToExel.mq5 erkennen wir, wie wir den Array mit den Wichtungen der Normalverteilung erhalten. Im Folgenden wird dieselbe Funktion GetQuadratureWeights von den Skripten verwendet:
//+------------------------------------------------------------------+ //| Gets array of quadrature weights | //+------------------------------------------------------------------+ bool GetQuadratureWeights(const double mu0,const int n,double &w[]) { CAlglib alglib; // static member of class CAlglib double alp[]; // array alpha coefficients double bet[]; // array beta coefficients ArrayResize(alp,n); ArrayResize(bet,n); ArrayInitialize(alp,1.0); // initializes a numeric array alpha ArrayInitialize(bet,1.0); // initializes a numeric array beta double out_x[]; int inf=0; //| Info - error code: | //| * -3 internal eigenproblem solver hasn't | //| converged | //| * -2 Beta[i]<=0 | //| * -1 incorrect N was passed | //| * 1 OK | alglib.GQGenerateRec(alp,bet,mu0,n,inf,out_x,w); if(inf!=1) { Print("Call error in CGaussQ::GQGenerateRec"); return(false); } return(true); }
Diese Funktion füllt den Array w[] mit den Wichtungskoeffizienten der Normalverteilung und überprüft auch das Ergebnis des Aufrufs der Funktion aus der Bibliothek ALGLIB durch die Analyse der Variable inf.
Für das Zeichnen von Schatten auf der Leinwand werden gespeicherte Daten (ResourceReadImage) verwendet, zum Beispiel wird der Array mit Daten aus einer graphischen Quellen gefüllt.
Bei der Arbeit mit Quellen sollten Sie darauf achten, die Pixelarrays im Format uint zu sichern (mehr dazu: ARGB Farbdarstellung). Sie sollten auch wissen, wie 2D Bilder mit Breite und Höhe in einen eindimensionalen Array konvertiert werden. Ein Verfahren dieser Konvertierung wäre: nacheinander die Zeilen des Bildes zu einer einzigen Zeile zusammen zu kleben. Unten sehen Sie zwei Bilder in den Größen 4 x 3 Pixel und 3 x 4 Pixel, die zu einem eindimensionalen Array konvertiert werden:
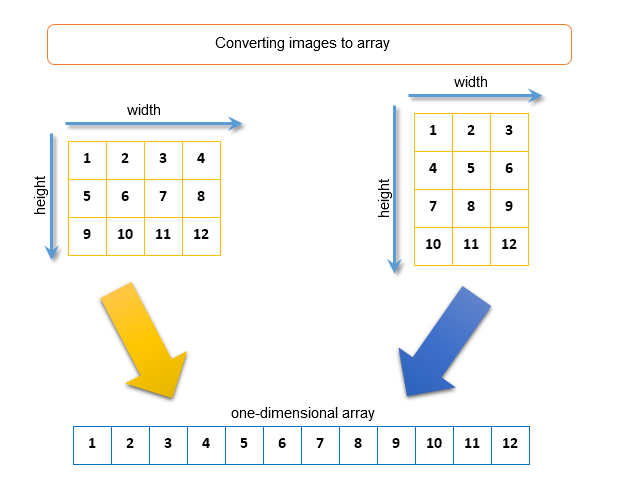
Fig. 8. Bildkonvertierung in einen eindimensionalen Array
4. Beispiel für den Gaußschen Unschärfealgorithmus
Eine Gaußsche Unschärfe wird beispielsweise durch ShadowTwoLayers.mq5 verdeutlicht. Die zwei Dateien Canvas.mqh und Numerik-Bibliothek ALGLIB werden für die Berechnung geladen:
#property script_show_inputs #include <Canvas\Canvas.mqh> #include <Math\Alglib\alglib.mqh>
Eingabe-Parameter:
//--- input input uint radius=4; // radius blur input color clrShadow=clrBlack; // shadow color input uchar ShadowTransparence=160; // transparency shadows input int ShadowShift=3; // shadow shift input color clrDraw=clrBlue; // shadow color input uchar DrawwTransparence=255; // transparency draws //---
Wir erstellen zwei Leinwände. Die untere Leinwand dient uns als Schicht, um die Schatten zu zeichnen, und auf der oberen Schicht zeichnen wir die Graphiken. Beide sind gleich groß wie der Chart (eine Anleitung, wie die Höhe und Breite des Charts abgefragt werden, wird nicht gegeben, dazu gibt es Beispiele im Dokumententeil Beispiele für das Arbeiten mit Charts):
//--- create canvas CCanvas CanvasShadow; CCanvas CanvasDraw; if(!CanvasShadow.CreateBitmapLabel("ShadowLayer",0,0,ChartWidth, ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return; } if(!CanvasDraw.CreateBitmapLabel("DrawLayer",0,0,ChartWidth ,ChartHeight,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return; }
Ok, zeichnen wir mal etwas auf der Leinwand. Zuerst zeichnen wir den Schatten der Figur (Schatten sind normalerweise durchsichtig) auf der unteren Leinwand und dann ein Rechteck auf der oberen.
//--- draw on canvas CanvasShadow.Erase(ColorToARGB(clrNONE,0)); CanvasShadow.FillRectangle(ChartWidth/10,ChartHeight/10, ChartWidth/2-ChartWidth/10,ChartHeight/10*9,ColorToARGB(clrShadow,ShadowTransparence)); CanvasShadow.FillRectangle(ChartWidth/2,ChartHeight/12,ChartWidth/3*2, ChartHeight/2,ColorToARGB(clrShadow,ShadowTransparence)); CanvasShadow.Update(); CanvasDraw.Erase(ColorToARGB(clrNONE,0)); CanvasDraw.FillRectangle(ChartWidth/10-ShadowShift,ChartHeight/10-ShadowShift,ChartWidth/2-ChartWidth/10-ShadowShift, ChartHeight/10*9-ShadowShift,ColorToARGB(clrDraw,DrawwTransparence)); CanvasDraw.Update();
Damit sollten wir folgendes Bild erhalten (Achtung: die Schatten des Rechtecks sind noch ohne Unschärfe):
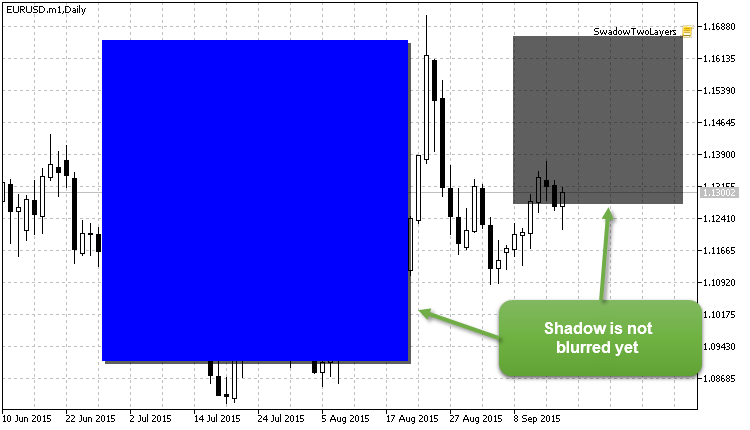
Fig. 9. Die Schatten noch ohne Unschärfe
Die Unschärfe wird auf der unteren Leinwand ausgeführt(CanvasShadow). Dafür müssen wir die Daten (ResourceReadImage) der Graphikquelle der unteren Leinwand lesen (CanvasShadow.ResourceName()) und müssen sie (res_data) in einen eindimensionalen Array kopieren:
//+------------------------------------------------------------------+ //| reads data from the graphical resource | //+------------------------------------------------------------------+ ResetLastError(); if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height)) { Print("Error reading data from the graphical resource ",GetLastError()); Print("attempt number two"); //--- attempt number two: now the picture width and height are known ResetLastError(); if(!ResourceReadImage(CanvasShadow.ResourceName(),res_data,res_width,res_height)) { Print("Error reading data from the graphical resource ",GetLastError()); return; } }
Für den nächsten Schritt benötigen wir den Array mit den Wichtungskoeffizienten der Normalverteilung von der Funktion GetQuadratureWeights, und wir zerlegen den eindimensionalen Array in vier Arrays: Alfa, Red, Green und Blue. Graphischen Effekte können nur auf einzelne Farbkomponenten angewendet werden, daher müssen die Farben zerlegt werden.
//+------------------------------------------------------------------+ //| decomposition of pictures on the components r, g, b | //+------------------------------------------------------------------+ ... if(!GetQuadratureWeights(1,NNodes,weights)) return; for(int i=0;i<size;i++) { clr_temp=res_data[i]; a_data[i]=GETRGBA(clr_temp); r_data[i]=GETRGBR(clr_temp); g_data[i]=GETRGBG(clr_temp); b_data[i]=GETRGBB(clr_temp); }
Der Code im nächsten Teil ist verantwortlich für die "Magie" der Unschärfe. Zuerst wird die Unschärfe des Bildes auf der X-Achse erzeugt, dann in gleicher Weise auf der Y-Achse. Dieser Ansatz ergibt sich aus den Trenneigenschaften der Gaußschen Filter, die eine Beschleunigung der Berechnung ohne Qualitätseinbußen erlaubt. Hier das Beispiel für die Unschärfe der X Achse des Bildes:
//+------------------------------------------------------------------+ //| blur horizontal (axis X) | //+------------------------------------------------------------------+ uint XY; // pixel coordinate in the array double a_temp=0.0,r_temp=0.0,g_temp=0.0,b_temp=0.0; int coef=0; int j=(int)radius; for(uint Y=0;Y<res_height;Y++) // cycle on image width { for(uint X=radius;X<res_width-radius;X++) // cycle on image height { XY=Y*res_width+X; a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0; coef=0; for(int i=-1*j;i<j+1;i=i+1) { a_temp+=a_data[XY+i]*weights[coef]; r_temp+=r_data[XY+i]*weights[coef]; g_temp+=g_data[XY+i]*weights[coef]; b_temp+=b_data[XY+i]*weights[coef]; coef++; } a_data[XY]=(uchar)MathRound(a_temp); r_data[XY]=(uchar)MathRound(r_temp); g_data[XY]=(uchar)MathRound(g_temp); b_data[XY]=(uchar)MathRound(b_temp); } //--- remove artifacts on the left for(uint x=0;x<radius;x++) { XY=Y*res_width+x; a_data[XY]=a_data[Y*res_width+radius]; r_data[XY]=r_data[Y*res_width+radius]; g_data[XY]=g_data[Y*res_width+radius]; b_data[XY]=b_data[Y*res_width+radius]; } //--- remove artifacts on the right for(uint x=res_width-radius;x<res_width;x++) { XY=Y*res_width+x; a_data[XY]=a_data[(Y+1)*res_width-radius-1]; r_data[XY]=r_data[(Y+1)*res_width-radius-1]; g_data[XY]=g_data[(Y+1)*res_width-radius-1]; b_data[XY]=b_data[(Y+1)*res_width-radius-1]; } }
Wir sehen die zwei verschachtelten Schleifen:
for(uint Y=0;Y<res_height;Y++) // cycle on image width { for(uint X=radius;X<res_width-radius;X++) // cycle on image height { ... } }
Diese Verschachtelung stellt sicher, dass alle Pixel des Bildes bearbeitet werden:
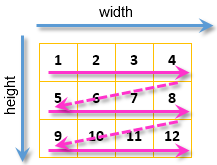
Fig. 10. Der Weg über alle Pixel des Bildes
Eine verschachtelte Schleife stellt sicher, dass alle Pixel des Bildes berechnet werden:
for(uint X=radius;X<res_width-radius;X++) // cycle on image height { XY=Y*res_width+X; a_temp=0.0; r_temp=0.0; g_temp=0.0; b_temp=0.0; coef=0; for(int i=-1*j;i<j+1;i=i+1) { a_temp+=a_data[XY+i]*weights[coef]; r_temp+=r_data[XY+i]*weights[coef]; g_temp+=g_data[XY+i]*weights[coef]; b_temp+=b_data[XY+i]*weights[coef]; coef++; } a_data[XY]=(uchar)MathRound(a_temp); r_data[XY]=(uchar)MathRound(r_temp); g_data[XY]=(uchar)MathRound(g_temp); b_data[XY]=(uchar)MathRound(b_temp); }
Die Zahl der rechts und links benachbarten Pixel werden entsprechend des Radius' für die Unschärfe ausgewählt. Erinnern wir uns, wir verwendeten die Funktion GetQuadratureWeights, um den Array mit den Wichtungskoeffizienten der Normalverteilung zu erhalten. Es stellt sich heraus, die Zahl benachbarter Pixel links + dem Pixel mit zu berechnender Unschärfe + der Zahl benachbarter Pixel rechts = der Zahl der Elemente im Array der Wichtungskoeffizienten. Auf diesem Weg entspricht jedem benachbarte Pixel ein spezifischer Wert im Array der Wichtungskoeffizienten.
Und so wird dann die Unschärfe einer Farbe berechnet: jeder benachbarte Pixel wird mit dem ihm entspr. Wichtungskoeffizienten multipliziert und aufsummiert. Unten ist ein Beispiel der Berechnung der Unschärfe von Rot und einem Unschärferadius von 4:
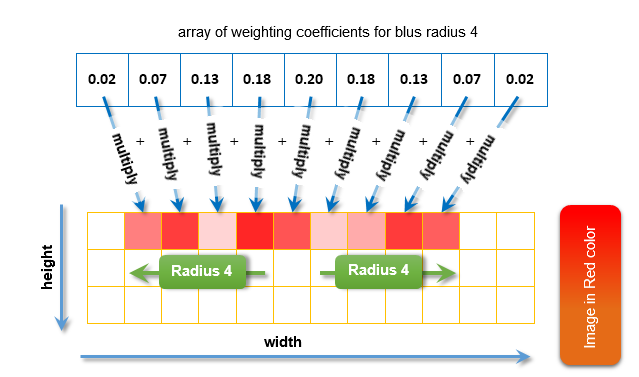
Fig. 11. Berechnung der Unschärfe
Mit diesem Algorithmus die Unschärfe verbleiben aber an den Rändern des Bildes Artefakte – Pixelstreifen ohne Unschärfe. Die Breite dieser Streifen ist gleich dem Radius der Unschärfe. Je größer dieser Unschärferadius ist, desto breiter sind die Streifen der Pixel ohne Unschärfe. Im Algorithmus werden diese Artefakte durch das Kopieren der Pixel mit Unschärfe entfernt:
//--- remove artifacts on the left for(uint x=0;x<radius;x++) { XY=Y*res_width+x; a_data[XY]=a_data[Y*res_width+radius]; r_data[XY]=r_data[Y*res_width+radius]; g_data[XY]=g_data[Y*res_width+radius]; b_data[XY]=b_data[Y*res_width+radius]; } //--- remove artifacts on the right for(uint x=res_width-radius;x<res_width;x++) { XY=Y*res_width+x; a_data[XY]=a_data[(Y+1)*res_width-radius-1]; r_data[XY]=r_data[(Y+1)*res_width-radius-1]; g_data[XY]=g_data[(Y+1)*res_width-radius-1]; b_data[XY]=b_data[(Y+1)*res_width-radius-1]; }
Ähnliche Unschärfeberechnungen führen wir für die Y-Achse durch. Als Ergebnis erhalten wir vier Arrays a1_data[], r1_data[], g1_data[], b1_data[] mit den Unschärfewerten jeweils für Alpha, Rot, Grün und Blau. Jetzt bleibt nur noch, die vier Farbkomponenten eines jeden Pixels zusammenzuführen und auf die Leinwand CanvasShadow zu übertragen:
//--- for(int i=0;i<size;i++) { clr_temp=ARGB(a1_data[i],r1_data[i],g1_data[i],b1_data[i]); res_data[i]=clr_temp; } for(uint X=0;X<res_width;X++) { for(uint Y=radius;Y<res_height-radius;Y++) { XY=Y*res_width+X; CanvasShadow.PixelSet(X,Y,res_data[XY]); } } CanvasShadow.Update(); CanvasDraw.Update(); Sleep(21000);
Das Ergebnis der Unschärfe einer Schicht mit Schatten:
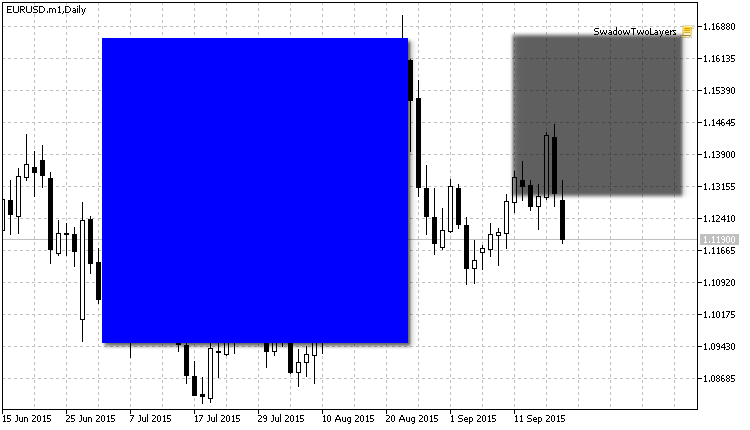
Fig. 12. Schatten sind jetzt unscharf
5. Klasse für das Zeichnen von Schatten
Das Beispiel einer Zeichnung auf einer Leinwand ist Teil der Klasse CGauss. Die Klasse CGauss erlaubt das Zeichnen solcher Primitives mit Schatten:
| Primitives | Beschreibung |
|---|---|
| LineVertical | Zeichnet eine Vertikale mit Schatten |
| LineHorizontal | Zeichnet eine Horizontale mit Schatten |
| Line | Zeichnet eine beliebige Linie mit Schatten |
| Polyline | Zeichnet eine Polylinie mit Schatten |
| Polygon | Zeichnet ein Polygon mit Schatten |
| Rectangle | Zeichnet ein Rechteck mit Schatten |
| Circle | Zeichnet einen Kreis mit Schatten |
| FillRectangle | Zeichnet ein gefülltes Rechteck mit Schatten |
| FillTriangle | Zeichnet ein gefülltes Dreieck mit Schatten |
| FillPolygon | Zeichnet ein gefülltes Polygon mit Schatten |
| FillCircle | Zeichnet einen gefüllten Kreis mit Schatten |
| FillEllipse | Zeichnet eine gefüllte Ellipse mit Schatten |
| Fill | Füllt einen Bereich mit Schatten |
| TextOut | Zeigt einen Text mit Schatten |
Demo-Video über das Skript Blur.mq5, das die Primitives mit Schatten zeichnet:
Video 2. Zeichnen von Primitives mit Schatten
Die Numerik-Bibliothek ALGLIB wird für die Berechnung der Schattenfarbe in der Klasse CGauss benötigt. Ein Schattentyp ist in dieser Klasse realisiert — ein außen und schräg nach rechts unten versetzter Schatten (siehe Fig. 4).
Die allgemeine Idee der Klasse CGauss ist die Verwendung zweier Leinwände. Die untere Leinwand dient uns als Schicht, um die Schatten zu zeichnen, und auf der oberen Schicht zeichnen wir die Graphiken. Die Größe beider Leinwände ist gleich der Größe des Charts. Wobei die untere Leinwand nach ihrer Erstellung einfach horizontal und vertikal um die Breite des Schattens verschoben werden — auf diese Weise wird die Berechnung der Koordinaten der Schatten leichter.
Der Algorithmus für das Zeichnen der Schatten folgt diesem Prinzip: Auf der unteren Leinwand werden der Reihe nach die Anzahl der Objekte mit Radius der Unschärfe gezeichnet. Die Farbe jedes Objekts wird anhand des Gaußschen Algorithmus erstellt, der einen weichen Übergang von der angegebenen Schattenfarbe bis zur kompletten Transparenz erzeugt.
Schlussfolgerung
In diesem Artikel beschrieben wir den Algorithmus der Kantenglättung der Klasse CCanvas, zusammen mit Beispielen der Berechnung und dem Zeichnen von unscharfen Objekten und Schatten. Wir verwendeten die Numerik-Bibliothek ALGLIB zur Berechnung der Unschärfe und Schatten.
Zusätzlich wurde die Klasse CGauss geschrieben, die graphische Primitives auf der Basis verschiedener Beispiele zeichnet.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1612
Thomas DeMarks Beitrag zur technischen Analyse
Schutz vor Falschauslöser bei Handelsroboter
Cross-Plattform Expert Advisor: Einführung
Universal Expert Advisor: Das Event-Modell und der Trading-Strategie Prototyp (Part 2)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.