Representaciones en el dominio de la frecuencia de series temporales: El espectro de potencia

Introducción

Las cotizaciones de precios que vemos en los gráficos representan datos dispersos a lo largo del tiempo. Se considera que la serie de precios se encuentra en el dominio del tiempo, pero esta no es la única forma de mostrar dicha información. Mostrar datos en diferentes dominios puede revelar características interesantes de una serie que pueden no resultar evidentes al realizar un análisis únicamente en el dominio del tiempo. Además, analizaremos algunas perspectivas prometedoras para el análisis de series temporales en el dominio de la frecuencia utilizando la transformada discreta de Fourier (DFT). Hoy nos centraremos en el análisis de funciones espectrales, ofreciendo ejemplos prácticos de cómo calcular y reconocer las características de las series temporales reveladas mediante este método de análisis. También revisaremos brevemente técnicas importantes de preprocesamiento que deben usarse antes de aplicar la transformada discreta de Fourier.

Transformada discreta de Fourier

Antes de demostrar las técnicas de análisis del espectro, primero deberemos comprender qué es la función espectral. El análisis de funciones espectrales de series temporales es un tema amplio en cuanto al procesamiento de señales. En el artículo "Indicadores técnicos y filtros digitales", el autor muestra cómo cualquier secuencia compleja se puede descomponer en ondas senoidales y cosenoidales ordinarias. Esto nos permite dividir un proceso complejo en componentes simples. Todo esto resulta posible gracias a la representación en el dominio de la frecuencia elegida. La base de la presentación es un conjunto de funciones que se utilizan para reproducir una serie temporal.

Una de las representaciones de series temporales más usadas en el dominio de la frecuencia es la transformada discreta de Fourier. La base son las ondas senoidales y cosenoidales que cubren un ciclo a lo largo de la serie. Su característica más valiosa es que cualquier serie temporal descrita de esta forma siempre estará definida de forma única, es decir, no hay dos series que tengan la misma representación en el dominio de la frecuencia. La función espectral muestra cuánta potencia o energía tiene una señal en diferentes frecuencias. En el contexto de los datos de series temporales, la función espectral ofrece información sobre la distribución de la energía en las diferentes frecuencias que componen la serie temporal.

Calculando la transformada discreta de Fourier

Para convertir cualquier serie al dominio de la frecuencia usando la DFT, se utilizará la siguiente fórmula.

Cada término de la ecuación es un número complejo, mientras que x es una serie de datos sin procesar. Cada término es un componente periódico que se repite exactamente j veces en todo el rango de valores. La transformada rápida de Fourier es un algoritmo que acelera el cálculo de transformadas discretas de Fourier. Divide recursivamente una serie por la mitad, transformando cada mitad y combinando después los resultados.

El espectro de potencia

Usando algunas matemáticas básicas, podremos calcular la cantidad de energía debida al componente de frecuencia. Trazando un número complejo en un plano cartesiano, con la parte real en el eje X y la parte imaginaria en el eje Y, podremos aplicar el teorema de Pitágoras, que establece que el valor absoluto será igual a la raíz cuadrada de la suma de los cuadrados de las partes real e imaginaria. Por tanto, la energía debida a una determinada frecuencia será igual al cuadrado de su valor absoluto. La potencia se calculará dividiendo el cuadrado del valor absoluto de la función por el cuadrado del número de valores en la serie en el dominio temporal.

Pero antes de aplicar a la serie el cálculo de la DFT sin procesar, deberemos superar varios pasos de preprocesamiento para obtener una estimación precisa de la potencia en una frecuencia específica. Esto es necesario porque la DFT opera en segmentos de datos de longitud finita y supone que la señal de entrada es periódica, lo cual puede provocar fugas de espectro y otras distorsiones si los valores no cumplen con este supuesto. Para mitigar estos problemas se usan las ventanas.

Función de ventana

Una ventana consiste en multiplicar una serie temporal por una función de ventana, que es una función matemática que asigna pesos a diferentes puntos de una serie temporal. Este es un paso importante en la preparación de los datos de las series temporales para el análisis de transformada discreta de Fourier.

Al analizar los datos de las series temporales utilizando la DFT, dividimos los datos en segmentos más pequeños. Si no añadimos un marco (en este caso una función de ventana) alrededor de cada segmento, podemos perder información importante y nuestro análisis quedará incompleto. La ventana de datos estrecha los extremos de la serie temporal, reduciendo las transiciones bruscas en los límites de la ventana de la DFT. La función de reducción suele estar diseñada para reducir suavemente la señal hasta cero en los bordes de la ventana, lo cual reduce la amplitud de cualquier componente de espectro cerca del borde de la ventana.

Por importante que resulte este proceso, potencialmente puede distorsionar o cambiar la forma original de los datos. Este problema se puede eliminar o minimizar centrando la serie antes de aplicar la función de ventana a la serie no procesada. Cuando una serie temporal está centrada, su media se resta de cada punto de datos de la serie, lo que da como resultado una nueva serie con una media de cero.

Hay muchas funciones de ventana disponibles, como la ventana rectangular, la ventana de Hamming, la ventana Hanning, la ventana de Blackman y la ventana de Kaiser, cada una de ellas con sus propiedades y usos únicos. En este texto usaremos la ventana de datos de Welch (Welch data window).  
    
La ventana se define con la siguiente fórmula.

Cada valor de la serie temporal original debe multiplicarse por el correspondiente m(i).

Para centrar los valores, calculamos el promedio ponderado de la serie usando una función de ventana. Luego, este promedio se resta de cada punto de la serie antes de aplicar la propia ventana.

Suavizado de funciones espectrales

Un espectro de potencia discreto suele ser difícil de interpretar porque normalmente existen muchos picos estrechos que sobresalen por todas partes. Es posible que resulte necesario suavizarlo un poco para comprender mejor lo que está sucediendo. Para estos fines se suele usar un filtro de Savitzky-Golay. Su función de filtrado está determinada por dos parámetros: la mitad de la longitud y el grado de polinomios. La mitad de la longitud indica el número de valores adyacentes (antes y después) del que se está filtrando. Los grados indican el grado del polinomio que debe ajustarse al valor actual y sus valores adyacentes.

La clase CSpectrum

En este apartado presentaremos una clase que nos permitirá analizar series fácilmente en mql5. Una de las características principales de la clase es el método de dibujado, que facilita la visualización de varios gráficos espectrales con unas pocas líneas de código.

La clase completa está más abajo.

//+------------------------------------------------------------------+
//|                                                     Spectrum.mqh |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\fasttransforms.mqh>
#include<Graphics\Graphic.mqh>

enum ENUM_SPECTRUM_PLOT
  {
   PLOT_POWER_SPECTRUM=0,//PowerSpectrum
   PLOT_FILTERED_POWER_SPECTRUM,//FilteredPowerSpectrum
   PLOT_CUMULATIVE_SPECTRUM_DEVIATION//CumulativeSpectrumDeviation
  };

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSpectrumAnalysis
  {
private:
   bool              m_window,m_initialized;
   int               m_n,m_cases;
   complex           m_dft[];
   double            m_real[];
   double            m_win,m_win2;
   double            m_wsq;
   double            m_wsum,m_dsum;
   int               m_window_size,m_poly_order;
   void              savgol(double &data[], double&out[], int window_size, int poly_order);
public:
   //---constructor
                     CSpectrumAnalysis(const bool window,double &in_series[]);
   //---destructor
                    ~CSpectrumAnalysis(void)
     {
      if(m_n)
        {
         ArrayFree(m_dft);
         ArrayFree(m_real);
        }
     }
   bool              PowerSpectrum(double &out_p[]);
   bool              CumulativePowerSpectrum(double & out_cp[]);
   double            CumulativeSpectrumDeviation(double &out_csd[]);
   void              Plot(ENUM_SPECTRUM_PLOT plot_series,int window_size=5, int poly_order=2, color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400);
  };

Para utilizarla, el usuario llamará al constructor paramétrico y le transmitirá dos parámetros. El primer parámetro indica si la función de ventana debe aplicarse a los datos. Debemos señalar que al utilizar la función de ventana, la fila también estará centrada. El segundo parámetro del constructor es una array que contiene los valores sin procesar para analizar.

La transformada de Fourier se realiza en el constructor y los valores complejos vinculados con el espectro se almacenan en un array de DFT.

void CSpectrumAnalysis::CSpectrumAnalysis(const bool apply_window,double &in_series[])
  {
   int n=ArraySize(in_series);

   m_initialized=false;

   if(n<=0)
      return;

   m_cases=(n/2)+1;
   m_n=n;

   m_window=apply_window;

   ArrayResize(m_real,n);

   if(m_window)
     {
      m_wsum=m_dsum=m_wsq=0;
      for(int i=0; i<n; i++)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
         m_wsum+=m_win;
         m_dsum+=m_win*in_series[i];
         m_wsq+=m_win*m_win;
        }
      m_dsum/=m_wsum;
      m_wsq=1.0/sqrt(n*m_wsq);
     }
   else
     {
      m_dsum=0;
      m_wsq=1.0;
     }


   for(int i=0; i<n; i++)
     {
      if(m_window)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
        }
      else
         m_win=1.0;
      m_win*=m_wsq;
      m_real[i]=m_win*(in_series[i]-m_dsum);
     }
   CFastFourierTransform::FFTR1D(m_real,n,m_dft);

   m_initialized=true;

  }

Para calcular y obtener los valores de la función espectral, la función espectral acumulativa y la desviación del espectro acumulativo, la clase dispone de los métodos PowerSpectrum(), CumulativePowerSpectrum() y CumulativeSpectrumDeviation(), respectivamente. Cada método requiere un parámetro de array en el que se copiarán los valores correspondientes.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::PowerSpectrum(double &out_p[])
  {
   if(!m_initialized)
      return false;

   ArrayResize(out_p,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::CumulativePowerSpectrum(double &out_cp[])
  {
   if(!m_initialized)
      return false;

   double out_p[];

   ArrayResize(out_p,m_cases);
   ArrayResize(out_cp,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   for(int i=0; i<m_cases; i++)
     {
      out_cp[i]=0;
      for(int j=i; j>=1; j--)
         out_cp[i]+=out_p[j];
     }

   ArrayFree(out_p);

   return true;

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSpectrumAnalysis::CumulativeSpectrumDeviation(double &out_csd[])
  {
   if(!m_initialized)
      return 0;

   ArrayResize(out_csd,m_cases);

   double sum=0;
   for(int i=0; i<m_cases; i++)
     {
      out_csd[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i==(m_cases-1))
         out_csd[i]*=0.5;
      sum+=out_csd[i];
     }
   double sfac=1.0/sum;
   double nfac=1.0/(m_cases-1);
   double dmax=sum=0;

   for(int i=1; i<m_cases-1; i++)
     {
      sum+=out_csd[i];
      out_csd[i]=sum*sfac - i*nfac;
      if(MathAbs(out_csd[i])>dmax)
         dmax=MathAbs(out_csd[i]);
     }
   out_csd[0]=out_csd[m_cases-1]=0;

   return dmax;
  }

El último método que merece la pena considerar es la función Plot(). Con su ayuda, el usuario podrá mostrar rápidamente un gráfico de los tres especificados en la enumeración ENUM_SPECTRUM_PLOT. El segundo y tercer parámetro del método Plot() determinan los parámetros de suavizado aplicados al filtro de Savitzky-Golay al construir el espectro de potencia acumulativo filtrado. Estas opciones no tienen ningún efecto al elegir otros gráficos. Los parámetros restantes de Plot() controlan el color del gráfico de líneas, el tiempo que se muestra el gráfico en segundos y el tamaño del gráfico, respectivamente.

void CSpectrumAnalysis::Plot(ENUM_SPECTRUM_PLOT plot_series,int windowsize=5, int polyorder=2,color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400)
  {
   double x[],y[];
   bool calculated=false;

   string header="";

   switch(plot_series)
     {
      case PLOT_POWER_SPECTRUM:
         ArrayResize(x,m_cases);
         calculated=PowerSpectrum(y);
         for(int i=0; i<m_cases; i++)
            x[i]=double(i)/double(m_n);
         header="Power Spectrum";
         break;
      case PLOT_FILTERED_POWER_SPECTRUM:
        {
         double ps[] ;
         calculated=PowerSpectrum(ps);
         savgol(ps,y,windowsize,polyorder);
         ArrayResize(x,ArraySize(y));
         for(int i=0; i<ArraySize(y); i++)
            x[i]=double((i+(windowsize/2))/double(m_n));
         header="Filtered Power Spectrum";
        }
      break;
      case PLOT_CUMULATIVE_SPECTRUM_DEVIATION:
         calculated=CumulativeSpectrumDeviation(y);
         ArrayResize(x,m_cases);
         for(int i=0; i<m_cases; i++)
            x[i]=i;
         header="Cumulative Spectrum Deviation";
         break;
     }

   if(!calculated)
     {
      ArrayFree(x);
      ArrayFree(y);
      return;
     }

   ChartSetInteger(0,CHART_SHOW,false);

   long chart=0;
   string name=EnumToString(plot_series);

   CGraphic graphic;
   if(ObjectFind(chart,name)<0)
      graphic.Create(chart,name,0,0,0,size_x,size_y);
   else
      graphic.Attach(chart,name);
//---
   graphic.BackgroundMain(header);
   graphic.BackgroundMainSize(16);
   graphic.CurveAdd(x,y,ColorToARGB(line_color),CURVE_LINES);
//---
   graphic.CurvePlotAll();
//---
   graphic.Update();
//---
   Sleep(display_time_seconds*1000);
//---
   ChartSetInteger(0,CHART_SHOW,true);
//---
   graphic.Destroy();
//---
   ChartRedraw();
//---

  }

Para facilitar su comprensión, analizaremos las características espectrales de algunas series hipotéticas con ciertas características, a saber, una serie autorregresiva con un término positivo o negativo, una serie con un marcado componente estacional y tendencias obvias. Finalmente, analizaremos la naturaleza espectral del proceso aleatorio.

Identificando patrones estacionales en una serie temporal

Normalmente, al crear modelos predictivos, debemos realizar un procesamiento previo antes de continuar. Es una práctica común eliminar cualquier característica obvia, como cualquier tendencia o estacionalidad, antes de usar una red neuronal para predecir una serie. Una forma de detectar dichas características es estimar la función espectral. Los componentes fuertes que definen una serie suelen aparecer como picos amplios. Vamos a tomar como ejemplo una serie determinista que tiene un componente estacional evidente. La serie se genera usando el código que se muestra a continuación.

input bool Add_trend=false;


//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int num_samples = 100; 
   double inputs[];
   ArrayResize(inputs,num_samples);
   MathSrand(2023);
//---
   for(int i=0;i<num_samples;i++)
     {
      inputs[i]=(Add_trend)?i*0.03*-1:0;
      inputs[i]+= cos(2*M_PI*0.1*(i+1)) + sin(2*M_PI*0.4*(i+1)) + (double)rand()/SHORT_MAX;
     } 
//---

La visualización de estos valores se muestra en los siguientes gráficos: el primero muestra los valores con una tendencia añadida, mientras que el último muestra el gráfico sin el componente de tendencia.

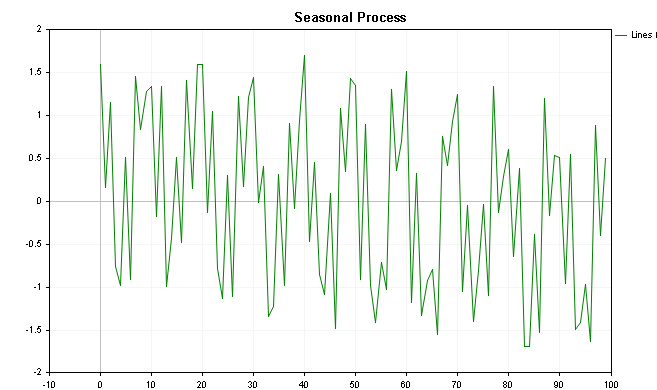
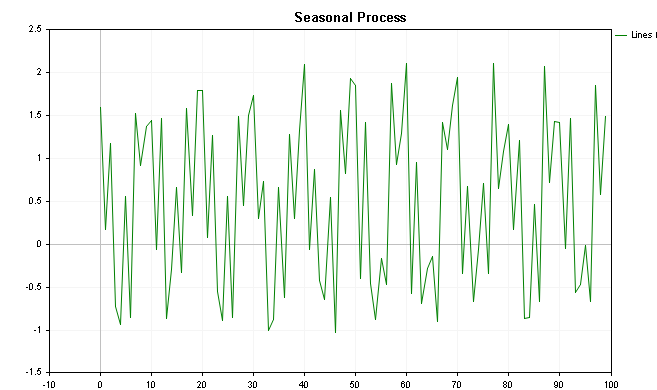
Al ejecutar la clase CSpectrum, podemos visualizar el espectro de potencia de la serie como se muestra a continuación. Podemos ver que el espectro de potencia muestra claramente varios picos prominentes.

CSpectrumAnalysis sp(true,inputs); 
       
   sp.Plot(PLOT_POWER_SPECTRUM);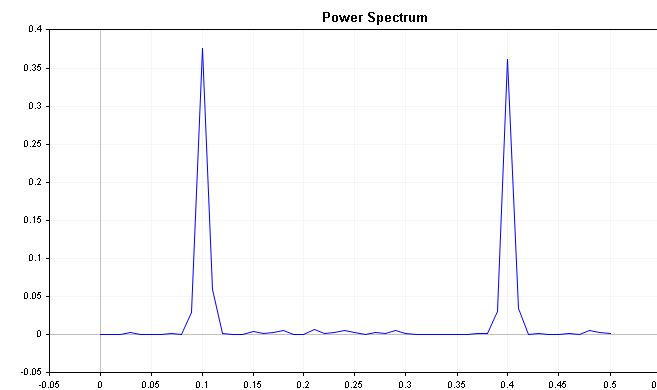 

El gráfico muestra claramente que la serie está fuertemente influenciada por componentes de frecuencia de 0,2 y 0,4, respectivamente.

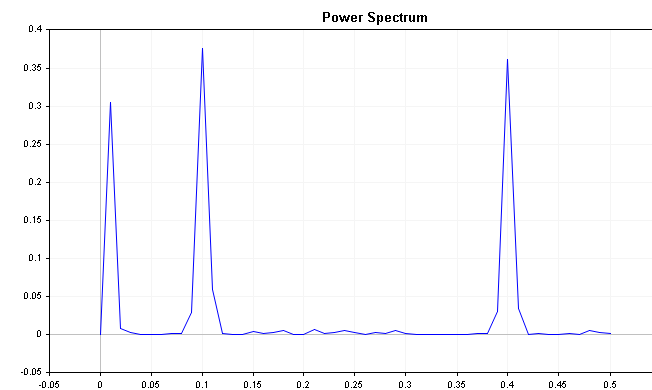
El espectro de una serie con una ligera tendencia descendente muestra un pico inicial junto con el componente estacional. En esta situación, sería razonable no solo diferenciar las series, sino también aplicar un ajuste estacional. Debemos señalar que la presencia de dichos picos no siempre supone una señal de tendencia y/o estacionalidad. El ejemplo mostrado tiene un pequeño componente de ruido, mientras que los conjuntos de datos reales, como las series financieras, sufren de ruido en mayor medida. La estacionalidad en una serie suele aparecer como un pico obvio en el gráfico del espectro de potencia.

Determinando el orden de un modelo autorregresivo (AR)

Los modelos autorregresivos se usan comúnmente en el análisis de series temporales para predecir valores futuros de una serie según sus valores pasados. El orden del modelo AR determina cuántos valores pasados ​​se usan para predecir el siguiente valor. Un método para determinar el orden apropiado para un modelo AR sería examinar el espectro de potencia de la serie temporal.

Normalmente, el espectro de potencia disminuirá a medida que aumente la frecuencia. Por ejemplo, una serie temporal definida por un término autorregresivo positivo de corto plazo tendrá la mayor parte de su energía espectral concentrada en frecuencias bajas, mientras que una serie con un término autorregresivo negativo de corto plazo desplazará su energía espectral hacia frecuencias altas.
Veamos qué aspecto tiene esto en la práctica, usando otra serie determinista definida por un componente autorregresivo positivo o negativo. El código para crear la fila se muestra a continuación.

double inputs[300];
   ArrayInitialize(inputs,0);

   MathSrand(2023);

   for(int i=1; i<ArraySize(inputs); i++)
     {
      inputs[i]= 0.0;
      
          switch(Coeff_Mult)
             {
              case positive:
               inputs[i]+= 0.9*inputs[i-1];
               break;
              case negative:
               inputs[i]+= -1*0.9*inputs[i-1];
               break;   
             }
             
      inputs[i]+=(double)rand() / double(SHORT_MAX);
     }

Cuando la serie se define por autorregresión positiva, el espectro de potencia muestra que la mayor parte de la energía se concentra en bajas frecuencias, mientras que la potencia en frecuencias más altas disminuye a medida que se asciende en la escala de valores.

La comparación con el gráfico de una serie autorregresiva con un término negativo muestra que la potencia aumenta a medida que se muestrean frecuencias más altas. Nuevamente, este es un ejemplo simple, pero demuestra características importantes que pueden usarse al construir modelos autorregresivos.

Estudiando el espectro de distribución del error para evaluar la efectividad de un modelo de pronóstico.

Finalmente, podemos utilizar el espectro de potencia de la distribución del error de un modelo de predicción para evaluar lo bien que este modela el proceso. Para ello, primero ajustaremos el modelo de pronóstico a los datos de la serie temporal y calcularemos los residuos o errores (la diferencia entre los valores previstos y reales).

A continuación, examinaremos el espectro de potencia de la distribución del error. Un buen modelo de predicción tendrá residuos que se comportarán como ruido blanco, lo cual significa que el espectro de potencia de la distribución del error deberá ser relativamente plano en todas las frecuencias. Los picos pronunciados en el espectro de potencia de cualquier frecuencia sugieren que el modelo de predicción no capta toda la información en los datos de la serie temporal y es posible que sea necesario realizar ajustes adicionales. El problema es que, en realidad, el espectro de potencia del ruido blanco no suele ser tan plano como se espera. Basta con mirar el espectro de la serie de ruido blanco generado por el siguiente código.

int num_samples = 500;
   double inputs[];
   MathSrand(2023);
   ArrayResize(inputs,num_samples);
   
   for (int i = 0; i < num_samples; i++) 
    {
        inputs[i] = ((double)rand() / SHORT_MAX) * 32767 - 32767/2;
    }

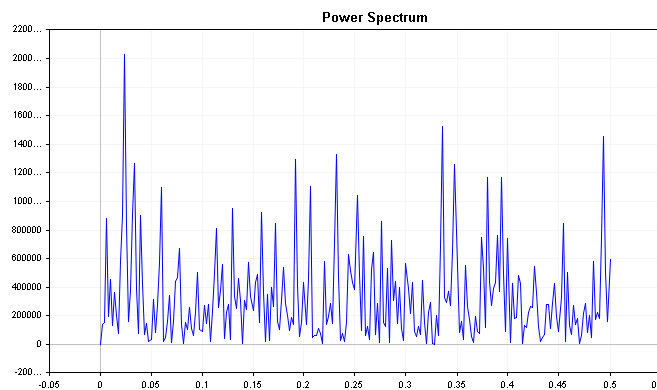
Para obtener una imagen más clara de los componentes de frecuencia, podemos usar el espectro de potencia acumulativo.

Teóricamente, si la serie temporal constituye ruido blanco, todos los términos espectrales serán iguales, por lo que se esperará que el gráfico del espectro de potencia acumulativo sea recto. En particular, la fracción de la potencia total contada para cada término individual deberá ser igual a la fracción del número total de términos acumulados. Matemáticamente, esto significará que la potencia total del ruido blanco tendrá una expectativa determinista. A continuación le mostramos la ecuación que determina la potencia total para cada banda de frecuencia seleccionada.

 
Si el espectro de potencia muestra una alta concentración de energía en frecuencias bajas o altas, veremos desviaciones de la forma de onda teórica del ruido blanco. Utilizando este hecho, podremos calcular la desviación entre los espectros acumulativos observados y teóricos, lo cual nos dará la desviación del espectro acumulativo.

Esta serie puede revelar información importante sobre la serie temporal. Por ejemplo, si la energía espectral se desplaza hacia la izquierda, la desviación comenzará cerca de cero y aumentará lentamente hasta converger mucho más tarde. Por el contrario, si la energía espectral se desplaza hacia la derecha, la desviación disminuirá inmediatamente a valores negativos y luego volverá lentamente a cero con el tiempo. El ruido blanco producirá valores de desviación que variarán mucho menos alrededor de cero.

Los gráficos a continuación muestran la desviación acumulada del espectro de procesos AR(1) positivos y negativos que definimos anteriormente. Compárelos con un gráfico del espectro acumulativo de ruido blanco y notará las diferencias de forma más clara.

 

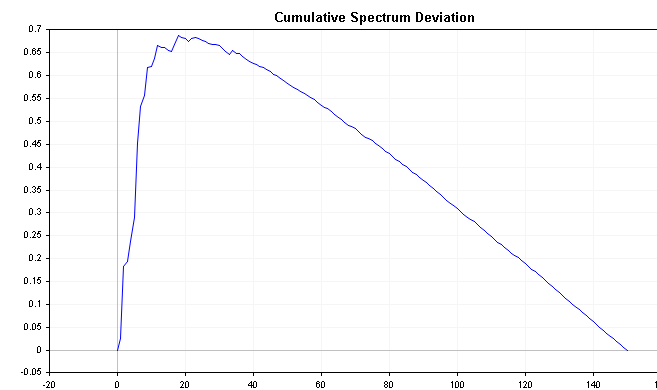
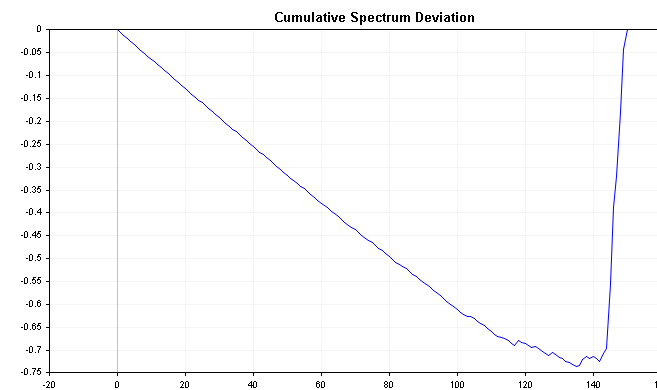
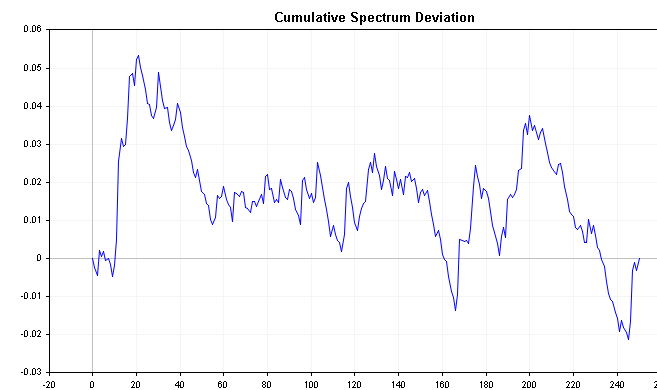
Como ya se sabe, la distribución del valor absoluto máximo de todas las desviaciones sigue . Aplicando la siguiente fórmula, podremos probar directamente la hipótesis de que la serie temporal es ruido blanco. Esta fórmula calcula la estadística D de una serie.

q define los grados de libertad si se aplica la DFT a una serie temporal real, q =n/2-1. Si se usa una ventana de datos Welch antes de la DFT, q deberá multiplicarse por 0,72 para compensar la pérdida de información causada por la ventana. Alfa es el nivel de significancia, generalmente expresado como porcentaje. Para probar la hipótesis del ruido blanco, obtendremos la diferencia o desviación máxima y la compararemos con la estadística D.

En la clase CSpectrum, podemos obtener la diferencia máxima determinada calculando la desviación acumulada del espectro llamando al método CumulativeSpectrumDeviation().

Conclusión

El artículo se ha centrado principalmente en la conocida DFT para estimar el espectro de potencia de una serie temporal. Sin embargo, existe un método alternativo llamado método de máxima entropía (ME), que a veces es superior al DFT. El espectro del ME permite ampliar elementos muy estrechos mientras suaviza áreas de baja energía espectral, lo cual permite una visualización completa. No obstante, el método ME tiende a detectar altos picos de energía espectral incluso cuando no existen, lo que lo hace inadecuado para su uso en solitario. Por consiguiente, recomendamos utilizar siempre el espectro de la DFT como confirmación.

En conclusión, el espectro de potencia de datos de series temporales puede ofrecer información valiosa sobre varios aspectos del análisis de series temporales, como, por ejemplo, determinando el orden del modelo AR, estableciendo la necesidad de diferencias estacionales como paso previo al procesamiento y examinando el rendimiento del modelo de pronóstico.

Nombre del archivo	Descripción
mql5files\include\Spectrum.mqh	Definición de la clase CSpectrum
mql5files\scripts\OrderOneARProcess.mql5	Script que genera una serie temporal autorregresiva y utiliza la clase CSpectrum
mql5files\scripts\SeasonalProcess.mql5	Script que genera una serie temporal con estacionalidad y aplica la clase CSpectrum
mql5files\scripts\WhiteNoise.mql5	Script que genera una serie temporal de ruido blanco y aplica la clase CSpectrum