Redes neuronales: así de sencillo (Parte 87): Segmentación de series temporales

Introducción

La previsión juega un papel esencial en el análisis de series temporales. Los modelos profundos han aportado mejoras significativas en esta esfera. No solo predicen con éxito valores futuros, sino que también extraen representaciones abstractas que pueden aplicarse a otras tareas como la clasificación y la detección de anomalías.

La arquitectura del Transformer, que comenzó su desarrollo en el Procesamiento del Lenguaje Natural (PLN), ha demostrado sus ventajas en la Visión por Computadora (CV) y ha encontrado con éxito aplicación en el análisis de series temporales. Su mecanismo de Self-Attention, capaz de identificar automáticamente las relaciones entre los elementos de la secuencia, se ha convertido en la base de modelos de predicción eficaces.

La creciente cantidad de datos disponibles para el análisis y las mejoras en las técnicas de aprendizaje automático nos permiten desarrollar modelos más precisos y eficaces para analizar datos temporales. No obstante, a medida que aumenta la complejidad de las series temporales, se hace necesario desarrollar métodos de análisis más eficaces y menos costosos para lograr predicciones precisas e identificar patrones ocultos.

Uno de estos métodos es el Transformer de segmentación de series temporales (Patch Time Series Transformer — PatchTST), presentado en el artículo "A Time Series is Worth 64 Words: Long-term Forecasting with Transformers". Este método se basa en dividir las series temporales en segmentos (parches) y utilizar el Transformer para predecir los valores futuros.

La previsión de series temporales pretende comprender la correlación entre los datos en cada paso temporal. Sin embargo, un paso temporal individual no posee significado semántico. Por lo tanto, la extracción de información semántica local resulta esencial para analizar sus relaciones. La mayoría de los trabajos anteriores solo utilizan tokens de pasos temporales puntuales de los datos de origen. PatchTST, por su parte, mejora la localización y recopila información semántica compleja que no está disponible a nivel de puntos mediante la agregación de pasos temporales en parches a nivel de subserie.

Además, la serie temporal multidimensional supone una señal multicanal, y cada token de los datos de origen puede representar datos de un solo canal o de varios canales. Según la estructura de los tokens de datos de origen, existen distintas variantes de la arquitectura del Transformer. La mezcla de canales se refiere a este último caso, cuando el token de entrada toma el vector de todas las características de las series temporales y lo proyecta en el espacio de incorporación para mezclar la información. Por otro lado, la independencia del canal implica que cada token de datos de origen contiene información de un solo canal. Se ha demostrado anteriormente que esto funciona bien en modelos de convolución y lineales. PatchTST demuestra la eficacia del enfoque de canales independientes en modelos basados en el Transformer.

Los autores de PatchTST destacan las siguientes ventajas del método propuesto:

1. Reducción de la complejidad: La segmentación reduce la complejidad temporal y espacial del modelo, lo cual mejora su rendimiento con grandes conjuntos de datos.
2. Mejora del aprendizaje durante periodos prolongados: Los parches permiten al modelo explorar periodos de tiempo mayores, mejorando potencialmente la calidad de las previsiones.
3. Aprendizaje de representaciones: El modelo propuesto no solo es eficaz en la predicción, sino que también es capaz de extraer representaciones abstractas más complejas de los datos, lo cual mejora su capacidad de generalización.

La investigación presentada en el trabajo del autor demuestra la eficacia del método propuesto y sus perspectivas para diversas tareas aplicadas de análisis de series temporales.

1. Algoritmo PatchTST

El método PatchTST está diseñado para el análisis y la previsión de series temporales multidimensionales en las que cada estado del sistema analizado se describe mediante un vector de parámetros. En este caso, el tamaño del vector de descripción de cada paso temporal contendrá el mismo número de parámetros con idéntica estructura de datos. Así, podemos dividir la serie temporal multidimensional global en varias series temporales unitarias según el número de parámetros que describen el estado del sistema.

Al igual que en los métodos anteriores, primero reduciremos los datos de origen obtenidos como entrada del modelo a una forma comparable normalizándolos. Este paso es muy importante. Hemos dicho muchas veces que el uso de datos normalizados como entrada en el modelo mejora mucho la estabilidad del proceso de entrenamiento del mismo. Además, aunque el método PatchTST implica el análisis independiente del canal de series temporales unitarias, estas se analizan con un único conjunto de parámetros entrenados. Por lo tanto, resulta esencial que los datos analizados de todos los canales sean comparables.

El siguiente paso será la segmentación de series temporales unitarias, que permite modelizar patrones locales y aumenta la generalizabilidad del modelo. En este paso, los autores del método PatchTST proponen dividir la secuencia temporal en parches de tamaño fijo y con paso fijo. El método funciona igual de bien con segmentos solapados y no solapados. En el primer caso, el paso será menor que el tamaño del parche, y en el segundo, ambos hiperparámetros serán iguales. Ambos enfoques de segmentación permiten aprender información semántica local. Y la elección de un método concreto dependerá en gran medida de la tarea que vayamos a realizar y del tamaño de la ventana de datos de origen que vayamos a analizar.

Obviamente, el número de segmentos será inferior a la longitud de la secuencia, y la diferencia será mayor cuanto mayor sea el tamaño del paso de segmentación. Por lo tanto, la máxima diferencia entre el número de segmentos y la longitud de la secuencia se conseguirá para parches no solapados. En este caso, la reducción se realizará en múltiplos del tamaño del paso. Esto permitirá analizar un mayor tamaño de los datos de la serie temporal de origen con los mismos o incluso menos recursos de memoria y computación.

Al analizar una ventana pequeña de datos de origen, se recomienda utilizar parches superpuestos, lo cual permitirá explorar mejor las dependencias semánticas locales.

Una vez más, crearemos parches para cada serie temporal unitaria individual, pero con los mismos parámetros de segmentación para todas ellas.

A continuación, trabajaremos con los parches ya creados. Formamos las incorporaciones para ellos. Añadimos la codificación de la posición entrenada. Y transmitimos en un bloque de varias capas del Transformer vainilla.

No vamos a profundizar en la arquitectura del Transformer, que ya presentamos con detalle anteriormente. Pero conviene señalar que el Codificador del Transformer analiza por separado las dependencias dentro de las series temporales unitarias. Sin embargo, para analizar todas las series temporales unitarias, se usan parámetros uniformes entrenados.

El Transformer permite extraer representaciones abstractas a partir de parches de datos de origen, dada su secuencia temporal y su contexto. Por consiguiente, las representaciones obtenidas a la salida del Codificador contienen información sobre las relaciones entre los parches y los patrones dentro de cada uno de ellos. Las representaciones de series temporales unitarias procesadas de este modo se concatenan, y el tensor obtenido puede utilizarse para resolver diversos problemas. Este se introduce en la "cabeza de decisión" para generar los resultados del modelo.

Aquí hay que decir que los autores del método proponen usar un modelo para resolver diferentes problemas sobre el mismo conjunto de datos de origen. Puede tratarse de la búsqueda de anomalías, la clasificación o la previsión de datos de series temporales posteriores para distintos horizontes de planificación. Basta con sustituir la "cabeza de decisión" y afinar (entrenar adicional) el modelo.

Al pronosticar los datos de series temporales posteriores en la salida del modelo, desnormalizaremos los datos devolviendo características estadísticas extraídas de los datos de origen.

A continuación le presentamos la visualización del método por parte del autor.

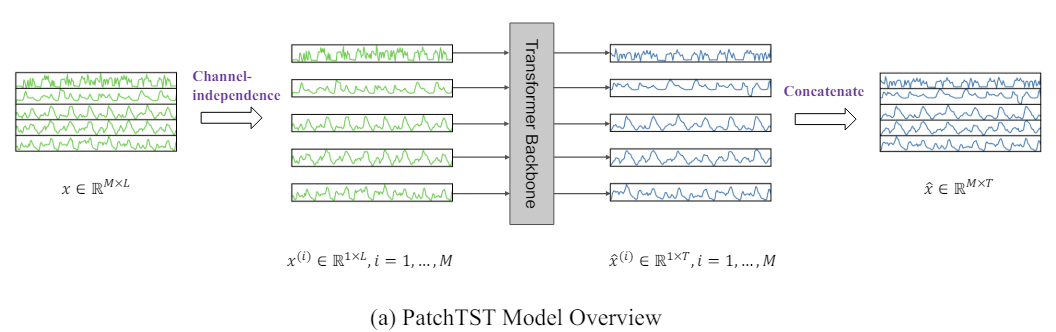
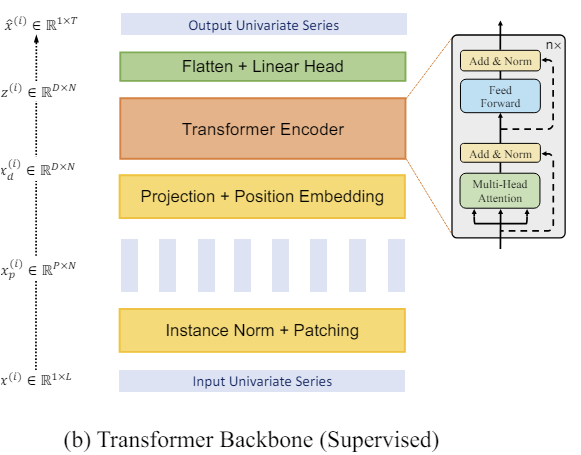
2. Implementación con MQL5

Tras considerar los aspectos teóricos del método, procederemos a la construcción de los planteamientos propuestos usando MQL5.

Conviene aclarar aquí que aplicaremos precisamente nuestra visión de los planteamientos propuestos, y este puede diferir de la percepción del autor.

Como se desprende de la descripción teórica anterior del método PatchTST, este se basa en la segmentación de los datos de origen y la división de las series temporales multidimensionales en secuencias unitarias separadas.

Lo primero en el flujo de procesamiento de datos es la segmentación, que consiste en dividir los datos de origen en bloques de información más pequeños. En el caso de los parches no solapados, se puede pensar en reformatear el tensor bidimensional de los datos de origen en un tensor tridimensional. En el caso de los parches solapados, resulta un poco más complicado, ya que deberemos copiar los datos. Pero en cualquier caso obtendremos un tensor tridimensional "número de variables * número de parches * tamaño del parche" como salida.

Obviamente, la transformación del tensor de datos de origen implica operaciones de copiado de información. Y nos gustaría eliminar las operaciones innecesarias, incluido el copiado. Al fin y al cabo, cada operación adicional supone para nosotros un gasto de tiempo y recursos.

Nos centraremos en las operaciones siguientes. Y lo que sigue en el flujo de operaciones es la incorporación de datos. Así, existe un deseo legítimo de combinar las dos operaciones. Esencialmente solo realizaremos la operación de incorporación de datos, solo que para realizar esta, tomaremos del tensor de datos de origen los bloques individuales correspondientes a nuestros parches.

Y aquí nos acordamos de las capas de convolución. En ellas también tomamos un bloque de datos de origen del tamaño de una ventana dada y tras la operación de convolución con varios filtros obtendremos un vector de proyección de la ventana de datos analizada en algún subespacio. Parece que eso es lo que necesitamos. Pero la capa de convolución que creamos antes funciona con un tensor unidimensional de los datos de origen. Y no permite distinguir las series temporales unitarias separadas del tensor general de las series temporales multidimensionales. Así que tenemos que crear algo similar, pero con la capacidad de funcionar dentro de secuencias unitarias individuales.

2.1 Segmentación en el lado OpenCL

Primero aumentaremos el programa OpenCL creando en él los kernels de pasada directa e inversa de segmentación de datos, proyectándolos en algún subespacio de incorporaciones. Y empezaremos con el kernel de pasada directa PatchCreate.

En los parámetros del kernel, transmitiremos los punteros a 3 búferes de datos: los datos de origen (inputs), la matriz de coeficientes de peso (weights) y los resultados (outputs). Además, añadiremos 4 constantes a los parámetros del kernel. En ellos, especificaremos el tamaño completo del tensor de datos de origen para evitar el error de superación de sus dimensiones. Luego especificaremos el tamaño del parche y el paso. Y también ofreceremos una opción para que el usuario añada una función de activación. 

__kernel void PatchCreate(__global float *inputs,
                          __global float *weights,
                          __global float *outputs,
                          int inputs_total,
                          int window_in,
                          int step,
                          int activation
                         )
  {
   const int i = get_global_id(0);
   const int w = get_global_id(1);
   const int v = get_global_id(2);
   const int window_out = get_global_size(1);
   const int variables = get_global_size(2);

Después planificaremos la ejecución del kernel para que se realice en un espacio de tareas tridimensional: el número de parches, la posición del elemento en el vector de incorporación del parche analizado y el ID de la variable en los datos de origen Recordemos que estamos construyendo la segmentación dentro de series temporales unitarias independientes.

En el cuerpo del kernel, implementaremos el ID del flujo en las 3 dimensiones del espacio de tareas. También definiremos las dimensiones del espacio de tareas.

A continuación, basándonos en los datos obtenidos, podremos determinar el desplazamiento en los búferes de datos hacia los elementos analizados.

   const int shift_in = i * step * variables + v;
   const int shift_out = (i * variables + v) * window_out + w;
   const int shift_weights = (window_in + 1) * (v * window_out + w);

Tenga en cuenta que al determinar el desplazamiento en el búfer de datos de origen, realizaremos las siguientes suposiciones:

1. El tensor de datos de origen contiene una secuencia de vectores de descripción del estado del entorno en un paso temporal concreto. En otras palabras, el tensor de datos de origen es una matriz bidimensional cuyas filas contienen descripciones del estado del entorno en un paso temporal concreto. Y las columnas de la matriz se corresponderán con los parámetros (variables) aparte de la descripción del estado del entorno analizado.
2. El método PatchTST analiza series temporales unitarias individuales. Por lo tanto, cada parámetro (variable) de la descripción del estado del entorno contendrá solo 1 elemento en el vector y se segmentará independientemente de los demás (dentro de toda la serie temporal).

Recuerde estos supuestos. Según ellos, deberemos preparar los datos de entrada en la parte del programa principal antes de transmitirlos al modelo.

A continuación, organizaremos un ciclo para multiplicar el vector de segmentos por el correspondiente vector de coeficientes de peso. En el cuerpo del ciclo, controlaremos el desplazamiento en el búfer de datos de origen para evitar accesos fuera del array.

   float res = weights[shift_weights + window_in];
   for(int p = 0; p < window_in; p++)
      if((shift_in + p * variables) < inputs_total)
         res += inputs[shift_in + p * variables] * weights[shift_weights + p];
   if(isnan(res))
      res = 0;

Nótese aquí que al acceder a los datos del tensor de origen, utilizaremos un paso igual al número de variables en la descripción de un estado del entorno. Es decir, nos desplazaremos una columna de la matriz de datos de origen, lo cual se corresponde con el requisito de segmentación de una serie temporal unitaria.

En caso de que obtendremos NaN como resultado de la operación de multiplicación del vector; lo sustituiremos por "0".

A continuación, todo lo que deberemos hacer es ejecutar la función de activación especificada y guardar el valor obtenido en el búfer de resultados correspondiente.

   switch(activation)
     {
      case 0:
         res = tanh(res);
         break;
      case 1:
         res = 1 / (1 + exp(-clamp(res, -20.0f, 20.0f)));
         break;
      case 2:
         if(res < 0)
            res *= 0.01f;
         break;
      defaultд:
         break;
     }
//---
   outputs[shift_out] = res;
  }

Una vez realizada la pasada directa, procederemos a construir los kernels del pasada inversa. Y primero crearemos el kernel de distribución del gradiente de error a la capa anterior PatchHiddenGradient. En los parámetros de este kernel transmitiremos 4 punteros a búferes de datos:

• inputs — búfer de datos de entrada (necesario para corregir gradientes de error en la derivada de la función de activación);
• inputs_gr — búfer de gradientes de error a nivel de datos de entrada (en este caso, el búfer para registrar los resultados);
• weights — matriz de parámetros de la capa entrenada;
• outputs_gr — tensor de gradiente en el nivel de resultados de la capa (en este caso, los datos de origen para calcular los gradientes de error).

Además, transmitiremos 5 constantes al kernel, cuyo propósito podrá adivinarse fácilmente a partir de los nombres de las variables.

__kernel void PatchHiddenGradient(__global float *inputs,
                                  __global float *inputs_gr,
                                  __global float *weights,
                                  __global float *outputs_gr,
                                  int window_in,
                                  int step,
                                  int window_out,
                                  int outputs_total,
                                  int activation
                                 )
  {
   const int i = get_global_id(0);
   const int v = get_global_id(1);
   const int variables = get_global_size(1);

Tenemos previsto usar el kernel en un espacio de tareas bidimensional: la longitud de la secuencia de datos de origen y el número de parámetros del estado del entorno (variables) que deben analizarse.

Obsérvese que al construir los kernels, orientaremos el espacio del problema en la dimensionalidad del tensor de resultados. En la pasada directa, nos centramos en el tensor tridimensional de incorporación de datos, mientras que en la pasada inversa nos centramos en el tensor bidimensional de los datos de origen, o más bien en sus gradientes de error. Este enfoque permite que cada flujo individual se configure para recuperar un único valor en el búfer de resultados del kernel.

En el cuerpo del kernel, identificaremos el flujo en el espacio de tareas y definiremos las dimensiones necesarias. Luego calcularemos los índices de desplazamiento.

   const int w_start = i % step;
   const int r_start = max((i - window_in + step) / step, 0);
   int total = (window_in - w_start + step - 1) / step;
   total = min((i + step) / step, total);

A continuación, organizaremos un sistema de ciclos anidados para recopilar los gradientes de error.

   float grad = 0;
   for(int p = 0; p < total; p ++)
     {
      int row = r_start + p;
      if(row >= outputs_total)
         break;
      for(int wo = 0; wo < window_out; wo++)
        {
         int shift_g = (row * variables + v) * window_out + wo;
         int shift_w = v * (window_in + 1) * window_out + w_start + (total - p - 1) * step + wo * (window_in + 1);
         grad += outputs_gr[shift_g] * weights[shift_w];
        }
     }

Obsérvese que un elemento de los datos de origen afectará al valor de todos los elementos del vector de incorporación de un parche individual con distintos coeficientes de peso. Por lo tanto, el ciclo anidado recopilará los gradientes de error de todo el vector de incorporación del parche individual.

Además, en el caso de los parches superpuestos, existirá la posibilidad de que el elemento de los datos de origen analizado entre en la ventana de datos de origen de múltiples parches. El ciclo exterior de nuestro sistema de ciclos anidados servirá para recopilar el gradiente de error de dichos parches.

El gradiente de error recopilado (total) sobre el elemento analizado de los datos de origen lo corregiremos mediante la derivada de la función de activación.

   float inp = inputs[i * variables + v];
   if(isnan(grad))
      grad = 0;
//---
   switch(activation)
     {
      case 0:
         grad = clamp(grad + inp, -1.0f, 1.0f) - inp;
         grad = grad * (1 - pow(inp == 1 || inp == -1 ? 0.99999999f : inp, 2));
         break;
      case 1:
         grad = clamp(grad + inp, 0.0f, 1.0f) - inp;
         grad = grad * (inp == 0 || inp == 1 ? 0.00000001f : (inp * (1 - inp)));
         break;
      case 2:
         if(inp < 0)
            grad *= 0.01f;
         break;
      default:
         break;
     }

Y el resultado de las operaciones se escribirá en el elemento correspondiente del búfer de gradiente de error de la capa neuronal precedente.

   inputs_gr[i * variables + v] = grad;
  }

Tras distribuir el gradiente de error, tendremos que ajustar los parámetros entrenados del modelo para minimizar el error. Para implementar esta funcionalidad, crearemos el kernel PatchUpdateWeightsAdam, en el que construiremos la optimización de los parámetros utilizando el método de Adam.

En los parámetros del kernel transmitiremos los punteros a 5 búferes de datos. Además de los conocidos búferes inputs, weights y output_gr, añadiremos búferes auxiliares para los momentos 1 y 2 de los gradientes de error a nivel de la matriz de pesos weights_m y weights_v, respectivamente. Además, también transmitiremos los coeficientes de entrenamiento en los parámetros del kernel.

__kernel void PatchUpdateWeightsAdam(__global float *weights,
                                     __global const float *outputs_gr,
                                     __global const float *inputs,
                                     __global float *weights_m,
                                     __global float *weights_v,
                                     const int inputs_total,
                                     const float l,
                                     const float b1,
                                     const float b2,
                                     int step
                                    )
  {
   const int c = get_global_id(0);
   const int r = get_global_id(1);
   const int v = get_global_id(2);
   const int window_in = get_global_size(0) - 1;
   const int window_out = get_global_size(1);
   const int variables = get_global_size(2);

Como nuestro tensor de coeficientes de peso es tridimensional, el espacio de tareas también se formará en 3 dimensiones:

• tamaño del parche + bias,
• tamaño del vector de incorporación,
• número de variables.

Aquí, seguiremos la lógica anterior donde cada flujo individual ajustará el valor de 1 parámetro entrenado.

En el cuerpo del kernel, identificaremos el flujo en las 3 dimensiones del espacio de tareas. También definiremos la dimensionalidad de las dimensiones. A continuación, definiremos las constantes de desplazamiento en los búferes de datos.

   const int start_input = c * variables + v;
   const int step_input = step * variables;
   const int start_out = v * window_out + r;
   const int step_out = variables * window_out;
   const int total = inputs_total / (variables * step);

Y organizaremos un ciclo de recopilación de gradientes de error en el nivel del parámetro entrenado corregido....

   float grad = 0;
   for(int p = 0; p < total; p++)
     {
      int i = start_input + i * step_input;
      int o = start_out + i * step_out;
      grad += (c == window_in ? 1 : inputs[i]) * outputs_gr[0];
     }
   if(isnan(grad))
      grad = 0;

Una vez determinado el gradiente de error, pasaremos al algoritmo de ajuste de parámetros. En primer lugar, definiremos los momentos de primer y segundo orden.

   const int shift_weights = (window_in + 1) * (window_out * v + r) + c;
//---
   float weight = weights[shift_weights];
   float mt = b1 * weights_m[shift_weights] + (1 - b1) * grad;
   float vt = b2 * weights_v[shift_weights] + (1 - b2) * pow(grad, 2);

A continuación, calcularemos la magnitud del ajuste de los parámetros.

   float delta = l * (mt / (sqrt(vt) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));

Y por último corregiremos los valores en los búferes de datos.

   if(fabs(delta) > 0)
      weights[shift_weights] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);
   weights_m[shift_weights] = mt;
   weights_v[shift_weights] = vt;
  }

Tenga en cuenta que solo cambiaremos el coeficiente de ponderación en el búfer de datos si el valor de cambio del parámetro es distinto de "0". Desde un punto de vista matemático, añadir "0" al valor actual no modificará el parámetro. Pero introduciremos una operación de comprobación adicional en la variable local para eliminar la operación innecesaria y más costosa de acceder al búfer de datos global.

Esto completará el trabajo en el lado OpenCL, así que podemos pasar al trabajo en el lado del programa principal.

2.2 Clase de segmentación de datos

Para llamar y mantener los kernels creados anteriormente en el lado del programa principal, crearemos la clase CNeuronPatching, que es heredera de nuestra clase básica de todas las capas neuronales CNeuronBaseOCL.

En el cuerpo de la clase, declararemos las variables para almacenar los parámetros básicos de la arquitectura del objeto. Así como los búferes de los parámetros entrenados y los momentos correspondientes. Luego declararemos todos los búferes como objetos estáticos, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos".

class CNeuronPatching   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindowIn;
   uint              iStep;
   uint              iWindowOut;
   uint              iVariables;
   uint              iCount;
   //---
   CBufferFloat      cPatchWeights;
   CBufferFloat      cPatchFirstMomentum;
   CBufferFloat      cPatchSecondMomentum;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronPatching(void){};
                    ~CNeuronPatching(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, 
                          uint step, uint window_out, uint count, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronPatchingOCL; }
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

El conjunto de métodos de clase redefinidos es bastante estándar. La inicialización de los objetos y variables de la clase se realizará en el método Init. En los parámetros, el método obtendrá toda la información necesaria para crear el objeto, la arquitectura requerida.

bool CNeuronPatching::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window_in, uint step, uint window_out,
                           uint count, uint variables,
                           ENUM_OPTIMIZATION optimization_type, uint batch
                          )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count * variables, 
                                                                optimization_type, batch))
      return false;

En el cuerpo del método, primero llamaremos al método homónimo de la clase padre, que ejecutará el control mínimo necesario de los valores obtenidos y la inicialización de los objetos y variables heredados. El resultado de las operaciones en el método de la clase padre está controlado por el valor lógico retornado.

Una vez ejecutadas con éxito las operaciones en el método de la clase padre, guardaremos los valores obtenidos de la descripción de la arquitectura del objeto en las variables locales.

   iWindowIn = MathMax(window_in, 1);
   iWindowOut = MathMax(window_out, 1);
   iStep = MathMax(step, 1);
   iVariables = MathMax(variables, 1);
   iCount = MathMax(count, 1);

Después inicializaremos el búfer de parámetros entrenados.

   int total = int((window_in + 1) * window_out * variables);
   if(!cPatchWeights.Reserve(total))
      return false;
   float k = float(1 / sqrt(total));
   for(int i = 0; i < total; i++)
     {
      if(!cPatchWeights.Add((2 * GenerateWeight()*k - k)*WeightsMultiplier))
         return false;
     }
   if(!cPatchWeights.BufferCreate(OpenCL))
      return false;

Así como los búferes de momentos del gradiente de error al nivel de los parámetros entrenados.

   if(!cPatchFirstMomentum.BufferInit(total, 0) ||
      !cPatchFirstMomentum.BufferCreate(OpenCL))
      return false;
   if(!cPatchSecondMomentum.BufferInit(total, 0) ||
      !cPatchSecondMomentum.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Tras inicializar el objeto, pasaremos a construir el método de pasada directa CNeuronPatching::feedForward. En este método, implementaremos la colocación en cola del kernel de pasada directa creado anteriormente. Ya hemos descrito los procedimientos para colocar un kernel en la cola de ejecución más de una vez como parte de esta serie de artículos. Aquí deberemos prestar especial atención a la correcta especificación de la dimensionalidad del espacio de tareas y de los parámetros a transmitir.

Como mencionamos al construir el kernel, en este caso utilizaremos un espacio de tareas tridimensional:

• número de parches;
• dimensionalidad de la incorporación de 1 parche;
• número de parámetros analizados en la descripción de las condiciones del entorno.

bool CNeuronPatching::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !OpenCL)
      return false;
//---
   uint global_work_offset[3] = {0, 0, 0};
   uint global_work_size[3] = {iCount, iWindowOut, iVariables};

Tras crear los arrays de especificación del espacio de tareas y el desplazamiento en él, organizaremos el proceso de transmisión de parámetros al kernel.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PatchCreate, def_k_ptc_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchCreate, def_k_ptc_weights, cPatchWeights.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchCreate, def_k_ptc_outputs, Output.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchCreate, def_k_ptc_activation, (int)activation))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchCreate, def_k_ptc_inputs_total, (int)NeuronOCL.Neurons()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchCreate, def_k_ptc_window_in, (int)iWindowIn))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchCreate, def_k_ptc_step, (int)iStep))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Al mismo tiempo, no nos olvidaremos de controlar que las operaciones sean correctas. Y después de transferir con éxito todos los parámetros requeridos, colocaremos el kernel en la cola de ejecución.

   if(!OpenCL.Execute(def_k_PatchCreate, 3, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

De forma similar, pondremos en la cola el kernel de distribución del gradiente de error a los elementos de la capa precedente según su influencia en el resultado final del modelo en el método CNeuronPatching::calcInputGradients. Solo que la llamada al kernel PatchHiddenGradient se realizará en el espacio de tareas bidimensional.

bool CNeuronPatching::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !OpenCL)
      return false;
//---
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2] = {NeuronOCL.Neurons() / iVariables, iVariables};

Obsérvese aquí que hemos definido el tamaño de la secuencia inicial de una serie temporal multivariante como la relación entre el tamaño del búfer de resultados de la capa precedente y el número de variables analizadas de la descripción de un estado del entorno.

Recordemos que se supone que el método PatchTST utiliza como datos de entrada una serie temporal multidimensional en la que cada estado del entorno se describe mediante un vector de longitud fija. Y cada elemento del vector contiene el valor del parámetro correspondiente de la descripción del estado del sistema.

A continuación, transmitiremos los parámetros al kernel con control del tiempo de ejecución.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PatchHiddenGradient, def_k_pthg_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchHiddenGradient, def_k_pthg_inputs_gr, NeuronOCL.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchHiddenGradient, def_k_pthg_weights, cPatchWeights.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchHiddenGradient, def_k_pthg_outputs_gr, Gradient.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchHiddenGradient, def_k_pthg_activation, (int)NeuronOCL.Activation()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchHiddenGradient, def_k_pthg_outputs_total, (int)iCount))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchHiddenGradient, def_k_pthg_window_in, (int)iWindowIn))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchHiddenGradient, def_k_pthg_step, (int)iStep))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchHiddenGradient, def_k_pthg_window_out, (int)iWindowOut))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Y pondremos el kernel en la cola de ejecución.

   if(!OpenCL.Execute(def_k_PatchHiddenGradient, 2, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

El último método para construir la funcionalidad principal de la clase será el método para ajustar los parámetros entrenados del modelo CNeuronPatching::updateInputWeights. Este método pondrá en cola el kernel PatchUpdateWeightsAdam, cuyo algoritmo hemos descrito antes. Creo que ya se habrá dado cuenta de que el algoritmo para poner el kernel en la cola de ejecución es idéntico a los dos métodos descritos anteriormente. La diferencia está en los detalles. Aquí se usa un espacio de tareas tridimensional.

bool CNeuronPatching::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || !OpenCL)
      return false;
//---
   uint global_work_offset[3] = {0, 0, 0};
   uint global_work_size[3] = {iWindowIn + 1, iWindowOut, iVariables};

En la primera dimensión, añadiremos 1 elemento de desplazamiento bayesiano al tamaño del parche. En las dimensiones segunda y tercera, especificaremos el tamaño de la incorporación de 1 parche y el número de canales independientes analizados almacenados en nuestras variables de clase.

Y luego implementaremos la transmisión de parámetros al kernel con el control de los resultados de las operaciones.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_outputs_gr, getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_weights, cPatchWeights.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_weights_m, 
                                                                            cPatchFirstMomentum.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_weights_v, 
                                                                           cPatchSecondMomentum.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_inputs_total, (int)NeuronOCL.Neurons()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_l, lr))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_b1, b1))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_step, (int)iStep))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PatchUpdateWeightsAdam, def_k_ptuwa_b2, b2))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

A continuación, el kernel se colocará en la cola de ejecución.

   if(!OpenCL.Execute(def_k_PatchUpdateWeightsAdam, 3, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

El algoritmo de los métodos de trabajo con los archivos se ha simplificado al máximo, y le sugiero que se familiarice con el código de estos métodos en el archivo adjunto. Allí también encontrará el código completo de todas las clases y sus métodos para crear y entrenar modelos.

Ya hemos implementado un método para crear incorporaciones de los parches creados para las series temporales unitarias independientes que sean componentes de las series temporales multidimensionales que estamos analizando. Sin embargo, esto supone solo la mitad del método PatchTST propuesto. El segundo bloque (no menos importante) de este método será el Transformer de análisis de las dependencias entre parches dentro de una serie temporal unitaria. Y aquí hay una aclaración importante: los análisis de dependencia solo se realizarán dentro de canales independientes, sin analizar las dependencias cruzadas entre elementos de distintos canales unitarios.

Y aquí deberemos recordar que todas las variantes consideradas anteriormente para la implementación de la arquitectura del Transformer utilizaban la mezcla de canales, lo cual contradice los principios del método PatchTST. Pero hay una excepción, el Conformer. El Conformer, a diferencia del Transformer vainilla utilizado por los autores del método PatchTST, tiene una arquitectura más compleja. Este utiliza Continuous-Attention e introduce bloques NeuralODE para mejorar la eficacia del modelo, lo cual suele dar resultados positivos. Y esto lo confirman nuestros experimentos anteriores. Por lo tanto, como parte de nuestra implementación, hemos sustituido el Transformer utilizado por los autores del método PatchTST por la implementación del bloque Conformer que creamos anteriormente en la clase CNeuronConformer.

2.3 Arquitectura del modelo

Tras haber realizado el trabajo de implementación de los "bloques de construcción" para la aplicación del método PatchTST, pasaremos a crear la arquitectura de los modelos entrenados. El método analizado se ha propuesto para la previsión de series temporales multidimensionales. Y creo que resulta bastante obvio que implementamos este método dentro del Codificador del estado del entorno. La arquitectura de este modelo se describe en el método CreateEncoderDescriptions, con un único puntero a un array dinámico transmitido en sus parámetros para preservar la arquitectura del modelo.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En el cuerpo del método comprobaremos la relevancia del puntero recibido al objeto y, de ser necesario, crearemos una nueva instancia del array dinámico.

Luego introduciremos el conjunto completo de datos históricos en la entrada del modelo.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí cabe señalar que el procedimiento de creación de los parches no permite utilizar como datos de entrada una historia con una profundidad inferior a 1 parche. Obviamente, solo podemos introducir datos históricos con una profundidad de 1 parche en la entrada del modelo en cada llamada, y al mismo tiempo, acumular toda la profundidad de la historia analizada en la pila interna, como hicimos anteriormente en la capa incorporación. Pero este enfoque tiene una serie de limitaciones. En primer lugar, el modelo deberá especificar un paso entre parches igual al propio parche (parches no solapados), mientras que el paso real será igual a la frecuencia de la llamada al modelo.

Creo que resulta evidente que existe cierta confusión y dificultad a la hora de alinear los programas de recopilación de datos de entrenamiento, de entrenamiento y de explotación de modelos.

El segundo punto es que con este enfoque, si cambiamos el tamaño del parche o el tamaño del paso, tendríamos que volver a recopilar la muestra de entrenamiento, lo que introducirá restricciones y costes adicionales en el proceso de entrenamiento del modelo.

Por lo tanto, utilizaremos un método más sencillo y versátil para suministrar la profundidad completa del modelo analizado a la entrada del modelo. Y estableceremos el parche y el tamaño de paso según los parámetros en la arquitectura de la capa del modelo correspondiente.

Como siempre, suministraremos los datos "brutos" sin procesar a la entrada del modelo, que normalizaremos directamente en la capa de normalización por lotes.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, debemos notar que en este modelo, hemos puesto una capa de codificación posicional entrenada con el nivel de datos de origen en lugar de con las incorporaciones, como hicimos anteriormente. De este modo quería destacar la posición de los parámetros específicos. Al fin y al cabo, al utilizar parches superpuestos, un parámetro puede ir en varios parches.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronLearnabledPE;
   descr.count = prev_count;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, hemos añadido una capa Dropout, que utilizaremos para enmascarar valores individuales de los datos de origen mientras entrenamos el modelo.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDropoutOCL;
   descr.count = prev_count;
   descr.probability = 0.4f;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Asimismo, hemos fijado el coeficiente de enmascaramiento de datos en un 40%, como en artículos anteriores.

Luego añadimos una capa de generación de parches. En este artículo, hemos añadido parches no solapados con una ventana y un tamaño de paso igual a 3.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPatchingOCL;
   descr.window = 3;
   prev_count = descr.count = (HistoryBars+descr.window-1)/descr.window;
   descr.step = descr.window;
   descr.layers=BarDescr;
   int prev_wout = descr.window_out = EmbeddingSize / 2;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí también cabe destacar que la incorporación del parche se entrena en 2 etapas. En primer lugar, generaremos incorporaciones de parches con la mitad de tamaño. Y luego en la capa de convolución, aumentaremos el tamaño del parche.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count*BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Recordemos que hemos introducido la codificación de la posición al nivel de los datos de origen. Así que tras generar las incorporaciones, suministraremos inmediatamente los datos a un bloque de 10 capas del Conformer.

//--- layer 6-16
   for(int i = 0; i < 10; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronConformerOCL;
      descr.count = prev_count;
      descr.window = prev_wout;
      descr.step = 8;
      descr.window_out = EmbeddingSize;
      descr.layers = BarDescr;
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }
     }

Después tendremos una cabeza de decisión formada por 3 capas totalmente conectadas. Haremos que el tamaño de la última capa sea suficiente para contener la información recuperada de los datos históricos y predecir los estados posteriores para una profundidad dada.

//--- layer 17
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation=SIGMOID;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 18
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation=LReLU;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 19
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count=descr.count = BarDescr*(HistoryBars+NForecast);
   descr.activation=TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Al final del modelo, desnormalizaremos los valores recuperados y predichos añadiendo los indicadores estadísticos eliminados de los datos de origen.

//--- layer 20
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   prev_count = descr.count = prev_count;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Obsérvese que hemos mantenido el tamaño de los datos de entrada y los resultados del modelo similares a los del artículo anterior. Esto nos ha permitido trasladar completamente la arquitectura de los modelos del Actor y el Crítico sin modificaciones. Además, en el nuevo experimento, podremos utilizar plenamente la muestra de entrenamiento y los asesores expertos del artículo anterior sin modificaciones. De este modo, podremos comparar el efecto de diferentes arquitecturas del Codificador del estado del entorno en el rendimiento del entrenamiento de las políticas del Actor.

La descripción completa de la arquitectura de todos los modelos entrenados y los programas utilizados en la preparación de este artículo se puede encontrar en el archivo adjunto.

3. Simulación

En los anteriores apartados de este de este artículo, hemos presentado un nuevo método de predicción de series temporales multidimensionales, el PatchTST. Asimismo, hemos implementado nuestra propia visión de los enfoques propuestos usando MQL5. Y ahora ha llegado el momento de poner a prueba el trabajo realizado. En esta etapa, primero entrenaremos los modelos utilizando datos históricos reales. Y luego probaremos los modelos entrenados en el Simulador de Estrategias de MetaTrader 5 en un intervalo histórico más allá de la muestra de entrenamiento.

Al igual que antes, entrenaremos los modelos con datos históricos de 2023 para EURUSD y el marco temporal H1. Las pruebas del modelo entrenado se realizarán con datos históricos de enero de 2024, conservando el instrumento financiero y el marco temporal. Los parámetros de todos los indicadores analizados durante la recogida de la muestra de entrenamiento y la comprobación de la política entrenada se utilizarán por defecto.

El entrenamiento de los modelos se realizará en 2 fases. En el primer paso, entrenaremos el Codificador del estado del entorno. Este modelo aprende a analizar y resumir únicamente los datos históricos de una serie temporal multidimensional de la dinámica de precios de los instrumentos y de los indicadores analizados. Sin tener en cuenta el estado de la cuenta y las posiciones abiertas. Por lo tanto, entrenaremos el modelo con la muestra de entrenamiento inicial sin recoger datos adicionales hasta obtener un resultado aceptable de recuperación de datos enmascarados y predicción de estados posteriores.

En la segunda etapa, aplicaremos el entrenamiento de la política de comportamiento del Actor y la corrección de la evaluación de las acciones del Crítico. Esta etapa es iterativa e implicará 2 subprocesos:

1. Entrenamiento de modelos para el Actor y el Crítico.
2. Recopilación de datos del entorno adicionales con respecto a la política actual del Actor.

Tras varias iteraciones de entrenamiento de la política del Actor, podremos obtener un modelo capaz de generar rendimientos tanto con los datos históricos de la muestra de entrenamiento como con datos nuevos. A continuación le presentamos los resultados del modelo entrenado con los nuevos datos.

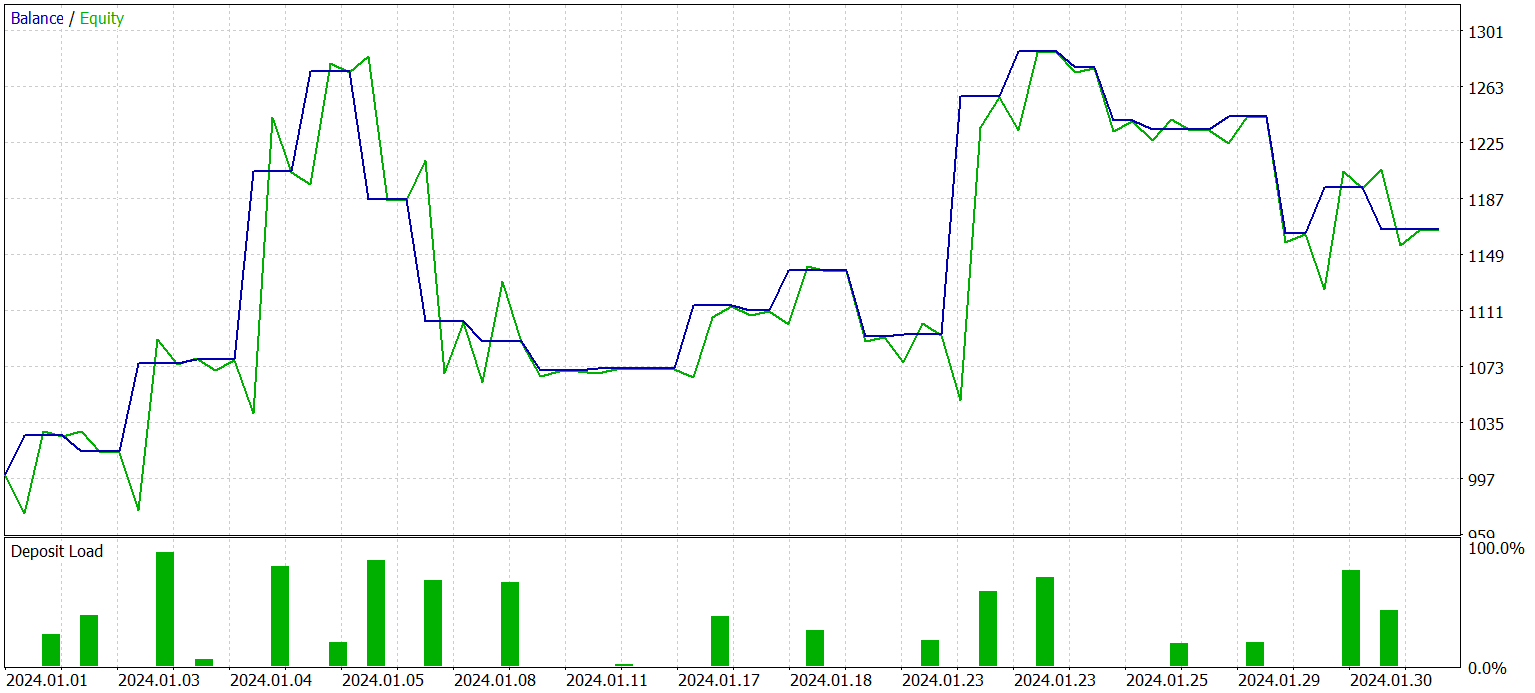
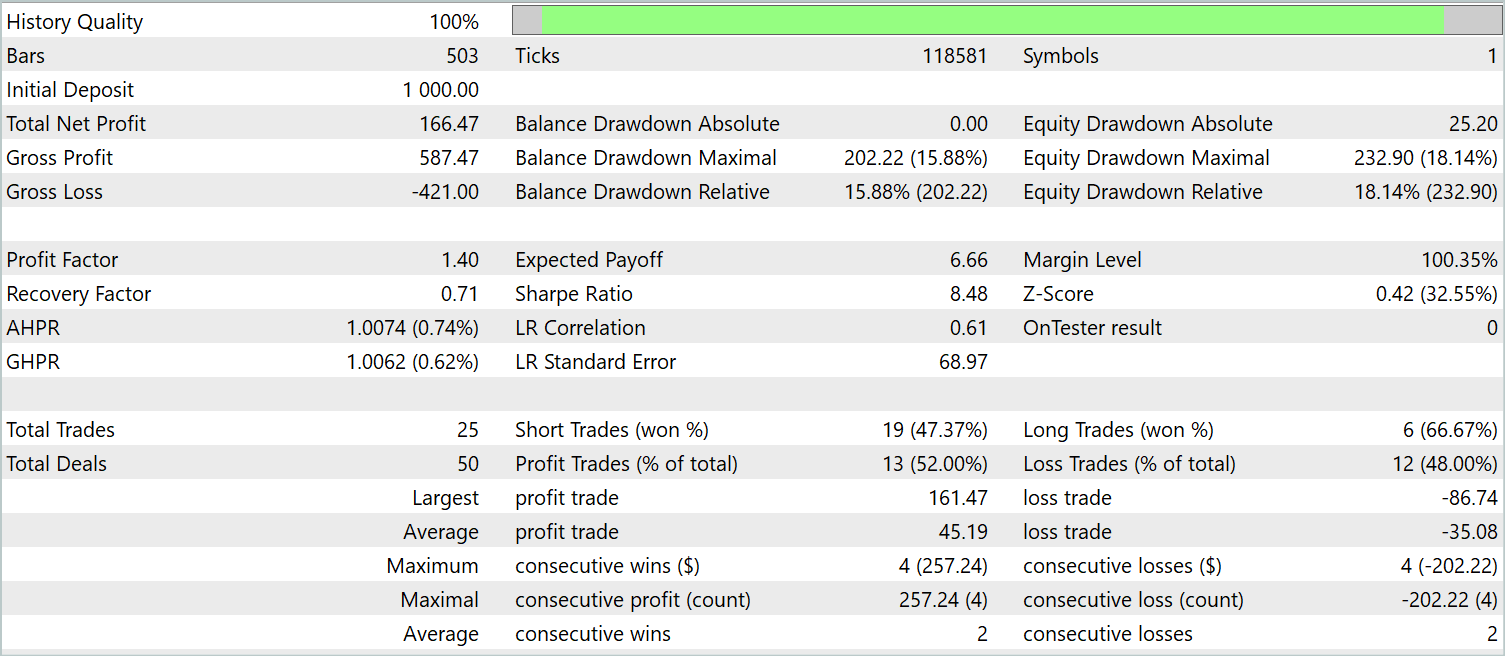
No podemos decir que el gráfico de balance sea un gráfico de crecimiento uniforme. No obstante, durante el periodo de prueba el modelo ha realizado 25 transacciones, 13 de las cuales se han cerrado con beneficios. Esto supone el 52,0% de las transacciones rentables. Un indicador cercano a la paridad. Sin embargo, la transacción rentable máxima supera a la pérdida máxima en un 87,2% mientras que la transacción rentable media supera a la pérdida media en un 28,6%. Como resultado, durante el periodo de prueba, el factor de beneficio ha sido de 1,4.

Conclusión

En este artículo, hemos presentado un nuevo método de análisis y predicción de series temporales multidimensionales, el PatchTST, que combina las ventajas de la segmentación de datos, el uso de transformadores y el aprendizaje de representaciones. La segmentación de datos permite al modelo captar mejor los patrones temporales locales y el contexto, lo cual mejora la calidad del análisis y las previsiones. Y el uso del Transformer permite extraer representaciones abstractas de los datos y analizar su secuencia temporal y su interrelación.

En la parte práctica del artículo, hemos implementado nuestra propia visión de los enfoques propuestos usando MQL5. Y también hemos entrenado el modelo con datos históricos reales. Asimismo, hemos probado la política entrenada del Actor con nuevos datos fuera de la muestra de entrenamiento. Los resultados demuestran la viabilidad del uso del método PatchTST para construir y entrenar modelos capaces de generar beneficios.

Así pues, el método PatchTST supone una potente herramienta de análisis y previsión de series temporales multidimensionales, que puede aplicarse con éxito en diversas tareas prácticas.

Enlaces

• A Time Series is Worth 64 Words: Long-term Forecasting with Transformers
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de cobros de ejemplo Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL