Using OpenCL to test candlestick patterns

Introduction

When traders start mastering OpenCL, they are confronted with the question of where to apply it. Such illustrative examples as multiplication of matrices or sorting large amounts of data are not widely used in the development of indicators or automated trading systems. Another common application — working with neural networks — requires certain knowledge in the area. Studying neural networks can cost a lot of time for a common programmer without guaranteeing any results in trading. This circumstance may turn down those who would like to feel the full power of OpenCL when solving elementary tasks.

In this article we will consider the use of OpenCL for solving the simplest task of algorithmic trading — finding candlestick patterns and testing them on history. We will develop the algorithm of testing a single pass and optimizing two parameters in the "1 minute OHLC" trading mode. After that, we will compare the performance of the built-in strategy tester with the OpenCL one and find out which of them (and to what degree) is faster.

It is assumed that the reader is already familiar with OpenCL basics. Otherwise, I recommend reading the articles "OpenCL: The bridge to parallel worlds" and "OpenCL: From naive towards more insightful programming". It would also be good to have the OpenCL Specification Version 1.2 on hand. The article will focus on the algorithm of building a tester without dwelling on OpenCL programming basics.

• Introduction
• 1. Implementation in MQL5    
  
• 1.1 Searching for patterns
• 1.2 Assembling the EA
• 1.3 Testing
• 2. Implementation in OpenCL
• 2.1 Uploading price data
• 2.2 Single test
• 2.2.1. Searching for patterns in OpenCL
• 2.2.2. Moving orders to M1 timeframe
• 2.2.3. Obtaining trade results
• 2.3. Launching a test
• 2.4. Optimization
• 2.4.1. Preparing orders
• 2.4.2. Obtaining trade results
• 2.4.3. Searching for patterns and forming test results
• 2.5. Launching optimization
• 3. Comparing performance
• 3.1. Optimization on EURUSD
• 3.2. Optimization on GBPUSD
• 3.3. Optimization on USDJPY
• 3.4. Performance summary table
• Conclusion
  

1. Implementation in MQL5

We need to rely on something to make sure that the implementation of the tester on OpenCL works correctly. First, we will develop an MQL5 EA. Then we will compare its results of testing and optimizing using a regular tester with the ones obtained by the OpenCL tester.

The test object is a simple EA trading the following candlestick patterns.

• Bearish pin bar
• Bullish pin bar
• Bearish engulfing
• Bullish engulfing

The strategy is simple:

• Bearish pin bar or bearish engulfing  — sell
• Bullish pin bar or bullish engulfing — buy
• The number of simultaneously opened positions — unlimited
• Maximum position holding time — limited, user-defined
  
• Take Profit and Stop Loss levels — fixed, user-defined

The presence of the pattern is to be checked on fully closed bars. In other words, we search for a pattern on three previous bars as soon as a new one appears.

Pattern detection conditions are as follows:

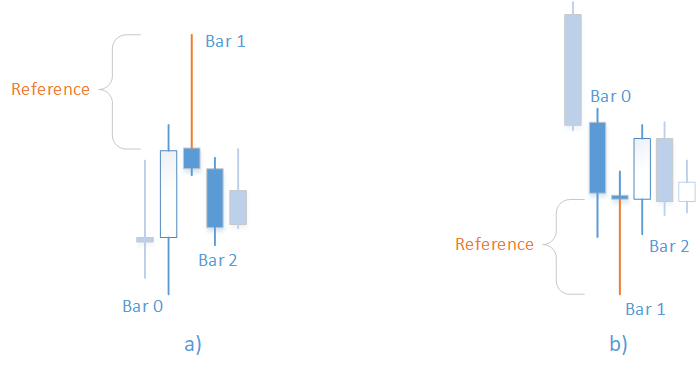
Fig. 1. "Bearish pin bar" (a) and "Bullish pin bar" (b) patterns

For the bearish pin bar (Fig. 1, a):

• The upper shadow ("tail") of the first bar is greater than the specified reference value: tail>=Reference
  
• The zero bar is bullish: Close[0]>Open[0]
• The second bar is bearish: Open[2]>Close[2]
  
• High price of the first bar is a local maximum: High[1]>MathMax(High[0],High[2])
• The body of the first bar is smaller than its upper shadow: MathAbs(Open[1]-Close[1])<tail
• tail = High[1]-max(Open[1],Close[1])

For the bullish pin bar (Fig. 1, b):

• The lower shadow ("tail") of the first bar is greater than the specified reference value: tail>=Reference
• The zero bar is bearish: Open[0]>Close[0]
• The second bar is bullish: Close[2]>Open[2]
  
• Low price of the first bar is a local minimum: Low[1]<MathMin(Low[0],Low[2])
• The body of the first bar is smaller than its lower shadow: MathAbs(Open[1]-Close[1])<tail

• tail = min(Open[1],Close[1])-Low[1]

Fig. 2. "Bearish engulfing" (a) and "Bullish engulfing" (b)

For bearish engulfing (Fig. 2, a):

• The first bar is bullish, its body is larger than the specified reference value: (Close[1]-Open[1])>=Reference
• High price of the zero bar is lower than the Close price of the first bar: High[0]<Close[1]
• Open price of the second bar exceeds the Close price of the first bar: Open[2]>CLose[1]
• Close price of the second bar is lower than the Open price of the first bar: Close[2]<Open[1]

For bullish engulfing (Fig. 2, b):

• The first bar is bearish, its body is larger than the specified reference value: (Open[1]-Close[1])>=Reference
• Low price of the zero bar is higher than the Close price of the first bar: Low[0]>Close[1]
• Open price of the second bar is lower than the Close price of the first bar: Open[2]<Close[1]
• Close price of the second bar exceeds the Open price of the first bar: Close[2]>Open[1]

1.1 Searching for patterns

Pattern definition code is provided below.

ENUM_PATTERN Check(MqlRates &r[],uint flags,double ref)
  {
//--- bearish pin bar  
   if((flags&PAT_PINBAR_BEARISH)!=0)
     {//
      double tail=H(1)-MathMax(O(1),C(1));
      if(tail>=ref && C(0)>O(0) && O(2)>C(2) && H(1)>MathMax(H(0),H(2)) && MathAbs(O(1)-C(1))<tail)
         return PAT_PINBAR_BEARISH;
     }
//--- bullish pin bar
   if((flags&PAT_PINBAR_BULLISH)!=0)
     {//
      double tail=MathMin(O(1),C(1))-L(1);
      if(tail>=ref && O(0)>C(0) && C(2)>O(2) && L(1)<MathMin(L(0),L(2)) && MathAbs(O(1)-C(1))<tail)
         return PAT_PINBAR_BULLISH;
     }
//--- bearish engulfing
   if((flags&PAT_ENGULFING_BEARISH)!=0)
     {//
      if((C(1)-O(1))>=ref && H(0)<C(1) && O(2)>C(1) && C(2)<O(1))
         return PAT_ENGULFING_BEARISH;
     }
//--- bullish engulfing
   if((flags&PAT_ENGULFING_BULLISH)!=0)
     {//
      if((O(1)-C(1))>=ref && L(0)>C(1) && O(2)<C(1) && C(2)>O(1))
         return PAT_ENGULFING_BULLISH;
     }
//--- nothing found   
   return PAT_NONE;
  }

Here we should pay attention to the ENUM_PATTERN enumerator. Its values are flags that can be combined and passed as one argument using bitwise OR:

enum ENUM_PATTERN
  {
   PAT_NONE=0,
   PAT_PINBAR_BEARISH = (1<<0),
   PAT_PINBAR_BULLISH = (1<<1),
   PAT_ENGULFING_BEARISH = (1<<2),
   PAT_ENGULFING_BULLISH = (1<<3)
  };

Also, the macros have been introduced for more compact record:

#define O(i) (r[i].open)
#define H(i) (r[i].high)
#define L(i) (r[i].low)
#define C(i) (r[i].close)

The Check() function is called from the IsPattern() function meant for checking the presence of specified patterns at the time of opening a new bar:

ENUM_PATTERN IsPattern(uint flags,uint ref)
  {
   MqlRates r[];
   if(CopyRates(_Symbol,_Period,1,PBARS,r)<PBARS)
      return 0;
   ArraySetAsSeries(r,false);
   return Check(r,flags,double(ref)*_Point);
  }

1.2 Assembling the EA

At first, the input parameters have to be defined. We have a reference value in the pattern definition conditions. This is the minimum length of the "tail" for a pin bar or an area for the intersection of bodies during an engulfing. We will specify it in points:

input int      inp_ref=50;

Besides, we have a set of patterns we work with. For more convenience, we will not use the register of flags in the inputs. Instead, we will divide it into four bool type parameters:

input bool     inp_bullish_pin_bar = true;
input bool     inp_bearish_pin_bar = true;
input bool     inp_bullish_engulfing = true;
input bool     inp_bearish_engulfing = true;

And assemble them into an unsigned variable in the initialization function:

   p_flags = 0;
   if(inp_bullish_pin_bar==true)
      p_flags|=PAT_PINBAR_BULLISH;
   if(inp_bearish_pin_bar==true)
      p_flags|=PAT_PINBAR_BEARISH;
   if(inp_bullish_engulfing==true)
      p_flags|=PAT_ENGULFING_BULLISH;
   if(inp_bearish_engulfing==true)
      p_flags|=PAT_ENGULFING_BEARISH;

Next, we set the acceptable position holding time expressed in hours, Take Profit and Stop Loss levels, as well as lot volume:

input int      inp_timeout=5;
input bool     inp_bullish_pin_bar = true;
input bool     inp_bearish_pin_bar = true;
input bool     inp_bullish_engulfing = true;
input bool     inp_bearish_engulfing = true;
input double   inp_lot_size=1;

For trading, we will use the CTrade class from the standard library. To define the tester speed, we will use the CDuration class that allows measuring time intervals between control points of the program execution in microseconds and display them in a convenient form. In this case, we will measure the time between the OnInit() and OnDeinit() functions. The full class code is contained in the attached Duration.mqh file.

CDuration time;

int OnInit()
  {
   time.Start();
   // ... 
   return(INIT_SUCCEEDED);
  }

void OnDeinit(const int reason)
  {
   time.Stop();
   Print("Test lasted "+time.ToStr());
  }

The EA work is extremely simple and consists of the following.

The OnTick() function's primary task is handling open positions. It closes a position if its holding time exceeds the value specified in the inputs. This is followed by checking the opening of a new bar. If the check is passed, check the presence of the pattern using the IsPattern () function. When finding a pattern, open a buy or sell position according to the strategy. The full OnTick() function code is provided below:

void OnTick()
  {
//--- handle open positions
   int total= PositionsTotal();
   for(int i=0;i<total;i++)
     {
      PositionSelect(_Symbol);
      datetime t0=datetime(PositionGetInteger(POSITION_TIME));
      if(TimeCurrent()>=(t0+(inp_timeout*3600)))
        {
         trade.PositionClose(PositionGetInteger(POSITION_TICKET));
        }
      else
         break;
     }
   if(IsNewBar()==false)
      return;
//--- check if the pattern is present
   ENUM_PATTERN pat=IsPattern(p_flags,inp_ref);
   if(pat==PAT_NONE)
      return;
//--- open positions
   double ask=SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   double bid=SymbolInfoDouble(_Symbol,SYMBOL_BID);
   if((pat&(PAT_ENGULFING_BULLISH|PAT_PINBAR_BULLISH))!=0)//buy     
      trade.Buy(inp_lot_size,_Symbol,ask,NormalizeDouble(ask-inp_sl*_Point,_Digits),NormalizeDouble(ask+inp_tp*_Point,_Digits),DoubleToString(ask,_Digits));
   else//sell
      trade.Sell(inp_lot_size,_Symbol,bid,NormalizeDouble(bid+inp_sl*_Point,_Digits),NormalizeDouble(bid-inp_tp*_Point,_Digits),DoubleToString(bid,_Digits));
  }

1.3 Testing

First of all, launch optimization to find out the best input values for the EA to trade profitably or at least open positions. We will optimize two parameters — a reference value for patterns and Stop Loss level in points. Set Take Profit level to 50 points and select all patterns for testing.

Optimization is to be performed on EURUSD M5. Time interval: 01.01.2018  — 01.10.2018. Fast optimization (genetic algorithm), trading mode: "1 minute OHLC".

The values of the optimized parameters are selected in a wide range with a large number of gradations:

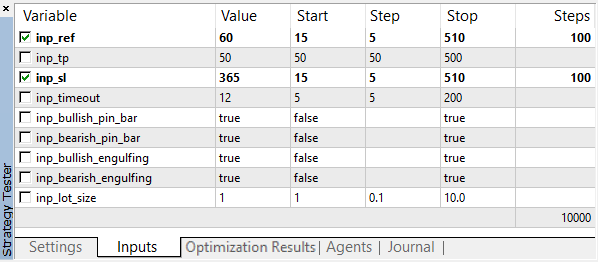
Fig. 3. Optimization parameters

After optimization completion, results are sorted by profit:

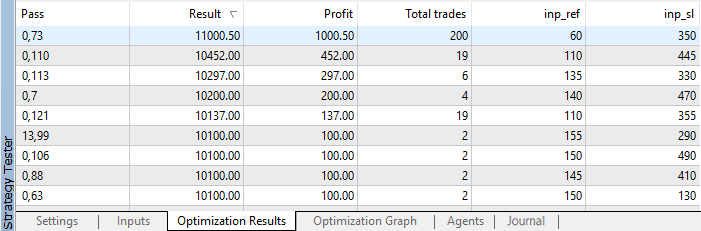
Fig. 4. Optimization results

As we can see, the best result with the profit of 1000.50 was received with a reference value of 60 points and on Stop Loss level of 350 points. Launch testing with these parameters and pay attention to its execution time.

Fig. 5. Single pass testing time by the built-in tester

Remember these values and proceed to testing the same strategy without involving a regular tester. Let's develop a custom tester using OpenCL features.

2. Implementation in OpenCL

To work with OpenCL, we will use the COpenCL class from the standard library with small modifications. The purpose of the improvements is to get as much information as possible about occurring errors. However, while doing so, we should not overload the code by conditions and outputting data to the console. To do this, create the COpenCLx class. Its full code can be found in the OpenCLx.mqh file attached below:

class COpenCLx : public COpenCL
  {
private:
   COpenCL          *ocl;
public:
                     COpenCLx();
                    ~COpenCLx();
   STR_ERROR         m_last_error;  // last error structure
   COCLStat          m_stat;        // OpenCL statistics                    
   //--- work with buffers
   bool              BufferCreate(const ENUM_BUFFERS buffer_index,const uint size_in_bytes,const uint flags,const string function,const int line);
   template<typename T>
   bool              BufferFromArray(const ENUM_BUFFERS buffer_index,T &data[],const uint data_array_offset,const uint data_array_count,const uint flags,const string function,const int line);
   template<typename T>
   bool              BufferRead(const ENUM_BUFFERS buffer_index,T &data[],const uint cl_buffer_offset,const uint data_array_offset,const uint data_array_count,const string function,const int line);
   template<typename T>
   bool              BufferWrite(const ENUM_BUFFERS buffer_index,T &data[],const uint cl_buffer_offset,const uint data_array_offset,const uint data_array_count,const string function,const int line);
   //--- set arguments
   template<typename T>
   bool              SetArgument(const ENUM_KERNELS kernel_index,const int arg_index,T value,const string function,const int line);
   bool              SetArgumentBuffer(const ENUM_KERNELS kernel_index,const int arg_index,const ENUM_BUFFERS buffer_index,const string function,const int line);
   //--- work with kernel
   bool              KernelCreate(const ENUM_KERNELS kernel_index,const string kernel_name,const string function,const int line);
   bool              Execute(const ENUM_KERNELS kernel_index,const int work_dim,const uint &work_offset[],const uint &work_size[],const string function,const int line);
   //---
   bool              Init(ENUM_INIT_MODE mode);
   void              Deinit(void);
  };

As we can see, the class contains a pointer to the COpenCL object, as well as several methods used as wrappers for the COpenCL class methods of the same name. Each of these methods has the name of the function and the string it was called from among the arguments. In addition, enumerators are used instead of kernel indices and buffers. This is done to enable applying EnumToString() in the error message, which is much more informative than just an index.

Let's consider one of these methods in more detail.

bool COpenCLx::KernelCreate(const ENUM_KERNELS kernel_index,const string kernel_name,const string function,const int line)
  {
   if(ocl==NULL)
     {
      SET_UERRx(UERR_NO_OCL,"OpenCL object does not exist",function,line);
      return false;
     }
//--- Launch kernel execution
   ::ResetLastError();
   if(!ocl.KernelCreate(kernel_index,kernel_name))
     {
      string comment="Failed to create kernel "+EnumToString(kernel_index)+", name \""+kernel_name+"\"";
      SET_ERRx(comment,function,line);
      if(!m_last_error.code)
         SET_UERRx(UERR_KERNEL_CREATE,comment,function,line);
      return(false);
     }
//---
   return true;
  }

There are two checks here: for the presence of the COpenCL class object and kernel creation method success. But instead of displaying a text using the Print() function, the messages are passed to macros together with the error code, the function name and the call string. These macros store error information in the m_last_error class error. Its structure is displayed below:

struct STR_ERROR
  {
   int               code;       // code 
   string            comment;    // comment 
   string            function;   // function the error has occurred in
   int               line;       // string the error has occurred in
  };

There are four such macros in total. Let's consider them one by one.

The SET_ERR macro writes the last execution error, the function and the string it has been called from, as well as the comment passed as a parameter:

#define SET_ERR(c) do {m_last_error.function = __FUNCTION__; \
      m_last_error.line =__LINE__; \
      m_last_error.code=::GetLastError(); m_last_error.comment=c;} while(0)

The SET_ERRx macro is similar to the SET_ERR one:

#define SET_ERRx(c,f,l) do {m_last_error.function = f; m_last_error.line = l; \
      m_last_error.code=::GetLastError(); m_last_error.comment=c;} while(0)

It differs in that the function name and string are passed as parameters. Why was this done? Suppose that an error has occurred in the KernelCreate() method. When using the SET_ERR macro, we can see the KernelCreate() method name, but it is much more useful to know where the method has been called from. To achieve this, we pass the function and the method call string as arguments inserting them to the macro.

The SET_UERR macro goes next. It is meant for writing custom errors:

#define SET_UERR(err,c) do {m_last_error.function = __FUNCTION__; \
      m_last_error.line =__LINE__; \
      m_last_error.code=ERR_USER_ERROR_FIRST+err; m_last_error.comment=c;} while(0)

In the macro, an error code is passed as a parameter rather than calling GetLastError(). In other aspects, it is similar to the SET_ERR macro.

The SET_UERRx macro is meant for writing custom errors and passing the function name and the call string as parameters:

#define SET_UERRx(err,c,f,l) do {m_last_error.function = f; m_last_error.line = l; \
      m_last_error.code=ERR_USER_ERROR_FIRST+err; m_last_error.comment=c;} while(0)

Thus, in case of an error, we have all the necessary information. Unlike the errors sent to the console from the COpenCL class, this is a specification of the target kernel and where the method of its creation has been called from. Simply compare the output from the COpenCL class (upper string) and the extended output from the COpenCLx class (two lower lines):

Fig. 6. Kernel creation error

Let's consider another example of a wrapper method: the buffer creation method:

bool COpenCLx::BufferCreate(const ENUM_BUFFERS buffer_index,const uint size_in_bytes,const uint flags,const string function,const int line)
  {
   if(ocl==NULL)
     {
      SET_UERRx(UERR_NO_OCL,"OpenCL object does not exist",function,line);
      return false;
     }
//--- consider and check free memory
   if((m_stat.gpu_mem_usage+=size_in_bytes)==false)
     {
      CMemsize cmem=m_stat.gpu_mem_usage.Comp(size_in_bytes);
      SET_UERRx(UERR_NO_ENOUGH_MEM,"No free GPU memory. Insufficient "+cmem.ToStr(),function,line);
      return false;
     }
//--- create the buffer
   ::ResetLastError();
   if(ocl.BufferCreate(buffer_index,size_in_bytes,flags)==false)
     {
      string comment="Failed to create buffer "+EnumToString(buffer_index);
      SET_ERRx(comment,function,line);
      if(!m_last_error.code)
         SET_UERRx(UERR_BUFFER_CREATE,comment,function,line);
      return(false);
     }
//---
   return(true);
  }

Apart from checking the presence of the COpenCL class object and operation result, it also contains the function for accounting and checking free memory. Since we deal with relatively large amounts of memory (hundreds of megabytes), we need to control the process of its consumption. This task is assigned to СMemsize. The complete code is contained in the Memsize.mqh file.

However, there is a drawback. Despite the convenient debugging, the code becomes cumbersome. For example, the buffer creation code will look as follows:

if(BufferCreate(buf_ORDER_M1,len*sizeof(int),CL_MEM_READ_WRITE,__FUNCTION__,__LINE__)==false)
   return false;

There is too much unnecessary information that makes focusing on the algorithm difficult. The macros come to the rescue here once again. Each of the wrapper methods is duplicated by a macro making its call more compact. For the BufferCreate() method, it is _BufferCreate macro:

#define _BufferCreate(buffer_index,size_in_bytes,flags) \
      if(BufferCreate(buffer_index,size_in_bytes,flags,__FUNCTION__,__LINE__)==false) return false

Thanks to the macro, the call of the buffer creation method takes the form:

_BufferCreate(buf_ORDER_M1,len*sizeof(int),CL_MEM_READ_WRITE);

Creation of kernels looks as follows:

_KernelCreate(k_FIND_PATTERNS,"find_patterns");

Most of these macros end in return false, while _KernelCreate ends in break. This should be considered when developing the code. All macros are defined in the OCLDefines.mqh file.

The class also contains initialization and deinitialization methods. Apart from creating the COpenCL class object, the first one also checks support for 'double', creates kernels and receives the size of available memory:

bool COpenCLx::Init(ENUM_INIT_MODE mode)
  {
   if(ocl) Deinit();
//--- create the object of the COpenCL class
   ocl=new COpenCL;
   while(!IsStopped())
     {
      //--- initialize OpenCL
      ::ResetLastError();
      if(!ocl.Initialize(cl_tester,true))
        {
         SET_ERR("OpenCL initialization error");
         break;
        }
      //--- check if working with 'double' is supported
      if(!ocl.SupportDouble())
        {
         SET_UERR(UERR_DOUBLE_NOT_SUPP,"Working with double (cl_khr_fp64) is not supported by the device");
         break;
        }
      //--- set the number of kernels
      if(!ocl.SetKernelsCount(OCL_KERNELS_COUNT))
         break;
      //--- create kernels         
      if(mode==i_MODE_TESTER)
        {
         _KernelCreate(k_FIND_PATTERNS,"find_patterns");
         _KernelCreate(k_ARRAY_FILL,"array_fill");
         _KernelCreate(k_ORDER_TO_M1,"order_to_M1");
         _KernelCreate(k_TESTER_STEP,"tester_step");
        }else if(mode==i_MODE_OPTIMIZER){
         _KernelCreate(k_ARRAY_FILL,"array_fill");
         _KernelCreate(k_TESTER_OPT_PREPARE,"tester_opt_prepare");
         _KernelCreate(k_TESTER_OPT_STEP,"tester_opt_step");
         _KernelCreate(k_FIND_PATTERNS_OPT,"find_patterns_opt");
        }
      else
         break;
      //--- create buffers
      if(!ocl.SetBuffersCount(OCL_BUFFERS_COUNT))
        {
         SET_UERR(UERR_SET_BUF_COUNT,"Failed to create buffers");
         break;
        }
      //--- receive the RAM size          
      long gpu_mem_size;
      if(ocl.GetGlobalMemorySize(gpu_mem_size)==false)
        {
         SET_UERR(UERR_GET_MEMORY_SIZE,"Failed to receive RAM value");
         break;
        }
      m_stat.gpu_mem_size.Set(gpu_mem_size);
      m_stat.gpu_mem_usage.Max(gpu_mem_size);
      return true;
     }
   Deinit();
   return false;
  }

The mode argument sets the initialization mode. This may be optimization or single testing. Various kernels are created based on this.

Kernel and buffer enumerators are declared in the OCLInc.mqh file. The kernels' source codes are attached as a resource there, like the cl_tester string.

The Deinit() method deletes OpenCL programs and objects:

void COpenCLx::Deinit()
  {
   if(ocl!=NULL)
     {
      //--- remove OpenCL objects
      ocl.Shutdown();
      delete ocl;
      ocl=NULL;
     }
  }

Now that all the conveniences have been developed, it is time to start the main work. We already have a relatively compact code and comprehensive information about errors.

But first we need to upload data we are to work with. This is not as easy as it might seem at first glance.

2.1 Uploading price data

The CBuffering class uploads the data.

class CBuffering
  {
private:
   string            m_symbol;
   ENUM_TIMEFRAMES   m_period;
   int               m_maxbars;
   uint              m_memory_usage;   //amount of used memory
   bool              m_spread_ena;     //upload spread buffer
   datetime          m_from;
   datetime          m_to;
   uint              m_timeout;        //upload timeout in milliseconds
   ulong             m_ts_abort;       //time label in microseconds when the operation should be interrupted
   //--- forced upload
   bool              ForceUploading(datetime from,datetime to);
public:
                     CBuffering();
                    ~CBuffering();
   //--- amount of data in buffers
   int               Depth;
   //--- buffers
   double            Open[];
   double            High[];
   double            Low[];
   double            Close[];
   double            Spread[];
   datetime          Time[];
   //--- get real time boundaries of the uploaded data
   datetime          TimeFrom(void){return m_from;}
   datetime          TimeTo(void){return m_to;}
   //--- 
   int               Copy(string symbol,ENUM_TIMEFRAMES period,datetime from,datetime to,double point=0);
   uint              GetMemoryUsage(void){return m_memory_usage;}
   bool              SpreadBufEnable(void){return m_spread_ena;}
   void              SpreadBufEnable(bool ena){m_spread_ena=ena;}
   void              SetTimeout(uint timeout){m_timeout=timeout;}
  };

We will not dwell on it too much, since data upload has no direct relation to the current topic. Anyway, we should consider its application briefly.

The class contains the Open[], High[], Low[], Close[], Time[] and Spread[] buffers. You can work with them after the Copy() method has successfully worked out. Please note that the Spread[] buffer is of 'double' type and is expressed not in points, but in price difference. Besides, copying the Spread[] buffer is initially disabled. If necessary, it should be enabled using the SpreadBufEnable() method.

The Copy() method is used for upload. The preset point argument is used only to recalculate the spread from points into price difference. If the spread copying is off, this argument is not used.

The main reasons for creating a separate class for uploading data are:

• Inability to download data in the amount exceeding TERMINAL_MAXBARS using the CopyTime() function and the like.
• No guarantee that the terminal has the data locally.
  

The CBuffering class is able to copy large volumes of data exceeding TERMINAL_MAXBARS, as well as initiate the upload of missing data from the server and wait for it to finish. Due to this waiting, we need to pay attention to the SetTimeout() method meant for setting the maximum data upload time (including waiting) in milliseconds. By default, the class constructor is equal to 5000 (5 seconds). Setting timeout to zero disables it. This is highly undesirable, but in some cases it may be useful.

There are some limitations though: M1 period data are not uploaded for the period exceeding one year, which to some extent narrows the range of our tester.

2.2 Single test

Single test consists of the following points:

1. Downloading timeseries buffers
   
2. Initializing OpenCL
3. Copying timeseries buffers to OpenCL buffers
4. Launching the kernel that finds patterns on the current chart and adds results to the order buffer as market entry points
5. Launching the kernel that moves orders to M1 chart
6. Launching the kernel that counts trade results by orders on chart M1 and adds them to buffer
7. Processing the result buffer and calculating test results
8. Deinitializing OpenCL
9. Removing timeseries buffers

The CBuffering download timeseries. Then these data should be copied to the OpenCL buffers, so that kernels are able to work with them. This task is assigned to the LoadTimeseriesOCL() method. Its code is provided below:

bool CTestPatterns::LoadTimeseriesOCL()
  {
//--- Open buffer:
   _BufferFromArray(buf_OPEN,m_sbuf.Open,0,m_sbuf.Depth,CL_MEM_READ_ONLY);
//--- High buffer:
   _BufferFromArray(buf_HIGH,m_sbuf.High,0,m_sbuf.Depth,CL_MEM_READ_ONLY);
//--- Low buffer:
   _BufferFromArray(buf_LOW,m_sbuf.Low,0,m_sbuf.Depth,CL_MEM_READ_ONLY);
//--- Close buffer:
   _BufferFromArray(buf_CLOSE,m_sbuf.Close,0,m_sbuf.Depth,CL_MEM_READ_ONLY);
//--- Time buffer:
   _BufferFromArray(buf_TIME,m_sbuf.Time,0,m_sbuf.Depth,CL_MEM_READ_ONLY);
//--- Open (M1) buffer:
   _BufferFromArray(buf_OPEN_M1,m_tbuf.Open,0,m_tbuf.Depth,CL_MEM_READ_ONLY);
//--- High (M1) buffer:
   _BufferFromArray(buf_HIGH_M1,m_tbuf.High,0,m_tbuf.Depth,CL_MEM_READ_ONLY);
//--- Low (M1) buffer:
   _BufferFromArray(buf_LOW_M1,m_tbuf.Low,0,m_tbuf.Depth,CL_MEM_READ_ONLY);
//--- Close (M1) buffer:
   _BufferFromArray(buf_CLOSE_M1,m_tbuf.Close,0,m_tbuf.Depth,CL_MEM_READ_ONLY);
//--- Spread (M1) buffer:
   _BufferFromArray(buf_SPREAD_M1,m_tbuf.Spread,0,m_tbuf.Depth,CL_MEM_READ_ONLY);
//--- Time (M1) buffer:
   _BufferFromArray(buf_TIME_M1,m_tbuf.Time,0,m_tbuf.Depth,CL_MEM_READ_ONLY);
//--- copying successful
   return true;
  }

So the data have been downloaded. Now it is time to implement the test algorithm.

2.2.1 Searching for patterns in OpenCL

The pattern definition code on OpenCL is not much different from the code in MQL5:

//--- patterns
#define  PAT_NONE                0
#define  PAT_PINBAR_BEARISH      (1<<0)
#define  PAT_PINBAR_BULLISH      (1<<1)
#define  PAT_ENGULFING_BEARISH   (1<<2)
#define  PAT_ENGULFING_BULLISH   (1<<3)
//--- prices
#define  O(i) Open[i]
#define  H(i) High[i]
#define  L(i) Low[i]
#define  C(i) Close[i]
//+------------------------------------------------------------------+
//| Check for presence of patterns                                   |
//+------------------------------------------------------------------+
uint Check(__global double *Open,__global double *High,__global double *Low,__global double *Close,double ref,uint flags)
  {
//--- bearish pin bar  
   if((flags&PAT_PINBAR_BEARISH)!=0)
     {//
      double tail=H(1)-fmax(O(1),C(1));
      if(tail>=ref && C(0)>O(0) && O(2)>C(2) && H(1)>fmax(H(0),H(2)) && fabs(O(1)-C(1))<tail)
         return PAT_PINBAR_BEARISH;
     }
//--- bullish pin bar  
   if((flags&PAT_PINBAR_BULLISH)!=0)
     {//
      double tail=fmin(O(1),C(1))-L(1);
      if(tail>=ref && O(0)>C(0) && C(2)>O(2) && L(1)<fmin(L(0),L(2)) && fabs(O(1)-C(1))<tail)
         return PAT_PINBAR_BULLISH;
     }
//--- bearish engulfing
   if((flags&PAT_ENGULFING_BEARISH)!=0)
     {//
      if((C(1)-O(1))>=ref && H(0)<C(1) && O(2)>C(1) && C(2)<O(1))
         return PAT_ENGULFING_BEARISH;
     }
//--- bullish engulfing
   if((flags&PAT_ENGULFING_BULLISH)!=0)
     {//
      if((O(1)-C(1))>=ref && L(0)>C(1) && O(2)<C(1) && C(2)>O(1))
         return PAT_ENGULFING_BULLISH;
     }
//--- nothing found   
   return PAT_NONE;
  }

One of the small differences is that the buffers are passed by the pointer, not the reference. Besides, there is the __global modifier, which indicates that the timeseries buffers are in the global memory. All OpenCL buffers we are to create are located in the global memory.

The Check() function calls the find_patterns() kernel:

__kernel void find_patterns(__global double *Open,__global double *High,__global double *Low,__global double *Close,
                            __global int *Order,       // order buffer
                            __global int *Count,       // number of orders in the buffer
                            const double ref,          // pattern parameter 
                            const uint flags)          // what patterns to look for
  {
//--- work in one dimension  
//--- bar index  
   size_t x=get_global_id(0);
//--- pattern search space size   
   size_t depth=get_global_size(0)-PBARS;
   if(x>=depth)
      return;
//--- check if patterns are present
   uint res=Check(&Open[x],&High[x],&Low[x],&Close[x],ref,flags);
   if(res==PAT_NONE)
      return;
//--- set orders
   if(res==PAT_PINBAR_BEARISH || res==PAT_ENGULFING_BEARISH)
     {//sell
      int i=atomic_inc(&Count[0]);
      Order[i*2]=x+PBARS;
      Order[(i*2)+1]=OP_SELL;
     }
   else if(res==PAT_PINBAR_BULLISH || res==PAT_ENGULFING_BULLISH)
     {//buy
      int i=atomic_inc(&Count[0]);
      Order[i*2]=x+PBARS;
      Order[(i*2)+1]=OP_BUY;
     }
  }

We will use it to search for patterns and locating orders in a specially designated buffer.

The find_patterns() kernel works in a one-dimensional task space. During its launch, we will create the number of work-items we are to specify in the task space for the dimension 0. In this case, it is the number of bars in the current period. To understand which bar is being handled, you need to get the task index:

size_t x=get_global_id(0);

Where zero is a measurement index.

If the Check() function execution result shows the presence of the pattern, set the order in the order buffer of the current period. Each order is to occupy two cells since it consists of the bar index in the timeseries buffers and operation (buy or sell). Since all passed arrays are one-dimensional, it is necessary to implement two-dimensionality on our own. Use the i*2 equation for locating bar indices in timeseries by even indices of the order array and the (i*2)+1 equation for locating operations by odd indices, where i is an order serial number:

      Order[i*2]=x+PBARS;
      Order[(i*2)+1]=OP_SELL;

To obtain the order serial number, use the atomic_inc() atomic function. When executing a task, we have no idea what tasks and bars have already been completed. These are parallel computations, and there is absolutely no sequence in anything here. A task index is not related to the number of already completed tasks. Consequently, we do not know how many orders are already placed in the buffer. If we try to read their number located in cell 0 of the Count [] buffer, another task may write something there at the same time. To avoid that, we use atomic functions.

In our case, the atomic_inc() function disables access of other tasks to the Count[0] cell. After that, it increases its value by one, while the previous value is returned as a result.

int i=atomic_inc(&Count[0]);

Of course, this slows down the work, since other tasks have to wait till access to Count[0] is blocked. But in some cases (like ours), there is simply no other solution.

After all the tasks have been completed, we get the formed Order[] buffer of orders and their number in the Count[0] cell.

2.2.2 Moving orders to M1 timeframe

So, we found patterns on the current timeframe, but testing should be done on M1 timeframe. This means that the appropriate bars should be found on M1 for all entry points found on the current period. Since trading patterns provides for a relatively small number of entry points even on small timeframes, we will choose a rather rough but quite suitable method — enumeration. We will compare the time of each found order with the time of each M1 timeframe bar. To do this, create the order_to_M1() kernel:

__kernel void order_to_M1(__global ulong *Time,__global ulong *TimeM1,
                          __global int *Order,__global int *OrderM1,
                          __global int *Count,
                          const ulong shift) // time shift in seconds
  {
//--- work in two dimensions
   size_t x=get_global_id(0); //index of Time index in Order
   if(OrderM1[x*2]>=0)
      return;
   size_t y=get_global_id(1); //index in TimeM1
   if((Time[Order[x*2]]+shift)==TimeM1[y])
     {
      atomic_inc(&Count[1]);
      //--- set indices in the TimeM1 buffer by even indices
      OrderM1[x*2]=y;
      //--- set (OP_BUY/OP_SELL) operations by odd indices
      OrderM1[(x*2)+1]=Order[(x*2)+1];
     }
  }

Here we have two-dimensional task space. The 0 space dimension is equal to the number of placed orders, while dimension of the space 1 is equal to the number of bars of M1 period. When the open time of an order bar and M1 bar coincide, the operation of the current order is copied to the OrderM1[] buffer and the detected bar index in the timeseries of M1 period is set.

There are two things here that should not exist at first glance.

• The first one is the atomic_inc() atomic function, which for some reason counts the entry points found on M1 period. In the dimension 0, each order works with its index, while there can be no more than one match in the index 1. This means the shared access attempt is completely out of question. Why then do we need to count?
  
• The second one is the shift argument added to the current period bar time. 

There are special reasons for this. The world is not perfect. The presence of a bar on M5 chart with the open time of 01:00:00 does not mean that a bar with the same open time is present on M1 chart.

The appropriate bar on M1 chart may have an open time of either 01:01:00, or 01:04:00. In other words, the number of variations is equal to the ratio of the timeframes' duration. The function of counting the number of detected entry points for M1 is introduced for that:

atomic_inc(&Count[1]);

If after the completion of the kernel operation, the number of found M1 orders is equal to the number of orders detected on the current timeframe, then the task has been completed in full. Otherwise, a restart with another shift argument is required. There may be as many restarts as the number of M1 periods contained in the current period.

The following check has been introduced to make sure that detected entry points are not rewritten by other values during a restart with a non-zero shift argument value:

   if(OrderM1[x*2]>=0)
      return;

To let it work, fill the OrderM1[] buffer with the value of -1 before launching the kernel. To do this, create the array_fill() buffer filling kernel:

__kernel void array_fill(__global int *Buf,const int value)
  {
//--- works in one dimension    
   size_t x=get_global_id(0);
   Buf[x]=value;
  }

2.2.3 Obtaining trade results

After M1 entry points are found, we can start obtaining trade results. To do this, we need a kernel that will accompany open positions. In other words, we should wait till they are closed for one of the four reasons:

• Reaching Take Profit
• Reaching Stop Loss
• Expiration of the open position maximum holding time
• End of the test period

The task for the kernel is one-dimensional, and its size is equal to the number of orders. The kernel is to iterate over the bars starting with the position open one and check the conditions described above. Inside the bar, the ticks are simulated in the "1 minute OHLC" mode described in the "Testing Trading Strategies" section of the documentation.

The important thing is that some positions are closed almost immediately after opening, some are closed later, while others are closed by timeout or when the test ends. This means that the task execution time for different entry points differs significantly.

The real practice has shown that accompanying a position before closing in one pass is not efficient. In contrast, dividing the test space (the number of bars before the forced closure by position holding timeout) into several parts and performing the handling in several passes yield significantly better results in terms of performance.

The tasks that are not completed on the current pass are postponed till the next one. Thus, the size of the task space is decreased with each pass. But to implement this, you need to use another buffer to store task indices. Each task is an index of an entry point in the order buffer. At the time of the first launch, the contents of the task buffer fully corresponds to the orders buffer. During the next launches, it will contain indices of the orders, positions for which have not yet been closed. In order to work with the task buffer and store the tasks for the next run there simultaneously, it should have two banks: one bank is used during the current launch, while another one is used to form tasks for the next one.

In actual work, this looks like this. Suppose that we have 1000 entry points, for which we need to get trade results. The holding time of an open position is equivalent to 800 bars. We decided to break the test into 4 passes. Graphically, it looks as displayed on Fig. 7.

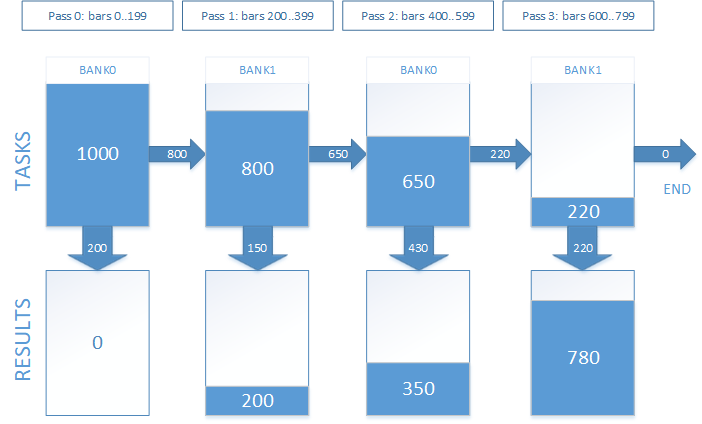
Fig. 7. Tracking open positions in several passes

By trial and error, we have determined the optimal number of passes equal to 8 for a position holding timeout of 12 hours (or 720 minute bars). This is the default value. It varies for different timeout values and OpenCL devices. Thorough selection is recommended for maximum performance.

Thus, the Tasks[] buffer and the index of the task bank we work with are added to the kernel arguments apart from the timeseries. Besides, we add the Res[] buffer to save the results.

The amount of actual data in the task buffer is returned via the Left[] buffer, which has a size of the two elements — for each of the banks, respectively.

Since the test is performed in parts, the values of the start and end bars for position tracking should be passed among the kernel arguments. This is a relative value that is summed up with the position opening bar index to get the absolute index of the current bar in the timeseries. Also, the maximum allowable bar index in the timeseries should be passed to the kernel so as not to exceed the buffers.

As a result, the set of the tester_step() kernel arguments, which is to track open positions, looks as follows:

__kernel void tester_step(__global double *OpenM1,__global double *HighM1,__global double *LowM1,__global double *CloseM1,
                          __global double *SpreadM1, // in price difference, not in points
                          __global ulong *TimeM1,
                          __global int *OrderM1,     // orders buffer, where [0] is an index in OHLC(M1), [1] - (Buy/Sell) operation
                          __global int *Tasks,       // task buffer (of open positions) stores indices for orders in the OrderM1 buffer
                          __global int *Left,        // number of remaining tasks, two elements: [0] - for bank0, [1] - for bank1
                          __global double *Res,      // result buffer 
                          const uint bank,           // current bank                           
                          const uint orders,         // number of orders in OrderM1
                          const uint start_bar,      // serial number of the handled bar (as a shift from the specified index in OrderM1)
                          const uint stop_bar,       // the last bar to be handled
                          const uint maxbar,         // maximum acceptable bar index (the last bar of the array)
                          const double tp_dP,        // TP in price difference
                          const double sl_dP,        // SL in price difference
                          const ulong timeout)       // when to forcibly close a trade (in seconds) 

The tester_step() kernel works in one dimension. The size of the dimension tasks changes at each call starting with the number of orders decreasing with each pass.

We obtain the task ID at the start of the kernel code:

   size_t id=get_global_id(0);

Then, based on the index of the current bank, which is passed via the bank argument, calculate the index of the following:

   uint bank_next=(bank)?0:1;

Calculate the index of the order we are to work with. During the first launch (when start_bar is equal to zero), the task buffer corresponds to the orders buffer, therefore the order index is equal to the task index. During the subsequent launches, the order index is obtained from the task buffer considering the current bank and the task index:

   if(!start_bar)
      idx=id;
   else
      idx=Tasks[(orders*bank)+id];

Knowing the order index, we get the bar index in the timeseries, as well as the operation code:

//--- index of the bar the position has been opened at in the buffer M1
   uint iO=OrderM1[idx*2];
//--- (OP_BUY/OP_SELL) operation
   uint op=OrderM1[(idx*2)+1];

Based on the timeout argument value, calculate the time of the forced position closing:

   ulong tclose=TimeM1[iO]+timeout;

The open position is then handled. Let's consider this using the BUY operation as an example (the case is similar for SELL).

   if(op==OP_BUY)
     {
      //--- position open price
      double open=OpenM1[iO]+SpreadM1[iO];
      double tp = open+tp_dP;
      double sl = open-sl_dP;
      double p=0;
      for(uint j=iO+start_bar; j<=(iO+stop_bar); j++)
        {
         for(uint k=0;k<4;k++)
           {
            if(k==0)
              {
               p=OpenM1[j];
               if(j>=maxbar || TimeM1[j]>=tclose)
                 {
                  //--- forced closing by time
                  Res[idx]=p-open;
                  return;
                 }
              }
            else if(k==1)
               p=HighM1[j];
            else if(k==2)
               p=LowM1[j];
            else
               p=CloseM1[j];
            //--- check if TP or SL is triggered
            if(p<=sl)
              {
               Res[idx]=sl-open;
               return;
              }
            else if(p>=tp)
              {
               Res[idx]=tp-open;
               return;
              }
           }
        }
     }

If none of the conditions for exiting the kernel is triggered, the task is postponed till the next pass:

   uint i=atomic_inc(&Left[bank_next]);
   Tasks[(orders*bank_next)+i]=idx;

After handling all the passes, the Res[] buffer stores the results of all trades. To obtain the test result, they should be summed up.

Now that the algorithm is clear and the kernels are ready, we should start launching them.

2.3 Launching a test

The CTestPatterns class will help us with that:

class CTestPatterns : private COpenCLx
  {
private:
   CBuffering       *m_sbuf;  // Current period timeseries
   CBuffering       *m_tbuf;  // M1 period timeseries
   int               m_prepare_passes;
   uint              m_tester_passes;
   bool              LoadTimeseries(datetime from,datetime to);
   bool              LoadTimeseriesOCL(void);
   bool              test(STR_TEST_STAT &stat,datetime from,datetime to,STR_TEST_PARS &par);
   bool              optimize(STR_TEST_STAT &stat,datetime from,datetime to,STR_OPT_PARS &par);
   void              buffers_free(void);
public:
                     CTestPatterns();
                    ~CTestPatterns();
   //--- launch a single test                    
   bool              Test(STR_TEST_STAT &stat,datetime from,datetime to,STR_TEST_PARS &par);
   //--- launch optimization   
   bool              Optimize(STR_TEST_STAT &stat,datetime from,datetime to,STR_OPT_PARS &par);
   //--- get the pointer to the program execution statistics   
   COCLStat         *GetStat(void){return &m_stat;}
   //--- get the code of the last error   
   int               GetLastError(void){return m_last_error.code;}
   //--- get the structure of the last error
   STR_ERROR         GetLastErrorExt(void){return m_last_error;}
   //--- reset the last error  
   void              ResetLastError(void);
   //--- number of passes the testing kernel launch is divided into
   void              SetTesterPasses(uint tp){m_tester_passes=tp;}
   //--- number of passes the orders preparation kernel launch is divided into
   void              SetPrepPasses(int p){m_prepare_passes=p;}
  };

Let's consider the Test() method in more details:

bool CTestPatterns::Test(STR_TEST_RESULT &result,datetime from,datetime to,STR_TEST_PARS &par)
  {
   ResetLastError();
   m_stat.Reset();
   m_stat.time_total.Start();
//--- upload the timeseries data   
   m_stat.time_buffering.Start();
   if(LoadTimeseries(from,to)==false)
      return false;
   m_stat.time_buffering.Stop();
//--- initialize OpenCL
   m_stat.time_ocl_init.Start();
   if(Init(i_MODE_TESTER)==false)
      return false;
   m_stat.time_ocl_init.Stop();
//--- launch the test
   bool result=test(stat,from,to,par);
   Deinit();
   buffers_free();
   m_stat.time_total.Stop();
   return result;
  }

At the entry, it has a date range, in which it is necessary to test the strategy, as well as the links to the structure of parameters and test results.

If successful, the method returns "true" and writes results to the 'result' argument. If an error has occurred during the execution, the method returns 'false'. To receive error details, call GetLastErrorExt().

First, upload timeseries data. Then initialize OpenCL. This includes creating objects and kernels. If all is well, call the test() method containing the entire test algorithm. In fact, the Test() method is a wrapper for test(). This is done to make sure that deinitialization is performed at any exit from the 'test' method and timeseries buffers are released.

In the test() method, all starts with uploading timeseries buffers to the OpenCL buffers:

   if(LoadTimeseriesOCL () ==false)returnfalse;

This is done using the LoadTimeseriesOCL() method discussed above.

The find_patterns() kernel, to which the k_FIND_PATTERNS enumerator corresponds, is launched first. Before the launch, we should create order and result buffers:

   _BufferCreate(buf_ORDER,m_sbuf.Depth*2*sizeof(int),CL_MEM_READ_WRITE);
   int  count[2]={0,0};
   _BufferFromArray(buf_COUNT,count,0,2,CL_MEM_READ_WRITE);

The order buffer has a size twice the number of bars on the current timeframe. Since we do not know how many patterns will be found, we assume that the pattern will be found on each bar. This precaution may seem absurd at first glance given the patterns we are working with at the moment. Further on, when adding other patterns, this may save you from many issues.

Set the arguments:

   _SetArgumentBuffer(k_FIND_PATTERNS,0,buf_OPEN);
   _SetArgumentBuffer(k_FIND_PATTERNS,1,buf_HIGH);
   _SetArgumentBuffer(k_FIND_PATTERNS,2,buf_LOW);
   _SetArgumentBuffer(k_FIND_PATTERNS,3,buf_CLOSE);
   _SetArgumentBuffer(k_FIND_PATTERNS,4,buf_ORDER);
   _SetArgumentBuffer(k_FIND_PATTERNS,5,buf_COUNT);
   _SetArgument(k_FIND_PATTERNS,6,double(par.ref)*_Point);
   _SetArgument(k_FIND_PATTERNS,7,par.flags);

For the find_patterns() kernel, set a one-dimensional task space with an initial zero offset:

   uint global_size[1];
   global_size[0]=m_sbuf.Depth;
   uint work_offset[1]={0};

Launch the execution of the find_patterns() kernel:

   _Execute(k_FIND_PATTERNS,1,work_offset,global_size);

It should be noted that exiting the Execute() method does not mean that the program is executed. It may still be executed or queued for execution. To find out its current status, use the CLExecutionStatus() function. If we need to wait for the program completion, we can survey its status periodically or read the buffer the program places the results to. In the second case, waiting for the program completion occurs in the BufferRead() buffer reading method.

   _BufferRead(buf_COUNT,count,0,0,2);

Now at the index 0 of the count[] buffer, we can find the number of detected patterns or the number of orders located in the corresponding buffer. The next step is to find the corresponding entry points on M1 timeframe. The order_to_M1() kernel accumulates the detected quantity into the same count[] buffer, although at index 1. Triggering of the (count[0]==count[1]) condition is considered successful.

But first we need to create the buffer of orders for M1 and fill it with the value of -1. Since we already know the number of orders, specify the exact size of the buffer without a margin:

   int len=count[0]*2;
   _BufferCreate(buf_ORDER_M1,len*sizeof(int),CL_MEM_READ_WRITE);

Set the arguments for the array_fill() kernel:

   _SetArgumentBuffer(k_ARRAY_FILL,0,buf_ORDER_M1);
   _SetArgument(k_ARRAY_FILL,1,int(-1));

Set the one-dimensional task space with an initial shift equal to zero and the size equal to the buffer size. Start execution:

   uint opt_init_work_size[1];
   opt_init_work_size[0]=len;
   uint opt_init_work_offset[1]={0};
   _Execute(k_ARRAY_FILL,1,opt_init_work_offset,opt_init_work_size);

Next, we should prepare the launch of the order_to_M1() kernel execution:

//--- set the arguments
   _SetArgumentBuffer(k_ORDER_TO_M1,0,buf_TIME);
   _SetArgumentBuffer(k_ORDER_TO_M1,1,buf_TIME_M1);
   _SetArgumentBuffer(k_ORDER_TO_M1,2,buf_ORDER);
   _SetArgumentBuffer(k_ORDER_TO_M1,3,buf_ORDER_M1);
   _SetArgumentBuffer(k_ORDER_TO_M1,4,buf_COUNT);
//--- task space for the k_ORDER_TO_M1 kernel is two-dimensional
   uint global_work_size[2];
//--- the first dimension consists of orders left by the k_FIND_PATTERNS kernel
   global_work_size[0]=count[0];
//--- the second dimension consists of all M1 chart bars
   global_work_size[1]=m_tbuf.Depth;
//--- the initial offset in the task space for both dimensions is equal to zero
   uint global_work_offset[2]={0,0};

The argument with the index of 5 is not set since its value will be different and it will be set immediately before the kernel execution launch. For the reason stated above, the execution of the order_to_M1() kernel may be executed several times with different offset value in seconds. The maximum number of launches is limited by the ratio of durations of the current and M1 charts:

   int maxshift=PeriodSeconds()/PeriodSeconds(PERIOD_M1);

The entire loop looks as follows:

   for(int s=0;s<maxshift;s++)
     {
      //--- set the offset for the current pass
      _SetArgument(k_ORDER_TO_M1,5,ulong(s*60));
      //--- execute the kernel
      _Execute(k_ORDER_TO_M1,2,global_work_offset,global_work_size);
      //--- read the results
      _BufferRead(buf_COUNT,count,0,0,2);
      //--- at index 0, you can find the number of orders on the current chart
      //--- at index 1, you can find the number of detected appropriate bars on М1 chart
      //--- both values match, exit the loop
      if(count[0]==count[1])
         break;
      //--- otherwise, move to the next iteration and launch the kernel with other offset
     }
//--- check if the number of orders is valid once again just in case we have exited the loop not by 'break'
   if(count[0]!=count[1])
     {
      SET_UERRt(UERR_ORDERS_PREPARE,"M1 orders preparation error");
      return false;
     }

Now it is time to launch the tester_step() kernel that calculates the results of trades opened by detected entry points. First, let's create the missing buffers and set the arguments:

//--- create the Tasks buffer where the number of tasks for the next pass is formed
   _BufferCreate(buf_TASKS,m_sbuf.Depth*2*sizeof(int),CL_MEM_READ_WRITE);
//--- create the Result buffer where trade results are stored
   _BufferCreate(buf_RESULT,m_sbuf.Depth*sizeof(double),CL_MEM_READ_WRITE);
//--- set the arguments for the single test kernel   
   _SetArgumentBuffer(k_TESTER_STEP,0,buf_OPEN_M1);
   _SetArgumentBuffer(k_TESTER_STEP,1,buf_HIGH_M1);
   _SetArgumentBuffer(k_TESTER_STEP,2,buf_LOW_M1);
   _SetArgumentBuffer(k_TESTER_STEP,3,buf_CLOSE_M1);
   _SetArgumentBuffer(k_TESTER_STEP,4,buf_SPREAD_M1);
   _SetArgumentBuffer(k_TESTER_STEP,5,buf_TIME_M1);
   _SetArgumentBuffer(k_TESTER_STEP,6,buf_ORDER_M1);
   _SetArgumentBuffer(k_TESTER_STEP,7,buf_TASKS);
   _SetArgumentBuffer(k_TESTER_STEP,8,buf_COUNT);
   _SetArgumentBuffer(k_TESTER_STEP,9,buf_RESULT);
   uint orders_count=count[0];
   _SetArgument(k_TESTER_STEP,11,uint(orders_count));
   _SetArgument(k_TESTER_STEP,14,uint(m_tbuf.Depth-1));
   _SetArgument(k_TESTER_STEP,15, double(par.tp)*_Point);
   _SetArgument(k_TESTER_STEP,16, double(par.sl)*_Point);
   _SetArgument(k_TESTER_STEP,17,ulong(par.timeout));

Next, convert the maximum position holding time into the number of bars on M1 chart:

   uint maxdepth=(par.timeout/PeriodSeconds(PERIOD_M1))+1;

Next, check if the specified number of kernel execution passes is valid. By default, it is equal to 8, but in order to define the optimal performance for various OpenCL devices, it is allowed to set other values using the SetTesterPasses() method.

   if(m_tester_passes<1)
      m_tester_passes=1;
   if(m_tester_passes>maxdepth)
      m_tester_passes=maxdepth;
   uint step_size=maxdepth/m_tester_passes;

Set the task space size for a single dimension and launch the trade results calculation loop:

   global_size[0]=orders_count;
   m_stat.time_ocl_test.Start();
   for(uint i=0;i<m_tester_passes;i++)
     {
      //--- set the current bank index
      _SetArgument(k_TESTER_STEP,10,uint(i&0x01));
      uint start_bar=i*step_size;
      //--- set the index of the bar the test in the current pass starts from
      _SetArgument(k_TESTER_STEP,12,start_bar);
      //--- set the index of the last bar the test is performed at during the current pass
      uint stop_bar=(i==(m_tester_passes-1))?(m_tbuf.Depth-1):(start_bar+step_size-1);
      _SetArgument(k_TESTER_STEP,13,stop_bar);
      //--- reset the number of tasks in the next bank 
      //--- it is to store the number of orders remaining for the next pass
      count[(~i)&0x01]=0;
      _BufferWrite(buf_COUNT,count,0,0,2);
      //--- launch the test kernel
      _Execute(k_TESTER_STEP,1,work_offset,global_size);
      //--- read the number of orders remaining for the next pass
      _BufferRead(buf_COUNT,count,0,0,2);
      //--- set the new number of tasks equal to the number of orders
      global_size[0]=count[(~i)&0x01];
      //--- if no tasks remain, exit the loop
      if(!global_size[0])
         break;
     }
   m_stat.time_ocl_test.Stop();

Create the buffer for reading the trade results:

   double Result[];
   ArrayResize(Result,orders_count);
   _BufferRead(buf_RESULT,Result,0,0,orders_count);

To obtain results comparable with the built-in teste ones, the read values should be divided into _Point. The result and statistics calculation code is provided below:

   m_stat.time_proc.Start();
   result.trades_total=0;
   result.gross_loss=0;
   result.gross_profit=0;
   result.net_profit=0;
   result.loss_trades=0;
   result.profit_trades=0;
   for(uint i=0;i<orders_count;i++)
     {
      double r=Result[i]/_Point;
      if(r>=0)
        {
         result.gross_profit+=r;
         result.profit_trades++;
           }else{
         result.gross_loss+=r;
         result.loss_trades++;
        }
     }
   result.trades_total=result.loss_trades+result.profit_trades;
   result.net_profit=result.gross_profit+result.gross_loss;
   m_stat.time_proc.Stop();

Let's write a short script allowing us to launch our tester.

#include <OCL_Patterns\TestPatternsOCL.mqh>

CTestPatterns tpat;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   datetime from=D'2018.01.01 00:00';
   datetime to=D'2018.10.01 00:00';
//--- set test parameters
   STR_TEST_PARS pars;
   pars.ref= 60;
   pars.sl = 350;
   pars.tp = 50;
   pars.flags=15;  // all patterns
   pars.timeout=12*3600;
//--- results structure
   STR_TEST_RESULT res;
//--- launch the test
   tpat.Test(res,from,to,pars);
   STR_ERROR oclerr=tpat.GetLastErrorExt();
   if(oclerr.code)
     {
      Print(oclerr.comment);
      Print("code = ",oclerr.code,", function = ",oclerr.function,", line = ",oclerr.line);
      return;
     }
//--- test results  
   Print("Net Profit: ",   res.net_profit);
   Print("Gross Profit: ", res.gross_profit);
   Print("Gross Loss: ",   res.gross_loss);
   Print("Trades Total: ", res.trades_total);
   Print("Profit Trades: ",res.profit_trades);
   Print("Loss Trades: ",  res.loss_trades);
//--- execution statistics
   COCLStat ocl_stat=tpat.GetStat();
   Print("GPU memory size: ",       ocl_stat.gpu_mem_size.ToStr());
   Print("GPU memory usage: ",      ocl_stat.gpu_mem_usage.ToStr());
   Print("Buffering: ",             ocl_stat.time_buffering.ToStr());
   Print("OpenCL init: ",           ocl_stat.time_ocl_init.ToStr());
   Print("OpenCL buffering: ",      ocl_stat.time_ocl_buf.ToStr());
   Print("OpenCL prepare orders: ", ocl_stat.time_ocl_orders.ToStr());
   Print("OpenCL test: ",           ocl_stat.time_ocl_test.ToStr());
   Print("OpenCL total execution: ",ocl_stat.time_ocl_exec.ToStr());
   Print("Post-processing: ",       ocl_stat.time_proc.ToStr());
   Print("Total: ",                 ocl_stat.time_total.ToStr());
  }

The applied test time range, symbol and period are the ones we already used to test the EA implemented in MQL5. The applied reference and Stop Loss level values are the ones found during the optimization. Now we only have to run the script and compare the obtained result with the built-in tester's one.

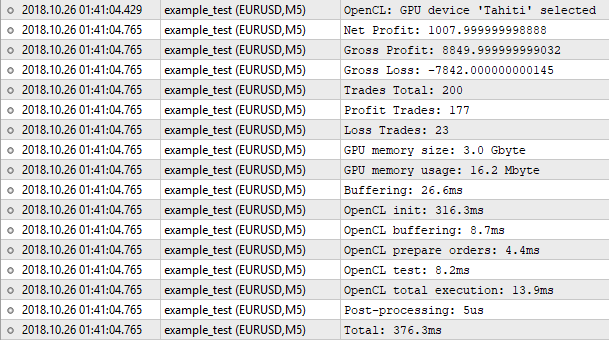
Fig. 8. Results of the tester implemented in OpenCL

Thus, the number of trades is the same, while the net profit value is not. The built-in tester shows the number of 1000.50, while our tester yields 1007.99. The reason for this is as follows. To achieve the same results, we need to consider a swap among other things. But implementing it into our tester is not justified. For a rough estimate, where the "1 minute OHLC" mode is applied, such trifles can be neglected. The important thing is that the result is very close, which means our algorithm works correctly.

Now let's have a look at the program execution statistics. Only 16 MB of memory was used. OpenCL initialization took the most time. The entire process took 376 milliseconds, which is almost similar to the built-in tester. It is pointless to expect some gain in performance here. With 200 trades, we will spend more time on preparatory operations, like initialization, copying buffers and so on. To feel the difference, we need hundreds of times more orders for testing. It is time to move on to optimization.

2.4. Optimization

The optimization algorithm is to be similar to the single test algorithm with one fundamental difference. While in the tester we search for patterns and then count the trade results, here the sequence of actions is different. First, we count the trade results and start searching patterns afterwards. The reason is that we have two optimized parameters. The first one is a reference value for finding the patterns. The second one is a Stop Loss level participating in the trade result calculation. Thus, one of them affects the number of entry points, while the second one has influence over trade results and open position tracking duration. If we keep the same sequence of actions as in the single test algorithm, we will not avoid a re-test of the same entry points causing a huge loss of time, since the pin bar with a "tail" of 300 points is found at any reference value equal or less than this value.

Therefore, in our case, it is much more reasonable to calculate the results of trades with entry points at each bar (including both buying and selling) and then operate with these data during the pattern search. Thus, the sequence of actions during optimization will be as follows:

1. Downloading timeseries buffers
   
2. Initializing OpenCL
3. Copying timeseries buffers to OpenCL buffers
4. Launching the orders preparation kernel (two orders - buy and sell ones - per each bar of the current timeframe)
5. Launching the kernel that moves orders to M1 chart
6. Launching the kernel that counts trade results by orders
   
7. Launching the kernel that finds the patterns and forms the test results for each combination of optimized parameters from ready-made trade results
   
8. Handling result buffers and searching for optimized parameters matching the best result
   
9. Deinitializing OpenCL
10. Removing timeseries buffers

In addition, the number of tasks for searching patterns is multiplied by the number of reference variable values, while the number of tasks for calculating the trade results is multiplied by the number of Stop Loss level values.

2.4.1 Preparing orders

We assume that the desired patterns can be found on any bar. This means we need to place a buy or a sell order on each bar. The buffer size can be defined by the following equation:

N = Depth*4*SL_count;

where Depth is a size of timeseries buffers, while SL_count is a number of Stop Loss values.

Besides, the bar indices should be from the M1 timeseries. The tester_opt_prepare() kernel searches the timeseries for M1 bars with the open time corresponding to the current period's bars opening time and place them into the order buffer in the format specified above. In general, its work is similar to the order_to_M1() kernel's one:

__kernel void tester_opt_prepare(__global ulong *Time,__global ulong *TimeM1,
                                 __global int *OrderM1,// order buffer
                                 __global int *Count,
                                 const int   SL_count,      // number of SL values
                                 const ulong shift)         // time shift in seconds
  {
//--- work in two dimensions   
   size_t x=get_global_id(0); //index in Time
   if(OrderM1[x*SL_count*4]>=0)
      return;
   size_t y=get_global_id(1); //index in TimeM1
   if((Time[x]+shift)==TimeM1[y])
     {
      //--- find the maximum bar index for М1 period along the way
      atomic_max(&Count[1],y);
      uint offset=x*SL_count*4;
      for(int i=0;i<SL_count;i++)
        {
         uint idx=offset+i*4;
         //--- add two orders (buy and sell) for each bar
         OrderM1[idx++]=y;
         OrderM1[idx++]=OP_BUY |(i<<2);
         OrderM1[idx++]=y;
         OrderM1[idx]  =OP_SELL|(i<<2);
        }
      atomic_inc(&Count[0]);
     }
  }

However, there is one important difference — finding the maximum index of M1 timeseries. Let me explain why this is done.

When testing a single pass, we deal with a relatively small number of orders. The number of tasks equal to the number of orders multiplied by the size of buffers of M1 timeseries is also relatively small. If we consider the data we performed the test on, these are 200 orders multiplied by 279 039 М1 bars ultimately providing 55.8 million tasks.

In the current situation, the number of tasks will be much larger. For example, these are 279 039 M1 bars multiplied by 55 843 bars of the current period (M5), which equals to 15.6 billion tasks. It is also worth considering that you have to run this kernel again with a different time shift value. The enumeration method is too resource-intensive here.

To resolve this issue, we still leave the enumeration, although we divide the current period bars handling range into several parts. Besides, we should limit the range of appropriate minute bars. However, since the calculated index value of the upper border of minute bars will in most cases exceed the actual one, we will return the maximum index of a minute bar after Count[1] to start the next pass from this point.

2.4.2 Obtaining trade results

After preparing the orders, it is time to start receiving trade results.

The tester_opt_step() kernel is very similar to tester_step(). Therefore, I will not provide the entire code focusing mainly on the differences. First, the inputs have changed:

__kernel void tester_opt_step(__global double *OpenM1,__global double *HighM1,__global double *LowM1,__global double *CloseM1,
                              __global double *SpreadM1,// in price difference, not in points
                              __global ulong *TimeM1,
                              __global int *OrderM1,     // order buffer, where [0] is an index in OHLC(M1), [1] - (Buy/Sell) operation
                              __global int *Tasks,       // buffer of tasks (open positions) storing indices for orders in the OrderM1 buffer
                              __global int *Left,        // number of remaining tasks, two elements: [0] - for bank0, [1] - for bank1
                              __global double *Res,      // buffer of results filled as soon as they are received, 
                              const uint bank,           // the current bank                           
                              const uint orders,         // number of orders in OrderM1
                              const uint start_bar,      // the serial number of a handled bar (as a shift from the specified index in OrderM1) - in fact, "i" from the loop launching the kernel
                              const uint stop_bar,       // the final bar to be handled - generally, equal to 'bar'
                              const uint maxbar,         // maximum acceptable bar index (last bar of the array)
                              const double tp_dP,        // TP in price difference
                              const uint sl_start,       // SL in points - initial value
                              const uint sl_step,        // SL in points - step
                              const ulong timeout,       // trade lifetime (in seconds), after which it is forcibly closed 
                              const double point)        // _Point

Instead of the sl_dP argument used to pass the SL level value expressed in price difference, we now have two arguments: sl_start and sl_step, as well as the 'point' argument. Now, the following equation should be applied to calculate the SL level value:

SL = (sl_start+sl_step*sli)*point;

where sli is a value of the Stop Loss index contained in the order.

The second difference is a code of receiving the sli index from the order buffer:

//--- operation (bits 1:0) and SL index (bits 9:2)
   uint opsl=OrderM1[(idx*2)+1];
//--- get SL index   
   uint sli=opsl>>2;

The rest of the code is identical to the tester_step() kernel.

After the execution, we obtain buy and sell results for each bar and each Stop Loss value in the Res[] buffer.

2.4.3 Searching for patterns and forming test results

Unlike testing, here we sum up the results of trades directly in the kernel, not in the MQL code. However, there is an unpleasant disadvantage — we have to convert the results into an integer type necessarily resulting in a loss of accuracy. Therefore, in the point argument, we should pass the _Point value divided by 100.

The forced conversion of results into the 'int' type is due to the fact that atomic functions do not work with the 'double' type. atomic_add() is to be used for summing up the results.

The find_patterns_opt() kernel is to work in the three-dimensional task space:

• Dimension 0: bar index on the current timeframe
• Dimension 1: reference value index for patterns
• Dimension 2: Stop Loss level value index
  

In the course of work, a buffer of results is generated. The buffer contains test statistics for each combination of Stop Loss level and reference value. The test statistics is a structure containing the following values:

• Total profit
• Total loss
• Number of profitable trades
• Number of loss-making trades

All of them are of 'int' type. Based on them, you can also calculate the net profit and the total number of trades. The kernel code is provided below:

__kernel void find_patterns_opt(__global double *Open,__global double *High,__global double *Low,__global double *Close,
                                __global double *Test,     // buffer of test results for each bar, size 2*x*z ([0]-buy, [1]-sell ... )
                                __global int *Results,     // result buffer, size 4*y*z 
                                const double ref_start,    // pattern parameter
                                const double ref_step,     // 
                                const uint flags,          // what patterns to search for
                                const double point)        // _Point/100
  {
//--- works in three dimensions
//--- bar index 
   size_t x=get_global_id(0);
//--- ref value index
   size_t y=get_global_id(1);
//--- SL value index
   size_t z=get_global_id(2);
//--- number of bars
   size_t x_sz=get_global_size(0);
//--- number of ref values
   size_t y_sz=get_global_size(1);
//--- number of sl values
   size_t z_sz=get_global_size(2);
//--- pattern search space size   
   size_t depth=x_sz-PBARS;
   if(x>=depth)//do not open near the buffer end
      return;
//
   uint res=Check(&Open[x],&High[x],&Low[x],&Close[x],ref_start+ref_step*y,flags);
   if(res==PAT_NONE)
      return;
//--- calculate the trade result index in the Test[] buffer
   int ri;
   if(res==PAT_PINBAR_BEARISH || res==PAT_ENGULFING_BEARISH) //sell
      ri = (x+PBARS)*z_sz*2+z*2+1;
   else                                                      //buy
      ri=(x+PBARS)*z_sz*2+z*2;
//--- get the result by the calculated index and convert into cents
   int r=Test[ri]/point;
//--- calculate the test results index in the Results[] buffer
   int idx=z*y_sz*4+y*4;
//--- add a trade result to the current pattern
   if(r>=0)
     {//--- profit
      //--- sum up the total profit in cents
      atomic_add(&Results[idx],r);
      //--- increase the number of profitable trades
      atomic_inc(&Results[idx+2]);
     }
   else
     {//--- loss
      //--- sum up the total loss in cents
      atomic_add(&Results[idx+1],r);
      //--- increase the number of loss-making trades
      atomic_inc(&Results[idx+3]);
     }
  }

The Test[] buffer in the arguments is the results obtained after executing the tester_opt_step() kernel.

2.5 Launching optimization

The code of launching kernels from MQL5 during optimization is constructed similarly to the testing process. The Optimize() public method is a wrapper of the optimize() method where the order of preparing and launching kernels is implemented.

bool CTestPatterns::Optimize(STR_TEST_RESULT &result,datetime from,datetime to,STR_OPT_PARS &par)
  {
   ResetLastError();
   if(par.sl.step<=0 || par.sl.stop<par.sl.start || 
      par.ref.step<=0 || par.ref.stop<par.ref.start)
     {
      SET_UERR(UERR_OPT_PARS,"Optimization parameters are incorrect");
      return false;
     }
   m_stat.Reset();
   m_stat.time_total.Start();
//--- upload timeseries data   
   m_stat.time_buffering.Start();
   if(LoadTimeseries(from,to)==false)
      return false;
   m_stat.time_buffering.Stop();
//--- initialize OpenCL
   m_stat.time_ocl_init.Start();
   if(Init(i_MODE_OPTIMIZER)==false)
      return false;
   m_stat.time_ocl_init.Stop();
//--- launch optimization
   bool res=optimize(result,from,to,par);
   Deinit();
   buffers_free();
   m_stat.time_total.Stop();
   return res;
  }

We are not going to consider each string in detail. Let's focus only on differences instead, in particular, launching the tester_opt_prepare() kernel.

First, create the buffer for managing the number of handled bars and returning the maximum index of M1 bar:

   int count[2]={0,0};
   _BufferFromArray(buf_COUNT,count,0,2,CL_MEM_READ_WRITE);

Then, set the arguments and size of the task space.

   _SetArgumentBuffer(k_TESTER_OPT_PREPARE,0,buf_TIME);
   _SetArgumentBuffer(k_TESTER_OPT_PREPARE,1,buf_TIME_M1);
   _SetArgumentBuffer(k_TESTER_OPT_PREPARE,2,buf_ORDER_M1);
   _SetArgumentBuffer(k_TESTER_OPT_PREPARE,3,buf_COUNT);
   _SetArgument(k_TESTER_OPT_PREPARE,4,int(slc)); // number of SL values
//--- the k_TESTER_OPT_PREPARE kernel is to have two-dimensional task space
   uint global_work_size[2];
//--- 0 dimension - current period orders 
   global_work_size[0]=m_sbuf.Depth;
//--- 1 st dimension - all М1 bars   
   global_work_size[1]=m_tbuf.Depth;
//--- for the first launch, set the offset in the task space to be equal to zero for both dimensions   
   uint global_work_offset[2]={0,0};

The offset of the 1 st dimension in the task space is increased after handling part of the bars. Its value is to be equal to the maximum value of М1 bar that is to return the kernel increased by 1.

   int maxshift=PeriodSeconds()/PeriodSeconds(PERIOD_M1);
   int prep_step=m_sbuf.Depth/m_prepare_passes;
   for(int p=0;p<m_prepare_passes;p++)
     {
      //offset for the current period task space
      global_work_offset[0]=p*prep_step;
      //offset for the M1 period task space
      global_work_offset[1]=count[1];
      //size of tasks for the current period
      global_work_size[0]=(p<(m_prepare_passes-1))?prep_step:(m_sbuf.Depth-global_work_offset[0]);
      //size of tasks for M1 period
      uint sz=maxshift*global_work_size[0];
      uint sz_max=m_tbuf.Depth-global_work_offset[1];
      global_work_size[1]=(sz>sz_max)?sz_max:sz;
      //
      count[0]=0;
      _BufferWrite(buf_COUNT,count,0,0,2);
      for(int s=0;s<maxshift;s++)
        {
         _SetArgument(k_TESTER_OPT_PREPARE,5,ulong(s*60));
         //--- execute kernel
         _Execute(k_TESTER_OPT_PREPARE,2,global_work_offset,global_work_size);
         //--- read the result (number should coincide with m_sbuf.Depth)
         _BufferRead(buf_COUNT,count,0,0,2);
         if(count[0]==global_work_size[0])
            break;
        }
      count[1]++;
     }
   if(count[0]!=global_work_size[0])
     {
      SET_UERRt(UERR_ORDERS_PREPARE,"Failed to prepare M1 orders");
      return false;
     }

The m_prepare_passes parameter means the number of passes the orders preparation should be divided into. By default, its value is 64, although it can be changed using the SetPrepPasses() method.

After reading the test results in the OptResults[] buffer, the search is performed for the combination of optimized parameters leading to a maximum net profit.

   int max_profit=-2147483648;
   uint idx_ref_best= 0;
   uint idx_sl_best = 0;
   for(uint i=0;i<refc;i++)
      for(uint j=0;j<slc;j++)
        {
         uint idx=j*refc*4+i*4;
         int profit=OptResults[idx]+OptResults[idx+1];
         //sum+=profit;
         if(max_profit<profit)
           {
            max_profit=profit;
            idx_ref_best= i;
            idx_sl_best = j;
           }
        }

After that, recalculate the results in 'double' and set the desired values of optimized parameters into the appropriate structure.

   uint idx=idx_sl_best*refc*4+idx_ref_best*4;
   result.gross_profit=double(OptResults[idx])/100;
   result.gross_loss=double(OptResults[idx+1])/100;
   result.profit_trades=OptResults[idx+2];
   result.loss_trades=OptResults[idx+3];
   result.trades_total=result.loss_trades+result.profit_trades;
   result.net_profit=result.gross_profit+result.gross_loss;
//---
   par.ref.value= int(par.ref.start+idx_ref_best*par.ref.step);
   par.sl.value = int(par.sl.start+idx_sl_best*par.sl.step);

Keep in mind that converting 'int' into 'double' and vice versa will surely affect the results making them differ slightly from the ones obtained during the single test.

Write a small script for launching optimization:

#include <OCL_Patterns\TestPatternsOCL.mqh>

CTestPatterns tpat;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   datetime from=D'2018.01.01 00:00';
   datetime to=D'2018.10.01 00:00';
//--- set optimization parameters
   STR_OPT_PARS optpar;
   optpar.ref.start = 15;
   optpar.ref.step  = 5;
   optpar.ref.stop  = 510;
   optpar.sl.start = 15;
   optpar.sl.step  = 5;
   optpar.sl.stop  = 510;
   optpar.flags=15;
   optpar.tp=50;
   optpar.timeout=12*3600;
//--- result structure
   STR_TEST_RESULT res;
//--- launch optimization
   tpat.Optimize(res,from,to,optpar);
   STR_ERROR oclerr=tpat.GetLastErrorExt();
   if(oclerr.code)
     {
      Print(oclerr.comment);
      Print("code = ",oclerr.code,", function = ",oclerr.function,", line = ",oclerr.line);
      return;
     }
//--- values of optimized parameters
   Print("Ref: ",optpar.ref.value,", SL: ",optpar.sl.value);
//--- test results  
   Print("Net Profit: ",   res.net_profit);
   Print("Gross Profit: ", res.gross_profit);
   Print("Gross Loss: ",   res.gross_loss);
   Print("Trades Total: ", res.trades_total);
   Print("Profit Trades: ",res.profit_trades);
   Print("Loss Trades: ",  res.loss_trades);
//--- execution statistics
   COCLStat ocl_stat=tpat.GetStat();
   Print("GPU memory size: ",       ocl_stat.gpu_mem_size.ToStr());
   Print("GPU memory usage: ",      ocl_stat.gpu_mem_usage.ToStr());
   Print("Buffering: ",             ocl_stat.time_buffering.ToStr());
   Print("OpenCL init: ",           ocl_stat.time_ocl_init.ToStr());
   Print("OpenCL buffering: ",      ocl_stat.time_ocl_buf.ToStr());
   Print("OpenCL prepare orders: ", ocl_stat.time_ocl_orders.ToStr());
   Print("OpenCL test: ",           ocl_stat.time_ocl_test.ToStr());
   Print("OpenCL total execution: ",ocl_stat.time_ocl_exec.ToStr());
   Print("Post-processing: ",       ocl_stat.time_proc.ToStr());
   Print("Total: ",                 ocl_stat.time_total.ToStr());
  }

The inputs are the same ones we used when optimizing on the built-in tester. Perform a launch:

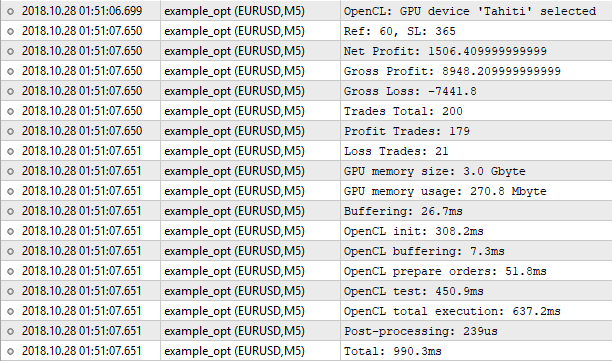
Fig. 9. Optimizing on the OpenCL tester

As we can see, the results do not coincide with the ones of the built-in tester. Why? Could the loss of accuracy when converting 'double' into 'int' and vice versa play a decisive role here? Theoretically, this could happen if the results differed in fractions after the decimal point. But the differences are significant.

The built-in tester shows Ref = 60 and SL = 350 with the net profit of 1000.50. The OpenCL tester shows Ref = 60 and SL = 365 with the net profit of 1506.40. Let's try to run a regular tester with the values found by the OpenCL tester:

Fig. 10. Checking the optimization results found by the OpenCL tester

The result is very similar to ours. So, this is not the loss of accuracy. The genetic algorithm has skipped this combination of optimized parameters. Let's launch the built-in tester in the slow optimization mode with complete enumeration of parameters.

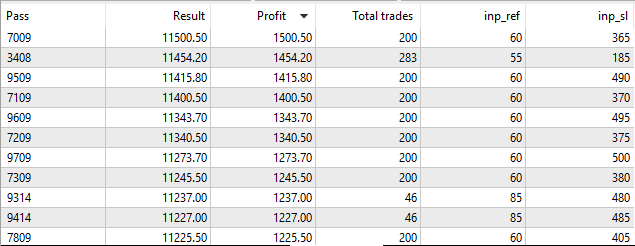
Fig. 11. Launching the built-in strategy tester in the slow optimization mode

As we can see, in case of a complete enumeration of parameters, the built-in tester finds the same desired values Ref = 60 and SL = 365, as the OpenCL tester. This means the optimization algorithm we have implemented works correctly.

3. Comparing performance

Now it is time to compare the performance of the built-in and OpenCL testers.

We will compare the time spent on optimization of the parameters of the strategy described above. The built-in tester is to be launched in two modes: fast (genetic algorithm) and slow optimization (complete enumeration of parameters). The launch will be performed on a PC with the following characteristics:

Operating system	Windows 10 (build 17134) x64
CPU	AMD FX-8300 Eight-Core Processor, 3600MHz
RAM	24 574 Mb
Type of media MetaTrader is installed on	HDD

6 cores out of 8 are allocated for test agents.

OpenCL tester is to be launched on AMD Radeon HD 7950 video 3Gb RAM and 800Mhz GPU frequency.

Optimization is to be performed on three pairs: EURUSD, GBPUSD and USDJPY. On each pair, the optimization is performed on four time ranges for each optimization mode. We will use the following abbreviations:

Optimization mode	Description
Tester Fast	Built-in strategy tester, genetic algorithm
Tester Slow	Built-in strategy tester, complete enumeration of parameters
Tester OpenCL	Tester implemented using OpenCL

Designating test ranges:

Period	Time range
1 month	2018.09.01 - 2018.10.01
3 months	2018.07.01 - 2018.10.01
6 months	2018.04.01 - 2018.10.01
9 months	2018.01.01 - 2018.10.01

The most important results for us are the values of the desired parameters, net profit, number of trades and optimization time.

3.1. Optimization on EURUSD

H1, 1 month:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	15	15	15
Stop Loss	330	510	500
Net profit	942.5	954.8	909.59
Number of trades	48	48	47
Optimization duration	10 sec	6 min 2 sec	405.8 ms

H1, 3 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	50	65	70
Stop Loss	250	235	235
Net profit	1233.8	1503.8	1428.35
Number of trades	110	89	76
Optimization duration	9 sec	8 min 8 sec	457.9 ms

H1, 6 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	15	20	20
Stop Loss	455	435	435
Net profit	1641.9	1981.9	1977.42
Number of trades	325	318	317
Optimization duration	15 sec	11 min 13 sec	405.5 ms

H1, 9 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	15	15	15
Stop Loss	440	435	435
Net profit	1162.0	1313.7	1715.77
Number of trades	521	521	520
Optimization duration	20 sec	16 min 44 sec	438.4 ms

M5, 1 month:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	135	45	45
Stop Loss	270	205	205
Net profit	47	417	419.67
Number of trades	1	39	39
Optimization duration	7 sec	9 min 27 sec	418 ms

M5, 3 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	120	70	70
Stop Loss	440	405	405
Net profit	147	342	344.85
Number of trades	3	16	16
Optimization duration	11 sec	8 min 25 sec	585.9 ms

M5, 6 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	85	70	70
Stop Loss	440	470	470
Net profit	607	787	739.6
Number of trades	22	47	46
Optimization duration	21 sec	12 min 03 sec	796.3 ms

M5, 9 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	60	60	60
Stop Loss	495	365	365
Net profit	1343.7	1500.5	1506.4
Number of trades	200	200	200
Optimization duration	20 sec	16 min 44 sec	438.4 ms

3.2. Optimization on GBPUSD

H1, 1 month:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	175	90	90
Stop Loss	435	185	185
Net profit	143.40	173.4	179.91
Number of trades	3	13	13
Optimization duration	10 sec	4 min 33 sec	385.1 ms

H1, 3 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	175	145	145
Stop Loss	225	335	335
Net profit	93.40	427	435.84
Number of trades	13	19	19
Optimization duration	12 sec	7 min 37 sec	364.5 ms

H1, 6 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	165	170	165
Stop Loss	230	335	335
Net profit	797.40	841.2	904.72
Number of trades	31	31	32
Optimization duration	18 sec	11 min 3 sec	403.6 ms

H1, 9 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	165	165	165
Stop Loss	380	245	245
Net profit	1303.8	1441.6	1503.33
Number of trades	74	74	75
Optimization duration	24 sec	19 min 23 sec	428.5 ms

M5, 1 month:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	335	45	45
Stop Loss	450	485	485
Net profit	50	484.6	538.15
Number of trades	1	104	105
Optimization duration	12 sec	9 min 42 sec	412.8 ms

M5, 3 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	450	105	105
Stop Loss	440	240	240
Net profit	0	220	219.88
Number of trades	0	16	16
Optimization duration	15 sec	8 min 17 sec	552.6 ms

M5, 6 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	510	105	105
Stop Loss	420	260	260
Net profit	0	220	219.82
Number of trades	0	23	23
Optimization duration	24 sec	14 min 58 sec	796.5 ms

M5, 9 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	185	195	185
Stop Loss	205	160	160
Net profit	195	240	239.92
Number of trades	9	9	9
Optimization duration	25 sec	20 min 58 sec	4.4 ms

3.3. Optimization on USDJPY

H1, 1 month:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	60	50	50
Stop Loss	425	510	315
Net profit	658.19	700.14	833.81
Number of trades	18	24	24
Optimization duration	6 sec	4 min 33 sec	387.2 ms

H1, 3 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	75	55	55
Stop Loss	510	510	460
Net profit	970.99	1433.95	1642.38
Number of trades	50	82	82
Optimization duration	10 sec	6 min 32 sec	369 ms

H1, 6 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	150	150	150
Stop Loss	345	330	330
Net profit	273.35	287.14	319.88
Number of trades	14	14	14
Optimization duration	17 sec	11 min 25 sec	409.2 ms

H1, 9 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	190	190	190
Stop Loss	425	510	485
Net profit	244.51	693.86	755.84
Number of trades	16	16	16
Optimization duration	24 sec	17 min 47 sec	445.3 ms

M5, 1 month:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	30	35	35
Stop Loss	225	100	100
Net profit	373.60	623.73	699.79
Number of trades	53	35	35
Optimization duration	7 sec	4 min 34 sec	415.4 ms

M5, 3 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	45	40	40
Stop Loss	335	250	250
Net profit	1199.34	1960.96	2181.21
Number of trades	71	99	99
Optimization duration	12 sec	8 min	607.2 ms

M5, 6 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	130	40	40
Stop Loss	400	130	130
Net profit	181.12	1733.9	1908.77
Number of trades	4	229	229
Optimization duration	19 sec	12 min 31 sec	844 ms

M5, 9 months:

Result	Tester Fast	Tester Slow	Tester OpenCL
Reference	35	30	30
Stop Loss	460	500	500
Net profit	3701.30	5612.16	6094.31
Number of trades	681	1091	1091
Optimization duration	34 sec	18 min 56 sec	1 sec

3.4. Performance summary table

The obtained results show that the built-in tester often skips the best results in the fast optimization mode (genetic algorithm). Therefore, it is more fair to compare the performance relative to the OpenCL in the complete parameter enumeration mode. For more visibility, let's arrange a summary table of time spent on optimization.

Optimization conditions	Tester Slow	Tester OpenCL	Ratio
EURUSD, H1, 1 month	6 min 2 sec	405.8 ms	891
EURUSD, H1, 3 months	8 min 8 sec	457.9 ms	1065
EURUSD, H1, 6 months	11 min 13 sec	405.5 ms	1657
EURUSD, H1, 9 months	16 min 44 sec	438.4 ms	2292
EURUSD, M5, 1 month	9 min 27 sec	418 ms	1356
EURUSD, M5, 3 months	8 min 25 sec	585.9 ms	861
EURUSD, M5, 6 months	12 min 3 sec	796.3 ms	908
EURUSD, M5, 9 months	17 min 39 sec	1 sec	1059
GBPUSD, H1, 1 month	4 min 33 sec	385.1 ms	708
GBPUSD, H1, 3 months	7 min 37 sec	364.5 ms	1253
GBPUSD, H1, 6 months	11 min 3 sec	403.6 ms	1642
GBPUSD, H1, 9 months	19 min 23 sec	428.5 ms	2714
GBPUSD, M5, 1 month	9 min 42 sec	412.8 ms	1409
GBPUSD, M5, 3 months	8 min 17 sec	552.6 ms	899
GBPUSD, M5, 6 months	14 min 58 sec	796.4 ms	1127
GBPUSD, M5, 9 months	20 min 58 sec	970.4 ms	1296
USDJPY, H1, 1 month	4 min 33 sec	387.2 ms	705
USDJPY, H1, 3 months	6 min 32 sec	369 ms	1062
USDJPY, H1, 6 months	11 min 25 sec	409.2 ms	1673
USDJPY, H1, 9 months	17 min 47 sec	455.3 ms	2396
USDJPY, M5, 1 month	4 min 34 sec	415.4 ms	659
USDJPY, M5, 3 months	8 min	607.2 ms	790
USDJPY, M5, 6 months	12 min 31 sec	844 ms	889
USDJPY, M5, 9 months	18 min 56 sec	1 sec	1136

As we can see in the table, in some cases, the OpenCL tester is able to get results 2714 times faster than the built-in one. This is a good speed boost for those who value their time.

Conclusion

In this article, we have implemented the algorithm for constructing a tester for the simplest trading strategy using OpenCL. Of course, this implementation is just one of the possible solutions, and it has many drawbacks. Among them are:

• Working in "1 minute OHLC" mode suitable only for rough estimates
• No accounting for swaps and commissions
• Incorrect work with cross rates
• No trailing stop
• No consideration for the number of simultaneously opened positions
  
• No drawback among returned parameters

Despite all this, the algorithm can greatly help when you need to quickly and roughly assess the performance of the simplest patterns, since it allows you to do so thousand times faster than the built-in tester running in the complete parameters enumeration mode and dozens of times faster than the tester using a genetic algorithm.