MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 62): Nutzung der Muster von ADX und CCI mit Reinforcement-Learning TRPO

Einführung

Wir setzen unseren Blick darauf fort, wie technische Indikatoren, die verschiedene Teile des Preisgeschehens verfolgen, beim maschinellen Lernen miteinander verbunden werden können. Im letzten Beitrag haben wir gesehen, wie das überwachte Lernen in einem Multi-Layer-Perceptron (MLP) die Grundlage für die Vorhersage von Kursbewegungen bildet. Wir bezeichnen die Eingaben des MLP als Merkmale und seine Prognoseausgaben als Zustände. Die Art und Weise, wie wir unsere Merkmale im letzten Artikel definiert haben, unterschied sich geringfügig von unserem Ansatz in den Beiträgen 57-60, da wir einen kontinuierlichen Eingabevektor anstrebten, im Gegensatz zu der diskreten Option, die wir verwendet hatten. Die Entwicklung hin zu kontinuierlichen Daten und Regression und weg von diskreten Daten und Klassifizierung lässt sich vielleicht am besten durch einen Blick auf unsere KI-Trends verdeutlichen.

Um ein Computerprogramm zu einer brauchbaren oder praktischen Antwort zu veranlassen, musste diese Antwort früher von Hand in das Programm eingegeben werden. Im Grunde genommen war die if-Klausel das Herzstück der Programmierung der meisten Programme. Und wenn man darüber nachdenkt, bedeutete die Abhängigkeit von if-Klauseln, dass die vom Nutzer eingegebenen oder vom Programm verarbeiteten Daten bestimmten Kategorien angehören mussten. Es musste diskret sein. Daher kann man sagen, dass unsere Entwicklung und Verwendung von diskreten Daten größtenteils eine Reaktion auf Programmierungszwänge war und nicht auf die Daten oder das zu lösende Problem bezogen war.

Und dann kam OpenAI im Herbst 2023 mit ihrem ersten öffentlichen GPT, und all dies änderte sich. Die Entwicklung von Transformernetzen und GPTs geschah nicht über Nacht, da die ersten Perceptrons in den späten 60er Jahren entwickelt wurden, aber man kann mit Sicherheit sagen, dass die Einführung von ChatGPT ein wichtiger Meilenstein war. Mit der weiten Verbreitung von Modellen für große Sprachen ist klar geworden, dass Tokenisierung, Worteinbettung und natürlich Selbstaufmerksamkeit entscheidende Komponenten sind, damit die Modelle mit dem, was sie verarbeiten können, skalieren können. Keine Wenn-Klauseln mehr. Vor dem Hintergrund der Tokenisierung und der Einbettung von Wörtern, um die Netzwerkeingaben so kontinuierlich wie möglich zu gestalten, haben wir auch die Eingaben unseres MLP mit überwachtem Lernen „kontinuierlicher“ gemacht.

Um dies zu veranschaulichen, wird unser zweites Merkmal, Feature_1, wie folgt für das MLP von Python dargestellt:

def feature_1(adx_df, cci_df):
    """
    Creates a modified 3D signal array with:
    1. ADX > 25 (1 when above 25, else 0)
    2. CCI crosses from below 0 to above +50 (1 when condition met, else 0)
    3. CCI crosses from above 0 to below -50 (1 when condition met, else 0)
    """
    # Initialize empty array with 3 dimensions
    feature = np.zeros((len(adx_df), 5))
    
    # Dimension 1: ADX above 25 (continuous, not just crossover)
    feature[:, 0] = (adx_df['adx'] > 25).astype(int)
    
    # Dimension 2: CCI crosses from <0 to >+50
    feature[:, 1] = (cci_df['cci'] > 50).astype(int)
    feature[:, 2] = (cci_df['cci'].shift(1) < 0).astype(int)
    
    # Dimension 3: CCI crosses from >0 to <-50
    feature[:, 3] = (cci_df['cci'] < -50).astype(int)
    feature[:, 4] = (cci_df['cci'].shift(1) > 0).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

Wenn wir die Methode beibehalten würden, die wir für die Artikel 57 bis 60 verwendet haben, dann wäre sie wie folgt verarbeitet worden:

def feature_1(adx_df, cci_df):
    """
    """
    # Initialize empty array with 3 dimensions and same length as input
    feature = np.zeros((len(dem_df), 3))
    
    # Dimension 1:
    feature[:, 0] = (adx_df['adx'] > 25).astype(int)
    feature[:, 1] = ((cci_df['cci'] > 50) &
                     (cci_df['cci'].shift(1) < 0)).astype(int)
    feature[:, 2] = ((cci_df['cci'] < -50) &
                     (cci_df['cci'].shift(1) > 0)).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

Dieser Ansatz neigt dazu, die Signale in Übereinstimmung mit den typischerweise erwarteten Mustern für auf- oder abwärts zu klassifizieren, da die zweite Position im Ausgangsvektor ausschließlich Merkmale für ein Aufwärtssignal erfasst. Der dritte Punkt erfasst nur Abwärts-Eigenschaften. Da sich dieser Ansatz an bereits als auf- oder abwärts definierte Muster hält, ist er eher klassifizierend und daher diskret. Unsere Testergebnisse ergaben, dass nur 3 der 10 getesteten Muster in der Lage waren, von 2024.01.01 bis 2025.01.01 den Vorwärtstest zu bestehen, nachdem sie von 2020.01.01 bis 2024.01.01 getestet/trainiert worden waren. Das verwendete Symbol war EUR USD und der Zeitrahmen war der tägliche Zeitrahmen.

In Anbetracht des großen Zeitrahmens und des relativ langen Trainingsfensters, das wir verwendet haben, könnte es daher sinnvoll sein, mit diskreteren Eingabedaten für unseren ersten MLP zu arbeiten. Ein weiteres Argument dafür könnte auch aus den LLM-Eingaben abgeleitet werden. Ja, die Tokenisierung und das Einbetten von Wörtern machen die Eingabedaten kontinuierlicher, aber die „Geheimsoße“ der Selbstaufmerksamkeit von LLM ist von Natur aus diskret. Dies liegt daran, dass versucht wird, jedem der in der Eingabeaufforderung angegebenen Wörter eine relative Bedeutung beizumessen.

Wir machen so etwas nicht, und deshalb könnte das eine Erklärung sein. Die Leser können daher verschiedene Formate von Eingaben ändern und testen, da der gesamte MQL5-Quellcode beigefügt ist. Wir für unseren Teil werden bei diesem Ansatz bleiben und sehen, welche Ergebnisse wir mit Reinforcement Learning erzielen.

Reinforcement-Learning

Wir bauen auf dem Modell des überwachten Lernens aus unserem letzten Artikel auf, indem wir Aktionen und Belohnungen einführen. Wir erinnern uns, dass wir Merkmale als Eingaben für unser MLP und Zustände (prognostizierte Preisänderungen) als Ausgaben hatten. Die Aktionen in dieser Phase stellen das Wie dar, was wir tun müssen, wenn wir wissen, was unsere MLP vorhersagt. Wenn zum Beispiel ein Preisrückgang prognostiziert wird, könnten wir ein Verkaufslimit, einen Verkaufsstopp oder einen sofortigen Marktverkauf durchführen. Der Aufbau und die Ausbildung eines politischen Netzwerks können dazu beitragen, diese Entscheidung zu verbessern.

In einem Szenario wie in unserem obigen Beispiel, in dem verschiedene Arten von Verkaufsaufträgen ausgeführt werden, entspricht die Größe des Ausgangsvektors für das Politik-Netz in der Regel der Anzahl der möglichen Aktionen. In diesem Fall wären es 3, für die 3 Optionen: Limit-Order, Stop-Order und Market-Order. Das Training mit diesen Einstellungen sollte zu Unterschieden in der Leistung führen, und der Leser ist eingeladen, dies zu untersuchen. Wir bleiben dabei, dass es sich bei den Aktionen um einen einzelnen Dim-Vektor handelt, der im Wesentlichen eine Nachbildung des Ausgabevektors unserer Zustände aus dem MLP im letzten Artikel ist. Welchem Zweck dient dies dann? Sie dient als Bestätigung der Kauf- oder Verkaufs-Prognose, die das überwachte Lernnetz erstellt hat.

Darüber hinaus werden Belohnungen verwendet, um die Höhe des Gewinns aus jedem platzierten Handel zu erhöhen. Belohnungen sind der Output des Wertenetzes, und auch wenn wir sie wieder als eindimensionalen Vektor betrachten, können auch sie mehrdimensional sein. Denn die Analyse nach dem Handel kann mehr als nur Gewinn oder Verlust berücksichtigen, sondern auch Ausreißer. Diese sind günstig und ungünstig, daher kann der Belohnungsvektor auch in 3 Dimensionen unterteilt werden, indem er die ungünstige Ausdehnung, die günstige Ausdehnung und den Nettogewinn enthält.

Optimierung der Vertrauensbereichspolitik

Trust Region Policy Optimization (TRPO) ist ein Reinforcement-Learning-Algorithmus, bei dem es um die Verbesserung von Richtlinien geht. Dies geschieht iterativ, indem die Gewichte und Biases des Politik-Netzes aktualisiert werden, während sie gleichzeitig innerhalb einer „Vertrauensregion“ der aktuellen Politik bleiben.

Die Schlüsselkomponenten für die Umsetzung dieses Konzepts sind das Politik-Netz, die Vertrauensregion und die KL-Divergenz. Das Politik-Netz ist ein neuronales Netz, das die Handlungsauswahl durch Zuordnung von Zuständen zu einer Wahrscheinlichkeitsverteilung über mögliche Handlungen darstellt. Die Vertrauensregion ist eine Einschränkung, die die Änderung der Strategie bei jeder Iteration begrenzt. Sie sorgt dafür, dass die neue Politik nicht zu sehr von der alten abweicht, und vermeidet so Instabilität. Die KL-Divergenz schließlich misst den Unterschied zwischen der prognostizierten und der vertrauenswürdigen Wahrscheinlichkeitsverteilung. Sie definiert im Wesentlichen die Beschränkung der Vertrauensregion.

Der Trainingsprozess umfasst: das Sammeln von Daten, idealerweise in Form von Trajektorien-Batches, unter Verwendung der aktuellen Politik; die Schätzung der Vorteilsfunktion für jedes Zustands-Aktions-Paar in den gesammelten Daten, um ein Gefühl dafür zu bekommen, wie viel besser eine Aktion im Vergleich zur durchschnittlichen Aktion ist; die Formulierung des Optimierungsproblems, um geeignete Netzwerkgewichte und -biases für die Politik- und Werte-Netze zu finden, die die Belohnungen unter Berücksichtigung von KL-Divergenz-Beschränkungen maximieren, die die Divergenz zwischen einer neuen und einer alten Politik innerhalb eines bestimmten Schwellenwerts halten; Lösung des Optimierungsproblems durch Techniken wie Gradientenabstieg; schließlich die Aktualisierung der Gewichte der Politik und die Werte der Netze.

Die Hauptvorteile von TRPO sind: eine gleichmäßige Verbesserung, wodurch die Verbesserungen der Politik garantiert sind; Stabilität, da die vertrauenswürdige Region verhindert, dass die Politik unnötig große Aktualisierungen vornimmt, die instabil sein könnten; und Effizienz, da TRPO dazu neigt, mit weniger Stichproben effektiv zu lernen als andere Politik-Gradientenmethoden. Zusammenfassend lässt sich sagen, dass die Kernidee von TRPO darin besteht, den erwarteten Vorteil einer neuen Politik gegenüber einer alten Politik zu maximieren, vorbehaltlich einer Beschränkung hinsichtlich des Ausmaßes, in dem die Politik geändert werden darf. Dies wird durch die folgenden Gleichungen erfasst;

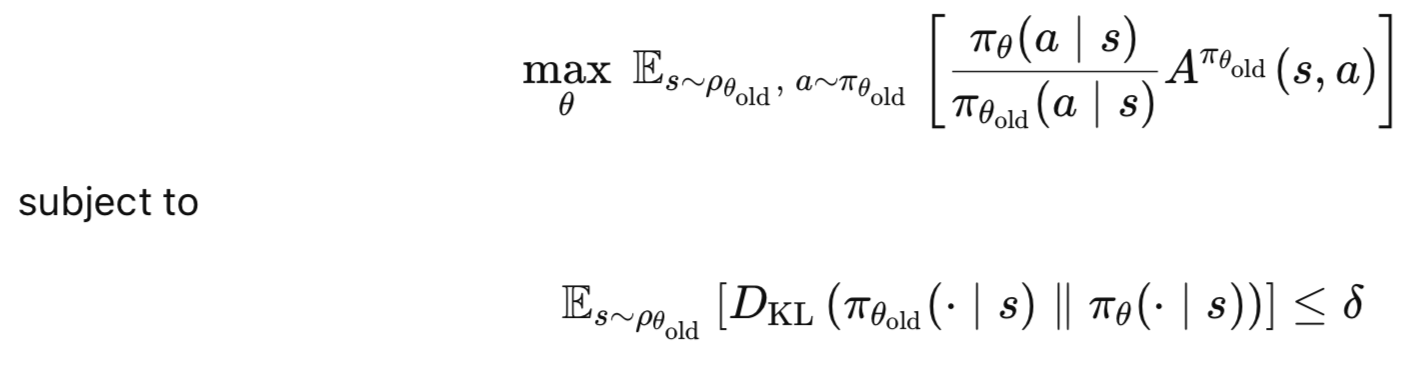
wobei:

• θ: neue Parameter der Politik.
• θold: alte Parameter der Politik vor der Aktualisierung.
• πθ(a∣s): Wahrscheinlichkeit der Handlung a unter der neuen Politik πθ
• πθold(a∣s): Wahrscheinlichkeit der Handlung a unter der alten Politik πθold
• Aπθold(s,a): Vorteilsfunktion, die abschätzt, um wie viel besser a als die durchschnittliche Aktion im Zustand s ist.
• ρθold (s): Staatliche Besuchsverteilung nach der alten Politik.
• DKL : Divergenz nach Kullback-Leibler (KL), die den Unterschied zwischen alter und neuer Politik misst.
• δ: Vertrauensbereichsbeschränkung (kleiner positiver Wert).

Das Politik-Netzwerk

Wir implementieren unsere Politik und Wertnetzwerke in Python wie folgt;

class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_size=64, discrete=False):
        super(PolicyNetwork, self).__init__()
        self.discrete = discrete
        
        self.fc1 = nn.Linear(state_dim, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)

        self.export_mode = False
        
        if self.discrete:
            self.fc3 = nn.Linear(hidden_size, action_dim)
        else:
            self.mean = nn.Linear(hidden_size, action_dim)
            self.log_std = nn.Parameter(torch.zeros(action_dim))
    
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        
        if self.discrete:
            action_probs = F.softmax(self.fc3(x), dim=-1)
            dist = Categorical(action_probs)
        else:
            mean = self.mean(x)
            std = torch.exp(self.log_std)
            
            if self.export_mode:
                return mean, std  # return raw tensors
            
            cov_mat = torch.diag_embed(std).unsqueeze(dim=0)
    
            dist = MultivariateNormal(mean, cov_mat)
        
        return dist

Das Politik-Netz erbt vom nn.module, was es zu einem PyTorch-Netzwerkmodul macht. Die Parameter sind: state-dimension, die Größe des Eingabezustandsraums; action-dimension, die Größe des Aktionsraums; hidden-size, die Größe der versteckten Schichten, für die wir 64 vorgeben. Als Eingabe dient auch ein boolesches Flag mit der Bezeichnung diskret, das angibt, ob der Aktionsraum diskret oder kontinuierlich ist. Diese diskrete Markierung bestimmt schließlich auch die Struktur der Ausgabeschicht und die Art der verwendeten Verteilung.

Dieser Aufbau macht unser Netzwerk vielseitig in der Handhabung sowohl diskreter als auch kontinuierlicher Aktionsräume in RL-Umgebungen. So können Spiele wie CartPole die Option discrete ist gleich true verwenden, während in unserem Fall des Handels oder sogar der Robotik diese Option auf False gesetzt ist. In TRPO definiert das Politik-Netz die Politik des Agenten, die eine Abbildung von Zuständen auf Aktionen ist. Die Flexibilität im Umgang mit verschiedenen Arten von Handlungsräumen kann sich daher als wichtig für die allgemeine Anwendbarkeit erweisen. Für Händler könnten wir unsere Aktionen auf die 3 oben erwähnten Ordertypen Limits, Stops und Market Orders beschränken, und in diesem Fall würde diskrete True zugewiesen werden. 

Bei der Umsetzung ist darauf zu achten, dass die Zustandsdimension und die Aktionsdimension mit den Vorgaben der Umgebung oder den verwendeten Datensätzen übereinstimmen. Das diskrete Flag sollte auch mit dem Aktionsraumtyp der Umgebung übereinstimmen. Die versteckte Größe von 64 ist ein einstellbarer Hyperparameter, der je nach Komplexität der Umgebung/des verwendeten Datensatzes eine Erhöhung oder sogar das Hinzufügen weiterer versteckter Schichten rechtfertigen könnte.

Die Netzarchitektur besteht aus 2 vollständig verbundenen linearen Schichten, wobei fc1 den Eingangszustand einer versteckten Schicht und fc2 einer weiteren versteckten Schicht derselben Größe zuordnet. „Export Mode“ ist ein Flag, mit dem gesteuert wird, ob das Netz rohe Tensoren für den Export oder eine Verteilung für Training/Sampling liefert. 

Diese Schichten bilden das Rückgrat des Politik-Netzes, da sie rohe Zustandsdaten in eine übergeordnete Darstellung einer geeigneten Aktion für die Auswahl umwandeln. Durch eine einfache zweischichtige Architektur mit ReLU-Aktivierungen erhalten wir eine ausreichende Ausdruckskraft und halten das Modell gleichzeitig leicht. In TRPO muss das Politik-Netzwerk differenzierbar sein. Dies ist wichtig für die Berechnung der Gradienten der Politikaktualisierungen. Mit diesen beiden linearen Systemen ist diese Anforderung erfüllt. 

Die Wahl von zwei versteckten Schichten mit einer Größe von 64 ist für eine Standardeinstellung vernünftig, kann aber oft eine Anpassung erfordern, wenn die Umgebung/getesteten Datensätze komplexer oder größer werden. In Fällen, in denen mehr als zwei Indikatoren gepaart werden, um Merkmalsmuster zu erhalten, oder in denen komplexere Zustände in das Politik-Netz eingegeben werden, müsste diese Zahl nach oben skaliert werden. 

Je nachdem, ob unser Netz im diskreten Modus läuft oder nicht, wird unsere endgültige Ausgabeschicht aus einem einzigen Netz oder aus zwei Netzen bestehen. Für diskrete Räume ist die Ausgabe der linearen Schicht fc3 eine Darstellung der Logik jeder Aktion. Wird dagegen diskret auf false gesetzt, dann handelt es sich um kontinuierliche Räume, in denen zwei Netze jeweils einen eigenen Vektor ausgeben. Der erste ist der Mittelwert einer Gauß-Verteilung für jede Handlungsdimension. Zweitens haben wir einen logarithmischen Standardabweichungsvektor der Gaußschen Verteilung jeder Handlungsdimension.

Dies ist wichtig, weil die Bifurkation die Modellierung in verschiedenen Aktionsraumtypen ermöglicht. Die Option „discrete-on“ gibt eine Wahrscheinlichkeitsverteilung über eine vorgegebene Anzahl von Aktionen aus. Die kontinuierliche oder diskrete Alternative gibt eine multivariate Gauß-Verteilung aus. Dabei handelt es sich einfach um zwei Vektoren, von denen einer, der Mittelwert, einen indikativen Mittelwert und damit eine Gewichtung für jede Aktion liefert, während der andere Vektor der logarithmischen Verteilungen eine logarithmische Verteilung oder eine Konfidenzmetrik für jede der mittleren Vorhersagen liefert.

In TRPO wird die Politik-Verteilung verwendet, um Aktionen zu stichprobenartig zu erfassen und Log-Wahrscheinlichkeiten für Politik-Gradienten-Updates zu berechnen. Die Wahl zwischen diskret und kontinuierlich wirkt sich daher auf die Anzahl der erforderlichen Berechnungen und die Effizienz des Netzes aus. Die Standardabweichung der logarithmischen Wahrscheinlichkeiten ist ein erlernbarer Parameter, der es dem Netz ermöglicht, das Explorationsniveau (Varianz) während des Trainings anzupassen. Dies ist wichtig, um ein Gleichgewicht zwischen Erkunden und Nutzen herzustellen.

Bei diskreten Aktionen sollte die Aktionsdimension der Anzahl der möglichen Aktionen entsprechen. Wir bleiben bei einer einzigen Dimension, da es sich um eine kontinuierliche Variable handelt, aber wir werden uns in späteren Artikeln wieder mit diskreten Handlungsoptionen befassen. Für unsere aktuellen kontinuierlichen Aktionen ist es jedoch immer wichtig, log_std sorgfältig zu initialisieren. Der Start mit Torch.zeros(action_dim) bedeutet, dass die anfänglichen Standardabweichungen exp(0)=1 sind, was je nach Aktionsskala zu breit oder zu schmal sein kann. Es sollte eine umgebungsspezifische Skalierungsmethode vorhanden sein.

Auch in TRPO werden die logarithmischen Wahrscheinlichkeiten der Politik in der Zielfunktion und den KL-Divergenzbeschränkungen verwendet. Das bedeutet, dass die numerische Stabilität innerhalb der Verteilung unbedingt gewährleistet sein muss. In Fällen, in denen die Umgebung begrenzte Aktionen verwendet, werden die Netzausgänge zwangsläufig manchmal außerhalb des Anwendungsbereichs liegen. Daher müssten die Mittelwerte beschnitten oder skaliert werden, um sicherzustellen, dass sie in den vorgesehenen Bereich passen.

Der Vorwärtsdurchlauf zum Politik-Netzwerk führt eine gemeinsame Verarbeitung durch, bei der der Eingangszustand x durch fc1 und fc2 geleitet wird, wobei ReLU-Aktivierungen angewendet werden, um Nichtlinearität hinzuzufügen. Wenn die Aktionen diskret sind, dann durchläuft die Ausgabe von fc3 einen Softmax, um Aktionswahrscheinlichkeiten zu erzeugen. Ist sie hingegen kontinuierlich, wird der Mittelwert über die Mittelwertschicht berechnet; die Standardabweichung wird als exp(log_std) ermittelt, um sicherzustellen, dass sie positiv ist; wenn export_mode auf true gesetzt ist, werden die Standardabweichungen als rohe Tensoren zurückgegeben. Wenn export_mode false ist, wird eine diagonale Kovarianzmatrix (cov_mat) erstellt und eine Multivariate-Normalverteilung für die Stichprobenziehung der Protokolle erzeugt.

Der Vorwärtsdurchlauf definiert die Art und Weise, in der die Politik Zustände auf Aktionsverteilungen abbildet, und dies ist der Kern der Entscheidungsfindung des RL-Agenten. In TRPO umfasst die Politikverteilung: das Sammeln von Aktionen während der Interaktion mit der Umgebung, das Berechnen von Log-Wahrscheinlichkeiten für das Politikgradienten-Ziel und das Bewerten der Vertrauensbereichsbeschränkung. Die Verwendung von kategorialen und multivariaten Normalverteilungen gewährleistet die Kompatibilität mit Standard-RL-Bibliotheken wie torch.distributions von PyTorch. Die Option „Exportmodus“ ermöglicht einen praktischen Einsatz, da Rohdaten verwendet werden, die dann je nach Bedarf nachbearbeitet werden können.

Die Softmax im diskreten Fall stellt sicher, dass sich die Wahrscheinlichkeiten zu 1 addieren. Numerische Instabilität kommt in den Logik häufig vor, daher sollte bei Bedarf auf NaNs geachtet und Torch.Clamp verwendet werden. Bei kontinuierlichen Handlungen geht die diagonale Kov-Matrix von unabhängigen Handlungsdimensionen aus. Sind die Handlungen hingegen korreliert, sollte eine vollständige Kovarianzmatrix verwendet werden. Dies führt zu höheren Rechenkosten. In TRPO sollten die Log-Wahrscheinlichkeiten der Politik effizient und genau berechnet werden, da sie in den Schritten des konjugierten Gradienten und der Liniensuche verwendet werden.

Das Netzwerk der Werte

Wir setzen unser Netzwerk der Werte wie folgt um:

class ValueNetwork(nn.Module):
    def __init__(self, state_dim, hidden_size=64):
        super(ValueNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, 1)
    
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

Bei der Gestaltung und Umsetzung des Wertenetzes gibt es eine Reihe von Überschneidungen mit dem Politiknetz. Ich werde daher das meiste davon auslassen. Im Prinzip schätzt das Wertenetz jedoch den Zustandswert für die Berechnung des Vorteils (oder der Belohnung) und die Verringerung der Varianz. Wir verwenden ebenfalls eine einfache Architektur wie beim Politik-Netz und unsere Ausgabe ist ein einziger Skalar. Dieses Netz ist für stabile Aktualisierungen der Politik in TRPO durch genaue Belohnungsschätzungen unerlässlich.

TRPO-Agent

Wir implementieren unsere TRPO-Agentenklasse in Python wie folgt:

class TRPO_Agent:
    def __init__(self, state_dim, action_dim, discrete=False, 
                 hidden_size=64, lr_v=0.001, gamma=0.99, 
                 delta=0.01, lambda_=0.97, max_kl=0.01, cg_damping=0.1, 
                 cg_iters=10, device='cpu'):
        
        self.policy = PolicyNetwork(state_dim, action_dim, hidden_size, discrete).to(device)
        self.value_net = ValueNetwork(state_dim, hidden_size).to(device)
        self.value_optimizer = optim.Adam(self.value_net.parameters(), lr=lr_v)
        
        self.gamma = gamma
        self.delta = delta
        self.lambda_ = lambda_
        self.max_kl = max_kl
        self.cg_damping = cg_damping
        self.cg_iters = cg_iters
        
        self.discrete = discrete
        self.device = device
        self.state_dim = state_dim
    
    def get_action(self, state):
        # Convert state to tensor and add batch dimension
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        
        # Get action distribution from policy
        dist = self.policy(state)
        
        # Sample action from distribution
        action = dist.sample()
        
        # Get log probability BEFORE converting to numpy/item
        log_prob = dist.log_prob(action)
        
        # Convert action to appropriate format
        if self.discrete:
            action = action.item()  # For discrete actions
        else:
            action = action.detach().cpu().numpy()[0]  # For continuous actions
        
        # Clip continuous actions to [-1, 1] range (optional for discrete)
        if not self.discrete:
            action = np.clip(action, -1, 1)
        
        return action, log_prob
        
    def update_value_net(self, states, targets):
        # Convert inputs to proper tensor format
        if torch.is_tensor(states):
            states = states.detach().cpu().numpy()
        if torch.is_tensor(targets):
            targets = targets.detach().cpu().numpy()
        
        states = np.array(states, dtype=np.float32)
        targets = np.array(targets, dtype=np.float32)
        
        # Ensure proper shapes
        if len(states.shape) == 1:
            states = np.expand_dims(states, 0)
        if len(targets.shape) == 0:
            targets = np.expand_dims(targets, 0)
        
        states_tensor = torch.FloatTensor(states).to(self.device)
        targets_tensor = torch.FloatTensor(targets).to(self.device)
        
        # Forward pass
        self.value_optimizer.zero_grad()
        values = self.value_net(states_tensor)
        
        # Ensure matching shapes for loss calculation
        values = values.view(-1)
        targets_tensor = targets_tensor.view(-1)
        
        loss = F.mse_loss(values, targets_tensor)
        loss.backward()
        self.value_optimizer.step()

    def update_policy(self, states, actions, old_log_probs, advantages):
        # Handle tensor conversion safely
        def safe_convert(x):
            if torch.is_tensor(x):
                return x.detach().cpu().numpy()
            return np.array(x, dtype=np.float32)
        
        states = safe_convert(states)
        actions = safe_convert(actions)
        old_log_probs = safe_convert(old_log_probs)
        advantages = safe_convert(advantages)
        
        # Convert to tensors with proper shapes
        states_tensor = torch.FloatTensor(states).to(self.device)
        actions_tensor = torch.FloatTensor(actions).to(self.device)
        old_log_probs_tensor = torch.FloatTensor(old_log_probs).to(self.device)
        advantages_tensor = torch.FloatTensor(advantages).to(self.device)
        
        # Get old distribution
        with torch.no_grad():
            old_dist = self.policy(states_tensor)
        
        # Compute gradient of surrogate loss
        def get_loss():
            dist = self.policy(states_tensor)
            if self.discrete:
                log_probs = dist.log_prob(actions_tensor.long())
            else:
                log_probs = dist.log_prob(actions_tensor)
            return -self.surrogate_loss(log_probs, old_log_probs_tensor, advantages_tensor)
        
        # Rest of the TRPO update remains the same...
        loss = get_loss()
        grads = torch.autograd.grad(loss, self.policy.parameters(), create_graph=True)
        flat_grad = torch.cat([grad.view(-1) for grad in grads]).detach()
        
        step_dir = self.conjugate_gradient(states_tensor, old_dist, flat_grad, nsteps=self.cg_iters)
        
        shs = 0.5 * torch.dot(step_dir, self.hessian_vector_product(states_tensor, old_dist, step_dir))
        step_size = torch.sqrt(self.max_kl / (shs + 1e-8))
        full_step = step_size * step_dir
        
        old_params = torch.cat([param.view(-1) for param in self.policy.parameters()])
        
        def line_search():
            for alpha in [0.5**x for x in range(10)]:
                new_params = old_params + alpha * full_step
                self.set_policy_params(new_params)
                
                with torch.no_grad():
                    new_dist = self.policy(states_tensor)
                    new_loss = get_loss()
                    kl = self.kl_divergence(old_dist, new_dist)
                
                if kl <= self.max_kl and new_loss < loss:
                    return True
            return False
        
        if not line_search():
            self.set_policy_params(old_params)
    
    def set_policy_params(self, flat_params):
        prev_idx = 0
        for param in self.policy.parameters():
            flat_size = param.numel()
            param.data.copy_(flat_params[prev_idx:prev_idx + flat_size].view(param.size()))
            prev_idx += flat_size
    
    def compute_advantages(self, rewards, values, dones):
        advantages = np.zeros_like(rewards)
        last_advantage = 0
        
        for t in reversed(range(len(rewards))):
            if dones[t]:
                delta = rewards[t] - values[t]
                last_advantage = delta
            else:
                delta = rewards[t] + self.gamma * values[t+1] - values[t]
                last_advantage = delta + self.gamma * self.lambda_ * last_advantage
            advantages[t] = last_advantage
        
        advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
        return advantages
    
    def surrogate_loss(self, new_probs, old_probs, advantages):
        ratio = torch.exp(new_probs - old_probs)
        return torch.mean(ratio * advantages)
    
    def kl_divergence(self, old_dist, new_dist):
        if self.discrete:
            return torch.mean(torch.sum(old_dist.probs * (torch.log(old_dist.probs) - torch.log(new_dist.probs)), dim=1))
        else:
            return torch.distributions.kl.kl_divergence(old_dist, new_dist).mean()
    
    def hessian_vector_product(self, states, old_dist, vector):
        kl = self.kl_divergence(old_dist, self.policy(states))
        
        # First compute gradient of KL
        grads = torch.autograd.grad(kl, self.policy.parameters(), create_graph=True)
        flat_grad_kl = torch.cat([grad.view(-1) for grad in grads])
        
        # Compute gradient of (grad_KL * vector)
        grad_vector_product = torch.sum(flat_grad_kl * vector)
        grad_grad = torch.autograd.grad(grad_vector_product, self.policy.parameters(), retain_graph=True)
        flat_grad_grad = torch.cat([grad.contiguous().view(-1) for grad in grad_grad])
        
        return flat_grad_grad + self.cg_damping * vector
    
    def conjugate_gradient(self, states, old_dist, b, nsteps=10, residual_tol=1e-10):
        x = torch.zeros_like(b)
        r = b.clone()
        p = b.clone()
        rdotr = torch.dot(r, r)
        
        for i in range(nsteps):
            Avp = self.hessian_vector_product(states, old_dist, p)
            alpha = rdotr / torch.dot(p, Avp)
            x += alpha * p
            r -= alpha * Avp
            new_rdotr = torch.dot(r, r)
            if new_rdotr < residual_tol:
                break
            beta = new_rdotr / rdotr
            p = r + beta * p
            rdotr = new_rdotr
        
        return x

Die TRPO-Agentenklasse funktioniert sowohl für kontinuierliche Aktionsräume als auch für diskrete Räume, indem sie ein Politik-Netz zur Auswahl von Aktionen und ein Wertnetzwerk zur Schätzung der Belohnungen für jeden Zustand verwendet. Ein wichtiger Unterschied zu TRPO-Wertnetzen besteht darin, dass die Eingaben nur Zustände sind und keine Aktionen enthalten, wie es bei anderen RL-Algorithmen oft der Fall ist. TRPO optimiert die Politik, indem es ein Ersatzziel maximiert und gleichzeitig die Politikaktualisierungen darauf beschränkt, innerhalb einer durch KL-Divergenz definierten Vertrauensregion zu bleiben. Diese Klasse umfasst Methoden zur Auswahl von Aktionen, zur Aktualisierung von Wertfunktionen, zur Optimierung von Richtlinien, zur Schätzung von Belohnungen und zu anderen Berechnungen.

Die Funktion def __init__() startet den TRPO-Agenten mit Richtlinien- und Wertnetzen, Optimierern und Hyperparametern für die TRPO-Optimierung der Vertrauensregion. Die Eingaben umfassen Hyperparameter, von denen einige TRPO-spezifisch sind, wie 'max_kl' und 'cg_damping', andere sind RL-spezifisch, wie Gamma und Lambda. Bei der Abstimmung dieser Hyperparameter sind die Standardwerte von max_kl=0,01, cg_damping=0,1 und lambda=0,97 vernünftig, aber umfeld- und datensatzspezifisch.

Für komplexere Umgebungen, wie z. B. hochdimensionale Datensätze, könnte ein kleineres max_kl von etwa 0,005 für strengere Einschränkungen oder ein größeres cg_iters von etwa 20 für die Konvergenz des konjugierten Gradienten besser sein. Die Wahl des Optimierers von Adam für das Wertnetz ist Standard, aber das Politiknetz hängt von der nutzerdefinierten Aktualisierung von TRPO ohne den Optimierer ab. Es ist auch eine gute Idee, dafür zu sorgen, dass die Lernrate des Netzwerks ausreichend klein ist, um die Stabilität des Netzwerks zu verbessern.

Die Funktion, die die Aktion abruft, wandelt den Eingabezustand in einen PyTorch-Tensor um. Der Zustand wird durch das Politik-Netzwerk verarbeitet, um eine Aktionsverteilung zu erhalten, eine Aktion aus der Verteilung zu entnehmen, um ihre Log-Wahrscheinlichkeit zu berechnen, und schließlich die Aktion in ein mit der Umgebung kompatibles Format zu konvertieren. Dieses Format ist ein Skalar für diskrete Aktionen und ein geclipptes NumPy-Array für kontinuierliche Aktionen. 

Diese Funktion stellt die Schnittstelle des Agenten mit der Umwelt dar, da sie die Auswahl von Aktionen auf der Grundlage von Richtlinien ermöglicht. Die logarithmische Wahrscheinlichkeit ist für die Gradientenberechnungen von TRPO von entscheidender Bedeutung, da sie in den Ersatzverlusten zur Bewertung der politischen Leistung verwendet wird. Durch die Begrenzung von kontinuierlichen Aktionen auf einen Bereich von [-1,1] kann sichergestellt werden, dass die Ergebnisse des Politik-Netzes mit den Erwartungen der Umwelt in Bezug auf begrenzte Aktionen kompatibel sind. Bei kontinuierlichen Maßnahmen sollte die Standardabweichung überwacht werden, um degenerierte Verteilungen zu vermeiden. Bei der verwendeten Dosierungsmethode wird von Eingaben mit einem einzigen Zustand ausgegangen, bei vektorisierten oder mehrdimensionalen Zuständen kann dies jedoch erweitert werden, um Zustände effizienter zu handhaben.

Die Aktualisierung des Wertnetzes wandelt die Eingangszustände in den Q-Wert der Vorhersagen des Politik-Netzes, auch Belohnungen genannt, um. Sie berechnet den mittleren quadratischen Fehlerverlust gegenüber den Zielen und aktualisiert das Wertnetzwerk durch Backpropagation mit dem Adam-Optimierer. Genaue Wertschätzungen verringern die Varianz der politischen Gradienten und verbessern somit die Stabilität der TRPO. Der MSE-Verlust stellt sicher, dass das Wertenetz lernt, die erwartete diskontierte Rendite vorherzusagen, und entspricht somit dem RL-Ziel. Bei der Berechnung der Ziele für das Training des Wertnetzes verwenden wir Ziele mit zeitlicher Differenz. Diese müssen genau berechnet werden, da ungenaue Schätzungen zu instabilen politischen Aktualisierungen führen können.

Die Verlustfunktion ist der Standard-MSE, doch könnte auch Huber-Loss in Betracht gezogen werden, um in Umgebungen/Datensätzen mit hoher Varianz robuster gegenüber Ausreißern zu sein. Die Logik der Formkorrektur scheint ebenfalls geeignet zu sein, kann jedoch bei großen Datensätzen eine Herausforderung darstellen. Dies kann eine Voroptimierung der Formen der Eingaben erfordern, um sicherzustellen, dass sie mit den richtigen Formen vorverarbeitet werden. Auch Gradientenbeschneidung kann über Module wie Torch.nn.utils.clip_grd_norm_ integriert werden, um übergroße Aktualisierungen zu begrenzen und so das Training des Netzes zu stabilisieren.

Die Funktion zur Aktualisierung von Richtlinien ändert Zustände, Aktionen, alte log-Wahrscheinlichkeiten und Belohnungen in Tensoren mit den entsprechenden Formen. Außerdem wird die Verteilung der alten Strategie für die Berechnung der KL-Divergenz ermittelt und die Ersatzverlustfunktion definiert, mit der die erwartete Belohnung unter der neuen Strategie gegenüber der alten Strategie gemessen werden kann. Darüber hinaus berechnet die Aktualisierungsfunktion der Politik den Politik-Gradienten, verwendet den konjugierten Gradienten, um die Suchrichtung zu finden, und bestimmt die Schrittgröße auf der Grundlage der Beschränkung „max-kl“ für die Vertrauensregion. Es führt eine Zeilensuche durch, die sicherstellt, dass die neue Strategie die KL-Divergenzbedingungen erfüllt, und verbessert auch den Surrogatverlust oder kehrt zu den alten Parametern zurück, wenn die Suche fehlschlägt. 

In vielerlei Hinsicht ist dies das Herzstück von TRPO, da es die Optimierung der Vertrauensbereiche implementiert, die ein Gleichgewicht zwischen der Verbesserung der Richtlinien und der Stabilität schafft. Der Ersatzverlust schätzt den Gradienten der Politik, während die KL-Divergenz-Beschränkung sicherstellt, dass es nicht zu großen Politikänderungen kommt, die die Leistung beeinträchtigen können. Mit anderen Worten: Die konjugierte Gradientenmethode löst die Suchrichtung effizient, während die Liniensuche robuste Aktualisierungen gewährleistet.

In TRPO ist der Parameter max-kl entscheidend. Ein zu kleiner Wert, z. B. unter 0,005, kann die Aktualisierungen zu sehr einschränken, was zu einem sehr langsamen Lernen führen kann. Umgekehrt kann ein zu großer Wert, z. B. über 0,05, zu destabilisierenden Aktualisierungen führen, also genau zu dem Problem, das TRPO zu beseitigen versucht. Der Parameter „cg-iters“ (conjugate-gradient iterations) sollte eine ausreichende Größe haben, um Konvergenz zu erreichen. Die Restmenge sollte ebenfalls überwacht werden, um die Genauigkeit der Lösung zu überprüfen.

Die Funktion, die die Parameter der Politik festlegt, aktualisiert die Parameter des Politik-Netzes, indem sie eine Kopie der Werte aus einem reduzierten Vektor anfertigt und sie dann so umformt, dass sie der Größe der einzelnen Parameter entsprechen. Dies ermöglicht die Aktualisierung der nutzerdefinierten TRPO-Parameter, die während der Suche nach konjugierten Gradientenlinien als flacher Vektor berechnet werden. Mit dieser Funktion wird sichergestellt, dass das Politik-Netz nach jeder Aktualisierung optimierte Parameter aufweist.

Die Berechnung der Belohnungen, die im Code als compute-advantage bezeichnet wird, bestimmt die Belohnungen unter Verwendung der Generalized Advantage Estimation (GAE). Dabei wird der Fehler der zeitlichen Differenz für jeden Zeitschritt berechnet. Die Kombination von TD-Fehlern und lambda_ hilft, Verzerrungen und Varianz auszugleichen. Außerdem wird die Belohnung/der Vorteil am Ende jeder Episode zurückgesetzt, wie durch den Parameter dones[t] verfolgt, und diese Belohnungen werden so normalisiert, dass sie einen Mittelwert von Null und eine Einheitsvarianz haben.

Die Verlustfunktion des Surrogats berechnet den Surrogatverlust als den Erwartungswert des Wahrscheinlichkeitsverhältnisses πneu(a∣s)/πalt(a∣s) multipliziert mit Vorteilen. Der Surrogatverlust schätzt das Ziel des Politikgradienten, indem er misst, wie sich die Änderungen der Politik auf die erwarteten Gewinne auswirken. In TRPO wird dieser Verlust maximiert und somit in get-loss negiert, innerhalb der Beschränkung der Vertrauensregion.

Die kl-Divergenzfunktion gibt an, wie weit die alten Politikverteilungen von den neuen Politikverteilungen entfernt sind. Wenn die Aktionen diskret sind, wird eine analytische Formel für kategoriale Verteilungen verwendet. Für kontinuierliche Aktionen verwendet PyTorch Multivariate-Normalverteilungen. Diese Messungen helfen dabei, die TRPO-Beschränkung der Vertrauensregion durchzusetzen.

Die Hessian-Vektorprodukt-Funktion berechnet, wie der Name schon sagt, das Hessian-Produkt, das für die KL-Divergenz bei der konjugierten Gradientenmethode verwendet wird. Bei den Berechnungen wird der Gradient der KL-Divergenz ermittelt, mit dem Eingangsvektor multipliziert und dann der Gradient zweiter Ordnung berechnet. Es fügt eine Dämpfung hinzu, um die numerische Stabilität zu verbessern. Durch Annäherung der Wirkung der Fischer-Informationsmatrix auf einen Vektor ermöglichen wir eine effiziente Berechnung der Suchrichtung in TRPO. Der Dämpfungsterm stellt sicher, dass die Hessian positiv definiert ist und der konjugierte Gradient konvergiert.

Schließlich implementiert die konjugierte Gradientenfunktion die Methode zur Lösung von Hx = g, wobei H die Fischer-Matrix ist, die durch die Funktion hessian_vector_product angenähert wird, und g der Politikgradient ist. Es verfeinert iterativ seine Lösung x oder die Suchrichtung, bis entweder Konvergenz eintritt oder n Iterationsschritte durchgeführt werden.

Testläufe

Wenn wir Forward Walks nur für die drei Merkmalsmuster durchführen, die im letzten Artikel vorwärts gehen konnten, nämlich die Merkmale 2, 3 und 4, erhalten wir die unten stehenden Berichte. Wir testen das Paar EUR USD von 2020.01.01 bis 2025.01.01. Das Training wurde in Python auf den Daten von 805 aus diesem Zeitraum oder vom 2020.01.01 bis 2024.01.01 durchgeführt. 

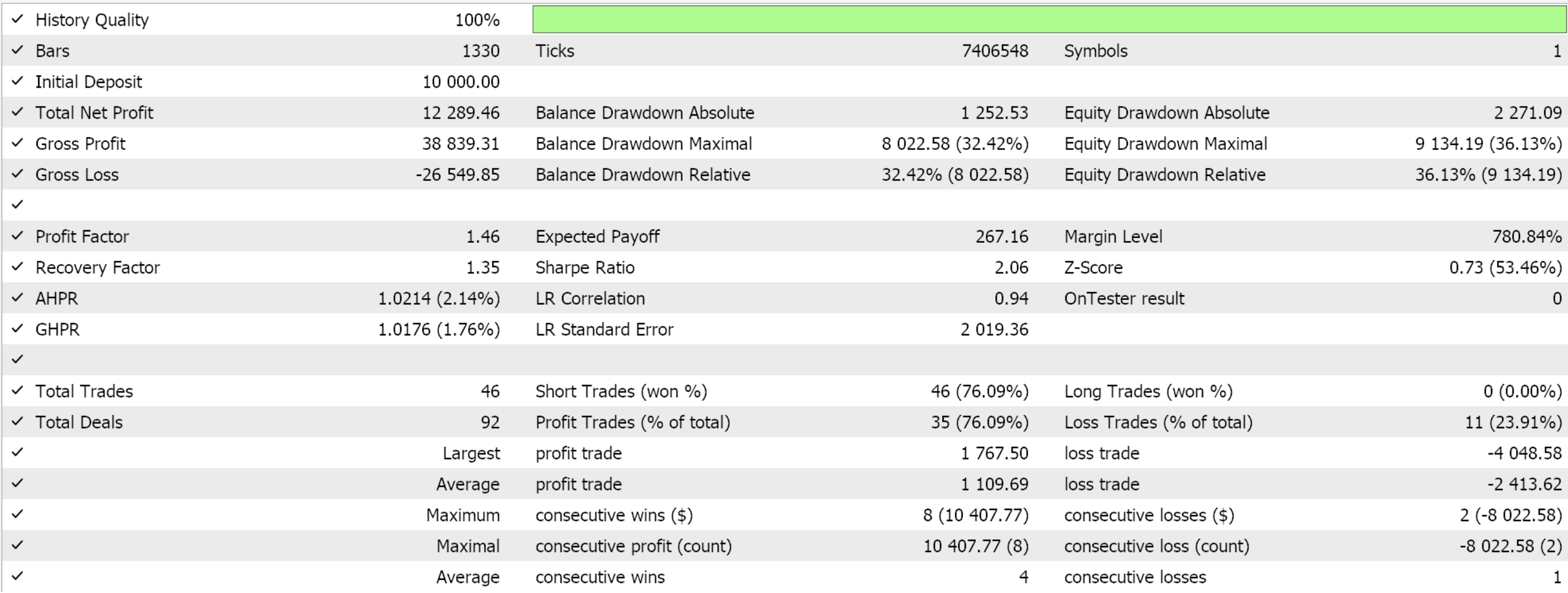
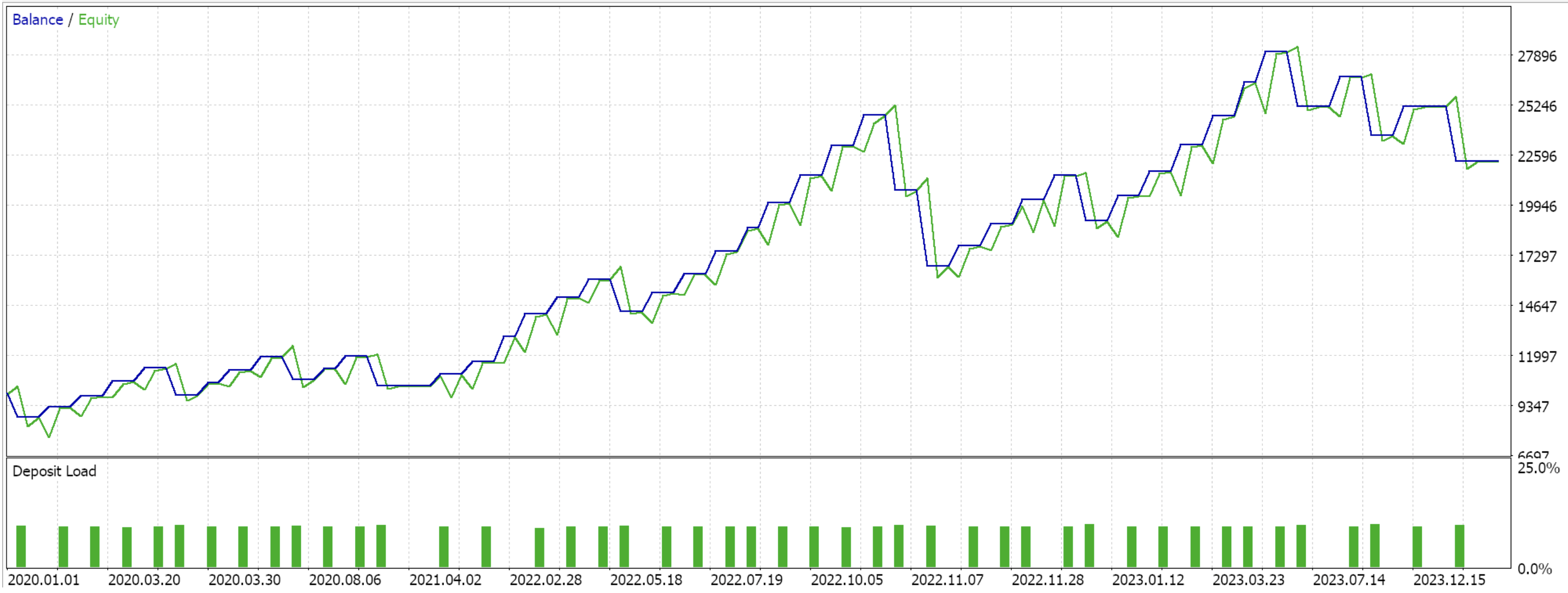
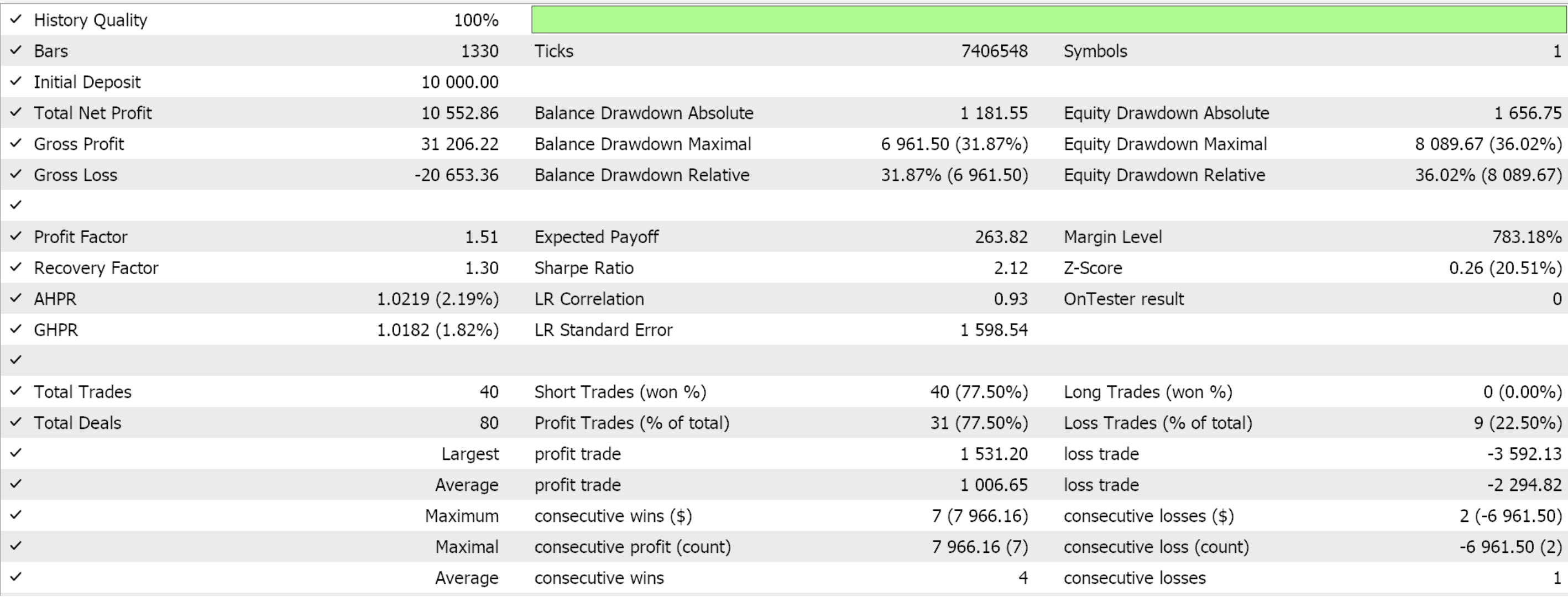
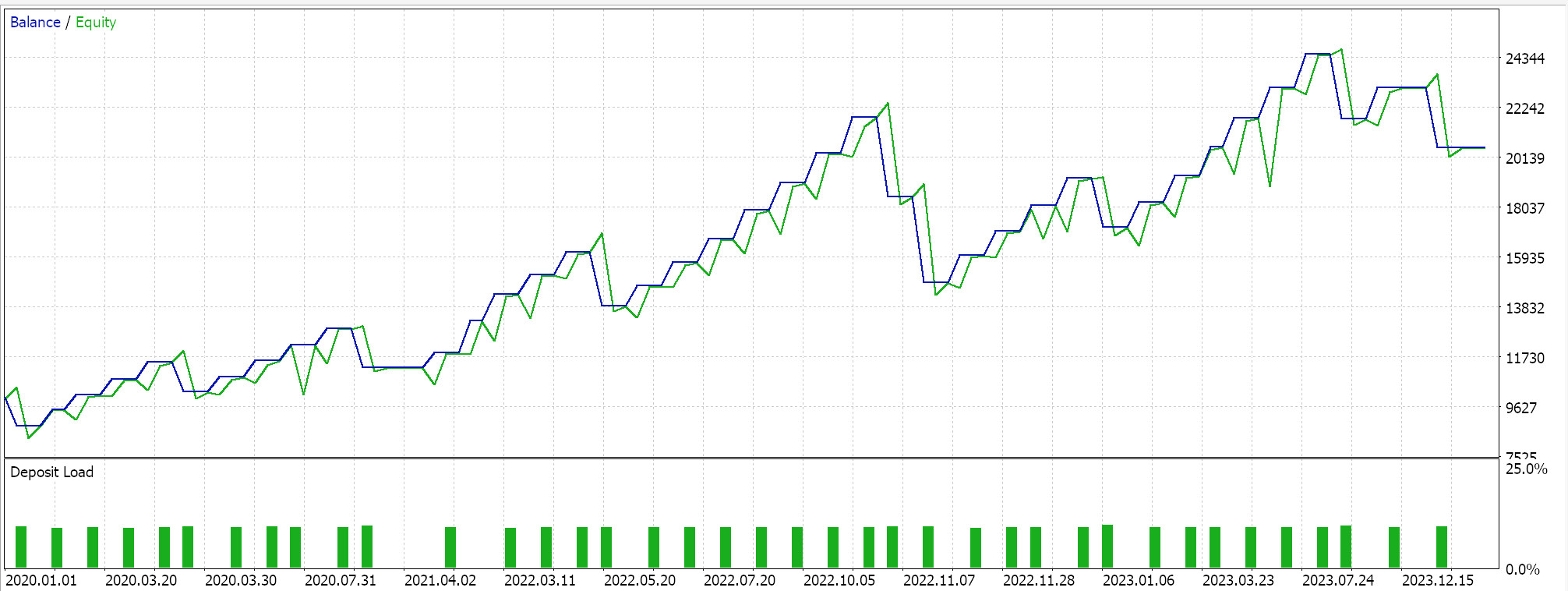
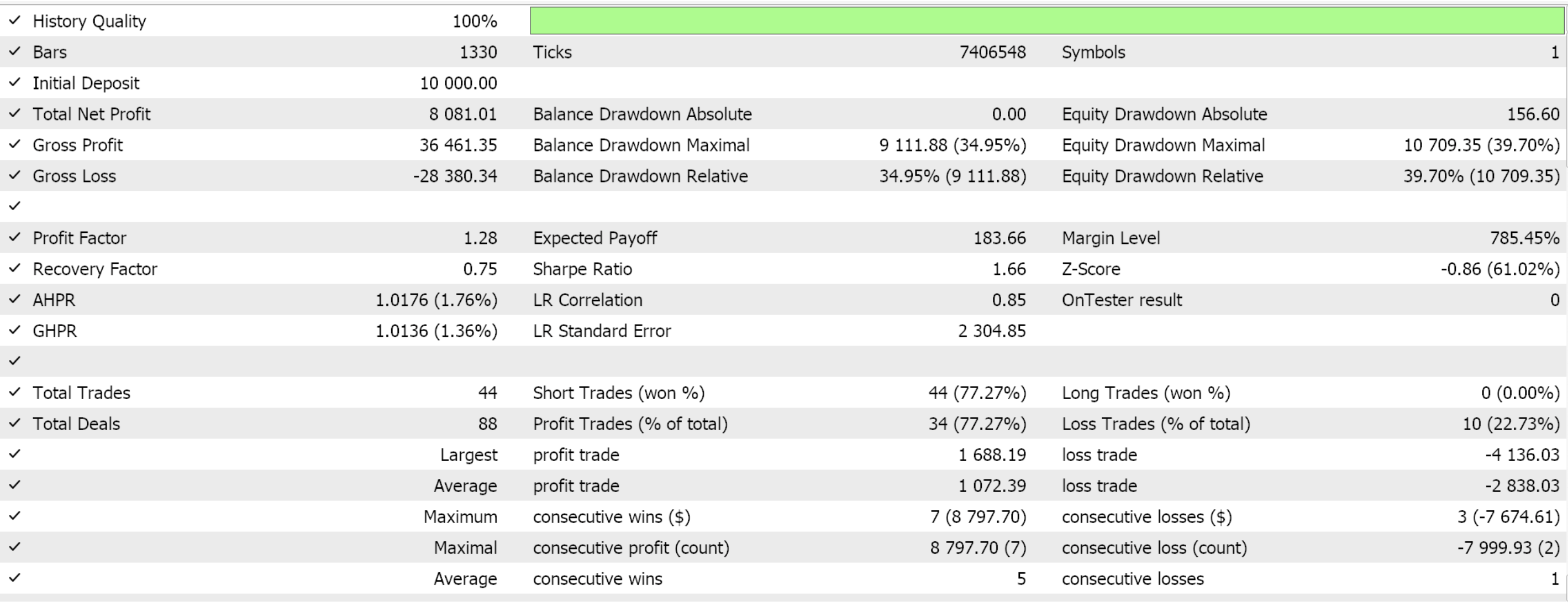
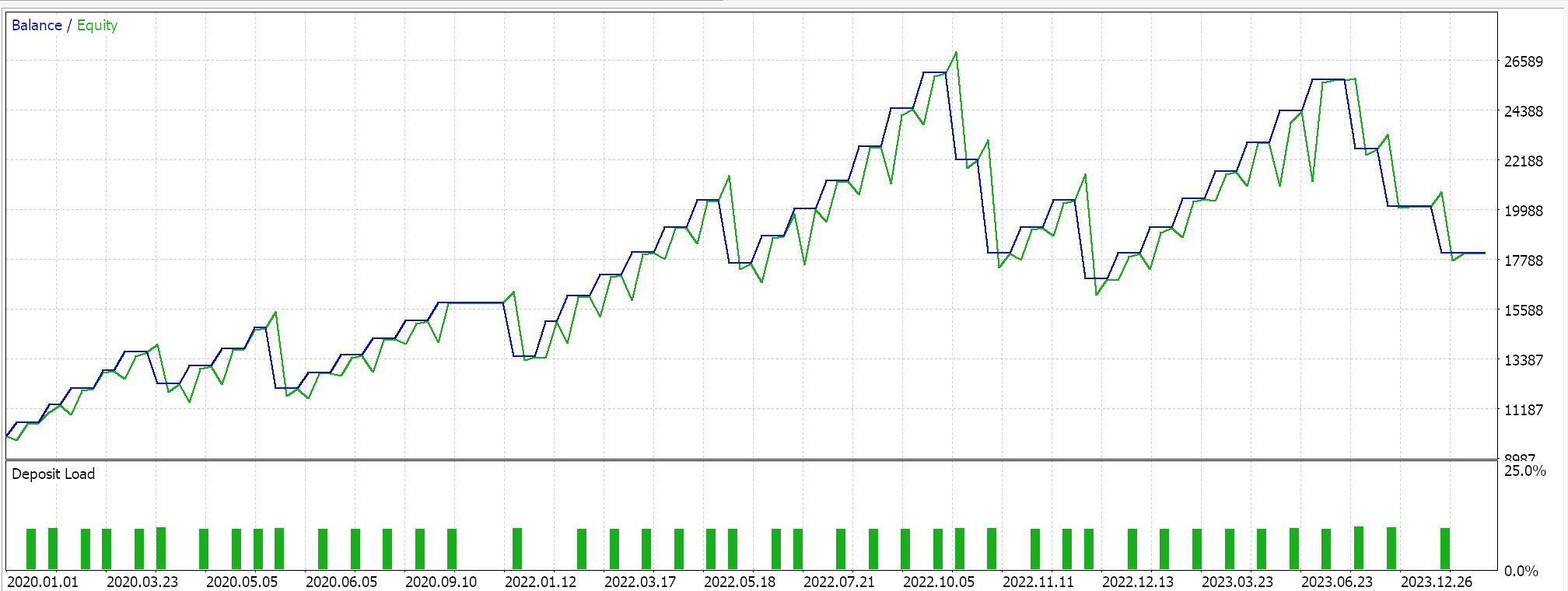
Wenn wir bedenken, dass der Zeitraum für die Vorwärtstest nur bis zum Jahr 2024 reicht, dann scheinen nur die Muster 2 und 3 in der Lage gewesen zu sein, zu bestehen. Wie immer spielen viele Faktoren eine Rolle, und es wird immer empfohlen, vor der Verwendung von Code/Materialien, die in diesen Artikeln vorgestellt werden, eine unabhängige Prüfung durchzuführen. Um Expert Advisors wie den in den obigen Tests verwendeten zusammenzustellen und zu verwenden, muss man Dateien des beigefügten Codes mit dem MQL5-Assistenten verwenden. Für neue Leser gibt es hier und hier eine Anleitung, wie man das macht.

Schlussfolgerung

Im Anschluss an unseren letzten Artikel über die Entwicklung eines Expert Advisors aus einem Modell des überwachten Lernens, das die Muster des ADX und des CCI als Inputs verwendet, haben wir einen weiteren Artikel verfasst. In diesem Artikel werden die gleichen Indikatoren verwendet, jedoch im Rahmen des Verstärkungslernens. RL zielt darauf ab, den früher entwickelten Expert Advisor durch eine vorsichtige Erweiterung seines Lernfensters robuster zu machen.

Ein zusammenfassender Artikel, der für diese Indikatormuster folgen soll, sollte sich mit der Inferenz befassen. Wir verwenden Inferenz hier als Mittel zur Zusammenfassung und „Archivierung“ des Gelernten beim überwachten Lernen und beim Verstärkungslernen. Dieser Artikel enthält Beispiele für diesen Ansatz. Wir überlassen jedoch die Verwendung von Inferenzen dem Leser, da wir zu einem einfacheren Artikelformat zurückkehren werden, das abwechselnd einige Ideen zum maschinellen Lernen enthält. 

Name	Beschreibung
wz_62.mq5	Assistent Assemblierter Expert Advisor, dessen Kopfzeile die enthaltenen Dateien anzeigt
SignalWZ_62.mqh	Nutzerdefinierte Signalklassendatei
61_2.onnx	Feature_2 ONNX Modell für überwachtes Lernen
61_3.onnx	Feature_3 ONNX Modell für überwachtes Lernen
61_4.onnx	Feature_4 ONNX Modell für überwachtes Lernen
62_policy_2.onnx	Feature_2 Reinf. Lernender Akteur
62_policy_3.onnx	Feature_3 Reinf. Lernender Akteur
62_policy_4.onnx	Feature_4 Reinf. Lernender Akteur
62_value_2.onnx	Feature_2 Reinf. Lernender Kritiker
62_value_3.onnx	Feature_3 Reinf. Lernender Kritiker
62_value_4.onnx	Feature_4 Reinf. Lernender Kritiker