Brute-Force-Ansatz zur Mustersuche

Einführung

In diesem Artikel werden wir nach Marktmustern suchen, Expert Advisors basierend auf den identifizierten Mustern erstellen und prüfen, wie lange diese Muster gültig bleiben, wenn sie überhaupt ihre Gültigkeit behalten. Ich denke, dieser Artikel wird für diejenigen, die selbstanpassende Handelssysteme erstellen, äußerst nützlich sein. Ich möchte mit einer Erklärung beginnen, was ich mit dem Konzept der Brute-Force im Zusammenhang mit dem Forex-Handel meine. Im Allgemeinen wollen wir beim Brute-Force-Ansatz eine Zahlenfolge für einen Code oder einen anderen Zweck bestimmen, die es letztendlich ermöglicht, das gewünschte Ergebnis mit der maximalen Wahrscheinlichkeit oder mit der maximal verfügbaren Wahrscheinlichkeit zu erreichen, indem wir diese Folge verwenden. Das gewünschte Ergebnis kann sein, Kryptowährung zu schürfen oder ein Konto oder Wi-Fi-Passwort zu hacken. Der Anwendungsbereich ist sehr groß. Im Fall von Forex sollte unsere Sequenz den maximalen Gewinn bringen und dabei so lange wie möglich funktionieren. Die Sequenz kann von beliebiger Art und Länge sein. Die einzige erforderliche Bedingung ist ihre Effizienz. Der Sequenztyp hängt letztlich von unserem Algorithmus ab.

Was ist so besonders an dieser Technik, dass ich mich entschlossen habe, sie zu behandeln?

Ich versuche immer, meine Gedanken so auszudrücken, dass sie die maximale praktische Anwendung für andere Händler haben. Warum mache ich das? Das ist eine gute Frage. Ich möchte meine Erfahrungen mit anderen Händler teilen. Ich würde mich freuen, wenn jemand meine Ideen nutzen und etwas Interessantes und Profitables umsetzen könnte, unabhängig davon, ob ich etwas davon habe oder nicht. Ich verstehe natürlich, dass die Ideen vielleicht nicht ganz von mir sind und dass ich das Rad neu erfinden könnte. Ich glaube, dass wir Erfahrungen austauschen und so produktiv wie möglich zusammenarbeiten sollten. Vielleicht ist das das Geheimnis des Erfolgs. Es ist schwer, etwas Bedeutendes alleine zu erreichen, wenn man isoliert von allen anderen arbeitet. Meiner Meinung nach ist das Thema Muster von fundamentaler Bedeutung für das Verständnis der Physik des Marktes. Ihre Karriere als Händler kann genau vom Verständnis der grundlegenden Ideen abhängen, auch wenn der Ausdruck "Karriere als Händler" vielleicht komisch klingt. Ich hoffe, dass ich für die Leute, die diese Fragen erforschen, nützlich sein kann.

Über Brute Force und seine Unterschiede zu Neuronalen Netzwerken

Ein Neuronales Netzwerk ist im Grunde auch eine Art von Brute Force. Aber seine Algorithmen unterscheiden sich stark von einfachen Brute-Force-Algorithmen. Ich werde nicht auf die Details spezifischer neuronaler Netzwerkarchitekturen und ihrer Elemente eingehen, sondern versuchen, eine allgemeine Beschreibung zu geben. Ich denke, wenn wir an einer bestimmten Architektur festhalten, schränken wir die Fähigkeiten unseres Algorithmus im Voraus ein. Eine feste Architektur ist eine irreparable Einschränkung. Ein Neuronales Netzwerk ist in unserem Fall eine Art Architektur einer möglichen Strategie. Daher entspricht die Konfiguration eines neuronalen Netzes immer einer bestimmten Datei mit einer Netzwerkstruktur. Diese verweist immer auf eine Sammlung von bestimmten Einheiten. Es ist wie bei einem 3D-Drucker: Man definiert einen Gegenstand und der Drucker wird ihn produzieren. Ein Neuronales Netz ist also ein allgemeiner Code, der ohne eine Karte keinen Sinn macht. Das ist so, als würde man eine beliebige fortgeschrittene Programmiersprache nehmen und einfach ein leeres Projekt erstellen, ohne alle seine Möglichkeiten zu nutzen. Das Ergebnis ist, dass die leere Vorlage nichts tut. Das Gleiche gilt für das neuronale Netzwerk. Im Gegensatz zur Brute-Force-Methode kann ein Neuronales Netz eine fast unbegrenzte Variabilität der Strategien, eine beliebige Anzahl von Kriterien und eine höhere Effizienz bieten. Der einzige Nachteil dieses Ansatzes ist, dass die Effizienz stark von der Codequalität abhängt. Eine steigende Systemkomplexität kann zu einer erhöhten Ressourcenintensität des Programms führen. Daher wird unsere Strategie in eine Netzwerkstruktur umgewandelt, die ihr Äquivalent ist. Das Gleiche wird beim Brute-Force-Ansatz gemacht, aber hier arbeiten wir mit einer einfachen Sequenz einiger Zahlen. Diese Sequenz ist viel einfacher als eine Netzwerkstruktur, sie ist leichter zu berechnen, aber sie hat auch eine Grenze in Bezug auf die Effizienz. Das folgende Schema zeigt die obige Erklärung.

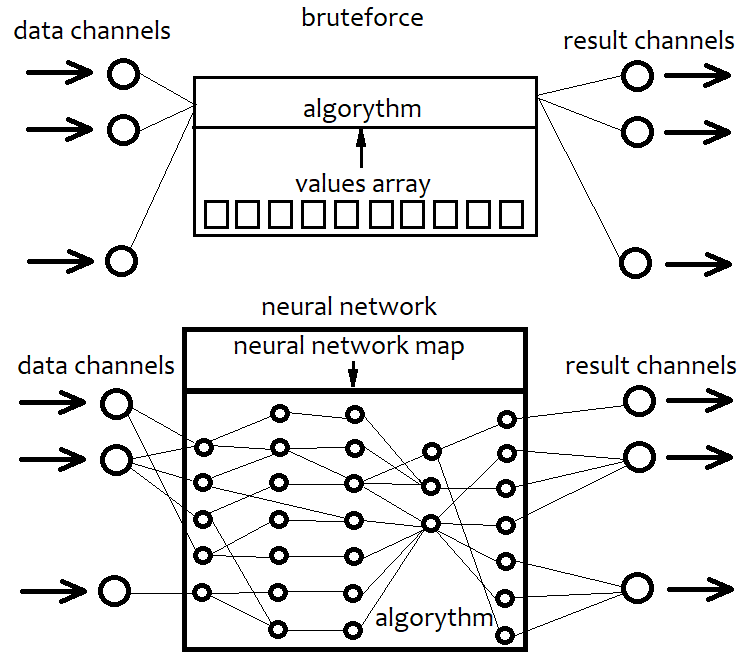
Mit anderen Worten: Bei einem Brute-Force-Ansatz wählen wir eine Zahlenfolge aus, die mit unserem Code interagiert und unterschiedliche Ergebnisse liefert. Da der Algorithmus jedoch feststeht, ist seine gesamte Flexibilität in dem Array von Zahlen enthalten. Seine Länge ist fest und die Struktur ist sehr einfach. Wenn wir mit einem neuronalen Netzwerk arbeiten, suchen wir nach einer Netzwerkstruktur, die das beste Ergebnis liefert. In jedem Fall suchen wir nach einer bestimmten Sequenz von Bytes, oder den Daten, die schließlich in den resultierenden Algorithmus umgewandelt werden. Der einzige Unterschied liegt in den Fähigkeiten und der Komplexität. 

Mein Brute-Force- und Optimierungsalgorithmus

Ich habe in meinem Algorithmus die multivariate Taylor-Erweiterung verwendet. Hier ist der Grund, warum ich diesen Ansatz gewählt habe. Ich wollte einen Algorithmus erstellen, der so variabel wie möglich ist und sehr einfach ist. Ich wollte mich nicht an eine bestimmte Formel halten, da jede Funktion letztendlich in eine Taylorreihe oder eine Fourierreihe expandiert werden kann. Ich denke, die Fourier-Reihe ist für diesen Zweck nicht sehr geeignet. Außerdem bin ich mit dem mehrdimensionalen Äquivalent nicht vertraut. Deshalb habe ich mich für die erste Variante entschieden. Außerdem ist ihre Implementierung viel einfacher. Eine eindimensionale Taylor-Reihe sieht wie folgt aus:

Y = Cs[0]+Cs[1]*(x-x0)^1 + Cs[2]*(x-x0) ^2 + ... + Cs[i]*(x-x0)^n

wobei die Koeffizienten vor den Potenzen als Ableitungen der Ordnung von 0 bis n dienen. Dies kann in eine einfachere Form umgewandelt werden, indem die Klammern erweitert werden:

Y = C[0]+C[1]*x^1 + C[2]*x^2 + ... + C[i]*x^n + ...= Sum(0,+Unendlich)(C[i]x^i)

In diesem Fall haben wir nur eine Variable. Diese Reihe kann jede kontinuierliche und differenzierbare Funktion in der Nähe eines beliebigen ausgewählten x0-Punktes imitieren. Je mehr Terme die Formel hat, desto genauer beschreibt sie unsere Funktion. Wenn ihre Anzahl unendlich ist, dann würde unsere Funktion perfekt entsprechen. Ich werde hier nicht zeigen, wie man eine beliebige Funktion in eine Taylorreihe in der Nähe eines beliebigen Punktes erweitert. Diese Information ist in jedem Mathebuch zu finden. Aber die eindimensionale Variante reicht für uns nicht aus, da wir die Daten von mehreren Balken verwenden wollen, um die Variabilität der allgemeinen Formel zu erhöhen. Deshalb soll die mehrdimensionale Variante verwendet werden:

Y = Sum(0,+Unendlich)( C[i]*Arbeitsvariante(x1^p1*x2^p2...*xN^pN) ) 

Andere Varianten der Formel sind eher schwierig. Sie folgt der gleichen Logik wie die eindimensionale Variante. Wir müssen alle möglichen partiellen Ableitungen angeben. Wenn wir die höchste Potenz der Terme begrenzen, dann können wir die Gesamtzahl solcher Terme durch Kombinationen und Summen berechnen. Unser Algorithmus wird die Begrenzung des höchsten Grades nutzen, um den Verbrauch von Rechenressourcen zu begrenzen. 

Aber das ist immer noch nicht genug, um unsere Brute-Force-Funktion bequemer zu machen. Es ist besser, den ersten Term C[0] zu entfernen und der Funktion eine maximale Symmetrie in Bezug auf negative oder positive Werte zu geben, die wir in sie einspeisen werden. Außerdem wäre es eine bequeme Lösung, einen positiven Funktionswert als Kaufsignal und einen negativen Wert als Verkaufssignal zu interpretieren. Eine Erhöhung der unteren Grenze des Moduls dieses Signals sollte idealerweise zu einer Erhöhung des erwarteten Gewinns und des Gewinnfaktors führen, wird aber auch unweigerlich zu einer Verringerung der Anzahl der Signale führen. Je näher die Funktion an diesen Anforderungen liegt, desto besser. Wir werden in die Funktionen (Close[i]-Open[i]) Werte einer bestimmten Kerze als Variablen eingeben.

Was wir nun tun müssen, ist, zufällige Varianten dieser Koeffizienten zu erzeugen und zu prüfen, wie sich die Varianten im Tester verhalten. Natürlich wird niemand diese Koeffizienten manuell iterieren. Wir brauchen also einen Expert Advisor, der solche Varianten erzeugen kann und dabei Tausende solcher Varianten verwaltet, oder eine Lösung eines Drittanbieters, der einige der Funktionen des Strategietesters implementiert. Ursprünglich musste ich einen solchen Expert Advisor in MQL4 schreiben - dieser EA ist dem Artikel zusammen mit einer Anleitung beigefügt, so dass er von jedem verwendet werden kann. Ich werde aber eine andere Anwendung verwenden, die ich in C# entwickelt habe. Leider kann ich diese Anwendung aus offensichtlichen Gründen nicht frei zugänglich zur Verfügung stellen. Ihre Möglichkeiten gehen weit über den Bereich der Forschung hinaus. Ich werde aber alle Möglichkeiten beschreiben und demonstrieren, so dass jeder, der programmieren kann, diese Anwendung nachbauen kann. Die Screenshots werden später in diesem Artikel zur Verfügung gestellt, wo wir die Ergebnisse der Operation analysieren werden.

Hier sind die Hauptfunktionen der Anwendung. Die Suche nach Arrays von Koeffizienten wird in 2 Stufen durchgeführt. Die erste Stufe durchsucht einfach einen geladenen Kurs in Arrays, die entweder den maximalen erwarteten Gewinn oder den maximalen Gewinnfaktor bei der nächsten Kerze erzeugen. Es werden ähnliche Durchläufe wie beim Strategietester ausgeführt. Tatsächlich wird einfach versucht, eine Formel zu finden, die die Richtung des nächsten Balkens mit maximaler Genauigkeit vorhersagt. Eine bestimmte Anzahl der besten Ergebnisse wird im Speicher und auf der Festplatte als Array-Varianten gespeichert. Es kann nur ein Teil der Preise getestet werden - hier sollte Prozent relativ zur geladenen Kursdatei angegeben werden. Dies wird verwendet, um das Verwerfen von Zufallswerten in der zweiten Stufe zu ermöglichen. In der zweiten Stufe werden Marktaufträge und eine Gleichgewichtskurve simuliert - dies geschieht für den gesamten geladenen Bereich. Gleichzeitig wird ein sanfter Anstieg der Signalgröße und eine Suche nach besseren Qualitätsoptionen durchgeführt. Diese Stufe verfügt auch über verschiedene Filter, mit denen wir glattere Charts erhalten können. Je glatter das Diagramm ist, desto besser ist die gefundene Formel. Nach Abschluss der zweiten Suchstufe gibt es eine bestimmte Anzahl der besten Optionen, die visuell in der Liste zu sehen sind. Nachdem Sie die gewünschte Option ausgewählt haben, können Sie in der dritten Registerkarte einen Handelsroboter für MetaTrader 4 und MetaTrader 5 generieren. Der EA wird nach einer vorkompilierten Vorlage generiert, in der die erhaltenen Zahlen an bestimmten Stellen angegeben sind.

Erstellen einer einfachen Vorlage für die Aufgabe

Die Vorlage wurde ursprünglich in MQL4 erstellt und dann nach MQL5 konvertiert. Der Code ist für beide Plattformen angepasst (ähnlich wie der Code im vorherigen Artikel). Ich versuche, diese Kompatibilität zu gewährleisten, um weniger Zeit für die Anpassung der Lösung aufzuwenden. Um vordefinierte Arrays wie in MQL4 zu verwenden, sollte etwas zusätzlicher Code zum Expert Advisor hinzugefügt werden, der in meinem vorherigen Artikel beschrieben wurde. Lesen Sie also bitte diesen Artikel für Details. Dieses Wissen ist für diesen Artikel erforderlich. Eigentlich ist es nicht schwierig, und jeder Entwickler kann diese Kompatibilität implementieren. Beginnen wir mit der Beschreibung der Variablen und Arrays, die zur Zeit der Robotergenerierung automatisch gefüllt werden.

double C1[] = { %%%CVALUES%%% };//array of coefficients
int CNum=%%%CNUMVALUE%%%;//number of candlesticks in the formula
int DeepBruteX=%%%DEEPVALUE%%%;//formula depth
int DatetimeStart=%%%DATETIMESTART%%%;//start point in time
input bool bInvert=%%%INVERT%%%;//inverted trading
input double DaysToTrade=%%%DAYS%%%;//number of days into the future to trade

Hier ist C1 das Array der Koeffizienten vor den Graden, die wir ausgewählt haben. CNum ist die Anzahl der letzten Kerzen auf dem Preisdiagramm, die zur Berechnung des Polynomwertes verwendet werden. Als Nächstes kommt die Tiefe der Formel, die der maximale Grad des mehrdimensionalen Polynoms ist. Ich verwende in der Regel 1, da im Gegensatz zur eindimensionalen Taylorreihe die mehrdimensionale mit zunehmendem Grad eine viel größere Berechnungskomplexität aufweist, da die Gesamtzahl der Koeffizienten mit zunehmendem Grad deutlich steigt. Der Startpunkt in der Zeit wird benötigt, um die EA-Operationszeit zu begrenzen, da eine solche Begrenzung die Information darüber verwendet, wo die Operation begonnen hat. Die inverse Funktion wird verwendet, um sicherzustellen, dass das Polynom in der richtigen Richtung arbeitet. Wenn wir alle Vorzeichen vor den Gradkoeffizienten invertieren, dann ändert sich das Polynom selbst nicht, während nur die Zahlen, die durch das Polynom ausgegeben werden, ein anderes Vorzeichen haben. Der wichtigste Teil ist hier das Verhältnis der Koeffizienten. Wenn ein negativer Wert des Polynoms Verkaufen und ein positiver Wert Kaufen bedeutet, dann ist die Umkehrung = falsch. Wenn nicht, dann wahr. Wir weisen also den Algorithmus an, "die Werte des Polynoms mit umgekehrtem Vorzeichen zu verwenden". Außerdem ist es besser, diese Variable zu einem Eingabewert zu machen, da wir möglicherweise in der Lage sein müssen, den Handel umzukehren, ebenso wie die Anzahl der Tage für den Handel in der Zukunft.

Wenn Sie die Größe eines Arrays mit Koeffizienten berechnen müssen, können Sie dies wie folgt tun:

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {       
         DeepN(Nums,deepC-1);
         } 
      else 
         {
         NumCAll++;
         }
      }   
   }

void CalcDeepN(int Nums,int deepC=1)//to launch calculations
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ )
      {
      DeepN(Nums,i+1);
      }   
   }

Die fraktale Zwischenfunktion zählt die Anzahl der Terme, die den gleichen Gesamtgrad aller Faktoren haben. Dies geschieht der Einfachheit halber, weil es für uns nicht so wichtig ist, in welcher Reihenfolge die Terme summiert werden. Die zweite Funktion ruft einfach die erste in einer Schleife so oft auf, wie es Arten von Termen gibt. Wenn die mehrdimensionale Reihenentwicklung zum Beispiel auf, sagen wir, 4 begrenzt ist, dann rufen wir die erste Funktion mit allen natürlichen Zahlen von 1 bis 4 auf.

Die Funktion, die den Wert des Polynoms berechnen wird, ist fast identisch. Allerdings wird in diesem Fall das Array selbst erzeugt und seine Größe muss nicht festgelegt werden. So sieht das Ganze aus:

double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC=1,double Val0=1.0)//calculate the sum of one degree
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;      
         Deep(Ci0,Nums,deepC-1,ValW);
         } 
      else 
         {
         ValStart+=Ci0[NumC]*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }   
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)//calculate the entire polynomial
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ )
      {
      Deep(Ci0,Nums,i+1);
      }   
   }

Alles, was berechnet wird, wird zu ValStart hinzugefügt, d. h. das Ergebnis wird zu einer globalen Variablen hinzugefügt. Eine weitere globale Variable wird benötigt - ValW. Sie wird verwendet, um das bereits vorhandene Produkt mit einem Wert zu multiplizieren. In unserem Fall ist dies die Bewegung des entsprechenden Balkens in Punkten. Die Bewegung kann sowohl nach oben als auch nach unten erfolgen, was durch das Vorzeichen angezeigt wird. Diese Funktionen haben also eine sehr interessante Struktur. Sie rufen sich selbst im Inneren auf, und die Anzahl und Struktur dieser Aufrufe ist immer unterschiedlich. Das ist eine Art von Aufrufbaum. Ich verwende diese Funktionen sehr gerne, da sie sehr variabel sind. Diesmal haben wir die mehrdimensionale Taylorreihe auf eine einfache und elegante Weise implementiert.

Es ist auch möglich, eine zusätzliche Funktion für den Fall zu implementieren, dass nur eine eindimensionale Version des Polynoms verwendet wird. In diesem Fall wird die gesamte Reihe stark vereinfacht. Sie verwandelt sich in eine Summe von Koeffizienten, multipliziert mit der Bewegung eines der Balken im ersten Grad. Ihre Anzahl wird identisch mit der Anzahl der verwendeten Balken. Dadurch werden alle Berechnungen vereinfacht. Wenn der Grad eins ist, dann wird eine vereinfachte Version verwendet. Ansonsten wird eine universellere Methode für jeden Grad verwendet.

double Val;
double PolinomTrade()//optimized polynomial
   {
   Val=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<ArraySize(C1); i++ )
         {
         Val+=C1[i]*(Close[i+1]-Open[i+1])/Point;
         }
      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }      
   }

Bei einer einfachen Variante werden die Ergebnisse in die Variable Val eingefügt.

Lassen Sie uns nun die Hauptmethode schreiben, die aufgerufen wird, wenn ein neuer Balken erscheint:

void Trade()
   {
   double Value;
   Value=PolinomTrade();
   
   if ( Value > ValueCloseE)
      {
      if ( !bInvert )
         {
         CloseBuyF();
         }      
      else 
         {
         CloseSellF();
         }
      }
      
   if ( Value < -ValueCloseE)
      {
      if ( !bInvert )
         {
         CloseSellF();
         }      
      else 
         {
         CloseBuyF();
         }      
      }   
   
   if ( double(TimeCurrent()-DatetimeStart)/86400.0 <= DaysToTrade && Value > ValueOpenE && Value <= ValueOpenEMax )
      {
      if ( !bInvert ) SellF();
      else BuyF();
      }
      
   if ( double(TimeCurrent()-DatetimeStart)/86400.0 <= DaysToTrade && Value < -ValueOpenE && Value >= -ValueOpenEMax )
      {
      if ( !bInvert ) BuyF();
      else SellF();
      }

   }

Diese Funktion ist sehr einfach. Alles, was Sie tun müssen, ist, unsere gewünschten Funktionen zum Öffnen und Schließen der Position zu implementieren.

Das Auftauchen des Balkens kann wie folgt erkannt werden:

void CalcTimer()
   {
   if ( Time[1] > PrevTimeAlpha )
       {
       if ( PrevTimeAlpha > 0 )
          {
          Trade();
          }
       PrevTimeAlpha=Time[1];
       }
   }

Ich finde den Code sehr einfach und übersichtlich.

Die von meinem Code generierten Koeffizienten werden anhand der vier oben erläuterten Modelle erstellt. Der Einfachheit halber liegen alle diese Koeffizienten im Bereich [-1,1], weil die Verhältnisse der Werte wichtiger sind als die Werte selbst. Die Funktion, die diese Zahlen aus meinem MQL5-Programmprototyp generiert, sieht wie folgt aus:

   void GenerateC()
      {
      double RX;
      if ( DeepBrute > 1 ) CalcDeepN(CandlesE,DeepBrute);
      else NumCAll=CandlesE;
      for ( int j=0; j<VariantsE; j++ )
         {
         ArrayResize(Variants[j].Ci,NumCAll,0);
         Variants[j].CNum=CandlesE;
         Variants[j].ANum=NumCAll;
         Variants[j].DeepBruteX=DeepBrute;
         RX=MathRand()/32767.0;
         for ( int i=0; i<Variants[j].ANum; i++ )
            {
            if ( RE == RANDOM_TYPE_1 ) Variants[j].Ci[i]=double(MathRand())/32767.0;
            if ( RE == RANDOM_TYPE_2 )
               {
               if ( MathRand()/32767.0 >= 0.5  )
                  {
                  Variants[j].Ci[i]=double(MathRand())/32767.0;                  
                  }
               else
                  {
                  Variants[j].Ci[i]=double(-MathRand())/32767.0;                  
                  }
               }
            if ( RE == RANDOM_TYPE_3 )
               {
               if ( MathRand()/32767.0 >= RX  )
                  {
                  if ( MathRand()/32767.0 >= RX+(1.0-RX)/2.0  )
                     {
                     Variants[j].Ci[i]=double(MathRand())/32767.0;
                     ///Print(Variants[j].Ci[i]);
                     }
                  else
                     {
                     Variants[j].Ci[i]=double(-MathRand())/32767.0;                  
                     }        
                  }
               else
                  {
                  Variants[j].Ci[i]=0.0;                  
                  }
               }
            if ( RE == RANDOM_TYPE_4 )
               {
               if ( MathRand()/32767.0 >= RX  )
                  {
                  Variants[j].Ci[i]=double(MathRand())/32767.0;
                  }
               else
                  {
                  Variants[j].Ci[i]=0.0;                  
                  }
               }                              
            }
         }
      }

Der Brute-Force-Prototyp in MQL4 und MQL5 ist im Anhang des Artikels verfügbar. Ich stelle hier nicht meine Handelsfunktionsimplementierungen zur Verfügung, da der Zweck nur darin besteht, zu zeigen, wie der Ansatz im Rahmen einer Vorlage implementiert werden kann. Wenn Sie daran interessiert sind, die gesamte Implementierung zu sehen, schauen Sie bitte im Anhang nach. Alle Expert Advisors und andere benötigte Materialien sind im Anhang dieses Artikels. Generell hat mein Template ziemlich viele überflüssige Dinge, wie z.B. unnötige Funktionen oder Variablen und könnte irgendwie optimiert werden. Persönlich kümmere ich mich nicht darum. Wenn irgendetwas den Betrieb stört, werde ich es entfernen. Wichtiger ist für mich, dass jetzt alles gut funktioniert. Ich bin ständig dabei, etwas zu entwickeln, daher habe ich nicht die Zeit, jedes Detail zu perfektionieren. Ich sehe auch keinen Grund, alle Prozeduren und Variablen in Klassen zu speichern, obwohl das die Ordnung und Lesbarkeit des Codes verbessern könnte. Die Vorlage ist sehr einfach. Die Dateien mit den Anführungszeichen, die vom Programm verwendet werden, werden von einem speziellen Expert Advisor generiert, der auf der Historie läuft und die Balken-Daten in eine Textdatei mit einer Struktur schreibt, die vom Programm leicht gelesen werden kann. Ich werde den Code dieses EAs hier nicht zur Verfügung stellen, da er leicht entwickelt werden kann.

Verwendung des Programms zum Finden und Analysieren von Mustern

Ich habe drei Marktbereiche für die Analyse ausgewählt, sie haben jeweils eine Monatslänge und folgen aufeinander. EURUSD, M5.

• Erstes Intervall:  2020.01.13 - 2020.02.16
• Zweites Intervall:  2020.02.13 - 2020.03.15
• Drittes Intervall:  2020.03.13 - 2020.04.18

Die Intervalle sind so gewählt, dass der letzte Tag immer der Freitag ist. Und Freitag ist ja bekanntlich der letzte Handelstag der Woche. Die Auswahl der Intervalle auf diese Weise erlaubt es, zwei ganze Tage Zeit zu haben, um nach Mustern zu suchen, bis die Börse wieder mit dem Handel beginnt. Dies ist eine Art kleiner Life Hack. In unserem Fall spielt das keine Rolle, weil wir den EA in einem Tester testen. Ich habe mich entschieden, hier 12 Varianten der gefundenen Muster zu beschreiben. Sechs davon werden Polynome mit einem maximalen Grad von 1 sein. Die anderen sechs werden den maximalen Grad von 2 haben. Ich denke, das ist ausreichend.

So sieht die erste Registerkarte meines Programms aus:

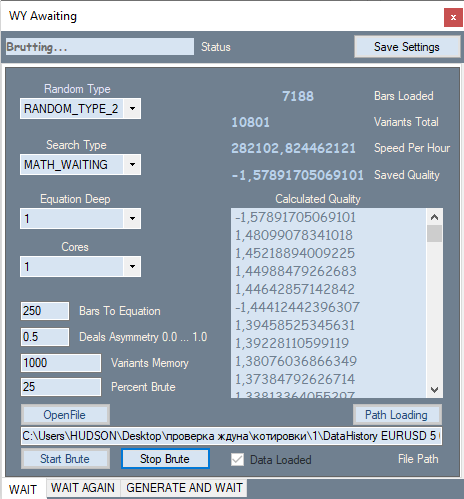
Sie bietet die Möglichkeit, die Art der Zahlengenerierung zu ändern, z. B. nur positiv, positiv und negativ, positiv und Null, positiv, negativ und Null. Das Suchkriterium wird in der zweiten ComboBox konfiguriert. Es gibt zwei mögliche Optionen: Erwartungswert in Punkten und mein Analogon der Gewinnfaktor-Formel. In meiner Formel reicht dieser Wert von -1 bis +1. Außerdem kann es keine Fälle geben, in denen der Gewinnfaktor aufgrund eines Fehlers bei der Nullteilung nicht berechnet werden kann.

P_Factor=(Profit-Loss)/(Profit+Loss).

Dann folgen der maximale Grad des Polynoms und die Anzahl der Prozessorkerne, die für die Berechnungen verwendet werden sollen. In Textblöcken geben Sie die Anzahl der Balken für das Polynom oder die Anzahl der Berechnungen an, sowie den von mir erfundenen Deal-Asymmetrie-Koeffizienten, der der vorherigen Formel sehr ähnlich ist

D_Asymmetry=|(BuyTrades-SellTrades)|/(BuyTrades+SellTrades).

Seine Werte liegen im Bereich von 0 bis 1. Dieser Filter wird benötigt, wenn wir das Programm anweisen müssen, eine ähnliche Anzahl von Kauf- und Verkaufssignalen zu haben, um Situationen zu vermeiden, in denen alle Positionen in die gleiche Richtung während eines globalen Trends ausgeführt werden. Als Nächstes folgt die Anzahl der besten Varianten aus allen gefundenen, die im Speicher gespeichert werden sollen, sowie welcher Prozentsatz des geladenen Kurses für die Brute-Force-Iteration verwendet werden soll. Dieser Abschnitt wird ab dem letzten Balken durch die Eröffnungszeit gemessen, und der Abschnitt dahinter wird für die Optimierung verwendet. Den Rest der Indikatoren und die Liste mit Varianten werde ich nicht erklären, da sie einfach genug sind.

Die zweite Registerkarte sieht wie folgt aus:

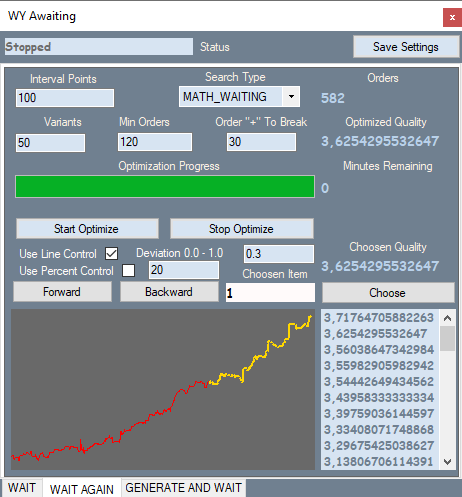
Die Registerkarte entspricht der ersten Variante für den ersten Abschnitt des Roboters. Sie können die Grafik in meinem Programm mit der Grafik des Testers vergleichen. Dieser wird im Folgenden dargestellt. Aufträge in dem Teil des Angebots, in dem die Brute-Force durchgeführt wurde, sind gelb dargestellt, andere sind rot. Ich werde hier keine Screenshots von allen Varianten zur Verfügung stellen - alle sind im Anhang verfügbar.

Schauen wir uns an, was sich in der Registerkarte befindet. Intervallpunkte — Aufteilung des Intervalls der Werte unseres Polynoms. Wenn wir auf der ersten Registerkarte Brute-Force anwenden, werden die Hauptparameter der Variante sowie der Modulo-Maximalwert dieses Polynoms berechnet. So kennen wir das Wertefenster des Polynoms und können dieses Fenster in gleiche Teile aufteilen, wobei wir den Wert schrittweise erhöhen und versuchen, stärkere Signale zu erkennen. Dies geschieht in der zweiten Registerkarte. Diese Registerkarte enthält auch den Suchtyp und die Anzahl der besten Varianten, die im Optimierungsspeicher abgelegt werden. Weitere Filter erlauben uns, unnötige Varianten herauszufiltern, die nicht in unsere Definition eines Musters passen. Line Control ermöglicht für jede Variante einen zusätzlichen Durchlauf, in dem die relative Abweichung der Linie des Graphen von der geraden Linie, die den Anfang und das Ende des Graphen verbindet, berechnet wird. 

Deviation = Max(|Profit[i]-LineProfit[i]|)/EndProfit.

Dabei ist Profit[i] der Wert der Saldenkurve an der i-ten Stelle, LineProfit[i] ist der gleiche Wert auf der Geraden, EndProfit ist der Wert am Ende der Grafik.

Alle Werte werden in Punkten gemessen. Use Percent Control ist ein Prozentsatz des roten Teils des Charts (ich habe diesen Filter in diesem Fall nicht verwendet). Es gibt auch einen Filter für die Mindestanzahl von Aufträgen.

Die folgende Abbildung zeigt die Registerkarte "Bot-Generierung":

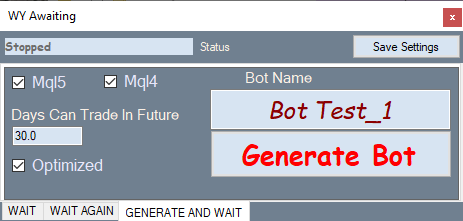
So funktioniert es: Wählen Sie die gewünschte Variante in der Optimierungs-Registerkarte, wechseln Sie zu dieser Registerkarte und generieren Sie einen Expert Advisor.

Lassen Sie uns nun die generierten Bots im Strategietester des MetaTrader 4 testen. Ich habe ihn gewählt, weil er es erlaubt, den Spread gleich 1 zu setzen und damit seinen Einfluss auf die Chartdarstellung praktisch zu eliminieren. Tatsächlich wird der erwartete Payoff der Mehrheit der auf diese Weise gefundenen Roboter etwas höher sein als der durchschnittliche Spread auf einem Paar, so dass wir nicht in der Lage wären, Muster mit einem kleinen erwarteten Payoff visuell zu analysieren. Jede Variante wurde etwa zwei Stunden lang "brute-forced" und optimiert, was für das Finden eines hochwertigen Musters nicht ausreicht. Es ist besser, es ein oder zwei Tage dauern zu lassen. Aber das reicht für diesen Artikel, der darauf abzielt, die gefundenen Muster zu analysieren und nicht die besten von ihnen zu finden. Wenn Sie meine Roboter im Tester testen wollen, achten Sie bitte auf die Variable DaysToTrade. Ihr Wert ist standardmäßig auf 3 Tage eingestellt. Daher kann es sein, dass es nach dem Brute-Force-Abschnitt fast nicht .gehandelt wird.

Wenden wir uns zunächst den Roboter zu, die auf der Basis eines Polynoms ersten Grades generiert wurden.

Erster Abschnitt.  2020.01.13 - 2020. 02.16

Roboter 1:

                                                             

Brute-Force-Teil

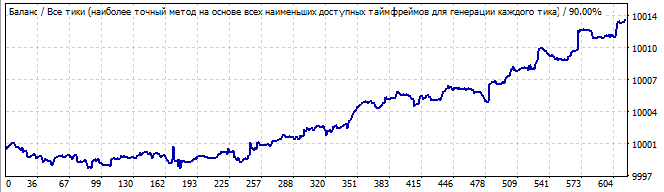
                                                              10 Tage in die Zukunft 

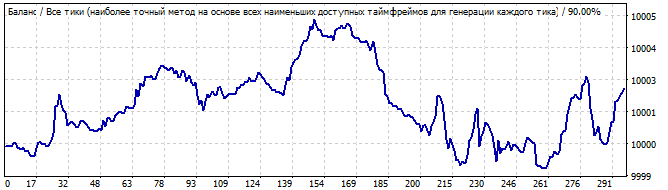
Die erste Grafik zeigt eine Variante aus dem Screenshot der zweiten Registerkarte meines Programms. Das zweite Diagramm ist ein Test desselben Roboters über 10 Tage in die Zukunft. Ich denke, 10 Tage sind genug, um zu sehen, wie es funktioniert. Wie Sie sehen können, setzt sich das Muster für einige Zeit fort, und dann dreht es sich plötzlich und geht in die entgegengesetzte Richtung. Man könnte meinen, dass dieses Muster ausreichen würde, um zwei oder drei Tage lang Gewinn zu erzielen. Lassen Sie uns den zweiten Roboter im gleichen Marktbereich betrachten:

                                                             

Brute-Force-Teil

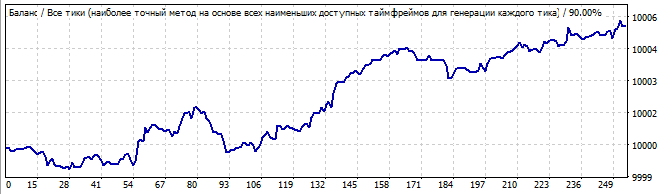
                                                             10 Tage in die Zukunft

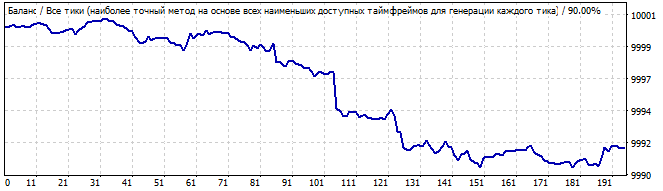
Hier ist das Ergebnis nicht so glatt. Warum wohl? Es wurde erwartet, dass das Muster ein oder zwei Tage lang funktioniert, aber es beginnt von der ersten Sekunde an abwärts zu gehen, obwohl die Umkehrung ziemlich glatt ist. Wahrscheinlich ist dies nicht das Ergebnis, das Sie erwartet haben. Aber es kann erklärt werden. Wir werden später darauf zurückkommen.

Gehen Sie nun zum zweiten Testintervall über.  2020.02.13 - 2020.03.15

Der dritte Roboter:

                                                             

Brute-Force-Teil

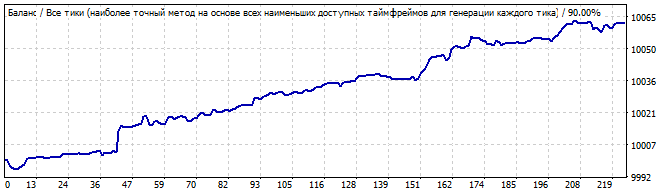
                                                             10 Tage in die Zukunft

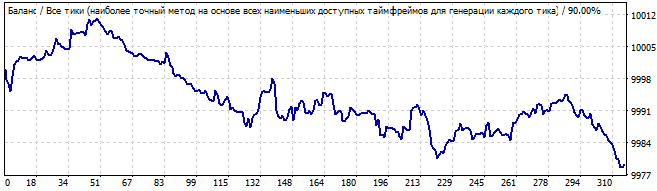
Dieses Mal sieht die Situation besser aus. Das Diagramm ist flach und kommt einer geraden Linie sehr nahe. Dies deutet darauf hin, dass das Muster stabil ist und wahrscheinlich für einige Zeit anhalten wird. Und es hat sich fortgesetzt. Die Bewegung in der Zukunft ähnelt ebenfalls einer Linie, was bedeutet, dass die vielen Parameter des Musters auch in der Zukunft weiter funktionieren.

Hier ist der vierte Roboter:

                                                             

Brute-Force-Teil

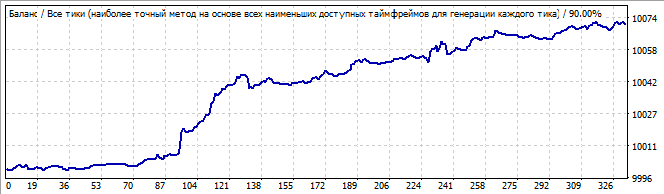
                                                             10 Tage in die Zukunft

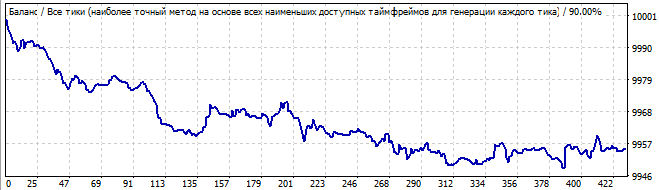
Er hat eine ziemlich gute Aufwärtsbewegung, und alles sieht glatt und stabil aus, mit Ausnahme des starken Anstiegs am Anfang des Charts. Aber dieser Anstieg sollte nicht ignoriert werden: diese Asymmetrie deutet darauf hin, dass dies nur ein Zufall oder ein zufälliges Ergebnis sein kann. Natürlich sehen wir in der Zukunft eine Umkehrung des gesamten Musters in die entgegengesetzte Richtung.

Gehen wir nun zum dritten Testintervall über.  2020.03.13 - 2020.04.18

Fünfter Roboter:

                                                             

Brute-Force-Teil

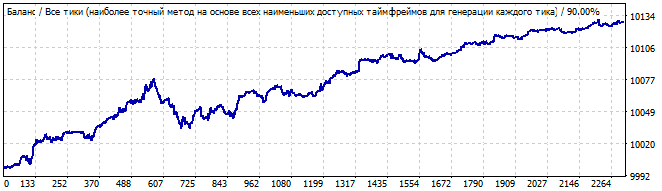
                                                             10 Tage in die Zukunft

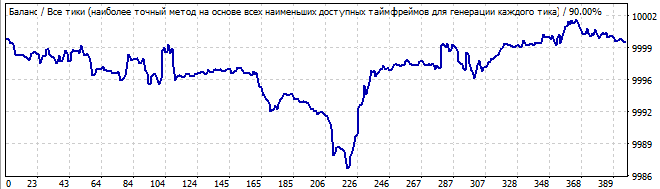
Die Situation ist ähnlich. Es zeigt sichtbare Asymmetrie, Wellen am Anfang und Dämpfung am Ende. Dies sieht nicht wie ein zuverlässiges Muster aus. Ich würde die Fortsetzung des Musters nicht handeln. Auch hier sehen wir in der Zukunft eine sofortige Umkehrung des Graphen und eine Umkehrung der gesamten Formel. Ich werde den sechsten Roboter hier nicht zeigen - sein Graph ist im Archiv verfügbar. Er ist den obigen Graphen sehr ähnlich.

Lassen Sie uns nun die Roboter testen, die auf einem Polynom zweiten Grades basieren.

Erster Abschnitt.  2020.01.13 - 2020. 02.16

Der siebte Roboter sieht folgendermaßen aus:

                                                         

   

Brute-Force-Teil

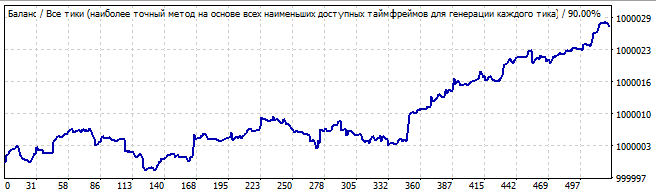
                                                             10 Tage in die Zukunft

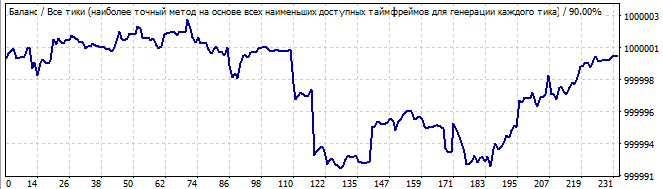
Die Besonderheit dieser Roboter ist, dass sie im Brute-Force-Intervall besser arbeiten. Im Intervall, das dem Brute-Force-Teil vorausgeht, sind die Ergebnisse nicht so gut. Das Brute-Force-Intervall zeigt immer eine scharfe positive Halbwelle. Aber das restliche Intervall ist ein einziges Durcheinander. Dies sind die Ergebnisse einer bestimmten Formel, das Verhalten ist ähnlich. Es gibt eine kleine Zufälligkeit am Anfang, gefolgt von einer Bewegung in die entgegengesetzte Richtung.

Die achte Variante:

                                                             

Brute-Force-Teil

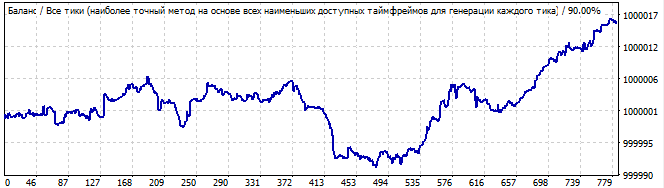
                                                             10 Tage in die Zukunft

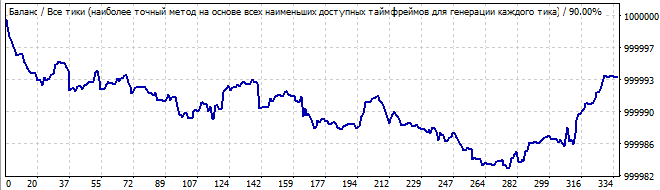
Es ist viel schlimmer. Es gibt keine globalen Muster, aber es zeigt trotzdem eine Aufwärtsbewegung im Brute-Force-Intervall. Es handelt sich nicht um ein Muster, also dreht sich der Graph nach unten.

Nun prüfen Sie das zweite Testintervall.  2020.02.13 - 2020.03.15

Der neunte Roboter:

                                                             

Brute-Force-Teil

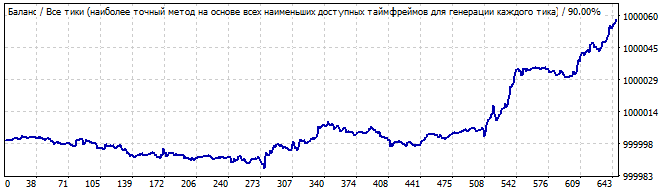
                                                             10 Tage in die Zukunft

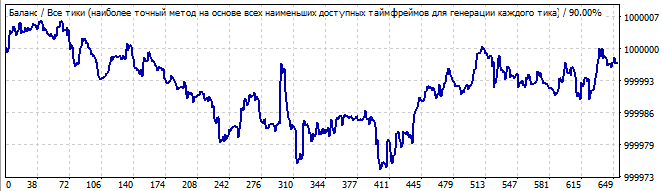
Ich sehe den Beginn einer Welle in der ersten Grafik und ihr Ende in der Zukunft. Es gibt kein globales Muster, aber die Umkehrung ist glatt genug, um zu versuchen, davon zu profitieren.

Der zehnte Roboter ist wie folgt:

                                                             

Brute-Force-Teil

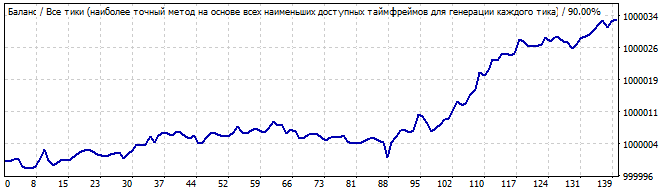
                                                             10 Tage in die Zukunft

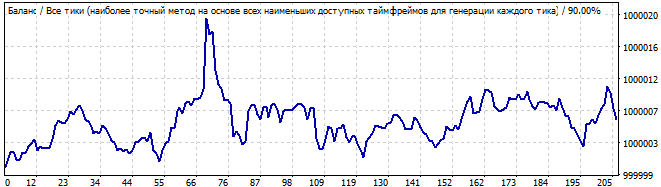
Diesmal ist die Grafik besser. Diesmal ähnelt sie einem Muster. Das Muster hält maximal ein bis zwei Tage an. Ich würde jedoch nicht riskieren, nach einem solchen Graphen zu handeln. Er weist eine signifikante Abweichung von einer Geraden auf. 

Nun gehen wir zum dritten Testintervall.  2020.03.13 - 2020.04.18 Elfter Roboter:

Der elfte Roboter:

                                                       

     

  Brute-Force-Teil

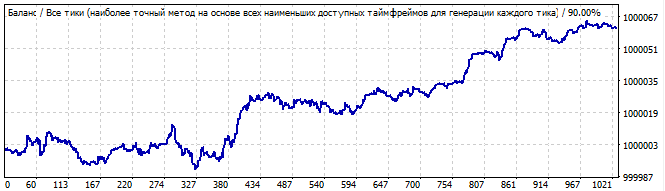
                                                              10 Tage in die Zukunft  

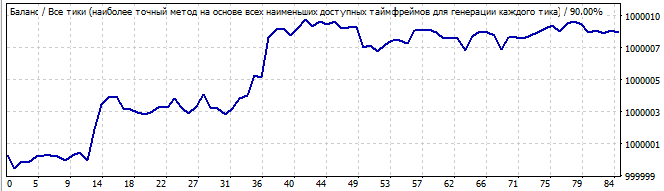
Der Graph ist nicht sehr schön, aber es gibt eine gewisse Ähnlichkeit mit der geraden Linie. Das Muster setzt sich in die Zukunft fort, aber ich denke, es ist eher Glück als die regelmäßigen Ergebnisse, da es zu viel zufälliges Rauschen hat. Es kann auch nicht alles Rauschen sein, sondern kleine Wellen. 

Zwölfter Roboter:

                                                              

  Brute-Force-Teil

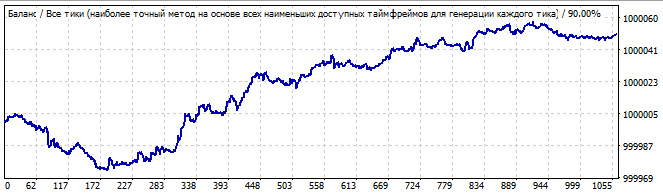
                                                               10 Tage in die Zukunft  

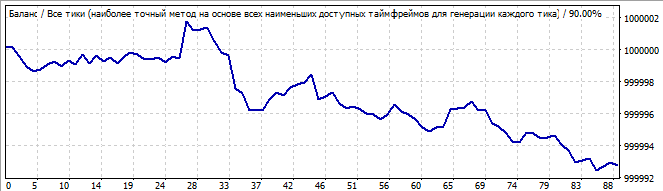
Ein ziemlich hässliches Diagramm, aber es hat ein ausgeprägtes Ende einer Welle und eine weitere riesige Welle, die ihr folgt. In der Zukunft kehrt sich diese riesige Welle langsam um und invertiert schließlich irgendwann. Es schien mir, dass die Trendumkehr bei Robotern mit einem Polynom höheren Grades als 2 reibungsloser verläuft. Sie zeigen also weniger Überraschungen. Ich denke, es macht Sinn, etwas Zeit zu investieren und den dritten Grad zu testen. Regelmäßigkeiten können besser beschrieben werden, wenn das Polynom eine höhere höchste Gesamtpotenz der Faktoren in den Termen hat.

Schlussfolgerungen und mathematische Wahrheiten aus unseren Untersuchungen

Nun können wir alle Testergebnisse unserer Expert Advisors zusammenfassen. Dies mag schwierig erscheinen, da Brute-Force- und Optimierungsintervalle Muster zeigen, während die Zukunftssegmente ein unklares Bild zeigen. Nicht wirklich:

• In jedem der Future-Tests gibt es immer einen Punkt, an dem sich der Chart umkehrt und die Formel invertiert wird.
• Eine Umkehrung kann fließend oder sofort erfolgen, aber sie ist immer da.
• Die überwiegende Mehrheit der Graphen geht in der Zukunft generell nach unten.
• Manchmal hält das Muster zu Beginn noch eine Weile an.
• Alle Tests in der Zukunft haben gezeigt, dass das Muster in die entgegengesetzte Richtung wirkt.
• Wenn die Gleichgewichtskurve von der geraden Linie abweicht, dann sind die Chancen auf eine Fortsetzung viel geringer.
• In der besten der gefundenen Varianten funktioniert das Muster ein oder zwei Tage lang weiter.

Ich werde nun versuchen, diese Fakten zu erklären. Die erste und wichtigste Tatsache habe ich schon vor langer Zeit entdeckt, als es noch keine solchen Programme gab. Dies ist eine einfache mathematische Wahrheit. Ich habe unten ein Gleichgewichtsdiagramm für eine beliebige Strategie gezeichnet. Die schwarze Linie ist die mit einem kleinen Muster, und die lila Linie hat ein Muster. Der Graph zeigt ihr ungefähres Verhalten, wenn wir sie im Laufe der Geschichte gehandelt haben, und nicht nur im Brute-Force-Intervall:

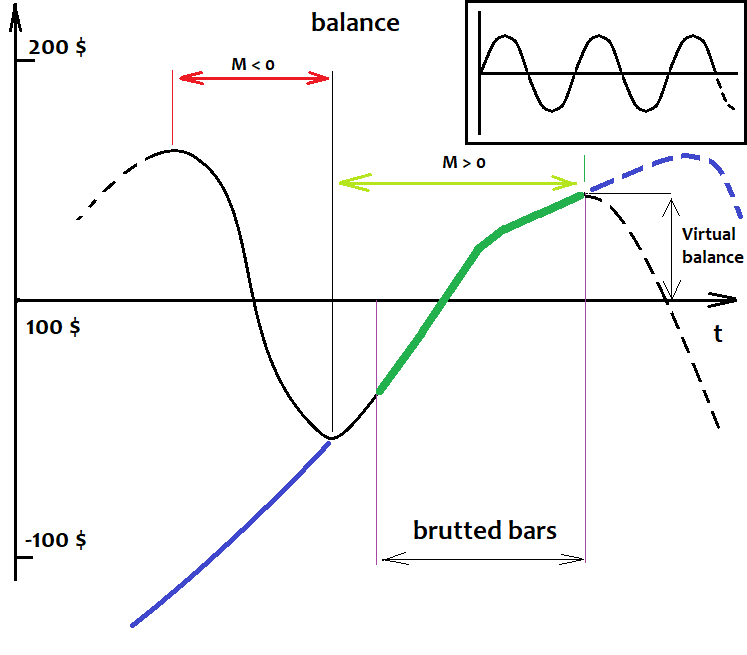
Ich füge hier keine Kurse ein, da in unserem Fall die analysierte Basis die Saldenkurve sein kann. Es sollte uns egal sein, wie sich die Kurse verhalten. Wir werden in den Kursen nicht mehr erkennen können als unsere Strategie.

Stellen Sie sich vor, wir würden alle unsere Roboter von Beginn der Geschichte an und weiter in die Zukunft testen. Wir haben eben keine zukünftigen Kurse, dennoch können wir mit 100%iger Genauigkeit annehmen, was passieren wird. Klingt nach Unsinn? Nein, es ist kein Unsinn. Stellen wir uns zunächst einmal vor, dass wir Roboter anhand der gesamten verfügbaren Kurshistorie testen würden. Was werden wir sehen? Einige verwirrende Bewegungen, auf und ab und so weiter. Was sollten wir hier erkennen können? Wellen. Ihre Form, Wellenlänge und Amplitude sind nicht wichtig. Es handelt sich nicht um eine Sinuskurve, aber das interessiert uns nicht. Was zählt, ist, dass dieser Vorgang periodisch ist. Darüber hinaus tendiert der Erwartungswert einer Strategie, die auf einer Zufallsformel basiert, basierend auf meiner mathematischen Forschung, die ich in meinem vorherigen Artikel vorgestellt habe, gegen Null, wenn die Anzahl der historischen Daten gegen unendlich tendiert. Was ist die Auswirkung davon? Aufgrund der obigen Annahme können wir sagen, dass jede Saldenkurve mit einer unendlichen Anzahl von Positionen die Startgleichgewichtslinie unendlich oft kreuzen wird. Selbst wenn der Saldo aus irgendeinem Grund sofort nach oben oder unten geht und die ganze Zeit dort bleibt, können wir diese Linie leicht nach unten oder oben verschieben und diesen Gleichgewichtspunkt finden, in dessen Nähe die Balance schwankt.

Wir werden nicht die Formeln berücksichtigen, die zu einem ausgeprägten Gewinn oder Verlust im Laufe der Geschichte führen, obwohl diese Varianten auch dieser Kategorie zugeordnet werden können - es ist nur die positive oder negative Halbwelle einer riesigen Welle, die größer als unsere gesamte Geschichte ist. Nach diesen Annahmen sind die gefundenen Muster nur Teile von positiven Halbwellen. Je größer der gefundene Teil ist, desto wahrscheinlicher ist es, dass der Gleichgewichtspunkt weit darunter liegt. Wenn es jetzt eine positive Halbwelle gibt, dann sollte demnach bald eine negative erscheinen. Aus mathematischer Sicht gilt: Je größer die gefundene Halbwelle ist, desto größer ist die Wahrscheinlichkeit einer Bewegung in die negative Richtung. Und umgekehrt, wenn wir eine negative Halbwelle feststellen, dann ist die Wahrscheinlichkeit, dass eine positive Halbwelle beginnt, umso größer, je größer diese Halbwelle ist. Es geht noch einfacher: Wenn wir eine Strategie mit einem erwarteten Payoff von Null in der gesamten Geschichte haben, dann besteht diese ganze Geschichte aus Segmenten mit negativen und positiven erwarteten Payoffs, die aufeinander folgen und sich ständig abwechseln. Ich habe einen Expert Advisor, der dieses Prinzip implementiert und der für jedes Währungspaar in der gesamten Geschichte der Kurse funktioniert. Die obigen Annahmen werden also auch von Expert Advisors bestätigt. Generell kann dieses Prinzip nicht nur skaliert, sondern auch unendlich geschichtet werden, was die Effizienz des Systems erhöht. Natürlich ist es möglich, die Trendfortsetzung zu handeln, aber ich empfehle, dies nur zu tun, wenn das Muster sehr ausgeprägt und gleichmäßig ist, und bis zu 5-10% des gefundenen Musters in die Zukunft zu handeln. Die Risiken sind sehr hoch. Außerdem ist es dumm, gegen die Mathematik zu handeln. Man könnte versuchen, wenn es irgendwie möglich wäre, die ungefähre Restlebensdauer dieses Musters abzuschätzen. Aber das ist unmöglich, da die Natur des Musters nicht klar ist. Und selbst wenn die Natur des Musters klar ist, ist eine solche Analyse extrem schwierig durchzuführen.

Wie kann man den Pegel bestimmen, relativ zu dem Fluktuationen auftreten?

Was die Fluktuationen betrifft, werde ich versuchen zu beantworten, wie man das Niveau definiert, relativ zu dem man die Wellen und ihre Bewegung bestimmen sollte. Die Antwort ist sehr einfach. Es gibt keine Möglichkeit, es zu bestimmen. Das bedeutet nicht, dass die Ebene nicht existiert und dass wir keinen richtigen Handel durchführen können. Dieses Niveau ist nicht festgelegt, und es existiert nur in unserem Kopf. Noch wichtiger ist es, Folgendes zu verstehen: Wenn die Größe einer Halbwelle gegen unendlich tendiert, tendiert auch das Verhältnis der Größe dieser Halbwelle zum Abstand des Niveaus vom Ausgangsniveau gegen unendlich. Mit anderen Worten, je stärker die Halbwelle ist, desto weniger können wir darüber nachdenken, wo dieses Niveau ist, da mit einer Zunahme der Anzahl der Positionen dieses Niveau zum Nullpunkt tendiert. Alles, was wir tun müssen, ist, sehr starke Halbwellen zu finden. Eine weitere Tatsache, die dasselbe zeigt, ist, dass je größer und besser die Halbwelle ist, desto unwahrscheinlicher ist es, dass eine Welle mit einer vergleichbaren Größe im Rest des virtuellen Tests gefunden werden kann. Ich werde versuchen, das Gesagte in der Abbildung visuell darzustellen:

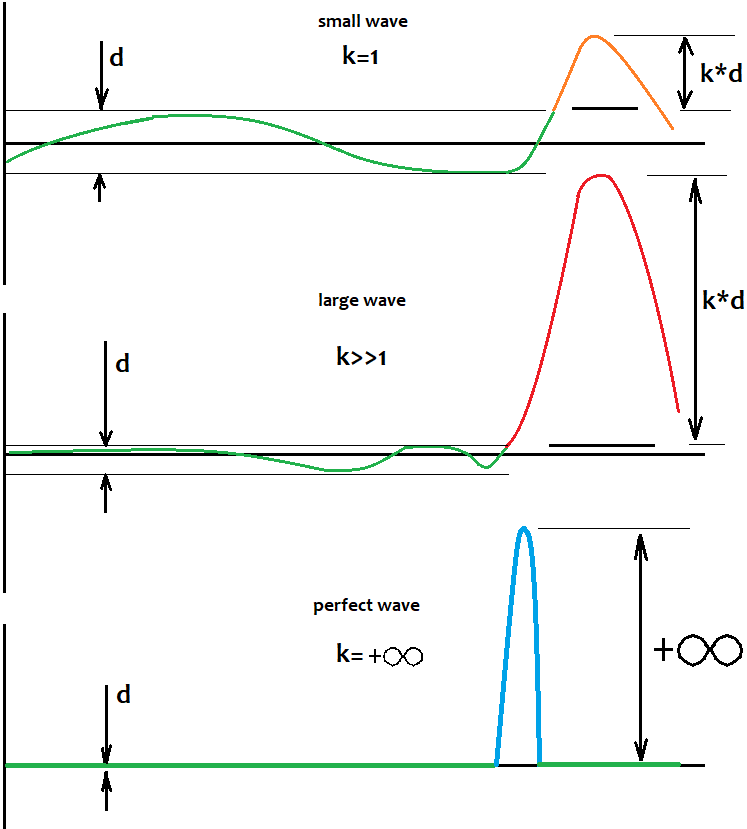
Dieses Niveau garantiert nicht, dass sich das Muster mit 100%iger Wahrscheinlichkeit drehen wird. Wichtiger ist, dass allein die Tatsache der Existenz eines Musters, das Teil der Halbwelle ist, uns sagt, dass es höchstwahrscheinlich mehr als eine solche Welle geben wird, und sie könnten sogar während der gesamten Geschichte existieren. In diesem Fall besteht eine große Chance, dass es einen großen Rücksetzer geben wird. Wir sollten versuchen, ihn zu erwischen. Selbst als ich verschiedene Expert Advisors getestet habe, die auf globaler Ebene nicht funktionierten, funktionierte dies lokal auf eine direkte oder umgekehrte Weise. Es gab lebendige Wellen und der Chart war klar strukturiert.

Um das Bild zu vervollständigen

werde ich versuchen zu zeigen, wie diese Wellen meiner Meinung nach am effizientesten gehandelt werden sollten. Lassen Sie mich Ihnen zunächst einige Illustrationen geben:

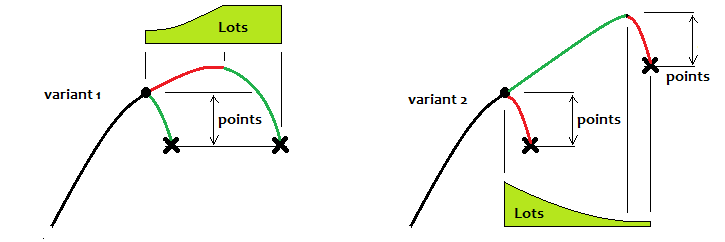
Die erste Option ist der Handel auf die Musterumkehr, und die zweite ist der Handel auf die Fortsetzung. Wenn wir die erste Option besprechen, dann sollten Sie idealerweise immer ein bestimmtes Niveau erreichen und den Handelszyklus dort stoppen und dann auf den nächsten warten. Wenn Sie ein partielles Martingal verwenden, wird es eine Verbesserung geben, aber nur, wenn bekannt ist, dass der Chart bald umkehren sollte. Wenn nicht, wird die erwartete Auszahlung immer noch "0" sein. Sie können die Trendfortsetzung nur dann handeln, wenn das Muster nahe am Ideal ist. Aber dieser Handel sollte nur für eine kurze Zeit sein. In der zweiten Variante können Sie meiner Meinung nach das umgekehrte Martingal verwenden. Um ehrlich zu sein, beweisen alle Strategien, die ich getestet habe, diese mathematische Tatsache: Wenn Sie mit einer festen Losgröße handeln und Sie nicht wissen, wie sich der Preis in der Zukunft verhalten wird (und das ist fast nie bekannt), dann wird das Ergebnis immer "0" sein.

Aber es gibt Situationen, in denen wir zufällig ein globales Muster erwischen und es funktioniert sehr weit. Meiner Meinung nach ist es jedoch besser, nicht auf solche Situationen zu warten. Es ist besser, ein Handelsschema zu wählen und ihm zu folgen. Es gibt keine Einheitslösungen. Ich habe noch keine Zeit gehabt, dies auch auf Demokonten zu testen, da dies 2-3 Monate dauern wird. In einem Monat gibt es vier Wochen, und jedes Wochenende sollte die zweitägige Brute-Force durchgeführt werden. Und dann sollte es auf einem Computer getestet werden, der rund um die Uhr arbeitet. Ich habe jetzt keine Möglichkeit, dies zu tun. Vielleicht werde ich in der Zukunft auf einem Demokonto experimentieren und ein separates Signal erstellen.

Schlussfolgerung

In diesem Artikel haben wir einfache, aber sehr wichtige Schlussfolgerungen über die Muster und ihre Physik in Bezug auf den Markt gemacht. Sie lauten wie folgt: Der Markt ist nicht chaotisch und es gibt viele Muster, die in ihm auf verschiedenen Perioden der Charts versteckt sind. Sie überlagern sich und erzeugen die Illusion von Chaos. Ein Muster ist ein periodischer Prozess, der sich wiederholen und umkehren kann. Da sich die Muster wiederholen, können diese Wellen eine begrenzte Amplitude haben, die in Handelsstrategien genutzt werden kann. Ich habe versucht, diesen Artikel so klar wie möglich zu gestalten und ein Minimum an Mathematik zu vermitteln. Ich hoffe, dass diese Informationen Ihnen bei der Entwicklung von Handelssystemen helfen werden. Wenn Sie andere Schlussfolgerungen haben, fügen Sie bitte Ihre Kommentare hinzu. Leider war ich nicht in der Lage, Brute Force auf höheren Zeitrahmen durchzuführen, da dies zu viel Zeit in Anspruch nimmt. Wenn die Leser an einer tieferen Analyse interessiert sind, bin ich bereit, dieses Thema in weiteren Artikeln fortzusetzen. Dieser Artikel stellt eher eine Themeneinführung und Demonstration dar.