
Grundlegende Mathematik hinter dem Forex-Handel
Einführung
Ich bin ein Entwickler von automatischen Strategien und Software mit über 5 Jahren Erfahrung. In diesem Artikel werde ich den Schleier der Geheimhaltung für diejenigen lüften, die gerade erst mit dem Handel am Forex oder an einer anderen Börse beginnen. Außerdem werde ich versuchen, die am häufigsten gestellten Handelsfragen zu beantworten.
Ich hoffe, der Artikel wird sowohl für Anfänger als auch für erfahrene Händler nützlich sein. Beachten Sie bitte auch, dass dies nur meine Sichtweise ist, die auf tatsächlichen Erfahrungen und Recherchen basiert.
Einige der erwähnten Roboter und Indikatoren können in meinen Produkten gefunden werden. Dies ist aber nur ein kleiner Teil. Ich habe eine Vielzahl von Robotern entwickelt, die eine Fülle von Strategien anwenden. Ich werde versuchen zu zeigen, wie der beschriebene Ansatz es ermöglicht, einen Einblick in die wahre Natur des Marktes zu bekommen und welche Strategien es wert sind, beachtet zu werden.
Warum ist es so schwierig, Einstiegs- und Ausstiegspunkte zu finden?
Wenn Sie wissen, wo Sie in den Markt ein- und aussteigen können, brauchen Sie wahrscheinlich nichts anderes zu wissen. Leider ist das Thema Einstiegs- und Ausstiegspunkte ein schwer fassbares Thema. Auf den ersten Blick kann man immer ein Muster erkennen und ihm eine Zeit lang folgen. Aber wie kann man es ohne ausgeklügelte Tools und Indikatoren erkennen? Die einfachsten und immer wiederkehrenden Muster sind TREND und Seitwärtsbewegung. Trend ist eine langfristige Bewegung in eine Richtung, während die Seitwärtsbewegung häufigere Umkehrungen impliziert.
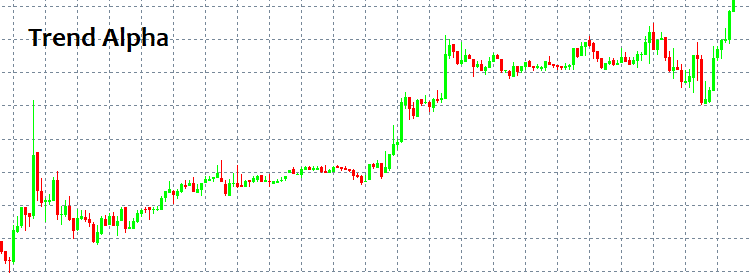
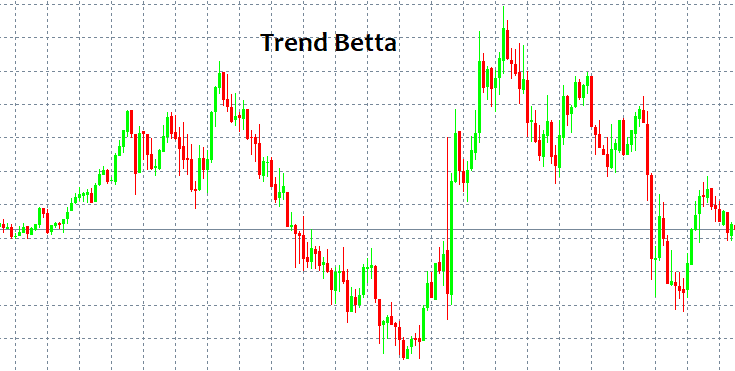

Diese Muster können leicht erkannt werden, da ein menschliches Auge sie ohne jegliche Indikatoren finden kann. Das Hauptproblem hier ist, dass wir ein Muster nur sehen können, nachdem es ausgelöst wurde. Außerdem kann niemand garantieren, dass es überhaupt ein Muster gegeben hat. Kein Muster kann Ihr Depot unabhängig von einer Strategie vor der Zerstörung bewahren. Ich werde versuchen, mögliche Gründe dafür zu liefern, indem ich die Sprache der Mathematik verwende.
Marktmechanismen und Niveaus
Lassen Sie mich Ihnen ein wenig über die Preisbildung und die Kräfte, die den Marktpreis bewegen, erzählen. Es gibt zwei Kraftpositionen auf dem Markt — im Markt und an der Grenze. Ebenso gibt es zwei Arten von Aufträgen — Markt- und Limit-Aufträge. Die Limit-Käufer und -Verkäufer füllen die Markttiefe auf, während die Markt-Käufer und -Verkäufer sie wieder leeren. Die Markttiefe ist im Grunde eine vertikale Preisskala, die anzeigt, wer bereit ist, etwas zu kaufen oder zu verkaufen. Es gibt immer eine Lücke zwischen Limit-Verkäufern und -Käufern. Diese Lücke wird als Spread bezeichnet. Der Spread ist ein Abstand zwischen den besten Kauf- und Verkaufspreisen, gemessen in der Anzahl der minimalen Preisbewegungen. Käufer wollen zum günstigsten Preis kaufen, während Verkäufer zum höchsten Preis verkaufen wollen. Daher befinden sich Limit-Orders von Käufern immer am unteren Rand, während sich die Orders von Verkäufern immer am oberen Rand befinden. Markt-Käufer und -Verkäufer treten in die Markttiefe ein und zwei Orders (Limit- und Markt-Order) werden miteinander verbunden. Die Marktbewegung erfolgt, wenn eine Limit-Order ausgelöst wird.
Wenn eine aktive Markt-Order erscheint, hat sie normalerweise Stop Loss und Take Profit. Ähnlich wie bei Limit-Orders sind diese Stop-Levels über den ganzen Markt verstreut und bilden Preisbeschleunigungs- oder Umkehrlevels. Alles hängt von der Menge und der Art der Stop-Levels ab, sowie vom Handelsvolumen. Wenn wir diese Levels kennen, können wir sagen, wo der Preis beschleunigen oder umkehren kann.
Limit-Orders können auch Fluktuationen und Cluster bilden, die schwer zu durchlaufen sind. Sie treten normalerweise an wichtigen Preispunkten auf, wie z.B. bei einer Tages- oder Wocheneröffnung. Wenn von niveaubasiertem Handel die Rede ist, meinen Händler in der Regel die Verwendung von Limit-Order-Levels. All dies kann kurz wie folgt dargestellt werden.
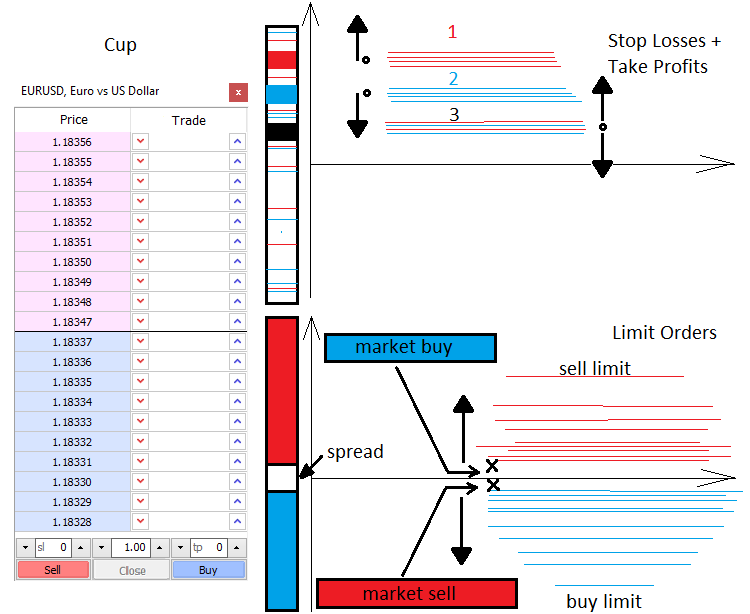
Mathematische Beschreibung des Marktes
Was wir im MetaTrader-Fenster sehen, ist eine diskrete Funktion mit dem Argument t, wobei t die Zeit ist. Die Funktion ist diskret, weil die Anzahl der Ticks endlich ist. Im aktuellen Fall sind Ticks Punkte, die nichts dazwischen enthalten. Ticks sind die kleinsten Elemente der möglichen Preisdiskretisierung, größere Elemente sind Balken, M1, M5, M15 Kerzen, usw. Der Markt weist sowohl das Element des Zufalls als auch Muster auf. Die Muster können verschiedene Größenordnungen und Dauer haben. Der Markt ist jedoch zum größten Teil eine probabilistische, chaotische und fast unvorhersehbare Umgebung. Um den Markt zu verstehen, sollte man ihn durch die Konzepte der Wahrscheinlichkeitsrechnung betrachten. Diskretisierung ist notwendig, um die Konzepte der Wahrscheinlichkeit und der Wahrscheinlichkeitsdichte einzuführen.
Um das Konzept der Erwartung einzuführen, müssen Sie zuerst das Konzept eines Ereignisses und eine vollständige Gruppe von Ereignissen einführen:
- C1 Ereignis — Gewinn, er ist gleich tp
- C2 Ereignis — Verlust, er ist gleich sl
- P1 — C1-Ereigniswahrscheinlichkeit
- P2 — C2-Ereigniswahrscheinlichkeit
Die Ereignisse С1 und С2 bilden eine vollständige Gruppe von antithetischen Ereignissen (d.h. eines dieser Ereignisse tritt auf jeden Fall ein). Deshalb ist die Summe dieser Wahrscheinlichkeiten gleich einem P2(tp,sl) + P2(tp,sl) = 1. Diese Gleichung kann sich später als nützlich erweisen.
Wenn wir einen EA oder eine manuelle Strategie mit einer zufälligen Eröffnung sowie einem zufälligen StopLoss und TakeProfit testen, erhalten wir immer noch ein nicht-zufälliges Ergebnis und die erwartete Auszahlung gleich "-(Spread)", was "0" bedeuten würde, wenn wir den Spread auf Null setzen könnten. Dies deutet darauf hin, dass wir auf dem Zufallsmarkt immer den erwarteten Gewinn von Null erhalten, unabhängig von den Stop-Levels. Auf dem nicht-zufälligen Markt erhalten wir immer einen Gewinn oder Verlust, vorausgesetzt, dass der Markt zusammenhängende Muster aufweist. Wir können zu den gleichen Schlussfolgerungen kommen, wenn wir annehmen, dass der erwartete Payoff (Tick[0].Bid - Tick[1].Bid) ebenfalls gleich Null ist. Dies sind recht einfache Schlussfolgerungen, die auf viele Arten erreicht werden können.
- M=P1*tp-P2*sl= P1*tp-(1- P1)*sl — für jeden Markt
- P1*tp-P2*sl= 0 — für einen chaotischen Markt
Dies ist die wichtigste Gleichung für den chaotischen Markt, die den erwarteten Gewinn einer chaotischen Order beim Öffnen und Schließen unter Verwendung von Stop-Werten beschreibt. Nachdem wir die letzte Gleichung gelöst haben, erhalten wir alle Wahrscheinlichkeiten, an denen wir interessiert sind, sowohl für den vollständigen Zufall als auch für den umgekehrten Fall, vorausgesetzt, wir kennen die Stop-Werte.
Die hier angegebene Gleichung ist nur für den einfachsten Fall gedacht, der für jede Strategie verallgemeinert werden kann. Genau das werde ich jetzt tun, um ein vollständiges Verständnis dafür zu erlangen, was den endgültigen erwarteten Gewinn ausmacht, den wir ungleich Null machen müssen. Außerdem wollen wir das Konzept des Gewinnfaktors einführen und die entsprechenden Gleichungen schreiben.
Nehmen wir an, dass unsere Strategie sowohl das Schließen durch Stop-Levels als auch einige andere Signale beinhaltet. Dazu werde ich den Ereignisraum С3, С4 einführen, in dem das erste Ereignis das Schließen durch Stop-Levels ist, während das zweite Ereignis das Schließen durch Signale ist. Sie bilden auch eine vollständige Gruppe von antithetischen Ereignissen, so dass wir die Analogie verwenden können, um zu schreiben:
M=P3*M3+P4*M4=P3*M3+(1-P3)*M4, wobei M3=P1*tp-(1- P1)*sl, und M4=Sum(P0[i]*pr[i]) - Sum(P01[j]*ls[j]); Sum( P0[i] )+ Sum( P01[j] ) =1
- M3 — erwartetes Ergebnis beim Schließen durch eine Stop-Order.
- M4 — erwartetes Ergebnis beim Schließen durch ein Signal.
- P1 , P2 — Wahrscheinlichkeiten der Aktivierung der Stoppniveaus, vorausgesetzt, dass eines der Stoppniveaus auf jeden Fall ausgelöst wird.
- P0[i] — Wahrscheinlichkeit der Schließung eines Geschäfts mit dem Gewinn von pr[i], vorausgesetzt, dass es keine Stoppniveaus ausgelöst hat. i — Nummer der schließenden Option
- P01[j] — Wahrscheinlichkeit einer Position mit einem Verlust von ls[j] unter der Annahme, dass keine Stop-Level ausgelöst wurden. j — Nummer der Schließoption
Mit anderen Worten, wir haben zwei antithetische Ereignisse. Ihre Ergebnisse bilden zwei weitere unabhängige Ereignisräume, in denen wir auch die vollständige Gruppe definieren. Allerdings sind die Wahrscheinlichkeiten P1, P2, P0[i] und P01[j] nun bedingte Wahrscheinlichkeiten, während P3 und P4 die Wahrscheinlichkeiten der Hypothesen sind. Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit für ein Ereignis, wenn eine Hypothese eintritt. Alles ist in strenger Übereinstimmung mit der Formel für die Gesamtwahrscheinlichkeit (Bayes-Formel). Ich empfehle dringend, sie gründlich zu studieren, um die Materie zu begreifen. Für einen völlig chaotischen Handel ist M=0.
Jetzt ist die Gleichung viel klarer und breiter geworden, da sie sowohl das Schließen durch Stop-Levels als auch durch Signale bespricht. Wir können diese Analogie noch weiter verfolgen und die allgemeine Gleichung für jede Strategie schreiben, die sogar dynamische Stop-Levels berücksichtigt. Das ist, was ich tun werde. Führen wir N neue Ereignisse ein, die eine komplette Gruppe bilden, d.h. Eröffnungsgeschäfte mit ähnlichen StopLoss und TakeProfit. CS[1] .. CS[2] .. CS[3] ....... CS[N] . ebenso, PS[1] + PS[2] + PS[3] + ....... +PS[N] = 1.
M = PS[1]*MS[1]+PS[2]*MS[2]+ ... + PS[k]*MS[k] ... +PS[N]*MS[N] , MS[k] = P3[k]*M3[k]+(1- P3[k])*M4[k], M3[k] = P1[k] *tp[k] -(1- P1[k] )*sl[k], M4[k] = Sum(i)(P0[i][k]*pr[i][k]) - Sum(j)(P01[j][k] *ls[j][k] ); Sum(i)( P0[i][k] )+ Sum(j)( P01[j][k] ) =1.
- PS[k] — Wahrscheinlichkeit der Einstellung der k-ten Stopp-Level-Option.
- MS[k] — erwarteter Payoff von geschlossenen Geschäften mit k-ten Stop-Levels.
- M3[k] — erwarteter Payoff beim Schließen durch eine Stop-Order mit k-ten Stop-Levels.
- M4[k] — erwarteter Payoff beim Schließen durch ein Signal mit k-ten Stopp-Levels.
- P1[k], P2[k] — Wahrscheinlichkeiten der Aktivierung der Stoppniveaus unter der Voraussetzung, dass eines der Stoppniveaus auf jeden Fall ausgelöst wird.
- P0[i][k] — Wahrscheinlichkeit, eine Position mit pr[i][k] Gewinn zu schließen, gemäß einem Signal mit k-ten Stoppniveaus. i — Nummer der schließenden Option
- P01[j][k] — Wahrscheinlichkeit, eine Position mit ls[j][k] Verlust zu schließen, nach einem Signal mit k-ten Stoppniveau. j — Nummer der schließenden Option
Wie in den vorherigen (einfacheren) Gleichungen, ist M=0 im Falle eines chaotischen Handels und des Fehlens eines Spreads. Man kann höchstens die Strategie ändern, aber wenn sie keine rationale Grundlage enthält, wird man einfach das Gleichgewicht dieser Variablen ändern und trotzdem 0 erhalten. Um dieses unerwünschte Gleichgewicht zu durchbrechen, müssen wir die Wahrscheinlichkeit der Marktbewegung in eine beliebige Richtung innerhalb eines festgelegten Bewegungssegments in Punkten oder die erwartete Auszahlung der Preisbewegung innerhalb einer bestimmten Zeitspanne kennen. In Abhängigkeit davon werden Einstiegs-/Ausstiegspunkte gewählt. Wenn es Ihnen gelingt, diese zu finden, dann haben Sie eine profitable Strategie.
Lassen Sie uns nun die Gleichung für den Gewinnfaktor aufstellen. PF = Gewinn/Verlust. Der Gewinnfaktor ist das Verhältnis von Gewinn zu Verlust. Wenn die Zahl größer als 1 ist, ist die Strategie profitabel, andernfalls ist sie es nicht. Dies kann mit Hilfe des erwarteten Payoffs umdefiniert werden. PrF=Mp/Ml. Das bedeutet das Verhältnis des erwarteten Nettogewinnauszahlungsbetrags zum erwarteten Nettoverlust. Lassen Sie uns die Gleichungen schreiben.
- Mp = PS[1]*MSp[1]+PS[2]*MSp[2]+ ... + PS[k]*MSp[k] ... +PS[N]*MSp[N] , MSp[k] = P3[k]*M3p[k]+(1- P3[k])*M4p[k] , M3p[k] = P1[k] *tp[k], M4p[k] = Sum(i)(P0[i][k]*pr[i][k])
- Ml = PS[1]*MSl[1]+PS[2]*MSl[2]+ ... + PS[k]*MSl[k] ... +PS[N]*MSl[N] , MSl[k] = P3[k]*M3l[k]+(1- P3[k])*M4l[k] , M3l[k] = (1- P1[k] )*sl[k], M4l[k] = Sum(j)(P01[j][k]*ls[j][k])
Sum(i)( P0[i][k] ) + Sum(j)( P01[j][k] ) =1.
- MSp[k] — erwarteter Payoff von abgeschlossenen Geschäften mit k-ten Stopp-Levels.
- MSl[k] — erwarteter Payoff von geschlossenen Geschäften mit k-ten Stop-Levels.
- M3p[k] — erwarteter Payoff beim Schließen durch eine Stop-Order mit k-ten Stop-Levels.
- M4p[k] — erwarteter Payoff beim Schließen durch ein Signal mit k-ten Stop-Levels.
- M3l[k] — erwarteter Verlust beim Schließen durch eine Stop-Order mit k-ten Stop-Levels.
- M4l[k] — erwarteter Verlust beim Schließen durch ein Signal mit k-ten Stop-Levels.
Für ein tieferes Verständnis werde ich alle verschachtelten Ereignisse abbilden:
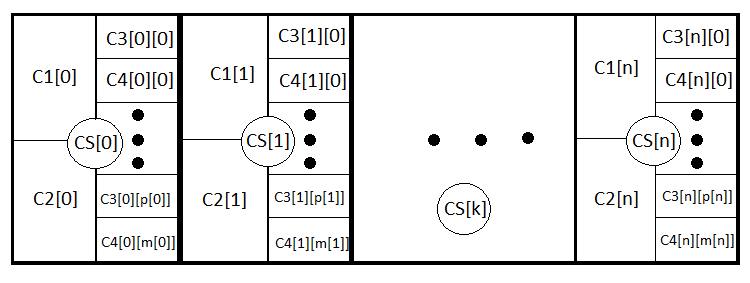
Tatsächlich sind das dieselben Gleichungen, obwohl in der ersten der Teil fehlt, der sich auf den Verlust bezieht, während in der zweiten der Teil fehlt, der sich auf den Gewinn bezieht. Im Falle des chaotischen Handels ist PrF = 1, vorausgesetzt, dass der Spread wieder gleich Null ist. M und PrF sind zwei Werte, die völlig ausreichend sind, um die Strategie von allen Seiten zu bewerten.
Insbesondere ist es möglich, den Trend oder die Seitwärtsbewegung eines bestimmten Instruments mit der gleichen Wahrscheinlichkeitstheorie und Kombinatorik zu bewerten. Außerdem ist es auch möglich, einige Unterschiede zur Zufälligkeit mit Hilfe der Wahrscheinlichkeitsverteilungsdichten zu finden.
Ich werde ein Wahrscheinlichkeitsdichte-Diagramm der Zufallswertverteilung für einen diskretisierten Preis bei einem festen H-Schritt in Punkten erstellen. Nehmen wir an, dass, wenn sich der Preis in eine beliebige Richtung H bewegt, ein Schritt gemacht wurde. Auf der X-Achse soll ein Zufallswert in Form einer vertikalen Preisbewegung im Chart, gemessen in der Anzahl der Schritte, dargestellt werden. In diesem Fall sind n Schritte zwingend erforderlich, da nur so die gesamte Kursbewegung bewertet werden kann.
- n — Gesamtzahl der Schritte (konstanter Wert)
- d — Anzahl der Schritte für die Preissenkung
- u — Anzahl der Schritte für die Preiserhöhung
- s — Gesamte Aufwärtsbewegung in Schritten
Nachdem Sie diese Werte definiert haben, berechnen Sie u und d:
Um die Gesamtzahl der "s"-Schritte nach oben bereitzustellen (der Wert kann negativ sein, was Schritte nach unten bedeutet), sollte eine bestimmte Anzahl von Auf- und Abwärtsschritten bereitgestellt werden: "u", "d". Die endgültige Auf- oder Abwärtsbewegung von "s" hängt von der Gesamtzahl der Schritte ab:
n=u+d;
s=u-d;
Dies ist ein System aus zwei Gleichungen. Löst man es, erhält man u und d:
u=(s+n)/2, d=n-u.
Allerdings sind nicht alle "s"-Werte für einen bestimmten "n"-Wert geeignet. Der Schritt zwischen den möglichen s-Werten ist immer gleich 2. Dies geschieht, um "u" und "d" mit natürlichen Werten zu versehen, da sie für die Kombinatorik, oder besser gesagt, für die Berechnung von Kombinationen verwendet werden sollen. Wenn diese Zahlen gebrochen sind, dann können wir die Fakultät nicht berechnen, die der Grundstein aller Kombinatorik ist. Im Folgenden sind alle möglichen Szenarien für 18 Schritte dargestellt. Die Grafik zeigt, wie umfangreich die Ereignisoptionen sind.
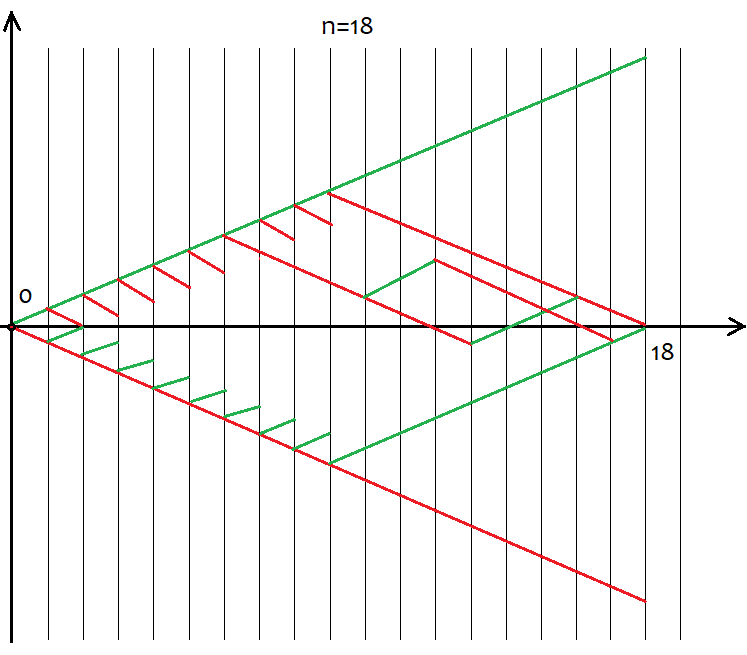
Es ist einfach zu definieren, dass die Anzahl der Optionen 2^n für die ganze Vielfalt der Preisoptionen umfasst, da es nur zwei mögliche Bewegungsrichtungen nach jedem Schritt gibt - aufwärts oder abwärts. Wir brauchen nicht zu versuchen, jede dieser Optionen zu erfassen, da dies unmöglich ist. Stattdessen müssen wir einfach nur wissen, dass wir n eindeutige Zellen haben, von denen u und d jeweils aufwärts und abwärts sein sollten. Die Optionen, die das gleiche u und d haben, ergeben letztlich das gleiche s. Um die Gesamtzahl der Optionen zu berechnen, die das gleiche "s" liefern, können wir die Kombinationsgleichung aus der Kombinatorik С=n!/(u!*(n-u)!), sowie die äquivalente Gleichung С=n!/(d!*(n-d)!) verwenden. Bei unterschiedlichen u und d erhalten wir den gleichen Wert von C. Da die Kombinationen sowohl durch aufsteigende als auch durch absteigende Segmente gebildet werden können, führt dies unweigerlich zu einem Déjà-vu. Welche Segmente sollten wir also verwenden, um Kombinationen zu bilden? Die Antwort ist beliebig, da diese Kombinationen trotz ihrer Unterschiede gleichwertig sind. Ich werde im Folgenden versuchen, dies anhand einer auf MathCad 15 basierenden Anwendung zu beweisen.
Nachdem wir nun die Anzahl der Kombinationen für jedes Szenario bestimmt haben, können wir die Wahrscheinlichkeit einer bestimmten Kombination (oder eines Ereignisses, wie Sie wollen) bestimmen. P = С/(2^n). Dieser Wert kann für alle "s" berechnet werden, und die Summe dieser Wahrscheinlichkeiten ist immer gleich 1, da eine dieser Optionen sowieso eintreten wird. Basierend auf dieser Wahrscheinlichkeitsmatrix können wir den Wahrscheinlichkeitsdichtegraphen in Bezug auf den Zufallswert "s" erstellen, wobei wir besprechen, dass der Schritt s 2 ist. In diesem Fall kann die Dichte bei einem bestimmten Schritt einfach durch Division der Wahrscheinlichkeit durch die Schrittgröße s, d. h. durch 2, ermittelt werden. Der Grund dafür ist, dass wir keine kontinuierliche Funktion für diskrete Werte bilden können. Diese Dichte bleibt einen halben Schritt nach links und rechts, d. h. durch 1, relevant. Sie hilft uns, die Knotenpunkte zu finden und ermöglicht die numerische Integration. Für negative "s"-Werte werde ich den Graphen einfach an der Achse der Wahrscheinlichkeitsdichte spiegeln. Bei geraden n-Werten beginnt die Nummerierung der Knoten bei 0, bei ungeraden Werten bei 1. Bei geraden n-Werten können wir keine ungeraden s-Werte angeben, während wir bei ungeraden n-Werten keine geraden s-Werte angeben können. Der Screenshot der Berechnungsanwendung unten verdeutlicht dies:
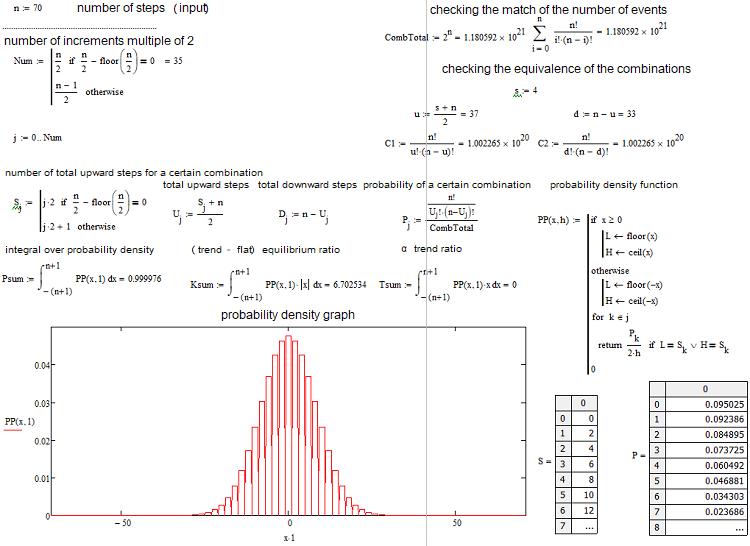
Es listet alles auf, was wir brauchen. Die Anwendung ist unten angehängt, damit Sie mit den Parametern herumspielen können. Eine der am häufigsten gestellten Fragen ist, wie man definieren kann, ob die aktuelle Marktsituation auf einem Trend oder einer Seitwärtsbewegung basiert. Ich habe mir meine eigenen Gleichungen ausgedacht, um die Trend- oder Seitwärtsbewegung eines Instruments zu quantifizieren. Ich habe Trends in Alpha- und Beta-Trends unterteilt. Alpha bedeutet eine Tendenz, entweder zu kaufen oder zu verkaufen, während Beta nur eine Tendenz ist, die Bewegung fortzusetzen, ohne dass es eine klar definierte Prävalenz von Käufern oder Verkäufern gibt. Seitwärtsbewegung schließlich bedeutet eine Tendenz, zum Anfangskurs zurückzukehren.
Die Definitionen von Trend und Seitwärtsbewegung variieren stark unter den Händlern. Ich versuche, all diesen Phänomenen eine starrere Definition zu geben, da selbst ein grundlegendes Verständnis dieser Dinge und Mittel zu ihrer Quantifizierung die Anwendung vieler Strategien ermöglicht, die bisher als tot oder zu einfach besprochen wurden. Hier sind die wichtigsten Gleichungen:
K=Integral(p*|x|)
oder
K=Summ(P[i]*|s[i]|)
Die erste Option gilt für eine kontinuierliche Zufallsvariable, während die zweite für eine diskrete Variable gilt. Der besseren Übersichtlichkeit halber habe ich den diskreten Wert kontinuierlich gemacht, also die erste Gleichung verwendet. Das Integral erstreckt sich von minus bis plus unendlich. Dies ist das Gleichgewichts- oder Trendverhältnis. Nachdem wir es für einen Zufallswert berechnet haben, erhalten wir einen Gleichgewichtspunkt, mit dem wir die reale Verteilung der Preise mit der Referenzverteilung vergleichen können. Wenn Кp > K ist, kann der Markt als tendenziell angesehen werden. Wenn Кp < K ist, befindet sich der Markt in einer Seitwärtsbewegung.
Wir können den maximalen Wert des Verhältnisses berechnen. Er ist gleich KMax=1*Max(|x|) oder KMax=1*Max(|s[i]|). Wir können auch den Minimalwert des Verhältnisses berechnen. Er ist gleich KMin=1*Min(|x|) = 0 oder KMin=1*Min(|s[i]|) = 0. Der KMid-Mittelwert, das Minimum und das Maximum reichen aus, um Trend oder Seitwärtsbewegung des analysierten Bereichs in Prozent zu bewerten.
if ( K >= KMid ) KTrendPercent=((K-KMid)/(KMax-KMid))*100 else KFletPercent=((KMid-K)/KMid)*100.
Das reicht aber immer noch nicht aus, um die Situation vollständig zu charakterisieren. Hier kommt das zweite Verhältnis T=Integral(p*x), T=Summe(P[i]*s[i]) zur Hilfe. Es zeigt im Wesentlichen den erwarteten Payoff der Anzahl der Aufwärtsschritte an und ist gleichzeitig ein Indikator für den Alpha-Trend. Tp > 0 bedeutet einen Kauftrend, während Tp < 0 einen Verkaufstrend bedeutet, d. h. T=0 steht für den Random Walk.
Finden wir den maximalen und minimalen Wert des Verhältnisses: TMax=1*Max(x) or TMax=1*Max(s[i]), das Minimum ist im absoluten Wert gleich dem Maximum, aber es ist einfach negativ TMin= - TMax. Wenn wir den Alpha-Trend-Prozentsatz von 100 bis -100 messen, können wir Gleichungen für die Berechnung des Wertes schreiben, die der vorherigen ähnlich sind:
AProzent=( T /TMax)*100.
Wenn der Prozentsatz positiv ist, ist es ein Aufwärtstrend, wenn er negativ ist, ein Abwärtstrend. Die Fälle können gemischt sein. Es kann eine Alpha-Seitwärtsbewegung und einen Alpha-Trend geben, aber nicht gleichzeitig einen Alpha-Trend und Alpha-Seitwärtsbewegung. Nachfolgend finden Sie eine grafische Veranschaulichung der obigen Aussagen und Beispiele für konstruierte Dichtegraphen für verschiedene Anzahlen von Schritten.
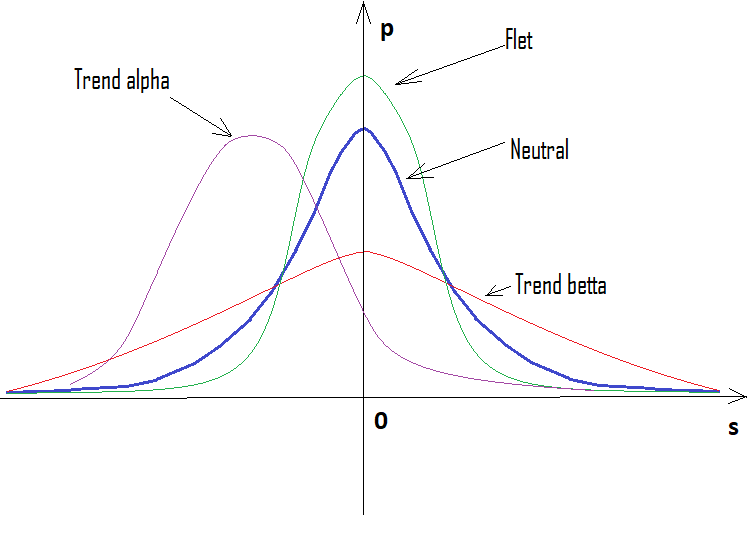
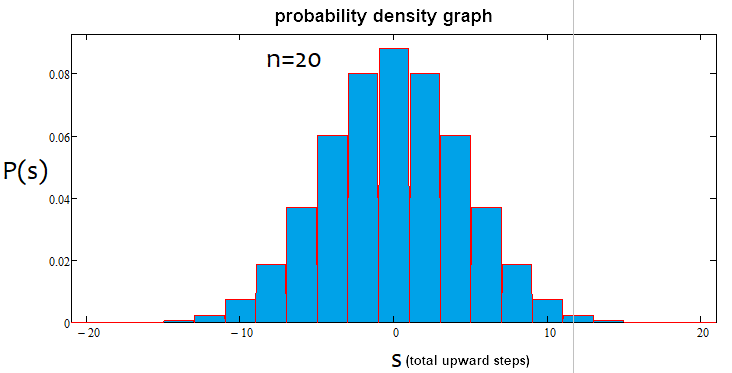
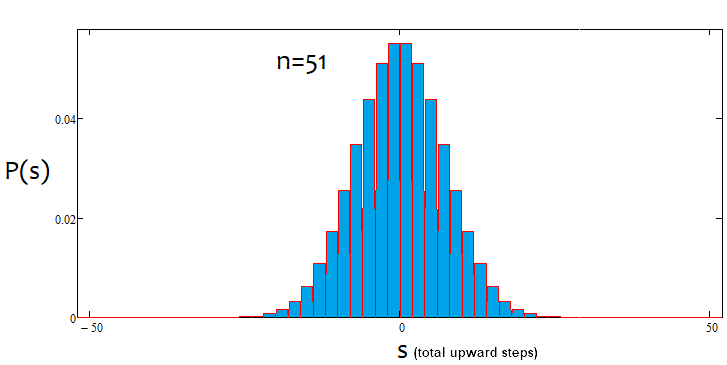
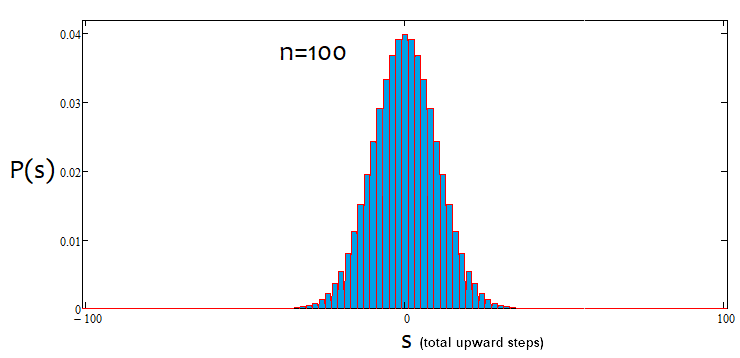
Wie wir sehen können, wird der Graph mit zunehmender Anzahl der Schritte schmaler und höher. Für jede Schrittanzahl sind die entsprechenden Alpha- und Beta-Werte unterschiedlich, genau wie die Verteilung selbst. Wenn Sie die Anzahl der Schritte ändern, sollte die Referenzverteilung neu berechnet werden.
Alle diese Gleichungen können verwendet werden, um automatisierte Handelssysteme zu erstellen. Diese Algorithmen können auch verwendet werden, um Indikatoren zu entwickeln. Einige Händler haben diese Dinge bereits in ihren EAs implementiert. Ich bin mir sicher: Es ist besser, diese Analysen anzuwenden, als sie zu vermeiden. Wer sich mit Mathematik auskennt, wird sofort auf neue Ideen kommen, wie man sie anwenden kann. Diejenigen, die es nicht sind, werden sich mehr Mühe geben müssen.
Einen einfachen Indikator schreiben
Hier werde ich meine einfache mathematische Forschung in einen Indikator umwandeln, der Markteintrittspunkte erkennt und als Grundlage für das Schreiben von EAs dient. Ich werde den Indikator in MQL5 entwickeln. Der Code soll aber weitestgehend für die Portierung auf MQL4 angepasst werden. Generell versuche ich, möglichst einfache Methoden zu verwenden und greife nur dann auf OOP zurück, wenn ein Code unnötig umständlich und unlesbar wird. Dies lässt sich jedoch in 90% der Fälle vermeiden. Unnötig bunte Panels, Buttons und eine Fülle von Daten, die in einem Chart angezeigt werden, behindern nur die visuelle Wahrnehmung. Stattdessen versuche ich immer, mit so wenig visuellen Hilfsmitteln wie möglich auszukommen.
Beginnen wir mit den Indikatoreingaben.
input uint BarsI=990;//Bars TO Analyse ( start calc. & drawing ) input uint StepsMemoryI=2000;//Steps In Memory input uint StepsI=40;//Formula Steps input uint StepPoints=30;//Step Value input bool bDrawE=true;//Draw Steps
Wenn der Indikator geladen ist, können wir die erste Berechnung einer bestimmten Anzahl von Schritten durchführen, indem wir bestimmte letzte Kerzen als Grundlage verwenden. Wir brauchen auch den Puffer, um Daten über unsere letzten Schritte zu speichern. Die neuen Daten sollen die alten ersetzen. Seine Größe soll begrenzt werden. Die gleiche Größe soll verwendet werden, um Schritte auf dem Chart zu zeichnen. Wir sollten die Anzahl der Schritte angeben, für die wir die Verteilung bilden und die notwendigen Werte berechnen sollen. Dann sollen wir dem System die Schrittgröße in Punkten mitteilen und ob wir eine Visualisierung der Schritte brauchen. Die Schritte sollen durch Zeichnen auf dem Chart visualisiert werden.
Ich habe den Indikatorstil in einem separaten Fenster gewählt, das die neutrale Verteilung und die aktuelle Situation anzeigt. Es gibt zwei Linien, obwohl es gut wäre, die dritte Linie zu haben. Leider sehen die Funktionen des Indikators das Zeichnen in einem separaten und Hauptfenster nicht vor, so dass ich auf das Zeichnen zurückgreifen musste.
Ich benutze immer den folgenden kleinen Trick, um auf die Balkendaten wie in MQL4 zugreifen zu können:
//variable to be moved in MQL5 double Close[]; double Open[]; double High[]; double Low[]; long Volume[]; datetime Time[]; double Bid; double Ask; double Point=_Point; int Bars=1000; MqlTick TickAlphaPsi; void DimensionAllMQL5Values()//set the necessary array size { ArrayResize(Close,BarsI,0); ArrayResize(Open,BarsI,0); ArrayResize(Time,BarsI,0); ArrayResize(High,BarsI,0); ArrayResize(Low,BarsI,0); ArrayResize(Volume,BarsI,0); } void CalcAllMQL5Values()//recalculate all arrays { ArraySetAsSeries(Close,false); ArraySetAsSeries(Open,false); ArraySetAsSeries(High,false); ArraySetAsSeries(Low,false); ArraySetAsSeries(Volume,false); ArraySetAsSeries(Time,false); if( Bars >= int(BarsI) ) { CopyClose(_Symbol,_Period,0,BarsI,Close); CopyOpen(_Symbol,_Period,0,BarsI,Open); CopyHigh(_Symbol,_Period,0,BarsI,High); CopyLow(_Symbol,_Period,0,BarsI,Low); CopyTickVolume(_Symbol,_Period,0,BarsI,Volume); CopyTime(_Symbol,_Period,0,BarsI,Time); } ArraySetAsSeries(Close,true); ArraySetAsSeries(Open,true); ArraySetAsSeries(High,true); ArraySetAsSeries(Low,true); ArraySetAsSeries(Volume,true); ArraySetAsSeries(Time,true); SymbolInfoTick(Symbol(),TickAlphaPsi); Bid=TickAlphaPsi.bid; Ask=TickAlphaPsi.ask; } ////////////////////////////////////////////////////////////
Jetzt wird der Code so weit wie möglich mit MQL4 kompatibel gemacht und wir sind in der Lage, ihn schnell und einfach in ein MQL4-Analogon zu verwandeln.
Um die Schritte zu beschreiben, müssen wir zunächst die Knoten beschreiben.
struct Target//structure for storing node data { double Price0;//node price datetime Time0;//node price bool Direction;//direction of a step ending at the current node bool bActive;//whether the node is active }; double StartTick;//initial tick price Target Targets[];//destination point ticks (points located from the previous one by StepPoints)
Zusätzlich benötigen wir einen Punkt, von dem aus der nächste Schritt gezählt wird. Der Knoten speichert Daten über sich selbst und den Schritt, der an ihm endete, sowie die boolesche Komponente, die angibt, ob der Knoten aktiv ist. Erst wenn der gesamte Speicher des Knoten-Arrays mit realen Knoten gefüllt ist, wird die reale Verteilung berechnet, da sie nach Schritten berechnet wird. Keine Schritte — keine Berechnung.
Weiterhin müssen wir die Möglichkeit haben, den Status der Schritte bei jedem Tick zu aktualisieren und bei der Initialisierung des Indikators eine ungefähre Berechnung nach Balken durchzuführen.
bool UpdatePoints(double Price00,datetime Time00)//update the node array and return 'true' in case of a new node { if ( MathAbs(Price00-StartTick)/Point >= StepPoints )//if the step size reaches the required one, write it and shift the array back { for(int i=ArraySize(Targets)-1;i>0;i--)//first move everything back { Targets[i]=Targets[i-1]; } //after that, generate a new node Targets[0].bActive=true; Targets[0].Time0=Time00; Targets[0].Price0=Price00; Targets[0].Direction= Price00 > StartTick ? true : false; //finally, redefine the initial tick to track the next node StartTick=Price00; return true; } else return false; } void StartCalculations()//approximate initial calculations (by bar closing prices) { for(int j=int(BarsI)-2;j>0;j--) { UpdatePoints(Close[j],Time[j]); } }
Beschreiben wir anschließend die Methoden und Variablen, die zur Berechnung aller Parameter der neutralen Linie erforderlich sind. Die Ordinate stellt die Wahrscheinlichkeit einer bestimmten Kombination oder eines bestimmten Ergebnisses dar. Ich mag es nicht, dies als Normalverteilung zu bezeichnen, da die Normalverteilung eine kontinuierliche Größe ist, während ich den Graphen eines diskreten Wertes aufbaue. Außerdem handelt es sich bei der Normalverteilung um eine Wahrscheinlichkeitsdichte und nicht um eine Wahrscheinlichkeit wie im Fall des Indikators. Es ist bequemer, einen Wahrscheinlichkeitsgraphen zu erstellen, als seine Dichte.
int S[];//array of final upward steps int U[];//array of upward steps int D[];//array of downward steps double P[];//array of particular outcome probabilities double KBettaMid;//neutral Betta ratio value double KBettaMax;//maximum Betta ratio value //minimum Betta = 0, there is no point in setting it double KAlphaMax;//maximum Alpha ratio value double KAlphaMin;//minimum Alpha ratio value //average Alpha = 0, there is no point in setting it int CalcNumSteps(int Steps0)//calculate the number of steps { if ( Steps0/2.0-MathFloor(Steps0/2.0) == 0 ) return int(Steps0/2.0); else return int((Steps0-1)/2.0); } void ReadyArrays(int Size0,int Steps0)//prepare the arrays { int Size=CalcNumSteps(Steps0); ArrayResize(S,Size); ArrayResize(U,Size); ArrayResize(D,Size); ArrayResize(P,Size); ArrayFill(S,0,ArraySize(S),0);//clear ArrayFill(U,0,ArraySize(U),0); ArrayFill(D,0,ArraySize(D),0); ArrayFill(P,0,ArraySize(P),0.0); } void CalculateAllArrays(int Size0,int Steps0)//calculate all arrays { ReadyArrays(Size0,Steps0); double CT=CombTotal(Steps0);//number of combinations for(int i=0;i<ArraySize(S);i++) { S[i]=Steps0/2.0-MathFloor(Steps0/2.0) == 0 ? i*2 : i*2+1 ; U[i]=int((S[i]+Steps0)/2.0); D[i]=Steps0-U[i]; P[i]=C(Steps0,U[i])/CT; } } void CalculateBettaNeutral()//calculate all Alpha and Betta ratios { KBettaMid=0.0; if ( S[0]==0 ) { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=1;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } else { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } KBettaMax=S[ArraySize(S)-1]; KAlphaMax=S[ArraySize(S)-1]; KAlphaMin=-KAlphaMax; } double Factorial(int n)//factorial of n value { double Rez=1.0; for(int i=1;i<=n;i++) { Rez*=double(i); } return Rez; } double C(int n,int k)//combinations from n by k { return Factorial(n)/(Factorial(k)*Factorial(n-k)); } double CombTotal(int n)//number of combinations in total { return MathPow(2.0,n); }
Alle diese Funktionen sollten an der richtigen Stelle aufgerufen werden. Alle Funktionen hier sind entweder für die Berechnung der Werte von Arrays vorgesehen, oder sie implementieren einige mathematische Hilfsfunktionen, außer den ersten beiden. Sie werden bei der Initialisierung zusammen mit der Berechnung der neutralen Verteilung aufgerufen und zum Einstellen der Größe der Arrays verwendet.
Erstellen Sie als Nächstes den Codeblock für die Berechnung der realen Verteilung und ihrer Hauptparameter auf die gleiche Weise.
double AlphaPercent;//alpha trend percentage double BettaPercent;//betta trend percentage int ActionsTotal;//total number of unique cases in the Array of steps considering the number of steps for checking the option int Np[];//number of actual profitable outcomes of a specific case int Nm[];//number of actual losing outcomes of a specific case double Pp[];//probability of a specific profitable step double Pm[];//probability of a specific losing step int Sm[];//number of losing steps void ReadyMainArrays()//prepare the main arrays { if ( S[0]==0 ) { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)-1); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)-1); ArrayResize(Sm,ArraySize(S)-1); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i+1]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } else { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)); ArrayResize(Sm,ArraySize(S)); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } } void CalculateActionsTotal(int Size0,int Steps0)//total number of possible outcomes made up of the array of steps { ActionsTotal=(Size0-1)-(Steps0-1); } bool CalculateMainArrays(int Steps0)//count the main arrays { int U0;//upward steps int D0;//downward steps int S0;//total number of upward steps if ( Targets[ArraySize(Targets)-1].bActive ) { ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); for(int i=1;i<=ActionsTotal;i++) { U0=0; D0=0; S0=0; for(int j=0;j<Steps0;j++) { if ( Targets[ArraySize(Targets)-1-i-j].Direction ) U0++; else D0++; } S0=U0-D0; for(int k=0;k<ArraySize(S);k++) { if ( S[k] == S0 ) { Np[k]++; break; } } for(int k=0;k<ArraySize(Sm);k++) { if ( Sm[k] == S0 ) { Nm[k]++; break; } } } for(int k=0;k<ArraySize(S);k++) { Pp[k]=Np[k]/double(ActionsTotal); } for(int k=0;k<ArraySize(Sm);k++) { Pm[k]=Nm[k]/double(ActionsTotal); } AlphaPercent=0.0; BettaPercent=0.0; for(int k=0;k<ArraySize(S);k++) { AlphaPercent+=S[k]*Pp[k]; BettaPercent+=MathAbs(S[k])*Pp[k]; } for(int k=0;k<ArraySize(Sm);k++) { AlphaPercent+=Sm[k]*Pm[k]; BettaPercent+=MathAbs(Sm[k])*Pm[k]; } AlphaPercent= (AlphaPercent/KAlphaMax)*100; BettaPercent= (BettaPercent-KBettaMid) >= 0.0 ? ((BettaPercent-KBettaMid)/(KBettaMax-KBettaMid))*100 : ((BettaPercent-KBettaMid)/KBettaMid)*100; Comment(StringFormat("Alpha = %.f %%\nBetta = %.f %%",AlphaPercent,BettaPercent));//display these numbers on the screen return true; } else return false; }
Hier ist alles einfach, aber es gibt viel mehr Arrays, da der Graph nicht immer an der vertikalen Achse gespiegelt ist. Um dies zu erreichen, benötigen wir zusätzliche Arrays und Variablen, aber die allgemeine Logik ist einfach: Berechnen Sie die Anzahl der spezifischen Fallergebnisse und teilen Sie diese durch die Gesamtzahl aller Ergebnisse. So erhalten wir alle Wahrscheinlichkeiten (Ordinaten) und die entsprechenden Abszissen. Ich werde nicht auf jede einzelne Schleife und Variable eingehen. All diese Komplexitäten sind nötig, um Probleme mit dem Verschieben von Werten in die Puffer zu vermeiden. Hier ist alles fast gleich: die Größe der Arrays definieren und sie zählen. Als Nächstes berechnen Sie die Alpha- und Beta-Trend-Prozentsätze und zeigen sie in der oberen linken Ecke des Bildschirms an.
Es bleibt zu definieren, was wo aufgerufen werden soll.
int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,NeutralBuffer,INDICATOR_DATA); SetIndexBuffer(1,CurrentBuffer,INDICATOR_DATA); CleanAll(); DimensionAllMQL5Values(); CalcAllMQL5Values(); StartTick=Close[BarsI-1]; ArrayResize(Targets,StepsMemoryI);//maximum number of nodes CalculateAllArrays(StepsMemoryI,StepsI); CalculateBettaNeutral(); StartCalculations(); ReadyMainArrays(); CalculateActionsTotal(StepsMemoryI,StepsI); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { CalcAllMQL5Values(); if ( UpdatePoints(Close[0],TimeCurrent()) ) { if ( CalculateMainArrays(StepsI) ) { if ( bDrawE ) RedrawAll(); } } int iterator=rates_total-(ArraySize(Sm)+ArraySize(S))-1; for(int i=0;i<ArraySize(Sm);i++) { iterator++; NeutralBuffer[iterator]=P[ArraySize(S)-1-i]; CurrentBuffer[iterator]=Pm[ArraySize(Sm)-1-i]; } for(int i=0;i<ArraySize(S);i++) { iterator++; NeutralBuffer[iterator]=P[i]; CurrentBuffer[iterator]=Pp[i]; } return(rates_total); }
CurrentBuffer und NeutralBuffer werden hier als Puffer verwendet. Zur besseren Übersichtlichkeit habe ich die Anzeige auf den nächstgelegenen Kerzen zum Markt eingeführt. Jede Wahrscheinlichkeit befindet sich auf einem separaten Balken. Dadurch konnten wir uns von unnötigen Komplikationen befreien. Zoomen Sie einfach den Chart ein und aus, um alles zu sehen. Die Funktionen CleanAll() und RedrawAll() werden hier nicht gezeigt. Sie können auskommentiert werden, und alles wird auch ohne Rendering funktionieren. Außerdem habe ich den Zeichenblock hier nicht eingefügt. Sie finden ihn im Anhang. Dort gibt es nichts Bemerkenswertes. Der Indikator ist auch unten in zwei Versionen angehängt — für MetaTrader 4 und MetaTrader 5.
Dieser sieht dann wie folgt aus.
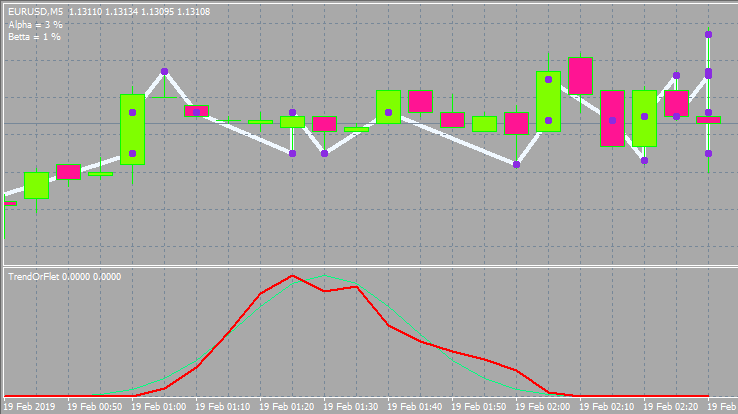
Unten ist die Variante mit anderen Eingaben und Fensterstil.
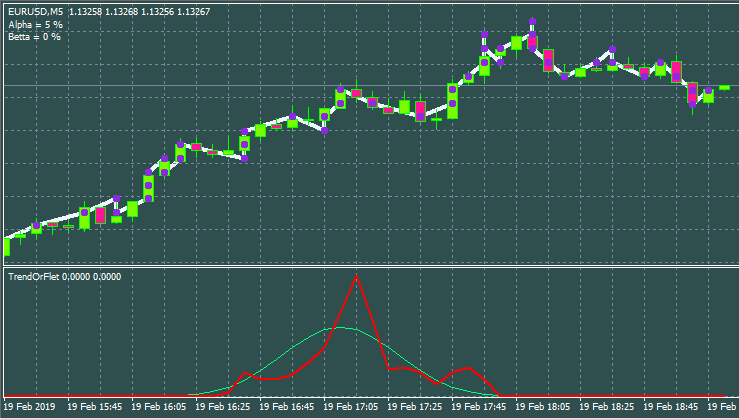
Rückblick auf die interessantesten Strategien
Ich habe viele Strategien entwickelt und gesehen. Meiner bescheidenen Erfahrung nach passieren die bemerkenswertesten Dinge, wenn man ein Grid oder Martingale oder beides verwendet. Streng genommen ist der erwartete Payoff sowohl bei Martingale als auch bei Grid 0. Lassen Sie sich nicht von aufwärtsgerichteten Charts täuschen, denn eines Tages werden Sie einen großen Verlust erleiden. Es gibt funktionierende Grids und sie können auf dem Markt gefunden werden. Sie funktionieren recht gut und zeigen sogar einen Gewinnfaktor von 3-6. Dies ist ein recht hoher Wert. Außerdem bleiben sie auf jedem Währungspaar stabil. Aber es ist nicht einfach, Filter zu finden, die es Ihnen ermöglichen, zu gewinnen. Die oben beschriebene Methode erlaubt es Ihnen, diese Signale auszusortieren. Das Grid erfordert einen Trend, während die Richtung nicht wichtig ist.
Martingale und Grid sind die Beispiele für die einfachsten und beliebtesten Strategien. Allerdings ist nicht jeder in der Lage, sie richtig anzuwenden. Selbstanpassende Expert Advisors sind ein bisschen komplexer. Sie sind in der Lage, sich an alles anzupassen, sei es eine Seitwärtsbewegung, ein Trend oder ein anderes Muster. Bei ihnen wird in der Regel ein bestimmter Teil des Marktes genommen, um nach Mustern zu suchen und eine kurze Zeitspanne zu handeln, in der Hoffnung, dass das Muster für einige Zeit bestehen bleibt.
Eine separate Gruppe bilden die exotischen Systeme mit geheimnisvollen, unkonventionellen Algorithmen, die versuchen, von der chaotischen Natur des Marktes zu profitieren. Solche Systeme basieren auf reiner Mathematik und sind in der Lage, auf jedem Instrument und in jeder Zeitperiode einen Gewinn zu erzielen. Der Gewinn ist nicht groß, aber stabil. Ich habe mich in letzter Zeit mit solchen Systemen beschäftigt. Zu dieser Gruppe gehören auch Brute-Force-basierte Roboter. Die Brute-Force kann mit zusätzlicher Software durchgeführt werden. Im nächsten Artikel werde ich meine Version eines solchen Programms zeigen.
Die oberste Nische wird von Robotern besetzt, die auf neuronalen Netzen und ähnlicher Software basieren. Diese Roboter zeigen sehr unterschiedliche Ergebnisse und weisen den höchsten Grad an Raffinesse auf, da das neuronale Netzwerk ein Prototyp der KI ist. Wenn ein neuronales Netzwerk richtig entwickelt und trainiert wurde, ist es in der Lage, die höchste Effizienz zu zeigen, die von keiner anderen Strategie erreicht wird.
Was die Arbitrage betrifft, so sind deren Möglichkeiten meiner Meinung nach mittlerweile fast gleich Null. Ich habe die entsprechenden EAs, die keine Ergebnisse liefern.
Ist es die Mühe wert?
Jemand handelt aus Aufregung an den Märkten, jemand sucht nach einfachem und schnellem Geld, während jemand die Marktprozesse über Gleichungen und Theorien studieren möchte. Außerdem gibt es Händler, die einfach keine andere Wahl haben, da es für sie keinen Weg zurück gibt. Ich gehöre meistens zu der letzteren Kategorie. Mit all meinem Wissen und meiner Erfahrung habe ich derzeit kein profitables, stabiles Konto. Ich habe EAs, die gute Testläufe zeigen, aber alles ist nicht so einfach, wie es scheint.
Diejenigen, die danach streben, schnell reich zu werden, werden höchstwahrscheinlich das gegenteilige Ergebnis erleben. Schließlich ist der Markt nicht dafür geschaffen, dass ein gewöhnlicher Händler gewinnt. Er hat genau das gegenteilige Ziel. Wenn Sie jedoch mutig genug sind, sich an das Thema heranzuwagen, dann stellen Sie sicher, dass Sie viel Zeit und Geduld haben. Das Ergebnis wird nicht schnell eintreten. Wenn Sie keine Programmierkenntnisse haben, dann haben Sie praktisch überhaupt keine Chance. Ich habe eine Menge Pseudo-Händler gesehen, die mit Ergebnissen prahlen, nachdem sie 20-30 Geschäfte gemacht haben. In meinem Fall, nachdem ich einen anständigen EA entwickelt habe, funktioniert er vielleicht ein oder zwei Jahre, aber dann versagt er unweigerlich...In vielen Fällen funktioniert er von Anfang an nicht.
Natürlich gibt es so etwas wie manuelles Trading, aber ich glaube, dass es eher einer Kunst ähnelt. Alles in allem ist es möglich, an der Börse Geld zu verdienen, aber Sie werden viel Zeit investieren. Ich persönlich glaube nicht, dass es das wert ist. Aus der mathematischen Perspektive ist der Markt nur eine langweilige zweidimensionale Kurve. Ich möchte sicherlich nicht mein ganzes Leben lang auf Kerzen schauen.
Gibt es den Gral und wo kann man ihn suchen?
Ich glaube, dass der Gral mehr als möglich ist. Ich habe relativ einfache EAs, die das beweisen. Leider deckt deren erwarteter Payoff kaum den Spread. Ich denke, fast jeder Entwickler hat Strategien, die dies bestätigen. Der Markt hat viele Roboter, die in jeder Hinsicht als Gral bezeichnet werden können. Aber mit solchen Systemen Geld zu verdienen ist extrem schwierig, da man um jeden Pip kämpfen muss, sowie Spread-Return und Partnerschaftsprogramme aktivieren muss. Grale mit beachtlichen Gewinnen und geringen Einzahlungsbeträgen sind selten.
Wenn Sie selbst einen Gral entwickeln wollen, dann ist es besser, sich nach neuronalen Netzwerken umzusehen. Sie haben viel Potenzial in Bezug auf den Gewinn. Natürlich können Sie versuchen, verschiedene exotische Ansätze und Brute-Force zu kombinieren, aber ich empfehle, sich gleich mit neuronalen Netzwerken zu beschäftigen.
Seltsamerweise ist die Antwort auf die Fragen, ob es einen Gral gibt und wo man nach einem solchen suchen sollte, ziemlich einfach und für mich nach Tonnen von EAs, die ich entwickelt habe, offensichtlich.
Tipps für gewöhnliche Händler
Alle Händler wollen drei Dinge:
- Erzielen eines positiven erwarteten Payoffs
- Gewinn der gewinnbringenden Positionen erhöhen
- Verlust der Verlustpositionen reduzieren
Der erste Punkt ist hier der wichtigste. Wenn Sie eine profitable Strategie haben (unabhängig davon, ob es sich um eine manuelle oder algorithmische handelt), werden Sie immer eingreifen wollen. Dies sollte nicht erlaubt sein. Situationen, in denen weniger gewinnbringende Positionen als verlierende gibt, üben einen erheblichen psychologischen Einfluss aus und ruinieren ein Handelssystem. Am wichtigsten ist, dass Sie sich nicht beeilen, Ihre Verluste zurückzugewinnen, wenn Sie im Minus sind. Andernfalls könnten es noch mehr Verlusten werden. Denken Sie an einen erwarteten Payoff. Es spielt keine Rolle, wie hoch der Kapitalverlust der aktuellen Position ist. Was wirklich zählt, ist die Gesamtzahl der Positionen und das Gewinn/Verlust-Verhältnis.
Die nächste wichtige Sache ist die Losgröße, die Sie bei Ihrem Handel anwenden. Wenn Sie derzeit im Gewinn sind, sollten Sie die Losgröße schrittweise reduzieren. Andernfalls erhöhen Sie sie. Es sollte jedoch nur bis zu einem bestimmten Schwellenwert erhöht werden. Dies ist ein Forward- und Reverse-Martingale. Wenn Sie sorgfältig nachdenken, können Sie Ihren eigenen EA entwickeln, der rein auf der Variationen der Losgrößen basiert. Das wird dann kein Grid oder Martingal mehr sein, sondern etwas Komplexeres und Sichereres. Außerdem kann ein solcher EA auf allen Währungspaaren in der gesamten Geschichte der Preise funktionieren. Dieses Prinzip funktioniert auch in einem chaotischen Markt, und es spielt keine Rolle, wo und wie Sie einsteigen. Bei richtiger Anwendung werden Sie alle Spreads und Kommissionen kompensieren, und bei meisterhafter Anwendung werden Sie mit einem Gewinn herauskommen, auch wenn Sie den Markt an einem zufälligen Punkt und in einer zufälligen Richtung betreten.
Um Verluste zu reduzieren und Gewinne zu erhöhen, versuchen Sie, auf einer negativen Halbwelle zu kaufen und auf einer positiven Halbwelle zu verkaufen. Eine Halbwelle zeigt in der Regel die vorherige Aktivität von Käufern oder Verkäufern im aktuellen Marktbereich an, was wiederum bedeutet, dass einige von ihnen auf dem Markt waren, während offene Positionen früher oder später geschlossen werden und den Preis in die entgegengesetzte Richtung drücken. Das ist der Grund, warum der Markt eine Wellenstruktur hat. Wir können diese Wellen überall sehen. Auf einen Kauf folgt ein Verkauf und andersherum. Schließen Sie auch Ihre Positionen nach dem gleichen Kriterium.
Schlussfolgerung
Die Sichtweise eines jeden ist subjektiv. Am Ende hängt alles von Ihnen ab, so oder so. Trotz aller Nachteile und verschwendeter Zeit möchte jeder sein eigenes Supersystem schaffen und die Früchte seiner Entschlossenheit ernten. Ansonsten sehe ich keinen Sinn darin, sich überhaupt mit dem Forex-Handel zu beschäftigen. Irgendwie bleibt diese Tätigkeit für viele Händler, mich eingeschlossen, attraktiv. Jeder weiß, wie dieses Gefühl genannt wird, aber es wird kindisch klingen. Deshalb werde ich es nicht benennen, um Trolling zu vermeiden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8274
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Parallele Partikelschwarmoptimierung
Parallele Partikelschwarmoptimierung
 Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
 Fortschrittliches Resampling und Auswahl von CatBoost-Modellen durch die Brute-Force-Methode
Fortschrittliches Resampling und Auswahl von CatBoost-Modellen durch die Brute-Force-Methode
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Vielen Dank für diesen Artikel. Ich war nie wirklich gut in Mathe, aber ich werde weiter versuchen, es zu verstehen, damit ich ein besserer Händler werden kann.
Toller Artikel! Ich danke Ihnen!
Danke, ich habe seit diesem Artikel eine Menge anderer Artikel geschrieben. Lesen Sie sie und schauen Sie, ob Sie noch etwas Nützliches finden.