
Erforschung des maschinellen Lernens im unidirektionalen Trendhandel am Beispiel von Gold
Einführung
In jüngster Zeit haben wir uns mit der Umsetzung symmetrischer Handelssysteme unter dem Aspekt der binären Klassifizierung befasst. Wir sind davon ausgegangen, dass Kauf- und Verkaufstransaktionen im Merkmalsraum gut getrennt werden können, d. h. es gibt eine Trennlinie (Hyperebene), die es dem Algorithmus für maschinelles Lernen ermöglicht, sowohl Kauf- und Verkaufstransaktionen gleich gut vorherzusagen.
In der Realität ist dies nicht immer der Fall, vor allem nicht bei Trendhandelsinstrumenten wie einigen Metallen und Indizes sowie bei Kryptowährungen. In Situationen, in denen ein Vermögenswert einen klar definierten unidirektionalen Trend aufweist, können Handelssysteme, die Käufe und Verkäufe implizieren, zu riskant sein. Und die Gesamtverteilung solcher Handelsgeschäfte kann sehr asymmetrisch sein, was zu Fehlklassifizierungen mit einer großen Anzahl von Fehlern führt.
In diesem Fall kann ein bidirektionales Handelssystem unwirksam sein, und es wäre besser, sich auf den Handel in eine Richtung zu konzentrieren. Dieser Artikel soll die Möglichkeiten des maschinellen Lernens zur Entwicklung solcher unidirektionalen Strategien beleuchten.
Ich schlage vor, dass die Ansätze für kausale Schlussfolgerungen neu konzipiert und an die Aufgabe des unidirektionalen Handels angepasst werden müssen.
Nehmen wir die Materialien aus früheren Artikeln als Grundlage:
- Die Kreuzvalidierung und die Grundlagen der kausalen Inferenz in CatBoost-Modellen, Export ins ONNX-Format
- Kausalschluss in den Problemen bei Zeitreihenklassifizierungen
- Schneller Handelsstrategie-Tester in Python mit Numba
Ich empfehle dringend die Lektüre dieser Artikel, um ein umfassenderes Verständnis der Idee des Kausalschlusses und der Kausalprüfung zu erlangen.
Erstellen eines Samplers von Handelsgeschäften in einer bestimmten Richtung
Da wir früher Kauf- und Verkaufsgeschäfte gleichzeitig markiert haben, müssen wir den Handelsmarker so ändern, dass er nur Handelsgeschäfte für die ausgewählte Richtung markiert. Nachstehend finden Sie ein Beispiel für einen solchen Probenehmer, der in diesem Artikel verwendet wird:
@njit def calculate_labels_one_direction(close_data, markup, min, max, direction): labels = [] for i in range(len(close_data) - max): rand = random.randint(min, max) curr_pr = close_data[i] future_pr = close_data[i + rand] if direction == "sell": if (future_pr + markup) < curr_pr: labels.append(1.0) else: labels.append(0.0) if direction == "buy": if (future_pr - markup) > curr_pr: labels.append(1.0) else: labels.append(0.0) return labels def get_labels_one_direction(dataset, markup, min = 1, max = 15, direction = 'buy') -> pd.DataFrame: close_data = dataset['close'].values labels = calculate_labels_one_direction(close_data, markup, min, max, direction) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() return dataset
Es gibt einen neuen Parameter „Richtung“, mit dem Sie die erforderliche Richtung für die Kennzeichnung von Kauf- oder Verkaufsgeschäften festlegen können. Eine Klasse mit der Bezeichnung „1“ zeigt an, dass ein Handel in der gewählten Richtung möglich ist, und eine Klasse mit der Bezeichnung „0“ bedeutet, dass es besser ist, zu diesem Zeitpunkt keinen Handel zu eröffnen. Die Parameter geben auch eine zufällige Dauer des Handels im Bereich {min, max} an. Die Dauer wird in der Anzahl der Balken gemessen, die seit der Eröffnung des Handelsgeschäfts vergangen sind. Dies ist ein einfaches Stichprobenverfahren, das sich für diese Art von Strategie als sehr effektiv erwiesen hat.
Modifizierung des nutzerdefinierten Strategietesters
Für unidirektionale Strategien ist nun eine andere Prüflogik erforderlich. Daher muss der Strategietester selbst geändert werden, um die Logik anzupassen. Dem Modul 'tester_lib.py' wurden Funktionen für unidirektionales Testen hinzugefügt. Schauen wir sie uns genauer an.
Die Funktion process_data_one_direction() verarbeitet Daten für den Handel in einer Richtung:
@jit(nopython=True) def process_data_one_direction(close, labels, metalabels, stop, take, markup, forward, backward, direction): last_deal = 2 last_price = 0.0 report = [0.0] chart = [0.0] line_f = 0 line_b = 0 for i in range(len(close)): line_f = len(report) if i <= forward else line_f line_b = len(report) if i <= backward else line_b pred = labels[i] pr = close[i] pred_meta = metalabels[i] # 1 = allow trades if last_deal == 2 and pred_meta == 1: last_price = pr last_deal = 2 if pred < 0.5 else 1 continue if last_deal == 1 and direction == 'buy': if (-markup + (pr - last_price) >= take) or (-markup + (last_price - pr) >= stop): last_deal = 2 profit = -markup + (pr - last_price) report.append(report[-1] + profit) chart.append(chart[-1] + profit) continue if last_deal == 1 and direction == 'sell': if (-markup + (pr - last_price) >= stop) or (-markup + (last_price - pr) >= take): last_deal = 2 profit = -markup + (last_price - pr) report.append(report[-1] + profit) chart.append(chart[-1] + (pr - last_price)) continue # close deals by signals if last_deal == 1 and pred < 0.5 and direction == 'buy': last_deal = 2 profit = -markup + (pr - last_price) report.append(report[-1] + profit) chart.append(chart[-1] + profit) continue if last_deal == 1 and pred < 0.5 and direction == 'sell': last_deal = 2 profit = -markup + (last_price - pr) report.append(report[-1] + profit) chart.append(chart[-1] + (pr - last_price)) continue return np.array(report), np.array(chart), line_f, line_b
Der Hauptunterschied zur Basisfunktion besteht darin, dass jetzt Flags verwendet werden, die ausdrücklich angeben, welche Art von Handelsgeschäften im Tester verwendet wird: Kauf oder Verkauf. Die Funktion ist dank der Beschleunigung durch Numba sehr schnell und führt einen Durchlauf durch die Kurshistorie durch, wobei der Gewinn aus jedem Handel berechnet wird. Bitte beachten Sie, dass der Tester in der Lage ist, Handelsgeschäfte auf der Grundlage von Modellsignalen sowie von Stop-Loss und Take-Profit zu schließen, je nachdem, welche Bedingung früher ausgelöst wurde. Dies ermöglicht die Auswahl von Modellen, die sich bereits in der Lernphase befinden, vorbehaltlich der für Sie akzeptablen Risiken.
Die Funktion tester_one_direction() verarbeitet einen markierten Datensatz, der Preise und Beschriftungen enthält, und übergibt diese Daten an die Funktion process_data_one_direction(), die dann das Ergebnis für die anschließende Darstellung im Chart abruft.
def tester_one_direction(*args): ''' This is a fast strategy tester based on numba List of parameters: dataset: must contain first column as 'close' and last columns with "labels" and "meta_labels" stop: stop loss value take: take profit value forward: forward time interval backward: backward time interval markup: markup value direction: buy/sell plot: false/true ''' dataset, stop, take, forward, backward, markup, direction, plot = args forw = dataset.index.get_indexer([forward], method='nearest')[0] backw = dataset.index.get_indexer([backward], method='nearest')[0] close = dataset['close'].to_numpy() labels = dataset['labels'].to_numpy() metalabels = dataset['meta_labels'].to_numpy() report, chart, line_f, line_b = process_data_one_direction(close, labels, metalabels, stop, take, markup, forw, backw, direction) y = report.reshape(-1, 1) X = np.arange(len(report)).reshape(-1, 1) lr = LinearRegression() lr.fit(X, y) l = 1 if lr.coef_[0][0] >= 0 else -1 if plot: plt.plot(report) plt.axvline(x=line_f, color='purple', ls=':', lw=1, label='OOS') plt.axvline(x=line_b, color='red', ls=':', lw=1, label='OOS2') plt.plot(lr.predict(X)) plt.title("Strategy performance R^2 " + str(format(lr.score(X, y) * l, ".2f"))) plt.xlabel("the number of trades") plt.ylabel("cumulative profit in pips") plt.show() return lr.score(X, y) * l
Die Funktion test_model_one_direction() ermittelt Modellvorhersagen auf der Grundlage der ausgewählten Daten. Diese Vorhersagen werden an die Funktion tester_one_direction() übergeben, um das Testergebnis dieses Modells zu drucken.
def test_model_one_direction(dataset: pd.DataFrame, result: list, stop: float, take: float, forward: float, backward: float, markup: float, direction: str, plt = False): ext_dataset = dataset.copy() X = ext_dataset[ext_dataset.columns[1:]] ext_dataset['labels'] = result[0].predict_proba(X)[:,1] ext_dataset['meta_labels'] = result[1].predict_proba(X)[:,1] ext_dataset['labels'] = ext_dataset['labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0) ext_dataset['meta_labels'] = ext_dataset['meta_labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0) return tester_one_direction(ext_dataset, stop, take, forward, backward, markup, direction, plt)
Meta-Learner als Herzstück eines Handelssystems
Betrachten wir den ersten Meta-Learner aus dem Artikel über die Kreuzvalidierung, und ich werde versuchen, eine logische Erklärung dafür zu geben, warum er im Fall von unidirektionalen Strategien besser funktioniert als im Fall von bidirektionalen.
def meta_learner(folds_number: int, iter: int, depth: int, l_rate: float) -> pd.DataFrame: dataset = get_labels_one_direction(get_features(get_prices()), markup=hyper_params['markup'], min=1, max=15, direction=hyper_params['direction']) data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy() X = data[data.columns[1:-2]] y = data['labels'] B_S_B = pd.DatetimeIndex([]) # learn meta model with CV method meta_model = CatBoostClassifier(iterations = iter, max_depth = depth, learning_rate=l_rate, verbose = False) cv = StratifiedKFold(n_splits=folds_number, shuffle=False) predicted = cross_val_predict(meta_model, X, y, method='predict_proba', cv=cv) coreset = X.copy() coreset['labels'] = y coreset['labels_pred'] = [x[0] < 0.5 for x in predicted] coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1) # select bad samples (bad labels indices) diff_negatives = coreset['labels'] != coreset['labels_pred'] B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index) to_mark = B_S_B.value_counts() marked_idx = to_mark.index data['meta_labels'] = 1.0 data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0 data.loc[data.index.isin(marked_idx), 'labels'] = 0.0 return data[data.columns[:]]
Zur Verdeutlichung ist unten ein Diagramm der Meta-Learner in Form von Schlüsselblöcken abgebildet, die für verschiedene Funktionen zuständig sind.
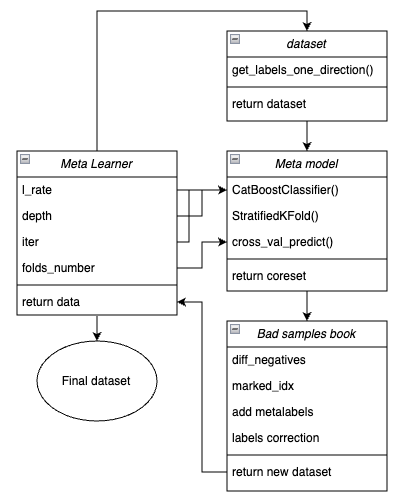
Abbildung 1. Schematische Darstellung der Funktion meta_learner()
Es sei daran erinnert, dass der Meta-Learner ein Übersetzungsgetriebe zwischen den Ausgangsdaten und dem endgültigen Modell ist. Es übernimmt die Hauptlast der effektiven Vorverarbeitung, indem es durch ein Metamodell Meta-Kennzeichnungen erstellt. Die Einzigartigkeit der von mir entwickelten Funktion liegt in der Tatsache, dass sie geklärte und gut aufbereitete Datensätze erzeugt, aufgrund derer robuste Modelle und Handelssysteme entstehen.
Funktionseingabeparameter:
- l_rate (Lernrate) ist der Gradientenschritt für das Metamodell oder den CatBoost-Klassifikator. Er wird in einem Bereich von {0,01, 0,5} festgelegt. Der Algorithmus ist empfindlich gegenüber diesem Parameter.
- depth ist für die Tiefe der Entscheidungsbäume verantwortlich, die bei jeder Iteration des CatBoost-Klassifikator-Trainings erstellt werden. Der empfohlene Wertebereich ist {1, 6}.
- iter ist die Anzahl der Trainingswiederholungen, empfohlen wird ein Wert im Bereich {5, 25}.
- folds_number ist die Anzahl der Faltungen für die Kreuzvalidierung. In der Regel sind {5, 15} Falten ausreichend.
Der Mechanismus der Funktionsweise:
- Es wird ein Datensatz mit Merkmalen und Bezeichnungen erstellt. Die zuvor beschriebene Funktion get_labels_one_direction() wird als Sampler verwendet.
- Ein Meta-Learner mit den angegebenen Parametern wird auf diesen Daten im Kreuzvalidierungsmodus mit der Funktion StratifiedKFold() trainiert. Die Funktion unterteilt die Trainingsdaten in mehrere Faltungen, abhängig von der Ausgewogenheit der Klassen. Für jede Falte wird ein Metamodell trainiert, und anschließend werden alle Vorhersagen gespeichert. Dies ist notwendig, um eine unverzerrte Schätzung der Modellfehler bei den Trainingsdaten zu erhalten. Diese Vorhersagen werden zum Vergleich mit den ursprünglichen Kennzeichnungen verwendet.
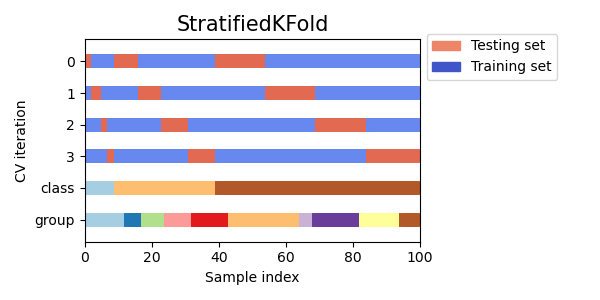
Abb. 2. Ein Schema zur Aufteilung von Daten in Faltungen unter Verwendung der Funktion StratifiedKFold()
- Es wird ein separater Kerndatensatz erstellt, der sowohl die ursprünglichen als auch die vorhergesagten Bezeichnungen durch Kreuzvalidierung erfasst.
- Es wird eine separate Variable diff_negatives erstellt, die binäre Flags für Übereinstimmungen zwischen dem Original und den vorhergesagten Bezeichnungen speichert.
- Ein Buch mit schlechten Proben B_S_B (Bad Samples Book) wird erstellt. Sie zeichnet die Zeitindizes derjenigen Datensatzzeilen auf, deren Vorhersagen nicht mit den ursprünglichen Bezeichnungen übereinstimmten.
- Es werden eindeutige Indizes der falsch vorhergesagten Beispiele für alle Faltungen ermittelt.
- Im Originaldatensatz wird eine zusätzliche Spalte „meta_labels“ erstellt, und allen Beobachtungen wird „1“ zugewiesen (Sie können handeln).
- Für alle Beispiele, die während der Kreuzvalidierung falsch vorhergesagt wurden, wird in der Spalte „meta_labels“ eine „0“ vergeben (nicht handeln).
- Für alle falsch vorhergesagten Proben wird in der Spalte „Labels“, die Kennzeichnungen für das Hauptmodell enthält, ebenfalls „0“ zugewiesen (kein Handel).
- Die Funktion gibt einen geänderten Datensatz zurück.
Ein zuverlässigerer Kausalschluss
Im vorangegangenen Abschnitt haben wir den grundlegenden Meta-Learner erörtert, dessen Beispiel die Erklärung des Grundkonzepts erleichtert. In diesem Abschnitt wird der Ansatz etwas komplizierter und wir befassen uns direkt mit dem Prozess der kausalen Schlussfolgerung selbst. Ich habe die Funktion für das kausale Sehließen aus dem verlinkten Artikel für den Fall des unidirektionalen Handels angepasst. Sie ist fortschrittlicher und hat eine flexiblere Funktionalität.
def meta_learners(models_number: int, iterations: int, depth: int, bad_samples_fraction: float): dataset = get_labels_one_direction(get_features(get_prices()), markup=hyper_params['markup'], min=1, max=15, direction=hyper_params['direction']) data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy() X = data[data.columns[1:-2]] y = data['labels'] BAD_WAIT = pd.DatetimeIndex([]) BAD_TRADE = pd.DatetimeIndex([]) for i in range(models_number): X_train, X_val, y_train, y_val = train_test_split( X, y, train_size = 0.5, test_size = 0.5, shuffle = True) # learn debias model with train and validation subsets meta_m = CatBoostClassifier(iterations = iterations, depth = depth, custom_loss = ['Accuracy'], eval_metric = 'Accuracy', verbose = False, use_best_model = True) meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False) coreset = X.copy() coreset['labels'] = y coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1] coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1) # add bad samples of this iteration (bad labels indices) coreset_w = coreset[coreset['labels']==0] coreset_t = coreset[coreset['labels']==1] diff_negatives_w = coreset_w['labels'] != coreset_w['labels_pred'] diff_negatives_t = coreset_t['labels'] != coreset_t['labels_pred'] BAD_WAIT = BAD_WAIT.append(diff_negatives_w[diff_negatives_w == True].index) BAD_TRADE = BAD_TRADE.append(diff_negatives_t[diff_negatives_t == True].index) to_mark_w = BAD_WAIT.value_counts() to_mark_t = BAD_TRADE.value_counts() marked_idx_w = to_mark_w[to_mark_w > to_mark_w.mean() * bad_samples_fraction].index marked_idx_t = to_mark_t[to_mark_t > to_mark_t.mean() * bad_samples_fraction].index data['meta_labels'] = 1.0 data.loc[data.index.isin(marked_idx_w), 'meta_labels'] = 0.0 data.loc[data.index.isin(marked_idx_t), 'meta_labels'] = 0.0 data.loc[data.index.isin(marked_idx_t), 'labels'] = 0.0 return data[data.columns[:]]
Nachfolgend gibt es ein Schema der Funktion des Meta-Learners in Form von Schlüsselblöcken, die für verschiedene Funktionen zuständig sind.
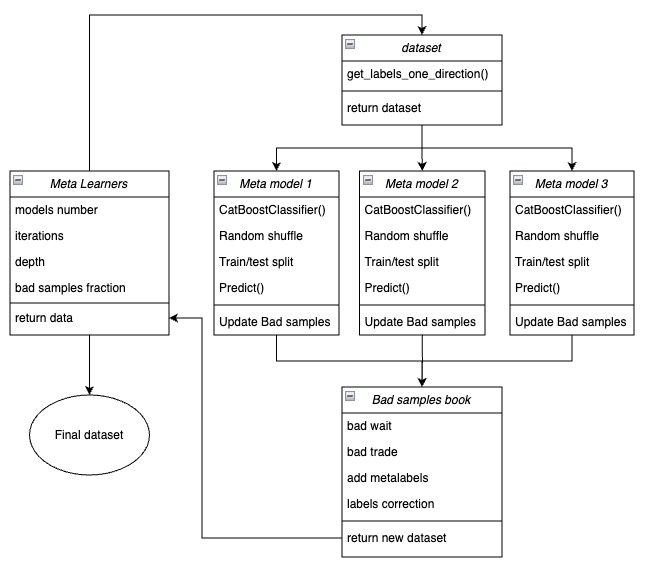
Abbildung 3. Schematische Darstellung der Funktion meta_learners()
Eine Besonderheit dieser Funktion ist, dass sie mehrere „Köpfe“ von Metamodellen hat, die auf zufälligen Teilproben des ursprünglichen Datensatzes trainiert werden, die mit der Bootstrap-Methode mit Rücklauf ausgewählt werden. Diese Methode ermöglicht die mehrfache Erzeugung von Teilstichproben aus dem Quelldatensatz. Statistische und probabilistische Merkmale können auf dieser Menge von Pseudostichproben geschätzt werden.
Wir interessieren uns zum Beispiel für den Durchschnittswert, wie gut ein bestimmtes Beispiel aus der Grundgesamtheit vorhergesagt wird, wenn wir Modelle auf verschiedenen Teilstichproben dieser Grundgesamtheit trainieren. Auf diese Weise erhalten wir eine weniger voreingenommene Sicht auf jedes der aggregierten Beispiele, die dann mit einem höheren Maß an Sicherheit als schlechte oder gute Beispiele eingestuft werden können.
Funktionseingabeparameter:
- models number ist die Anzahl der Metamodelle, die im Algorithmus verwendet werden. Empfohlener Wertebereich {5, 100}
- iterations ist die Anzahl der Trainingsiterationen für jedes Modell. Empfohlener Wertebereich {15, 35}
- depth ist die Tiefe der Entscheidungsbäume, die bei jeder Iteration des CatBoost-Klassifikator-Trainings erstellt werden. Der empfohlene Wertebereich ist {1, 6}.
- bad samples fraction ist die Anzahl der Proben, die als „schlecht“ markiert werden. Der empfohlene Wertebereich ist {0.4, 0.9}.
Der Mechanismus der Funktionsweise:
- Es wird ein Datensatz mit Merkmalen und Bezeichnungen für eine bestimmte Handelsrichtung erstellt.
- In der Schleife wird jedes der Metamodelle mit Hilfe der Bootstrap-Methode auf zufällig ausgewählten Trainings- und Validierungsdaten trainiert.
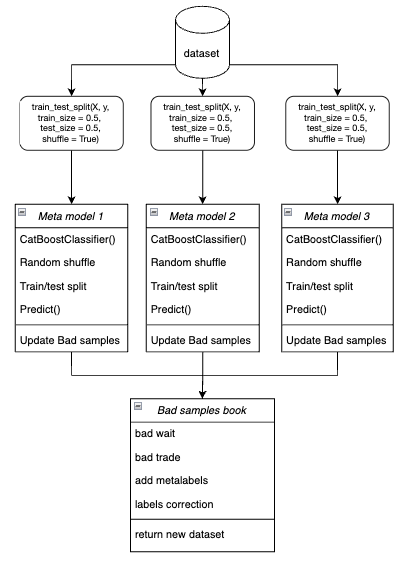
Abbildung 4. Schematische Darstellung der Bootstrap-Stichprobe
- Für jedes Modell werden die Vorhersagen mit den wahren Bezeichnungen verglichen. Die Indizes der falsch eingestuften Fälle werden im Buch der schlechten Proben gespeichert.
- Es wird die durchschnittliche Anzahl der falsch vorhergesagten Indizes über alle Durchgänge hinweg ermittelt.
- Die Indizes mit der größten Anzahl falsch vorhergesagter Labels, die den mit dem Schwellenwert multiplizierten Durchschnitt überschreiten, werden in der Spalte „meta_labels“ als Nullen hinzugefügt (Handelsverbot).
- Die Kennzeichnungen, 'labels', werden nach dem gleichen Prinzip auf Null gesetzt.
Die Philosophie hinter der Verwendung des Meta-Learners für unidirektionalen Handel:
- Der Code des Meta-Learners löst das Problem der Filterung „schlechter“ Signale in einem markierten Datensatz.
- Vereinfachung der Klassifizierungsaufgabe. Die Merkmale sind nur für eine bestimmte Art von Mustern optimiert (z. B. Trendfortsetzung).
- Auch bei der Ausgewogenheit der Klassen (50 % der Käufe/ 50 % der Verkäufe) bleibt die Asymmetrie im Trend erhalten. Trendkäufe haben stabilere Muster, während Verkäufe gegen den Trend oft mit schwer vorhersehbaren Ereignissen (Korrekturen, falsche Umkehrungen) verbunden sind.
- Bei Verkäufen in einem Aufwärtstrend sind die meisten Signale zunächst falsch (False Positives), was zu Klassifizierungsfehlern führt. Dementsprechend sind im Falle des bidirektionalen Handels Kauf- und Verkaufsgeschäfte unterschiedlicher Natur und können nicht verglichen werden.
- In einem unidirektionalen System sind Fehler nur mit falschen Eingängen in einen Trendhandel verbunden (z.B. Einstieg vor der Korrektur). Der Meta-Learner findet solche Fälle effektiv, da sie klare Anzeichen aufweisen (z. B. überkauft). In einem bidirektionalen System gehören zu den Fehlern auch falsche Käufe und Verkäufe, die ähnliche Muster aufweisen können. Der Meta-Learner kann das „Rauschen“ nicht zuverlässig von echten Signalen trennen, da die Merkmale für Käufe/Verkäufe gemischt sind.
- In einem unidirektionalen System konzentriert sich das Modell auf eine Art von Nicht-Stationarität (z. B. Trendverstärkung) und die Merkmale passen sich der aktuellen Marktphase an.
- In einem bidirektionalen System gibt es zwei Nicht-Stationaritäten (Trend + Korrektur), was doppelt so viele Daten erfordern würde und schwieriger zu verallgemeinern wäre.
Ergebnis:
- Die Klassifizierungsaufgabe wird vereinfacht – es reicht aus, eine statt zwei Klassen richtig vorherzusagen.
- Das Rauschen wird reduziert – das endgültige Metamodell filtert nur eine Art von Fehler.
- Die Kreuzvalidierung verbessert sich, weil die Stratifizierung korrekt funktioniert.
- Die Nicht-Stationarität der Trends wird berücksichtigt – das Modell passt sich nur einer Marktphase an.
Ein wichtiges Merkmal von Meta-Learner:
Meta-Learner sind nicht zu verwechseln mit dem endgültigen Metamodell, das auf den von Meta-Learnern erstellten Kennzeichnungen trainiert wird. Meta-Learner sind keine endgültigen Modelle und werden nur in der Vorverarbeitungsphase verwendet. Als grundlegende Lernverfahren können alle binären Klassifizierungsalgorithmen verwendet werden, einschließlich logistischer Regression, neuronaler Netze, „baumbasierter“ Modelle und anderer exotischer Modelle. Darüber hinaus können Regressionsmodelle mit geringfügigen Codeänderungen verwendet werden, was den Rahmen dieses Artikels sprengen würde und in späteren Artikeln behandelt werden kann. Der Einfachheit halber verwende ich den binären Klassifikator CatBoost, weil ich mit ihm zu arbeiten gewohnt bin.
Merkmale in Bezug auf die Lernattribute
Es wurde bereits erwähnt, dass der Handel in eine Richtung die Klassifizierung vereinfacht. Die Merkmale werden nur für eine Art von Mustern optimiert (z. B. Einkäufe), sodass keine Notwendigkeit für symmetrische Merkmale besteht. Als symmetrische Merkmale können sowohl die ursprüngliche Zeitreihe mit unterschiedlichen Zeitverzögerungen, deren Werte Kauf- und Verkaufsgeschäften entsprechen, als auch verschiedene Derivate (Preisinkremente) und andere Oszillatoren bezeichnet werden. Zu den nicht-symmetrischen Merkmalen gehört die Volatilität in verschiedenen Zeitfenstern, da sie nur die Änderungsrate der Preise, nicht aber deren Richtung widerspiegelt. In diesem Projekt wird die Volatilität mit verschiedenen Zeitfenstern verwendet, die in der Variablen „Perioden“ festgelegt sind.
Hier ist der vollständige Code, der die Erstellung von Merkmalen implementiert:
def get_features(data: pd.DataFrame) -> pd.DataFrame: pFixed = data.copy() pFixedC = data.copy() count = 0 for i in hyper_params['periods']: pFixed[str(count)] = pFixedC.rolling(i).std() count += 1 return pFixed.dropna()
Und die Zeiträume der gleitenden Fenster für die Berechnung solcher Merkmale sind im Wörterbuch angegeben. Sie können willkürlich geändert werden und die Leistung des Modells zu variieren.
hyper_params = {
'periods': [i for i in range(5, 300, 30)],
}
In diesem Beispiel erstellen wir 10 Merkmale, von denen das erste eine Periode von 5 hat und jede weitere Periode sich um 30 erhöht, und so weiter bis 300:
>>> [i for i in range(5, 300, 30)] [5, 35, 65, 95, 125, 155, 185, 215, 245, 275]
Training und Test von unidirektionalen Modellen
hyper_params = {
'symbol': 'XAUUSD_H1',
'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Mean reversion/',
'model_number': 0,
'markup': 0.25,
'stop_loss': 10.0000,
'take_profit': 5.0000,
'direction': 'buy',
'periods': [i for i in range(5, 300, 30)],
'backward': datetime(2020, 1, 1),
'forward': datetime(2024, 1, 1),
'full forward': datetime(2026, 1, 1),
}
models = []
for i in range(10):
print('Learn ' + str(i) + ' model')
models.append(fit_final_models(meta_learner(5, 15, 3, 0.1)))
# models.append(fit_final_models(meta_learners(25, 15, 3, 0.8)))Zunächst wird der erste Meta-Learner getestet, der zweite wird auskommentiert. Die Richtung des Kaufhandels ist die bevorzugte, denn Gold befindet sich derzeit in einem Aufwärtstrend. Das Training wird von Anfang 2020 bis 2024 durchgeführt. Für den Testzeitraum wurde der Zeitraum von Anfang 2024 bis zum 1. April 2025 gewählt.
Der Meta-Learner hat die folgenden Einstellungen:
- 5 Falten für die Kreuzvalidierung
- 15 Trainingsiterationen für den CatBoost-Algorithmus
- die Tiefe des Baums beträgt bei jeder Iteration 3
- die Lernrate beträgt 0,1
So sieht das beste Modell im Strategietester für die Richtung „Kaufen“ aus:
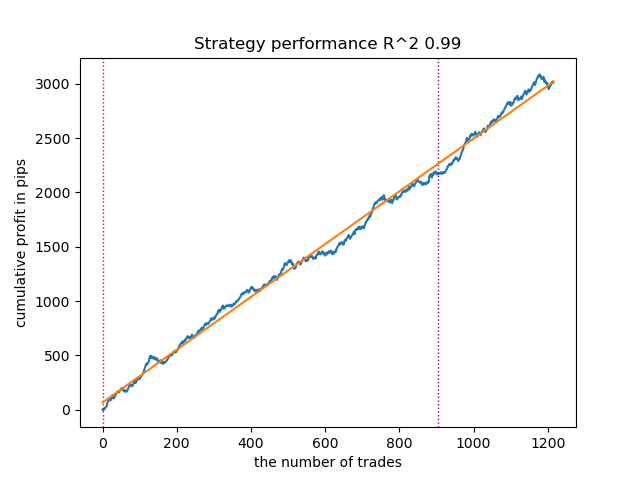
Abbildung 5. Ergebnisse der Prüfung von Merkmalen der Funktion meta_learner() in Kaufrichtung
Zum Vergleich: So sieht das beste Modell für die Richtung „Verkaufen“ aus:
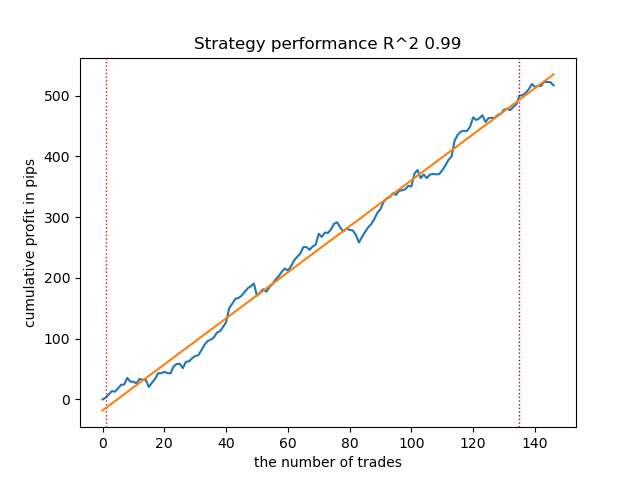
Abbildung 6. Ergebnisse der Prüfung von Merkmalen der Funktion meta_learner() in der Verkaufsrichtung
Der Algorithmus hat gelernt, Abschlüsse sowohl in Kauf- als auch in Verkaufsrichtung vorherzusagen. Aber es gab viel weniger Verkaufstransaktionen, was bei einem Markt mit einem Aufwärtstrend normal ist. Das Metamodell hat auch ohne die Auswahl seiner Hyperparameter recht effektiv gearbeitet, was sich sowohl im Trainingsbereich als auch im Vorwärtstest widerspiegelt.
Diskutieren Sie nun über einen fortgeschrittenen Meta-Lernenden. Führen Sie ähnliche Manipulationen für die Funktion meta_learners() durch. Lassen Sie uns diesen Kommentar entfernen und den vorherigen kommentieren:
models = [] for i in range(10): print('Learn ' + str(i) + ' model') # models.append(fit_final_models(meta_learner(5, 15, 3, 0.1))) models.append(fit_final_models(meta_learners(25, 15, 3, 0.8)))
Der Meta-Learner hat die folgenden Einstellungen:
- 25 „Köpfe“ oder Metamodelle
- 15 Trainingsiterationen für den CatBoost-Algorithmus für jedes der Modelle
- die Tiefe des Baums beträgt bei jeder Iteration 3
- 0,8 für den Parameter „bad_samples_fraction“, der den Prozentsatz der im Trainingsdatensatz verbliebenen schlechten Proben bestimmt. 0,1 entspricht einer sehr starken Filterung, und 0,9 filtert wenige schlechte Proben heraus.
So sieht das beste Modell im Strategietester für die Richtung „Kaufen“ aus:
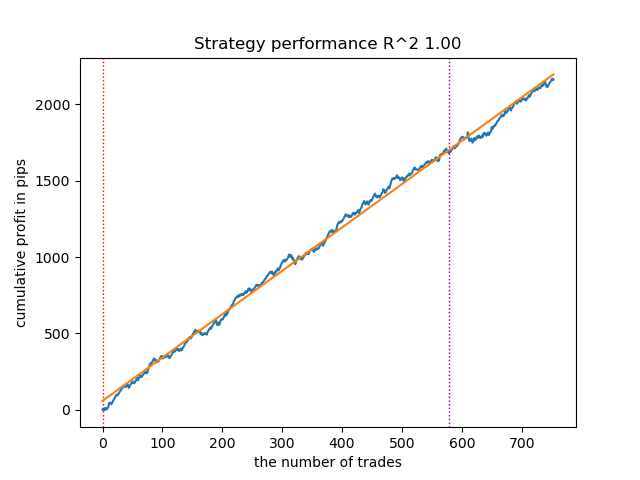
Abbildung 7. Ergebnisse der Prüfung von Merkmalen der Funktion meta_learners() in Kaufrichtung
Zum Vergleich: So sieht das beste Modell für die Richtung „Verkaufen“ aus:
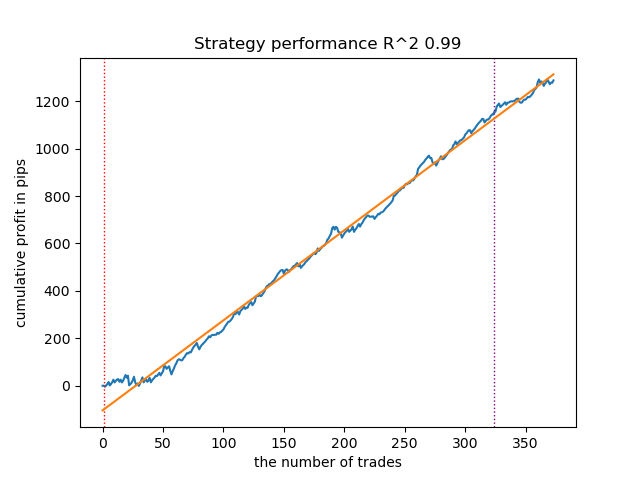
Abbildung 8. Ergebnisse der Prüfung von Merkmalen der Funktion meta_learners() in der Verkaufsrichtung
Eine fortgeschrittenere Funktion des Meta-Learners zeigte schönere Kurven. Der Saldo für Kauf- und Verkaufsgeschäfte wurde gespeichert. Die beste Strategie ist natürlich eine Kaufstrategie. Nachdem die Modelle trainiert und das beste Modell ausgewählt wurde, können Sie sie in das Meta Trader 5-Terminal exportieren. Sie können beide Strategien anwenden, aber da die Strategie der Eröffnung von Verkaufspositionen weniger effektiv ist, wählen wir nur die Strategie für Kaufpositionen.
Nachstehend finden Sie eine Tabelle mit den Abhängigkeiten der Lernergebnisse von fortgeschrittenen Parameter des Meta-Learner:
| Name des Parameters: | Auswirkungen auf die Qualität der Filterung: |
|---|---|
| models_number: int | Je mehr „Köpfe“ oder Metamodelle es gibt, desto weniger voreingenommen ist die Bewertung von schlechten Proben. Die Größe des Trainingsdatensatzes beeinflusst die Wahl der Anzahl der Modelle. Je länger die Vorgeschichte ist, desto mehr Modelle benötigen Sie möglicherweise. Es ist notwendig, diesen Parameter in einem Bereich von 5 bis 100 zu variieren. |
| iterations: int | Beeinflusst in hohem Maße die Filtrationsrate. Je mehr Iterationen jeder Meta-Learner trainiert, desto langsamer ist die Rate. Kleine Werte können zu einem unzureichenden Training führen, was zu einer stärkeren Filterung und einer geringen Anzahl von Handelsgeschäften am Ausgang führen kann. Es wird empfohlen, den Wert im Bereich von 5 bis 50 einzustellen. |
| depth: int | Die Tiefe des Baums wird im Bereich von 1 bis 6 festgelegt. Bei jeder Iteration vervollständigt der Algorithmus den Baum mit einer bestimmten Tiefe. Ich verwende eine Tiefe von 3, aber Sie können mit diesem Parameter experimentieren. |
| bad_samples_fraction: float | Sie wirkt sich auf die endgültige Auswahl der schlechten Stichproben und die Anzahl der Abschlüsse aus. 0,9 entspricht einer „weichen“ Filterung und einer großen Anzahl von Handelsgeschäften am Ausgang. 0,5 entspricht einer „harten“ Filterung und infolgedessen einer geringen Anzahl von Handelsgeschäften am Ausgang. |
Feinschliff: Export von Modellen und Erstellung eines Handelsberaters
Die Modelle werden genau so exportiert, wie sie in anderen Artikeln verwendet werden. Wählen Sie dazu das gewünschte Modell aus der sortierten Liste der Modelle aus und rufen Sie die Exportfunktion auf.
models.sort(key=lambda x: x[0]) data = get_features(get_prices()) test_model_one_direction(data, models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], hyper_params['forward'], hyper_params['backward'], hyper_params['markup'], hyper_params['direction'], plt=True) export_model_to_ONNX(models[-1], 0)
Die Logik des Trading Bots wurde so geändert, dass er nur noch in eine Richtung handelt, je nachdem, welches Modell Sie exportiert haben.
input bool direction = true; //True = Buy, False = Sell
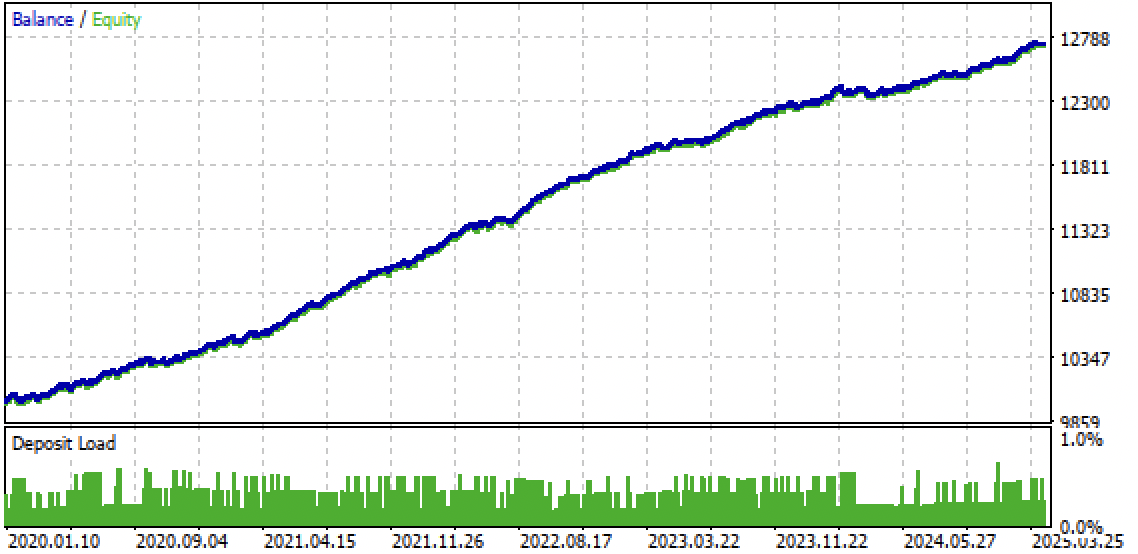
Abb. 9. Testen des Bots im Meta Trader 5-Terminal
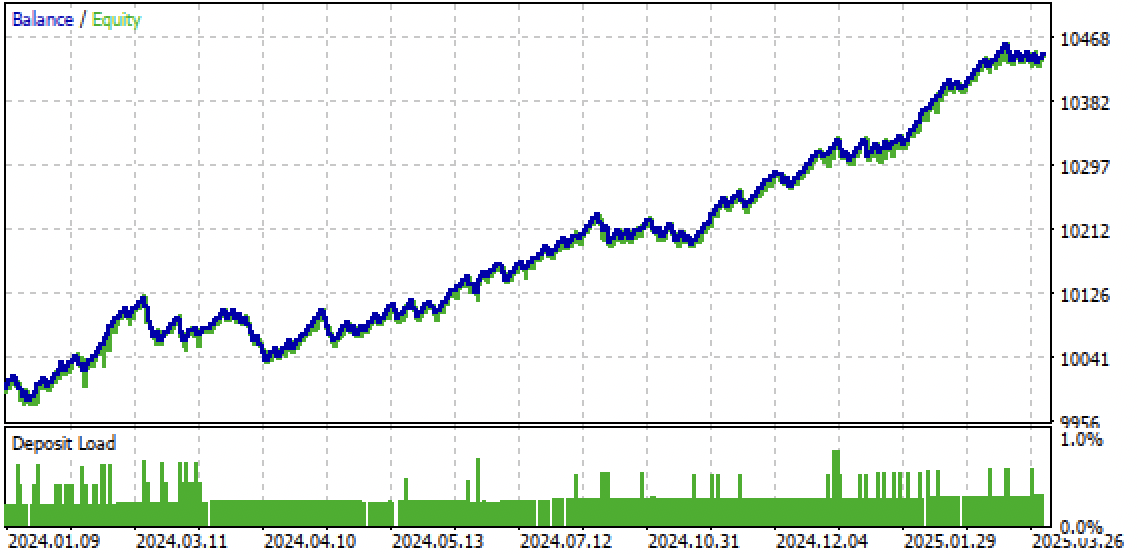
Abb. 10. Prüfung nur für den Terminzeitraum ab Anfang 2024
Schlussfolgerung
Die Idee unidirektionaler Strategien mit Hilfe von maschinellem Lernen erschien mir interessant, und so habe ich eine Reihe von Experimenten durchgeführt, darunter auch den in diesem Artikel vorgeschlagenen Ansatz. Sie ist nicht die einzig mögliche, aber sie erfüllt die Aufgabe gut. Solche trendabhängigen Strategien können eine gute Performance aufweisen, wenn der Trend anhält. Daher ist es wichtig, globale Trendänderungen zu beobachten und solche Systeme an die aktuelle Marktsituation anzupassen.
Das Archiv Python files.zip enthält die folgenden Dateien für die Entwicklung in Python:
| Dateiname | Beschreibung |
|---|---|
| causal one direction.py | Das wichtigste Skript zum Lernen von Modellen |
| labeling_lib.py | Aktualisiertes Modul mit Handelsmarkern |
| tester_lib.py | Aktualisierter nutzerdefinierter Tester für auf maschinellem Lernen basierende Strategien |
| XAUUSD_H1.csv | Die vom MetaTrader 5-Terminal exportierte Kursdatei |
Das Archiv MQL5 files.zip enthält Dateien für MetaTrader 5:
| Dateiname | Beschreibung |
|---|---|
| one direction.ex5 | Zusammengestelltes Bot aus diesem Artikel |
| one direction.mq5 | Die Quelle des Bot aus dem Artikel |
| Ordner Include//Trend following | Speicherort der ONNX-Modelle und der Header-Datei für die Verbindung mit dem Bot. |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17654
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Die Komponenten View und Controller für Tabellen im MQL5 MVC-Paradigma: Container
Die Komponenten View und Controller für Tabellen im MQL5 MVC-Paradigma: Container
 Integration von Computer Vision in den Handel in MQL5 (Teil 1): Erstellen von Grundfunktionen
Integration von Computer Vision in den Handel in MQL5 (Teil 1): Erstellen von Grundfunktionen
 Neuronale Netze im Handel: Hybride Graphsequenzmodelle (letzter Teil)
Neuronale Netze im Handel: Hybride Graphsequenzmodelle (letzter Teil)
 Visualisierung von Strategien in MQL5: Verteilung der Optimierungsergebnisse auf die Kriteriendiagramme
Visualisierung von Strategien in MQL5: Verteilung der Optimierungsergebnisse auf die Kriteriendiagramme
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.