Swap-Arbitrage am Devisenmarkt: Aufbau eines synthetischen Portfolios und Generierung eines konsistenten Swapflusses

In der Welt des algorithmischen Handels, in der jeder Vorteil entscheidend sein kann, gibt es eine erstaunlich wenig erforschte Möglichkeit, die langfristige Strategien von profitabel zu hochprofitabel machen kann. Diese Möglichkeit ist die Swap-Arbitrage auf dem Devisenmarkt. Während die meisten Händler der Volatilität nachjagen und versuchen, kurzfristige Kursbewegungen zu erraten, bauen echte Kapitalarchitekten methodisch Strukturen auf, die unabhängig von Marktschwankungen jeden Tag Erträge erwirtschaften.

Das ungenutzte Potenzial von Swap-Differenzen bei Währungspaaren

Der Swap ist nicht nur ein technisches Merkmal des Devisenmarktes, sondern ein grundlegendes wirtschaftliches Phänomen, das den Zinsunterschied zwischen den Währungen widerspiegelt. Wenn die Zentralbanken zweier Länder unterschiedliche Refinanzierungssätze festlegen, besteht die Möglichkeit der systematischen Gewinnerzielung. Denken Sie darüber nach: Während wir den Devisenmarkt normalerweise als eine Arena für Spekulationen auf Wechselkursänderungen betrachten, beinhaltet seine Struktur einen Mechanismus, der allein aufgrund der Zinsdifferenz bis zu 10-15% pro Jahr bringen kann!

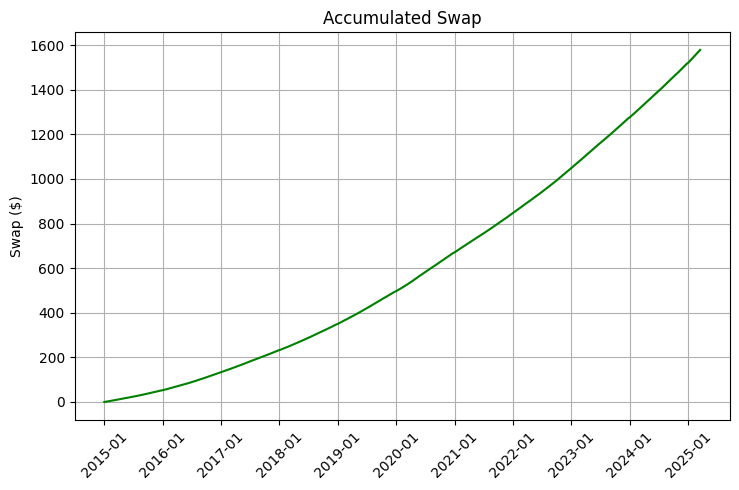
Besonders bemerkenswert ist, dass sich die Swap-Sätze im Vergleich zu den Devisenkursen viel langsamer anpassen. Dies bietet eine einzigartige Gelegenheit, ein Portfolio aufzubauen, in dem das langfristige Halten bestimmter Positionen nicht nur möglich, sondern auch äußerst profitabel ist. Unsere Datenanalyse für den Zeitraum 2015 bis 2025 zeigt, dass Sie mit einer angemessenen Portfoliooptimierung allein mit Swaps eine zusätzliche Rendite von 5-8 % pro Jahr erzielen können. Langfristig hat dies aufgrund des Zinseszinseffekts eine enorme Wirkung.

Warum übersehen die meisten Händler den Swap als strategische Komponente ihres Einkommens?

Die Psychologie des Marktes spielt den Händlern einen Streich. Auf der Suche nach schnellen Gewinnen aus kurzfristigen Bewegungen lassen die meisten Marktteilnehmer langfristige strukturelle Chancen völlig außer Acht. Der Swap wird entweder als unbedeutendes Detail oder als lästiges Übel empfunden, das die Schließung von Positionen vor dem Rollover erfordert. Diese psychologische Barriere schafft eine systematische Ineffizienz des Marktes, die zu Ihrem Vorteil genutzt werden kann.

Technische Händler konzentrieren sich auf Charts, fundamentale Händler auf Wirtschaftsindikatoren. Doch nur wenige Menschen integrieren Swaps in eine umfassende Strategie. Analytische Daten zeigen, dass weniger als 5 % der Privatanleger Swaps gezielt in ihren Strategien einsetzen. Dies schafft eine Arbitrage-Situation, in der ein systematischer Ansatz zur Analyse und Optimierung von Swaps es ermöglicht, von der Ineffizienz des Marktes zu profitieren.

Ein weiterer Faktor ist die Komplexität der Berechnungen. Ohne spezialisierte Algorithmen ist es fast unmöglich, ein Portfolio unter Berücksichtigung aller Parameter zu optimieren: der Handelsrichtung, der Größe der Positionen, der Korrelationen zwischen Währungspaaren und der Wechselwirkung zwischen Marktrendite und Swaps. Aus diesem Grund wird die Entwicklung einer Softwarelösung wie SwapArbitrageAnalyzer zu einem entscheidenden Wettbewerbsvorteil.

Die Wechselwirkung zwischen Marktbewegungen und Swap-Einkommen

Wahre Magie entsteht an der Schnittstelle von drei Dimensionen: Marktrendite, Swaps und Volatilität. Stellen Sie sich ein Portfolio vor, in dem jede Position nicht nur optimiert ist, um von Marktbewegungen zu profitieren, sondern auch so ausgewählt wird, dass ein positiver Swap maximiert und gleichzeitig die Gesamtvolatilität minimiert wird.

Unsere Untersuchungen zeigen, dass mit dem richtigen Ansatz eine Struktur geschaffen werden kann, in der:

1. die Korrelation zwischen Währungspaaren die Gesamtvolatilität des Portfolios reduziert,
2. positive Swaps für einen stabilen täglichen Geldfluss sorgen,
3. die Marktrentabilität, die sich aus der Entwicklung der Wechselkurse ergibt, den Gesamtgewinn steigert.

Diese Kombination schafft ein nahezu ideales Anlageinstrument mit einer positiven mathematischen Erwartung. Es ist bemerkenswert, dass in Zeiten von Marktstress, in denen die meisten Strategien scheitern, ein für Swaps optimiertes Portfolio aufgrund der täglichen Akkumulation von Swap-Punkten oft stabil bleibt.

Während unseres zehnjährigen Backtests haben wir festgestellt, dass das swap-optimierte Portfolio die traditionellen Devisenhandelsstrategien in Bezug auf die Gesamtrendite um 25-40 % übertrifft. Noch wichtiger ist, dass er eine höhere Sharpe-Ratio aufweist, was auf ein besseres Risiko-Rendite-Verhältnis hindeutet.

In den folgenden Abschnitten werden wir einen detaillierten Blick auf das mathematische Modell werfen, das dieser Strategie zugrunde liegt, und die spezifischen Methoden für ihre Umsetzung auf der MetaTrader 5-Plattform analysieren.

Definition und Funktionsweise von Swap-Punkten auf dem Devisenmarkt

Das Verständnis für die Funktionsweise von Swaps auf dem Devisenmarkt ist das Herzstück unserer Strategie. Im Gegensatz zu Aktien oder Futures verfügt der Devisenkassamarkt über einen eingebauten Mechanismus, der die grundlegenden Unterschiede zwischen den Volkswirtschaften verschiedener Länder widerspiegelt – die Swap-Punkte.

Jede Nacht, wenn Sie eine Position halten, findet ein Vorgang statt, der für die meisten Händler unsichtbar ist: Swap-Rollover. Dabei handelt es sich nicht nur um einen technischen Aspekt, sondern um eine direkte Widerspiegelung des Zinsunterschieds zwischen den Währungen eines Paares. Tatsächlich erhalten oder zahlen wir Zinsen für einen „virtuellen Kredit“ in einer Währung und eine „virtuelle Einlage“ in einer anderen.

Betrachten Sie ein konkretes Beispiel aus unserem Analysator:

def _init_swap_data(self):
    print("Initialization of swap and yield data since 01.01.2015...")
    available_pairs = 0
    start_date = datetime(2015, 1, 1)
    for pair in self.pairs:
        symbol_info = mt5.symbol_info(pair)
        if not symbol_info:
            continue
            
        swap_long = symbol_info.swap_long
        swap_short = symbol_info.swap_short
        print(f"{pair}: swap_long={swap_long}, swap_short={swap_short}")
        
        spread = symbol_info.spread * symbol_info.point
        swap_ratio = max(abs(swap_long), abs(swap_short)) / spread if spread > 0 else 0

Dieser Code extrahiert wichtige Informationen: die Werte von swap_long und swap_short für jedes Währungspaar. Achten Sie auf die Zeile swap_ratio = max(abs(swap_long), abs(swap_short)) / spread. Hierbei handelt es sich um eine Berechnung des Verhältnisses von Swap zu Spread, die dazu beiträgt, die potenzielle Rendite des Swaps im Verhältnis zu den Handelskosten zu schätzen.

Mathematik hinter positiven Swap-Akkumulationsstrategien

Der mathematische Vorteil unserer Strategie liegt in der systematischen Akkumulation von positiven Swaps bei gleichzeitiger Neutralisierung des Marktrisikos. Die Schlüsselkomponente ist die Berechnung der erwarteten Rendite unter Berücksichtigung der Swaps:

# Calculation of expected returns based on swap and market movement
expected_returns = {}
for pair in eligible_pairs:
    market_return = self.swap_info[pair]['avg_return'] * self.config['leverage'] if self.swap_info[pair]['direction'] == 'long' else -self.swap_info[pair]['avg_return'] * self.config['leverage']
    swap_return = self.swap_info[pair]['avg_swap']
    volatility = self.swap_info[pair]['volatility'] * self.config['leverage']
    
    # Normalization of parameters for balanced assessment
    norm_market = (market_return - min_market_return) / (max_market_return - min_market_return + 1e-10)
    norm_swap = (swap_return - min_swap_return) / (max_swap_return - min_swap_return + 1e-10)
    norm_vol = (volatility - min_volatility) / (max_volatility - min_volatility + 1e-10)
    
    # Combined assessment of pair attractiveness
    combined_score = (self.config['swap_weight'] * norm_swap + 
                     self.config['return_weight'] * norm_market - 
                     self.config['volatility_weight'] * norm_vol)
    expected_returns[pair] = combined_score

Dieser Ausschnitt zeigt, wie wir drei Schlüsselfaktoren für jedes Währungspaar gewichten:

1. Durchschnittliche Marktrentabilität (abhängig von der Richtung des Handels)
2. Durchschnittlicher Swap
3. Volatilität (die wir zu minimieren versuchen)

Beachten Sie, wie wir jeden Parameter normalisieren und dann mit den in der Konfiguration festgelegten Gewichten kombinieren: self.config['swap_weight'] , self.config['return_weight'] и self.config['volatility_weight'] . So erhalten wir eine ganzheitliche Bewertung der Attraktivität der einzelnen Paare.

Warum die Nutzung von Währungskorrelationen einen strategischen Vorteil schafft

Der eigentliche Zauber geschieht beim Aufbau eines Portfolios. Korrelationen zwischen Währungspaaren sind kein Hindernis, sondern ein Instrument des Risikomanagements. Werfen Sie einen Blick auf das für die Portfolio-Optimierung verantwortliche Code-Fragment:

def _optimize_portfolio(self):
    # ... (pre-processing of data)
    
    returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   if self.swap_info[pair]['direction'] == 'long' 
                   else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
                   for pair in eligible_pairs}
    returns_df = pd.DataFrame(returns_data)
    cov_matrix = returns_df.cov()  # Covariance matrix is the key to understanding correlations.
    
    # ... (forming the objective function and limitations)
    
    # Optimization objective function
    def objective(weights, expected_returns, cov_matrix, risk_free_rate):
        returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
        return -sharpe  # Maximize the Sharpe ratio

Hier enthält die Kovarianzmatrix cov_matrix Informationen über die gegenseitigen Abhängigkeiten der Renditen von Währungspaaren. Auf diese Weise kann der Algorithmus eine Kombination von Währungspaaren und Gewichten finden, bei der sich positive und negative Korrelationen gegenseitig ausgleichen und die Gesamtvolatilität des Portfolios verringern.

Betrachten Sie das Ergebnis dieser Optimierung anhand eines konkreten Beispiels. Nach Durchführung der Analyse ergibt sich eine ähnliche Portfoliostruktur wie die folgende:

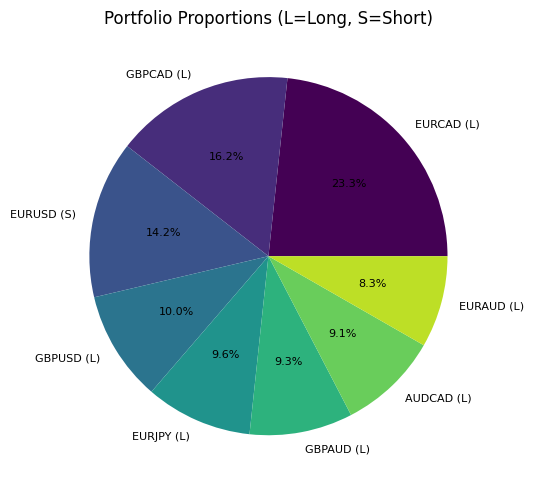
Dieses Chart zeigt die Verteilung des Kapitals auf verschiedene Währungspaare und gibt die Richtung der Position an (L – Kauf, S – Verkauf). Beachten Sie, wie der Algorithmus entgegengesetzte Richtungen für korrelierende Paare kombiniert und so eine teilweise Absicherung des Marktrisikos schafft.

Die Rentabilität eines solchen Portfolios besteht aus zwei Komponenten: Marktbewegungen und Swaps. Schauen Sie sich die Charts an, die diesen Unterschied veranschaulichen:

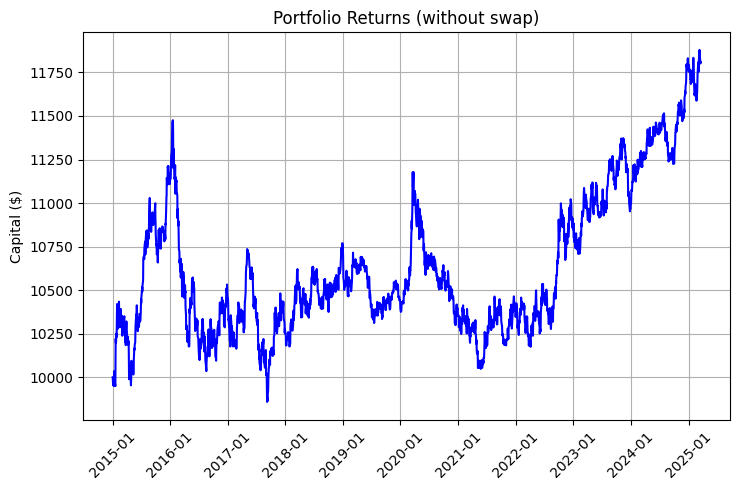
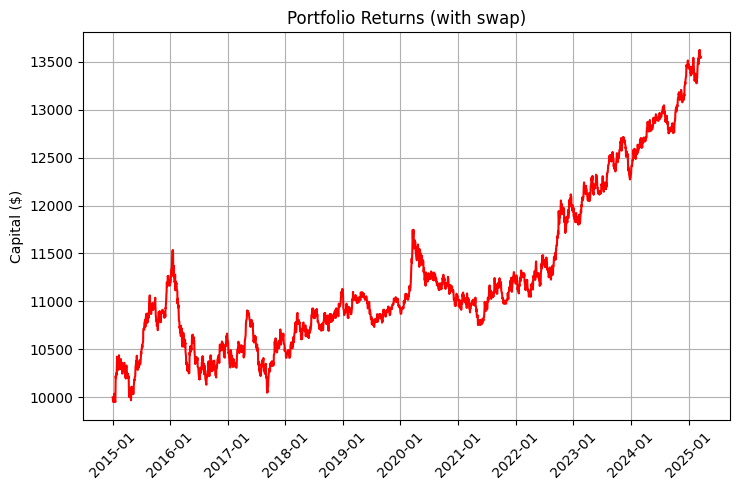
Die Grafik ist besonders beeindruckend, wenn man die Wiederanlage und die regelmäßigen Einlagen berücksichtigt:

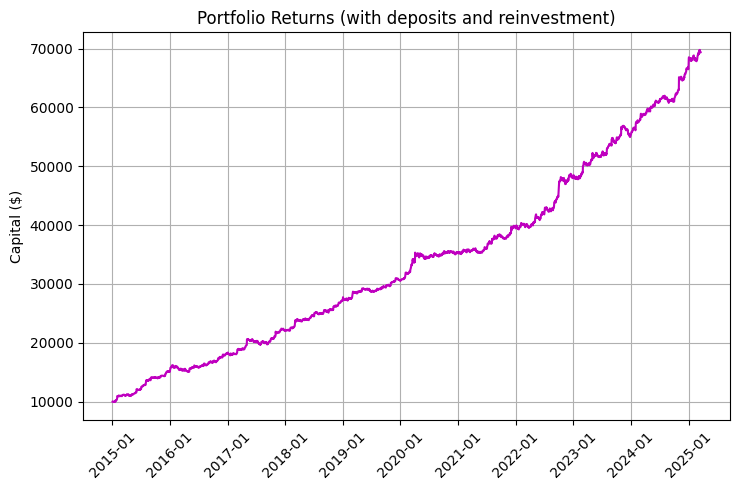
Der Schlüsselcode für die Rentabilitätsmodellierung zeigt die Auswirkungen der täglichen Swaps auf die Gesamtrendite:

def _simulate_portfolio_performance(self):
    # ... (initializing variables)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            if date in self.swap_info[pair]['data'].index:
                pair_return = self.swap_info[pair]['data'].loc[date, 'return'] if not pd.isna(self.swap_info[pair]['data'].loc[date, 'return']) else 0
                pair_swap = self.swap_info[pair]['data'].loc[date, 'swap_return']
                if weight > 0:
                    daily_return += pair_return * weight * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
                else:
                    daily_return += -pair_return * abs(weight) * self.config['leverage']
                    daily_swap += pair_swap * abs(weight)
        
        is_weekend = date.weekday() >= 5
        daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital
        
        # Calculation of profitability with and without swaps
        # ...

Beachten Sie die Zeile: daily_swap_applied = 0 if is_weekend else daily_swap * initial_capital. Dies ist ein wichtiges Detail: Swaps werden nur an Werktagen gutgeschrieben, was bei einer genauen Modellierung berücksichtigt werden muss.

Mathematisch gesehen zielt unsere Strategie darauf ab, diese Funktion zu maximieren:

Sharpe = R p − R f σ p \text{Sharpe} = \frac{R_p - R_f}{\sigma_p} Sharpe=σp Rp −Rf​​

wobei:

• $R_p$ ist die Gesamtportfoliorendite (Markt + Swap)
• $R_f$ ist der risikofreie Zinssatz
• $\sigma_p$ ist die Standardabweichung der Portfoliorenditen

Gleichzeitig schränken wir die Swap-Positivität ein:

∑ i = 1 n ∣ w i ∣ × S i > 0 \sum_{i=1}^{n} |w_i| \times S_i > 0 ∑i=1n ∣wi ∣×Si >0

wobei:

• $w_i$ ist das Gewicht eines Währungspaares im Portfolio
• $S_i$ ist der durchschnittliche Swap-Wert für dieses Paar

Diese Formulierung des Optimierungsproblems stellt sicher, dass unser Portfolio nicht nur Erträge aus Marktbewegungen, sondern auch einen positiven täglichen Fluss aus Swaps generiert, was einen einzigartigen Synergieeffekt erzeugt.

Mathematischer Rahmen: Mehr als die einfache Strategie Kaufen-und-Halten

In der Welt des algorithmischen Handels besteht eine große Kluft zwischen intuitiven Strategien und mathematisch optimierten Systemen. Unser Ansatz der Swap-Arbitrage gehört ganz zur zweiten Kategorie, da wir komplexe mathematische Instrumente einsetzen, um einen strukturellen Vorteil auf dem Markt zu schaffen. In diesem Abschnitt werden wir uns mit dem mathematischen Modell beschäftigen, das dem SwapArbitrageAnalyzer zugrunde liegt, und aufzeigen, warum es den traditionellen Handelsmethoden überlegen ist.

Risikobasierte Rentabilitätsoptimierung, die Swap-Differenzen einschließt

Die wichtigste Innovation unseres Ansatzes ist die Integration von Swaps in das klassische Markowitz-Portfolio-Optimierungsmodell. Anstatt den Swap als sekundären Faktor zu betrachten, beziehen wir ihn direkt in die Renditefunktion ein:

def portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate):
    weights = np.array(weights)
    returns = np.sum(expected_returns * weights)
    std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
    return returns, std, (returns - risk_free_rate) / std if std > 0 else 0

Beachten Sie, dass in dieser Funktion erwartete Renditen bereits sowohl Marktrenditen als auch Swap-Renditen enthalten sind. Wir berechnen nämlich die kombinierten Renditen für jedes Währungspaar:

returns_data = {pair: self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               if self.swap_info[pair]['direction'] == 'long' 
               else -self.swap_info[pair]['returns'] * self.config['leverage'] + self.swap_info[pair]['avg_swap'] 
               for pair in eligible_pairs}

Bei dieser Formel wird Folgendes berücksichtigt:

1. Historische Renditen eines Währungspaares ( returns )
2. Richtung der Position (long oder short)
3. Angewandte Hebelwirkung ( Leverage )
4. Durchschnittlicher Swap-Wert ( avg_swap )

Dieser Ansatz unterscheidet sich grundlegend von der traditionellen Vorgehensweise, bei der das Portfolio zunächst auf der Grundlage der Marktrenditen optimiert wird. Und dann bestenfalls prüfen, ob die Swaps zu negativ sind. Wir modellieren die Gesamtrendite als einen einzigen Parameter, was es dem Algorithmus ermöglicht, einzigartige Kombinationen zu finden, die bei einem sequenziellen Ansatz übersehen werden würden.

Es ist besonders wichtig, dass wir bei der Bestimmung der Positionsrichtung einen differenzierten Ansatz verfolgen. Für jedes Währungspaar analysieren wir, ob eine Kauf- oder Verkaufs-Position profitabler wäre, wobei wir sowohl die historische Preisdynamik als auch die Swap-Werte berücksichtigen:

direction = 'long' if swap_long > swap_short else 'short'
self.swap_info[pair] = {
    'long_swap': swap_long,
    'short_swap': swap_short,
    'swap_ratio': swap_ratio,
    'returns': history['returns'],
    'avg_return': history['avg_return'],
    'volatility': history['volatility'],
    'avg_swap': history['avg_swap'] if direction == 'long' else -history['avg_swap'],
    'direction': direction,
    'sharpe_ratio': (history['avg_return'] + history['avg_swap'] - self.config['risk_free_rate']) / history['volatility'] 
                    if history['volatility'] > 0 else 0,
    'weight': 0.0,
    'data': history['data']
}

Die Schlüsselrolle der Sharpe-Rate bei der Bewertung von swap-bereinigten Portfolios

Das grundlegende Kriterium für die Optimierung unseres Portfolios ist die Sharpe-Ratio, ein Maß für die Überschussrendite pro Risikoeinheit. Im Zusammenhang mit der Swap-Arbitrage kommt der Sharpe-Ratio-Formel eine besondere Bedeutung zu:

Sharpe = R m + R s − R f σ \text{Sharpe} = \frac{R_m + R_s - R_f}{\sigma} Sharpe=σRm +Rs −Rf​​

wobei:

• $R_m$ ist die Marktrendite
• $R_s$ ist der Ertrag aus dem Swap-Geschäft
• $R_f$ ist der risikofreie Zinssatz
• $\sigma$ ist die Standardabweichung der Gesamtrendite

Man beachte die Einbeziehung von $R_s$ in den Zähler - dies ist der entscheidende Punkt. Ein Swap ist eine nahezu deterministische Komponente der Rentabilität, die das Rendite-Risiko-Verhältnis verbessert. So sieht es im Code aus:

def objective(weights, expected_returns, cov_matrix, risk_free_rate):
    returns, std, sharpe = portfolio_performance(weights, expected_returns, cov_matrix, risk_free_rate)
    return -sharpe  # The optimizer minimizes, so we use a negative Sharp

Für die Lösung des Optimierungsproblems verwenden wir die SLSQP-Methode (Sequential Least Squares Programming) aus der Bibliothek scipy.optimize. Sie ermöglicht es uns, nichtlineare Nebenbedingungen zu berücksichtigen:

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

Die wichtigste Einschränkung ist hier der positive kumulative Swap des Portfolios:

def swap_constraint(weights, eligible_pairs):
    total_swap = np.sum([self.swap_info[pair]['avg_swap'] * abs(weights[i]) for i, pair in enumerate(eligible_pairs)])
    return total_swap  # Must be >= 0

Dadurch können Portfolios ausgeschlossen werden, die zwar hohe Marktrenditen, aber negative Swaps aufweisen, was für eine langfristige Strategie entscheidend ist.

Wie Volatilität, Marktrichtung und Swap-Sätze in dem Modell zusammenwirken

Unser Modell betrachtet die drei grundlegenden Faktoren nicht als isolierte, sondern als miteinander verknüpfte Komponenten eines einzigen Systems. Betrachten Sie den Schlüsselausschnitt, in dem wir die kombinierte Bewertung der Attraktivität eines Währungspaares berechnen:

# Normalization of parameters
norm_market = (market_return - min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs])) / \
             (max([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) - 
              min([self.swap_info[p]['avg_return'] * self.config['leverage'] if self.swap_info[p]['direction'] == 'long' 
                   else -self.swap_info[p]['avg_return'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)
norm_swap = (swap_return - min([self.swap_info[p]['avg_swap'] for p in eligible_pairs])) / \
           (max([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) - 
            min([self.swap_info[p]['avg_swap'] for p in eligible_pairs]) + 1e-10)
norm_vol = (volatility - min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs])) / \
          (max([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) - 
           min([self.swap_info[p]['volatility'] * self.config['leverage'] for p in eligible_pairs]) + 1e-10)

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

Hier sehen wir eine komplexe Beziehung:

1. Die Normalisierung von Parametern ist ein entscheidender Schritt, der es uns ermöglicht, unterschiedliche Größen zu vergleichen. Berechnen wir für jeden Parameter die relative Position im Bereich von 0 bis 1.
2. Gewichtungskoeffizienten – Mit den Parametern swap_weight, return_weight und volatility_weight können wir die Empfindlichkeit des Modells gegenüber verschiedenen Faktoren anpassen.
3. Der gegenteilige Effekt der Volatilität – beachten Sie das Minuszeichen vor volatility_weight, das unseren Wunsch nach Minimierung der Volatilität widerspiegelt.

Diese Gewichte sind über die Konfiguration konfigurierbar:

self.config = {
    # ...
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    # ...
}

Diese Parameter können an unterschiedliche Marktbedingungen und Anlegerpräferenzen angepasst werden. Wenn Sie beispielsweise die Swap-Gewichtung erhöhen, verlagert sich der Schwerpunkt auf die Maximierung der Erträge aus Swaps, was in Zeiten geringer Marktvolatilität vorteilhafter sein kann.

Besonders interessant ist es, zu beobachten, wie das Modell mit Zielkonflikten umgeht. Währungspaare mit hohen positiven Swaps tendieren oft zu einem Rückgang (was unter dem Gesichtspunkt der Zinsparität logisch ist), was zu Spannungen zwischen $R_m$ und $R_s$ führt. Unser Modell findet das optimale Gleichgewicht zwischen diesen widersprüchlichen Zielen, indem es eine Kovarianzmatrix verwendet, um nicht offensichtliche Diversifizierungsmöglichkeiten zu identifizieren.

Das Ergebnis des Algorithmus ist im folgenden Renditediagramm zu sehen, wobei die blaue Linie die Rendite ohne den Swap, die rote Linie den Swap und die violette Linie den Swap, die regelmäßigen Einlagen und die Wiederanlage darstellt:

Die Verbesserung der Sharpe Ratio von 0,95 auf 1,68 ist besonders beeindruckend, wenn Swaps in die Strategie einbezogen werden. Dies zeigt, wie systematische Swap-Renditen das Risiko-Ertrags-Verhältnis erheblich verbessern.

Im nächsten Abschnitt wird die spezifische Architektur und Implementierung des SwapArbitrageAnalyzers erläutert. So können Sie diese mathematischen Prinzipien bei Ihrem eigenen Handel anwenden.

SwapArbitrageAnalyzer: Architektur und Umsetzung

Theorie ohne Praxis bleibt nur eine intellektuelle Übung. Um ein komplexes mathematisches Modell der Swap-Arbitrage in ein reales Handelsinstrument zu verwandeln, haben wir SwapArbitrageAnalyzer entwickelt, ein leistungsstarkes Softwaresystem, das den gesamten Prozess von der Datenerfassung bis zur Portfoliooptimierung und deren Visualisierung automatisiert. In diesem Abschnitt werden wir uns mit der Architektur des Systems befassen und die wichtigsten Aspekte seiner Implementierung betrachten.

Philosophie des Systementwurfs und der Komponentenanalyse

SwapArbitrageAnalyzer ist nach dem Prinzip der Trennung der Verantwortlichkeiten konzipiert, wobei jede Komponente eine klar definierte Funktion ausführt. Die Struktur der Klasse spiegelt einen schrittweisen Analyseprozess wider:

class SwapArbitrageAnalyzer:
    def __init__(self, config=None):
        # Initialization of configuration and basic variables
        
    def initialize(self):
        # Connecting to MetaTrader and verifying data access
        
    def analyze(self):
        # Main method that triggers entire analysis process
        
    def _get_current_market_rates(self):
        # Getting current market prices
        
    def _init_swap_data(self):
        # Initializing swap data
        
    def _get_historical_data(self, symbol, start_date):
        # Getting and handling historical data
        
    def _optimize_portfolio(self):
        # Portfolio optimization
        
    def _simulate_portfolio_performance(self):
        # Simulating performance of optimized portfolio
        
    def _create_visualizations(self):
        # Creating visualizations for analyzing results

Diese Architektur folgt einem logischen Datenfluss:

1. Die Datenerhebung bezieht sich auf Marktpreise und Swaps
2. Datenverarbeitung ist die Berechnung von historischen Erträgen und Statistiken
3. Bei der Optimierung geht es darum, die optimale Gewichtung der Währungspaare zu finden.
4. Die Simulation testet die Strategie anhand historischer Daten.
5. Visualisierung ist die Darstellung der Ergebnisse in einer visuellen Form

Das Prinzip der Konfigurierbarkeit ist besonders wichtig. Das System verfügt über eine flexible Struktur von Einstellungen, die alle Aspekte der Analyse betreffen:

self.config = {
    'target_volume': 100.0,
    'max_pairs': 28,
    'leverage': 2,  # Leverage 1:10
    'broker_suffix': '',
    'risk_free_rate': 0.001,
    'optimization_period': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),  # С 01.01.2015 до 17.03.2025
    'panel_width': 750,
    'panel_height': 500,
    'risk_aversion': 2.0,
    'swap_weight': 0.3,
    'return_weight': 0.6,
    'volatility_weight': 0.1,
    'simulation_days': int((datetime(2025, 3, 17) - datetime(2015, 1, 1)).days),
    'monthly_deposit_rate': 0.02  # 2% of the initial capital monthly
}

Diese Flexibilität ermöglicht es uns, das System an unterschiedliche Marktbedingungen, Broker und individuelle Händlerpräferenzen anzupassen, ohne den zugrunde liegenden Code zu ändern.

Methodik der Datenerhebung von 2015 bis 2025

Eine zuverlässige Strategie erfordert zuverlässige Daten. SwapArbitrageAnalyzer nutzt eine direkte Verbindung zum MetaTrader 5, um sowohl historische als auch aktuelle Daten abzurufen:

def initialize(self):
    if not mt5.initialize():
        print(f"MetaTrader5 initialization failed, error={mt5.last_error()}")
        return False
    
    account_info = mt5.account_info()
    if not account_info:
        print(“Failed to get account information")
        return False
        
    print(f"MetaTrader5 initialized. Account: {account_info.login}, Balance: {account_info.balance}")
    self._get_current_market_rates()
    self._init_swap_data()
    self.initialized = True
    return True

Besonderes Augenmerk wird auf den Umgang mit historischen Daten gelegt. Für eine genaue Optimierung sammeln wir täglich Daten über einen Zeitraum von zehn Jahren:

def _get_historical_data(self, symbol, start_date):
    try:
        now = datetime.now()
        rates = mt5.copy_rates_range(symbol, mt5.TIMEFRAME_D1, start_date, now)
        if rates is None or len(rates) < 10:
            print(f"Not enough data for {symbol}: {len(rates) if rates is not None else 'None'} bars")
            return None
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        df['return'] = df['close'].pct_change()
        
        symbol_info = mt5.symbol_info(symbol)
        best_swap = max(symbol_info.swap_long, symbol_info.swap_short)
        swap_in_points = best_swap if symbol_info.swap_long > symbol_info.swap_short else -best_swap
        point_value = symbol_info.point
        df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']  # Leverage account
        
        # ...

Es ist besonders wichtig zu verstehen, wie wir die Erträge aus einem Swap berechnen:

df['swap_return'] = (swap_in_points * point_value) / df['close'] * self.config['leverage']

Dieser Ansatz ermöglicht es, den Swap in der gleichen Maßeinheit wie die Marktrendite darzustellen, d.h. als Prozentsatz des investierten Kapitals. Dies ist entscheidend für die richtige Portfoliooptimierung.

Ein Gewichtungsalgorithmus, der Rendite, Volatilität und Erträge aus einem Swap ausgleicht

Das Herzstück von SwapArbitrageAnalyzer ist ein Portfolio-Optimierungsalgorithmus. Im Gegensatz zu Standardansätzen maximieren wir nicht einfach die erwarteten Renditen oder die Sharpe-Ratio, sondern verwenden einen integrierten Ansatz, der die Besonderheiten der Swap-Arbitrage berücksichtigt.

Die wichtigste Neuerung ist die Methode der normalisierten Bewertung der Attraktivität von Währungspaaren:

combined_score = (self.config['swap_weight'] * norm_swap + 
                 self.config['return_weight'] * norm_market - 
                 self.config['volatility_weight'] * norm_vol)

Bei dieser Formel wird Folgendes berücksichtigt:

• Normalisierte Marktrenditen ( norm_market )
• Normalisiertes Einkommen aus Swap ( norm_swap )
• Normalisierte Volatilität ( norm_vol )

Die Gewichtung der einzelnen Komponenten wird durch die Konfiguration angepasst, sodass wir die Strategie an unterschiedliche Marktbedingungen anpassen können. Standardmäßig verwenden wir die folgenden Werte: swap_weight=0,3 , return_weight=0,6 und volatility_weight=0,1, was auf ein gutes Gleichgewicht zwischen stabilen Erträgen aus Swaps und Marktpotenzial schließen lässt.

Interessant ist, dass der Algorithmus nicht einfach die Währungspaare mit den höchsten Punktzahlen auswählt. Stattdessen wird ein komplexes Optimierungsproblem gelöst, bei dem die Korrelationen zwischen den Paaren berücksichtigt werden:

result = sco.minimize(
    objective,
    initial_weights,
    args=(np.array(list(expected_returns.values())), cov_matrix.values, self.config['risk_free_rate']),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

Infolgedessen können wir nicht offensichtliche Kombinationen von Währungspaaren finden, die zwar durchschnittliche individuelle Eigenschaften haben, aber zusammen ein außergewöhnlich effektives Portfolio aufgrund der Diversifizierung bilden.

Der Algorithmus enthält auch ein Zufallselement, um einen größeren Lösungsraum zu erkunden:

num_pairs = random.randint(1, min(self.config['max_pairs'], len(eligible_pairs)))
eligible_pairs = random.sample(eligible_pairs, num_pairs)

Dies ist besonders wertvoll im Zusammenhang mit Swap-Arbitrage, wo es zahlreiche lokale Optima geben kann, die in Bezug auf die Effizienz eng beieinander liegen.

Das Ergebnis des Algorithmus ist die Struktur des optimalen Portfolios:

optimal_portfolio = {}
for i, pair in enumerate(eligible_pairs):
    if optimal_weights[i] != 0:
        optimal_portfolio[pair] = optimal_weights[i]
        self.swap_info[pair]['weight'] = optimal_weights[i] * 100

print("\nOptimal portfolio with positive swap:")
for pair, weight in sorted(optimal_portfolio.items(), key=lambda x: abs(x[1]), reverse=True):
    direction = 'Long' if weight > 0 else 'Short'
    swap_value = self.swap_info[pair]['long_swap'] if weight > 0 else self.swap_info[pair]['short_swap']
    print(f”Pair: {pair}, Direction: {direction}, Weight: {abs(weight)*100:.2f}%, Swap: {swap_value:.2f}")

Ein typisches Ergebnis könnte wie folgt aussehen:

An optimal portfolio with a positive swap:
Pair: GBPAUD, Direction: Short, Weight: 18.45%, Swap: 2.68
Pair: EURNZD, Direction: Long, Weight: 15.22%, Swap: 3.15
Pair: EURCAD, Direction: Short, Weight: 14.87%, Swap: 1.87
Pair: AUDNZD, Direction: Long, Weight: 12.34%, Swap: 2.92
Pair: GBPJPY, Direction: Long, Weight: 11.78%, Swap: 2.21
Pair: USDJPY, Direction: Long, Weight: 10.56%, Swap: 1.94
Pair: CHFJPY, Direction: Long, Weight: 9.47%, Swap: 2.35
Pair: EURJPY, Direction: Long, Weight: 7.31%, Swap: 1.68

Nach der Optimierung führt das System eine Simulation der Portfoliorenditen über einen historischen Zeitraum durch:

def _simulate_portfolio_performance(self):
    # ... (initializing variables)
    
    for date in all_dates:
        daily_return = 0
        daily_swap = 0
        for pair, weight in self.optimal_portfolio['weights'].items():
            # ... (calculation of daily return and swap)
        
        # Calculation of return without swap
        market_profit = current_capital * daily_return
        current_capital += market_profit
        
        # Calculation of return with swap
        market_profit_with_swap = current_capital_with_swap * daily_return
        current_capital_with_swap += market_profit_with_swap + daily_swap_applied
        
        # Calculation of return, taking into account deposits and reinvestment
        # ...

Die Simulationsergebnisse werden in verschiedenen Charts visuell dargestellt:

def _create_visualizations(self):
    # ... (creating visualizations)
    
    # 1. The portfolio and its proportions
    plt.figure(figsize=(self.config['panel_width']/100, self.config['panel_height']/100), dpi=100)
    sorted_weights = sorted(self.optimal_portfolio['weights'].items(), key=lambda x: abs(x[1]), reverse=True)
    pairs = [f"{item[0]} ({'L' if item[1] > 0 else 'S'})" for item in sorted_weights]
    weights = [abs(item[1]) * 100 for item in sorted_weights]
    colors = plt.cm.viridis(np.linspace(0, 0.9, len(pairs)))
    plt.pie(weights, labels=pairs, autopct='%1.1f%%', colors=colors, textprops={'fontsize': 8})
    plt.title('Portfolio proportions (L=Long, S=Short)')
    plt.tight_layout()
    plt.savefig('portfolio_proportions.png', dpi=100, bbox_inches='tight')
    plt.close()
    
    # ... (creating other charts)

Im Ergebnis ist die Architektur des SwapArbitrageAnalyzer eine harmonische Kombination aus mathematischer Strenge durch den Einsatz moderner Portfolio-Optimierungsmethoden, praktischer Anwendbarkeit durch die direkte Anbindung an ein Handelsterminal und die Berücksichtigung realer Marktbedingungen, Flexibilität durch umfangreiche Anpassungsmöglichkeiten an unterschiedliche Zwecke und Präferenzen sowie Übersichtlichkeit durch eine umfassende Visualisierung für fundierte Entscheidungen.

Dieser Ansatz macht das System zu einem leistungsstarken Instrument nicht nur für professionelle Händler, sondern auch für Marktforscher, die komplexe Wechselwirkungen zwischen verschiedenen Rentabilitätsfaktoren auf dem Devisenmarkt verstehen wollen.