MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 43): Reinforcement Learning mit SARSA

Einführung

Bestärkendes Lernen (Reinforcement Learning, RL) ermöglicht es Handelssystemen, von ihrer Umgebung oder von Marktdaten zu lernen und so ihre Fähigkeit zum Handel im Laufe der Zeit zu verbessern. RL ermöglicht die Anpassung an sich ändernde Marktbedingungen und ist daher für bestimmte dynamische Finanzmärkte und Wertpapiere geeignet. Die Finanzmärkte sind unberechenbar, da sie oft mit einem hohen Maß an Unsicherheit behaftet sind. RL zeichnet sich dadurch aus, dass es Entscheidungen unter Unsicherheit trifft, indem es seine Handlungen kontinuierlich auf der Grundlage der erhaltenen Rückmeldungen (Belohnungen) anpasst, was für Händler sehr hilfreich ist, wenn sie mit volatilen Marktbedingungen umgehen müssen.

Ein paralleler Vergleich hierzu könnte ein Expert Advisor sein, der auf ein Chart gestartet worden ist und sich ebenfalls regelmäßig anhand der jüngsten Kursentwicklung selbst optimiert, um seine Parameter fein abzustimmen. RL zielt darauf ab, dasselbe zu tun, aber mit weniger Fanfare. In dem Teil dieser Serie, der sich mit RL befasst hat, haben wir es im Sinne seiner strengen Definition als dritten Ansatz für das Training beim maschinellen Lernen (neben überwachtem und unüberwachtem Lernen) verwendet. Wir haben es noch nicht als unabhängiges Modell betrachtet, das für Prognosen verwendet werden kann.

Das ändert sich in diesem Artikel. Wir führen nicht nur einen anderen RL-Algorithmus ein, SARSA, sondern versuchen, diesen innerhalb einer anderen nutzerdefinierten Signalklasse der von Wizard zusammengestellten Expert Advisors als unabhängiges Signalmodell zu implementieren. Als Signalmodell eingesetzt, automatisiert RL den Entscheidungsfindungsprozess und reduziert die Notwendigkeit ständiger menschlicher Eingriffe, was wiederum (zumindest theoretisch) den Hochfrequenzhandel und die Reaktion auf Marktbewegungen in Echtzeit ermöglichen könnte. Durch die ständige Rückkopplung mit dem Belohnungsmechanismus lernen RL-Modelle außerdem, Risiken besser zu steuern. Dies wird dadurch erreicht, dass risikoreiche Handlungen mit geringen Belohnungen bestraft werden, was im Endeffekt dazu führt, dass RL die Exposition gegenüber volatilen oder verlustreichen Geschäften minimiert.

Im RL geht es aber im Prinzip auch um das Gleichgewicht zwischen Erkundung und Ausbeutung, d.h. um die Abwägung zwischen dem Ausprobieren neuer Strategien und der Nutzung bereits profitabler Strategien. Ermöglicht wird dies durch einen „Epsilon-Greedy“-Ansatz zur Aktualisierung der Q-Map, einer Matrix von Aktionen über die möglichen Umweltzustände hinweg, aus der ein Agent eine Aktion auswählen kann.

Es gibt noch ein paar andere Vorteile von RL, die zwar anekdotisch erscheinen mögen, aber angesichts der zunehmenden Rolle von RL in der KI dennoch erwähnenswert sind.

Es kann dazu beitragen, die Handelsausführung zu optimieren, indem es auf der Grundlage historischer Daten und Echtzeit-Feedback den besten Zeitpunkt und die besten Preispunkte für den Kauf oder Verkauf ermittelt und so die Rentabilität verbessert. Dies kann erreicht werden, wenn es als Basissignalmodell, wie in diesem Artikel, mit einem anderen Signal gepaart wird, sodass seine Rolle darin besteht, in Situationen, in denen schwebende Aufträge verwendet werden, das Wie zu bestimmen. Wenn die Q-Map z.B. 3 Aktionen von Limit-Orders, Stop-Orders und Market-Orders enthält, können die Einstiegspunkte einer bereits etablierten und vertrauten Strategie feinabgestimmt werden.

RL ist ein wenig unkonventionell und eignet sich im Gegensatz zu traditionellen linearen Modellen vielleicht zum Erlernen und Ausführen komplexer, nichtlinearer Handelsstrategien, die das reale Marktverhalten wohl besser widerspiegeln. RL ist auch skalierbar, um mehrere Anlageklassen oder Strategien gleichzeitig zu handhaben, je nachdem, wie man seine Q-Map und die dazugehörigen Aktionen definiert, was es zu einer vielseitigen Lösung für das Portfoliomanagement oder den algorithmischen Handel über verschiedene Finanzinstrumente hinweg macht. Schließlich ist es besonders für Echtzeit-Entscheidungssysteme geeignet, die nicht nur vollautomatische Expert Advisors umfassen, sondern je nach Strategie und aktuellem Set-up auch teilweise manuelle Handelssysteme und Expert Advisors umfassen können.

Einführung in die SARSA

SARSA, ein Akronym für State-Action-Reward-State-Action, verdankt seinen Namen der Art und Weise, wie die Q-Map-Werte aktualisiert werden. Diese Methode zur Aktualisierung der Q-Werte unterscheidet sich deutlich von dem Q-Learning-Ansatz, den wir in einem früheren Artikel untersucht haben, da es sich um einen On-Policy-Ansatz handelt, im Gegensatz zu dem damals untersuchten Off-Policy-Ansatz. Tatsächlich ist unsere SARSA-Implementierung für diesen Artikel identisch mit der, die wir in jenem Artikel verwendet haben, als wir Q-Learning vorstellten, mit Ausnahme der Art und Weise, wie die Q-Map-Werte aktualisiert werden.

Der On-Policy-Algorithmus von SARSA bedeutet, dass es die Q-Werte auf der Grundlage der Aktionen lernt, die es bereits durchgeführt hat, indem es seiner aktuellen Politik folgt, und nicht die Aktionen, die es auf der Grundlage des aktuellen Umgebungszustands durchführen wird. Er aktualisiert die Q-Werte unter Verwendung der Aktion, die von derselben Politik gewählt wurde, die er verfolgt. Q-Learning hingegen ist ein Off-Policy-Algorithmus, d. h., er aktualisiert die Q-Werte anhand der bestmöglichen Aktion des nächsten Umgebungszustands, unabhängig von der Aktion, die die aktuelle Politik durchgeführt hat. Es lernt die optimale Strategie unabhängig von den aktuellen Aktionen des Agenten. Wir implementieren diese Aktualisierung der Q-Werte für SARSA wie folgt:

//+------------------------------------------------------------------+
// Update Q-value using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q-action from Q-Map
   double _action = Q[act[1]][e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _action *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  if(i == act[0])
      {  continue;
      }
      Q[i][e_row[1]][e_col[1]] += THIS.alpha * (Reward + (THIS.gamma * _action) - Q[act[0]][e_row[1]][e_col[1]]);
   }
}

Die SARSA-Aktualisierungsregel verwendet die im nächsten Zustand tatsächlich durchgeführte Aktion (Zustand → Aktion → Belohnung → Zustand → Aktion). Es folgt der Epsilon-Greedy-Strategie für Erkunden und Lernen. Dies ist sehr ähnlich zu dem, was mit Q-Learning untersucht wurde. Was damals nicht klar war, aber jetzt in den Vordergrund gerückt wurde, ist, wie die Epsilon-Greedy-Auswahl zu sehr inkonsistenten Ergebnissen führen kann, da der Prozess der Aktualisierung der Q-Map randomisiert ist. In der Regel gilt: Je kleiner der Epsilon-Wert ist, desto geringer sind die zufälligen Effekte.

Wenn es darum geht, ein Gleichgewicht zwischen Erkundung und Ausbeutung herzustellen, verfolgt SARSA einen ausgewogeneren Ansatz, da es sowohl beim Lernen als auch beim Handeln dieselbe Strategie verfolgt, was auf dem Papier bedeutet, dass es in unsicheren Umgebungen wie einigen Finanzmärkten sicherer ist. Q-Learning hingegen neigt dazu, aggressiver zu sein, da es immer die maximale Belohnung aus dem nächsten Zustand anstrebt, was es möglicherweise anfälliger für risikoreiche Entscheidungen in volatilen Umgebungen macht.

SARSA eignet sich daher besser für Szenarien, in denen die Aufrechterhaltung des Gleichgewichts zwischen Exploration und Ausbeutung von entscheidender Bedeutung ist und das Umfeld risikoreich oder instationär ist, und das beste Szenario, das mir dazu einfällt, wäre zum Beispiel der Handel mit einem der JPY-Paare. Umgekehrt ist Q-Learning besser geeignet, wenn das Umfeld relativ stabil ist und das Finden der optimalen Strategie wichtiger ist als das Management des laufenden Risikos. Das beste Beispiel hierfür ist wohl das Paar EUR-CHF.

Wir haben in diesem Artikel auch einen anderen RL-Algorithmus, Deep-Q-Networks, betrachtet, der sich ebenfalls in einigen Punkten von SARSA unterscheidet. Der Hauptunterschied besteht darin, dass SARSA wie Q-Learning eine Q-Tabelle zur Speicherung von Zustands- und Aktionswerten verwendet. Dies beschränkt SARSA auf Umgebungen mit kleinen Zustandsräumen, da größere Umgebungen die Pflege einer Q-Tabelle unpraktisch machen. Wie wir in diesem Artikel gesehen haben, verwenden DQNs jedoch neuronale Netze, um Q-Werte für jedes Zustands-Aktionspaar zu approximieren, was sie skalierbarer und effektiver in Umgebungen mit großen oder kontinuierlichen Zustandsräumen macht.

SARSA verwendet keine Erfahrungswiederholung, da es aus jeder Erfahrung nacheinander lernt. Dies kann zu ineffizientem Lernen führen, da der Agent nur aus den jüngsten Erfahrungen lernt. Auf der anderen Seite kann DQN aber auch Erfahrungswiederholungen implementieren, bei denen vergangene Erfahrungen zwischengespeichert und während des Trainings zufällig abgerufen werden. Dies kann dazu beitragen, die Korrelation zwischen aufeinanderfolgenden Erfahrungen zu verringern, was wiederum zu einem stabileren Lernprozess führen kann.

Ein weiterer Unterschied zwischen SARSA und DQN ergibt sich aus der Verwendung von Zielnetzen. SARSA hat kein solches Konzept, da es die Q-Werte in jedem Schritt direkt auf der Grundlage der aktuellen Politik aktualisiert. Andererseits ist, wie wir im DQN-Artikel gesehen haben, die Verwendung eines Zielnetzes neben dem Haupt-Q-Netz zur Stabilisierung des Lernens obligatorisch. Bei DQNs wird das Zielnetz in regelmäßigen Abständen aktualisiert, was zu stabilen Q-Wert-Aktualisierungen führt und große Schwankungen beim Lernen verhindert.

Skalierbarkeit und Komplexität sind ein weiterer abstruser Unterschied zwischen DQN und SARSA, da SARSA aufgrund der Beschränkungen der Q-Tabellengröße und des On-Policy-Learnings am besten für kleinere, einfachere Probleme geeignet ist. DQN ist für komplexere, hochdimensionale Probleme konzipiert, wie sie bei bildbasierten Aufgaben oder in Umgebungen mit einer großen Anzahl von Zuständen auftreten. In diesem Artikel über SARSA beschränken wir uns, genau wie im Artikel über Q-Learning, der Kürze halber auf 9 Umgebungszustände.

Zur Erinnerung: Diese basieren auf 3 vereinfachten Marktzuständen: steigend, fallend und seitwärts. Jeder dieser Zustände wird dann auf einen kurzen und einen langen Zeitrahmen angewandt, um eine 3 x 3-Matrix zu erstellen, die 9 mögliche Zustände impliziert. In Fällen, in denen zusätzliche Parameter wie Wirtschaftsnachrichten oder die Kursentwicklung von Wertpapieren berücksichtigt werden müssen, kann das Kontinuum der Werte dieser Daten die Anwendbarkeit von SARSA einschränken.

Schließlich stellt die Lerngeschwindigkeit einen weiteren wichtigen Unterschied zwischen SARSA und DQN dar, da SARSA in komplexen Umgebungen aufgrund des sequentiellen Aktualisierungsprozesses und der fehlenden Generalisierung des neuronalen Netzes langsamer sein kann. DQN ist jedoch in großen Umgebungen tendenziell schneller, da ein neuronales Netz über ähnliche Zustände hinweg verallgemeinern kann, insbesondere wenn dies mit Batch-Lernen über Erfahrungswiedergabe gekoppelt ist.

Einrichten der MQL5-Umgebung für SARSA

Um unsere nutzerdefinierte Signalklasse zu implementieren, die RL und nicht einen MLP oder einen anderen maschinellen Lernalgorithmus als Basismodell verwendet, müssen wir im Wesentlichen die Signalklasse vereinfachen, die wir im Einführungsartikel zu RL gesehen haben, der sich auf Q-Learning konzentrierte. Dieser Artikel stützte sich für seine Prognosen auf ein MLP, wobei sich RL auf die Verarbeitung der Verlustfunktion während des Trainings beschränkte. Das RL verwendet damals wie auch heute bei SARSA den Epsilon-Greedy-Ansatz, der den Agenten bei der zufälligen Auswahl der besten Aktion unterstützt.

Als wir die RL lediglich zur Steuerung des Trainingsprozesses einer MLP nutzten, waren diese oft zufälligen Entscheidungen „tolerierbar“, da der beim Training ermittelte Verlustwert nicht so empfindlich auf die Gesamtleistung der MLP reagierte. Da nun aber das RL das Modell ist und nicht ein anderes MLP, hat die Auswahl zufälliger Aktionen einen unverhältnismäßig großen Einfluss auf die Gesamtleistung.

Beim maschinellen Lernen gibt es häufig eine Trainingsstichprobe und eine Teststichprobe. Aus Gewohnheit stelle ich diese jedoch nicht zur Verfügung, sondern erwähne sie und fordere den Leser auf, sich diese beiden unabhängigen Datensätze zu besorgen. Normalerweise ist der Trainingsdatensatz etwas größer als der Testdatensatz, und wenn wir diesem Protokoll der Trennung von Training und Test folgen, kann die Verwendung von Epsilon für das Modell als Ganzes tatsächlich konstruktiv sein. Die Q-Map, die einfach ein Matrix-Array ist, wird von keiner Funktion im beigefügten Code exportiert, aber das ist relativ einfach und jeder, der daran interessiert ist, dies zu einem unabhängigen Training und Testen weiterzuentwickeln, müsste dieses Matrix nach dem Training als bin- oder CSV-Datei auf seinem System exportieren, bevor er es beim Testen liest.

Kodierung der nutzerdefinierten Signalklasse

Unsere nutzerdefinierte Signalklasse ist, wie oben erwähnt, eine Vereinfachung dessen, was wir im Artikel über den Q-Learning-Algorithmus hatten, und eine der wichtigsten Anpassungen ist die Get-Output-Funktion, die wir wie unten angegeben überarbeitet haben:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSARSA::GetOutput(int &Output, Cql *QL)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.SetOnPolicy(_reward, _in_e);
      Output = QL.transition_act;
   }
}

Der Einbau dieses Codes in einen Expert Advisor kann anhand der Richtlinien erfolgen, die hier und hier für neue Leser zu finden sind. Der zusammengesetzte Expert Advisor wird mit einem optimierten Epsilon-Wert getestet, da wir lediglich die Nutzbarkeit des Expert Advisors demonstrieren wollen. In der Praxis sollte dieser Wert idealerweise durch das eigene Wissen über die relative Bedeutung und Wichtigkeit der verschiedenen Umweltzustände und ihrer jeweiligen Handlungen bestimmt werden.

Testen und Debuggen Ihres SARSA-basierten Signals

Um das nutzerdefinierte SARSA-Signal besser testen und nutzbar machen zu können, müssten einige Änderungen an dieser Signalklasse vorgenommen werden, von denen die vielleicht wichtigste die Hinzufügung einer Funktion zum Export des Q-Map-Matrix-Arrays ist. Dies ermöglicht eine unabhängige Prüfung und Ausbildung im traditionellen Sinne. Diese Fähigkeiten zur Kreuzvalidierung sind jedoch in Strategietester eingebaut, da dort ein Vorwärtstest verfügbar ist.

Zusätzliche Anpassungen können an der Art und Weise vorgenommen werden, wie wir die Umweltzustände definiert haben, indem wir alternative Marktzustände wie absolute Preisniveaus, Indikatorwerte des RSI oder Bollinger Bands in Betracht ziehen und diese mit alternativen Zeitrahmen für jeden dieser Datenpunkte kreuzen. Im Debugger wird zunächst prüfen, wie diese Zustandsvariablen erfasst und aktualisiert werden.

Die Belohnungsfunktion sollte auch die Handelsergebnisse genau widerspiegeln. Für diesen Artikel verwendet unser Code günstige Ausschläge als Prozentsatz der Preisspanne bei jedem neuen Balken. Das liegt daran, dass wir gleichzeitig eine Q-Map trainieren und Handelsentscheidungen auf der Grundlage ihrer Q-Wert-Gewichtung zu diesem Zeitpunkt treffen.  Dies ist sicherlich nicht ideal, denn man sollte sich um eigene, unabhängige Test- und Trainingsdatensätze bemühen. Die Belohnungsmetriken können jedoch langfristiger sein als die, die wir hier verwenden, wenn sie zum Beispiel die Rentabilität und die Leistung eines Expert Advisors über längere Zeiträume hinweg berücksichtigen.

Um nicht blindlings der Profitabilität des Expert Advisors hinterher zu jagen, wäre es auch eine gute Idee, einzelne State-Action-Paare zu testen und sicherzustellen, dass der EA wie erwartet korrekt auf die Marktbedingungen reagiert. Wenn man zum Beispiel die Gewichtung der Q-Werte in der Q-Map in unserer vereinfachten Version für diesen Artikel an der ersten Gitterkoordinate von 0 & 0 prüft, die kurzfristigen und langfristigen Abwärts-Bedingungen kennzeichnet, sollte die höchste Gewichtung für die Aktion 0 gelten, die einen Verkauf darstellt, und nicht für einen „Kurvenanpassungswert“, der nicht mit dem übereinstimmt, was man in Abwärts-Märkten tun sollte.

Die Überprüfung eines angemessenen Gleichgewichts zwischen Erkundung und Ausbeutung, wie es durch die Epsilon-Greedy-Strategie erreicht wird, ist ebenfalls von entscheidender Bedeutung, kann jedoch durch die Optimierung des idealen Epsilon-Werts erreicht werden. Diese Optimierung müsste jedoch an einem separaten Trainingsdatensatz durchgeführt werden, bei dem die Q-Maps auf Durchgängen mit besserer Leistung gesichert werden. Nach dem Training auf einem separaten Datensatz kann das Testen (Vorwärtstest) den verwendeten Epsilon-Wert bestätigen oder widerlegen.

Die Optimierung sollte mit Datensätzen von angemessener Qualität durchgeführt werden. Die Berichte der Strategietester zeigen die Qualität der verwendeten Daten nach einem bestandenen Strategietest an und sind somit immer ein guter Indikator für die Zuverlässigkeit der Schulung. Bei diesem Training werden jedoch am Ende jedes Durchgangs Q-Maps exportiert, wenn die Testergebnisse besser sind als die vorherigen Benchmarks. Die exportierten Q-Maps würden dann in den nachfolgenden Back-Training-Runden wiederverwendet, sodass diese zusätzlichen Trainingsdurchgänge beim Training neuronaler Netze als Epochen fungieren.

Am Ende des Trainingsprozesses würde die endgültige Q-Map, die die zufriedenstellendste Leistung des Expert Advisors erbringt, in einem einzigen Vorwärts-Testdurchgang verwendet, um zu sehen, ob die vorausgegangene Trainingsleistung mit dieser speziellen Q-Map auf einem noch „ungesehenen“ Testdatensatz repliziert werden kann. Vorwärtstests sind eine Eigenart von Strategietestern, und dieser Artikel hier kann als Leitfaden für Leser dienen, die neu in diesem Bereich sind.

Neben der Kreuzvalidierung anhand historischer Datensätze könnte dies auch für Live-Konten in Betracht gezogen werden, bevor sie vollständig eingesetzt werden. Leistungsprotokollierung, in der die verschiedenen Q-Maps neben ihrer jeweiligen Testleistung tabellarisch aufgeführt sind. Dies kann durch die Implementierung einer detaillierten Protokollierung in Echtzeit-Forward-Tests noch weiter vorangetrieben werden, um Marktzustände, Aktionen, Belohnungen und Q-Wert-Aktualisierungen zu erfassen, was zumindest auf dem Papier dabei helfen sollte, Entscheidungsfehler aufzuspüren und Parameter wie Lernrate oder ε-Decay bei Bedarf anzupassen.

Berichte des Strategietesters

Testläufe auf dem täglichen Zeitrahmen für EUR JPY für das Jahr 2022, die ausschließlich der Demonstration der Nutzbarkeit des Expert Advisors dienen, liefern uns folgende Ergebnisse:

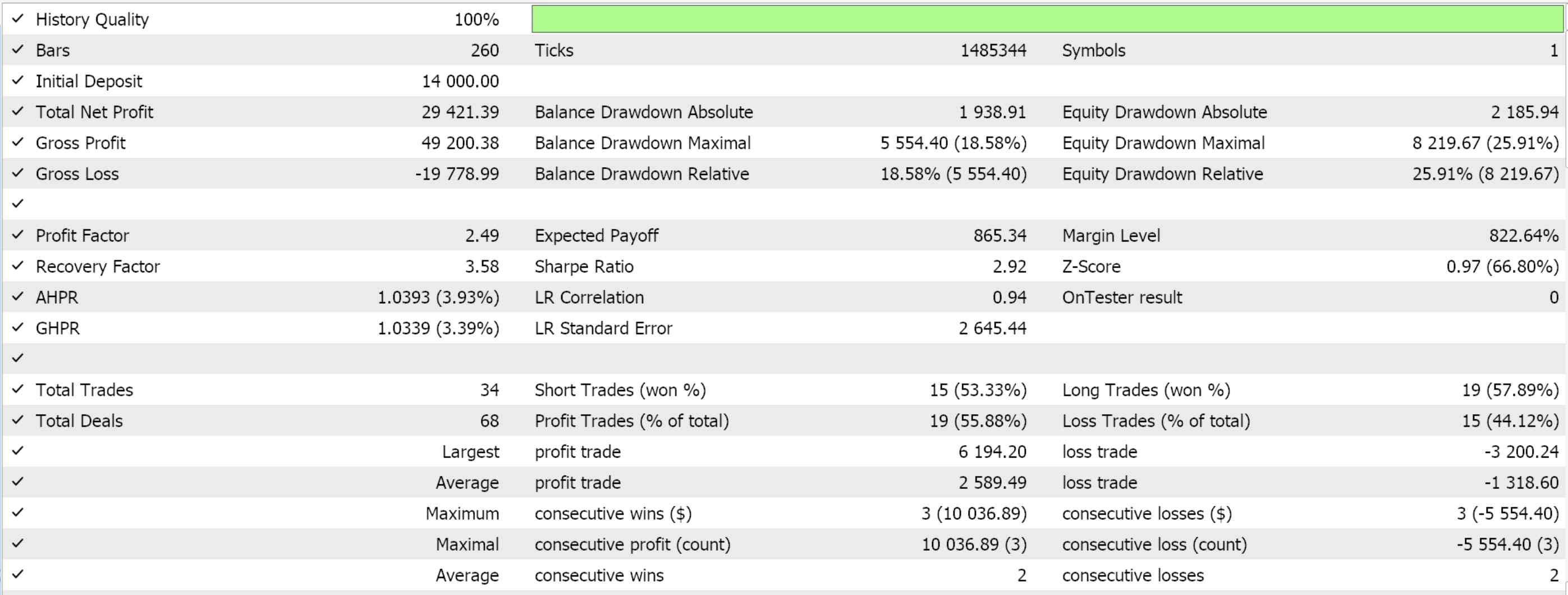
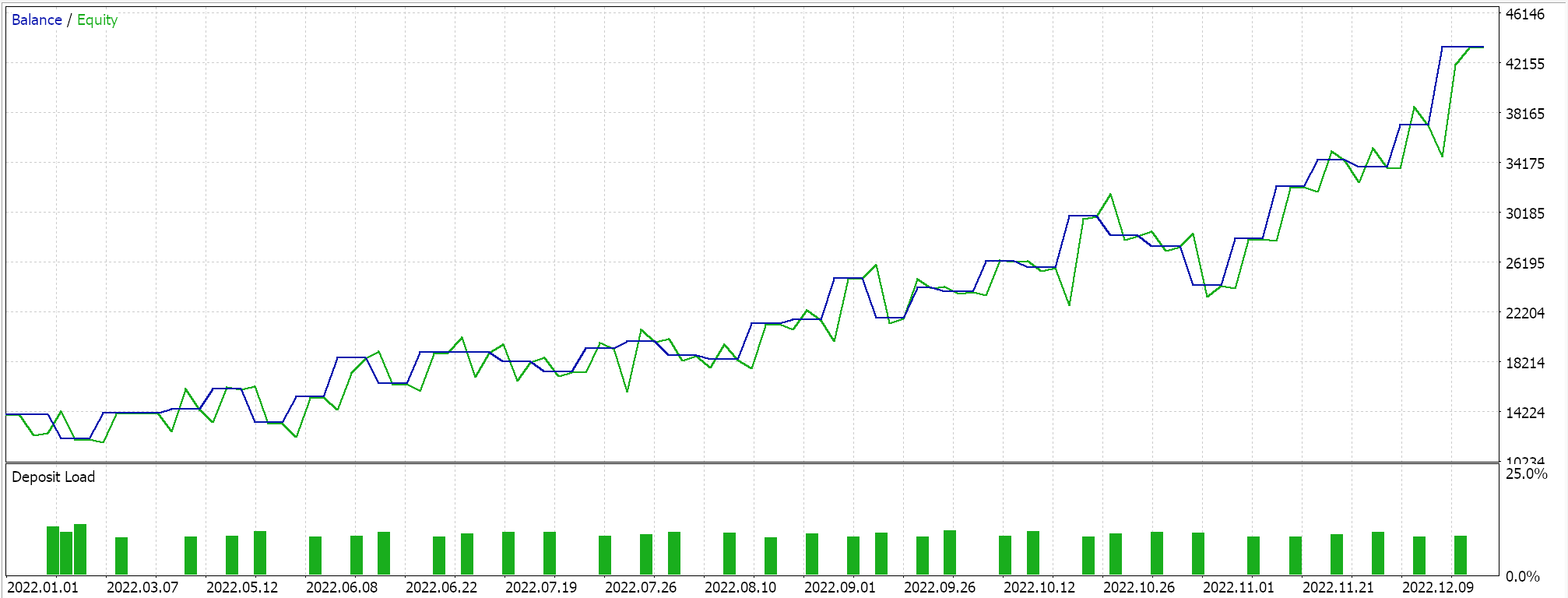
Praktische Überlegungen zu SARSA im Live-Handel

Da es sich bei SARSA um einen On-Policy-Algorithmus handelt, bezieht er die Aktionen der Politik direkt in den Lernprozess ein, was ihn anpassungsfähiger an verrauschte Daten macht. Die von uns verwendete Q-Map-Methode aktualisiert alle Q-Werte in der Map im Verhältnis zu ihrem Abstand zur aktuellen Aktion, wie im obigen On-Policy-Code gezeigt. Diese Aktualisierung folgt der Epsilon-Greedy-Aktualisierung, die in der Action-Funktion durchgeführt wird, um ein Gleichgewicht zwischen Exploration (Entdeckung neuer Strategien) und Exploitation (Nutzung bekannter Strategien) herzustellen und das Modell dabei zu unterstützen, eine Überanpassung an kurzfristiges Rauschen in den Marktdaten zu vermeiden. Die Auswahl der nächsten vom Agenten zu verwendenden Aktion erfolgt durch einen Markov-Entscheidungsprozess, unabhängig davon, ob eine Markov-Gewichtung auf den Q-Wert-Aktualisierungsprozess angewandt wird, wie wir es bereits im Artikel über Q-Learning getan haben. Dies wird in der Action-Funktion wie unten gezeigt gehandhabt:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//
   int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   transition_act = 0;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q[i][_next_row][_next_col] > Q[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
}

Zeitliche Glättung durch einen Belohnungsmechanismus hilft, kurzfristige Störungen zu glätten, indem er sich auf die kumulative Belohnung über mehrere Zeititerationen konzentriert. Dadurch ist der Algorithmus in der Lage, Muster jenseits des unmittelbaren Rauschens in den Daten zu lernen. Außerdem wird durch eine kontinuierliche Anpassung der Politik sichergestellt, dass die Politik sowohl auf aktuellen als auch auf zukünftigen Zuständen basiert. Dies kann dazu beitragen, die Auswirkungen verrauschter Daten abzuschwächen, da sich der Algorithmus anpassen kann, wenn mehr Daten zur Verfügung stehen, insbesondere wenn sich die Marktbedingungen schnell ändern.

SARSA ist recht robust im Umgang mit volatilen Märkten, da es eine inhärente Struktur bei der Auswahl der Übergangsaktion hat, wie in der Aktionsfunktion angegeben, deren Code oben geteilt wird. Bei einem Koordinatenpaar für den aktuellen Umgebungszustand müssten diese beiden Werte in einen einzigen Index umgewandelt werden, der von der Markov-Matrix der QL-Klasse erkannt wird. Dazu verwenden wir die Funktion „Get Markov“, deren Code unten aufgeführt ist:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

Sobald wir diesen Index haben, können wir aus der Zeile unserer Markov-Matrix (die durch diesen Index dargestellt wird) ablesen, welche Spalte den höchsten Wahrscheinlichkeitswert hat. Diese Markov-Matrix ist dafür besonders geeignet, da sie nicht wie die meisten gängigen Indikatoren gepuffert oder in irgendeiner Weise gespeichert wird. Sie hat kein Gedächtnis, was sie sehr anpassungsfähig an unsichere Umgebungen macht, z. B. wenn die Volatilität hoch ist. Wir lesen also aus der Zeile der Markov-Matrix für den aktuellen Umgebungszustand die Spalte mit der höchsten Wahrscheinlichkeit ab, und ihr Index würde uns die ganze Zahl für den nächsten Umgebungszustand liefern. Diese Ganzzahl müsste wiederum in zwei Werte zerlegt werden, ähnlich wie zu Beginn, die wir als Zeilenindex und Spaltenindex bezeichnen.

Sobald wir diese Zeilen- und Spaltenwerte haben, die die Koordinaten für den nächsten Zustand darstellen, können wir die Aktion mit dem höchsten Q-Wert aus unserer Q-Map ablesen. Der Index dieser Aktion würde das darstellen, was wir als „Übergangsaktion“ bezeichnet haben. Zur Erinnerung: Es gibt drei mögliche Aktionen, nämlich 0 - verkaufen, 1 - nichts tun und 2 - kaufen. Außerdem ist die Umgebung auf 3 Zustände in den 3 „Zeitrahmen“ beschränkt, die die Q-Map berücksichtigt.

Ich spreche von „Zeitrahmen“, weil wir wirklich nur einen Zeitrahmen verwenden. Der Leser kann natürlich den Code modifizieren und entsprechende Änderungen vornehmen. Der Eingabeparameter „m_scale“ legt fest, um wie viel die größeren „Zeitrahmen“-Änderungen bei der Ermittlung dieser zweistufigen Änderungen, die wir bei der Abbildung und Definition der Umgebungszustände verwenden, verfolgt werden.

SARSA berücksichtigt sowohl Aktionen als auch Belohnungen im Rahmen der aktuellen Politik und trägt dazu bei, den Lernprozess in Zeiten hoher Marktvolatilität zu stabilisieren. Dies verhindert extreme Schwankungen in der Entscheidungsfindung, die durch plötzliche Marktveränderungen entstehen könnten, und ist daher für volatile Märkte besser geeignet als Algorithmen, die außerhalb der Strategie arbeiten, wie das Q-Learning. Wie aus unserem oben geteilten On-Policy-Funktionscode ersichtlich ist, aktualisieren wir die Werte für die Aktion mit dem Index 1 und nicht mit dem Index 0, wie es beim Q-Learning-Algorithmus der Fall war.

Da SARSA die von der aktuellen Politik ergriffenen Maßnahmen direkt bewertet, wird es in sehr volatilen Umgebungen ohne viel Aufhebens vorsichtiger und vermeidet so zu optimistische Schätzungen des Aktionswerts, die bei unerwarteten Marktveränderungen zu schlechten Entscheidungen führen könnten. In volatilen Märkten ermöglicht die ε-greedy-Exploration von SARSA dem Modell außerdem, sicherere Strategien zu erkunden, anstatt risikoreiche Maßnahmen zu ergreifen. Dadurch wird die Wahrscheinlichkeit großer Verluste in Zeiten extremer Kursschwankungen verringert, während das Modell weiterhin die Möglichkeit hat, neue profitable Strategien zu entdecken. Die Erkundung sicherer Strategien ergibt sich daraus, dass Epsilon eine zufällige Auswahl von Aktionen zulässt und nicht notwendigerweise die derzeit am besten lohnenden Aktionen, die sich in einem volatilen Umfeld schnell in unvorteilhafte Belohnungen verwandeln können. 

Die langfristige Annäherung von SARSA an die optimale Politik hängt von der kontinuierlichen Interaktion mit der Umwelt ab. Auf den Finanzmärkten, wo langfristige Trends und strukturelle Veränderungen die Regel sind, stellt die iterative Politikbewertung von SARSA sicher, dass die Q-Werte im Laufe der Zeit konvergieren und damit diese langfristigen Muster widerspiegeln. 

Anpassung von SARSA für komplexere Strategien

Die State-Space-Aggregation in SARSA kann eine Möglichkeit sein, komplexe Zustandsräume aufzuschlüsseln, insbesondere auf den Finanzmärkten, wo der Zustandsraum (Preisbewegungen, Indikatoren, Marktbedingungen, Wirtschaftsnachrichten) sehr groß und kontinuierlich sein kann. Die Aggregation des Zustandsraums würde diese Komplexität verringern, indem ähnliche Zustände zu „aggregierten“ oder „abstrakten“ Zuständen zusammengefasst werden. Das gröbste Beispiel dafür sind unsere Umgebungszustände für diesen Artikel, die einfach 3 über sofortige Änderungen und längerfristige Änderungen sind. Eine einfallsreichere Verwendung könnte jedoch auch darin bestehen, ein Umfeld zu betrachten, das vielschichtiger ist, wie z. B. eine Q-Map, die auf jeder Achse z. B. Informationen über 10-jährige Renditen, Benchmark-Zinssätze, PPI, CPI und die Arbeitslosenquote enthält.

Da Q-Maps zweiachsig sind, wären diese Informationen für jede Währung eines gehandelten Devisenpaares anwendbar. Anstatt sich also mit den einzelnen Werten für jede dieser Kennzahlen auseinander zu setzen, könnte man sie auf die gleiche Weise zusammenfassen, wie wir es für diesen Artikel getan haben, indem man einfach betrachtet, ob jede dieser Kennzahlen gestiegen, gleich geblieben oder gesunken ist. Anhand dieser Ergebnisse würde dann bestimmt, welche Art von Index an jedem Punkt der Q-Map-Matrix zugewiesen werden muss, so wie wir in der Q-Map für diesen Artikel Indexwerte zugewiesen haben.

Schlussfolgerung

Wir haben in diesem Artikel einen anderen Algorithmus für Reinforcement Learning, SARSA, betrachtet, und es ist erwähnenswert, dass die Implementierung, die wir für den ersten RL-Algorithmus hatten, der Q-Learning berücksichtigte, sowie die nachfolgende, die Deep-Q-Networks betrachtete, den Markov-Entscheidungsprozess bei der Auswahl der nächsten Aktion nicht richtig nutzte. Stattdessen wurden Markov-Ketten lediglich als Mechanismus zur Gewichtung des Aktualisierungsprozesses bereitgestellt. Dies wurde für diesen Artikel korrigiert. Der vollständige Quellcode ist beigefügt.