MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 36): Q-Learning mit Markov-Ketten

Einführung

Nutzerdefinierte Signalklassen für assistentengestützte Expert Advisors können verschiedene Rollen übernehmen, die es wert sind, erforscht zu werden. Wir setzen diese Suche fort, indem wir untersuchen, wie der Algorithmus von Q-Lernen zusammen mit Markov-Ketten den Lernprozess eines mehrschichtigen Perzeptron-Netzwerks verfeinern kann. Q-Learning ist einer der verschiedenen (ca. 12) Algorithmen des Reinforcement-Learnings. Im Wesentlichen geht es also auch darum, wie dieses Thema als nutzerdefiniertes Signal implementiert und in einem von einem Assistenten zusammengestellten Expert Advisor getestet werden kann.

Die Struktur dieses Artikels geht also davon aus, was Reinforcement-Learning ist, beschäftigt sich mit dem Q-Learning-Algorithmus und seinen Zyklusphasen, betrachtet, wie Markov-Ketten in Q-Learning integriert werden können und schließt dann wie immer mit den Berichten des Strategietesters. Das Verstärkungslernen kann als unabhängiger Signalgeber genutzt werden, da seine Zyklen („Episoden“) im Wesentlichen eine Form des Lernens sind, die Ergebnisse als „Belohnungen“ für jede der „environments“ (Umgebungen) quantifiziert, an denen der „Akteur“ beteiligt ist. Diese in Anführungszeichen gesetzten Begriffe werden im Folgenden erläutert. Wir verwenden das Reinforcement Learning jedoch nicht als reines Signal, sondern nutzen seine Fähigkeiten, um den Lernprozess zu fördern, indem wir es als Ergänzung zu einem Multi-Layer-Perceptron einsetzen.

In Anbetracht der Position des Reinforcement-Learnings als dritter Standard im maschinellen Lerntraining neben dem überwachten und dem unbeaufsichtigten Lernen dachte ich, dass wir es mehr in die Verlustfunktion eines MLP einbeziehen könnten, da es gewissermaßen als Übergang zwischen Überwachung und Nicht-Überwachung fungiert, indem es „CriticReward“ (Kritikerbelohnungen) bzw. „environments“ (Umgebungszustände) verwendet. Die beiden zitierten Begriffe werden im nächsten Abschnitt eingeführt; dies bedeutet jedoch, dass der größte Teil der Vorhersage nach wie vor dem MLP obliegt und das Verstärkungslernen eher eine untergeordnete Rolle spielt. Darüber hinaus ist die Verwendung von Markov-Ketten auch eine Ergänzung zum Reinforcement Learning, da die Auswahl der „Akteure“ aus der „Q-Map“ oft ausreicht, um den Q-Learning-Algorithmus zu implementieren, aber wir fügen sie hier ein, um ein Gefühl für den Unterschied in den Testergebnissen zu bekommen, wenn überhaupt.

Überblick über Reinforcement Learning

Das Verstärkungslernen, das wir oben als drittes Standbein des maschinellen Lernens eingeführt haben, ist ein Weg, um während des Trainingsprozesses ein Gleichgewicht zwischen Erkunden und Gewinnen herzustellen. Ermöglicht wird dies durch den zyklischen Ansatz bei der Bewertung der einzelnen Ausbildungsrunden, wobei die Ausbildungsrunden als Episoden bezeichnet werden. Dieser Zyklus kann in dem folgenden Chart dargestellt werden:

Quelle

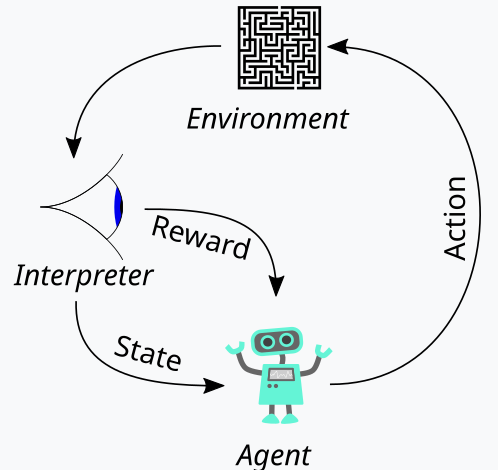
Damit haben wir also eine Abfolge von Schritten im Prozess des Verstärkungslernens. Am Anfang steht ein „Agent“, der im Auftrag einer primären Partei, in unserem Fall einer MLP, handelt, um angesichts einer aktualisierten Q-Learning-Zuordnung (map), eines Kerns oder einer Matrix die ideale Vorgehensweise zu wählen.  Diese Zuordnung besteht aus einer Aufzeichnung aller möglichen Umgebungszustände sowie einer Wahrscheinlichkeitsverteilung darüber, welche möglichen Aktionen für jeden der verfügbaren Zustände zu ergreifen sind.

Am besten lässt sich dies veranschaulichen, wenn wir die Implementierung der Umgebung durchgehen, die wir für diesen Artikel gewählt haben. Als Händler versuchen wir oft, Märkte nicht nur durch ihre kurzfristigen Aktionen zu definieren, sondern auch durch ihre trendigen oder langfristigen Merkmale. Wenn wir uns also auf 3 grundlegende Richtungen konzentrieren, nämlich auf, ab- und seitwärts, dann kann jeder dieser drei Indikatoren auf einem kürzeren und einem längeren Zeitrahmen haben. Unser „Umfeld“ ist also im Wesentlichen ein 9-Index-Raum (3 x 3 für kurzfristig und langfristig), in dem der Index 0 eine Abwärtstrend auf kurze und lange Sicht anzeigt, der Index 4 eine Seitwärtsbewegung sowohl auf kurze als auch auf lange Sicht, während der Index 8 einen Aufwärtstrend auf beiden Zeithorizonten anzeigt usw.

Die Umgebungen werden mit Hilfe einer gleichnamigen Funktion ausgewählt, deren Quelle unten angegeben ist:

//+------------------------------------------------------------------+
// Indexing new Environment data to conform with states
//+------------------------------------------------------------------+
void Cql::Environment(vector &E_Row, vector &E_Col, vector &E)
{  if(E_Row.Size() == E_Col.Size() && E_Col.Size() > 0)
   {  E.Init(E_Row.Size());
      E.Fill(0.0);
      for(int i = 0; i < int(E_Row.Size()); i++)
      {  if(E_Row[i] > 0.0 && E_Col[i] > 0.0)
         {  E[i] = 0.0;
         }
         else if(E_Row[i] > 0.0 && E_Col[i] == 0.0)
         {  E[i] = 1.0;
         }
         else if(E_Row[i] > 0.0 && E_Col[i] < 0.0)
         {  E[i] = 2.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] > 0.0)
         {  E[i] = 3.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] == 0.0)
         {  E[i] = 4.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] < 0.0)
         {  E[i] = 5.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] > 0.0)
         {  E[i] = 6.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] == 0.0)
         {  E[i] = 7.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] < 0.0)
         {  E[i] = 8.0;
         }
      }
   }
}

Dieser Code gilt ausschließlich für unsere 9-Index-Umgebung und kann nicht in Umgebungsmatrizen anderer Größe verwendet werden. Bei der Definition dieser Umgebungsmatrix verwenden wir einen zusätzlichen Eingabeparameter, der als „Maßstab“ bezeichnet wird. Diese Skala trägt dazu bei, unseren langfristigen Rahmenhorizont zu unserem kurzfristigen Rahmenfenster ins Verhältnis zu setzen. Der Standardwert hierfür ist 5, was bedeutet, dass wir auf einer Achse der Umgebungsmatrix den Zustand als auf-, ab- oder seitwärts markieren, basierend auf den Preisänderungen über einen Zeitraum, der fünfmal länger ist als ein anderer Zeitraum, dessen Werte auf der anderen Achse „gezeichnet“ werden. Ich sage „gezeichnet“, weil diese beiden Achsen einfach Koordinatenpunkte für den aktuellen Zustand liefern. Die Indizierung von 0 bis 8 ist einfach eine Abflachung dieser Matrix in ein Array, aber wie Sie aus dem beigefügten Quellcode sehen können, verweist der kontinuierliche Verweis auf „row“ und „col“ (Reihe und Spalte) einfach auf die möglichen x- und y-Koordinatenwerte aus der Umgebungsmatrix, die den aktuellen Zustand definieren.

Die Q-Learning-Zuordnung reproduziert diese Reihe von Umgebungszuständen, indem sie die möglichen Aktionen, die in jedem dieser Umgebungszustände durchgeführt werden können, gewichtet. Da wir in unserem Fall 3 mögliche Aktionen betrachten, die in jedem Zustand durchgeführt werden können, nämlich Kaufen, Verkaufen oder Warten, hat jeder Zustand in der Q-Learning-Zuordnung ein 3-großes Array, das festhält, welche Aktion am besten geeignet ist. Je höher der Punktwert, desto geeigneter ist es. Die andere wichtige Instanz in unserem obigen Zyklusdiagramm ist der Beobachter, den wir als „Kritiker“ bezeichnen werden. Es ist der Kritiker, der in erster Linie die Aufgabe hat, die „Belohnung“ für das Handeln des Akteurs zu bestimmen. Und was sind Belohnungen? Nun, das hängt davon ab, wofür das Reinforcement Learning eingesetzt wird, aber für unsere Zwecke, basierend auf den 3 möglichen Aktionen des Akteurs, verwenden wir den rohen Tickwertgewinn aus der Preisänderung als Belohnung.

Wenn diese Preisveränderung also negativ ist und unsere letzte Aktion ein Verkauf war, dann wirkt das Ausmaß dieser Veränderung wie eine Belohnung. Das Gleiche gilt, wenn die Veränderung nach einer vorangegangenen Kaufaktion positiv ist. Wenn jedoch die letzte Aktion ein Kauf war und wir eine negative Preisveränderung haben, dann wirkt die Größe dieses negativen Wertes wie eine Strafe, genauso wie Preisveränderungen nach einem Verkauf immer mit dem negativen Wert eins multipliziert werden, was bedeutet, dass jedes sich ergebende negative Produkt als Strafe für unsere Aktionen in diesem bestimmten Zustand wirken würde (was unsere Umgebung oder die Indexierung der kurzfristigen und langfristigen Preisaktion des Marktes ist).  

Dieser Belohnungswert muss jedoch normalisiert werden, und deshalb verwenden wir die Funktion „CriticReward“, die ihn im Bereich von 0,0 bis 1,0 hält. Alle negativen Werte liegen zwischen 0,0 und 0,5, während die positiven Werte auf 0,5 bis 1,0 normiert sind. Der Quellcode für diese Funktion ist unten angegeben:

//+------------------------------------------------------------------+
// Normalize reward via off-policy
//+------------------------------------------------------------------+
double Cql::CriticReward(double MaxProfit, double MaxLoss, double Float)
{  double _reward = 0.0;
   if(MaxProfit >= Float && Float >= MaxLoss && MaxLoss < MaxProfit)
   {  _reward = (Float - MaxLoss) / (MaxProfit - MaxLoss);
   }
   return(_reward);
}

Die Aktualisierung des Belohnungswertes würde immer in der Mitte des Trainingsprozesses erfolgen und nicht nur einmal zu Beginn. Das bedeutet, dass wir ständig Parameter, die die Werte von Reward-Max, Reward-Min und Reward-Float aktualisieren, an die Back-Propagation-Funktion weitergeben müssen, damit sie in den Prozess integriert werden können. Um dies zu erreichen, beginnen wir mit einer Änderung der Lernstruktur, die zum Speichern von Lernvariablen verwendet wird, die bei jedem Backpropagation-Durchgang aufgerufen werden können. Die Verwendung einer Struktur macht unseren Code leicht veränderbar, da wir nur die zusätzlichen neuen Variablen, die wir benötigen, zur bestehenden Liste der Variablen innerhalb der Struktur hinzufügen müssen. Dies ist deutlich weniger fehleranfällig und steht im krassen Gegensatz dazu, dass die Liste der Eingabeparameter in eine Funktion geändert werden muss, die die Variablen in dieser Struktur benötigt. Dann wäre es sicherlich unhandlich. Die geänderte Lernstruktur sieht nun wie folgt aus:

//+------------------------------------------------------------------+
//| Learning Struct                                                  |
//+------------------------------------------------------------------+
struct Slearning
{  Elearning         type;
   int               epochs;
   double            rate;
   double            initial_rate;
   double            prior_rate;
   double            min_rate;
   double            decay_rate_a;
   double            decay_rate_b;
   int               decay_epoch_steps;
   double            polynomial_power;
   double            ql_reward_max;
   double            ql_reward_min;
   double            ql_reward_float;
   vector            ql_e;

                     Slearning()
   {  type = LEARNING_FIXED;
      rate = 0.005;
      prior_rate = 0.1;
      epochs = 50;
      initial_rate = 0.1;
      min_rate = __EPSILON;
      decay_rate_a = 0.25;
      decay_rate_b = 0.75;
      decay_epoch_steps = 10;
      polynomial_power = 1.0;
      ql_reward_max = 0.0;
      ql_reward_min = 0.0;
      ql_reward_float = 0.0;
      ql_e.Init(1);
      ql_e.Fill(0.0);
   };
                    ~Slearning() {};
};

Außerdem müssen wir zum Zeitpunkt des Aufrufs der Verlustfunktion einige Änderungen an der Backpropagation-Funktion vornehmen. Dies liegt daran, dass wir jetzt eine neue oder untergeordnete Enumeration für Verlustfunktionen eingeführt haben, deren Auflistung wie folgt lautet:

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2
};

Eine der Enumerationen ist „LOSS_SVR“, die sich mit der Messung des Verlustes mittels Support-Vektor-Regression befasst, ein Ansatz, den wir im letzten Artikel behandelt haben. Die anderen beiden sind „LOSS_TYPICAL“-Verlust, der, wenn er ausgewählt wird, die Liste der eingebauten Verlustfunktionen in MQL5 vorgibt, und der andere ist „LOSS_QL“, wobei QL für Q-Learning steht und, wenn dies ausgewählt wird, das Verstärkungslernen mit Q-Learning den Lernprozess informiert, indem es einen Zielvektor (oder Label) bereitstellt, mit dem die MLP-Prognosen verglichen werden können. Die If-Klauseln innerhalb der Backpropagation-Funktion prüfen dies wie folgt:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

   ...

   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      if(QL.act == 0)
      {  _reward *= -1.0;
      }
      else if(QL.act == 1)
      {  _reward = -1.0 * fabs(_reward);
      }
      QL.CriticState(_reward, Learning.ql_e);
      _last_loss = output.LossGradient(QL.Q_Loss(), THIS.loss_typical);
   }
   

...

}

Die Hinzufügung dieser nutzerdefinierten Verlustfunktion macht die alten Verlustfunktionen, die auf der Grundlage der eingebauten Enumerationen in MQL5 verwendet wurden, nicht unbedingt überflüssig. Wir haben ihn einfach von „loss“ in „typical_loss“ umbenannt, und wenn die Eingabe „custom_loss“ „LOSS_TYPICAL“ lautet, muss dieser Wert angegeben werden.

Nachdem der Belohnungswert normalisiert wurde, wird er zur Aktualisierung der Q-Learning-Zuordnung in der Funktion CriticState verwendet. Die Aktualisierung der Q-Werte erfolgt nach der folgenden Formel:

Wobei:

• Q(s,a): Der Q-Wert für die Durchführung von Aktion a im Zustand s. Dies ist die erwartete zukünftige Belohnung für dieses Zustands-Aktionspaar.
• α: Die Lernrate, ein Wert zwischen 0 und 1, der festlegt, wie stark neue Informationen die alten Informationen überlagern. Ein kleinerer α-Wert bedeutet, dass der Agent langsamer lernt, während ein größerer α-Wert bedeutet, dass er stärker auf die jüngsten Erfahrungen reagiert.
• r: Die jüngste Belohnung, die nach einer Aktion im Staat s.
• γ: Der Abzinsungsfaktor, ein Wert zwischen 0 und 1, mit dem zukünftige Gewinne abgezinst werden. Je höher γ ist, desto mehr legt der Agent Wert auf langfristige Belohnungen, während er sich bei einem niedrigeren γ eher auf unmittelbare Belohnungen konzentriert.
• max a′ ​Q(s′,a′): Der maximale Q-Wert für den nächsten Zustand s′ über alle möglichen Aktionen a′ Dies stellt die Schätzung des Agenten für die bestmögliche zukünftige Belohnung ausgehend vom nächsten Zustand s′ dar.

Und die eigentliche Aktualisierung der Q-Learning-Zuordnung kann in MQL5 wie folgt umgesetzt werden:

//+------------------------------------------------------------------+
// Update Q-value using off-policy (Q-learning formula)
//+------------------------------------------------------------------+
void Cql::CriticState(double Reward, vector &E)
{  int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   int _new_best_q = Action();
   double _weighting = Q[e_row[0]][e_col[0]][_new_best_q];
   if(THIS.use_markov)
   {  LetMarkov(e_row[1], e_col[1], E);
      int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _weighting *= markov[_old_index][_new_index];
   }
   Q[e_row[1]][e_col[1]][act] += THIS.alpha * (Reward + (THIS.gamma * _weighting) - Q[e_row[1]][e_col[1]][act]);
}

Bei der Aktualisierung der Zuordnung wird die Off-Policy-Regel der Aktualisierung angewendet, bei der die beste Aktion des nächsten Zustands verwendet wird, um die alte Aktion zu aktualisieren. Dies steht im Gegensatz zu On-Policy-Aktionen, bei denen die aktuelle Aktion im nächsten Zustand verwendet wird, um die gleiche Aktualisierung vorzunehmen. Das liegt daran, dass es für jeden Zustand, der durch eine Zeilenkoordinate und eine Spaltenkoordinate in der Umgebungsmatrix definiert ist, eine Standardreihe möglicher Aktionen gibt, die der Agent ausführen kann. Und bei Off-Policy-Updates, die Q-Learning verwendet, wird die am besten gewichtete Aktion gewählt. Bei Algorithmen, die On-Policy-Updates verwenden, wird die aktuelle Aktion bei der Durchführung der Aktualisierung beibehalten. Die Auswahl der besten Aktion erfolgt über die Funktion „Aktion“, deren Code unten angegeben ist:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy
//+------------------------------------------------------------------+
int Cql::Action()
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[e_row[0]][e_col[0]][0];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[e_row[0]][e_col[0]][i] > _best_value)
         {  _best_value = Q[e_row[0]][e_col[0]][i];
            _best_act = i;
         }
      }
   }
   //update last action
   act = _best_act;
   return(_best_act);
}

Das Verstärkungslernen ähnelt dem überwachten Lernen insofern, als es eine Belohnungsmetrik gibt, die zur Anpassung und Feinabstimmung der Gewichtung von Aktionen in jedem Umgebungszustand verwendet wird. Andererseits ist es so, als ob unüberwachtes Lernen die Verwendung einer Umgebungsmatrix voraussetzt, deren Koordinatenwerte (die beiden Werte für den Zeilenindex und den Spaltenindex) als Eingaben für den MLP dienen, der sie verwendet. Das MLP dient daher als Klassifikator, der versucht, die richtige Wahrscheinlichkeitsverteilung für die drei anwendbaren Aktionen zu bestimmen, wenn ihm die Koordinaten des Umgebungszustands als Eingaben vorgelegt werden. Das Training erfolgt dann wie bei jedem Klassifikator-MLP, aber dieses Mal zielen wir darauf ab, die Differenz zwischen der projizierten Wahrscheinlichkeitsverteilung des MLP und der Wahrscheinlichkeitsverteilung im Q-Learning-Kernel an den Q-Learning-Zuordnungnskoordinaten zu minimieren, die als Eingabe für den MLP bereitgestellt werden.

Die Rolle der Markov-Übergänge

Markov-Ketten sind stochastische Wahrscheinlichkeitsmodelle, die Übergangsmatrizen verwenden, um die Wahrscheinlichkeiten für den Übergang von einem Zustand in einen anderen abzubilden, wenn sie mit einer zeitlichen Abfolge dieser Zustände gefüttert werden. Diese Wahrscheinlichkeitsmodelle sind von Natur aus gedächtnislos, da die Wahrscheinlichkeit des Übergangs in den nächsten Zustand ausschließlich auf dem aktuellen Zustand basiert und nicht auf der Geschichte der vorherigen Zustände. Diese Übergänge können genutzt werden, um den verschiedenen Zuständen, die in der Umgebungsmatrix definiert sind, Bedeutung beizumessen.

Die Umgebungsmatrix aus unserem Anwendungsfall im nutzerdefinierten Signal berücksichtigt nur die drei Marktzustände auf-, ab- und seitwärts eines kurzen und eines langen Zeithorizonts, sodass es sich um eine 3 x 3-Matrix handelt, die somit neun mögliche Zustände impliziert. Da wir neun mögliche Zustände haben, bedeutet dies, dass unsere Markov-Übergangsmatrix eine 9 x 9-Matrix sein wird, um die Übergänge von einem Umgebungszustand zum anderen abzubilden. Daher muss man in der Lage sein, das Indexpaar in der Umgebungsmatrix in einen einzigen Index umzuwandeln, der in der Markov-Übergangsmatrix verwendet werden kann. Im Endeffekt benötigen wir zwei Funktionen, eine, um das Paar der Zeilen- und Spaltenindizes der Umgebung in einen einzigen Index für die Markov-Matrix umzuwandeln, und eine weitere, um die Zeilen- und Spaltenindizes der Umgebungsmatrix zu rekonstruieren, wenn ein Index der Markov-Übergangsmatrix vorliegt. Diese beiden Funktionen heißen „GetMarkov“ und „SetMarkov“, und ihr Ursprung ist unten angegeben:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

und:

//+------------------------------------------------------------------+
// Getting environment row & col from markov index
//+------------------------------------------------------------------+
void Cql::SetMarkov(int Index, int &Row, int &Col)
{  Col = int(floor(Index / THIS.environments));
   Row = int(fmod(Index, THIS.environments));
}

Wir müssen den Markov-Äquivalenzindex der beiden Umgebungszustandskoordinaten zu Beginn der Durchführung der Markov-Berechnungen erhalten, da wir von diesem Zustand aus übergehen würden. Sobald wir diesen Index erhalten haben, können wir die Übergangswahrscheinlichkeiten zu anderen Zuständen entlang dieser Spalte in der Übergangsmatrix abrufen, da jede dieser Spalten als Gewicht dient. Wie erwartet ergeben sie alle zusammen eins, und da der Akteur bereits den nächsten Zustand aus der Q-Map ausgewählt hat, verwenden wir seine Wahrscheinlichkeit als Zähler im Nenner von eins. Das bedeutet, dass nur seine Wahrscheinlichkeit als Gewicht verwendet wird, um den neuen Wert in der Q-Map während des Lernprozesses zu erhöhen. Der Quellcode, der dies implementiert, ist bereits oben in der Zustandsfunktion des Kritikers enthalten.

Bei diesem Lernprozess wird der Lernzuwachs im Wesentlichen im Verhältnis zu seiner Wahrscheinlichkeit in der Markov-Übergangsmatrix abgezogen.

Darüber hinaus führen wir die Berechnungen der Übergangsmatrix immer dann durch, wenn ein neuer Balken registriert wird und die Zeitreihe der Preise eine Aktualisierung erfährt. Der Code für die Durchführung dieser Berechnungen ist unten angegeben:

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Da es sich um eine speicherlose Übergangsmatrix handelt, beginnt unser obiger Code immer mit einer neu deklarierten Matrix, und die Klassenvariable, die die Wahrscheinlichkeiten enthält, wird ebenfalls mit Nullwerten gefüllt, um jegliche Vorgeschichte auszugleichen. Der Ansatz zur Berechnung der Übergänge ist einfach, da wir in der ersten for-Schleife eine Zählung der Sequenzen der einzelnen Zustände erhalten und darauf eine weitere for-Schleife folgen lassen, in der die kumulierten Zählungen, die wir für jeden Übergang erhalten haben, durch die Gesamtzahl der Zustände geteilt werden, von denen aus die Übergänge erfolgen.

Implementierung der nutzerdefinierten Signalklasse

Wie bereits erwähnt, verwenden wir ein MLP, das als Klassifikator für die Hauptprognose zuständig ist, wobei das Verstärkungslernen nur eine untergeordnete Rolle als Verlustfunktion spielt. Reinforcement Learning kann auch optimiert oder trainiert werden, um brauchbare Handelssignale auszugeben, indem die kritischen Belohnungen maximiert werden. Das ist jedoch nicht das, was wir hier tun, sondern seine Rolle ist dem mehrschichtigen Perzeptron untergeordnet, da es, wie beim überwachten Lernen und auch beim unbeaufsichtigten Lernen, zur Quantifizierung der Zielfunktion verwendet wird.

Wie in früheren Artikeln, in denen wir MLPs verwendet haben, verwenden wir Preisänderungen als Ausgangspunkt für unsere Dateneingabe. Die für diesen Artikel verwendete Umgebungsmatrix ist eine 3 x 3-Matrix, die als Raster möglicher Marktzustände dient, wenn sie auf dem kurzen und dem langen Zeithorizont gewogen wird. Jede der Achsen für den kurzen und den langen Zeitrahmen hat Metriken oder Zahlenwerte von auf-, ab- und seitwärts, die das 3 x 3 Raster bilden. Ähnlich dieser Matrix ist die Q-Learning-Matrix oder Zuordnung, die ebenfalls dieses 3 x 3-Raster hat, mit dem Zusatz eines Feldes möglicher Aktionen, die dem Akteur offen stehen, und die die Eignung jeder Aktion für jeden Zustand bewerten. Dieses Eignungsfeld dient als Kennzeichnung oder Trainingsziel für unser MLP.

Die Inputs für MLP sind jedoch nicht die rohen Preisänderungen, wie es in unseren letzten Artikeln über MLP der Fall war, sondern die Koordinaten des Umgebungszustands für die jüngste oder aktuelle Preisänderung im Kurz- und Langzeitraum. Die Verwendung des Begriffs „Zeitrahmen“ dient hier lediglich der Veranschaulichung der verschiedenen Zeitskalen oder Zeithorizonte, über die Preisänderungen gemessen werden. Wir haben nicht zwei getrennte Zeitrahmen als Eingaben in die Signalklasse, die die Messung dieser Veränderungen leiten, sondern wir haben einen einzigen ganzzahligen Eingabeparameter mit der Bezeichnung „m_scale“, der ein Vielfaches davon ist, wie viel größer der „lange Zeitrahmen“ im Vergleich zum kurzen ist. Da der kurze Zeitrahmen Veränderungen über einen einzelnen Preisbalken verwendet, erhält der lange Zeitrahmen Veränderungswerte über einen Zeitraum, der diesem Skaleneingangsparameter entspricht. Diese Verarbeitung wird in der Funktion getOutput wie folgt durchgeführt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalQLM::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(m_scale) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) &&
            _in_row.Size() == m_scale
            &&
            _in_row_old.Init(m_scale) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, m_scale) &&
            _in_row_old.Size() == m_scale
            &&
            _in_col.Init(m_scale) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) &&
            _in_col.Size() == m_scale
            &&
            _in_col_old.Init(m_scale) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale + ii + 1, m_scale) &&
            _in_col_old.Size() == m_scale
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            vector _in_e;
            _in_e.Init(m_scale);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
            _in.Init(__MLP_INPUTS);
            _in[0] = _row;
            _in[1] = _col;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_data;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  double _type = _target_data[0] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  m_learning.ql_e = _in_e;
                  m_learning.ql_reward_float = _in_row[m_scale - 1];
                  m_learning.ql_reward_max = _in_row.Max();
                  m_learning.ql_reward_min = _in_row.Min();
                  if(i == m_epochs && ii == m_train_set)
                  {  MLP.QL.Action();
                  }
                  MLP.Backward(m_learning, i);
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

Wie wir also aus unserem obigen Quellcode ersehen können, benötigen wir 4 Vektoren, um die Koordinatenwerte für unsere MLP-Eingänge zu erhalten. Sobald diese bestimmt sind, werden sie mit Hilfe der Funktion „Environment“, die die beiden Preisänderungen in einen einzigen Markov-Index umwandelt, und der Funktion „Set Markov“, die diese beiden Koordinaten aus dem MARKOV-Index liefert, in den „in“-Vektor eingetragen, der unsere Eingabe ist. Der MLP-Klassifikator hat eine sehr einfache Architektur von 2-8-3, die 2 Eingänge, 8 versteckte Schichten und 3 Ausgänge darstellt, die den drei möglichen Aktionen entsprechen, die dem Akteur offen stehen. Die Ausgabe des MLP ist im Wesentlichen eine Wahrscheinlichkeitszuordnung, die Werte für „verkaufen“ (Index 0), „warten“ (Index 1) und „kaufen“ (Index 2) liefert.

Der Trainingsprozess des Reinforcement-Learnings misst, wie weit diese Ausgaben von den ähnlichen Vektoren entfernt sind, die jedem Umgebungszustand zugeordnet sind.

Strategie-Testergebnisse

Wie immer führen wir also Optimierungen und Testläufe mit Real-Tick-Daten durch, um zu demonstrieren, wie ein Expert Advisor, der über den MQL5-Assistenten mit dieser Signalklasse zusammengestellt wurde, seine grundlegenden Funktionen ausführen kann. Anleitungen zur Verwendung des beigefügten Codes mit dem MQL5-Assistenten finden Sie hier und hier. Ein großer Teil der Sorgfaltsarbeit, um den zusammengestellten Expert Advisor oder das Handelssystem für den Live-Account bereit zu machen, wird in diesen Artikeln nicht behandelt und bleibt dem Leser überlassen. Wir führen Läufe für das Paar GBPJPY für das Jahr 2023 auf dem täglichen Zeitrahmen durch. Wir haben Markov-Ketten als Alternative zur Gewichtung der Q-Learning-Zuordnungswerte eingeführt und führen daher zwei Tests durch, einen ohne und einen mit der Markov-Ketten-Gewichtung. Und hier sind die Ergebnisse:

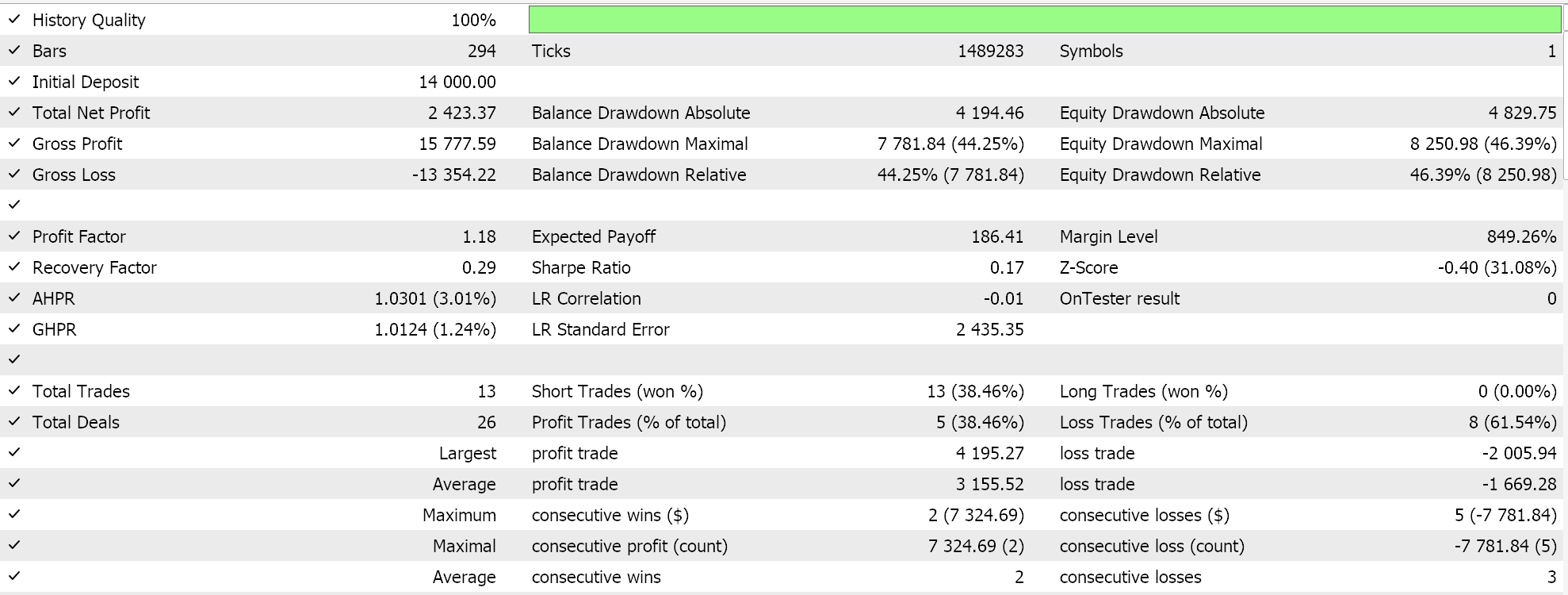
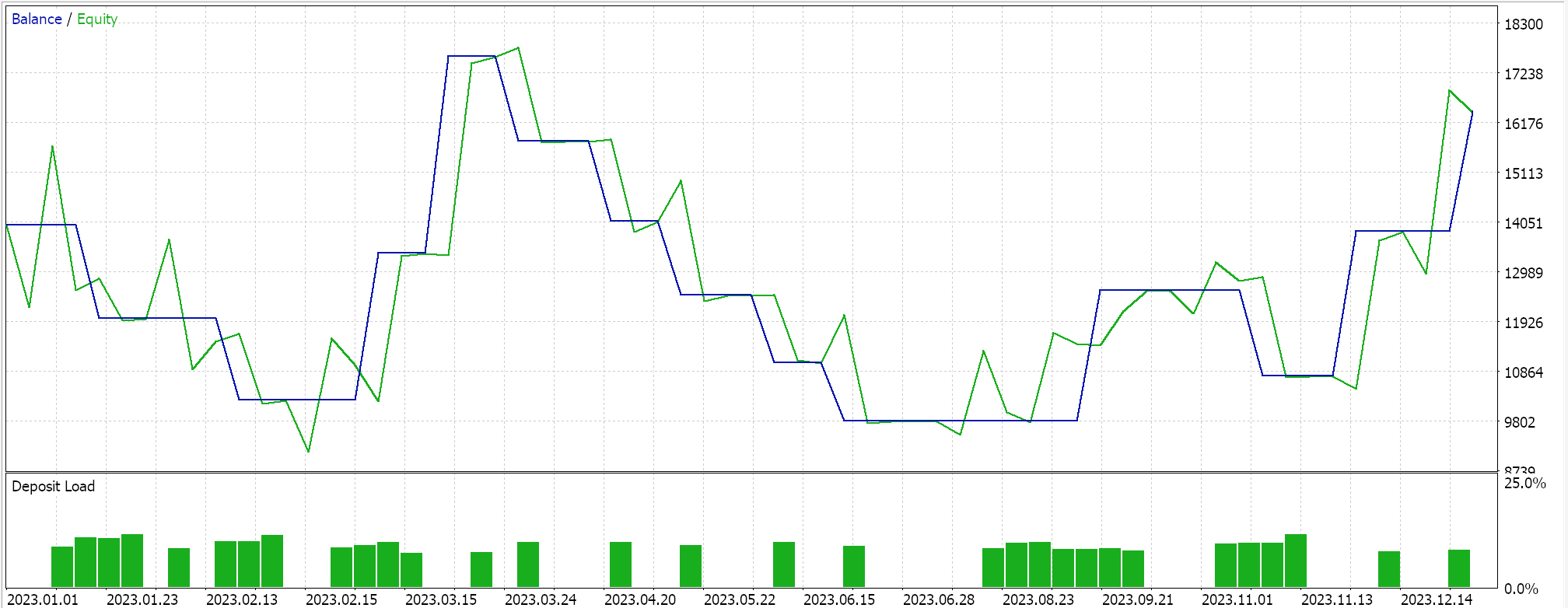
  Und dann sind die Ergebnisse ohne Markov-Gewichtung: 

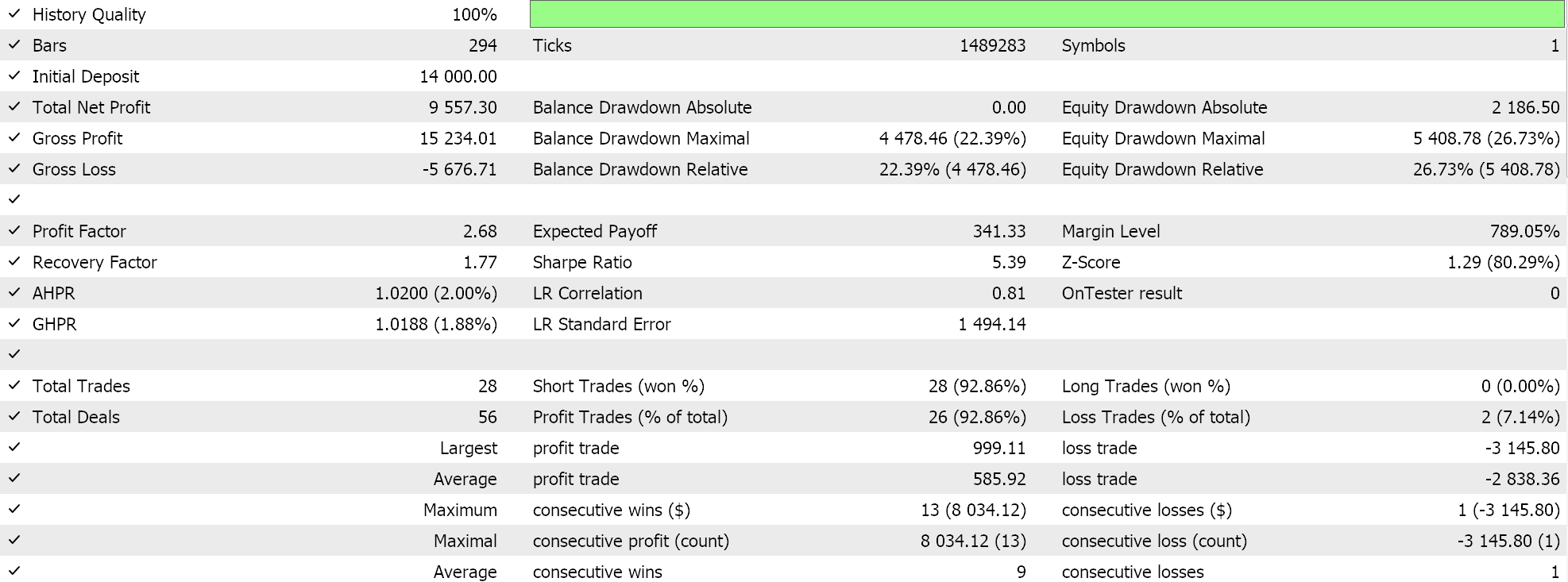
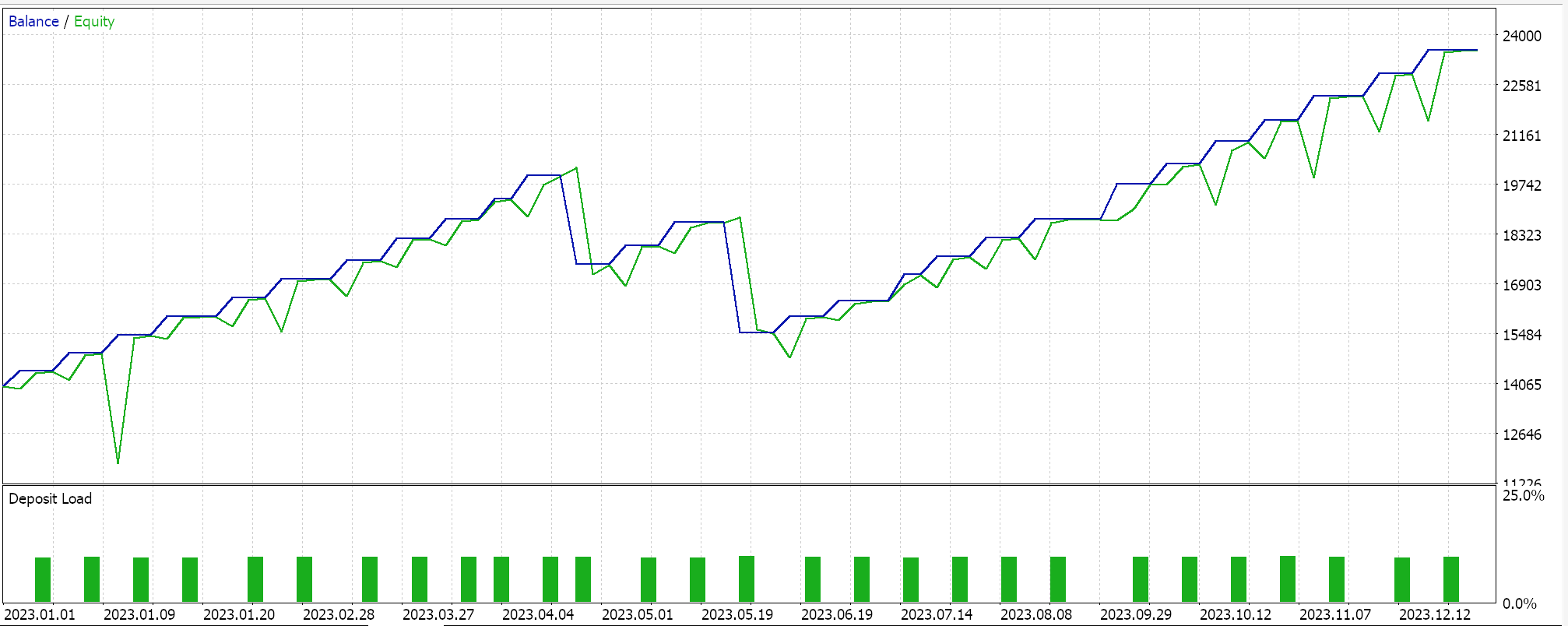
Diese Testergebnisse wurden weder mit den besten Optimierungseinstellungen erzielt, noch wurden mit diesen Einstellungen Walk-Forward-Tests durchgeführt; daher sind sie keine Empfehlung für die zusätzliche Verwendung von Markov-Ketten mit Q-Learning an sich, obwohl stichhaltige Argumente und ein umfassenderes Testregime für die Verwendung sprechen können.

Schlussfolgerung

In diesem Artikel haben wir aufgezeigt, was mit dem MQL5-Assistenten sonst noch möglich ist, indem wir das Reinforcement Learning eingeführt haben, eine Alternative im Machine-Learning-Training neben den etablierten Methoden des überwachten und des unüberwachten Lernens. Wir haben versucht, dies beim Training eines Klassifizierungs-MLP zu nutzen, indem wir es als Information und Anleitung für den Trainingsprozess verwenden, anstatt es als reinen Signalgenerator zu verwenden, was auch möglich ist. Dabei konzentrierten wir uns auf den Q-Learning-Algorithmus und nutzten Markov-Ketten, eine Übergangs-Wahrscheinlichkeits-Matrix, die als Gewicht für den Reinforcement-Learning-Trainingsprozess fungieren kann. Wir präsentierten Testläufe eines Trading Expert Advisors in zwei Szenarien: wenn er ohne Markov-Ketten trainiert wurde und wenn er mit ihnen trainiert wurde.

Dies war, denke ich, etwas komplexer als meine früheren Artikel, da wir 2 Klassen zu unserem nutzerdefinierten Signal referenzieren und viele empfindliche Eingangsparameter mit ihren Standardwerten ohne größere Anpassungen verwendet wurden, viele neue Begriffe mussten für diejenigen eingeführt werden, die mit dem Thema nicht vertraut sind. Es ist jedoch der Anfang unserer Auseinandersetzung mit diesem umfassenden und tiefgreifenden Thema, dem Verstärkungslernen, und ich hoffe, dass es in zukünftigen Artikeln, wenn wir dieses Thema erneut behandeln, nicht mehr so entmutigend sein wird.