Ökonometrische Instrumente zur Prognose der Volatilität: das GARCH-Modell

Einführung

Die Volatilität ist ein wichtiger Indikator für die Bewertung der Variabilität der Preise von Finanzanlagen. Bei der Analyse von Börsenkursen wird seit langem festgestellt, dass große Preisänderungen sehr oft zu noch größeren Veränderungen führen, insbesondere in Finanzkrisen. Auf kleine Veränderungen folgen in der Regel auch kleine Preisänderungen. Auf ruhige Zeiten folgen also Zeiten relativer Instabilität.

Das erste Modell, mit dem versucht wurde, dieses Phänomen zu erklären, war ARCH, entwickelt von Engle: „Autoregressive conditional heteroscedasticity (heterogeneity)“ (Autoregressive bedingte Heteroskedastizität (Heterogenität)). Neben dem Clustering-Effekt (Gruppierung der Renditen in Bündel von großen und kleinen Werten) erklärt das Modell auch das Auftreten von starken Ausläufer und positiver Kurtosis, die für alle Verteilungen von Preissteigerungen charakteristisch sind. Der Erfolg des bedingten Gauß-Modells ARCH führte zur Entstehung einer Reihe von Verallgemeinerungen dieses Modells. Ihr Ziel war es, Erklärungen für eine Reihe anderer Phänomene zu liefern, die bei der Analyse von Finanzzeitreihen beobachtet werden. Historisch gesehen ist eine der ersten Verallgemeinerungen von ARCH das Modell GARCH (verallgemeinertes ARCH) Modell.

Der Hauptvorteil von GARCH im Vergleich zu ARCH liegt in der Tatsache, dass es sparsamer ist und bei der Anpassung von Stichprobendaten keine langfristige Struktur erfordert. In diesem Artikel möchte ich das Modell GARCH beschreiben und vor allem ein fertiges Tool für die Volatilitätsprognose auf der Grundlage dieses Modells anbieten, da die Prognose eines der Hauptziele bei der Analyse von Finanzdaten ist.

Nichtparametrischer Ansatz zur Schätzung der Volatilität

Die Verwendung der Volatilität zur Risikobewertung ist unter Händlern ein recht beliebtes Thema. Die gängigste Methode zur Messung der Volatilität besteht darin, einfach die Standardabweichung über einen bestimmten Zeitraum zu berechnen.

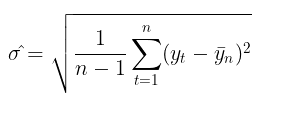
Dies ist der so genannte nicht-parametrische Ansatz zur Schätzung der Volatilität. Die auf diese Weise berechnete Volatilität wird als historische oder empirische Volatilität bezeichnet. Im Gauß'schen Random-Walk-Modell ist dies das wichtigste Maß für Unsicherheit und Variabilität, da es davon ausgeht, dass die Volatilität im Zeitablauf konstant ist.

Parametrischer Ansatz zur Schätzung der Volatilität

Beim GARCH-Modell wiederum wird davon ausgegangen, dass die Volatilität eine Zufallsvariable ist (die Volatilität selbst ist volatil). Dies ist bereits näher an der Realität. Der GARCH-Prozess wird anhand der folgenden Gleichungen festgelegt:

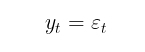
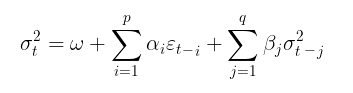
wobei:

• Yt – logarithmische Preissteigerungen,
• εt – Modellresiduen,
• σt² – bedingte Varianz,
• zt = i.e.S. N(0,1) – Gaußsche Standardverteilung,
• zt = i.i.d. t-Student(v) – standardisierte Studentsche t-Verteilung mit v Freiheitsgraden,
• (omega,alpha,beta,v) – Modellparameter, die anhand einer Datenstichprobe geschätzt werden sollen.

Für die Modellparameter gelten die folgenden Einschränkungen:

• omega >0, Bedingung der positiven Varianz,
• alpha≥0,
• beta≥0,
• ∑alphai + ∑betaj <1 , Stationaritätsbedingung,
• v>2

Wenn Beta = 0 ist, wird dasGARCH-Modell zum ARCH-Modell.

Das Modell GARCH wird in der Regel ergänzt durch ein Modell der bedingten oder unbedingten mathematischen Erwartung. So kann beispielsweise der autoregressive Prozess erster Ordnung AR(1) als Modell der bedingten mathematischen Erwartung verwendet werden:

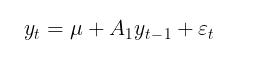
wobei:

• u – Verschiebungsparameter,
• A1 – Parameter des Autoregressionsmodells

Das Ziel der Modellierung des bedingten Mittelwerts ist die Bestimmung einer Reihe von quadrierten Residuen (εt²) zu bestimmen, die für die Suche nach der bedingten Varianz verwendet werden. Wenn es keine Autokorrelation in den Gewinnreihen gibt, was in der Regel der Fall ist, dann können wir zum unbedingten mathematischen Erwartungsmodell übergehen:

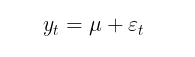
In diesem Artikel werde ich der Einfachheit halber ein Modell ohne Schätzung der Autokorrelation der Gewinne verwenden. Somit reduziert sich das Problem der Schätzung der Volatilität im GARCH-Modell auf das parametrische Problem der Ermittlung der Modellkennzahlen (μ, ω, alpha, beta, v).

Schätzung der Parameter des GARCH-Modells mit der Maximum-Likelihood-Methode

Die Maximum-Likelihood-Methode wird normalerweise verwendet, um unbekannte Parameter zu finden. Unter der Annahme einer Gaußschen Verteilung der Residuen von et hat die logarithmische Wahrscheinlichkeitsfunktion folgende Form:

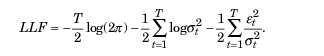
Wenn Abweichungen von der Normalität festgestellt werden, kann die standardisierte Studentsche t-Verteilung als geeignete Verteilung verwendet werden. Bei kleinen Werten des Parameters v (Freiheitsgrad) weist sie eine positive Kurtosis und einen stärkeren Schweif auf als die Normalverteilung. In diesem Fall hat die Wahrscheinlichkeitsfunktion folgende Form:

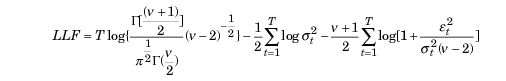
wobei,

• Г - Gamma-Funktion
• T – Volumen der Datenprobe

ALGLIB MinBLEIC-Optimierer

Um die Werte der Parameter des GARCH-Modells zu finden, müssen wir die Likelihood-Funktion maximieren. Dies erfordert Optimierungsmethoden. Die numerische Analysebibliothek ALGLIB kann dabei helfen. Um die Zielfunktion zu maximieren, habe ich den Algorithmus MinBLEIC (Bound Linear Equality Inequality Constraints) gewählt.

//+------------------------------------------------------------------+
//|  Objective Function: Gaussian loglikelihood                      |
//+------------------------------------------------------------------+
void CNDimensional_GaussianFunc::Func(CRowDouble &x,double &func,CObject &obj)
  {
//x[0] - mu;
//x[1] - omega;
//x[2] - alpha;
//x[3] - beta;
   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }

   double residuals[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   double condVar[];
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);  // Unconditional Variance

   for(int i=1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1]; // Conditional Variance
     }

   double LLF[],a[],b[];
   ArrayResize(LLF,N1);
   ArrayResize(a,N1);
   ArrayResize(b,N1);
   for(int i=0; i<N1; i++)
     {

      a[i]= 1/sqrt(2*M_PI*condVar[i]);
      if(!MathIsValidNumber(a[i]))
        {
         break;
        }

      b[i]= MathExp(- MathPow(residuals[i],2)/(2 * condVar[i]));
      if(!MathIsValidNumber(b[i]))
        {
         break;
        }

      LLF[i]=MathLog(a[i]*b[i]);
      if(!MathIsValidNumber(LLF[i]))
        {
         break;
        }
     }

   func = -MathSum(LLF); // Loglikelihood
  }

Bei der GARCH-Funktion, die sich direkt mit der Zielfunktion befasst und die optimalen Werte der Parameter ermittelt, ist es notwendig, :

• die Anfangswerte der Parameter anzugeben,
• die Datenskala festzulegen (ein sehr wichtiger Punkt, von dem der Erfolg der Optimierung abhängt),
• die Grenzen festzulegen, innerhalb derer sich Parameter ändern dürfen,
• lineare Ungleichheitsbedingungen aufzustellen (wir haben nur eine für die Stationarität Alpha + Beta < 1),
• die Bedingungen für das Anhalten des Optimierungsalgorithmus anzugeben,
• und den Differenzierungsschritt anzugeben.

//+------------------------------------------------------------------+
//|  Function GARCH  Gaussian                                        |
//+------------------------------------------------------------------+
vector GARCH()
  {
   double              x[],s[];
   int                 ct[];
   CMatrixDouble       c;
   CObject Obj;
   CNDimensional_GaussianFunc ffunc;
   CNDimensional_Rep frep;

   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }
   double returns_mean  = MathMean(returns);
   double returns_var = MathVariance(returns);
   double KurtosisReturns = MathKurtosis(returns);
// Print("KurtosisReturns= ",KurtosisReturns);

// Initial parameters ---------------------------
   ArrayResize(x,4);
   x[0]=returns_mean;  //  Mu
   x[1]=returns_var;  // Omega
   x[2]=0.0;         // alpha
   x[3]=0.0;        // beta
//------------------------------------------------------------
   double mu;
   if(NormalizeDouble(returns_mean,10)==0)
     {
      mu = 0.0000001;
     }
   else
      mu = NormalizeDouble(returns_mean,10);
// Set Scale-----------------------------------------------
   ArrayResize(s,4);
   s[0] = NormalizeDouble(returns_mean,10);  //  Mu
   s[1] = NormalizeDouble(returns_var,10); // omega
   s[2] =1;
   s[3] =1;
//---------------------------------------------------------------
// Linearly inequality constrained: --------------------------------
   c.Resize(1,5);
   c.Set(0,0,0);
   c.Set(0,1,0);
   c.Set(0,2,1);
   c.Set(0,3,1);
   c.Set(0,4,0.999); // alpha + beta <= 0.999
   ArrayResize(ct,1);
   ct[0]=-1; // {-1:<=},{+1:>=},{0:=}
//--------------------------------------------------------------
// Box constraints ------------------------------------------------
   double bndl[4];
   double bndu[4];

   bndl[0] = -0.01;  // mu
   bndl[1] = NormalizeDouble(returns_var/20,10);  // omega
   bndl[2] = 0.0;  // alpha
   bndl[3] = 0.0;  // beta

   bndu[0] = 0.01;  // mu
   bndu[1] = NormalizeDouble(returns_var,10);  // omega
   bndu[2] = 0.999;  // alpha
   bndu[3] = 0.999;  // beta
//--------------------------------------------------------------
   CMinBLEICStateShell state;
   CMinBLEICReportShell rep;
   double epsg=0;
   double epsf=0;
   double epsx=0.00001;
   double diffstep=0.0001;
//--- These variables define stopping conditions for the outer iterations:
//--- * epso controls convergence of outer iterations;algorithm will stop
//---   when difference between solutions of subsequent unconstrained problems
//---   will be less than 0.0001
//--- * epsi controls amount of infeasibility allowed in the final solution
   double epso=0.00001;
   double epsi=0.00001;

   CAlglib::MinBLEICCreateF(x,diffstep,state); //---  create optimizer
   CAlglib::MinBLEICSetBC(state,bndl,bndu);  //--- add boundary constraints
   CAlglib::MinBLEICSetLC(state,c,ct);
   CAlglib::MinBLEICSetScale(state,s);
   CAlglib::MinBLEICSetPrecScale(state); // Preconditioner
   CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);
   CAlglib::MinBLEICSetOuterCond(state,epso,epsi);
   CAlglib::MinBLEICOptimize(state,ffunc,frep,0,Obj);
   CAlglib::MinBLEICResults(state,x,rep);   // Get parameters
//---------------------------------------------------------

   double residuals[],resSquared[],Realised[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   MathPow(residuals,2,resSquared);
   ArrayCopy(resSquared_,resSquared,0,0,WHOLE_ARRAY);
   MathSqrt(resSquared,Realised);

   double condVar[],condStDev[];
   double ForecastCondVar,PriceConf_Upper,PriceConf_Lower;
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);
   for(int i = 1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1];
     }

   double PlotUncondStDev[];
   ArrayResize(PlotUncondStDev,N1);
   ArrayFill(PlotUncondStDev,0,N1,sqrt(condVar[0])); // for Plot
   ArrayCopy(PlotUncondStDev_,PlotUncondStDev,0,0,WHOLE_ARRAY);
   MathSqrt(condVar,condStDev);
// Print("math expectation of conditional standard deviation = "," ",MathMean(condStDev));

   ArrayCopy(Real,Realised,0,0,WHOLE_ARRAY);
   ArrayCopy(GARCH_,condStDev,0,0,WHOLE_ARRAY);

   vector v_Realised, v_condStDev;
   v_Realised.Assign(Realised);
   v_condStDev.Assign(condStDev);
   double MSE=v_condStDev.Loss(v_Realised,LOSS_MSE); // Mean Squared Error
//-----------------------------------------------------------------------------
//-------- Standardize Residuals--------------------------------------
   double z[];
   ArrayResize(z,N1);
   for(int i = 0; i<N1; i++)
     {
      z[i] = residuals[i]/sqrt(condVar[i]);
     }
   ArrayCopy(Z,z,0,0,WHOLE_ARRAY);
//----------------------------------------------------------------------------------

//-------------- JarqueBeraTest for Normality  ----------------------------------
   double pValueJB;
   int JBTestH;
   CAlglib::JarqueBeraTest(z,N1,pValueJB);
   if(pValueJB <0.05)
      JBTestH =1;
   else
      JBTestH=0; // H=0 - data Normal, H=1 data are not Normal
   double Kurtosis = MathKurtosis(z); // Kurosis = 0 for Normal distribution
//---------------------------------------------------------------------------------

//-------------------------------------------------------------------------------------
//-------- Forecast Conditional Variance for m bars
   double FCV[];
   ArrayResize(FCV,forecast_m);
   for(int i = 0; i<forecast_m; i++)
     {
      FCV[i] = sqrt(x[1]*((1-MathPow(x[2]+x[3],i+1))/(1-x[2]-x[3])) + MathPow(x[2]+x[3],i)*(x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])) ;
     }
   ArrayCopy(FCV_,FCV,0,0,WHOLE_ARRAY);
//-----------------------------------------------------------------------------------
   double LLF[];
   double Loglikelihood;
   ArrayResize(LLF,N1);
   for(int i = 0; i<N1; i++)
     {
      LLF[i] = MathLog(1/sqrt(2*M_PI*condVar[i])*MathExp(- MathPow(residuals[i],2)/(2*condVar[i])));
     }
   Loglikelihood = MathSum(LLF);
//--------------------------------------------------------------------------

   ForecastCondVar= x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1];
   int err1;
   PriceConf_Lower = close[N1]*MathExp(-MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])); // confidence interval pci%
   PriceConf_Upper = close[N1]*MathExp(MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1]));  // confidence interval pci%

//--------------------------------------------------------------------------------------
   vector result= {x[0],x[1],x[2],x[3],rep.GetTerminationType(),ForecastCondVar,PriceConf_Lower,PriceConf_Upper,MSE,Loglikelihood,condVar[0],returns_var,JBTestH,Kurtosis};
   return (result);
  }
//+------------------------------------------------------------------+

Volatilitätsprognose unter Verwendung des GARCH(1,1)-Modells

Prognose der Volatilitätspunkte

Sobald die Modellparameter gefunden sind, können wir uns der Hauptaufgabe zuwenden – der Prognose der Volatilität. Die Volatilitätsprognose für das Modell GARCH(1,1) für m Schritte in die Zukunft wird mit der folgenden Gleichung berechnet:

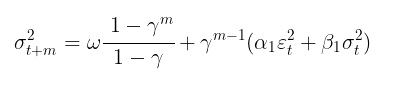
wobei:

• γ = α1 + β1.

Im Falle von m → ∞ konvergiert die Prognose mit der theoretischen unbedingten GARCH-Varianz (wenn die Bedingung der Modellstationarität α1+β1< 1 erfüllt ist).

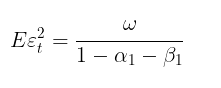
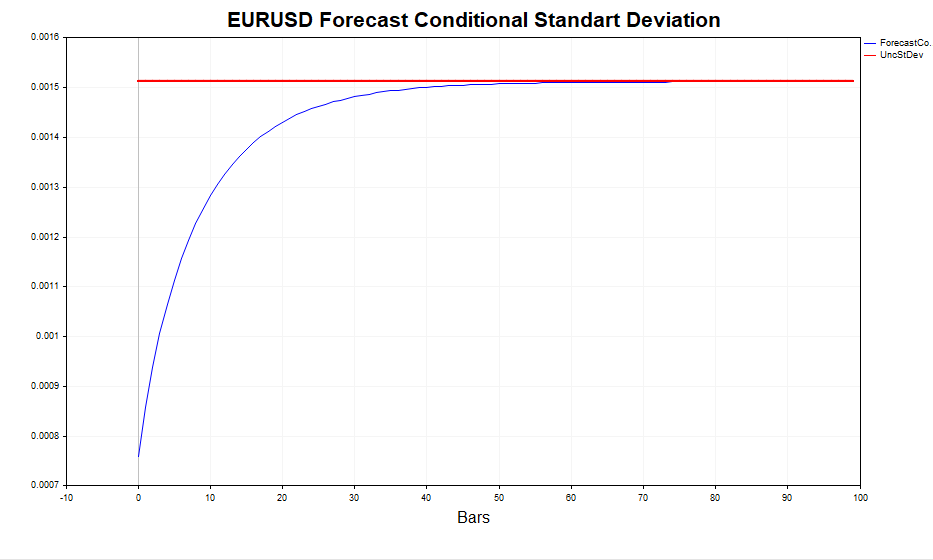
Mit anderen Worten, je weiter die Vorhersage entfernt ist, desto näher liegen ihre Werte am stationären Wert der unbedingten Varianz. Das GARCH-Skript ermöglicht die Berechnung der Volatilitätsprognose für m Schritte in der Zukunft und den Vergleich dieser Werte mit Eεt², wodurch bestätigt wird, dass dies tatsächlich der Fall ist.

Intervall-Prognose

Eine Punktprognose der Volatilität ist nützlich, aber es ist wichtiger, eine probabilistische Schätzung der Spanne zu erhalten, innerhalb derer künftige Preissteigerungen zu beobachten sind, d. h. Konfidenzintervalle mit einem bestimmten Signifikanzniveau zu erhalten.

Unter der Annahme der Normalität z t= i.i.d. N(0,1) Konfidenzintervalle werden nach folgender Gleichung berechnet:

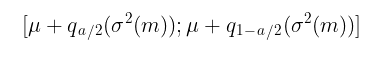
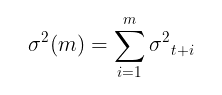
wobei:

• q – Quantil der Standardnormalverteilung

Für ein Konfidenzintervall mit einem Zuverlässigkeitsniveau von 90 % (a = 1-0,9) ist dies beispielsweise das Intervall:

[ u – 1,65σ ; u + 1,65σ ]

Die Dinge sind viel komplizierter, wenn angenommen wird, dass zt = i.i.d. t-Student(v). In diesem Fall gibt es keine analytische Gleichung für die inverse Verteilungsfunktion. Um Konfidenzintervalle zu erstellen, ist daher eine Monte-Carlo-Simulation erforderlich.

//+-------------------------------------------------------------------------+
//|Function calculate Forecast Confidence intervals using Monte-Carlo method|
//+-------------------------------------------------------------------------+
bool MCForecastStandardized_t(const double DoF,const double CondStDevForecast,const double prob, double & F_lower[],double & F_upper[])
  {

   double alpha = 1-prob;
   double qlower[1] = {alpha/2};       // q (a/2)
   double qupper[1] = {1-alpha/2};  // q (1-a/2)

   int N = 10000; //number Monte-Carlo simulates
   double h_St[];
   ArrayResize(h_St,N);
   for(int i=0;i<N;i++)
     {
      h_St[i] = CondStDevForecast * Standardized_t(DoF);   // GARCH-Student(1,1)
     }
   MathQuantile(h_St,qlower,F_lower);
   MathQuantile(h_St,qupper,F_upper);
   return(true);
  }

//+--------------------------------------------------------------------------+
//| Function calculate i.i.d. standardized t-distributed variable            |
//+--------------------------------------------------------------------------+
double  Standardized_t(const double DoF)
  {
   double randStandStudent;
   int err;
   randStandStudent = MathRandomNormal(0,1,err) * sqrt(DoF/((MathRandomGamma(DoF/2.0,1)*2.0)));
   randStandStudent = randStandStudent/sqrt(DoF/(DoF-2.0));
   return(randStandStudent);
  }
//+------------------------------------------------------------------+

Es ist klar, dass die Vorhersage umso genauer ist, je höher die Anzahl der Simulationen ist (die Standardeinstellung ist 10.000), aber auch die für die Berechnungen benötigte Zeit steigt. Die akzeptabelste Zahl ist 100.000. In diesem Fall sehen die Konfidenzintervalle symmetrischer aus.

Prüfung der Angemessenheit des bedingt Gaußschen GARCH-Modells

Um zu überprüfen, ob das GARCH-Modell in der Lage ist, die Heteroskedastizität der Volatilität (Heteroskedastizität = die Varianz der Störterme ist nicht konstant) zu erfassen, , ist es notwendig, die standardisierten Residuen auf Autokorrelation und auf Übereinstimmung mit der Standardnormalverteilung zu überprüfen. Standardisierte Residuen sind einfach die Kurssteigerungen abzüglich der bedingten (oder unbedingten) mathematischen Erwartung, geteilt durch die vom GARCH-Modell berechnete bedingte Standardabweichung.

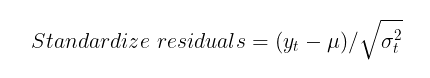
Wenn das GARCH-Modell den tatsächlichen Daten angemessen ist, dann sind die standardisierten Residuen unabhängige und identisch verteilte Standardnormalwerte.

Als Beispiel für die Residualanalyse nehmen wir die täglichen Daten zum EURUSD der letzten vier Jahre und berechnen die Modellparameter.

Überprüfen wir die Quadrate der Residuen auf Autokorrelation.

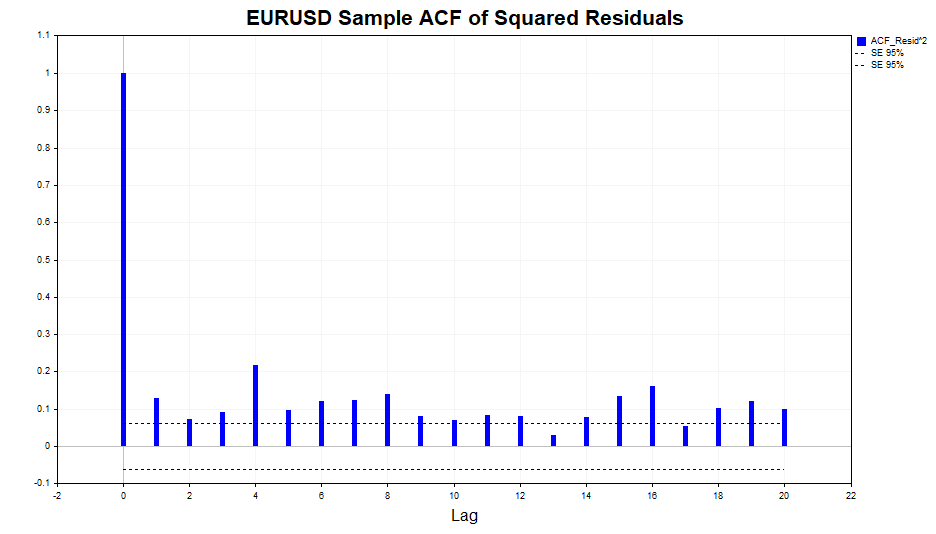
Wie wir sehen können, gibt es eine leichte Abhängigkeit in den Daten, bis einschließlich Lag 20. Überprüfen wir nun die Quadrate der standardisierten Residuen auf Autokorrelation und sehen wir, ob das Modell GARCH(1,1) diese Abhängigkeit angemessen beschreiben konnte.

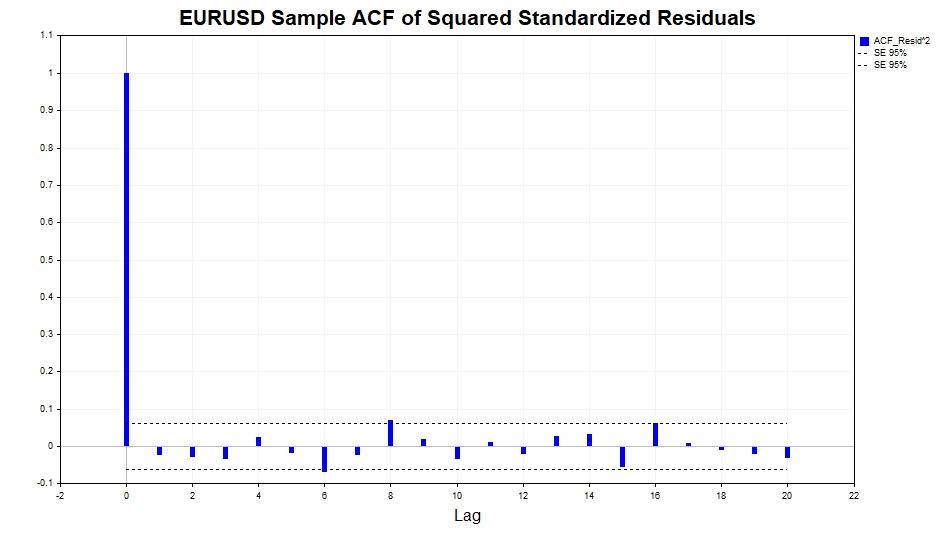
Wie wir sehen können, hat das Modell gute Arbeit geleistet. Es gibt keine signifikante Korrelation in den Daten.

Betrachten wir nun die berechnete realisierte Volatilität (das Quadrat der logarithmischen Kurssteigerungen) und die bedingte Standardabweichung (GARCH). Das Modell reagiert recht erfolgreich auf Veränderungen der Volatilität. Die unbedingte Standardabweichung dient als Mittelwert, um den die GARCH-Volatilität schwankt.

Überprüfen wir die Normalität der standardisierten Residuen.

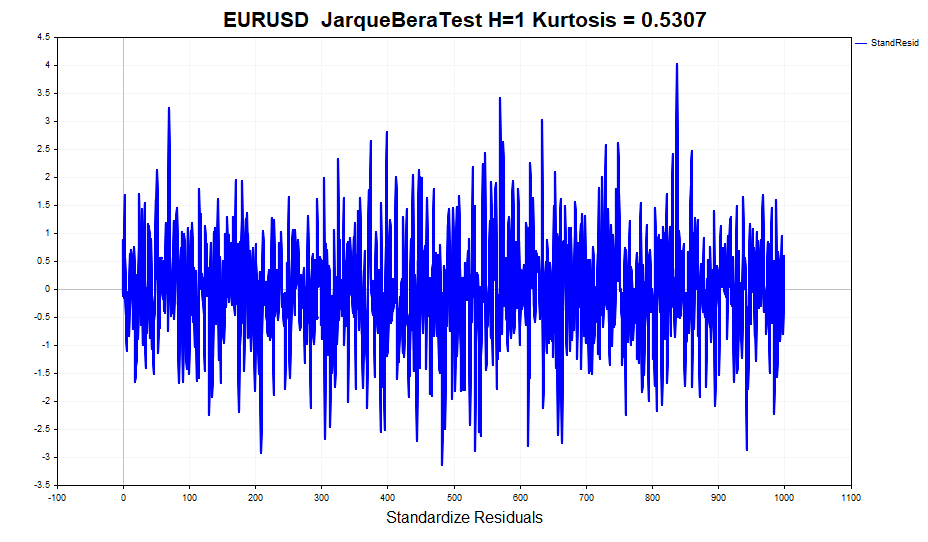
Auf den ersten Blick sehen die Daten ganz normal aus. Es gibt keine deutlich sichtbaren, dicke Ausläufer. Formale Normalitätstests, wie der JarqueBeraTest, weisen die Nullhypothese jedoch zurück. Der Grund liegt in der Überschreitung (0,5307), die sich leicht von der normalen Überschreitung unterscheidet. Gleichzeitig beträgt der Überschusswert für Gewinne 1,2904. Mit anderen Worten, das Modell GARCH hat den Effekt der Spitzenverteilung teilweise, wenn auch nicht vollständig, berücksichtigt. Wie Sie sich vielleicht erinnern, hat die unbedingte GARCH-Prozess-Verteilung dicke Enden. Dies ist darauf zurückzuführen, dass eine Mischung von Gauß-Verteilungen mit unterschiedlichen Varianzen zu einer Verteilung mit starken Ausläufern und positiver Kurtosis führt.

Daher ist eine der Annahmen des GARCH-Modells, dass die standardisierten Residuen eine bedingte Normalverteilung aufweisen, verletzt. Infolgedessen verlieren die mit der Maximum-Likelihood-Methode gewonnenen Schätzungen der Modellparameter einige nützliche Eigenschaften, nämlich dass sie nicht mehr asymptotisch effizient sind (mit anderen Worten, mit größeren Stichproben können genauere Parameterschätzungen gefunden werden).

In diesem Fall können wir als Alternative zur Normalverteilung die Studentsche Verteilung nehmen, da sie bei kleinen Freiheitsgraden einen positiven Überschuss und dicke Ausläufer aufweist. In diesem Fall wird die Anzahl der Freiheitsgrade zu einem zusätzlichen unbekannten Parameter, der anhand der Stichprobe geschätzt werden sollte.

Alle Aktionen im Zusammenhang mit der visuellen Darstellung verschiedener Statistiken, die wir gerade kurz besprochen haben, werden im GARCH-Skript festgelegt, um die Analyse zu erleichtern.

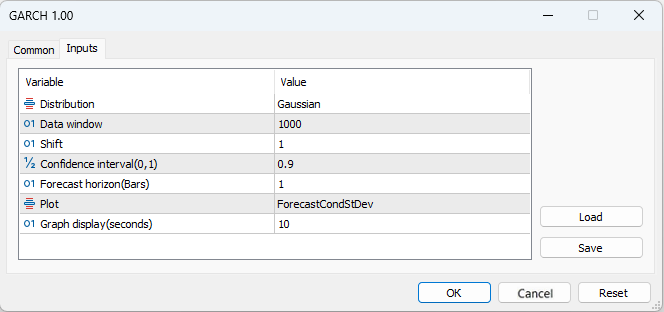
• Distribution – Standard-Normalverteilung oder standardisierte Studentsche t-Verteilung
• Data window – Datenfenster zur Berechnung der Modellparameter
• Shift – Verschiebung des Datenfensters (1 - vorletzter Balken im Chart)
• Confidence interval – Signifikanzniveau des Konfidenzintervalls (je höher das Signifikanzniveau, desto größer das Konfidenzintervall)
• Forecast horizon - Volatilitätsprognose für eine bestimmte Anzahl von Balken im Voraus
• Plot – zeigt: Volatilitätsprognose, standardisierte Residuen, Vergleich von realisierter und GARCH-Volatilität, Autokorrelationsfunktion der quadrierten Residuen und Autokorrelationsfunktion der standardisierten quadrierten Residuen im Chart.

iGARCH-Indikator

Um eine erste Vorstellung von dem Modell und den Daten zu bekommen, auf die wir dieses Modell anwenden wollen, ist das Skript GARCH genau richtig. Für die Bewertung und Vorhersage der Volatilität in Echtzeit wünschen wir uns jedoch einen Algorithmus, der die Modellparameter bei jedem neuen Balken neu berechnet und sich so schnell an den sich ständig verändernden Markt anpasst. Der adaptive iGARCH-Indikator ist die Lösung für dieses Problem.

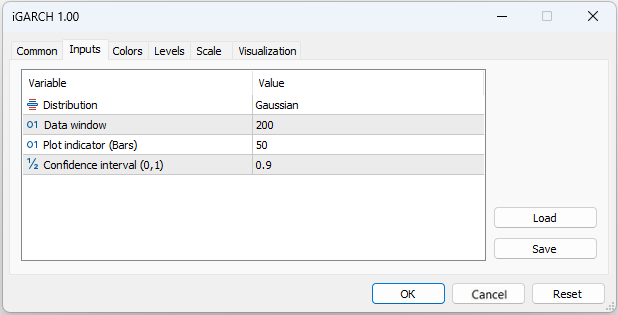
• Plot indicator – Anzahl der Balken, für die der Indikator berechnet wird

Der Indikator prognostiziert die Volatilität (bedingte Standardabweichung) und die Konfidenzintervalle für künftige Preiserhöhungen mit einer gewissen Zuverlässigkeit für einen Schritt im Voraus. Die Prognose wird auf dem Balken Null angezeigt, die Daten zur Berechnung der Parameter (Datenfenster) werden ab dem ersten Balken entnommen. Da die Modellparameter für jeden Balken optimiert werden, ist es nicht empfehlenswert, zu große Werte für den Plot-Indikator (Balken) einzustellen, da die Berechnung recht lange dauern kann (insbesondere für das Modell mit Studentscher Verteilung).

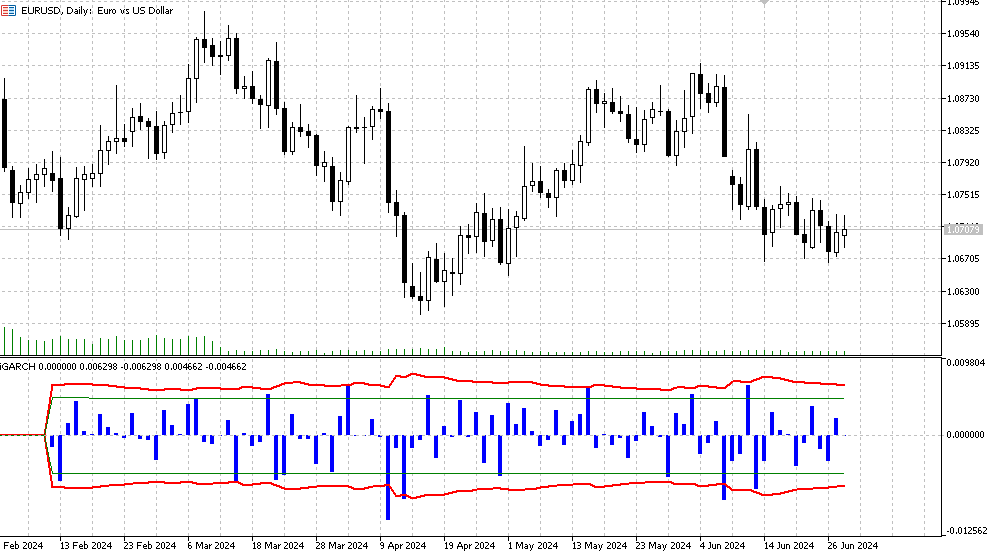
• Histogram – logarithmische Gewinnwerte LN(Yt/Yt-1),
• Die rote Linie ist die obere und untere Grenze der bedingten Standardabweichungsprognose, die für das Signifikanzniveau des Konfidenzintervalls (Standardwert ist 90 %) bestimmt wurde. Das bedeutet, dass in etwa 90 % der Fälle die logarithmischen Preiserhöhungen innerhalb dieser Grenzen liegen werden,
• Die grünen Linien stellen die normale historische Volatilität dar, also die untere bzw. obere Grenze.

Zusätzlich werden die folgenden Informationen im Journal angezeigt, das bei jedem neuen Takt aktualisiert wird:

• die neuesten Werte der optimierten Parameter (mu, omega, alpha, beta, v),
• Werte der Likelihood-Funktion (LLF),
• prognostizierte Preisniveaus für das gewählte Signifikanzniveau,
• Bericht über den erfolgreichen Abschluss der Optimierung,
• Werte der vorhergesagten bedingten Standardabweichung,
• Theoretische unbedingte Standardabweichungswerte von GARCH,
• historische Standardabweichungswerte.

Schlussfolgerung

Ich habe eines der populärsten Modelle der bedingten Heteroskedastizität betrachtet – das GARCH-Modell. Es hat sich gezeigt, dass die Standardmethoden zur Schätzung der Volatilität, bei denen von einer zeitlichen Konstanz ausgegangen wird, der Realität nicht gerecht werden. Im Gegensatz dazu berücksichtigt das GARCH-Modell die Variabilität der Volatilität im Zeitverlauf, was es für die Analyse der Marktbedingungen besser geeignet macht.

Am Beispiel des GARCH(1,1)-Modells wurde ein adaptiver Indikator entwickelt, der es ermöglicht, die Volatilität und die Konfidenzintervalle für die Logarithmen der Preissteigerungen einen Schritt in die Zukunft vorauszusagen. Dies bietet die Möglichkeit, eine probabilistische Einschätzung künftiger Preisänderungen zu erhalten und so die Risiken offener Positionen besser zu steuern.

Mit diesem Indikator können wir nicht nur das klassische Gauß'sche Residuenmodell wählen, sondern auch ein Modell, das davon ausgeht, dass die Residuen der Studentschen Verteilung folgen. Gleichzeitig wird bei jedem neuen Balken eine Optimierung der Modellparameter vorgenommen, sodass wir schnell auf die aktuelle Marktsituation reagieren können.

Zur Schätzung der Modellparameter mit Hilfe der Maximum-Likelihood-Methode verwendeten wir den Optimierungsalgorithmus MinBLEIC aus der ALGLIB-Bibliothek für numerische Analysen. Das GARCH-Skript berechnet alle notwendigen Statistiken, die mit dem Modell verbunden sind, und bietet visuelle Werkzeuge zur Bewertung der Abhängigkeiten in den Daten.

Somit ermöglicht die Anwendung des GARCH-Modells in der ökonometrischen Forschung und der Finanzanalyse genauere Volatilitätsprognosen, was das Risikomanagement und die Entscheidungsfindung bei Investitionen erheblich verbessert.