Diskussion zum Artikel "Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus"
Danke für den interessanten Artikel.
Es ist schade, dass es nur wenige Erklärungen zu Codes gibt.
Und etwas ist falsch mit dem Python-Code, ich habe alle Bibliotheken installiert, aber es gibt das folgende im Terminal:
learning time = 1228.5106182098389
solver = lbfgs
loss = 0.0024399556870102
iter = 300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)
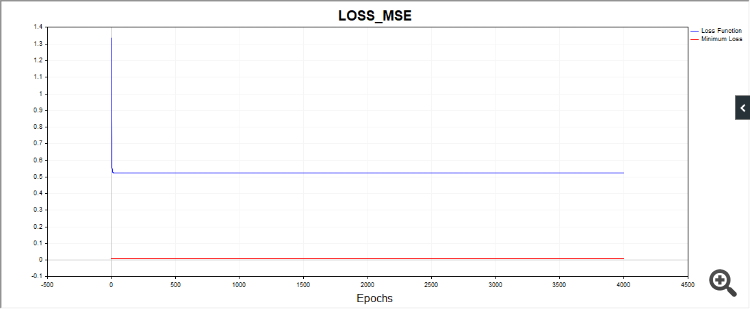
Und noch etwas, das SD-Skript zeichnet in einigen Fällen ein solches Bild:
D.h., der Algo bleibt scheinbar an einem einfachen Datum hängen.
Auch andere Codes liefern sehr unterschiedliche Konvergenzergebnisse. Daher ist es wünschenswert, Diagramme einer Reihe unabhängiger Tests zu erstellen, Bilder einzelner Tests sagen uns wenig (praktisch nichts).
Danke für das Feedback.
Zu Python. Es handelt sich nicht um einen Fehler, sondern um eine Warnung, dass der Algorithmus gestoppt wurde, weil wir die Iterationsgrenze erreicht haben. Das heißt, der Algorithmus wurde angehalten, bevor der Wert tol = 0,000001 erreicht wurde. Und dann wird gewarnt, dass der lbfgs-Optimierer kein "loss_curve"-Attribut hat, d. h. keine Verlustfunktionsdaten. Bei adam und sgd ist das der Fall, aber bei lbfgs aus irgendeinem Grund nicht. Wahrscheinlich hätte ich ein Skript erstellen sollen, das beim Start von lbfgs nicht nach dieser Eigenschaft fragt, damit es die Leute nicht verwirrt.
Zu SD. Da wir jedes Mal von verschiedenen Punkten im Parameterraum ausgehen, werden auch die Wege zur Lösung unterschiedlich sein. Ich habe viele Tests durchgeführt, und manchmal braucht es wirklich mehr Iterationen, um zu konvergieren. Ich habe versucht, eine durchschnittliche Anzahl von Iterationen anzugeben. Sie können die Anzahl der Iterationen erhöhen und Sie werden sehen, dass der Algorithmus am Ende konvergiert.
Zu SD. Da wir jedes Mal von einem anderen Punkt im Parameterraum ausgehen, sind auch die Wege zur Konvergenz mit einer Lösung unterschiedlich. Ich habe viele Tests durchgeführt, und manchmal braucht es wirklich mehr Iterationen, um zu konvergieren. Ich habe versucht, eine durchschnittliche Anzahl von Iterationen anzugeben. Sie können die Anzahl der Iterationen erhöhen und Sie werden sehen, dass der Algorithmus am Ende konvergiert.
Das ist es, worüber ich spreche. Es geht um die Robustheit bzw. Reproduzierbarkeit der Ergebnisse. Je größer die Streuung der Ergebnisse ist, desto näher ist der Algorithmus an RND für ein bestimmtes Problem.
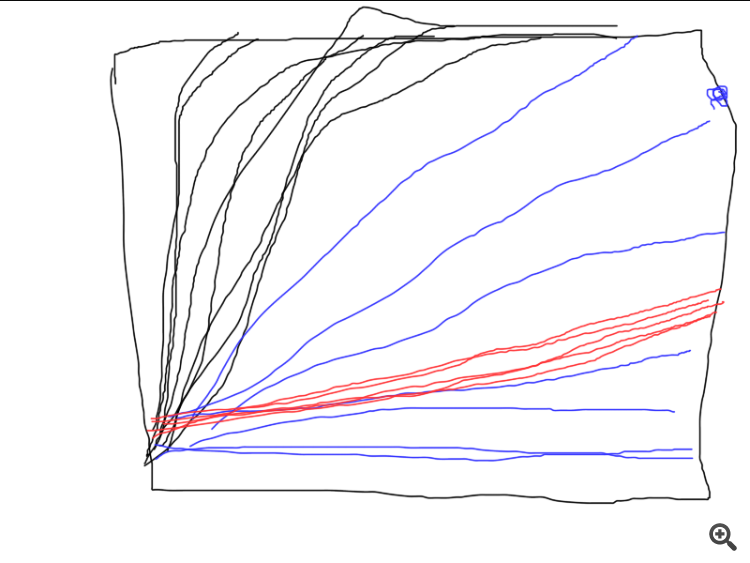
Hier ist ein Beispiel dafür, wie drei verschiedene Algorithmen funktionieren. Welcher ist der beste? Solange Sie nicht eine Reihe unabhängiger Tests durchführen und die durchschnittlichen Ergebnisse berechnen (idealerweise die Varianz der Endergebnisse berechnen und vergleichen), ist ein Vergleich unmöglich.
Das ist es, worüber ich spreche. Es geht um die Stabilität bzw. die Reproduzierbarkeit der Ergebnisse. Je größer die Streuung der Ergebnisse, desto näher ist der Algorithmus an RND für ein bestimmtes Problem.
Hier ist ein Beispiel dafür, wie drei verschiedene Algorithmen funktionieren. Welcher ist der beste? Solange Sie nicht eine Reihe unabhängiger Tests durchführen und die durchschnittlichen Ergebnisse berechnen (idealerweise die Varianz der Endergebnisse berechnen und vergleichen), ist ein Vergleich unmöglich.
Dann ist es notwendig, das Bewertungskriterium zu definieren.
Nein, in diesem Fall braucht man sich nicht so viel Mühe zu machen, aber wenn man verschiedene Methoden vergleicht, könnte man einen weiteren Zyklus (unabhängige Tests) hinzufügen und die Graphen der einzelnen Tests aufzeichnen. Es würde sehr deutlich werden, wer konvergiert, wie stabil es ist und wie viele Wiederholungen es braucht. Und so wurde es "wie beim letzten Mal", als das Ergebnis großartig war, aber nur einmal unter einer Million.
Wie auch immer, danke, der Artikel hat mir einige interessante Gedanken geliefert.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus :
Ziel dieses Artikels ist es, praktizierenden Händlern einen sehr effektiven Trainingsalgorithmus für neuronale Netze an die Hand zu geben - eine Variante der Newtonschen Optimierungsmethode, bekannt als Levenberg-Marquardt-Algorithmus. Er ist einer der schnellsten Algorithmen für das Training neuronaler Feed-Forward-Netze und wird nur vom Broyden-Fletcher-Goldfarb-Shanno-Algorithmus (L-BFGS) übertroffen.
Stochastische Optimierungsmethoden wie der stochastische Gradientenabstieg (SGD) und Adam eignen sich gut für das Offline-Training, wenn das neuronale Netz über lange Zeiträume hinweg eine Überanpassung aufweist. Wenn ein Händler, der neuronale Netze verwendet, möchte, dass sich das Modell schnell an die sich ständig ändernden Handelsbedingungen anpasst, muss er das Netz bei jedem neuen Balken oder nach einer kurzen Zeitspanne online neu trainieren. In diesem Fall sind die besten Algorithmen diejenigen, die zusätzlich zu den Informationen über den Gradienten der Verlustfunktion auch zusätzliche Informationen über die zweiten partiellen Ableitungen verwenden, was es ermöglicht, ein lokales Minimum der Verlustfunktion in nur wenigen Trainingsepochen zu finden.
Soweit ich weiß, gibt es derzeit keine allgemein verfügbare Implementierung des Levenberg-Marquardt-Algorithmus in MQL5. Es ist an der Zeit, diese Lücke zu schließen und dabei auch kurz auf die bekannten und einfachsten Optimierungsalgorithmen wie Gradientenabstieg, Gradientenabstieg mit Momentum und stochastischer Gradientenabstieg einzugehen. Am Ende des Artikels werden wir einen kleinen Test der Effizienz des Levenberg-Marquardt-Algorithmus und der Algorithmen aus der scikit-learn-Bibliothek für maschinelles Lernen durchführen.
Autor: Evgeniy Chernish