Wenn ich es richtig verstehe, wollen wir das Maximum der Hill-Funktion gleich 1 finden.
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //global max + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //global min. - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
Diese Funktion hat nur zwei Parameter.
Ich habe MinBleic angeschlossen.
Es scheint mir, dass wir nicht das durchschnittliche Ergebnis des Optimierers zählen sollten, sondern das maximale. Und natürlich kann man die Zeit sehen, sagenhafte 8 Millisekunden.
1. Wenn ich es richtig verstehe, wollen wir das Maximum der Hill-Funktion gleich 1 finden.
2. Diese Funktion hat nur zwei Parameter.
3. Verbundene MinBleic
Es scheint mir, dass wir nicht das durchschnittliche Ergebnis zählen sollten, das der Optimierer produziert, sondern das maximale. Und natürlich können Sie die Zeit sehen, sagenhafte 8 Millisekunden.
Vielen Dank für Ihren Kommentar.
1. Ja, das ist richtig. Alle Testfunktionen sind vereinheitlicht und ihre Werte liegen im Bereich [0.0; 1.0].
2. Alle Testfunktionen haben nur zwei Parameter. Beim Testen von Algorithmen verwenden wir jedoch einen mehrdimensionalen Suchraum (drei Arten von Tests, 5*2=10, 25*2=50, 500*2=1000 Parameter zur Bewertung der Skalierbarkeit von AO), indem wir eine zweidimensionale Funktion wiederholt duplizieren.
3. Das Problem mit zwei Parametern ist zu einfach, um die Algorithmen angemessen miteinander zu vergleichen, fast alle Algorithmen lösen ein solches Problem sofort mit 100% Konvergenz. Die Algorithmen haben Schwierigkeiten mit mehrdimensionalen Räumen.
Sollten wir das maximale Ergebnis nehmen? Der Punkt ist, dass die Streuung der Ergebnisse in den einzelnen Durchläufen der Algorithmen eine Rolle spielt. In allen Algorithmen bei der ersten Iteration zufällige Werte der Punkte Aussaat, die ganz zufällig sehr nahe an den Wert des globalen Extremum sein kann, in diesem Fall wird der Algorithmus unangemessen schnell das beste Ergebnis zu finden, so dass der Durchschnittswert aus den Ergebnissen der Läufe besser spiegelt die Eigenschaft des Algorithmus, um zufällige Abhängigkeit von der "Erfolg" des Algorithmus auszuschließen.
Dies hängt mit der Wahrscheinlichkeitsrechnung zusammen. Unabhängig davon, wie komplex die Zielfunktion ist, wenn es nur einen Parameter gibt, wird selbst nach der Erzeugung von 10 Zufallswerten einer von ihnen sehr nahe am globalen Extremwert liegen. ALGLIB-Methoden (Variationen des Gradientenabstiegs) reagieren empfindlich auf die Anfangsposition der Punkte im Raum und sind daher deterministisch. Mit zunehmender Dimensionalität des Suchraums steigt die Komplexität des Raums exponentiell an, und es gibt keine Möglichkeit, das globale Extremum durch die Erzeugung von Zufallszahlen zu erreichen.
Der Beweis dafür ist die Schwierigkeit dieser Methoden, selbst auf einem monotonen, glatten, unimodalen Paraboloid zu konvergieren, wenn die Dimensionalität des Problems zunimmt.
Je stabiler die Ergebnisse von AO unabhängig von den Anfangswerten im Suchraum sind, desto mehr kann diese Methode als zuverlässig bei der Lösung von Problemen angesehen werden. Aus diesem Grund wählen wir bei den Tests den Durchschnittswert aus mehreren Durchläufen von AO.
Die heutige Realität sieht so aus, dass viele Aufgaben die Optimierung von Millionen und sogar Milliarden von Parametern erfordern (KI, LLM, generative Netze, komplexe Steuerungsaufgaben in Produktion und Wirtschaft), und wir können nicht von Glattheit und Unimodalität der Aufgaben sprechen.
Vielen Dank für Ihren Kommentar.
1. Ja, richtig. Alle Testfunktionen sind vereinheitlicht und ihre Werte liegen im Bereich [0,0; 1,0].
2. Alle Testfunktionen haben nur zwei Parameter. Beim Testen von Algorithmen verwenden wir jedoch einen mehrdimensionalen Suchraum (drei Arten von Tests, 5*2=10, 25*2=50, 500*2=1000 Parameter zur Bewertung der Skalierbarkeit von AO), indem wir eine zweidimensionale Funktion wiederholt duplizieren.
3. Das Problem mit zwei Parametern ist zu einfach, um die Algorithmen angemessen miteinander zu vergleichen, fast alle Algorithmen lösen ein solches Problem sofort mit 100% Konvergenz. Die Algorithmen haben Schwierigkeiten mit mehrdimensionalen Räumen.
Sollten wir das maximale Ergebnis nehmen? Der Punkt ist, dass die Streuung der Ergebnisse in den einzelnen Durchläufen der Algorithmen eine Rolle spielt. In allen Algorithmen bei der ersten Iteration, zufällige Werte von Seeding-Punkte, die völlig zufällig sehr nahe an den Wert des globalen Extremum sein kann, in diesem Fall wird der Algorithmus unangemessen schnell das beste Ergebnis zu finden, so dass der Durchschnittswert aus den Ergebnissen der Läufe besser spiegelt die Eigenschaft des Algorithmus, um zufällige Abhängigkeit von der "Erfolg" des Algorithmus auszuschließen.
Dies hängt mit der Wahrscheinlichkeitsrechnung zusammen. Unabhängig davon, wie komplex die Zielfunktion ist, wenn es nur einen Parameter gibt, wird selbst nach der Erzeugung von 10 Zufallswerten einer von ihnen sehr nahe am globalen Extremwert liegen. ALGLIB-Methoden (Variationen des Gradientenabstiegs) sind empfindlich gegenüber der Anfangsposition der Punkte im Raum und daher deterministisch. Mit zunehmender Dimensionalität des Suchraums nimmt die Komplexität des Raums exponentiell zu, und es gibt keine Möglichkeit, das globale Extremum durch die Erzeugung von Zufallszahlen zu erreichen.
Der Beweis dafür ist die Schwierigkeit dieser Methoden, selbst auf einem monotonen, glatten, unimodalen Paraboloid zu konvergieren, wenn die Dimensionalität des Problems zunimmt.
Je stabiler die Ergebnisse von AO unabhängig von den Anfangswerten im Suchraum sind, desto mehr kann diese Methode als zuverlässig bei der Lösung von Problemen angesehen werden. Aus diesem Grund wählen wir bei den Tests den Durchschnittswert aus mehreren Durchläufen von AO.
Die heutige Realität sieht so aus, dass viele Aufgaben die Optimierung von Millionen und sogar Milliarden von Parametern erfordern (KI, LLM, generative Netze, komplexe Steuerungsaufgaben in Produktion und Wirtschaft), und wir können nicht von Glattheit und Unimodalität der Aufgaben sprechen.
Sie haben eine an sich sehr komplexe Funktion genommen. Da die Anzahl der Parameter wächst, ist die Suche nach optimalen Parametern für die Summe solcher Funktionen meiner Meinung nach von rein theoretischem Interesse. Ein mathematisches Prognosemodell für den Handel kann viele Parameter haben, aber die Verlustfunktion selbst ist sehr einfach, so dass die Suche dort viel einfacher ist. Und sicherlich kann es nicht eine Milliarde Parameter geben, sondern bescheidene 10-100, wenn wir nicht an Kurvafitting interessiert sind, natürlich, imho.
Wenn wir vom Standpunkt des Ergebnisses aus schauen. Ich bin an Parametern interessiert, die das Maximum der Funktion finden, warum brauche ich ein Durchschnittsergebnis? Ich interessiere mich für das Optimum und die Zeit, um dieses Optimum zu erreichen. Wenn diese Zeit akzeptabel ist, dann ist es mir egal, wie viel Aufwand der Computer betrieben hat, um den Startvektor der Parameter auszuwählen, Hauptsache, ich habe das Ergebnis.
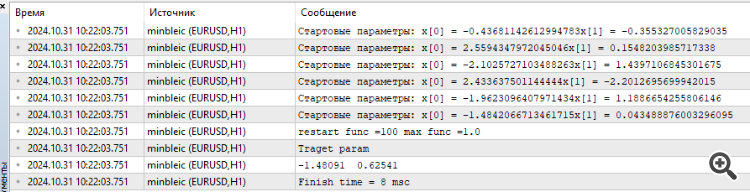
Hier ist ein Beispiel für die Summe von 5 Hilly-Funktionen
15 Sekunden Zeit und das Ergebnis ist 0,76. Nicht schlecht, denke ich. Vor allem, wenn man bedenkt, dass es um den Handel geht, bei dem wir einfach nicht wissen, was das globale Optimum ist und es auch nie wissen werden.
Wie auch immer, danke für den Artikel. Es gibt hier eine Menge zum Nachdenken. Ich werde die anderen Algorithmen ein wenig später testen und die Ergebnisse posten.
1) Sie haben eine an sich sehr komplexe Funktion genommen. Da die Zahl der Parameter wächst, ist die Suche nach den optimalen Parametern für die Summe solcher Funktionen meiner Meinung nach von rein theoretischem Interesse.
2) Ein mathematisches Prognosemodell für den Handel kann viele Parameter haben, aber die Verlustfunktion selbst ist sehr einfach, so dass die Suche dort viel einfacher ist. Und sicherlich kann es nicht eine Milliarde Parameter geben, sondern bescheidene 10-100, wenn wir natürlich nicht an Kurvafitting interessiert sind, imho.
3) Wenn wir vom Standpunkt des Ergebnisses aus schauen. Ich bin an Parametern interessiert, die das Maximum der Funktion finden, warum brauche ich ein durchschnittliches Ergebnis? Ich interessiere mich für das Optimum und die Zeit, um dieses Optimum zu erreichen. Wenn diese Zeit akzeptabel ist, dann ist es mir egal, wie viel Aufwand der Computer betrieben hat, um den Startvektor der Parameter auszuwählen, Hauptsache, ich habe das Ergebnis.
4) Hier ist ein Beispiel für die Summe von 5 Hilly-Funktionen
15 Sekunden Zeit und das Ergebnis ist 0,76. Nicht schlecht, denke ich. Vor allem in Anbetracht des Themas Handel, wenn wir einfach nicht wissen, was das globale Optimum gleich ist und es nie wissen werden.
5) Wie auch immer, danke für den Artikel. Es gibt hier eine Menge zum Nachdenken. Ich werde den Rest der Algorithmen ein wenig später testen und die Ergebnisse posten.
1) In den Artikeln betrachten wir die AOs nicht für sich allein als ein Pferd in einem Vakuum (Beispiel - PSO, sehr berühmt und daher beliebt, aber nicht leistungsfähig, und derselbe AEO - überhaupt nicht bekannt, aber hackt den glatten und diskreten Raum so schnell wie Chips fliegen), sondern zusammen mit der Analyse ihrer Logik und Vorrichtung betrachten wir ihre Suchfähigkeiten im Vergleich zueinander. Dies ermöglicht uns ein tieferes Verständnis ihrer Möglichkeiten bei praktischen Aufgaben. Und erst mit der Zunahme der Dimensionalität zeigen sich die wahren Möglichkeiten, und zwar im Vergleich der Algorithmen untereinander. Im wirklichen Leben gibt es praktisch keine einfachen Aufgaben, es sei denn natürlich, es handelt sich um Aufgaben, die analytisch gelöst werden können.
Ich habe oben erklärt, warum es notwendig ist, beim Vergleich von Algorithmen den Durchschnittswert der Endergebnisse zu verwenden - um den Einfluss des "zufälligen Erfolgs" auszuschließen und die Suchfähigkeiten der Algorithmen direkt aufzuzeigen.
Und wenn es um die praktische Anwendung von AO geht (nicht um den Vergleich von AOs), dann ist es in der Tat empfehlenswert, mehrere Optimierungsläufe durchzuführen, um das beste Ergebnis zu ermitteln. Aber wenn ein schwacher Algorithmus immer wieder neu gestartet werden muss und dabei wertvolle Durchläufe der Zielfunktion verschwendet, wird ein anderer Algorithmus das gleiche Ergebnis in viel weniger Durchläufen der Zielfunktion erreichen. Warum mehr bezahlen, wenn das Ergebnis dasselbe sein kann? Schwache Algorithmen bleiben stecken, verzetteln sich im Suchraum und erfordern mehrere Neustarts, und man kann nie sicher sein, dass man nicht schon zu Beginn der Optimierung stecken geblieben ist. Ich vermute, dass in der Praxis niemand an einer solchen Situation interessiert ist.
2) Versuchen Sie, die Verlustfunktion für ein praktisches Problem mit mindestens zwei Parametern mit einem Expert Advisor zu visualisieren, so wird sich herausstellen, dass die Oberfläche nicht glatt und keineswegs unimodal ist. Aufgrund des diskreten Charakters von Handelsaufgaben gibt es einfache und glatte Ziele einfach nicht. Daher werden Methoden, die selbst bei einem glatten Paraboloid Schwierigkeiten haben, beim Handel unwirksam sein.
3) Das durchschnittliche Ergebnis wird verwendet, um Algos untereinander zu vergleichen, nicht in der Praxis (siehe Punkt 1). Wenn Ihnen der Zeit- und Energieaufwand für die Suche egal ist, dann führen Sie eine vollständige Suche durch, es macht überhaupt keinen Sinn, AO zu verwenden. In der Praxis kommt dies jedoch nur sehr selten vor, da unsere Zeit- und Rechenressourcen immer begrenzt sind.
4) In den vorgelegten Ergebnissen fehlen Informationen über die Anzahl der Durchläufe der Zielfunktion, die erforderlich sind, um das angegebene Ergebnis zu erzielen. Dieser Indikator ist der Schlüssel zur Beurteilung der Wirksamkeit von AO. Die Wahl der AO sollte auf der Maximierung der Effizienz (Minimierung der Anzahl der Durchläufe) und der Minimierung der Wahrscheinlichkeit, stecken zu bleiben, beruhen, insbesondere bei praktischen Handelsaufgaben.
5) Danke, ich bin froh, dass die Artikel eine Grundlage für die Argumentation bieten. Es wäre toll, wenn Sie den Code der von Ihnen durchgeführten Tests zur Verfügung stellen könnten, obwohl der gesamte Code bereits im Artikel enthalten ist (anscheinend verwenden Sie eine eigene Testmethode). Wir werden es uns ansehen und herausfinden.
Ich arbeite an einem separaten Artikel über die in dieser Diskussion aufgeworfenen Fragen.
Probieren Sie verschiedene Algorithmen aus, wir haben viele in Betracht gezogen, vergleichen Sie sie miteinander. Alglib-Methoden sind sehr schnell und eignen sich meiner Meinung nach sehr gut für die Lösung von analytisch formulierten Problemen (das ist ein separates Thema), aber wenn die analytische Formel nicht bekannt ist, gibt es andere Möglichkeiten.
Für diejenigen, die analytisch formulierte Probleme lösen müssen, werden die Artikel ebenfalls sehr nützlich sein, da sie die Grundlagen der Arbeit mit ALGLIB-Methoden beschreiben.
Es ist nicht korrekt, metaevr. und Gradientenlöser auf diese Weise zu vergleichen. Sie sollten unter gleichen Bedingungen eingesetzt werden.
Metaevr. hat bereits gesetzte Punkte, während Gradientenlöser von einem Punkt ausgehen.
Um gleiche Bedingungen zu schaffen, müssen wir für letztere ein Batching durchführen. Oder eine mehrfache Initialisierung.
Aus diesem Grund müssen Gradientenlöser nach dem besten Ergebnis und nicht nach dem Durchschnittsergebnis bewertet werden. Und deshalb laufen sie auch schneller. So entsteht ein Gleichgewicht zwischen Geschwindigkeit und Genauigkeit beim Training neuronaler Netze.
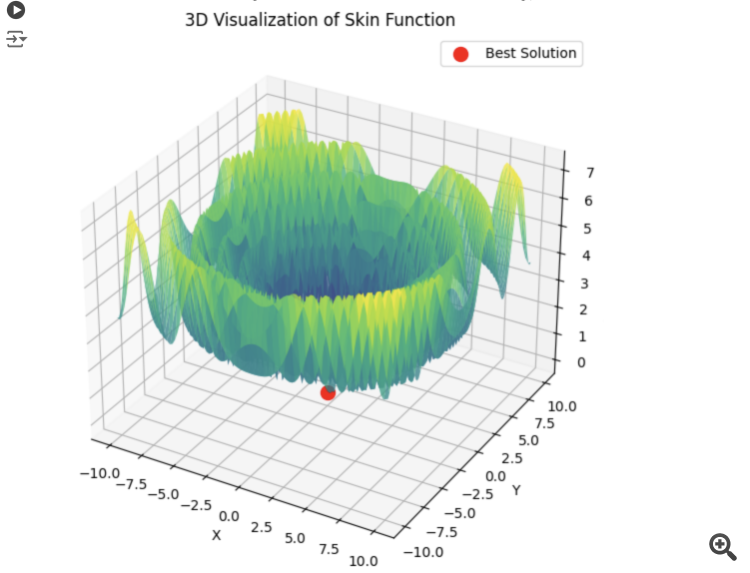
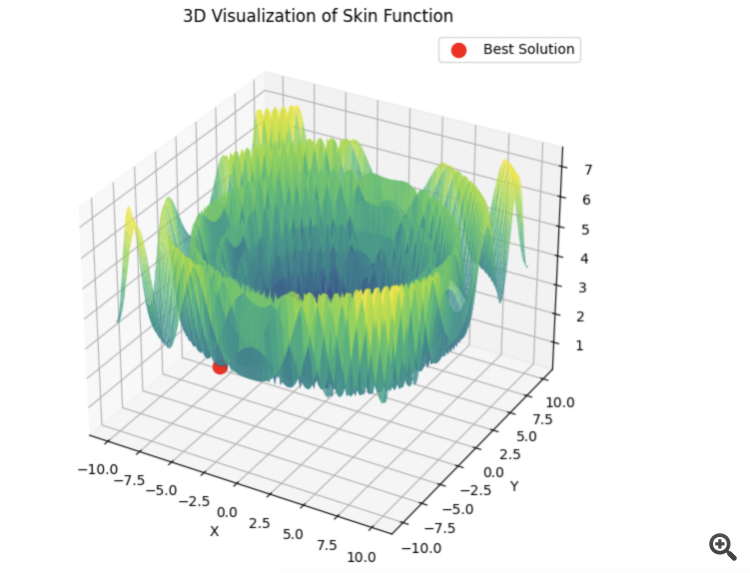
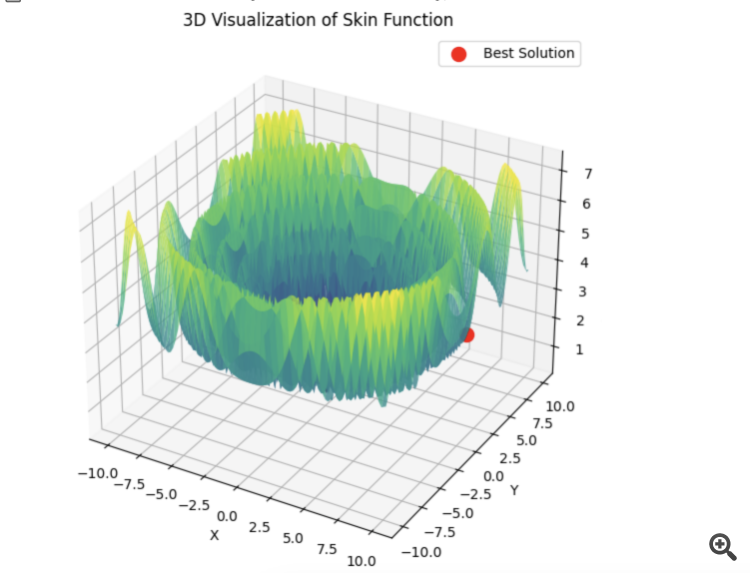
Wenn PSO sofort das richtige Minimum auswählt:
Dann springt lbfgs von Ort zu Ort, und das ist sein normales Verhalten. Aber es ist schnell und kann eine konfigurierbare Anzahl von Sprüngen durchführen, wobei die optimierte Funktion in Stapel aufgeteilt wird.
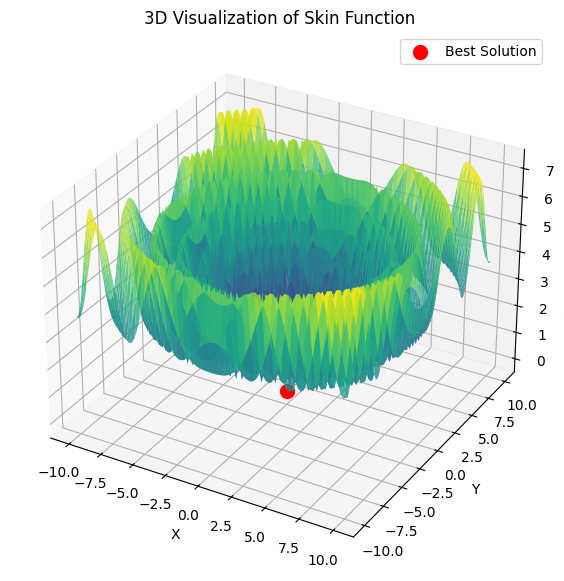
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.

Neuer Artikel Optimierungsmethoden der ALGLIB-Bibliothek (Teil II) :
Im ersten Teil unserer Untersuchung über die Optimierungsalgorithmen der ALGLIB-Bibliothek in der Standardauslieferung von MetaTrader 5 haben wir die folgenden Algorithmen gründlich untersucht: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden-Fletcher-Goldfarb-Shanno) und NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). Wir haben uns nicht nur mit ihren theoretischen Grundlagen beschäftigt, sondern auch eine einfache Möglichkeit diskutiert, sie auf Optimierungsprobleme anzuwenden.
In diesem Artikel werden wir die verbleibenden Methoden des ALGLIB-Arsenals näher betrachten. Besonderes Augenmerk wird dabei auf die Prüfung komplexer mehrdimensionaler Funktionen gelegt, die es uns ermöglichen, einen ganzheitlichen Blick auf die Effizienz der einzelnen Methoden zu werfen. Abschließend werden wir eine umfassende Analyse der erzielten Ergebnisse durchführen und praktische Empfehlungen für die Wahl des optimalen Algorithmus für bestimmte Aufgabentypen geben.
Autor: Andrey Dik