
Neuronale Netze im Handel: Punktwolkenanalyse (PointNet)
Einführung
Punktwolken sind einfache und einheitliche Strukturen, die kombinatorische Ungereimtheiten und die mit Gitternetzen verbundene Komplexität vermeiden. Da Punktwolken kein konventionelles Format haben, konvertieren die meisten Forscher solche Datensätze typischerweise in reguläre 3D-Voxel-Gitter oder Bildsätze, bevor sie in eine Deep-Network-Architektur übertragen werden. Durch diese Konvertierung werden die resultierenden Daten jedoch unnötig groß und es können Quantisierungsartefakte auftreten, die häufig die natürlichen Invarianten der Daten verschleiern.
Aus diesem Grund haben sich einige Forscher einer alternativen Darstellung der 3D-Geometrie zugewandt und verwenden direkt Punktwolken. Modelle, die mit solchen Rohdatendarstellungen arbeiten, müssen der Tatsache Rechnung tragen, dass eine Punktwolke lediglich eine Menge von Punkten ist und gegenüber Permutationen ihrer Elemente unveränderlich ist. Dies erfordert ein gewisses Maß an Symmetrisierung in den Berechnungen des Modells.
Eine solche Lösung wird in dem Artikel „PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation“ vorgestellt. Das in dieser Arbeit vorgestellte Modell mit dem Namen PointNet ist eine einheitliche architektonische Lösung, die eine Punktwolke direkt als Input nimmt und entweder Klassenlabels für den gesamten Datensatz oder Segmentierungslabels für einzelne Punkte innerhalb des Datensatzes ausgibt.
Die grundlegende Architektur des Modells ist bemerkenswert einfach. In der Anfangsphase wird jeder Punkt identisch und unabhängig bearbeitet. In der Standardkonfiguration wird jeder Punkt nur durch seine drei Koordinaten (x, y, z) dargestellt. Zusätzliche Dimensionen können durch die Berechnung von Normalen und anderen lokalen oder globalen Merkmalen einbezogen werden.
Der Schlüsselaspekt des PointNet-Ansatzes ist die Verwendung einer einzigen symmetrischen Funktion MaxPooling. Im Wesentlichen lernt das Netzwerk eine Reihe von Optimierungsfunktionen, die signifikante oder informative Elemente innerhalb der Punktwolke auswählen und die Gründe für ihre Auswahl kodieren. Die vollverknüpften Schichten in der Ausgangsstufe fassen diese erlernten optimalen Werte zu einem globalen Deskriptor für die gesamte Form zusammen.
Dieses Eingabedatenformat ist leicht mit starren oder affinen Transformationen kompatibel, da jeder Punkt unabhängig transformiert wird. Folglich führen die Autoren der Methode ein datenabhängiges räumliches Transformationsmodell ein, das versucht, die Daten vor der Verarbeitung in PointNet zu kanonisieren, um die Effizienz der Lösung weiter zu steigern.
1. Der Algorithmus PointNet
Die Autoren von PointNet haben ein Deep Learning-Framework entwickelt, das ungeordnete Punktmengen direkt als Eingabedaten verwendet. Eine Punktwolke wird als eine Menge von 3D-Punkten {Pi|i=1,…,n} dargestellt, wobei jeder Punkt Pi ein Vektor seiner Koordinaten (x, y, z) sowie zusätzlicher Merkmalskanäle, wie Farbe und anderer Attribute, ist.
Die Eingabedaten des Modells stellen eine Teilmenge von Punkten aus dem euklidischen Raum dar, die durch drei Schlüsseleigenschaften gekennzeichnet sind:
- Unsortiert. Im Gegensatz zu Pixelarrays in Bildern ist eine Punktwolke eine Menge von Elementen ohne definierte Reihenfolge. Mit anderen Worten, ein Modell, das einen Satz von N 3D-Punkten verbraucht, muss invariant gegenüber den N! Permutationen der Reihenfolge des Eingabedatensatzes sein.
- Punkt-Interaktionen. Die Punkte befinden sich in einem Raum mit einer Abstandsmetrik. Das bedeutet, dass sie nicht isoliert sind, sondern dass benachbarte Punkte sinnvolle Teilmengen bilden. Folglich muss das Modell in der Lage sein, sowohl lokale Strukturen von nahe gelegenen Punkten als auch kombinatorische Wechselwirkungen zwischen lokalen Strukturen zu erfassen.
- Transformationsinvarianz. Als geometrische Einheit sollte die gelernte Repräsentation einer Punktmenge invariant gegenüber bestimmten Transformationen sein. So sollte beispielsweise die gleichzeitige Rotation und Translation der Punkte die globale Kategorie der Punktwolke oder ihre Segmentierung nicht verändern.
Die Architektur von PointNet ist so konzipiert, dass Klassifizierungs- und Segmentierungsmodelle einen großen Teil ihrer Struktur gemeinsam haben. Es besteht aus drei Hauptmodulen:
- Eine Max-Pooling-Schicht als symmetrische Funktion zur Aggregation von Informationen aus allen Punkten.
- Eine Struktur zur Kombination lokaler und globaler Datendarstellungen.
- Zwei gemeinsame Alignment-Netzwerke, die sowohl die rohen Eingabepunkte als auch die gelernten Merkmalsdarstellungen abgleichen.
Um sicherzustellen, dass das Modell gegenüber der Permutation der Eingabedaten invariant ist, werden drei Strategien vorgeschlagen:
- Sortieren der Eingabedaten in eine kanonische Reihenfolge.
- Behandlung der Eingabedaten als Sequenz für das Training eines RNN, aber Ergänzung der Trainingsmenge mit allen möglichen Permutationen.
- Verwendung einer einfachen symmetrischen Funktion, um Informationen von jedem Punkt zu aggregieren. Eine symmetrische Funktion nimmt n Vektoren als Eingabe und gibt einen neuen Vektor aus, der sich nicht von der Reihenfolge der Eingabe unterscheidet.
Die Sortierung der Quelldaten klingt nach einer einfachen Lösung. In einem mehrdimensionalen Raum gibt es jedoch keine Ordnung, die bei punktuellen Störungen im allgemeinen Sinne stabil wäre. Daher löst das Sortieren das Ordnungsproblem nicht vollständig. Dies macht es dem Modell schwer, eine konsistente Zuordnung zwischen Eingabe- und Ausgabedaten zu erlernen. Experimentelle Ergebnisse haben gezeigt, dass die direkte Anwendung von MLP auf einen sortierten Satz von Punkten schlecht abschneidet, obwohl sie etwas besser ist als die Verarbeitung unsortierter Rohdaten.
Während RNNs für kurze Sequenzen (einige Dutzend Elemente) eine angemessene Robustheit gegenüber der Reihenfolge der Eingaben aufweisen, ist die Skalierung auf Tausende von Eingabeelementen eine Herausforderung. Die in der Originalarbeit vorgestellten empirischen Ergebnisse zeigen auch, dass ein RNN-basiertes Modell den vorgeschlagenen PointNet-Algorithmus nicht übertrifft.
Die Kernidee von PointNet ist die Annäherung an eine allgemeine Funktion, die über eine Menge von Punkten definiert ist, indem eine symmetrische Funktion auf transformierte Elemente innerhalb der Menge angewendet wird:
![]()
Empirisch gesehen schlagen die Autoren ein sehr einfaches Basismodul vor: Zunächst wird h mit Hilfe eines MLP approximiert, und g setzt sich aus einer einvariablen Funktion und einer Max-Pooling-Funktion zusammen. Die experimentelle Validierung bestätigt die Wirksamkeit dieses Ansatzes. Durch eine Reihe von h-Funktionen kann eine Reihe von f-Funktionen gelernt werden, um verschiedene Eigenschaften des Eingabedatensatzes zu erfassen.
Trotz der Einfachheit dieses Schlüsselmoduls weist es bemerkenswerte Eigenschaften auf und erreicht eine hohe Leistung bei verschiedenen Anwendungen.
Am Ausgang des vorgeschlagenen Schlüsselmoduls wird ein Vektor [f1,…,fK] gebildet, der als die globale Signatur des Eingabedatensatzes dient. Dies ermöglicht das Training eines SVM- oder MLP-Klassifikators auf der globalen Merkmalsform für Klassifikationsaufgaben. Die punktuelle Segmentierung erfordert jedoch eine Kombination aus lokalem und globalem Wissen. Dies lässt sich auf einfache, aber sehr effektive Weise erreichen.
Nach der Berechnung des globalen Merkmalsvektors für die gesamte Punktwolke schlagen die Autoren von PointNet vor, diesen Vektor durch Verkettung der globalen Repräsentation mit jedem Punkt in jedes einzelne Punktobjekt zurückzuführen. Auf diese Weise können neue punktuelle Merkmale auf der Grundlage der kombinierten punktweisen Objekte extrahiert werden, wobei nun sowohl lokale als auch globale Informationen berücksichtigt werden.
Mit dieser Modifikation kann PointNet Punktbewertungen auf der Grundlage sowohl der lokalen Geometrie als auch der globalen Semantik vorhersagen. So kann es beispielsweise die Normalen für jeden Punkt genau vorhersagen, was zeigt, dass das Modell in der Lage ist, Informationen aus der lokalen Umgebung des Punktes zusammenzufassen. Die experimentellen Ergebnisse der ursprünglichen Studie zeigen, dass das vorgeschlagene Modell die beste Leistung bei der Segmentierung von Formteilen und der Segmentierung von Szenen erzielt.
Die semantische Kennzeichnung von Punktwolken sollte unverändert bleiben, wenn die Punktwolke bestimmten geometrischen Transformationen unterliegt, z. B. starren Transformationen. Daher erwarten die Autoren, dass die gelernte Punktedarstellung gegenüber solchen Transformationen invariant ist.
Eine natürliche Lösung besteht darin, den gesamten Eingabesatz vor der Merkmalsextraktion an einem kanonischen Raum auszurichten. Das Punktwolken-Eingabeformat ermöglicht es uns, dieses Ziel auf einfache Weise zu erreichen. Wir müssen lediglich eine affine Transformationsmatrix mit Hilfe eines Mini-Netzes (T-Netz) vorhersagen und diese Transformation direkt auf die Koordinaten der Eingabepunkte anwenden. Das Mini-Netz selbst ähnelt dem größeren Netz und besteht aus Grundmodulen für punktunabhängige Merkmalsextraktion, Max-Pooling und vollständig verbundene Schichten.
Diese Idee kann auf die Ausrichtung im Merkmalsraum ausgedehnt werden. Ein zusätzliches Ausrichtungsnetzwerk kann auf der Ebene der Punktmerkmale eingefügt werden, um eine Merkmalstransformationsmatrix für die Ausrichtung von Objekten aus verschiedenen Eingabepunktwolken vorherzusagen. Die Merkmalsraum-Transformationsmatrix hat jedoch eine viel höhere Dimensionalität als die räumliche Transformationsmatrix, was die Optimierung erheblich erschwert. Daher führen die Autoren einen Regularisierungsterm in die Verlustfunktion SoftMax ein. Zu diesem Zweck muss die Transformationsmatrix der Merkmale einer orthogonalen Matrix nahekommen:
![]()
wobei A die durch das Mini-Netz vorhergesagte Merkmalsausrichtungsmatrix ist.
Orthogonale Transformationen führen nicht zu Informationsverlusten in der Eingabestufe und sind daher wünschenswert. Die Autoren von PointNet fanden heraus, dass das Hinzufügen dieses Regularisierungsterms die Optimierung stabilisiert und die Modellleistung verbessert.
Im Folgenden wird die Visualisierung der Methode PointNet durch den Autor vorgestellt.
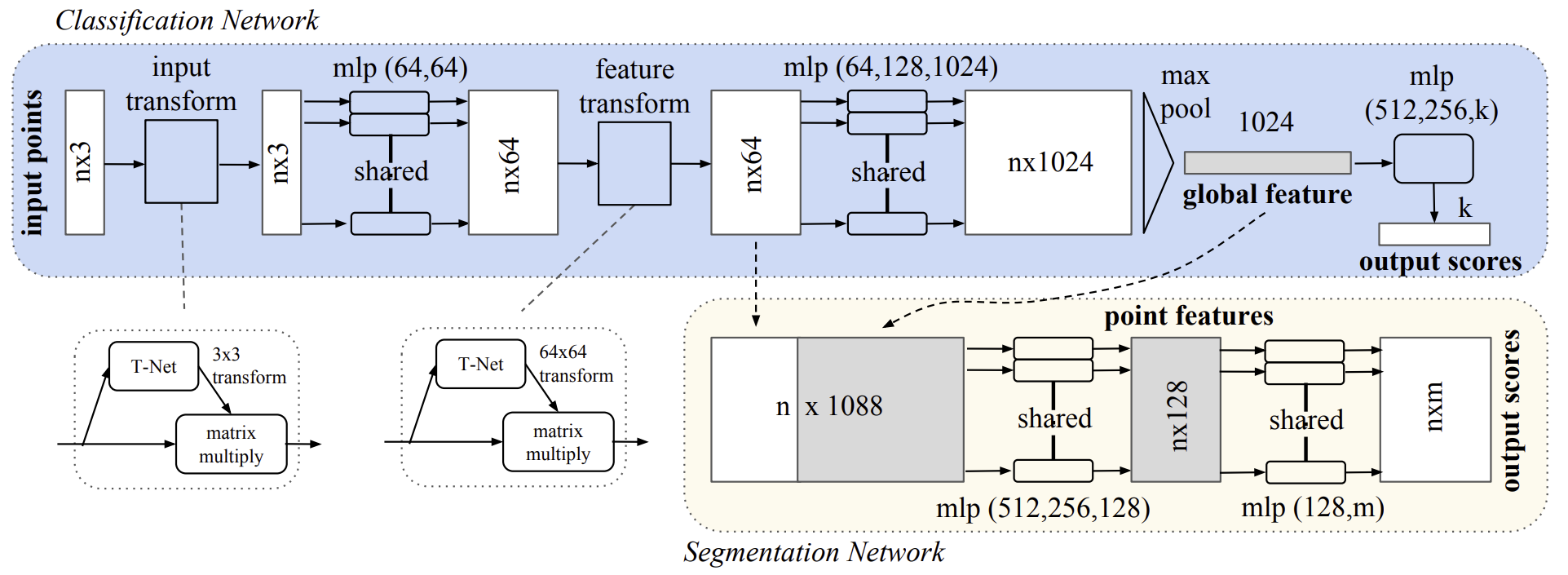
2. Implementation in MQL5
Im vorigen Abschnitt haben wir die theoretischen Grundlagen der in PointNet vorgeschlagenen Ansätze untersucht. Nun ist es an der Zeit, zum praktischen Teil dieses Artikels überzugehen, in dem wir unsere eigene Version der vorgeschlagenen Ansätze mit MQL5 implementieren werden.
2.1 Erstellen der PointNet-Klasse
Um PointNet-Algorithmen in Code zu implementieren, erstellen wir eine neue Klasse, CNeuronPointNetOCL, die die Basisfunktionalität von der vollständig verbundenen Schicht CNeuronBaseOCL erbt. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronPointNetOCL : public CNeuronBaseOCL { protected: CNeuronPointNetOCL *cTNet1; CNeuronBaseOCL *cTurned1; CNeuronConvOCL cPreNet[2]; CNeuronBatchNormOCL cPreNetNorm[2]; CNeuronPointNetOCL *cTNet2; CNeuronBaseOCL *cTurned2; CNeuronConvOCL cFeatureNet[3]; CNeuronBatchNormOCL cFeatureNetNorm[3]; CNeuronTransposeOCL cTranspose; CNeuronProofOCL cMaxPool; CNeuronBaseOCL cFinalMLP[2]; //--- virtual bool OrthoganalLoss(CNeuronBaseOCL *NeuronOCL, bool add = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronPointNetOCL(void) {}; ~CNeuronPointNetOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronPointNetOCL; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Sie sollten es bereits gewohnt sein, eine große Anzahl von verschachtelten Objekten in der Klassenstruktur zu sehen. Dieser Fall hat jedoch seine eigenen Nuancen. Erstens gibt es neben den statischen Objekten auch einige dynamische Objekte. Im Destruktor der Klasse müssen wir sie aus dem Speicher des Geräts entfernen.
CNeuronPointNetOCL::~CNeuronPointNetOCL(void) { if(!!cTNet1) delete cTNet1; if(!!cTNet2) delete cTNet2; if(!!cTurned1) delete cTurned1; if(!!cTurned2) delete cTurned2; }
Wir erstellen diese Objekte jedoch nicht im Klassenkonstruktor, sodass wir ihn leer lassen können.
Die zweite Nuance ist, dass zwei der verschachtelten dynamischen Objekte Instanzen der Klasse sind, die wir erstellen, CNeuronPointNetOCL. Sie sind also in verschachtelten Objekten verschachtelt.
Diese beiden Nuancen ergeben sich aus dem Ansatz der Autoren, die Eingabedaten und Merkmale an einem bestimmten kanonischen Raum auszurichten. Wir werden dies bei der Implementierung unserer Klassenmethoden weiter diskutieren.
Die Initialisierung einer neuen Instanz des Klassenobjekts wird wie üblich in der Methode Init durchgeführt. Die Parameter dieser Methode umfassen Schlüsselkonstanten, die die Architektur des erstellten Objekts definieren.
In diesem Fall ist der Algorithmus für die Klassifizierung von Punktwolken konzipiert. Die allgemeine Idee besteht darin, einen Encoder des Umgebungszustandes (Environmental State) unter Verwendung der Ansätze von PointNet zu entwickeln. Dieser Encoder liefert eine Wahrscheinlichkeitsverteilung, die den aktuellen Umgebungszustand einem bestimmten Typ zuordnet. Die Politik des Akteurs (Actor) ordnet dann einen bestimmten Umgebungszustand einer Reihe von Handelsparametern zu, die in dem gegebenen Zustand potenziell maximale Rentabilität erbringen. Daraus ergeben sich die wichtigsten Parameter der Klassenarchitektur:
- window — Größe des Parameterfensters für einen einzelnen Punkt in der analysierten Wolke;
- units_count — Anzahl der Punkte in der Wolke;
- output — Größe des Ergebnistensors;
- use_tnets — ob Modelle für die Projektion von Eingabedaten und Features in den kanonischen Raum erstellt werden sollen.
Der Ausgabeparameter gibt die Gesamtgröße des Ergebnispuffers an. Er ist nicht zu verwechseln mit dem früher verwendeten Parameter Ergebnisfenster. In diesem Fall erwarten wir, dass die Ausgabe ein Deskriptor des analysierten Umgebungszustands ist. Die Größe des Ergebnissensors entspricht logischerweise der Anzahl der möglichen Klassifizierungstypen des Umgebungszustands.
bool CNeuronPointNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, output, optimization_type, batch)) return false;
Im Körper der Methode rufen wir wie üblich zunächst die gleichnamige Methode der übergeordneten Klasse auf, die bereits die minimal notwendige Validierung der empfangenen Parameter und die Initialisierung der geerbten Objekte implementiert. Gleichzeitig stellen wir sicher, dass wir die Ausführungsergebnisse der Methodenoperationen überprüfen.
Als Nächstes fahren wir mit der Initialisierung der verschachtelten Objekte fort. Zunächst prüfen wir, ob es notwendig ist, interne Modelle für die Projektion der Quelldaten und Merkmale in den kanonischen Raum zu erstellen.
//--- Init T-Nets if(use_tnets) { if(!cTNet1) { cTNet1 = new CNeuronPointNetOCL(); if(!cTNet1) return false; } if(!cTNet1.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch)) return false;
Wenn Projektionsmodelle erstellt werden müssen, überprüfen wir zunächst die Gültigkeit des Zeigers auf das Modellobjekt und instanziieren, falls erforderlich, ein neues Objekt der Klasse CNeuronPointNetOCL. Anschließend wird mit der Initialisierung fortgefahren.
Beachten Sie, dass die Größe der Quelldaten für das Objekt zur Erzeugung der Projektionsmatrix mit der Größe der Quelldaten übereinstimmt, die die Hauptklasse von dem externen Programm erhält. Die Größe des Ergebnispuffers ist jedoch gleich dem Quadrat des Quelldatenfensters. Der Grund dafür ist, dass die Ausgabe dieses Modells eine quadratische Matrix zur Projektion der Quelldaten in den kanonischen Raum sein soll. Außerdem setzen wir den Parameter, der die Notwendigkeit der Erstellung von Projektionsmatrizen für die Quelldaten und -merkmale angibt, ausdrücklich auf false. Dies verhindert die unkontrollierte, rekursive Erstellung von Objekten. Außerdem wäre es unlogisch, Transformationsmodelle für Quelldaten in ein anderes Transformationsmodell für Quelldaten einzubetten.
Schließlich überprüfen wir den Zeiger auf das Objekt, das für die Aufzeichnung der korrigierten Daten zuständig ist, und erstellen gegebenenfalls eine neue Instanz des Objekts.
if(!cTurned1) { cTurned1 = new CNeuronBaseOCL(); if(!cTurned1) return false; } if(!cTurned1.Init(0, 1, OpenCL, window * units_count, optimization, iBatch)) return false;
Und wir initialisieren diese innere Schicht. Seine Größe entspricht dem Tensor der Originaldaten.
Wir führen ähnliche Operationen für das Modell der Merkmalsprojektion durch. Der einzige Unterschied besteht in den Abmessungen der inneren Schichten.
if(!cTNet2) { cTNet2 = new CNeuronPointNetOCL(); if(!cTNet2) return false; } if(!cTNet2.Init(0, 2, OpenCL, 64, units_count, 64 * 64, false, optimization, iBatch)) return false; if(!cTurned2) { cTurned2 = new CNeuronBaseOCL(); if(!cTurned2) return false; } if(!cTurned2.Init(0, 3, OpenCL, 64 * units_count, optimization, iBatch)) return false; }
Als Nächstes bilden wir ein MLP der primären Extraktion von Punktmerkmalen. In diesem Stadium schlagen die Autoren von PointNet eine unabhängige Extraktion von Punktmerkmalen vor. Daher ersetzen wir vollständig verbundene Schichten durch Faltungsschichten mit einer Schrittweite, die der Größe des Fensters der analysierten Daten entspricht. In unserem Fall sind sie gleich der Größe des Vektors, der einen Punkt beschreibt.
//--- Init PreNet if(!cPreNet[0].Init(0, 0, OpenCL, window, window, 64, units_count, optimization, iBatch)) return false; cPreNet[0].SetActivationFunction(None); if(!cPreNetNorm[0].Init(0, 1, OpenCL, 64 * units_count, iBatch, optimization)) return false; cPreNetNorm[0].SetActivationFunction(LReLU); if(!cPreNet[1].Init(0, 2, OpenCL, 64, 64, 64, units_count, optimization, iBatch)) return false; cPreNet[1].SetActivationFunction(None); if(!cPreNetNorm[1].Init(0, 3, OpenCL, 64 * units_count, iBatch, optimization)) return false; cPreNetNorm[1].SetActivationFunction(None);
Zwischen den Faltungsschichten fügen wir Stapel-Normalisierungsschichten ein und wenden die Aktivierungsfunktion auf sie an. In diesem Fall verwenden wir 2 Schichten von jedem Typ mit den von den Autoren der Methode vorgeschlagenen Abmessungen.
In ähnlicher Weise fügen wir ein dreischichtiges Perzeptron zur Extraktion von Merkmalen höherer Ordnung hinzu.
//--- Init Feature Net if(!cFeatureNet[0].Init(0, 4, OpenCL, 64, 64, 64, units_count, optimization, iBatch)) return false; cFeatureNet[0].SetActivationFunction(None); if(!cFeatureNetNorm[0].Init(0, 5, OpenCL, 64 * units_count, iBatch, optimization)) return false; cFeatureNet[0].SetActivationFunction(LReLU); if(!cFeatureNet[1].Init(0, 6, OpenCL, 64, 64, 128, units_count, optimization, iBatch)) return false; cFeatureNet[1].SetActivationFunction(None); if(!cFeatureNetNorm[1].Init(0, 7, OpenCL, 128 * units_count, iBatch, optimization)) return false; cFeatureNetNorm[1].SetActivationFunction(LReLU); if(!cFeatureNet[2].Init(0, 8, OpenCL, 128, 128, 512, units_count, optimization, iBatch)) return false; cFeatureNet[2].SetActivationFunction(None); if(!cFeatureNetNorm[2].Init(0, 9, OpenCL, 512 * units_count, iBatch, optimization)) return false; cFeatureNetNorm[2].SetActivationFunction(None);
Die Architektur der beiden letzten Blöcke ist im Wesentlichen identisch. Sie unterscheiden sich nur durch die Anzahl der Schichten und deren Größe. Logischerweise könnten sie in einem einzigen Block zusammengefasst werden. In diesem Fall werden sie jedoch nur getrennt, um die Einfügung eines Merkmalsumwandlungsblocks in den kanonischen Raum zwischen ihnen zu ermöglichen.
Der nächste Schritt nach der Extraktion der Punktmerkmale ist die Anwendung der Funktion MaxPooling, wie sie vom PointNet-Algorithmus vorgegeben wird. Diese Funktion wählt den maximalen Wert für jedes Element des Merkmalsvektors aus der gesamten analysierten Punktwolke aus. Als Ergebnis wird die Punktwolke durch einen Merkmalsvektor dargestellt, der die maximalen Werte der entsprechenden Elemente aller Punkte in der analysierten Wolke enthält.
Wir haben bereits die Klasse CNeuronProofOCL in unserem Toolkit, die eine ähnliche Funktion erfüllt, allerdings in einer anderen Dimension. Daher transponieren wir zunächst die erhaltene Punktmerkmalmatrix.
if(!cTranspose.Init(0, 10, OpenCL, units_count, 512, optimization, iBatch)) return false;
Und dann bilden wir einen Vektor der Maximalwerte.
if(!cMaxPool.Init(512, 11, OpenCL, units_count, units_count, 512, optimization, iBatch)) return false;
Der erhaltene Deskriptor der analysierten Punktwolke wird von einem dreischichtigen MLP verarbeitet. In diesem Fall habe ich jedoch zu einem kleinen Trick gegriffen und nur 2 interne, vollständig verbundene Schichten angegeben. Für die dritte Ebene verwenden wir das erstellte Objekt selbst, da es alle erforderlichen Funktionen von der übergeordneten Klasse geerbt hat.
//--- Init Final MLP if(!cFinalMLP[0].Init(256, 12, OpenCL, 512, optimization, iBatch)) return false; cFinalMLP[0].SetActivationFunction(LReLU); if(!cFinalMLP[1].Init(output, 13, OpenCL, 256, optimization, iBatch)) return false; cFinalMLP[1].SetActivationFunction(LReLU);
Am Ende der Initialisierungsmethode des Klassenobjekts geben wir die Aktivierungsfunktion explizit an und geben das logische Ergebnis der Operationen an das aufrufende Programm zurück.
SetActivationFunction(None); //--- return true; }
Nachdem wir die Implementierung der Initialisierungsmethode unserer neuen Klasse abgeschlossen haben, fahren wir mit der Konstruktion der Vorwärtsdurchgangs-Algorithmen für PointNet fort. Dies geschieht in der Methode feedForward. Wie zuvor erhalten wir in den Parametern dieser Methode einen Zeiger auf das Quelldatenobjekt.
bool CNeuronPointNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- PreNet if(!cTNet1) { if(!cPreNet[0].FeedForward(NeuronOCL)) return false; }
Im Hauptteil der Methode sehen wir sofort eine Verzweigung des Algorithmus, abhängig von der Notwendigkeit, die ursprünglichen Daten in den kanonischen Raum zu projizieren. Bitte beachten Sie, dass wir bei der Initialisierung des Objekts in den internen Variablen ein Flag gespeichert haben, das anzeigt, dass eine Datenprojektion durchgeführt werden muss. Um jedoch zu prüfen, ob eine Datenprojektion erforderlich ist, können wir die Validierung von Zeigern auf die entsprechenden Objekte verwenden. Das liegt daran, dass Projektionsmodelle nur bei Bedarf erstellt werden. Sie sind standardmäßig abwesend.
Wenn also kein gültiger Zeiger auf das Modellobjekt für die Erzeugung der Projektionsmatrix der Originaldaten vorhanden ist, übergeben wir einfach den erhaltenen Zeiger auf das Originaldatenobjekt an die Vorwärtsdurchgangs-Methode der ersten Faltungsschicht des Pre-Feature-Extraktionsblocks.
Wenn es notwendig ist, Daten in den kanonischen Raum zu projizieren, übergeben wir die empfangenen Daten an die Vorwärtsdurchgangs-Methode „FeedForward“ des Modells, um die Datentransformationsmatrix zu erzeugen.
else { if(!cTurned1) return false; if(!cTNet1.FeedForward(NeuronOCL)) return false;
Am Ausgang des Projektionsmodells erhalten wir eine quadratische Datentransformationsmatrix. Dementsprechend können wir die Dimension des Datenfensters anhand der Größe des Ergebnissensors bestimmen.
int window = (int)MathSqrt(cTNet1.Neurons());
Mit Hilfe der Matrixmultiplikation erhalten wir dann eine Projektion der ursprünglichen Punktwolke in den kanonischen Raum.
if(IsStopped() || !MatMul(NeuronOCL.getOutput(), cTNet1.getOutput(), cTurned1.getOutput(), NeuronOCL.Neurons() / window, window, window)) return false;
Die Projektion der Anfangspunkte in den kanonischen Raum wird dann in die erste Schicht des Blocks für die primäre Merkmalsextraktion eingegeben.
if(!cPreNet[0].FeedForward(cTurned1.AsObject())) return false; }
Unabhängig von der Notwendigkeit, die Originaldaten in den kanonischen Raum zu projizieren, haben wir in diesem Stadium bereits einen Vorwärtsdurchgang der ersten Schicht des primären Merkmalsextraktionsblocks durchgeführt. Dann rufen wir nacheinander die Methoden der Vorwärtsdurchgänge aller Schichten des angegebenen Blocks auf.
if(!cPreNetNorm[0].FeedForward(cPreNet[0].AsObject())) return false; if(!cPreNet[1].FeedForward(cPreNetNorm[0].AsObject())) return false; if(!cPreNetNorm[1].FeedForward(cPreNet[1].AsObject())) return false;
Als Nächstes stellt sich die Frage nach der Notwendigkeit, die Merkmale von Punkten in einen kanonischen Raum zu projizieren. Hier ist der Algorithmus ähnlich wie bei der Projektion der Anfangspunkte.
//--- Feature Net if(!cTNet2) { if(!cFeatureNet[0].FeedForward(cPreNetNorm[1].AsObject())) return false; } else { if(!cTurned2) return false; if(!cTNet2.FeedForward(cPreNetNorm[1].AsObject())) return false; int window = (int)MathSqrt(cTNet2.Neurons()); if(IsStopped() || !MatMul(cPreNetNorm[1].getOutput(), cTNet2.getOutput(), cTurned2.getOutput(), cPreNetNorm[1].Neurons() / window, window, window)) return false; if(!cFeatureNet[0].FeedForward(cTurned2.AsObject())) return false; }
Danach schließen wir die Operationen zur Extraktion von Merkmalen von Punkten der analysierten Wolke von Ausgangsdaten ab.
if(!cFeatureNetNorm[0].FeedForward(cFeatureNet[0].AsObject())) return false; uint total = cFeatureNet.Size(); for(uint i = 1; i < total; i++) { if(!cFeatureNet[i].FeedForward(cFeatureNetNorm[i - 1].AsObject())) return false; if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject())) return false; }
Im nächsten Schritt transponieren wir den resultierenden Merkmalstensor. Dann bilden wir einen Deskriptorvektor für die analysierte Wolke.
if(!cTranspose.FeedForward(cFeatureNetNorm[total - 1].AsObject())) return false; if(!cMaxPool.FeedForward(cTranspose.AsObject())) return false;
Als Nächstes müssen wir gemäß dem Klassifizierungsalgorithmus von PointNet die empfangenen Daten in MLP verarbeiten. Hier führen wir Operationen des Vorwärtsdurchgangs auf den 2 internen vollständig verbundenen Schichten durch.
if(!cFinalMLP[0].FeedForward(cMaxPool.AsObject())) return false; if(!cFinalMLP[1].FeedForward(cFinalMLP[0].AsObject())) return false;
Dann rufen wir eine ähnliche Methode der übergeordneten Klasse auf und übergeben einen Zeiger auf die innere Schicht.
if(!CNeuronBaseOCL::feedForward(cFinalMLP[1].AsObject())) return false; //--- return true; }
Ich möchte Sie daran erinnern, dass in diesem Fall die übergeordnete Klasse eine vollständig verbundene Schicht ist. Dementsprechend führen wir beim Aufruf der Vorwärtsdurchgangs-Methode der übergeordneten Klasse den Vorwärtsdurchgang der vollständig verbundenen Schicht aus. Der einzige Unterschied besteht darin, dass wir dieses Mal Objekte verwenden, die von der übergeordneten Klasse geerbt wurden, und nicht die einer verschachtelten Ebene.
Sobald alle Operationen unserer Vorwärtsdurchgangs-Methode erfolgreich abgeschlossen sind, geben wir dem aufrufenden Programm einen booleschen Wert zurück, der die ausgeführten Operationen angibt.
An dieser Stelle schließen wir unsere Arbeit über die Vorwärtsdurchgangs-Methode ab und gehen zu den Methoden der Rückwärtsdurchgänge über, die sich in zwei Teile gliedern: Verteilung der Fehlergradienten und Anpassung der Modellparameter.
Wie wir bereits mehrfach erwähnt haben, folgt die Fehlergradientenverteilung genau demselben Algorithmus wie der Vorwärtsdurchgang, nur dass der Informationsfluss umgedreht wird. In diesem Fall gibt es jedoch eine besondere Nuance. Für Datenprojektionsmatrizen haben die Autoren der PointNet-Methode eine Regularisierungstechnik eingeführt, die sicherstellt, dass die Projektionsmatrix einer orthogonalen Matrix so nahe wie möglich kommt. Diese Regularisierungsoperationen haben keinen Einfluss auf den Algorithmus des Vorwärtsdurchgangs; sie sind lediglich an der Optimierung der Modellparameter beteiligt. Außerdem erfordert die Durchführung dieser Operationen zusätzliche Berechnungen innerhalb des Programms von OpenCL.
Zu Beginn wollen wir die vorgeschlagene Regularisierungsformel untersuchen.
![]()
Es ist offensichtlich, dass die Autoren die Eigenschaft ausnutzen, dass die Multiplikation einer orthogonalen Matrix mit ihrer transponierten Kopie zu einer Identitätsmatrix führt.
Aufgeschlüsselt bedeutet die Multiplikation einer Matrix mit ihrer transponierten Kopie, dass jedes Element der resultierenden Matrix das Punktprodukt zweier entsprechender Zeilen darstellt. Bei einer orthogonalen Matrix sollte das Punktprodukt einer Zeile mit sich selbst 1 ergeben. In allen anderen Fällen ergibt das Punktprodukt aus zwei verschiedenen Zeilen 0.
Es ist jedoch wichtig zu beachten, dass es sich um eine Regularisierung innerhalb des Rückwärtsdurchgangs handelt. Das bedeutet, dass wir nicht nur den Fehler berechnen müssen, sondern auch den Fehlergradienten für jedes Element.
Um diesen Algorithmus innerhalb von OpenCL zu implementieren, erstellen wir einen Kernel namens OrthogonalLoss. Die Parameter dieses Kernels enthalten Zeiger auf zwei Datenpuffer. Eine davon enthält die ursprüngliche Matrix, die andere wird für die Speicherung der entsprechenden Fehlergradienten verwendet. Zusätzlich werden wir ein Flag einführen, um festzulegen, ob die Gradientenwerte überschrieben oder mit zuvor gespeicherten Werten akkumuliert werden sollen.
__kernel void OrthoganalLoss(__global const float *data, __global float *grad, const int add ) { const size_t r = get_global_id(0); const size_t c = get_local_id(1); const size_t cols = get_local_size(1);
In diesem Fall geben wir die Dimensionen der Matrizen nicht an. Aber hier ist alles ganz einfach. Wir planen, den Kernel in einem zweidimensionalen Aufgabenraum entsprechend der Anzahl der Zeilen und Spalten in der Matrix laufen zu lassen.
Im Kernelkörper identifizieren wir sofort den aktuellen Thread in beiden Dimensionen des Aufgabenraums.
Es sei auch daran erinnert, dass wir es mit einer quadratischen Matrix zu tun haben. Um den vollen Umfang der Matrix zu verstehen, müssen wir also nur die Anzahl der Threads in einer der Dimensionen bestimmen.
Um die Vektormultiplikationsoperationen auf mehrere Threads zu verteilen, erstellen wir lokale Arbeitsgruppen innerhalb der Zeilen der ursprünglichen Matrix. Und um den Prozess des Datenaustauschs zwischen Threads zu organisieren, werden wir ein Array im lokalen Speicher des Kontexts von OpenCL verwenden.
__local float Temp[LOCAL_ARRAY_SIZE]; uint ls = min((uint)cols, (uint)LOCAL_ARRAY_SIZE);
Als Nächstes definieren wir Offset-Konstanten zu den benötigten Objekten im Quelldatenpuffer.
const int shift1 = r * cols + c; const int shift2 = c * cols + r;
Wir laden die Werte der entsprechenden Elemente aus dem Datenpuffer.
float value1 = data[shift1]; float value2 = (shift1==shift2 ? value1 : data[shift2]);
Um die globalen Speicherzugriffe zu minimieren, vermeiden wir das erneute Einlesen diagonaler Elemente.
Hier überprüfen wir sofort die Gültigkeit der erhaltenen Werte, wobei ungültige Zahlen durch Nullwerte ersetzt werden.
if(isinf(value1) || isnan(value1)) value1 = 0; if(isinf(value2) || isnan(value2)) value2 = 0;
Danach berechnen wir ihr Produkt mit der obligatorischen Überprüfung des Ergebnisses auf Gültigkeit.
float v2 = value1 * value2; if(isinf(v2) || isnan(v2)) v2 = 0;
Der nächste Schritt ist die Organisation einer Schleife zur parallelen Summierung der erhaltenen Werte in den einzelnen Elementen des lokalen Arrays mit obligatorischer Synchronisierung der Arbeitsgruppen-Threads.
for(int i = 0; i < cols; i += ls) { //--- if(i <= c && (i + ls) > c) Temp[c - i] = (i == 0 ? 0 : Temp[c - i]) + v2; barrier(CLK_LOCAL_MEM_FENCE); }
Dann erstellen wir eine Schleife, um die erhaltenen Werte der Elemente des lokalen Arrays zu summieren.
uint count = min(ls, (uint)cols); do { count = (count + 1) / 2; if(c < ls) Temp[c] += (c < count && (c + count) < cols ? Temp[c + count] : 0); if(c + count < ls) Temp[c + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Besonderes Augenmerk wird auch auf die Synchronisierung von Arbeitsgruppen-Threads gelegt.
Als Ergebnis der im ersten Element des lokalen Arrays durchgeführten Operationen erhalten wir den Wert des Produkts der beiden analysierten Zeilen der Matrix. Jetzt können wir den Fehlerwert berechnen.
const float sum = Temp[0]; float loss = -pow((float)(r == c) - sum, 2.0f);
Dies ist jedoch nur ein Teil der Aufgabe. Als Nächstes müssen wir den Fehlergradienten für jedes Element der ursprünglichen Matrix bestimmen. Zunächst berechnen wir den Fehlergradienten auf der Ebene des Vektorprodukts.
float g = (2 * (sum - (float)(r == c))) * loss;
Dann wird der Fehlergradient auf das erste Element im Produkt der aktuellen Werte des Threads übertragen.
g = value2 * g;
Achten Sie darauf, die Gültigkeit des Wertes des erhaltenen Fehlergradienten zu überprüfen.
if(isinf(g) || isnan(g)) g = 0;
Danach speichern wir sie im entsprechenden Element des globalen Fehlergradientenpuffers.
if(add == 1) grad[shift1] += g; else grad[shift1] = g; }
Hier müssen wir das Flag überprüfen, das bestimmt, ob der Wert des Fehlergradienten addiert oder überschrieben werden soll, und wir führen die entsprechende Operation entsprechend aus.
Es ist wichtig zu beachten, dass wir innerhalb des Kerns den Fehlergradienten nur für eines der Elemente im Produkt berechnen. Der Gradient für das zweite Element im Produkt wird in einem separaten Thread berechnet, wobei die Zeilen- und Spaltenindizes der Matrix vertauscht werden.
Dieser Kernel wird mit der Methode CNeuronPointNetOCL::OrthogonalLoss in die Ausführungswarteschlange gestellt. Sein Algorithmus hält sich vollständig an die grundlegenden Prinzipien der Platzierung des Programmkernels von OpenCL in Ausführungswarteschlangen, die in früheren Artikeln ausführlich behandelt wurden. Ich empfehle Ihnen, den Code für diese Methode unabhängig zu überprüfen. Sie ist in der beigefügten Datei enthalten.
Schauen wir uns nun den Algorithmus der Methode calcInputGradients zur Verteilung von Fehlergradienten genauer an. Wie zuvor erhält diese Methode als Parameter einen Zeiger auf das Objekt der vorherigen Schicht, das in diesem Fall als Empfänger des Fehlergradienten auf der Rohdatenebene fungiert.
bool CNeuronPointNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Andernfalls ist es sinnlos, weiterzumachen.
Anschließend wird der Fehlergradient durch das Perzeptron zur Interpretation des Punktwolken-Deskriptors geleitet.
if(!CNeuronBaseOCL::calcInputGradients(cFinalMLP[1].AsObject())) return false; if(!cFinalMLP[0].calcHiddenGradients(cFinalMLP[1].AsObject())) return false;
Wir propagieren den Fehlergradienten durch die Schicht MaxPooling und transponieren ihn in die Merkmale der entsprechenden Punkte.
if(!cMaxPool.calcHiddenGradients(cFinalMLP[0].AsObject())) return false; if(!cTranspose.calcHiddenGradients(cMaxPool.AsObject())) return false;
Dann propagieren wir den Fehlergradienten durch die Merkmalsextraktionsschichten der Punkte, natürlich in umgekehrter Reihenfolge.
uint total = cFeatureNet.Size(); for(uint i = total - 1; i > 0; i--) { if(!cFeatureNet[i].calcHiddenGradients(cFeatureNetNorm[i].AsObject())) return false; if(!cFeatureNetNorm[i - 1].calcHiddenGradients(cFeatureNet[i].AsObject())) return false; } if(!cFeatureNet[0].calcHiddenGradients(cFeatureNetNorm[0].AsObject())) return false;
Bis zu diesem Punkt ist alles ziemlich normal. Aber wir sind auf der Ebene der Projektion von Punktmerkmalen in den kanonischen Raum angelangt. Wenn dies nicht erforderlich ist, wird der Fehlergradient natürlich einfach an den Block für die primäre Merkmalsextraktion weitergeleitet.
if(!cTNet2) { if(!cPreNetNorm[1].calcHiddenGradients(cFeatureNet[0].AsObject())) return false; }
Wenn wir dies umsetzen müssen, wird der Algorithmus komplexer sein. Zunächst propagieren wir den Fehlergradienten auf die Ebene der Datenprojektion hinunter.
else { if(!cTurned2) return false; if(!cTurned2.calcHiddenGradients(cFeatureNet[0].AsObject())) return false;
Danach verteilen wir den Fehlergradienten zwischen den Punktmerkmalen und der Projektionsmatrix. Wenn wir ein paar Schritte weitergehen, können wir sehen, dass der Fehlergradient durch das Modell zur Erzeugung der Projektionsmatrix auch auf die Ebene der Punktmerkmale übertragen wird. Um zu verhindern, dass kritische Daten später überschrieben werden, geben wir den Fehlergradienten in diesem Stadium nicht an die letzte Schicht des vorläufigen Merkmalsextraktionsblocks weiter, sondern an die vorletzte Schicht.
Zur Erinnerung: Die letzte Ebene im Block der vorläufigen Merkmalsextraktion ist die Ebene der Stapelnormalisierung. Die Schicht davor ist eine Faltungsschicht, die für die unabhängige Merkmalsextraktion aus einzelnen Punkten zuständig ist. Beide Schichten haben gleich große Fehlergradientenpuffer, sodass wir die Puffer sicher ersetzen können, ohne dass die Gefahr besteht, dass die Puffergrenzen überschritten werden.
int window = (int)MathSqrt(cTNet2.Neurons()); if(IsStopped() || !MatMulGrad(cPreNetNorm[1].getOutput(), cPreNet[1].getGradient(), cTNet2.getOutput(), cTNet2.getGradient(), cTurned2.getGradient(), cPreNetNorm[1].Neurons() / window, window, window)) return false;
Nach der Aufteilung des Fehlergradienten auf die beiden Datenstränge fügen wir den Regularisierungsfehlergradienten auf der Ebene der Projektionsmatrix hinzu.
if(!OrthoganalLoss(cTNet2.AsObject(), true)) return false;
Anschließend wird der Fehlergradient durch den Block zur Erzeugung der Projektionsmatrix propagiert.
if(!cPreNetNorm[1].calcHiddenGradients((CObject*)cTNet2)) return false;
Und wir summieren den Fehlergradienten von zwei Informationssträngen.
if(!SumAndNormilize(cPreNetNorm[1].getGradient(), cPreNet[1].getGradient(), cPreNetNorm[1].getGradient(), 1, false, 0, 0, 0, 1)) return false; }
Und dann können wir den Fehlergradienten durch den primären Merkmalsextraktionsblock auf die Ebene der ursprünglichen Datenprojektion übertragen.
if(!cPreNet[1].calcHiddenGradients(cPreNetNorm[1].AsObject())) return false; if(!cPreNetNorm[0].calcHiddenGradients(cPreNet[1].AsObject())) return false; if(!cPreNet[0].calcHiddenGradients(cPreNetNorm[0].AsObject())) return false;
Hier wenden wir einen Algorithmus an, der der Fehlergradientenverteilung mittels Merkmalsprojektion ähnelt. Die einfachste Version des Algorithmus ist diejenige ohne Datenprojektionsmatrix. Wir geben den Fehlergradienten einfach in den Puffer der vorherigen Schicht ein.
if(!cTNet1) { if(!NeuronOCL.calcHiddenGradients(cPreNet[0].AsObject())) return false; }
Wenn wir jedoch Daten projizieren müssen, propagieren wir zunächst den Fehlergradienten auf die Projektionsebene.
if(!cTurned1) return false; if(!cTurned1.calcHiddenGradients(cPreNet[0].AsObject())) return false;
Und dann verteilen wir den Fehlergradienten auf zwei Threads, je nach ihrem Einfluss auf das Ergebnis.
int window = (int)MathSqrt(cTNet1.Neurons()); if(IsStopped() || !MatMulGrad(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cTNet1.getOutput(), cTNet1.getGradient(), cTurned1.getGradient(), NeuronOCL.Neurons() / window, window, window)) return false;
Wir addieren den Regularisierungswert zu dem resultierenden Fehlergradienten.
if(!OrthoganalLoss(cTNet1, true)) return false;
Hier gibt es ein Problem mit dem Überschreiben des Fehlergradienten. Zu diesem Zeitpunkt haben wir keine freien Puffer für die Speicherung von Daten zur Verfügung. Wenn wir den Fehlergradienten in zwei Richtungen verteilen, schreiben wir ihn sofort in den Puffer der vorangehenden Schicht. Nun müssen wir den Fehlergradienten durch den Block zur Erzeugung der Projektionsmatrix propagieren, dessen Operationen die Gradientenwerte überschreiben, was zum Verlust der zuvor gespeicherten Daten führt. Um Datenverluste zu vermeiden, müssen wir die Gradientenwerte in einen geeigneten Datenpuffer kopieren. Aber wo können wir einen solchen Puffer finden? Bei der Initialisierung der Klasse haben wir keine Puffer für die Speicherung von Zwischendaten angelegt. Bei näherer Betrachtung fällt jedoch die Aufzeichnungsschicht der Datenprojektion auf. Seine Größe ist identisch mit der Größe des ursprünglichen Datentensors. Außerdem wurde der in dieser Schicht gespeicherte Fehlergradient bereits auf zwei Berechnungswege verteilt und wird bei den nachfolgenden Operationen nicht mehr verwendet.
Zugleich legt die Gleichheit der Puffergrößen einen alternativen Ansatz nahe. Anstatt die Daten direkt zu kopieren, könnten wir die Pufferzeiger vertauschen. Das Tauschen von Zeigern ist wesentlich einfacher als eine vollständige Datenkopie und ist unabhängig von der Puffergröße.
CBufferFloat *temp = NeuronOCL.getGradient(); NeuronOCL.SetGradient(cTurned1.getGradient(), false); cTurned1.SetGradient(temp, false);
Nachdem wir die Zeiger auf die Datenpuffer neu angeordnet haben, können wir den Fehlergradienten aus der Datenprojektionsmatrix an die Ebene der vorherigen Schicht weitergeben.
if(!NeuronOCL.calcHiddenGradients(cTNet1.AsObject())) return false; if(!SumAndNormilize(NeuronOCL.getGradient(), cTurned1.getGradient(), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; } //--- return true; }
Am Ende der Methodenoperationen summieren wir den Fehlergradienten aus den beiden Informationssträngen und geben das logische Ergebnis der Methodenoperationen an das aufrufende Programm zurück.
Die Aktualisierung der trainierbaren Modellparameter erfolgt über die Methode updateInputWeights. Wie üblich ist der Algorithmus einfach: Wir rufen nacheinander gleichnamige Methoden interner Objekte auf, die trainierbare Parameter enthalten. Gleichzeitig stellen wir sicher, dass die entsprechende Methode der übergeordneten Klasse aufgerufen wird, da ihre Funktionalität als dritte Schicht in der MLP-basierten Punktwolken-Deskriptor-Auswertung verwendet wird. In diesem Artikel werden wir nicht im Detail auf die Umsetzung dieser Methode eingehen. Ich möchte Sie ermutigen, den Code in den beigefügten Dateien unabhängig zu prüfen.
Damit sind unsere Überlegungen zu den Algorithmen für die Konstruktion von Methoden der Klasse CNeuronPointNetOCL abgeschlossen. Im Anhang zu diesem Artikel finden Sie den vollständigen Code dieser Klasse und alle ihre Methoden.
2.2 Modellarchitektur
Nachdem wir die Ansätze basierend auf PointNet mit MQL5 implementiert haben, gehen wir nun dazu über, ein neues Objekt in die Architektur unserer Modelle zu integrieren. Wie bereits erwähnt, ist unsere neue Klasse CNeuronPointNetOCL in das Encoder-Modell des Umgebungszustands integriert, das in der Methode CreateEncoderDescriptions definiert ist.
Es ist wichtig zu betonen, dass wir fast den gesamten Algorithmus in einem einzigen Block implementiert haben. Auf diese Weise können wir ein Modell mit einer prägnanten und kompakten High-Level-Architektur konstruieren. Ich betone hier den Begriff „High-Level-Architektur“. Trotz der einfachen Namensgebung des CNeuronPointNetOCL-Blocks kapselt er eine hochkomplexe und mehrschichtige neuronale Netzarchitektur.
Wie üblich besteht die Eingabe in das Modell aus unbearbeiteten Rohdaten, die zur Gewährleistung der Kompatibilität mit einer Batch-Normalisierungsschicht normalisiert werden.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Danach übergeben wir sie sofort an unseren neuen PointNet-Block.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPointNetOCL; descr.window = BarDescr; // Variables descr.count = HistoryBars; // Units descr.window_out = LatentCount; // Output Dimension descr.step = int(true); // Use input and feature transformation descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
An dieser Stelle sei angemerkt, dass wir die Aktivierungsfunktion am Ausgang unseres CNeuronPointNetOCL-Blocks nicht angegeben haben. Dieser Schritt wird absichtlich unternommen, um dem Nutzer die Möglichkeit zu geben, die Architektur des Punktwolkenidentifikationsblocks zu erweitern. In diesem Experiment fügen wir jedoch nur eine SoftMax-Schicht hinzu, um die erzielten Ergebnisse in den Bereich der Wahrscheinlichkeitswerte zu übertragen.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Damit ist die Architektur unseres neuen Encoder-Modells des Umgebungszustandes abgeschlossen.
Es sollte erwähnt werden, dass wir auch die Architektur der Modelle Akteur und Kritiker vereinfacht haben. Darin haben wir den mehrköpfigen Kreuzaufmerksamkeits-Block durch eine einfache Datenverkettungsschicht ersetzt. Ich schlage jedoch vor, dass Sie sich mit diesen spezifischen Änderungen in der Anlage vertraut machen.
Noch ein paar Worte zu dem Trainingsprogramm des Modells. Die Änderung der Modellarchitektur hatte keine Auswirkungen auf die Struktur der Quelldaten und -ergebnisse, sodass wir die zuvor erstellten Programme zur Interaktion mit der Umgebung und die von ihnen gesammelten Daten für das Offline-Training verwenden können. Dem zuvor gesammelten Datensatz fehlen jedoch die Klassenbezeichnungen für die ausgewählten Umgebungszustände. Ihre Erstellung würde zusätzliche Kosten verursachen. Wir beschlossen, einen anderen Weg einzuschlagen und den Encoder des Umgebungszustands (Environmental State) im Rahmen des Trainings der Politik des Akteurs zu schulen. Aus diesem Grund haben wir für den individuellen Encoder für den Umgebungszustand den Trainings-EA „StudyEncoder.mq5“ herausgenommen. Stattdessen haben wir geringfügige Änderungen an dem Trainings-EA für Akteur und Kritiker, „Study.mq5“, vorgenommen, damit sie den Encoder des Umgebungszustands trainieren kann. Ich schlage vor, dass Sie sich selbständig mit ihnen vertraut machen.
Ich möchte Sie daran erinnern, dass Sie im Anhang den vollständigen Code der in diesem Artikel vorgestellten Klasse und alle ihre Methoden sowie die Algorithmen aller bei der Erstellung des Artikels verwendeten Programme finden. Wir gehen nun zur letzten Phase unserer Arbeit über - dem Testen und der Bewertung der Ergebnisse unserer Arbeit.
3. Tests
In diesem Artikel haben wir die neue Methode PointNet zur Verarbeitung von Rohdaten in Form von Punktwolken vorgestellt und unsere Vision der von den Autoren vorgeschlagenen Ansätze mit MQL5 umgesetzt. Nun ist es an der Zeit, die Wirksamkeit der vorgeschlagenen Ansätze bei der Lösung unserer Aufgaben zu bewerten. Zu diesem Zweck werden wir die in diesem Artikel besprochenen Modelle anhand echter historischer Daten des Instruments EURUSD trainieren. Für unser Experiment werden wir historische Daten aus dem Jahr 2023 als Trainingsdatensatz verwenden. Die Modelle werden dann anhand der Daten vom Januar 2024 getestet. In beiden Fällen werden wir den H1-Zeitrahmen und die Standardparameter für alle analysierten Indikatoren verwenden.
Im Wesentlichen haben wir die Trainings- und Testparameter für die Modelle über mehrere Artikel hinweg unverändert übernommen. Daher wird das anfängliche Training mit zuvor gesammelten Datensätzen durchgeführt.
Das Training des Encoders für den Umgebungszustand erfolgt gleichzeitig mit dem Training der Actor Policy. Wie Sie wissen, wird die Akteurs-Politik iterativ trainiert, wobei der Trainingsdatensatz regelmäßig aktualisiert wird. Dieser Ansatz stellt sicher, dass der Trainingsdatensatz relevant und auf den aktuellen Handlungsraum der Akteurspolitik abgestimmt bleibt. Dies wiederum ermöglicht einen feiner abgestimmten Trainingsprozess.
Nach mehreren Iterationen beim Training der Modelle ist es uns gelungen, eine Akteurs-Politik zu finden, die sowohl in den Trainings- als auch in den Testdatensätzen Gewinne erzielt. Die Testergebnisse werden im Folgenden vorgestellt.
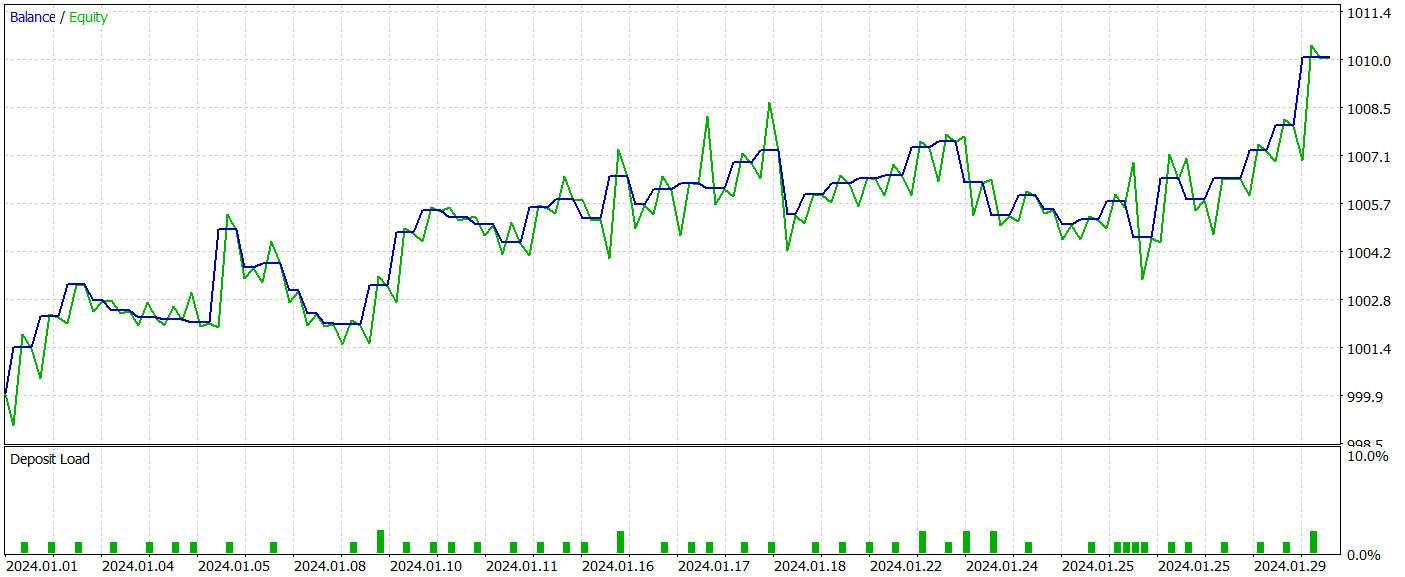
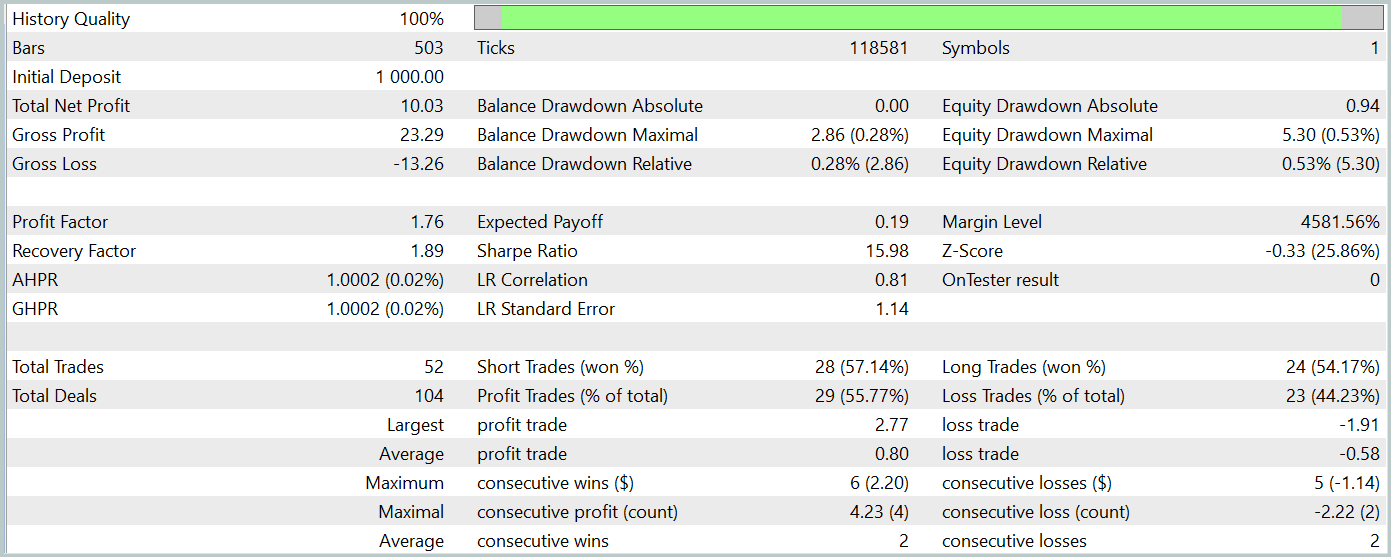
Während des Testzeitraums führte das Modell 52 Handelsgeschäfte aus, von denen 55,77 % gewinnbringend abgeschlossen wurden. Es ist erwähnenswert, dass das Modell eine praktische Parität zwischen Kauf- und Verkaufs-Positionen aufweist (24 bzw. 28). Sowohl die maximalen als auch die durchschnittlichen Gewinnpositionen übersteigen die entsprechenden Verlustpositionen. Der Gewinnfaktor erreichte 1,76. Die Saldenkurve zeigt einen klaren Aufwärtstrend. Der kurze Testzeitraum und die relativ geringe Anzahl von Handelsgeschäften lassen jedoch keine Rückschlüsse auf die Stabilität der erlernten Strategie über einen längeren Zeitraum zu.
Zusammenfassend lässt sich sagen, dass die umgesetzten Ansätze vielversprechend sind, aber weitere Tests erfordern.
Schlussfolgerung
In diesem Artikel haben wir eine neue Methode kennengelernt: PointNet, eine einheitliche architektonische Lösung, die direkt die Punktwolke als Eingabedaten verwendet. Die Anwendung von PointNet im Handel ermöglicht die effektive Analyse komplexer multidimensionaler Daten, wie z. B. Kursmuster, ohne dass diese in andere Formate konvertiert werden müssen. Dies eröffnet neue Möglichkeiten für eine genauere Vorhersage von Markttrends und die Verbesserung von Entscheidungsalgorithmen. Eine solche Analyse kann die Effizienz von Handelsstrategien auf den Finanzmärkten potenziell verbessern.
Im praktischen Teil des Artikels haben wir unsere Vision der vorgeschlagenen Ansätze in MQL5 implementiert, Modelle auf realen historischen Daten trainiert und den Expert Advisor unter Verwendung der erlernten Strategie im MetaTrader 5 Strategietester getestet. Auf der Grundlage der Testergebnisse haben wir vielversprechende Resultate erzielt. Es sei jedoch daran erinnert, dass alle in diesem Artikel vorgestellten Programme nur zu Informationszwecken bereitgestellt werden und nur dazu dienen, die Fähigkeiten der vorgeschlagenen Ansätze zu demonstrieren. Vor dem Einsatz in der Praxis sind erhebliche Verfeinerungen und umfassende Tests unter allen möglichen Bedingungen sowie gründliche Prüfungen erforderlich.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15747
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Die Direktive Include
Von der Grundstufe bis zur Mittelstufe: Die Direktive Include
 Entwicklung eines Expertenberaters für mehrere Währungen (Teil 17): Weitere Vorbereitung auf den realen Handel
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 17): Weitere Vorbereitung auf den realen Handel
 Einfache Lösungen für die komfortable Handhabung von Indikatoren
Einfache Lösungen für die komfortable Handhabung von Indikatoren
 USD- und EUR-Index-Charts — Beispiel für einen MetaTrader 5-Dienst
USD- und EUR-Index-Charts — Beispiel für einen MetaTrader 5-Dienst
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.